A&A 399, 919-929 (2003)
DOI: 10.1051/0004-6361:20021818
The X-ray Luminosity Distributions of the
high-metallicity open cluster Blanco 1
I. Pillitteri
1 -
G. Micela2 -
S. Sciortino2 -
F. Favata3
1 - Dipartimento di Scienze Fisiche e Astronomiche,
Sezione di Astronomia, Università di Palermo, Piazza del
Parlamento 1, 90134 Palermo, Italy
2 -
INAF - Osservatorio Astronomico di Palermo, Piazza del
Parlamento 1, 90134 Palermo, Italy
3 -
Astrophysics Division,
Research & Scientific Support Department of ESA, ESTEC,
Postbus 299, 2200 AG Noordwijk, The Netherlands
Received 22 October 2001 / Accepted 10 October 2002
Abstract
We present X-ray Luminosity Distributions (XLDs) of late-type members (dF, dG, dK, dM)
of the Blanco 1 cluster, based on ROSAT-HRI data and new astrometric-photometric membership
obtained from the GSC-II project. For the first time we present the XLD of dM stars of this
cluster. The high metallicity of Blanco 1 allows us to investigate the role of
chemical composition on the coronal emission of late-type stars.
Comparison between X-ray Luminosity Distributions of Blanco 1 and Pleiades,
NGC 2516 and 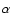 Per suggests a possible metallicity effect in dM
stars.
Per suggests a possible metallicity effect in dM
stars.
Key words: X-ray: stars - stars: activity - open clusters and
associations: individual: Blanco 1
Metal abundances can influence the X-ray emission of
solar type stars in different ways. High presence of
metals increases the radiative losses in the corona affecting the balance
between heating, conduction and radiative losses. Furthermore,
higher metallicity
produces a deeper convective zone in stars of a given mass
(through opacity changes in subphotospheric
layers). This increases the convective turnover time
leading to an enhancement of the dynamo efficiency that should produce
a larger coronal emission (Jeffries et al. 1997).
Metallicity can also influence the stellar
rotational history, thus affecting the efficiency of magnetic braking.
In this context the study of the Blanco 1 cluster is important because of its
peculiarities. In fact, Blanco 1 is a young open cluster, with an age
estimated in the range
50 - 100 Myr (de Epstein & Epstein 1985; Westerlund et al. 1988;
Edvardsson et al. 1995; Panagi & O'Dell 1997), a metallicity higher than the solar one
([Fe/H
![$] \sim +0.23$](/articles/aa/full/2003/09/aah3241/img8.gif) ,
Edvardsson et al. 1995) and also peculiar is its location
out of the galactic plane (
,
Edvardsson et al. 1995) and also peculiar is its location
out of the galactic plane (
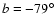 )
at a distance of
)
at a distance of  250 pc
from the Sun. In the following we will assume that the age of Blanco 1 is 100 Myr in
agreement with Panagi & O'Dell (1997).
The temperature scale adopted by Edvardsson et al. (1995) to derive the metallicity
of Blanco 1 is different from that used in studying other clusters like
the Pleiades (see Boesgaard & Friel 1990).
As pointed out by Jeffries & James (1999), when using the same scale adopted
for Pleiades, the metallicity value of Blanco 1 should be
reduced to +0.14, a value still higher than the solar one.
250 pc
from the Sun. In the following we will assume that the age of Blanco 1 is 100 Myr in
agreement with Panagi & O'Dell (1997).
The temperature scale adopted by Edvardsson et al. (1995) to derive the metallicity
of Blanco 1 is different from that used in studying other clusters like
the Pleiades (see Boesgaard & Friel 1990).
As pointed out by Jeffries & James (1999), when using the same scale adopted
for Pleiades, the metallicity value of Blanco 1 should be
reduced to +0.14, a value still higher than the solar one.
Previous membership studies have been largely based on photometric criteria
(Epstein 1968; de Epstein & Epstein 1985; Westerlund et al. 1988;
Panagi & O'Dell 1997). To
date, the most complete published member list is due to Panagi & O'Dell (1997).
This list does not include dM stars.
Membership lists for some F, G and early K stars based on stellar motions
(radial velocity measurements) are presented in Jeffries & James (1999) and Edvardsson et al. (1995) comprising a total
of 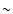 40 objects.
40 objects.
The X-ray properties of Blanco 1 have been investigated by Micela et al. (1999a;
hereafter Paper I).
The authors have analysed the data obtained from two ROSAT-HRI observations
for a total of 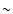 160 ksec, calculated the X-ray Luminosity Distributions (XLDs) for
the dG and dK stars of the cluster,
adopting the photometric member list of Panagi & O'Dell (1997),
and compared the XLDs with those of Pleiades and
160 ksec, calculated the X-ray Luminosity Distributions (XLDs) for
the dG and dK stars of the cluster,
adopting the photometric member list of Panagi & O'Dell (1997),
and compared the XLDs with those of Pleiades and
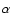 Per clusters. Furthermore, a list of unidentified
stellar-like sources, that were luminous in the X-ray band were reported.
Micela et al. (1999a) argued that a fraction of these X-ray sources are likely to be low
mass members of Blanco 1. The lack of membership information for dM stars has
not allowed them to compare the coronal properties of these stars
with the analogs of Pleiades and
Per clusters. Furthermore, a list of unidentified
stellar-like sources, that were luminous in the X-ray band were reported.
Micela et al. (1999a) argued that a fraction of these X-ray sources are likely to be low
mass members of Blanco 1. The lack of membership information for dM stars has
not allowed them to compare the coronal properties of these stars
with the analogs of Pleiades and 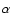 Per
and the possibility of contamination of the member list by older, less active
field stars made the results somewhat uncertain for dG and dK spectral types.
Per
and the possibility of contamination of the member list by older, less active
field stars made the results somewhat uncertain for dG and dK spectral types.
Taking advantage of the new analysis of proper motions (G. Hawkins,
private communication) for this cluster,
based on the GSC-II catalog data, we have derived membership probabilities and
recomputed unbiased XLDs using the two ROSAT-HRI observations in Paper I,
minimizing the contamination of field stars.
Furthermore, we can now calculate for the first time
the XLD of dM stars of Blanco 1. We will compare the Blanco 1 XLDs
with the XLDs of the stars in the Pleiades, NGC 2516 and 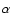 Per, discussing
the influence of age
and metallicity on the X-ray emission level. These comparison clusters have been chosen
because their properties are well known:
the Pleiades cluster is
Per, discussing
the influence of age
and metallicity on the X-ray emission level. These comparison clusters have been chosen
because their properties are well known:
the Pleiades cluster is 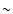 100 Myr old and has solar metallicity (Boesgaard & Friel 1990);
NGC 2516 has an age of
100 Myr old and has solar metallicity (Boesgaard & Friel 1990);
NGC 2516 has an age of 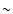 100 Myr and metallicity -0.3 dex lower than
the solar one (Jeffries et al. 1997);
100 Myr and metallicity -0.3 dex lower than
the solar one (Jeffries et al. 1997); 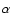 Per is 50 Myr
old and has solar metallicity (Mermilliod 1981).
Per is 50 Myr
old and has solar metallicity (Mermilliod 1981).
The structure of our paper is as follows: in Sect. 2 we
describe the method adopted for selecting members,
in Sect. 3 we present the XLDs and compare
them with the analogs of Pleiades, NGC 2516 and 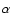 Per discussing the
implications of observed differences with respect to age and metallicity,
in Sect. 4 we present our conclusions.
Per discussing the
implications of observed differences with respect to age and metallicity,
in Sect. 4 we present our conclusions.
2.1 The method
An initial sample was selected of 8069 objects with instrumental R magnitude
down to 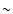 20, extracted from the GSC-II
20, extracted from the GSC-II![[*]](/icons/foot_motif.gif) catalog and falling in the region of
catalog and falling in the region of
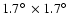 centered at
RA = 00:04:08.0 (J2000) Dec = -29:57:12.6 (J2000) which contains Blanco 1.
We calculated the membership probability for Blanco 1 on the basis of the
following criteria:
centered at
RA = 00:04:08.0 (J2000) Dec = -29:57:12.6 (J2000) which contains Blanco 1.
We calculated the membership probability for Blanco 1 on the basis of the
following criteria:
- 1.
- Photometric selection in order to reject the objects with photometry
clearly inconsistent with that of the cluster.
- 2.
- Spatial selection to keep only objects in the ROSAT-HRI fields of
view of the observations analyzed in Paper I.
- 3.
- Calculation of astrometric membership probability.
- 4.
- Second photometric selection based on the cluster main sequence
determined considering only the cluster high probability objects
(
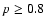 )
from step 3.
)
from step 3.
- 5.
- New astrometric membership probability for the photometric selected sample.
- 6.
- Final selection of stars with membership probability
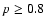 .
.
We give below a more detailed description of these steps.
From the initial sample of 8069 objects (their proper motions are
shown in Fig. 1) we selected 1650 objects,
with both colors and magnitudes in a "strip'' a few magnitudes broad
that approximately mimics the cluster sequence (Fig. 2, step 1)
in order to exclude a large fraction of faint objects not related to the cluster.
Since we are working on instrumental photometry, we have not attempted to use
a ZAMS model (which would require accurate color transformations) but have traced our strip by eye.
All the stars confirmed as members in Jeffries & James (1999) on the basis of their
radial velocity lie inside the selected strip.
In this phase we also rejected extended sources and those with very
large astrometric errors.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F1.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg11.gif) |
Figure 1:
Vector Point Diagram obtained from the 8069 GSC-II
objects in the Blanco 1 region.
The cluster is located at 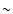 20 and 2 mas yr-1
along 20 and 2 mas yr-1
along 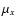 and
and 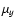 respectively, but the contamination from field objects is clearly
not negligible.
respectively, but the contamination from field objects is clearly
not negligible. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F2.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg12.gif) |
Figure 2:
R vs. B-R diagram of the complete GSC-II sample.
The lines show the first photometric selection
based on instrumental magnitudes B and R:
only the objects above the lines are retained ( step 1). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F3.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg13.gif) |
Figure 3:
R vs. B-R diagram showing the second photometric
selection ( step 4) based on instrumental magnitudes B and R.
Square symbols are the objects with
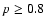 found in step 3.
Stars shown as open squares delineate the main sequence of Blanco 1,
while filled squares indicate the objects with
found in step 3.
Stars shown as open squares delineate the main sequence of Blanco 1,
while filled squares indicate the objects with
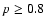 not on the same sequence.
Lines show the cut leading to the new photometric selection
obtained in step 4.
not on the same sequence.
Lines show the cut leading to the new photometric selection
obtained in step 4. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F4.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg14.gif) |
Figure 4:
Vector Point Diagram of photometrically and spatially selected
stars, crosses indicate stars with probability
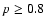 (calculated in step 5).
(calculated in step 5). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F5.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg15.gif) |
Figure 5:
Scatter plot and best fit of B-V vs. B-R instrumental values used
to obtain the B-V color index values for the Blanco 1
selected members as described in Sect. 2.1. |
| Open with DEXTER |
Since our main interest is to reliably select cluster members in the region
observed in the two ROSAT-HRI exposures, we restricted the analysis to
these regions (step 2).
We calculated the astrometric membership probability by
fitting the point density in a Vector Point Diagram
following the procedure described in Jones (1997) (step 3).
Figure 3 shows the R vs. B-R scatter plot of the
stars considered in this step, with
open and filled squares indicating the stars with probability
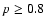 .
The objects with
.
The objects with
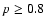 occupy two different regions;
in particular the open squares clearly delineate the main sequence of the cluster,
while the filled squares appear outside this sequence.
This behaviour prompted us to make a further cut in the
initial photometric strip and to retain only the objects lying above
the lines indicated in Fig. 3, thus allowing us to make the
further photometric selection implemented in step 4.
As a check, we note that this further photometric selection contains
the star members in Jeffries & James (1999).
We repeated the astrometric analysis (step 5) on the objects
selected by step 4.
occupy two different regions;
in particular the open squares clearly delineate the main sequence of the cluster,
while the filled squares appear outside this sequence.
This behaviour prompted us to make a further cut in the
initial photometric strip and to retain only the objects lying above
the lines indicated in Fig. 3, thus allowing us to make the
further photometric selection implemented in step 4.
As a check, we note that this further photometric selection contains
the star members in Jeffries & James (1999).
We repeated the astrometric analysis (step 5) on the objects
selected by step 4.
At the end of this procedure, we selected 93 stars as members of the
cluster with proper motion probability
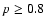 (step 6, Fig. 4).
By integrating the values (1 - p) for all the selected objects
(
(step 6, Fig. 4).
By integrating the values (1 - p) for all the selected objects
(
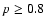 )
we estimated that
)
we estimated that  9 of the 93 members are likely to
be false members, thus implying a
fraction of
9 of the 93 members are likely to
be false members, thus implying a
fraction of 
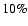 of contamination in our sample.
We found that the cluster has proper motion components
of contamination in our sample.
We found that the cluster has proper motion components
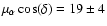 mas/yr and
mas/yr and
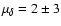 mas/yr in agreement with the values derived
by Robichon et al. (1999) (
mas/yr in agreement with the values derived
by Robichon et al. (1999) (
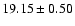 ,
,
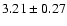 mas/yr respectively).
The values in Robichon et al. (1999) were derived from Hipparcos observations but from a
sample of only 13 members of Blanco 1.
We calculated the XLDs as discussed in Sect. 3 by considering a subsample
of 82 members comprising only stars in the range of dF-dM type,
namely 8 dF, 11 dG, 38 dK and 25 dM stars.
Five out of the remaining 11 are G-M type stars just on the edge of the
field of view with unreliable
mas/yr respectively).
The values in Robichon et al. (1999) were derived from Hipparcos observations but from a
sample of only 13 members of Blanco 1.
We calculated the XLDs as discussed in Sect. 3 by considering a subsample
of 82 members comprising only stars in the range of dF-dM type,
namely 8 dF, 11 dG, 38 dK and 25 dM stars.
Five out of the remaining 11 are G-M type stars just on the edge of the
field of view with unreliable 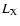 determination, and 6 of the remaining
have
determination, and 6 of the remaining
have
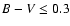 .
The selection method, based on photometry and proper motion analysis,
does not produce a bias from the point of view of X-ray emission,
making it suitable to estimate Blanco 1 X-ray properties.
.
The selection method, based on photometry and proper motion analysis,
does not produce a bias from the point of view of X-ray emission,
making it suitable to estimate Blanco 1 X-ray properties.
From the instrumental magnitude B and R we obtained
a standard B-V color index using conversion tables provided by G. Hawkins
(private communication). These tables report measurements of B-R for a
sample of stars with well assessed B-V index;
the reliably calibration is reported in Fig. 5.
We fitted a linear relation, after exclusion of some evident outliers,
and calculated the index color B-V from the instrumental B-R values of our
sample. The outliers are probably dM type stars with unreliable
B-V measurements. From Fig. 5 we can estimate that
our fitting is reliable just to
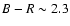 .
.
The fitted relation is:
The deduced B-V color index has been used to segregate the members in
"spectral type'' bins.
In the case of dM stars, for which the
B-V index is ineffective to distinguish the various spectral sub-types, we
used infrared photometry from the 2MASS catalog to assign the values of
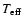 and spectral type.
We obtained a linear relation between
and spectral type.
We obtained a linear relation between
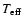 and the H-K color
index from the data reported in Leggett et al. (1996) and Leggett et al. (1998) and applied
this relation to our sample.
We found the relation:
and the H-K color
index from the data reported in Leggett et al. (1996) and Leggett et al. (1998) and applied
this relation to our sample.
We found the relation:
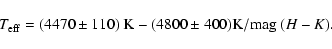 |
(1) |
The typical error in the estimated temperatures is 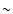
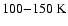 ,
corresponding to an uncertainty of
,
corresponding to an uncertainty of 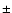 1 sub-spectral type in the dM range.
The temperature values from this calibration are in good agreement with those obtained
from the spectral classification of a subsample of stars with low-resolution
spectra (
1 sub-spectral type in the dM range.
The temperature values from this calibration are in good agreement with those obtained
from the spectral classification of a subsample of stars with low-resolution
spectra (
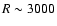 )
observed at the ESO 1.5 mt. telescope in
La Silla (Chile).
)
observed at the ESO 1.5 mt. telescope in
La Silla (Chile).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F6.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg30.gif) |
Figure 6:
Distribution of offsets between BLX sources and GSC-II stars.
The line represents the distribution of expected spurious identifications. |
| Open with DEXTER |
In order to identify new low-mass members among the X-ray
luminous sources that were unidentified in Paper I (BLX list hereafter),
we first cross-identified the positions of the BLX list
with the positions of the complete sample of 8069 GSC-II objects.
The positions in the BLX list are taken from Paper I, where the
systematic offsets had already been removed in the ROSAT pointing solution.
On the basis of the histogram shown in Fig. 6 we considered an
identification correct if the offset between the position of a given X-ray source and the
possible optical counterpart is 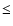
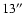 (the number of expected spurious
identifications with this criterion is 1.6).
We chose
(the number of expected spurious
identifications with this criterion is 1.6).
We chose
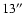 as
threshold for identifications on the basis of the local
minimum in the distribution shown in Fig. 6.
Of 88 BLX sources, 48 are identified in the GSC-II initial sample
of 8069 objects, while the other 40 sources are classified as follow:
as
threshold for identifications on the basis of the local
minimum in the distribution shown in Fig. 6.
Of 88 BLX sources, 48 are identified in the GSC-II initial sample
of 8069 objects, while the other 40 sources are classified as follow:
- 23 do not show GSC-II counterparts up to a distance of
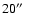 ,
i.e. the limit reported in Paper I for optical identification.
,
i.e. the limit reported in Paper I for optical identification.
- 11 show an object at the edge of the identification circle of
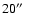 .
.
- 5 show a faint object in the Digitized Sky Survey not present in the GSC-II
catalog.
- 1 source is near a bright star that makes it impossible to calculate
accurate positions and proper motions.
In 8 cases, the determination of the extension of GSC-II counterparts suggests that these sources are
galaxies or galaxy clusters.
By adopting a radius of
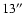 we then identified again the BLX sources
with the sample obtained
in steps 5 and 6 (second and final astrometric analysis),
and selected a subgroup of 28 objects.
For these 28 sources the distribution of membership probability is shown in
Fig. 7: 18 show a probability level higher than or equal to
80% which makes them probable low-mass members of the cluster.
This conclusion is supported by spectral identification of some high
probability BLX sources based on
low-resolution spectra obtained at the ESO 1.5 m telescope in La Silla; these sources also show strong emission in the H
we then identified again the BLX sources
with the sample obtained
in steps 5 and 6 (second and final astrometric analysis),
and selected a subgroup of 28 objects.
For these 28 sources the distribution of membership probability is shown in
Fig. 7: 18 show a probability level higher than or equal to
80% which makes them probable low-mass members of the cluster.
This conclusion is supported by spectral identification of some high
probability BLX sources based on
low-resolution spectra obtained at the ESO 1.5 m telescope in La Silla; these sources also show strong emission in the H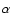 line (Fig. 8).
line (Fig. 8).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F7.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg35.gif) |
Figure 7:
Distribution of membership probability of identified stars in the BLX
list. |
| Open with DEXTER |
In order to verify the field star contamination present in the list
of photometric members used in previous studies,
we have applied the
same analysis to the members in the list of Panagi & O'Dell (1997) finding that
76 out of the 83 objects which lie in the
ROSAT-HRI fields are identified with objects in the GSC-II catalog.
A subsample of 68 of these 76 stars survives our selection, allowing us to
assign a value of astrometric membership to this group.
If we calculate the number of contaminants among these 68 stars by
integrating the value (1 - p) as done in Sect. 2.1,
we can estimate that 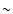 24 of the 68 stars are not members viz. a fraction
of
24 of the 68 stars are not members viz. a fraction
of 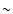
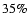 .
As a comparison, the fraction of contaminants in the Jeffries & James (1999) sample
is
.
As a comparison, the fraction of contaminants in the Jeffries & James (1999) sample
is 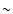
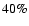 .
We obtained this estimate by considering the numbers of stars from
Tables 1 and 2 in Jeffries & James (1999); we also excluded 3 stars from the
non-member list because these probably belong to binary systems.
We conclude that the results (such as those presented in Paper I) based
on the photometric list of members in Panagi & O'Dell (1997) are likely to be heavily
contamined.
A mixture of age in a sample composed
by Blanco 1 stars and field stars can cause significant differences in derived
coronal activity, thus affecting the study of global properties that we discuss
in the following.
.
We obtained this estimate by considering the numbers of stars from
Tables 1 and 2 in Jeffries & James (1999); we also excluded 3 stars from the
non-member list because these probably belong to binary systems.
We conclude that the results (such as those presented in Paper I) based
on the photometric list of members in Panagi & O'Dell (1997) are likely to be heavily
contamined.
A mixture of age in a sample composed
by Blanco 1 stars and field stars can cause significant differences in derived
coronal activity, thus affecting the study of global properties that we discuss
in the following.
![\begin{figure}
\par\includegraphics[angle=-90,width=14.5cm,clip]{H3241F8.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg38.gif) |
Figure 8:
Low-resolution optical spectra of the couterpart of some BLX
source with membership probability 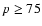 %.
The flux is normalized at 5550 Å and the spectra are shifted vertically for clarity.
We note in all cases the strong emission in the H %.
The flux is normalized at 5550 Å and the spectra are shifted vertically for clarity.
We note in all cases the strong emission in the H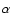 line at 6563 Å.
line at 6563 Å. |
| Open with DEXTER |
We calculated the upper limits to the X-ray luminosity
at a level corresponding to a source detection probability
of 4.5 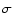 (consistent with the chosen detection threshold)
for the undetected cluster members (i.e. stars with
(consistent with the chosen detection threshold)
for the undetected cluster members (i.e. stars with
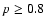 )
in the HRI fields using the
wavelet transform detection algorithm developed by Damiani et al. (1997).
For the detections
we cross-identified our optical catalog of 93 high probability members with
the X-ray sources identified in Paper I, choosing the threshold radius of 13
)
in the HRI fields using the
wavelet transform detection algorithm developed by Damiani et al. (1997).
For the detections
we cross-identified our optical catalog of 93 high probability members with
the X-ray sources identified in Paper I, choosing the threshold radius of 13
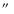 ,
already used when identifying the BLX sources.
This choice should minimize the loss of real identifications and the
probability of chance coincidence.
Coherently with the analysis carried out in Paper I,
we assumed a count rate to flux conversion factor of
,
already used when identifying the BLX sources.
This choice should minimize the loss of real identifications and the
probability of chance coincidence.
Coherently with the analysis carried out in Paper I,
we assumed a count rate to flux conversion factor of
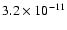 erg/(s cm-2 count-1), derived for an optically-thin plasma
model characterized by a single temperature of 1 keV (Raymond & Smith 1977) and
assuming a
erg/(s cm-2 count-1), derived for an optically-thin plasma
model characterized by a single temperature of 1 keV (Raymond & Smith 1977) and
assuming a
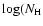 /cm
-2) = 20, derived from
E(B-V)= 0.02
(Westerlund et al. 1988).
Uncertainties in the temperature lead to an uncertainty of 20% in the
conversion factor as reported in Paper I.
To calculate the X-ray luminosity, we assumed a cluster distance of 250 pc as reported
in Panagi & O'Dell (1997).
When using the Hipparcos distance for Blanco 1 (262 pc, Robichon et al. 1999)
the X-ray luminosities should be systematically increased by
/cm
-2) = 20, derived from
E(B-V)= 0.02
(Westerlund et al. 1988).
Uncertainties in the temperature lead to an uncertainty of 20% in the
conversion factor as reported in Paper I.
To calculate the X-ray luminosity, we assumed a cluster distance of 250 pc as reported
in Panagi & O'Dell (1997).
When using the Hipparcos distance for Blanco 1 (262 pc, Robichon et al. 1999)
the X-ray luminosities should be systematically increased by 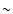 10%.
In the appendix, Table A.1 summarizes the optical, infrared and X-ray band
properties of the Blanco 1 members in the combined fields of view of the
two HRI observations as well as proper motion probabilities and identifiers.
Identifiers with prefix ZS are from de Epstein & Epstein (1985)
while the prefix BLX refers to BLX sources from Paper I; positions are taken from the
GSC-II catalog.
The
10%.
In the appendix, Table A.1 summarizes the optical, infrared and X-ray band
properties of the Blanco 1 members in the combined fields of view of the
two HRI observations as well as proper motion probabilities and identifiers.
Identifiers with prefix ZS are from de Epstein & Epstein (1985)
while the prefix BLX refers to BLX sources from Paper I; positions are taken from the
GSC-II catalog.
The
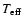 values are derived using the relationship of Lang (1992) for
stars with
values are derived using the relationship of Lang (1992) for
stars with
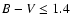 ,
otherwise we used Eq. (1) to assign a temperature.
The mass estimates are interpolated on the values of
,
otherwise we used Eq. (1) to assign a temperature.
The mass estimates are interpolated on the values of
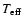 from
an isochrone model (Siess et al. 2000) calculated using metallicity Z = 0.03 and age 100 Myr.
from
an isochrone model (Siess et al. 2000) calculated using metallicity Z = 0.03 and age 100 Myr.
The new member list contains 46 of the 83 stars from the member list
given in Panagi & O'Dell (1997); for 31 of these 46 stars an X-ray detection is reported.
A further 18 members not included in the Panagi & O'Dell (1997) catalog are
identified with bright X-ray sources in the BLX list.
We have also found a number of faint members
for which we can only put an upper limit to their X-ray luminosity.
We selected dF, dG and dK type stars by the following (B-V)0 ranges:
0.3 - 0.5,
0.5 - 0.8 ,
0.8 - 1.45 respectively.
For dM stars we applied the combined criteria:
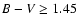 and
and
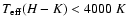 ,
using the
temperature estimate from 2MASS infrared photometry.
In Fig. 9 we plot
,
using the
temperature estimate from 2MASS infrared photometry.
In Fig. 9 we plot
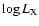 vs. (B-V)0assuming the correction
E(B-V) = 0.02 reported by Westerlund et al. (1988),
as
well as the medians of
vs. (B-V)0assuming the correction
E(B-V) = 0.02 reported by Westerlund et al. (1988),
as
well as the medians of
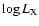 of dF, dG, dK and dM stars of
Blanco 1 in the present work and,
for comparison, that of the Pleiades (Micela et al. 1996 and Micela et al. 1999b).
The vertical lines indicate the 10%-90% range of the distributions;
in the case of dM stars the upper limit indicates that the X-ray
distribution does not reach the 0.9 level because of the significant fraction
of upper limits.
Medians and percentile ranges are calculated by interpolating the values of
of dF, dG, dK and dM stars of
Blanco 1 in the present work and,
for comparison, that of the Pleiades (Micela et al. 1996 and Micela et al. 1999b).
The vertical lines indicate the 10%-90% range of the distributions;
in the case of dM stars the upper limit indicates that the X-ray
distribution does not reach the 0.9 level because of the significant fraction
of upper limits.
Medians and percentile ranges are calculated by interpolating the values of
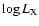 at which the XLD, as computed below, is equal to 0.5, 0.1 and 0.9 respectively.
Notice that the median value of
at which the XLD, as computed below, is equal to 0.5, 0.1 and 0.9 respectively.
Notice that the median value of
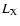 for dK stars is affected
by the low values for the latest types.
A change of
for dK stars is affected
by the low values for the latest types.
A change of 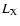 at
at
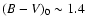 it is also evident.
We have decided to use this color binning for consistency with
the previous work on other clusters, but it is clear that the
obtained median value is strongly dependent on the chosen spectral type boundaries.
Table 1 shows the number of detections and upper limits for the
82 selected Blanco 1 members.
it is also evident.
We have decided to use this color binning for consistency with
the previous work on other clusters, but it is clear that the
obtained median value is strongly dependent on the chosen spectral type boundaries.
Table 1 shows the number of detections and upper limits for the
82 selected Blanco 1 members.
Table 1:
Numbers of detected stars in
X-ray and upper limits among the Blanco 1 members.
| Spectral Type |
Detections |
Upper Limits |
| dF |
6 |
2 |
| dG |
8 |
3 |
| dK |
22 |
16 |
| dM |
10 |
15 |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F9.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg48.gif) |
Figure 9:
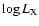 vs. B-V for the Blanco 1 stars. The arrows show the upper limits,
the horizontal lines are the medians of distribution of
vs. B-V for the Blanco 1 stars. The arrows show the upper limits,
the horizontal lines are the medians of distribution of
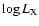 in
Blanco 1 (solid line) and Pleiades (dashed line), the vertical lines
show the 10%-90% of distribution range.
in
Blanco 1 (solid line) and Pleiades (dashed line), the vertical lines
show the 10%-90% of distribution range. |
| Open with DEXTER |
We note that the spread of Blanco 1 X-ray luminosities is
comparable to that of the Pleiades regardless of the differences in
metallicity, and also that the X-ray luminosity medians for dG and dK stars
in Blanco 1 are lower than those of the Pleiades.
In the case of dM stars, we note that the X-ray luminosity median in Blanco 1
dM stars is slightly higher than the analog for the Pleiades.
We estimate the XLDs following
the method described in Schmitt (1985) in the case of censored data
as done in Paper I. We do not find significant differences between XLDs
computed in the present work and those in Paper I.
The median of
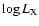 for dG stars is now larger than that in Paper I
(median
for dG stars is now larger than that in Paper I
(median
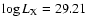 in Paper I, 29.4 in this work). In contrast,
in the case of dK stars the new median is lower than that in Paper I
(29.1 vs. 29.3),
the reason for this unexpected difference being that we have excluded contaminants
(that should lower the XLD), but have also included new late dK stars which are
less active than early dK stars.
in Paper I, 29.4 in this work). In contrast,
in the case of dK stars the new median is lower than that in Paper I
(29.1 vs. 29.3),
the reason for this unexpected difference being that we have excluded contaminants
(that should lower the XLD), but have also included new late dK stars which are
less active than early dK stars.
In order to investigate effects related to stellar metallicity,
in Figs. 10 and 11 we compare the XLDs of dF, dG, dK and dM stars in Blanco 1,
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H3241F10.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg50.gif) |
Figure 10:
XLDs for dF and dG stars of Blanco 1 (dotted line),
Pleiades (continuous line) and NGC 2516 (dashed line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H3241F11.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg51.gif) |
Figure 11:
XLDs for dK and dM stars of Blanco 1 (dotted line),
Pleiades (continuous line) and NGC 2516 (dashed line). |
| Open with DEXTER |
Pleiades (Micela et al. 1996; Micela et al. 1999b) and NGC 2516 (Harnden et al. 2001).
The XLDs of NGC 2516 are derived from Chandra data,
so that the comparison with other XLDs, obtained with a different instrument,
is not straightforward.
Furthermore the membership information for NGC 2516 is not yet as reliable as that
for the Pleiades, thus in this case the XLDs could still be affected by
contamination in the range of solar type stars. However, our primary comparison
relies on Blanco 1 vs. the Pleiades and 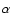 Per clusters for which we used ROSAT data
and for which astrometric membership is available.
We have not found any significant differences between Blanco 1 and Pleiades
stars for dG and dK spectral type when applying several statistical
"two sample'' tests (logrank, Gehan and Wilcoxon, see Schmitt 1985);
while we found a marginal difference at the 94% level in the case of
dM stars
Per clusters for which we used ROSAT data
and for which astrometric membership is available.
We have not found any significant differences between Blanco 1 and Pleiades
stars for dG and dK spectral type when applying several statistical
"two sample'' tests (logrank, Gehan and Wilcoxon, see Schmitt 1985);
while we found a marginal difference at the 94% level in the case of
dM stars![[*]](/icons/foot_motif.gif) .
.
The dG stars of Blanco 1 have a distribution of
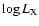 values similar to
that of Pleiades and NGC 2516, despite the differences in metal content.
The expected influence of metallicity on the coronal emission in this spectral
range is complex as pointed out by Pizzolato et al. (2001). A first, direct effect
is due to the radiative losses in the corona:
the X-ray coronal spectrum of late type stars, at temperatures of a
few million degrees, is dominated by line
emission produced by heavy ions so that the emissivity power scales
linearly with metal abundance.
values similar to
that of Pleiades and NGC 2516, despite the differences in metal content.
The expected influence of metallicity on the coronal emission in this spectral
range is complex as pointed out by Pizzolato et al. (2001). A first, direct effect
is due to the radiative losses in the corona:
the X-ray coronal spectrum of late type stars, at temperatures of a
few million degrees, is dominated by line
emission produced by heavy ions so that the emissivity power scales
linearly with metal abundance.
A second effect is related to the structural change in subphotospheric layers
due to the variation in metal abundance level. In fact, a higher metallicity increases the
opacity and produces deeper convection zones at a given mass.
This could result in a better efficiency of the dynamo, producing a higher coronal
activity, if the rotational period is kept fixed.
These two effects are likely to lead to an enhancement of X-ray coronal emission.
Another effect is related to the metallicity influence
on the mass vs. color-index relation:
stars with higher metallicity at a fixed B-V value are more massive than metal-poor stars
with the same B-V.
This effect produces variations in the convective turnover time of F-G
type stars of up to a factor 4, if modeled
with the Full-Spectrum-of-Turbulence theory (Canuto et al. 1996).
A lower convective turnover time would imply a lower activity in metal-rich solar type stars
with respect to metal-poor stars with the same color index because the compared stars have
different masses. More massive metal-rich stars should have less extended
convection zones and a less efficient dynamo mechanism than metal-poor stars
with the same color index.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H3241F12.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg52.gif) |
Figure 12:
XLDs for dG and dK stars of Blanco 1 (dotted line),
Pleiades (continuous line) and 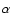 Per (dashed line). Per (dashed line). |
| Open with DEXTER |
As a result, when we compare dG stars with different metal abundances selected by the
same B-V color index, the effects on the convection zone and on the radiative losses tend
to compensate; for dK stars no effects on the convective zone are expected to be present
and only the radiative losses are affected by metal abundance (Pizzolato et al. 2001).
The XLD for dK stars of Blanco 1 is similar to that of the
Pleiades (Fig. 11), whereas based on the
Pizzolato et al. (2001) model estimates, we would expect a monotonic increase
of activity level with metal abundance.
Two hypotheses are possible: either the presence of contaminating less active field stars
lowers the overall distribution of
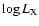 (but the threshold of
membership probability is high enough to minimize this effect),
or we are dealing with a real effect.
In particular, a distribution of rotational periods different from that of
Pleiades and NGC 2516 could overwhelm the metallicity effect in determining X-ray activity.
(but the threshold of
membership probability is high enough to minimize this effect),
or we are dealing with a real effect.
In particular, a distribution of rotational periods different from that of
Pleiades and NGC 2516 could overwhelm the metallicity effect in determining X-ray activity.
Measurements of
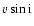 are given in Jeffries & James (1999)
for Blanco 1 G and K type stars selected from the list of
Panagi & O'Dell (1997) and filtered by means of radial velocity criteria.
The sample of members is very small but we note that the fraction of fast rotators is consistent with
that found in the Pleiades by Queloz et al. (1998). These stars should be in the saturated
coronal regime and this fact is consistent with the similarity of the high luminosity
tails of XLDs of dK stars in Pleiades and Blanco 1, so that differences are to be
looked for in the low velocity range (e.g.
are given in Jeffries & James (1999)
for Blanco 1 G and K type stars selected from the list of
Panagi & O'Dell (1997) and filtered by means of radial velocity criteria.
The sample of members is very small but we note that the fraction of fast rotators is consistent with
that found in the Pleiades by Queloz et al. (1998). These stars should be in the saturated
coronal regime and this fact is consistent with the similarity of the high luminosity
tails of XLDs of dK stars in Pleiades and Blanco 1, so that differences are to be
looked for in the low velocity range (e.g.
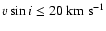 ).
The lack of measurements in this range for an extended sample of dK stars of Blanco 1
prevents us from testing for significant differences in the distributions of rotational periods.
).
The lack of measurements in this range for an extended sample of dK stars of Blanco 1
prevents us from testing for significant differences in the distributions of rotational periods.
For dM stars we note the relatively higher level of X-ray luminosity
for the Blanco 1 sample. Whereas the distributions of Pleiades and NGC 2516 are similar,
the XLD of Blanco 1 systematically presents higher values, although the high-luminosity
tail is similar to that of the other clusters. This can suggest
a possible metallicity effect on the X-ray emission of these stars.
If we assume that the expected fraction of contaminants (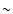 10%)
is concentrated in the lowest X-ray luminosity sources, we can correct the XLD,
excluding the 10% of less active stars and obtaining the "non-contaminated''
XLD. With this procedure we find that the probability level of a significant
difference between the XLD of dM stars in Blanco 1 and Pleiades increases
to 99.8%, thus reinforcing the indication that the
chemical abundances are likely to play a role in the coronae of dM stars.
10%)
is concentrated in the lowest X-ray luminosity sources, we can correct the XLD,
excluding the 10% of less active stars and obtaining the "non-contaminated''
XLD. With this procedure we find that the probability level of a significant
difference between the XLD of dM stars in Blanco 1 and Pleiades increases
to 99.8%, thus reinforcing the indication that the
chemical abundances are likely to play a role in the coronae of dM stars.
In Figs. 12 and 13 we compare the XLDs of Blanco 1, Pleiades and
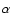 Per
to explore the effects related to age evolution. We note that in the case of dG and dK
stars,
Per
to explore the effects related to age evolution. We note that in the case of dG and dK
stars,
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{H3241F13.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg55.gif) |
Figure 13:
XLDs for dM stars of Blanco 1 (dotted line),
Pleiades (continuous line) and 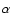 Per (dashed line). Per (dashed line). |
| Open with DEXTER |
the 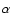 Per stars are more X-ray luminous than those of Pleiades and Blanco 1.
The dM stars of Blanco 1 appear, on the contrary, more X-ray luminous than those of Pleiades
and
Per stars are more X-ray luminous than those of Pleiades and Blanco 1.
The dM stars of Blanco 1 appear, on the contrary, more X-ray luminous than those of Pleiades
and 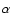 Per.
It appears that the age effect on the X-ray emission level
is relevant in the case of dG and dK stars while in
the case of dM stars the differences in the Blanco 1 sample could be
related to a metallicity effect.
Per.
It appears that the age effect on the X-ray emission level
is relevant in the case of dG and dK stars while in
the case of dM stars the differences in the Blanco 1 sample could be
related to a metallicity effect.
We give some caveats on this conclusion: the Blanco 1 dM sample contains
a small number of objects and the XLD is significantly influenced by upper limits.
Deeper observations already planned with XMM-Newton satellite
will allow us to give a firmer basis to this evidence.
We have calculated X-ray Luminosity Distributions for the Blanco 1 cluster
from ROSAT-HRI data, taking advantage of a new
astrometric-photometric membership selection.
In particular we
have calculated for the first time the XLD of Blanco 1 dM stars.
Spatial cross-correlation between the GSC-II catalog and unidentified X-ray sources
reported in Paper I allows us to identify new low-mass members characterized by
high X-ray luminosity.
We have also rejected a significant fraction of objects
from the photometric member list of Panagi & O'Dell (1997), as
having proper motions not compatible with those of the cluster.
The comparison of the new "uncontaminated'' XLDs
with the analogs of other clusters, allows us to explore effects related to age and
metallicity, and shows that the metal-rich dM stars of Blanco 1 appear more active (with
the caveats given in previous section)
than the analog ones (more metal poor) in Pleiades, NGC 2516 and 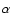 Per.
Our results suggest that chemical composition can influence coronal activity,
mainly through coronal radiative losses due to emission lines.
Deeper observations aimed to obtaining a larger sample of detections
are needed to confirm these results based in part on upper limits.
Per.
Our results suggest that chemical composition can influence coronal activity,
mainly through coronal radiative losses due to emission lines.
Deeper observations aimed to obtaining a larger sample of detections
are needed to confirm these results based in part on upper limits.
The dK stars of Blanco 1 do not follow the prediction based on Pizzolato et al. (2001)
according to which these stars should be more luminous than the dK stars in the Pleiades, thus
suggesting a possible difference (not measured up to now) in the rotational velocity
distribution of slow rotators with respect to the Pleiades.
The testing of this hypothesis will require an observational campaign to derive
rotational periods of "slowly" (
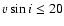 km s-1) rotating Blanco 1 members.
km s-1) rotating Blanco 1 members.
Acknowledgements
We wish to thank G. Hawkins for supplying GSC-II calibration and
the referee R. Jeffries for his useful comments.
We thank also D. Randazzo for significant help on revising the text.
The authors made use of the European Southern Observatory (ESO) Facilities
at La Silla, Chile.
The Guide Star Catalog-II is a joint project of the Space Telescope Science
Institute and the Osservatorio Astronomico di Torino.
The Two Micron All Sky Survey is a joint project of the University of Massachusetts
and the Infrared Analysis Processing and Analysis Center (California Institute of
Technology).
IP, GM and SS acknowledge financial support from ASI (Italian Space Agency)
and MIUR (Ministero della Istruzione, dell'Università e della Ricerca).
-
Boesgaard, A. M., & Friel, E. D. 1990, ApJ, 351, 467
In the text
NASA ADS
-
Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550
In the text
NASA ADS
-
Damiani, F., Maggio, A., Micela, G., & Sciortino, S. 1997, ApJ, 483,
350
In the text
NASA ADS
-
de Epstein, A. E. A., & Epstein, I. 1985, AJ, 90, 1211
In the text
NASA ADS
-
Edvardsson, B., Pettersson, B., Kharrazi, M., & Westerlund, B. 1995,
A&A, 293, 75
In the text
NASA ADS
-
Epstein, I. 1968, AJ, 73, 556
In the text
NASA ADS
-
Harnden, F. R. Jr., Adams, N. R., Damiani, F., et al. 2001, ApJ, 547,
L141
In the text
NASA ADS
-
Jeffries, R. D., & James, D. J. 1999, ApJ, 511, 218
In the text
NASA ADS
-
Jeffries, R. D., Thurston, M. R., & Pye, J. P. 1997, MNRAS, 287, 350
In the text
NASA ADS
-
Jones, B. 1997, Mem. Soc. Astron. It., 68, 833
In the text
NASA ADS
-
Lang, K. R. 1992, Astrophysical Data I. Planets and Stars (Astrophysical
Data I. Planets and Stars, X, 937 pp., 33 figs., Berlin: Springer-Verlag )
In the text
-
Leggett, S. K., Allard, F., Berriman, G., Dahn, C. C., & Hauschildt,
P. H. 1996, ApJS, 104, 117
In the text
NASA ADS
-
Leggett, S. K., Allard, F., & Hauschildt, P. H. 1998, ApJ, 509, 836
In the text
NASA ADS
-
Mermilliod, J. C. 1981, A&A, 97, 235
In the text
NASA ADS
-
Micela, G., Sciortino, S., Favata, F., Pallavicini, R., & Pye, J.
1999a, A&A, 344, 83
NASA ADS
-
Micela, G., Sciortino, S., Harnden F. R. Jr., et al. 1999b, A&A,
341, 751
In the text
NASA ADS
-
Micela, G., Sciortino, S., Kashyap, V., Harnden, F. R. Jr., & Rosner, R.
1996, ApJS, 102, 75
In the text
NASA ADS
-
Panagi, P. M., & O'Dell, M. A. 1997, A&AS, 121, 213
In the text
NASA ADS
-
Pizzolato, N., Ventura, P., D'Antona, et al. 2001, A&A, 373, 597
In the text
NASA ADS
-
Queloz, D., Allain, S., Mermilliod, J., Bouvier, J., & Mayor, M.
1998, A&A, 335, 183
In the text
NASA ADS
-
Raymond, J. C., & Smith, B. W. 1977, ApJS, 35, 419
In the text
NASA ADS
-
Robichon, N., Arenou, F., Mermilliod, J., & Turon, C. 1999, A&A, 345,
471
In the text
NASA ADS
-
Schmitt, J. H. M. M. 1985, ApJ, 293, 178
In the text
NASA ADS
-
Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593
In the text
NASA ADS
-
Westerlund, B. E., Lundgren, K., Pettersson, B., Garnier, R., &
Breysacher, J. 1988, A&AS, 76, 101
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F1.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg11.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F2.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg12.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F3.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg13.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F4.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg14.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F5.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg15.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F6.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg30.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F7.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg35.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=14.5cm,clip]{H3241F8.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg38.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{H3241F9.PS} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg48.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H3241F10.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg50.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H3241F11.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg51.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{H3241F12.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg52.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{H3241F13.eps} \end{figure}](/articles/aa/full/2003/09/aah3241/Timg55.gif)