A&A 399, L39-L42 (2003)
DOI: 10.1051/0004-6361:20030083
V. I. Denisov - S. I. Svertilov
Physics Department, Moscow State University, 119899, Moscow, Russia
Received 30 November 2001 / Accepted 15 January 2003
Abstract
Near a magnetic neutron star electromagnetic emission
should undergo nonlinear electrodynamic effects in strong
magnetic fields. Manifestations of this effect in detected
hard emission from magnetic neutron stars are discussed on
the base of nonlinear generalizations of the Maxwell
equation in vacuum. The dispersion equations for
electromagnetic waves propagating in the magnetic dipole
field were obtained in the framework of these theories.
Key words: pulsars: general - scattering - stars: neutron - waves
Studies of phenomena in the vicinity of a neutron star make it
possible to obtain information on the properties of matter
in states, which are unattainable in ground
laboratories. The last experiments on light-to-light
scattering made at Stanford (Burke et al. 1997) show that
electrodynamics in vacuum is really a nonlinear theory.
However, magnetic fields (
![]() G)
available in ground laboratories give no opportunity to test the
different models of nonlinear electrodynamics of vacuum
and their predictions because the typical value of
magnetic field induction necessary for essential
manifestation of electrodynamics nonlinearity in vacuum is about
G)
available in ground laboratories give no opportunity to test the
different models of nonlinear electrodynamics of vacuum
and their predictions because the typical value of
magnetic field induction necessary for essential
manifestation of electrodynamics nonlinearity in vacuum is about
![]() G. Since magnetic fields of some pulsars
can be characterized by such magnitudes, and for magnetars can reach
much greater values (
G. Since magnetic fields of some pulsars
can be characterized by such magnitudes, and for magnetars can reach
much greater values (
![]() G) (Thomson & Duncan 1995, 1996),
the nonlinear
effects of electrodynamics in vacuum should be most
pronounced in the vicinity of such astrophysical objects.
Different nonlinear electrodynamic effects in the vicinity of a
strongly magnetized neutron star were previously studied in the context of
quantum electrodynamics (Meszaros 1992; Gal'tsov & Nikitina 1983;
Bussard et al. 1986; De Lorenci et al. 2001). However,
the analysis presented above concentrated on the validity of quantum
electrodynamics without comparison with possible alternative theories. Thus,
we try to obtain some specific predictions by using post-Maxwellian items of
different nonlinear generalizations of electrodynamics.
G) (Thomson & Duncan 1995, 1996),
the nonlinear
effects of electrodynamics in vacuum should be most
pronounced in the vicinity of such astrophysical objects.
Different nonlinear electrodynamic effects in the vicinity of a
strongly magnetized neutron star were previously studied in the context of
quantum electrodynamics (Meszaros 1992; Gal'tsov & Nikitina 1983;
Bussard et al. 1986; De Lorenci et al. 2001). However,
the analysis presented above concentrated on the validity of quantum
electrodynamics without comparison with possible alternative theories. Thus,
we try to obtain some specific predictions by using post-Maxwellian items of
different nonlinear generalizations of electrodynamics.
Several nonlinear generalizations of the Maxwell equation in vacuum are considered in the framework of the field theory. The most well known among them are the Born-Infeld (BI) (Born & Infeld 1934) and the Heisenberg-Euler (HE) electrodynamics (Heisenberg & Euler 1936).
Born and Infeld proceeded from the idea of a limited value of the
electromagnetic field energy of a point particle. This and
some other reasons led them to the following Lagrangian of
the nonlinear electrodynamics in vacuum:
![\begin{displaymath}L=-{1\over 4\pi a^2}\Big[\sqrt{1+a^2\left({\vec B}^2-{\vec E}^2\right)-
a^4\left({\vec B}\times {\vec E}\right)^2}-1\Big],
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img13.gif) |
(1) |
![\begin{displaymath}L=-{1\over 8\pi }\left({\vec B}^2-{\vec E}^2\right)+{a^2\over...
...ec B}^2-{\vec E}^2\right)^2+4({\vec B}\times {\vec E})^2\Big].
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img17.gif)
![\begin{displaymath}L=-{1\over 8 \pi }\left[{\vec B}^2-{\vec E}^2\right]+{\alpha ...
...c B}^2-{\vec E}^2\right)^2+7({\vec B}\times {\vec E})^2\Big\},
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img21.gif)
In other theoretical models of nonlinear
electrodynamics the coefficients at the terms
![]() and
and
![]() in the
Lagrangian expansion can be absolutely arbitrary.
We will use a parameterized post-Maxwell
formalism, which was elaborated by Denisov & Denisova (2001a,b).
We will assume, that the main prerequisite for this formalism is
that the Lagrangian of nonlinear electrodynamics in
vacuum is an analytical function of invariants
in the
Lagrangian expansion can be absolutely arbitrary.
We will use a parameterized post-Maxwell
formalism, which was elaborated by Denisov & Denisova (2001a,b).
We will assume, that the main prerequisite for this formalism is
that the Lagrangian of nonlinear electrodynamics in
vacuum is an analytical function of invariants
![]() and
and
![]() at
least, near their zero values. Thus, in the case of a weak
electromagnetic field
at
least, near their zero values. Thus, in the case of a weak
electromagnetic field
![]() this Lagrangian can
be expanded into a converging set in integer powers of
these invariants:
this Lagrangian can
be expanded into a converging set in integer powers of
these invariants:
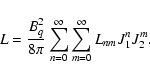 |
(2) |
For such an approach, a quite definite number of post-Maxwell
parameters Lnm will correspond to each nonlinear
electrodynamics. If we limit oneselves only to a few first terms in
expansion (2), then according to the parameterized post-Maxwell
formalism the generalized Lagrangian of the nonlinear
vacuum electrodynamics in the case of weak fields can be
represented as (Denisov & Denisova 2001a,b):
![\begin{displaymath}L={1\over 8\pi }\Big\{\left[{\vec E}^2-{\vec B}^2\right]+
\xi...
...}^2\right)^2+
4\eta_2({\vec B}\times {\vec E})^2\right]\Big\},
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img30.gif) |
(3) |
In particular, in the nonlinear HE electrodynamics parameters ![]() and
and ![]() have quite definite values
have quite definite values
![]() while in the BI theory they
can be expressed through the same unknown
constant a2:
while in the BI theory they
can be expressed through the same unknown
constant a2:
![]()
The electromagnetic ray is exactly the
agent, which passing through the neutron star magnetic field
undergoes nonlinear electromagnetic influence from this
field independently of the spectral range. Studying the main
parameters of incoming electromagnetic emission, such as
dependence of ray bending angle on impact distance, the
law of emission intensity decreasing in the course of time,
etc., it is possible (Denisov et al. 2001)
to reveal the main dependencies of nonlinear electrodynamic
interactions of electromagnetic fields.
We will assume that a "weak''
plane electromagnetic wave propagates through the permanent
magnetic field ![]() of a neutron star. Then in the
geometric optics approach we can write the following
relations:
of a neutron star. Then in the
geometric optics approach we can write the following
relations:
| |
= | ||
| = |
Under this approach the dispersion equation can be obtained
from Lagrangian (3) directly. To ensure the
necessary accuracy of calculations, we will add to Lagrangian (3) the terms of higher approximations and, hence, write
it with surplus accuracy:
| L | = | ||
![\begin{displaymath}\omega_{1,2}({\vec k})=ck\Big\{1-{2\eta_{1,2} \xi \over k^2}[...
... k}\times
{\vec B}_0]^2+O\left(\xi^2{\vec B}_0^4\right)\Big\},
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img49.gif) |
(4) |
As it was shown previously (Denisov 2000), the exact
dispersion equation for electromagnetic wave propagating in the
magnetic field
![]() in the BI theory (1) has the form
in the BI theory (1) has the form
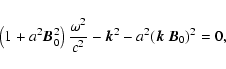 |
(5) |
The solution of the nonlinear electrodynamics equations for electromagnetic
waves propagating in the magnetic field shows that at
![]() the waves of both types with the
dispersion Eqs. (4) are polarized linearly in mutually
normal planes and propagate with different group velocities. This
property of electromagnetic waves is well known as birefringence.
the waves of both types with the
dispersion Eqs. (4) are polarized linearly in mutually
normal planes and propagate with different group velocities. This
property of electromagnetic waves is well known as birefringence.
At
![]() both types of electromagnetic waves
will coincide to the accuracy of terms proportional to
both types of electromagnetic waves
will coincide to the accuracy of terms proportional to ![]() .
As a result, electromagnetic waves of the same type
with arbitrary polarization will propagate in each direction.
.
As a result, electromagnetic waves of the same type
with arbitrary polarization will propagate in each direction.
Let us find now the eikonal equation for an electromagnetic
wave propagating in the dipole magnetic field of a neutron
star under the laws of nonlinear vacuum electrodynamics.
For this purpose we will raise relations (4) to the second power.
Retaining terms linear in ![]() and taking into account that
and taking into account that
![]() we obtain:
we obtain:
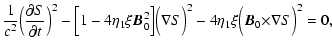 |
(6) | ||
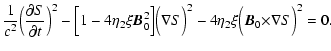 |
![\begin{displaymath}{1\over c^2}\Big({\partial S\over \partial t}\Big)^2\left[1+a...
...^2\right]-
({\bf\nabla }S)^2-a^2({\bf\nabla }S{\vec B}_0)^2=0.
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img62.gif) |
(7) |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{figure1.eps}
\end{figure}](/articles/aa/full/2003/09/aaek205/Timg65.gif) |
Figure 1:
The BI dependence
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{aaek205f2.eps}
\end{figure}](/articles/aa/full/2003/09/aaek205/Timg68.gif) |
Figure 2:
The HE
|
| Open with DEXTER | |
Let us denote the plane normal to the magnetic dipole
momentum vector ![]() ,
as plane XOY. In this case only
one component of the vector
,
as plane XOY. In this case only
one component of the vector
![]() will be
nonzero and vector
will be
nonzero and vector
![]() in this plane can be represented
as:
in this plane can be represented
as:
![]()
Hence the first of the eikonal Eq. (6) for electromagnetic wave
polarized in the XOY plane, which lie in the same plane, will be:
![\begin{displaymath}{1\over c^2}\Big({\partial S_1\over \partial t}\Big)^2-\left[...
...2}
\Big({\partial S_1\over \partial \varphi
}\Big)^2\right]=0.
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img72.gif) |
(8) |
As it is accepted in theoretical mechanics (Landau & Lifshitz 1984),
we will find the partial solution of Eq. (8) using the
variables separation method. As a result, we obtain:
![\begin{displaymath}S_1=-{\cal E}_0t+\alpha \varphi +\int\limits^r{\rm d}r
\sqrt{...
...{4\eta_1\xi {\vec m}^2
\over r^6}\right]-{\alpha^2\over r^2}},
\end{displaymath}](/articles/aa/full/2003/09/aaek205/img73.gif) |
(9) |
It should be noted, that in the magnetic equator plane the
expression (9) is also the solution of BI exact eikonal
Eq. (7), if we take into account, that in this theory
![]()
Using relation (9) we can determine the kinematic and dynamic parameters describing photon propagation in the dipole magnetic field.
Let us consider the case, when the
gamma ray source is located at a limited distance l1from a neutron star or even in its nearest vicinity.
Let us denote the distance from neutron star to the detector as l2.Then the
distance l1 is much smaller than l2 and comparable with
the neutron star radius R.Hence, the dependence of
impact distance on time for a circular orbit in the first
approximation can be represented as:
![]() where R1 is the orbit radius,
where R1 is the orbit radius, ![]() is the orbital
frequency.
is the orbital
frequency.
If we are considering the propagation of a X-ray or
gamma ray photon from a source located near a
galactic neutron star, it is convenient to direct the Xand Y axes in such a way, that a ray from the
source travels along the X axis with the impact distance b, the center of the dipole magnetic field is placed in the
center of the coordinate system and the spacecraft
with the detectors is located at the distance l2 from the
center of the coordinate system near the point
![]() .
.
Since the value
![]() is small, in order to find the
bending angles
is small, in order to find the
bending angles
![]() we can use the algorithm (Darwin 1961), well established for calculations of
angles of light gravitational bending.
For the case, when
we can use the algorithm (Darwin 1961), well established for calculations of
angles of light gravitational bending.
For the case, when
![]() and
and ![]() we obtained the following
relations for the bending angles:
we obtained the following
relations for the bending angles:
| |
= | ![$\displaystyle \arctan\left[{bQ_1\over \sqrt{Q_1^2l_1^2-1}}\right]
+{15\pi \eta_1\xi {\vec m}^2\over 4 b^6}$](/articles/aa/full/2003/09/aaek205/img84.gif) |
(10) |
![$\displaystyle -\left[1+{15 \eta_1\xi {\vec m}^2\over 4 b^6}\right]\arcsin\left({1\over Q_1l_1}\right)$](/articles/aa/full/2003/09/aaek205/img85.gif) |
|||
![$\displaystyle -{\eta_1\xi {\vec m}^2\over 16 b^6}\left\{\sin\left[4\arcsin\left({1\over Q_1l_1}\right)\right]\right.$](/articles/aa/full/2003/09/aaek205/img86.gif) |
|||
![$\displaystyle \left.-16\sin\left[2\arcsin\left({1\over Q_1l_1}\right)\right]\right\},$](/articles/aa/full/2003/09/aaek205/img87.gif) |
|||
| = | ![$\displaystyle \arctan\left[{bQ_2\over \sqrt{Q_2^2l_1^2-1}}\right]
+{15\pi \eta_2\xi {\vec m}^2\over 4 b^6}$](/articles/aa/full/2003/09/aaek205/img89.gif) |
||
![$\displaystyle -\left[1+{15 \eta_2\xi {\vec m}^2\over 4 b^6}\right]\arcsin\left({1\over
Q_2l_1}\right)$](/articles/aa/full/2003/09/aaek205/img90.gif) |
|||
![$\displaystyle -{\eta_2\xi {\vec m}^2\over 16 b^6}\left\{\sin\left[4\arcsin\left({1\over
Q_2l_1}\right)\right] \right.$](/articles/aa/full/2003/09/aaek205/img91.gif) |
|||
![$\displaystyle \left.-16\sin\left[2\arcsin\left({1\over Q_2l_1}\right)\right]\right\},$](/articles/aa/full/2003/09/aaek205/img92.gif) |
(11) |
![\begin{displaymath}Q_1={1\over b}\left[1+{2\eta_1\xi {\vec m}^2\over b^6}\right]...
...={1\over b}\left[1+{2\eta_2\xi {\vec m}^2\over b^6}\right]\cdot\end{displaymath}](/articles/aa/full/2003/09/aaek205/img93.gif)
Thus, nonlinear models of vacuum electrodynamics
with
![]() predict different angles of ray
bending for electromagnetic waves with different polarization.
predict different angles of ray
bending for electromagnetic waves with different polarization.
It should be noted, that besides the nonlinear electrodynamic bending (10) of electromagnetic rays will also undergo the well known
gravitational bending. However, because of the different bending
angle dependence on the impact distance b (1/b and 1/b2 in the
case of gravitational bending (Epstein & Shapiro 1980;
Meszaros & Riffert 1988; Riffert & Meszaros 1988) and 1/b6 in
the case of nonlinear electrodynamic bending) mathematical processing
allows to resolve each of these parts from the observational data if
the time dependence of impact distance b is harmonical
![]() For comparison, we present in Fig. 1
For comparison, we present in Fig. 1
![]() versus l1/b from gravitational bending
(
versus l1/b from gravitational bending
(
![]() for different
values of the attitude
for different
values of the attitude
![]() .
.
Although the observation of the manifestations of the nonlinear electrodynamics effects in astrophysical objects requires special conditions, in principle, they can be observed. The main astrophysical objects, where the nonlinear electrodynamic effects can be revealed more clearly, are certain kinds of gamma-ray pulsars and magnetars. These effects can be manifested as some peculiarities in the form of their hard emission pulsation.
Acknowledgements
We are grateful to Academician Georgiy T. Zatsepin for fruitful stimulating discussions. Authors would also like to express their warm thanks to Ekaterina D. Tolstaya for grammar corrections and Alexander A. Zubrilo, Vitaly V. Bogomolov, Oleg V. Morozov for the help with preparing this manuscript.
Part of this work was supported by the Russian Foundation of Basic Research at the Contract 02-02-16598.