A&A 399, 961-982 (2003)
DOI: 10.1051/0004-6361:20021842
The formation of a disk galaxy within a growing dark halo
M. Samland 1 - O. E. Gerhard 1
Astronomisches Institut der Universität Basel,
Venusstrasse 7, 4102 Binningen, Switzerland
Received 3 July 2002 / Accepted 29 November 2002
Abstract
We present a dynamical model for the formation and
evolution of a massive disk galaxy, within a growing dark halo
whose mass evolves according to cosmological simulations of
structure formation. The galactic evolution is simulated with a
new three-dimensional chemo-dynamical code, including dark matter,
stars and a multi-phase ISM. The simulations start at redshift z
= 4.85 with a small dark halo in a 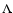 CDM universe and we follow
the evolution until the present epoch. The energy release by
massive stars and supernovae prevents a rapid collapse of the
baryonic matter and delays the maximum star formation until
redshift
CDM universe and we follow
the evolution until the present epoch. The energy release by
massive stars and supernovae prevents a rapid collapse of the
baryonic matter and delays the maximum star formation until
redshift
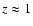 .
The metal enrichment history in this model
is broadly consistent with the evolution of [Zn/H] in damped
Ly
.
The metal enrichment history in this model
is broadly consistent with the evolution of [Zn/H] in damped
Ly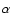 systems. The galaxy forms radially from inside-out and
vertically from halo to disk. As a function of metallicity, we
have described a sequence of populations, reminiscent of the
extreme halo, inner halo, metal-poor thick disk, thick disk, thin
disk and inner bulge in the Milky Way. The first galactic
component that forms is the halo, followed by the bulge, the
disk-halo transition region, and the disk. At redshift
systems. The galaxy forms radially from inside-out and
vertically from halo to disk. As a function of metallicity, we
have described a sequence of populations, reminiscent of the
extreme halo, inner halo, metal-poor thick disk, thick disk, thin
disk and inner bulge in the Milky Way. The first galactic
component that forms is the halo, followed by the bulge, the
disk-halo transition region, and the disk. At redshift
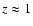 ,
a bar begins to form which later turns into a triaxial
bulge. Despite the still idealized model, the final galaxy
resembles present-day disk galaxies in many aspects. The bulge in
the model consists of at least two stellar subpopulations, an
early collapse population and a population that formed later in
the bar. The initial metallicity gradients in the disk are later
smoothed out by large scale gas motions induced by the bar. There
is a pronounced deficiency of low-metallicity disk stars due to
pre-enrichment of the disk ISM with metal-rich gas from the bulge
and inner disk ("G-dwarf problem''). The mean rotation and the
distribution of orbital eccentricities for all stars as a function
of metallicity are not very different from those observed in the
solar neighbourhood, showing that early homogeneous collapse
models are oversimplified. The approach presented here provides a
detailed description of the formation and evolution of an isolated
disk galaxy in a
,
a bar begins to form which later turns into a triaxial
bulge. Despite the still idealized model, the final galaxy
resembles present-day disk galaxies in many aspects. The bulge in
the model consists of at least two stellar subpopulations, an
early collapse population and a population that formed later in
the bar. The initial metallicity gradients in the disk are later
smoothed out by large scale gas motions induced by the bar. There
is a pronounced deficiency of low-metallicity disk stars due to
pre-enrichment of the disk ISM with metal-rich gas from the bulge
and inner disk ("G-dwarf problem''). The mean rotation and the
distribution of orbital eccentricities for all stars as a function
of metallicity are not very different from those observed in the
solar neighbourhood, showing that early homogeneous collapse
models are oversimplified. The approach presented here provides a
detailed description of the formation and evolution of an isolated
disk galaxy in a 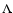 CDM universe, yielding new information about
the kinematical and chemical history of the stars and the
interstellar medium, but also about the evolution of the
luminosity, the colours and the morphology of disk galaxies with
redshift.
CDM universe, yielding new information about
the kinematical and chemical history of the stars and the
interstellar medium, but also about the evolution of the
luminosity, the colours and the morphology of disk galaxies with
redshift.
Key words: galaxies: formation - galaxies: evolution - galaxies: stellar
content - galaxies: structure - galaxies: kinematics and dynamics - galaxies: ISM
During the last decade, significant progress has been made in
understanding cosmic structure formation and galactic evolution.
With high-resolution cosmological simulations, the formation of
dark halos in different cosmologies has been studied in detail
(e.g. Navarro et al. 1996; Moore et al. 1998; Colín et al. 2000; Yoshida et al. 2000;
Avila-Reese et al. 2001; Jenkins et al. 2001; Klypin et al. 2001) to determine the large-scale mass
distribution, the halo merging histories, the structural
parameters of the dark halos, and finally the formation of
galaxies inside these dark halos (Steinmetz & Müller 1995; Kay et al. 2000;
Navarro & Steinmetz 2000b; Mosconi et al. 2001; Pearce et al. 2001).
In many respects, these simulations are in agreement with
observations, but there remain a number of difficulties. Firstly,
the universal cuspy halo density profiles (Navarro et al. 1997;
Moore et al. 1999; Fukushige & Makino 2001), while in agreement with observations of
galaxy clusters, are in apparent disagreement with the flat dark
matter density distributions inferred from observations in the
centres of galaxies (Salucci & Burkert 2000; Blais-Ouellette et al. 2001; Borriello & Salucci 2001;
de Blok et al. 2001). Secondly, the specific angular momenta and
scale lengths of the disk galaxies in the cosmological simulations
are too small compared to real galaxies (Navarro & Steinmetz 2000b). This
may be partially a numerical problem of SPH simulations, but is
more likely due to overly efficient cooling and strong angular
momentum transport from the baryons to the dark halos during
merger events (Navarro & Benz 1991). Thacker & Couchman (2001) and also
Sommer-Larsen et al. (1999) showed the angular momentum problem in CDM
simulations may be resolved by the inclusion of feedback
processes. Thirdly, the cold dark matter (CDM) simulations
predict a large number of satellite galaxies in the neighbourhood
of giant galaxies like the Milky Way Galaxy, but this is not
observed (Moore et al. 1999).
The cosmological simulations are used to describe the large-scale
evolution of the dark matter distribution from the primordial
density fluctuations to the time when the dark halos form. It is
inevitable in such simulations that structures on galactic and
sub-galactic scales are not well-resolved. Furthermore, it is
difficult to incorporate the detailed physics of the baryonic
component, that is of the multi-phase interstellar medium (ISM),
and the feedback processes between stars and ISM. These are
serious drawbacks, because feedback from stars can prevent a
proto-galactic cloud from rapid collapse and it can trigger large
scale gas motions (Samland et al. 1997). Both alter the galactic
formation process significantly.
Complementary ways to circumvent at least some of these problems
are (i) to combine the large-scale simulations with
semi-analytical galaxy models (Guiderdoni et al. 1998; Somerville & Primack 1999;
Boissier & Prantzos 2000; Cole et al. 2000; Kauffmann & Haehnelt 2000), or (ii) to simulate the
formation of only single galaxies or small galactic groups using
either cosmological initial conditions or a simplified, but
cosmologically motivated model of the dark matter background
(Navarro & Steinmetz 1997; Berczik 1999; Hultman & Pharasyn 1999; Sommer-Larsen et al. 1999;
Bekki & Chiba 2001; Thacker & Couchman 2001; Williams & Nelson 2001). While the semi-analytical
models are advantageous for investigating the global properties of
galaxy samples, the small-scale dynamical models provide
information about the detailed structure of galaxies, the
kinematics of the stellar populations and the ISM, and the star
formation histories. The dynamical models are called
chemo-dynamical (Theis et al. 1992; Samland et al. 1997; Bekki & Shioya 1998; Berczik 1999;
Williams & Nelson 2001), if they include different stellar populations, a
multi-phase ISM, and an interaction network that describes the
mass, momentum and energy transfer between these components.
The aim of the present work is to investigate how a large disk
galaxy forms inside a growing dark halo in a realistic 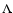 CDM
cosmogony. We present the results of a new three-dimensional
model, including dark matter, stars, and a multi-phase ISM. The
mass infall at the boundaries of the simulated volume is taken
from cosmological simulations (see
VIRGO-GIF-project; Kauffmann et al. 1999). We use a total dark matter
mass of
CDM
cosmogony. We present the results of a new three-dimensional
model, including dark matter, stars, and a multi-phase ISM. The
mass infall at the boundaries of the simulated volume is taken
from cosmological simulations (see
VIRGO-GIF-project; Kauffmann et al. 1999). We use a total dark matter
mass of
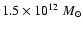 ,
a total baryonic mass of
,
a total baryonic mass of
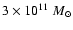 ,
a spin parameter
,
a spin parameter
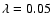 ,
and an
angular momentum profile similar to the universal profile found by
Bullock et al. (2001). Different from Bekki & Shioya (1998); Berczik (1999)
and Williams & Nelson (2001), we use an Eulerian grid-code for the ISM,
which we believe is better suited to describe the multi-phase
structure of the ISM and the feedback processes, especially in
low-density regions. The final galaxy model provides densities,
velocities, velocity dispersions, chemical abundances, and ages
for 614 500 stellar particles, and temperatures, chemical
abundances, densities, velocities, and pressures of the ISM. The
goal of the project is a self-consistent model for the formation
and evolution of large disk galaxies, which can be used to
understand observations of young galaxies as well as data on
stellar populations in the Milky Way.
,
and an
angular momentum profile similar to the universal profile found by
Bullock et al. (2001). Different from Bekki & Shioya (1998); Berczik (1999)
and Williams & Nelson (2001), we use an Eulerian grid-code for the ISM,
which we believe is better suited to describe the multi-phase
structure of the ISM and the feedback processes, especially in
low-density regions. The final galaxy model provides densities,
velocities, velocity dispersions, chemical abundances, and ages
for 614 500 stellar particles, and temperatures, chemical
abundances, densities, velocities, and pressures of the ISM. The
goal of the project is a self-consistent model for the formation
and evolution of large disk galaxies, which can be used to
understand observations of young galaxies as well as data on
stellar populations in the Milky Way.
The paper is organized as follows. Section 2
summarizes some observational material relating to the formation
and evolution of galaxies. Section 3 describes our
multi-phase ISM model and the underlying dark matter halo
model. In Sect. 4 we outline the formation history
of the model disk galaxy. The properties of the galactic halo,
bulge and disk components are discussed in Sect. 5. A summary and a short outlook conclude the paper
(Sect. 6).
2 Observations of the galaxy formation process
Galaxy evolution models can give a simplified description of the
evolution of real galaxies and can make predictions that can be
tested by observations. The high redshift observations show that
the first proto-galactic structures form at redshift z > 3 (e.g. Clements & Couch 1996; Dey et al. 1998; Steidel et al. 1999; Manning et al. 2000).
Surveys of high redshift galaxies reveal a wide range of galactic
morphologies with considerable substructure and clumpiness
(Pentericci et al. 2001). At redshift
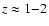 ,
the formation
of galactic components (spheroids, halos, bulges and disks) seems
to take place (Lilly et al. 1998; Kajisawa & Yamada 2001). However, the spatial
resolution of these high and intermediate redshift surveys
(e.g. Abraham et al. 1999; van den Bergh et al. 2000; Ellis et al. 2001;
Menanteau et al. 2001) is still too low to measure more than global
galactic properties (e.g. asymmetry and concentration
parameters). There are indications that most of the massive
galaxies form before or around z = 1 (Brinchmann & Ellis 2000), and
especially that the giant ellipticals form at redshifts z > 1 (Best et al. 1998), (but see van Dokkum et al. 1999), but not before
z = 2.4 (Pentericci et al. 2001). There is a general trend of early
type galaxies being older and having higher peak star formation
rates than late type galaxies (Sandage 1986). These general
star formation histories seem to be overlapped with star formation
bursts, triggered by infalling material or interactions with other
galaxies.
,
the formation
of galactic components (spheroids, halos, bulges and disks) seems
to take place (Lilly et al. 1998; Kajisawa & Yamada 2001). However, the spatial
resolution of these high and intermediate redshift surveys
(e.g. Abraham et al. 1999; van den Bergh et al. 2000; Ellis et al. 2001;
Menanteau et al. 2001) is still too low to measure more than global
galactic properties (e.g. asymmetry and concentration
parameters). There are indications that most of the massive
galaxies form before or around z = 1 (Brinchmann & Ellis 2000), and
especially that the giant ellipticals form at redshifts z > 1 (Best et al. 1998), (but see van Dokkum et al. 1999), but not before
z = 2.4 (Pentericci et al. 2001). There is a general trend of early
type galaxies being older and having higher peak star formation
rates than late type galaxies (Sandage 1986). These general
star formation histories seem to be overlapped with star formation
bursts, triggered by infalling material or interactions with other
galaxies.
Since we can observe galactic sub-structures down to the stellar
scale only in our Galaxy, the Milky Way observations are a
cornerstone for the understanding of the formation and evolution
of all spiral galaxies. From studies of Galactic stars we know
that the halo is old and that the disk and bulge contain a mixture
of old and young stars. This raises the question in what sequence
the galactic components halo, bulge and disk formed, and what was
the star formation history. Determinations of the star formation
history of the Milky Way and other nearby galaxies were attempted
by Bell et al. (2000); Hernandez et al. (2000) and Rocha-Pinto et al. (2000), based
on star counts, broad band colours, or chemical compositions of
stars.
The chemical and kinematical data from galactic halo stars have
been one of the starting points for different scenarios for the
formation and evolution of galaxies. Eggen et al. (1962) were the
first to propose a monolithic collapse galactic formation model in
which the Milky Way forms rapidly out of a collapsing
proto-galactic cloud. This was based on data for galactic halo
stars which are now known to have been plagued by selection
effects (Chiba & Beers 2000). Later, based on observations of halo
globular clusters, Searle & Zinn (1978) proposed a new model in which
the Milky Way forms out of merging lumps and fragments which all
have their individual star formation histories. The contrasting
nature of these two models and the proposed observable differences
(e.g. existence or non-existence of metallicity gradients, the
expected age spread for halo objects) seemed to offer a simple way
to deduce the formation history of disk galaxies from Milky Way
observations. However, new data especially from proper motion
catalogues, lead to the conclusion that at least the halo of the
Milky Way formed neither by a monolithic collapse nor by a pure
merging process (Sandage 1990; Unavane et al. 1996; Chiba & Beers 2000). In the
modern hybrid scenarios, a part of the Galactic halo formed during
a dissipative process (collapse) and another part shows signatures
of merging events. For example, Chiba & Beers (2000) proposed a
scenario in which "the outer halo is made up from merging
and/or accretion of sub-galactic objects, such as dwarf-type
satellite galaxies, whereas the inner part of the halo has
undergone a dissipative contraction on relatively short time
scales''. This is consistent with the findings of
Helmi et al. (1999), who found that 10% of the metal-poor stars in
the outer halo of the Milky Way are aligned in a single coherent
structure, which they identify as the remnant of a disrupted dwarf
galaxy. These hybrid scenarios are, in the general outline, also
consistent with the formation of galaxies in a hierarchical
universe (Chiba & Beers 2000).
3 The model
The formation and evolution of a galaxy is influenced by the
cosmological initial conditions and the environment, but also by
internal feedback processes. Heating by supernovae (SNe),
dissipation, radiative cooling, as well as in- and outflows
influence the evolution both locally and globally. Our new
three-dimensional galactic model takes into account the dynamics
of stars and the different phases of the ISM, as well as the
processes ("chemistry'') which connect the ISM and the stars.
These baryonic components are embedded in a collision-free dark
matter halo taken from simulations of cosmological structure
formation. The description of the ISM is based on that used in the
two-dimensional chemo-dynamical models of Samland & Hensler (1996);
Samland et al. (1997). The following subsections contain a brief outline of
our model.
3.1 The dark halo
Cosmological simulations (e.g. Navarro et al. 1995; Moore et al. 1999;
Pearce et al. 1999) show that in a hierarchical universe galaxies form out
of a few large fragments with an additional slow accretion of
mass. Thus each galaxy has its own formation history and
characteristic shape, depending on the masses, angular momenta and
merging histories of the fragments. Yet the formation of the CDM
halos can be described by some simple "universal'' formulae.
Wechsler et al. (2002) and van den Bosch (2002) calculated the
mass accretion history, Bullock et al. (2001) the angular momentum
distribution, Navarro et al. (1997) and others the density profiles
and Del Popolo (2001) and Wechsler et al. (2002) the evolution of
the concentration parameter.
In the hierarchical formation scenario, a dark halo may form early
and rapidly or grow slowly with time. For the model described in
this paper we take an average halo formation history, because at
present we cannot simulate the evolution of a galaxy for a large
number of different halo formation histories. We choose a 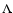 CDM
universe with
CDM
universe with
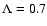 ,
,
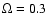 ,
a Hubble constant
h0 = 0.7 and a baryonic-to-dark matter ratio of 1:5. From the
cosmological N-body simulations of the VIRGO-GIF-project
(Kauffmann et al. 1999), we extracted the merging trees of 96 halos,
all with a final mass of
,
a Hubble constant
h0 = 0.7 and a baryonic-to-dark matter ratio of 1:5. From the
cosmological N-body simulations of the VIRGO-GIF-project
(Kauffmann et al. 1999), we extracted the merging trees of 96 halos,
all with a final mass of
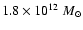 .
Figure
1 shows the average halo mass growth, which is in
agreement with the universal mass accretion histories found by
van den Bosch (2002) and Wechsler et al. (2002). The individual
merging histories can be quite different; two extreme cases with
early and late mass growth are shown in the small panels at the
top left and right of Fig. 1.
.
Figure
1 shows the average halo mass growth, which is in
agreement with the universal mass accretion histories found by
van den Bosch (2002) and Wechsler et al. (2002). The individual
merging histories can be quite different; two extreme cases with
early and late mass growth are shown in the small panels at the
top left and right of Fig. 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f1.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg29.gif) |
Figure 1:
The dots shows the average mass from 96 different halo
merging trees, which all result in a
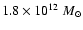 halo. The smooth line shows the
approximation which is used in our numerical model. The
most extreme halo merging trees and that which shows
the smallest deviations from the average are shown in
the smaller upper panels. Data from the
VIRGO-GIF-project (Kauffmann et al. 1999).
halo. The smooth line shows the
approximation which is used in our numerical model. The
most extreme halo merging trees and that which shows
the smallest deviations from the average are shown in
the smaller upper panels. Data from the
VIRGO-GIF-project (Kauffmann et al. 1999). |
| Open with DEXTER |
We assume that the growing dark halo has the universal density
profile as proposed by Navarro et al. (1997), and that its mass is
accreted in spherical shells. Given the current halo mass and the
evolution of the critical density, we can determine the outer halo
radius r200 (see Mo et al. 1998). A free parameter that
remains is the mass concentration c, which in the present
simulation is assumed to be c = 9.2. At redshift z = 0, this
leads to a circular velocity of
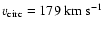 at
the
at
the
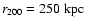 radius. Inside a galactocentric radius of
radius. Inside a galactocentric radius of
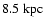 ,
the final mass of dark matter is
,
the final mass of dark matter is
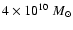 ,
comparable to the upper limit of the dark matter content
inside the solar circle (
,
comparable to the upper limit of the dark matter content
inside the solar circle (
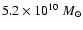 ;
Navarro & Steinmetz 2000a).
;
Navarro & Steinmetz 2000a).
Treating the growing dark matter halo as a spherical background
potential that does not respond to the baryonic component
minimizes gravitational torques during the collapse and thereby
circumvents the well-known angular momentum problem
(Navarro & Steinmetz 2000b). The accretion in this model is smoother as
compared to hierarchical models, where a fraction of the mass
accretion takes place through merging dark matter fragments,
unless the gas in these hierarchical fragments is dispersed by
early star formation and feedback.
During the hierarchical clustering, tidal torques induce shear
flows which lead to rotating proto-galactic systems. N-body
simulations show that, independent of the initial perturbation
spectrum and the cosmological model, the spin parameter of the
dark halos is in the range
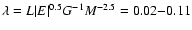 with an average value of
with an average value of
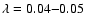 (Barnes & Efstathiou 1987; Steinmetz & Bartelmann 1995; Cole & Lacey 1996; van den Bosch 1998;
Gardner 2001).
(Barnes & Efstathiou 1987; Steinmetz & Bartelmann 1995; Cole & Lacey 1996; van den Bosch 1998;
Gardner 2001).
Bullock et al. (2001) studied the angular momentum profiles of dark
halos in a 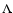 CDM cosmology. They found that the spatial
distribution of the angular momentum in most of the halos show a
certain degree of cylindrical symmetry, but that a spherically
symmetric angular momentum distribution with a power-law
CDM cosmology. They found that the spatial
distribution of the angular momentum in most of the halos show a
certain degree of cylindrical symmetry, but that a spherically
symmetric angular momentum distribution with a power-law
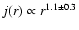 is also a good approximation. We consider
the following two rotation fields for the halo:
is also a good approximation. We consider
the following two rotation fields for the halo:
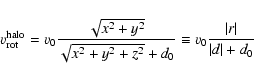 |
(1) |
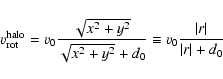 |
(2) |
v0 and d0 are constants which determine the total amount of
angular momentum and the rotation curve near the rotation axis,
respectively.
Assuming that initially the mass and velocity distributions of the
baryonic matter coincide with those of the dark matter, and that
baryonic mass and specific angular momentum is conserved during
the collapse to a disk (Mestel 1963; Fall & Efstathiou 1980), we can estimate
the disk surface density profiles corresponding to these rotation
fields. Figure 2 shows the results, calculated for
collapse in the pure NFW potential. As already pointed out by
Fall & Efstathiou (1980), disks with exponential surface density profiles
are found when the halo has a rising rotation curve at small radii
and a nearly constant rotation velocity in the outer parts. In the
present case, the cylindrical halo rotation model
(Eq. (2)) also produces an exponential disk, at least
in the inner
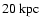 .
The spherical rotation model
(Eq. (1)) instead leads to higher surface densities
near the galactic centre which favours the formation of a
bulge. In the following we use the spherical rotation model with a
spin parameter
.
The spherical rotation model
(Eq. (1)) instead leads to higher surface densities
near the galactic centre which favours the formation of a
bulge. In the following we use the spherical rotation model with a
spin parameter
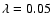 ,
to fix the initial angular
momentum distribution of the baryonic matter.
,
to fix the initial angular
momentum distribution of the baryonic matter.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f2.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg42.gif) |
Figure 2:
Surface density of the galactic disk if the specific
angular momentum is conserved during the proto-galactic
collapse in our NFW halo model. The cylindrical
rotation leads to an exponential disk in the inner
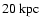 (dashed curve), while the spherical rotation
produces an exponential disk with an additional mass at
the centre (full line). The thin dash-dotted line shows
an exponential disk with a scale length of
(dashed curve), while the spherical rotation
produces an exponential disk with an additional mass at
the centre (full line). The thin dash-dotted line shows
an exponential disk with a scale length of
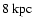 . . |
| Open with DEXTER |
The stellar motions have a considerable influence on the galactic
evolution, since the time-delayed stellar mass loss and energy
release connect different regions and also different galactic
evolution phases. The approximately 1011 stars in a large
galaxy form a collision-less system. Each star moves on its own
orbit, which is determined by the conditions under which the star
formed and the evolution of the galactic gravitational
potential. We use a particle-mesh method (Hockney & Eastwood 1988), in
which the passing of the stellar particles to the mesh and also
the interpolation of the gravitational forces at the particle
positions is done with a cloud-in-cell method. This method is fast
and second order accurate, but it is limited by the spatial
resolution of the underlying grid, which at present is
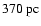 .
.
Each stellar particle represents an ensemble of stars with a
stellar mass function. In the present model, we assume a Salpeter
initial mass function (IMF) with lower and upper mass limits of
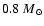 and
and
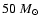 ,
and with an additional lock-up mass
fraction of 60%. The lock-up mass equals the mass of all stars
below
,
and with an additional lock-up mass
fraction of 60%. The lock-up mass equals the mass of all stars
below
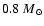 .
During a simulation the star formation rate is
calculated on the spatial grid, and in timesteps of
.
During a simulation the star formation rate is
calculated on the spatial grid, and in timesteps of
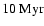 representative samples of 500 new stellar particles are
created. This yields 614 500 particles at the end of the
simulation. Depending on the star formation rate a single particle
represents 104 to 107 stars. The initial chemical
composition and velocity of a stellar particle is derived from the
chemical composition, velocity and velocity dispersion of the
parent molecular cloud medium.
representative samples of 500 new stellar particles are
created. This yields 614 500 particles at the end of the
simulation. Depending on the star formation rate a single particle
represents 104 to 107 stars. The initial chemical
composition and velocity of a stellar particle is derived from the
chemical composition, velocity and velocity dispersion of the
parent molecular cloud medium.
We assume that the evolution of the stars is determined only by
their initial mass and metallicity, neglecting effects of stellar
rotation or star-star interactions. From the stellar evolution
models of Maeder & Meynet (1989); Schaller et al. (1992) and Schaerer et al. (1993) we
get the lifetimes, energy releases and mass losses on the main
sequence. We can subdivide stars into three main classes.
First, the low mass stars which stay on the main sequence during
the whole galactic evolution. These stars become noticeable only
by their gravitational forces and because they lock-up a major
fraction of the galactic mass. The total lock-up mass has
influence on the galactic gas content and therefore on the
sequence of stellar generations. It is important in smaller
galaxies where SN-driven winds reduce the mass in gas, but not the
mass locked up in low mass stars.
The second class of stars are intermediate in mass. When they
leave the main sequence, they loose a substantial fraction of the
initial mass (asymptotic giant branch and planetary nebula phase);
however, the energy release of these stars is small compared to
other energy sources.
The third class of stars are the massive stars, typically with
masses in excess of 8-
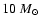 .
These stars are a major source
of both energy and mass return in a galaxy. The UV-radiation and
the kinetic energy release during the final explosion (SN type II)
ionize and accelerate the ISM. This can trigger large-scale gas
flows and star formation which both influence the galactic
evolution.
.
These stars are a major source
of both energy and mass return in a galaxy. The UV-radiation and
the kinetic energy release during the final explosion (SN type II)
ionize and accelerate the ISM. This can trigger large-scale gas
flows and star formation which both influence the galactic
evolution.
A rare but important galactic event is the explosion of SNe of
type Ia. The most probable progenitor candidates are close binary
stars consisting of a white dwarf and a main sequence star. We
include this process, since it is a major source of iron peak
elements (Nomoto et al. 1984).
3.3 The Interstellar Medium
The ISM in galaxies exists at different densities and
temperatures, and it shows phase transitions on short timescales
compared to the age of a galaxy. In the present galactic model we
use a simplified ISM description based on the three-phase model of
McKee & Ostriker (1977). The three phases are a cold, a warm and a hot
phase, with typical temperatures of
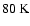 ,
,
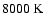 and
and
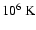 ,
respectively. The cold phase is found in the
dense cores of molecular clouds. These cores are embedded in warm
neutral or ionized gas envelopes. Outside the clouds the space is
filled with hot, dilute gas. The three-phase model is a
simplification, but it is realistic enough to use it in a global
galactic model. A critical discussion of the weak and strong
points of the three-phase model can be found in McKee (1990).
,
respectively. The cold phase is found in the
dense cores of molecular clouds. These cores are embedded in warm
neutral or ionized gas envelopes. Outside the clouds the space is
filled with hot, dilute gas. The three-phase model is a
simplification, but it is realistic enough to use it in a global
galactic model. A critical discussion of the weak and strong
points of the three-phase model can be found in McKee (1990).
Essentially, the temperatures and densities of the ISM phases
determine most of the physical processes in the ISM. However, the
geometry of the clouds is also important for processes that take
place in the phase transition regions (e.g. evaporation and
condensation) or that depend on the sizes of the clouds explicitly
(e.g. cloud-cloud collisions and star formation). In our model, we
assume spherical clouds which follow the mass-radius relation of
Elmegreen (1989)
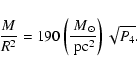 |
(3) |
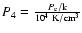 is the pressure in the ambient ISM. The mean cloud
mass is
is the pressure in the ambient ISM. The mean cloud
mass is
 ;
this is derived from the cloud mass spectrum
of Dame et al. (1986) for star forming giant molecular clouds in the
mass range of
;
this is derived from the cloud mass spectrum
of Dame et al. (1986) for star forming giant molecular clouds in the
mass range of
 to
to
 .
.
In the present dynamical description, we use only a two-phase
model for the ISM, containing hot gas with embedded (cold+warm)
clouds. The motions of both components are described by the
time-dependent hydrodynamical equations (mass, momentum and energy
conservation). Similar as in the two-dimensional chemo-dynamical
models (Samland et al. 1997) we use a fractional step method to split
the problem into source, sink and transport steps. The problem of
the three-dimensional transport is broken down into a number of
one-dimensional problems for the densities, metallicities, momenta
and energies (dimensional splitting). Using the van Leer advection
scheme (van Leer 1977) combined with the consistent advection
method (Norman et al. 1980) and the Strang splitting
(Strang 1968), the advection is second order accurate. In the
Strang splitting the three-dimensional transport is split into a
sequence of five one-dimensional transport steps:
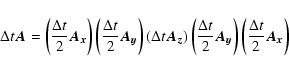 |
(4) |
where 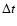 is the time step length,
is the time step length, 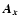 ,
,
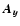 ,
,
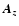 are the differential operators which
describe the transport in x, y, z direction, and
are the differential operators which
describe the transport in x, y, z direction, and 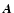 is the operator for the three-dimensional problem. Approximately
the same accuracy can be achieved by a simpler splitting scheme
which uses an alternating sequence of only three one-dimensional
transport steps:
is the operator for the three-dimensional problem. Approximately
the same accuracy can be achieved by a simpler splitting scheme
which uses an alternating sequence of only three one-dimensional
transport steps:
![$\displaystyle (\Delta t \vec{A})(\Delta t \vec{A}) = \left[ (\Delta t
\vec{A_x})(\Delta t \vec{A_y})(\Delta t \vec{A_z}) \right]$](/articles/aa/full/2003/09/aa2866/img62.gif) |
|
|
|
![$\displaystyle \left[ (\Delta t \vec{A_z})(\Delta t
\vec{A_y})(\Delta t \vec{A_x}) \right].$](/articles/aa/full/2003/09/aa2866/img63.gif) |
|
|
(5) |
For the 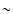 106 transport steps in our galactic evolution
simulations, both splitting schemes lead to identical
results. However, the second method is faster by a factor of 1.6.
106 transport steps in our galactic evolution
simulations, both splitting schemes lead to identical
results. However, the second method is faster by a factor of 1.6.
The interactions between stars and ISM are very important for the
galactic evolution. They determine the evolution timescale of a
galaxy to a large extent. In the following subsections we give a
short overview about the processes which we take into account, and
discuss the influence of the free parameters in the
parametrization of these processes.
Star formation is obviously one of the most important processes
during the galactic evolution, but it is one of the least
understood. Early on, Schmidt (1959) found that the star
formation rate in the solar neighbourhood varies with the square
of the surface gas density
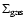 of the ISM. More
recently, Kennicutt (1998) found a star formation rate for
disk and starburst galaxies which is proportional to
of the ISM. More
recently, Kennicutt (1998) found a star formation rate for
disk and starburst galaxies which is proportional to
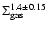 ,
with a sharp decline below a
critical surface density threshold (
,
with a sharp decline below a
critical surface density threshold (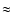 3-
3-
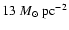 ). Remarkably, this simple law describes star formation
in galaxies for which the average gas consumption time can vary
from
). Remarkably, this simple law describes star formation
in galaxies for which the average gas consumption time can vary
from
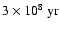 (starbursts) to
(starbursts) to
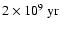 (normal
disks).
(normal
disks).
Motivated by these findings we use the following star formation
law:
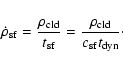 |
(6) |
Here
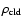 is the average density of the cloudy medium,
is the average density of the cloudy medium,
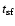 the star formation timescale, and
the star formation timescale, and
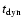 the dynamical timescale
for the average star forming cloud mass. For the cloud model
described in Sect. 3.3 the dynamical timescale of the
average star forming cloud is
the dynamical timescale
for the average star forming cloud mass. For the cloud model
described in Sect. 3.3 the dynamical timescale of the
average star forming cloud is
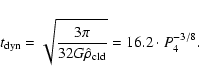 |
(7) |
Molecular clouds do not collapse and form stars on a single
dynamical timescale, because magnetic fields or turbulent motions
stabilize the clouds. To account for these processes, we include
the factor
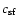 .
If we take into account that a part of the
clouds is only confined by pressure and that the timescales for
ambipolar diffusion and dissipation of turbulent energy are much
longer than the dynamical timescale, we expect
.
If we take into account that a part of the
clouds is only confined by pressure and that the timescales for
ambipolar diffusion and dissipation of turbulent energy are much
longer than the dynamical timescale, we expect
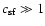 .
.
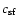 can be estimated from the observed number of OB stars in
the solar neighbourhood (Reed 2001). Assuming that the stellar
mass function follows a Salpeter law with lower and upper mass
limits of
can be estimated from the observed number of OB stars in
the solar neighbourhood (Reed 2001). Assuming that the stellar
mass function follows a Salpeter law with lower and upper mass
limits of
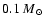 and
and
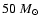 ,
we derive a local star
formation rate of
,
we derive a local star
formation rate of
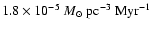 .
From the local
ISM density and pressure (
.
From the local
ISM density and pressure (
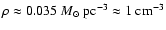 ,
,
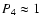 ), we find
), we find
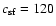 ,
which means that
the on average the star formation timescale exceeds the dynamical
timescale by factor of 120. The final star formation law can then
be written as
,
which means that
the on average the star formation timescale exceeds the dynamical
timescale by factor of 120. The final star formation law can then
be written as
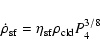 |
(8) |
with a star formation (gas depletion) timescale
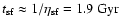 in the local Galactic disk. The star formation
rate is proportional to
in the local Galactic disk. The star formation
rate is proportional to
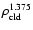 if the cloudy medium is
in pressure equilibrium (
if the cloudy medium is
in pressure equilibrium (
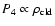 ). This is the
quiescent star formation mode in the model. During the collapse or
if large fragments merge, the pressure can increase and the star
formation can be more efficient.
). This is the
quiescent star formation mode in the model. During the collapse or
if large fragments merge, the pressure can increase and the star
formation can be more efficient.
Figure 3 shows the resulting star formation rate as a
function of the surface density of gas, in the forming disk galaxy
model described in Sect. 4. Both the average star
formation rates and the star formation rates in the strongest star
formation regions are slightly higher than, but consistent with
Kennicutt's 1998 data and mean
relation, over a range of surface densities extending from normal
disk galaxies into the starburst galaxy region. Had we calibrated
the factor
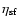 on Kennicutt's diagram, the resulting value
would have been about a factor of 2 smaller than that based on the
solar neighbourhood OB stars. The typical scatter in Kennicutt's
plot corresponds to a factor of 2.2 dispersion in
on Kennicutt's diagram, the resulting value
would have been about a factor of 2 smaller than that based on the
solar neighbourhood OB stars. The typical scatter in Kennicutt's
plot corresponds to a factor of 2.2 dispersion in
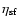 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f3.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg87.gif) |
Figure 3:
Star formation rate in the forming disk galaxy model
described in Sect. 4, versus the
projected surface density of the cloudy medium in a
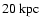 sphere. Open numbered circles are for average
star formation rates and surface densities within
sphere. Open numbered circles are for average
star formation rates and surface densities within
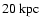 ;
the number denotes the galactic age in Gyr. The
filled numbered circles are for the most prominent star
formation region at the same galactic ages. The black
dots and black squares denote the data from
Kennicutt (1998) for disk galaxies and starburst
galaxies. The dashed line is Kennicutt's mean
relation. ;
the number denotes the galactic age in Gyr. The
filled numbered circles are for the most prominent star
formation region at the same galactic ages. The black
dots and black squares denote the data from
Kennicutt (1998) for disk galaxies and starburst
galaxies. The dashed line is Kennicutt's mean
relation. |
| Open with DEXTER |
Massive stars and SNe influence the galactic evolution in several
ways. They heat the ISM, produce shells and filaments and stir up
the cloudy medium. In addition, they are the most important source
of heavy elements and they determine the chemical evolution of a
galaxy. The lifetimes of the massive stars range from 3 to
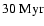 before they finally explode as SNe II. Only a stellar
remnant of
before they finally explode as SNe II. Only a stellar
remnant of 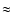
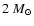 remains. The rest of the mass is
blown away by stellar winds or expelled during the explosion. On
average a massive star on the main sequence emits about
remains. The rest of the mass is
blown away by stellar winds or expelled during the explosion. On
average a massive star on the main sequence emits about
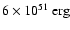 in photons (Schaerer & Vacca 1998) which ionize the
surrounding ISM and regulate the star formation. During the SN
explosion the star releases another
in photons (Schaerer & Vacca 1998) which ionize the
surrounding ISM and regulate the star formation. During the SN
explosion the star releases another
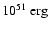 ,
creating a
fast expanding bubble. This influences the star formation process,
since it decreases the gas density in the surroundings of the SN
and it can trigger star formation in other regions.
,
creating a
fast expanding bubble. This influences the star formation process,
since it decreases the gas density in the surroundings of the SN
and it can trigger star formation in other regions.
In the model we can use only a simple description of these
processes.
(i) We assume that the mass return of a massive star takes place
instantaneously at the end of its evolution, when the SNe
explodes. This is a good approximation, because the time between
the stellar mass loss by a wind and the ejection of the SN shell
is short compared to galactic timescales.
(ii) We assume that the UV photons emitted by the massive stars
are absorbed and reradiated by the dense cloud medium. Since the
cooling time of this gas is short compared to the lifetime of the
massive stars (the typical timescale which we resolve in our
models), we do not simulate this heating and cooling process, but
assume that the clouds are in thermal equilibrium.
(iii) The SN explosion energy (
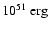 )
is released in a
short time and produces a bubble of hot gas and an expanding
shell. The shell interacts with the clouds and by this increases
the velocity dispersion
)
is released in a
short time and produces a bubble of hot gas and an expanding
shell. The shell interacts with the clouds and by this increases
the velocity dispersion
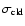 of the cloudy medium. The SN
energy is released locally, and we assume that
of the cloudy medium. The SN
energy is released locally, and we assume that
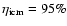 of
the SN energy heats the intercloud gas, and that the remaining
of
the SN energy heats the intercloud gas, and that the remaining
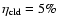 goes into the velocity dispersion of the cloudy
medium (McKee & Ostriker 1977). Thus
goes into the velocity dispersion of the cloudy
medium (McKee & Ostriker 1977). Thus
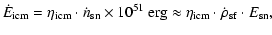 |
|
|
(9) |
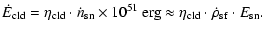 |
|
|
(10) |
In the second half of these equations we have related the heating
rates to the star formation rate; here
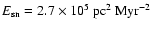 is the specific SN energy (per mass of stars formed for
one supernova II to occur). The parameters
is the specific SN energy (per mass of stars formed for
one supernova II to occur). The parameters
 ,
,
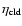 and
and
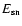 are not free, but are fixed in a narrow range by
observations and supernova models.
are not free, but are fixed in a narrow range by
observations and supernova models.
(iv) SNe are the most important sources of heavy elements. The
lack of self-consistent explosion models of massive stars causes
uncertainties in chemical yields by factors of two and more.
However, the detailed chemical composition is not important for
the galactic evolution. We therefore use a fiducial chemical
element which traces the fraction of heavy elements produced in
the hydrostatic burning phases and during the SN explosion of
massive stars. With the yield tables of Woosley & Weaver (1995) and
Thielemann et al. (1996), or the yield approximations of
Samland (1998) we can convert the abundances of the fiducial
SN II element into real chemical abundances. This method has the
advantage that it is not necessary redo the dynamical simulation
when new yield tables become available.
The progenitors of type Ia SN are believed to be close binary
stars consisting of an intermediate mass star and a white
dwarf. In the present model only a small fraction of the
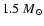 -
-
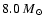 stars explode as SNe Ia. This fraction is
determined by the number ratio of SNe type Ia to type II. We take
a ratio of 1:8.5 (Samland 1998) which is consistent with the
observed SN rates in galaxies (Tammann et al. 1994) and can explain
the observed iron abundances and the Galactic evolution of the
[
stars explode as SNe Ia. This fraction is
determined by the number ratio of SNe type Ia to type II. We take
a ratio of 1:8.5 (Samland 1998) which is consistent with the
observed SN rates in galaxies (Tammann et al. 1994) and can explain
the observed iron abundances and the Galactic evolution of the
[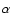 /Fe] ratio. In our model both the energy released by a SN Ia (
/Fe] ratio. In our model both the energy released by a SN Ia (
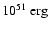 )
and the mass of the white dwarf progenitor
(
)
and the mass of the white dwarf progenitor
(
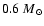 )
are given to the hot ISM. Because the mass return of
SN Ia is small compared to other stars and the total energy
released is an order of magnitude smaller than that from SNe type II, the SNe Ia do not influence the dynamical evolution
significantly. However, SNe type Ia are important for the chemical
evolution, because they are a main source of iron-peak, r- and
s-process elements. In the same way as for the SN II, we include a
fiducial chemical element to trace the enrichment with SN Ia
nucleosynthesis products. For the conversion into real abundances
we use the chemical yield table of Nomoto et al. (1984).
)
are given to the hot ISM. Because the mass return of
SN Ia is small compared to other stars and the total energy
released is an order of magnitude smaller than that from SNe type II, the SNe Ia do not influence the dynamical evolution
significantly. However, SNe type Ia are important for the chemical
evolution, because they are a main source of iron-peak, r- and
s-process elements. In the same way as for the SN II, we include a
fiducial chemical element to trace the enrichment with SN Ia
nucleosynthesis products. For the conversion into real abundances
we use the chemical yield table of Nomoto et al. (1984).
Intermediate mass stars act as a mass storage for the ISM. The
mass loss of these stars is significant only at the end of the
stellar evolution, when these stars enter the AGB and planetary
nebulae phase. Intermediate mass stars end as white dwarfs with
masses between
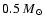 and
and
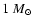 .
Unlike the massive
stars, the intermediate mass stars eject only weakly enriched gas
(van den Hoek & Groenewegen 1997) and, in total, they return twice as much
mass to the ISM as the massive stars, however with a much lower
energy and a significant time delay. In the model we neglect the
radiation of the intermediate mass stars, because they do not heat
the ISM efficiently, but include the mass return and the
enrichment in terms of a third fiducial element.
.
Unlike the massive
stars, the intermediate mass stars eject only weakly enriched gas
(van den Hoek & Groenewegen 1997) and, in total, they return twice as much
mass to the ISM as the massive stars, however with a much lower
energy and a significant time delay. In the model we neglect the
radiation of the intermediate mass stars, because they do not heat
the ISM efficiently, but include the mass return and the
enrichment in terms of a third fiducial element.
The heating of the ISM by SNe is mainly balanced by radiative
energy losses. This cooling process determines the temperature and
pressure of the hot ISM and by this has influence on the dynamics
of the ISM. We use the metallicity and temperature dependent
cooling functions
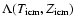 of Dalgarno & McCray (1972) and
Sutherland & Dopita (1993). These cooling functions provide lower
limits to the real energy loss, because they are calculated for a
homogeneous gas in thermal equilibrium. In a real ISM with density
fluctuations, the cooling rate can be enhanced by a factor
of Dalgarno & McCray (1972) and
Sutherland & Dopita (1993). These cooling functions provide lower
limits to the real energy loss, because they are calculated for a
homogeneous gas in thermal equilibrium. In a real ISM with density
fluctuations, the cooling rate can be enhanced by a factor
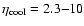 (McKee & Ostriker 1977), so that
(McKee & Ostriker 1977), so that
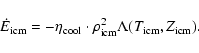 |
(11) |
We use an enhancement factor of
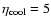 to describe the
radiative energy loss in the simulations. The radiative energy
loss
to describe the
radiative energy loss in the simulations. The radiative energy
loss
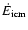 scales with the square of the gas density
scales with the square of the gas density
 because the ions are excited by collisions.
because the ions are excited by collisions.
3.4.6 Dissipation in the cloudy medium
The cloudy medium is described as a hydrodynamic fluid
characterized by its density, momentum, and kinetic energy. The
individual clouds are assumed to be at a thermal equilibrium
temperature. The kinetic energy density of the cloudy medium has
source and sink terms from the heating by SNe and dissipation by
cloud-cloud collisions. The description of the cloud-cloud
collisions is based on the inelastic cloud collision model of
Larson (1969). There, the energy loss of the cloudy medium
depends on the effective cross section
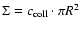 ,
which differs from the geometrical cross section by the
factor
,
which differs from the geometrical cross section by the
factor
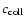 .
For a medium with density
.
For a medium with density
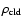 and velocity
dispersion
and velocity
dispersion
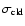 consisting of clouds of mass M and radius
R, the kinetic energy density then changes according to
consisting of clouds of mass M and radius
R, the kinetic energy density then changes according to
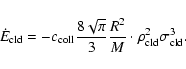 |
(12) |
With the cloud mass-radius relation of Elmegreen (1989) we
obtain
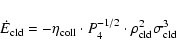 |
(13) |
with
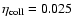 for
for
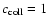 (geometrical cross
section). Unfortunately,
(geometrical cross
section). Unfortunately,
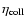 is not well constrained,
because magnetic fields, gravitational focusing, and self-gravity
can influence the effective cloud cross section significantly.
is not well constrained,
because magnetic fields, gravitational focusing, and self-gravity
can influence the effective cloud cross section significantly.
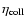 is the most uncertain parameter in our ISM description.
is the most uncertain parameter in our ISM description.
The different phases of the ISM exchange mass by evaporation as
well as condensation and cloud formation processes. These
processes depend mainly on the sizes of the cold clouds and the
density and temperature of the hot ambient gas. As in the
two-dimensional models (Samland et al. 1997), we use the model of
McKee & Begelman (1990) and Begelman & McKee (1990) for the description of
the evaporation,
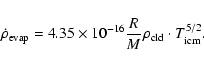 |
(14) |
For
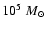 clouds in the simple spherical cloud model of
Sect. 3.3 we obtain an evaporation rate of
clouds in the simple spherical cloud model of
Sect. 3.3 we obtain an evaporation rate of
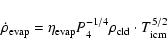 |
(15) |
with
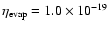 .
The value of
.
The value of
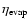 depends on the cloud model (cloud shapes, mass spectrum).
depends on the cloud model (cloud shapes, mass spectrum).
In small clouds, heat transfer by conduction is more efficient
than cooling by radiation (McKee & Begelman 1990). In large clouds (cloud
radius exceeds the Field-length) the cooling dominates and the
clouds can gain mass by condensation. The timescale for
condensation is of the order of the cooling time of the ambient
hot medium (McKee & Begelman 1990). In addition, clouds can form when the
hot gas becomes thermally unstable. This cloud formation process
is important in high density regions (e.g., shocks) or in regions
with no or low star formation activity. Since it is a cooling
instability, this process also has a timescale which is
approximately the cooling time. We use the following
parameterization for the condensation and cloud formation process:
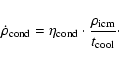 |
(16) |
It turns out that effectively
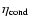 is not a free
parameter. Reasonable values for
is not a free
parameter. Reasonable values for
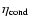 are in the range of 1.0 (cloud formation time = cooling time) to 0.3. Tests showed
that if
are in the range of 1.0 (cloud formation time = cooling time) to 0.3. Tests showed
that if
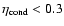 ,
the hot gas can cool to temperatures of
less than
,
the hot gas can cool to temperatures of
less than
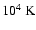 before condensation and cloud formation
are efficient. We use a value of
before condensation and cloud formation
are efficient. We use a value of
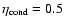 ,
which
guarantees a stable hot gas phase.
,
which
guarantees a stable hot gas phase.
The interaction network describes a self-regulated system in which
moderate changes of the parameters do not alter the results
significantly (see also Köppen et al. 1995). Star formation is
one example for such a self-regulation. An increase of the
efficiency
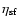 by a certain factor will not increase the star
formation rate by the same amount, because the ISM will be heated
by the stars, which in turn decreases the amount of available cold
gas to form stars. Another example is the phase transition between
hot and warm gas. A rise in the heating rate of the hot gas leads
to an enhanced evaporation of clouds. This increases the density
of the hot gas and enhances the cooling. The temperature of the
gas increases only by a small amount. If on the other hand the
heating rate decreases, condensation and cloud formation set
in. As a result, the hot gas density and therefore the cooling
efficiency drops and the gas temperature will stay nearly
constant.
by a certain factor will not increase the star
formation rate by the same amount, because the ISM will be heated
by the stars, which in turn decreases the amount of available cold
gas to form stars. Another example is the phase transition between
hot and warm gas. A rise in the heating rate of the hot gas leads
to an enhanced evaporation of clouds. This increases the density
of the hot gas and enhances the cooling. The temperature of the
gas increases only by a small amount. If on the other hand the
heating rate decreases, condensation and cloud formation set
in. As a result, the hot gas density and therefore the cooling
efficiency drops and the gas temperature will stay nearly
constant.
Some interactions are self-regulated by dynamical processes. For
example, a higher star formation efficiency delays the settling of
the clouds in the galactic disk, so that the average density of
the cloudy medium is lowered which in turn decreases the star
formation rate again. For the moment we neglect this (important)
dynamical self-regulation, discussing now only the influence of
the important model parameters on the velocity dispersion of the
clouds
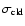 ,
the hot gas temperature
,
the hot gas temperature
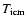 ,
and the mass
ratio between gas and clouds. We do this by calculating
equilibrium conditions first numerically and then in an analytical
approximation.
,
and the mass
ratio between gas and clouds. We do this by calculating
equilibrium conditions first numerically and then in an analytical
approximation.
The interaction network is a closed system of differential
equations, which can be solved numerically to find equilibrium
states for given densities of the ISM. The results are plotted in
Fig. 4. As expected for a self-regulated system, we
find that even density variations by five orders of magnitude have
only small effects, changing
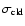 (
(
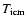 )
by factors of 3 (7).
)
by factors of 3 (7).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f4.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg126.gif) |
Figure 4:
The three panels show the density dependence of the
intercloud to cloud mass ratio, the cloud velocity
dispersion
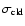 ,
and the hot gas temperature ,
and the hot gas temperature
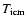 in a closed-box model where dynamical effects
are neglected. The dotted and dashed lines show the
[Fe/H] = 0 (solar metallicity) and the [Fe/H] = -4 cases and the full lines show the slopes given by the
analytical approximations of
Eqs. (17)-(19).
in a closed-box model where dynamical effects
are neglected. The dotted and dashed lines show the
[Fe/H] = 0 (solar metallicity) and the [Fe/H] = -4 cases and the full lines show the slopes given by the
analytical approximations of
Eqs. (17)-(19). |
| Open with DEXTER |
For the analytical approach, we assume that, most of the ISM mass
is in the cloudy medium and that the cloudy medium is in pressure
equilibrium with the surrounding gas. Balancing the heating by SNe
with the dissipation by cloud-cloud collisions and the cooling by
radiation, and assuming that evaporation rates are equal to
condensation rates, we get the following three relations:
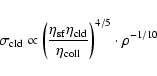 |
(17) |
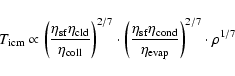 |
(18) |
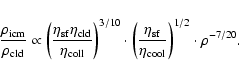 |
(19) |
Here 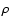 is the average density of the ISM (clouds and hot
gas). These equations confirm that there is only a weak dependence
of
is the average density of the ISM (clouds and hot
gas). These equations confirm that there is only a weak dependence
of
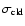 and
and
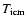 on the average ISM density. They are
shown in Fig. 4 for comparison with the numerical
results.
on the average ISM density. They are
shown in Fig. 4 for comparison with the numerical
results.
In the previous discussion, we neglected metallicity
effects. However, metallicity can be important because it
increases the cooling efficiency. The dashed lines in
Fig. 4 show the numerical equilibrium relations for an
extremely metal-poor gas ([Fe/H] = -4). The effects of low gas
metallicities are similar to a low cooling efficiency
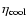 .
In both cases, the gas temperature
.
In both cases, the gas temperature
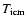 stays
nearly constant, because the lower cooling efficiency is balanced
by a higher gas density
stays
nearly constant, because the lower cooling efficiency is balanced
by a higher gas density
 .
The self-regulating character of
the interaction network again is obvious. The equilibrium system
is in a balance of forward and reverse reaction rates. Any stress
that alters one of these rates makes the system shift, so that the
two rates eventually equalize (Le Chatelier's principle).
.
The self-regulating character of
the interaction network again is obvious. The equilibrium system
is in a balance of forward and reverse reaction rates. Any stress
that alters one of these rates makes the system shift, so that the
two rates eventually equalize (Le Chatelier's principle).
In spite of the self-regulating character of the interaction
network it is necessary to solve the full interaction network
during a simulation, because processes on different timescales are
involved that compete with the dynamical evolution. For example,
heating processes or cloud dissipation may take longer than
dynamical changes. Equilibrium solutions of the interaction
network can be used only to study the general behaviour of a
star-gas system where dynamical processes are slow, but would not
be able to describe, e.g., the outflow of hot gas.
Most of the parameters in this multi-phase ISM description
(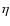 's) can be constrained either from theory or from
observations. The two most important parameters in the model are
the star formation efficiency
's) can be constrained either from theory or from
observations. The two most important parameters in the model are
the star formation efficiency
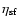 ,
and
,
and
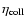 which
controls the dissipation rate. These parameters are of special
interest because they both influence the velocity dispersion of
the cloudy medium and thus the settling of the baryonic matter.
which
controls the dissipation rate. These parameters are of special
interest because they both influence the velocity dispersion of
the cloudy medium and thus the settling of the baryonic matter.
In Table 1 we list the parameters of the interaction
network together with their upper and lower limit values. These
are discussed in the subsections above. For
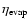 and
and
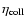 ,
where there is little constraint, we have used a large
range to illustrate that even in this case the resulting changes
to the equilibrium are not large. It is obvious from the
analytical model above that
,
where there is little constraint, we have used a large
range to illustrate that even in this case the resulting changes
to the equilibrium are not large. It is obvious from the
analytical model above that
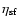 (
(
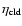 ,
,
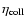 )
have
influence on
)
have
influence on
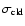 ,
,
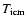 and
and
 ,
while
,
while
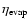 (
(
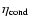 )
can change only
)
can change only
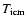 ,
and by varying
,
and by varying
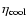 one can shift the gas-to-cloud mass ratio. Using the extreme
values for the parameters given in Table 1 we obtain
the uncertainties of
one can shift the gas-to-cloud mass ratio. Using the extreme
values for the parameters given in Table 1 we obtain
the uncertainties of
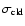 ,
,
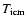 ,
and
,
and
 (Cols. 5-7 of Table 1). This shows that even large
changes of the parameter values lead only to moderate variations
in
(Cols. 5-7 of Table 1). This shows that even large
changes of the parameter values lead only to moderate variations
in
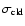 ,
,
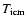 ,
and
,
and
 .
From these numbers we
conclude that
.
From these numbers we
conclude that
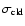 ,
,
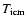 ,
and
,
and
 /
/
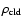 are
accurate to a factor of 2 in our model.
are
accurate to a factor of 2 in our model.
Gravitation is a long range force that couples the baryonic and
the dark matter and it is the main driver of the galactic
evolution. To determine the gravitational potential, we first map
all stars, the different phases of the ISM and the dark matter
onto one grid. Then, depending on the kind of grid (equidistant or
logarithmically spaced) we solve the Poisson equation with a FFT
(fast Fourier transformation) or a SOR (successive over-relaxation
with Chebeyshev acceleration) method. The gravitational forces are
calculated from the potential at every point.
The present simulations used a logarithmic 813 grid with a
spatial resolution of
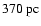 in the inner parts and
in the inner parts and
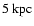 in
the outer halo. The timestep lengths, which in most cases are
limited by the interaction processes, are of the order of
104-
in
the outer halo. The timestep lengths, which in most cases are
limited by the interaction processes, are of the order of
104-
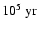 .
The simulations start at a redshift z = 4.85 corresponding to
.
The simulations start at a redshift z = 4.85 corresponding to
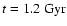 in a
in a 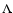 CDM cosmology. Initially
the dark halo has a mass of
CDM cosmology. Initially
the dark halo has a mass of
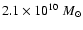 ,
distributed over a
,
distributed over a
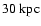 sphere. During the evolution, the
halo grows by accretion to a size of
sphere. During the evolution, the
halo grows by accretion to a size of
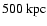 with an enclosed
mass of
with an enclosed
mass of
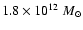 .
The baryonic-to-dark matter
ratio of the accreted mass is fixed at 1:5, which finally amounts
to
.
The baryonic-to-dark matter
ratio of the accreted mass is fixed at 1:5, which finally amounts
to
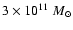 of baryonic matter inside the
r200 radius. The accretion rate, taken from cosmological
simulations (Kauffmann et al. 1999, see Sect. 3 and
Fig. 5) decreases from
of baryonic matter inside the
r200 radius. The accretion rate, taken from cosmological
simulations (Kauffmann et al. 1999, see Sect. 3 and
Fig. 5) decreases from
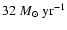 at z
= 4.85 (
at z
= 4.85 (
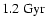 )
to
)
to
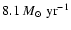 at z = 0 (
at z = 0 (
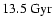 ). The baryonic matter outside the r200 radius consists
of ionized (T > 104 K) primordial gas at the virial
temperature. The cooling time of this gas is short compared to the
collapse time. On this time-scale clouds form which can then
dissipate kinetic energy and collapse inside the dark halo.
Thereafter the collapse is only delayed by stellar feedback
processes. We have confirmed that starting with a cloudy gas
medium leads to a very similar evolution. Initially, the accreted
baryonic matter, like the dark matter, is in spherical rotation
(Eq. (1)) with a spin parameter
). The baryonic matter outside the r200 radius consists
of ionized (T > 104 K) primordial gas at the virial
temperature. The cooling time of this gas is short compared to the
collapse time. On this time-scale clouds form which can then
dissipate kinetic energy and collapse inside the dark halo.
Thereafter the collapse is only delayed by stellar feedback
processes. We have confirmed that starting with a cloudy gas
medium leads to a very similar evolution. Initially, the accreted
baryonic matter, like the dark matter, is in spherical rotation
(Eq. (1)) with a spin parameter
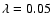 .
It
grows from inside-out and the mass with the highest specific
angular momentum is accreted at late times.
.
It
grows from inside-out and the mass with the highest specific
angular momentum is accreted at late times.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f5.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg149.gif) |
Figure 5:
Baryonic mass infall rate (MIR, full line) into inner
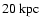 and across the r200 radius (dashed
line).
and across the r200 radius (dashed
line). |
| Open with DEXTER |
4 The formation history
The present simulation describes the formation and subsequent
evolution of a disk galaxy in a slowly growing dark halo. The halo
grows by accreting dark and baryonic matter in spherical shells
with an accretion rate that is derived from cosmological
simulations in a 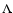 CDM universe (Kauffmann et al. 1999, see Sect. 3.1), with a baryonic mass fraction of 1/6. The dark and baryonic matter have initial
CDM universe (Kauffmann et al. 1999, see Sect. 3.1), with a baryonic mass fraction of 1/6. The dark and baryonic matter have initial
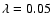 and specific angular momentum distribution similar to that from
Bullock et al. (2001). Star formation, feedback, and gas physics of
the baryonic component are described within a two-phase ISM model
(see Sect. 3.3). The dynamics of the gas and stars is
treated separately. The simulations start at z = 4.85 (
and specific angular momentum distribution similar to that from
Bullock et al. (2001). Star formation, feedback, and gas physics of
the baryonic component are described within a two-phase ISM model
(see Sect. 3.3). The dynamics of the gas and stars is
treated separately. The simulations start at z = 4.85 (
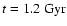 )
with a mixture of dark matter and gas, but no stars. At
redshift z = 4.85 the dark halo mass exceeds
)
with a mixture of dark matter and gas, but no stars. At
redshift z = 4.85 the dark halo mass exceeds
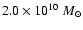 ,
which is twice the mass resolution of the cosmological
simulations on which our halo model is based.
,
which is twice the mass resolution of the cosmological
simulations on which our halo model is based.
The accreted primordial gas quickly reaches an equilibrium between
the cold and hot phases with most of the mass in the cold clouds.
It can then dissipate its kinetic energy and begins to collapse
inside the dark halo. The strong collapse takes place in a
redshift interval between z = 1.8 (
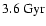 )
and z = 0.8 (
)
and z = 0.8 (
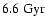 ). With a duration of
). With a duration of 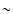
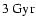 ,
its period
exceeds the free-fall time at the r200 radius by a factor of 3.4. This late and delayed collapse, which is in contradiction to
simple collapse scenarios, is caused by stellar feedback in
conjunction with the initially shallow gravitational potential of
the halo.
,
its period
exceeds the free-fall time at the r200 radius by a factor of 3.4. This late and delayed collapse, which is in contradiction to
simple collapse scenarios, is caused by stellar feedback in
conjunction with the initially shallow gravitational potential of
the halo.
The baryonic mass infall rate (MIR) across the r200 radius
and into the inner
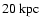 is shown in Fig. 5. At
early times the gas fallen through r200 has not yet reached
the inner
is shown in Fig. 5. At
early times the gas fallen through r200 has not yet reached
the inner
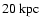 because of the delay from feedback. With the
growing mass of baryons the dissipation increases and the infall
into the centre accelerates, until the combination of feedback
from the growing star formation rate and decreasing infall rate
through r200 reverses this trend and the MIR into
because of the delay from feedback. With the
growing mass of baryons the dissipation increases and the infall
into the centre accelerates, until the combination of feedback
from the growing star formation rate and decreasing infall rate
through r200 reverses this trend and the MIR into
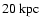 begins to decrease again at
begins to decrease again at
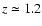 .
At late times (
.
At late times (
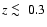 )
a significant fraction of the infalling gas has too much
angular momentum to arrive in the central
)
a significant fraction of the infalling gas has too much
angular momentum to arrive in the central
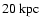 ,
so that the
rate of infall into
,
so that the
rate of infall into
 becomes lower than that through
r200. The mass of the galaxy increases rapidly and at z =
1.2 (
becomes lower than that through
r200. The mass of the galaxy increases rapidly and at z =
1.2 (
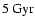 )
already
)
already
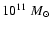 of baryonic matter has
been accreted. At z = 0, 2/3 of the total baryonic mass of
of baryonic matter has
been accreted. At z = 0, 2/3 of the total baryonic mass of
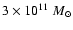 has collapsed into the inner
has collapsed into the inner
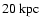 of
the dark matter halo and has formed the luminous galaxy, leading
to a dark-to-baryonic matter ratio of 3%, 10% and 30% inside
galactocentric radii of 1, 3, and
of
the dark matter halo and has formed the luminous galaxy, leading
to a dark-to-baryonic matter ratio of 3%, 10% and 30% inside
galactocentric radii of 1, 3, and
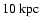 ,
respectively.
,
respectively.
The star formation rate integrated over the central
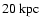 is
shown in Fig. 6. This increases steeply to a maximum
of
is
shown in Fig. 6. This increases steeply to a maximum
of 
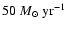 at z = 1 (
at z = 1 (
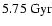 ). At that time,
the gas consumption by the star formation process is balanced to
80% by infall and to 20% by the stellar mass return. Afterwards
the infall rate decreases to
). At that time,
the gas consumption by the star formation process is balanced to
80% by infall and to 20% by the stellar mass return. Afterwards
the infall rate decreases to
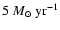 ,
at z = 0, while the
stellar mass return stays nearly constant at a rate of
,
at z = 0, while the
stellar mass return stays nearly constant at a rate of
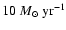 .
This explains the different shapes of the curves in
Figs. 5 and 6 at late times.
.
This explains the different shapes of the curves in
Figs. 5 and 6 at late times.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f6.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg163.gif) |
Figure 6:
Star formation rate (SFR) in the inner
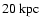 of the
dark halo. The star formation rate peaks slightly later
than the MIR (Fig. 5).
of the
dark halo. The star formation rate peaks slightly later
than the MIR (Fig. 5). |
| Open with DEXTER |
Figures 7, 8 show the spatial
distributions of the gas and stars as a function of redshift. In
general terms, star formation out of the dissipating cloud medium
proceeds from halo to disk and from inside out. Thus the earliest
stars at redshifts z > 2 form in the whole volume limited by the
r200 radius (halo formation), with a concentration to the
central bulge region. At a redshift of z = 1.3 (
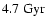 ), a
(thick) disk component first appears. Later the star formation is
concentrated to the equatorial plane, and at late times most of
the star formation occurs in the outer disk.
), a
(thick) disk component first appears. Later the star formation is
concentrated to the equatorial plane, and at late times most of
the star formation occurs in the outer disk.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS2866f7.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg166.gif) |
Figure 7:
Face-on surface density of the ionized gas, the cloudy
medium, the OB-associations and the stars at different
redshifts. Each column shows the evolution of one
component between redshift z = 2 and z = 0. Each
panel has a size of
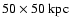 . . |
| Open with DEXTER |
Around z = 1.2 the infall of gas can no longer compensate the
gas consumption by star formation in the inner disk. This is
because the infalling molecular cloud medium now has higher
specific angular momentum, so that its infall timescale becomes
longer than the central star formation timescale. As a result, the
region of highest star formation density moves radially outwards
from the centre and a ring (Fig. 7, z = 1 panels)
forms. This ring grows to a radius of 
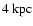 before, at
redshift z = 0.85 (
before, at
redshift z = 0.85 (
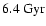 ), the disk becomes
unstable. Within
), the disk becomes
unstable. Within
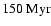 the ring then fragments, and for a
short time (
the ring then fragments, and for a
short time (
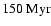 )
a very elongated bar is formed
with exponential major-axis scale-length of
)
a very elongated bar is formed
with exponential major-axis scale-length of
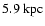 and axis
ratio of 12:2:1. Figure 9 shows that after this
transient period the bar length decreases, and a bar-bulge with
axial ratios
and axis
ratio of 12:2:1. Figure 9 shows that after this
transient period the bar length decreases, and a bar-bulge with
axial ratios  3:1.4:1 develops which includes the old bulge
component formed in the early collapse.
3:1.4:1 develops which includes the old bulge
component formed in the early collapse.
Already during this bar formation process the galaxy starts to
build up the outer disk. This disk is the youngest component in
the model galaxy, even though the oldest disk stars are as old as
the halo stars. The disk grows from inside-out, because the early
accreted mass has low specific angular momentum (see the last
columns of Figs. 7 and 8). In
parallel, the vertical scale-height in a fixed radial range
decreases; this is shown in Fig. 10 for the range
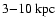 .
The more pronounced settling of the cloudy medium to the
equatorial plane at late times is due to (i) more efficient
cooling because of higher metallicity, (ii) higher gas density
and, thus, dissipation rate for gas near the angular momentum
barrier in a deeper potential well. The final disk thickness in
Fig. 10 of
.
The more pronounced settling of the cloudy medium to the
equatorial plane at late times is due to (i) more efficient
cooling because of higher metallicity, (ii) higher gas density
and, thus, dissipation rate for gas near the angular momentum
barrier in a deeper potential well. The final disk thickness in
Fig. 10 of 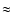
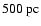 is set by the resolution
the present model.
is set by the resolution
the present model.
After the bar-bulge has formed, two trailing spiral arms appear in
the disk which are connected to the bar-bulge. At the beginning
the two spiral arms are symmetric and of the same size. However,
in the further evolution a persistent lopsidedness of the galaxy
develops. The resulting off-centre motion of the bulge-bar brings
one arm nearer to the bulge-bar, and the more distant spiral arm
becomes more prominent over a wider winding angle
(Fig. 7). The lopsidedness may be produced by the
dark halo which is here described as an external spherically
symmetric potential component, even though in the inner galaxy the
baryonic matter dominates the gravitational potential. The effect
that such perturbations can produce lopsided galaxies is well
known (Levine & Sparke 1998; Swaters et al. 1999).
We expect this evolutionary sequence to be more or less typical of
any dissipative collapse in a growing dark matter halo, unless it
is interrupted by substantial mergers. The following modelling
uncertainties may further modify the evolution as described above.
(i) The assumed dissipation parameter is uncertain. If in reality
dissipation is significantly more efficient than in the model, and
in addition stars form only above a certain density threshold
(Kennicutt 1998), the gas would fall into the disk much more
rapidly without significant star formation. In this case formation
of stars in the halo and thick disk may be substantially
suppressed. Also, in this case the velocity dispersion of the
cloudy medium in the disk would decrease. Then the gaseous disk
may fragment in local instabilities before a global disk
instability sets in, so that more material would dissipate to the
centre and contribute to the bulge. (ii) The precise angular
momentum distribution (as compared to the universal average
distribution assumed) will influence the detailed inside-out
formation of the disk. For example, the formation of a ring in the
present model would likely be suppressed by increasing the amount
of low angular momentum gas falling in at redshift
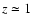 .
(iii) When small-scale initial fluctuations lead to the
formation of sub-galactic fragments that merge before the main
collapse, the mass of the bulge component would be substantially
greater, and its dynamical structure determined by the merging
process (Steinmetz & Navarro 2002).
.
(iii) When small-scale initial fluctuations lead to the
formation of sub-galactic fragments that merge before the main
collapse, the mass of the bulge component would be substantially
greater, and its dynamical structure determined by the merging
process (Steinmetz & Navarro 2002).
4.3 Global chemical evolution
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f9.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg175.gif) |
Figure 9:
Evolution of the bar-bulge axis ratios. z indicates the
vertical direction and x and y the major and minor axes
of the bar. The bar forms from a disk instability at
time
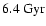 and settles to a triaxial bulge with
axis ratios
and settles to a triaxial bulge with
axis ratios 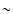 3:1.4:1 at late times. 3:1.4:1 at late times. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f10.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg176.gif) |
Figure 10:
Evolution of the vertical scale height of the stellar
disk between radial distances
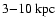 .
This part of
the disk forms later than the average of all stars
shown in Fig. 5. The scale heights in
small rings are shown as dots and the radial average is
drawn as a full line. The dashed line indicates the
spatial resolution limit of .
This part of
the disk forms later than the average of all stars
shown in Fig. 5. The scale heights in
small rings are shown as dots and the radial average is
drawn as a full line. The dashed line indicates the
spatial resolution limit of
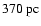 . . |
| Open with DEXTER |
The chemical evolution of the model proceeds in three
steps. First, there is the collapse phase, lasting until
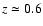 .
Then two quasi-equilibrium phases follow in which first (
z
= 0.6-0.3) the mass infall and later (
z = 0.3-0.0) the stellar
mass return determines the star formation rate (see
Figs. 5 and 6). These three phases are
clearly visible in the chemical enrichment history of the cloudy
medium. This is shown in Fig. 11, where we have plotted
the Zn/H metallicity normalized to the solar value because Zn is
believed to not be depleted onto dust grains. The Zn/H abundance
was reconstructed from the fiducial SN I and SN II elements as
described in Sect. 3.
.
Then two quasi-equilibrium phases follow in which first (
z
= 0.6-0.3) the mass infall and later (
z = 0.3-0.0) the stellar
mass return determines the star formation rate (see
Figs. 5 and 6). These three phases are
clearly visible in the chemical enrichment history of the cloudy
medium. This is shown in Fig. 11, where we have plotted
the Zn/H metallicity normalized to the solar value because Zn is
believed to not be depleted onto dust grains. The Zn/H abundance
was reconstructed from the fiducial SN I and SN II elements as
described in Sect. 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f11.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg178.gif) |
Figure 11:
Average Zn/ H abundance (linear
scale) of the ISM and the stars in the inner
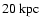 of the model galaxy.
of the model galaxy. |
| Open with DEXTER |
The initial collapse of the baryonic material produces a first
generation of stars which already at z = 2 has synthesized
enough metals to increase the average metallicity to 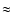 -1. During the late collapse phase the star formation rate
exceeds the MIR and the metallicity increases fast. Then in the
second phase, the star formation rate is proportional to the MIR
and the metallicity increases only slowly. In the final phase, the
star formation rate is again higher than the MIR and the
metallicity increases more rapidly (Fig. 11).
-1. During the late collapse phase the star formation rate
exceeds the MIR and the metallicity increases fast. Then in the
second phase, the star formation rate is proportional to the MIR
and the metallicity increases only slowly. In the final phase, the
star formation rate is again higher than the MIR and the
metallicity increases more rapidly (Fig. 11).
The chemical enrichment histories of the hot gas, cloudy medium,
and stars (shown separately in Fig. 11) are very
different from the predictions of multi-phase closed box models.
In these models the hot ionized gas always has the highest
metallicity, followed by the molecular cloud medium and the stars.
This is different in our model, because stars, clouds and gas have
different spatial distributions. Most of the ionized hot gas is
located in the halo, while the molecular clouds and stars are
preferentially found in the disk and bulge, where the gas
densities and metallicities are high. After a brief initial period
the average metallicity of the stars exceeds that of the cloudy
medium, because the stars form from gas that is more concentrated
to the equatorial plane and thus more metal-rich than the average
cold gas medium.
An interesting feature in Fig. 11 is the constant
[Zn/H
![$] \approx 0.4$](/articles/aa/full/2003/09/aa2866/img179.gif) of the hot gas from redshift z = 1 until
the present epoch. A large fraction of this gas occupies the
galactic halo, where the star formation rate is low. Two processes
keep the halo metallicity at a constant level: Gas flows from the
bulge and the disk transport heavy elements into the halo. There
it mixes with the existing ISM and with infalling low metallicity
gas. In this way the metallicity in the halo gas can remain
constant over a long time.
of the hot gas from redshift z = 1 until
the present epoch. A large fraction of this gas occupies the
galactic halo, where the star formation rate is low. Two processes
keep the halo metallicity at a constant level: Gas flows from the
bulge and the disk transport heavy elements into the halo. There
it mixes with the existing ISM and with infalling low metallicity
gas. In this way the metallicity in the halo gas can remain
constant over a long time.
A similar enrichment can be observed in the disk. During the
collapse the star formation and the metal production is
concentrated to the inner galaxy. From there, the metal-rich gas
expands into the disk. This disk pre-enrichment causes a lack of
metal-poor stars ("G-dwarf problem''![[*]](/icons/foot_motif.gif) , see Sect. 5), similar
to that observed in the Milky Way.
, see Sect. 5), similar
to that observed in the Milky Way.
We find a global age-metallicity relation and also a [O/Fe] to
[Fe/H] relation, which are consistent with Milky Way observations.
These relations are much more influenced by the choice of stellar
yields, resp. the star formation history, than by the details of
the galactic model, and have been found in previous galactic
models as well (e.g. Steinmetz & Müller 1994; Timmes et al. 1995;
Samland 1998). However, the pre-enrichment of the galactic disk,
explaining the so-called "G-dwarf problem'' and the sub-solar
abundances in the outer halo gas are a result of dynamical
processes and are therefore strongly influenced by the galactic
model. The same is true for relations connecting the kinematics
and chemical composition of stars; see Sect. 5.7.
In Fig. 12 we compare our results with the [Zn/H] data
for damped Ly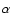 systems (Pettini et al. 1999; Prochaska et al. 2001),
using [Zn/H] because [Fe/H] may be depleted by dust. Damped
Ly
systems (Pettini et al. 1999; Prochaska et al. 2001),
using [Zn/H] because [Fe/H] may be depleted by dust. Damped
Ly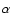 systems are an important test for galactic models. If
they are associated with forming disk galaxies, they can be used
to measure the metallicity of the ISM of young, gas rich galaxies
at high redshifts. The Ly
systems are an important test for galactic models. If
they are associated with forming disk galaxies, they can be used
to measure the metallicity of the ISM of young, gas rich galaxies
at high redshifts. The Ly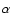 systems on average show only a
mild evolution in [Zn/H] for
systems on average show only a
mild evolution in [Zn/H] for
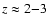 .
Even though we
consider only a single model with its specific evolutionary
history, the predicted metallicity range as a function of redshift
is consistent with the data. From the model we thus infer that the
time needed to increase the disk metallicity to the typical values
observed in Ly
.
Even though we
consider only a single model with its specific evolutionary
history, the predicted metallicity range as a function of redshift
is consistent with the data. From the model we thus infer that the
time needed to increase the disk metallicity to the typical values
observed in Ly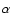 systems is
systems is 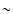
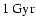 .
The shaded area
in Fig. 12 shows the range of metallicities from
different locations in the model at redshifts z > 1.6.
Figure 12 also shows the early [Zn/H] evolution of the
hot ionized gas (dashed line). This should be representative for
the average metallicity of metal-enriched clouds forming in the
low density halo ISM, and thus for absorption of background
quasars along halo lines-of-sight.
.
The shaded area
in Fig. 12 shows the range of metallicities from
different locations in the model at redshifts z > 1.6.
Figure 12 also shows the early [Zn/H] evolution of the
hot ionized gas (dashed line). This should be representative for
the average metallicity of metal-enriched clouds forming in the
low density halo ISM, and thus for absorption of background
quasars along halo lines-of-sight.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f12.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg182.gif) |
Figure 12:
Redshift evolution of the average zinc abundance [Zn/H]
of the cloudy medium (full line) inside a
galactocentric radius of
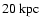 .
The shaded area
shows the range of [Zn/H] metallicities in the model
over this region. The points are data for damped
Ly .
The shaded area
shows the range of [Zn/H] metallicities in the model
over this region. The points are data for damped
Ly systems from Pettini et al. (1999) and
Prochaska et al. (2001), plotted as squares and rhombi,
respectively. The general trend of the model curve is
consistent with the observed damped Ly
systems from Pettini et al. (1999) and
Prochaska et al. (2001), plotted as squares and rhombi,
respectively. The general trend of the model curve is
consistent with the observed damped Ly abundances. The dashed line indicates the metallicity
evolution of the hot gas component, which fills most of
the galactic halo.
abundances. The dashed line indicates the metallicity
evolution of the hot gas component, which fills most of
the galactic halo. |
| Open with DEXTER |
At z = 0,
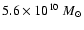 (15.7%) of the initial
baryonic mass of
(15.7%) of the initial
baryonic mass of
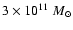 is still in the form of
gas. The distribution of this late ISM is spatially more extended
than that of the stars and the mass ratio of ISM to stars
increases with distance from the galactic centre. Inside
is still in the form of
gas. The distribution of this late ISM is spatially more extended
than that of the stars and the mass ratio of ISM to stars
increases with distance from the galactic centre. Inside
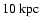 ,
only about 2% of the baryonic mass is still in the ISM,
but inside
,
only about 2% of the baryonic mass is still in the ISM,
but inside
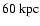 the fraction is already 43%. 75% of the ISM
mass is in the cold and warm phases (molecular and atomic gas),
but a significant fraction of 25% is hot and ionized. This hot
gas extends far out into the halo and fills most of the halo
volume (see Fig. 8). As discussed in the previous
subsection, the hot gas is the chemically least enriched component
at late times.
the fraction is already 43%. 75% of the ISM
mass is in the cold and warm phases (molecular and atomic gas),
but a significant fraction of 25% is hot and ionized. This hot
gas extends far out into the halo and fills most of the halo
volume (see Fig. 8). As discussed in the previous
subsection, the hot gas is the chemically least enriched component
at late times.
5 Formation of galactic components
The model presented in this paper describes the formation of a
massive disk galaxy with a total luminous mass of
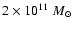 inside
inside
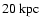 and a disk rotation velocity of
and a disk rotation velocity of
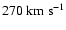 at a radius
at a radius
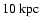 ,
about 2.5 times more massive
than the Milky Way. The galaxy model forms from inside-out
radially and from halo to disk vertically. In Fig. 6
one can clearly see halo, bulge, and disk components, which as
described in Sect. 4 form sequentially in this
order. The model contains the full spatially resolved dynamical
and chemical information for all of these components. With this
information it is possible to study the detailed consequences for
the stellar kinematics and abundances, that are implied by the
assumptions made for the galaxy formation scenario and the
modelling of the various physical processes involved, and to
compare to a variety of observational data.
,
about 2.5 times more massive
than the Milky Way. The galaxy model forms from inside-out
radially and from halo to disk vertically. In Fig. 6
one can clearly see halo, bulge, and disk components, which as
described in Sect. 4 form sequentially in this
order. The model contains the full spatially resolved dynamical
and chemical information for all of these components. With this
information it is possible to study the detailed consequences for
the stellar kinematics and abundances, that are implied by the
assumptions made for the galaxy formation scenario and the
modelling of the various physical processes involved, and to
compare to a variety of observational data.
Figure 13 shows average properties of the model
stars at redshift z = 0: age, metallicity, [O/Fe], and rotational
velocity. These vary continuously as a function of position in the
meridional plane (R,Z), in a way that reflects the interplay
between star formation and enrichment on the one hand, and the
vertically top-down and radially inside-out dynamical formation on
the other hand. Thus, the oldest stars can be found at low radial
distances in the halo and the youngest stellar populations are
located in the outer galactic disk. Because mean age and mean
metallicity vary as a function of position, global mean values for
age or metallicity are not sufficient to characterize the stellar
population of a galaxy. Notice also that stars at a given mean age
or metallicity can be found in a variety of positions.
![\begin{figure}
\par\includegraphics[width=17.1cm,clip]{MS2866f13.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg188.gif) |
Figure 13:
The panels show the mean stellar age, [Fe/H], [O/Fe],
and mean rotation velocity V of the model stars at
redshift z = 0, in the meridional plane as a function
of radial (R) and vertical distance (Z) from the
galaxy's centre. The mean stellar ages are given in Gyr,
and the units of the velocities are
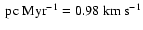 . . |
| Open with DEXTER |
In Fig. 14 we plot the complete distribution of model
stars at redshift z = 0 in the plane of rotational velocity
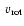 versus metallicity [Fe/H]. This shows the expected
evolution from non-rotating, low-metallicity stars formed early in
the collapse to a rotating disk-like, metal-rich population formed
at late times. However, this evolution is by no means described by
a single dependence of
versus metallicity [Fe/H]. This shows the expected
evolution from non-rotating, low-metallicity stars formed early in
the collapse to a rotating disk-like, metal-rich population formed
at late times. However, this evolution is by no means described by
a single dependence of
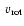 on [Fe/H]; rather there is large
scatter in
on [Fe/H]; rather there is large
scatter in
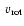 at given metallicity, especially at low [Fe/H]
values. In addition, there are also at least two concentrations of
stars visible, at [Fe/H
at given metallicity, especially at low [Fe/H]
values. In addition, there are also at least two concentrations of
stars visible, at [Fe/H
![$] \simeq -0.4$](/articles/aa/full/2003/09/aa2866/img190.gif) and [Fe/H
and [Fe/H
![$] \simeq 0.1$](/articles/aa/full/2003/09/aa2866/img191.gif) .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f14.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg193.gif) |
Figure 14:
Lower panel: distribution of model stars in the
metallicity-rotation velocity plane. Rotation
velocities are perpendicular to the total angular
momentum vector and are in
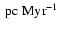 .
Upper panel: total
metallicity distribution of all model stars, projecting
along the rotation velocity axis. The dashed lines
separate the subpopulations discussed in the text. .
Upper panel: total
metallicity distribution of all model stars, projecting
along the rotation velocity axis. The dashed lines
separate the subpopulations discussed in the text. |
| Open with DEXTER |
The top panel of Fig. 14 shows a [Fe/H] histogram of
all stars, projecting along the
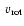 axis. Based on this
histogram, we will now study the stellar populations in the
different parts of Fig. 14 separated by the dashed
lines. In first order these might be described as extreme halo,
inner halo, metal-weak thick disk, thick disk, thin disk, and
central bulge components, somewhat reminiscent of the similar
components known in the Milky Way. However, we do not intend to
imply a detailed correspondence with the Milky Way components;
there are significant differences with the present model. Recall
that the dark and baryonic masses of this model are larger than in
the Milky Way, and especially the dissipation parameter of the
model may not be typical for the Milky Way. Nonetheless, studying
these components is useful to understand the course of the
dynamical evolution and chemical enrichment in dissipative,
star-forming collapse, and we will for definiteness use the Milky
Way terminology in the following discussion of the properties of
these populations.
axis. Based on this
histogram, we will now study the stellar populations in the
different parts of Fig. 14 separated by the dashed
lines. In first order these might be described as extreme halo,
inner halo, metal-weak thick disk, thick disk, thin disk, and
central bulge components, somewhat reminiscent of the similar
components known in the Milky Way. However, we do not intend to
imply a detailed correspondence with the Milky Way components;
there are significant differences with the present model. Recall
that the dark and baryonic masses of this model are larger than in
the Milky Way, and especially the dissipation parameter of the
model may not be typical for the Milky Way. Nonetheless, studying
these components is useful to understand the course of the
dynamical evolution and chemical enrichment in dissipative,
star-forming collapse, and we will for definiteness use the Milky
Way terminology in the following discussion of the properties of
these populations.
5.1 [Fe/H] <-1.9 ("Extreme halo'')
This component comprises all stars with [Fe/H] <-1.9; these
stars form before the collapse and simultaneous spin-up of the gas
goes under way. As the left row of Fig. 15 shows,
these stars form mostly in the first two Gyr after the start of
the simulation (at time
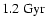 ), but there is a small ongoing
star formation in the halo even to late times from infalling
low-metallicity gas (remember that we have not imposed a density
threshold for star formation in this model). These stars have
[O/Fe] near 0.4 typical for enrichment by SNe II. Their spatial
distribution is nearly spherical, they rotate slowly if at all,
and they have an asymmetric, broad distribution of eccentricities
biased towards radial orbits. Here we have defined eccentricity
as
), but there is a small ongoing
star formation in the halo even to late times from infalling
low-metallicity gas (remember that we have not imposed a density
threshold for star formation in this model). These stars have
[O/Fe] near 0.4 typical for enrichment by SNe II. Their spatial
distribution is nearly spherical, they rotate slowly if at all,
and they have an asymmetric, broad distribution of eccentricities
biased towards radial orbits. Here we have defined eccentricity
as
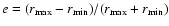 where
where
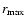 and
and
 are the maximum and minimal
three-dimensional radii of the orbit. The relative lack of
low-eccentricity orbits at these metallicities (see Sect. 5.7) may be due to our neglect of small-scale structure
in the initial conditions; compare with Bekki & Chiba (2001).
are the maximum and minimal
three-dimensional radii of the orbit. The relative lack of
low-eccentricity orbits at these metallicities (see Sect. 5.7) may be due to our neglect of small-scale structure
in the initial conditions; compare with Bekki & Chiba (2001).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2866f15a.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg198.gif) |
Figure 15:
Properties of model subcomponent selected by
metallicity according to the dashed lines in
Fig. 14. Columns from left to right show
all stars with [Fe/H] <-1.9 ("Extreme halo''),
-1.9< [Fe/H] <-0.85 ("Inner halo''), -0.85<
[Fe/H] <-0.6 ("Metal-weak thick disk''), -0.6<
[Fe/H] <-0.15 ("Thick disk''), -0.15< [Fe/H]
<0.17 ("Thin disk''), and [Fe/H] >0.17 ("Inner
bulge''). For each of these components, the panels
from top to bottom show the face-on projection onto
the disk plane, edge-on projection, distribution of
formation times, [O/Fe] distribution, eccentricity
distribution, and distribution of rotation
velocities. The top two panels in each row show an
area of
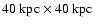 .
Star formation in
the model starts at time .
Star formation in
the model starts at time
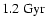 . . |
| Open with DEXTER |
5.2 -1.9< [Fe/H] <-0.85 ("Inner halo'')
Stars in this component have a metallicity range -1.9< [Fe/H]
<-0.85, covering the spin-up phase until the first minimum in
the [Fe/H] histogram in Fig. 14. These stars form a
more flattened spheroidal distribution with a flat density
profile. They rotate with 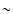
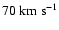 ,
and the eccentricity
distribution is less radially biased than for the extreme halo
component. This component forms partly during the phase of rapid
increase in the global star formation rate (Fig. 6),
but there is also a younger part forming until late times. Here
the selection in metallicity is important: the older part of these
stars forms at relatively small radii when the metallicity there
reaches the selected range, while the younger component forms at
progressively larger radii from infalling low-density gas mixed
with outflowing enriched material. This younger component may not
form in real galaxies if stars can only form above a density
threshold, as inferred from observations by
Kennicutt (1998). Further simulations also showed that a
larger dissipation parameter (see Sect. 3.4.6)
leads to a faster settling of the clouds into the disk and this
suppresses the star formation in the halo at late times.
,
and the eccentricity
distribution is less radially biased than for the extreme halo
component. This component forms partly during the phase of rapid
increase in the global star formation rate (Fig. 6),
but there is also a younger part forming until late times. Here
the selection in metallicity is important: the older part of these
stars forms at relatively small radii when the metallicity there
reaches the selected range, while the younger component forms at
progressively larger radii from infalling low-density gas mixed
with outflowing enriched material. This younger component may not
form in real galaxies if stars can only form above a density
threshold, as inferred from observations by
Kennicutt (1998). Further simulations also showed that a
larger dissipation parameter (see Sect. 3.4.6)
leads to a faster settling of the clouds into the disk and this
suppresses the star formation in the halo at late times.
5.3 -0.85< [Fe/H] <-0.6 ("Metal-weak thick disk'')
These stars with -0.85< [Fe/H] <-0.6 are intermediate in their
rotational properties between a halo and a disk population (see
Fig. 14). As Fig. 15 shows their spatial
distribution is already strongly flattened. They have a sizeable
rotation with peak of the distribution at
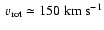 ,
around 50-60% of the circular velocity. The eccentricity
distribution is broad and centred around 0.5. The oldest stars of
this component form at around the peak of the global star
formation rate when the gas still has [O/Fe
,
around 50-60% of the circular velocity. The eccentricity
distribution is broad and centred around 0.5. The oldest stars of
this component form at around the peak of the global star
formation rate when the gas still has [O/Fe
![$] \simeq 0.3$](/articles/aa/full/2003/09/aa2866/img202.gif) .
A
slightly larger fraction of stars in this range of [Fe/H] forms
continuously until late times, at progressively larger radii,
again favoured by the lack of star formation threshold. These
stars are already enriched by SN Ia, as visible in their [O/Fe]
distribution.
.
A
slightly larger fraction of stars in this range of [Fe/H] forms
continuously until late times, at progressively larger radii,
again favoured by the lack of star formation threshold. These
stars are already enriched by SN Ia, as visible in their [O/Fe]
distribution.
5.4 -0.6< [Fe/H] <-0.15 ("Thick disk'')
This component with -0.6< [Fe/H] <-0.15 is one of the distinct
components in Fig. 14, and is clearly dominated by a
disk component in its rotational properties and eccentricity
distribution. However, Fig. 14 shows that it also
contains intermediate metallicity retrograde stars, showing that
this metallicity selection also includes part of the bulge. These
bulge stars cause the peak in the age distribution at 
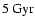 ,
with high [O/Fe]. The disk part has a relatively narrow
distribution in [O/Fe] centred around
,
with high [O/Fe]. The disk part has a relatively narrow
distribution in [O/Fe] centred around 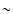 0.13.
0.13.
5.5 -0.15< [Fe/H] <0.17 ("Thin disk'')
The thin disk component, selected in the interval -0.15< [Fe/H]
<0.17, is characterized by near-circular orbits and a high
rotation velocity, about
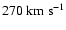 .
This component forms with an
approximately constant star formation rate and has mostly
near-solar [O/Fe]. As in the previous thick disk component, a
contribution from bulge stars is included by the metallicity
selection. The thin disk shows the bar and spiral arms clearest;
see the top panels in Fig. 15. In time, it forms from
inside out due to the accretion of material with progressively
larger angular momentum.
.
This component forms with an
approximately constant star formation rate and has mostly
near-solar [O/Fe]. As in the previous thick disk component, a
contribution from bulge stars is included by the metallicity
selection. The thin disk shows the bar and spiral arms clearest;
see the top panels in Fig. 15. In time, it forms from
inside out due to the accretion of material with progressively
larger angular momentum.
The thin disk shows only a shallow radial metallicity gradient of
0.02 dex/kpc, which is due to efficient mixing of the disk ISM
by the galactic bar. Beyond
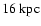 ,
where the mixing is not
very efficient, a steeper metallicity gradient of 0.07 dex/kpc
is established. See also Martinet & Friedli (1997) who found strong
metallicity gradients only in non-barred galaxies. The metal
production by the bulge and the mixing by the bar lead to a
pronounced pre-enrichment of the disk, which is visible in
Fig. 16 by the lack of metal-poor stars.
,
where the mixing is not
very efficient, a steeper metallicity gradient of 0.07 dex/kpc
is established. See also Martinet & Friedli (1997) who found strong
metallicity gradients only in non-barred galaxies. The metal
production by the bulge and the mixing by the bar lead to a
pronounced pre-enrichment of the disk, which is visible in
Fig. 16 by the lack of metal-poor stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f16.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg206.gif) |
Figure 16:
Distribution function of oxygen abundances of G-dwarfs,
selected by mass, in the model galaxy at redshift
z=0. All G-dwarfs in the equatorial plane with
galactocentric distances between
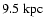 and
and
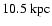 are plotted. The dotted curve shows predictions
of an instantaneous simple model with an effective
yield
are plotted. The dotted curve shows predictions
of an instantaneous simple model with an effective
yield
 . . |
| Open with DEXTER |
5.6 [Fe/H] >0.17 ("Inner bulge'')
The final metallicity component with [Fe/H] >0.17 consists
mainly of stars in the central bulge. Notice that these most
metal-rich stars do not form preferentially at late times; their
age distribution is similar to that of the thick disk
component. As the lower panels of Fig. 15 show, the
metal rich inner bulge forms from
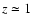 in this model,
rotates relatively slowly and has a broad eccentricity
distribution.
in this model,
rotates relatively slowly and has a broad eccentricity
distribution.
The total bulge population includes this inner component and a
second, more metal-poor component included in the metallicity
range of the "thick disk''. Two subpopulations in the bulge is
consistent with the observations of Prugniel et al. (2001), who find
that galactic bulges in general consist of two different stellar
components, an early collapse population and a population that
formed later out of accreted disk mass.
5.7 Kinematics-abundance relations
The previous subsections have shown that while it is useful to
select stellar components by metallicity, such a selection is not
ideal because it lacks spatial and kinematical
information. Vice versa, a purely kinematical selection would mix
stars from halo and bulge, or metal-poor and metal-rich disk. A
more physical separation would involve spatial, kinematic, and
abundance information. This is possible with models such as this,
because the complete population of model stars is available, but
will be deferred to a later paper. Here, we will only show two
relations between kinematic and abundance parameters for all stars
in the model, which further illustrate some of its properties.
Figure 17 shows the mean stellar rotation velocity as a
function of metallicity [Fe/H] for all model stars. For [Fe/H
![$]
<-2 ~{~v_{\rm rot}}$](/articles/aa/full/2003/09/aa2866/img207.gif) is independent of metallicity, at about
is independent of metallicity, at about
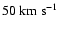 .
It then rises roughly linearly with [Fe/H] until the disk
rotation velocity is reached at [Fe/H
.
It then rises roughly linearly with [Fe/H] until the disk
rotation velocity is reached at [Fe/H
![$] \simeq 0.4$](/articles/aa/full/2003/09/aa2866/img209.gif) .
As is
apparent from Fig. 14, there is a large dispersion
around the mean value except in the disk components. Figure 18 shows the mean orbital eccentricity and a sample of
individual stellar eccentricities (defined in Sect. 5.1) as a function of metallicity. It is clear that
at any metallicity, there is a large scatter in the orbital
shapes. One of the causes of this is the very substantial
deepening of the gravitational potential during the prolonged
infall, which also affect orbits of stars formed early in the
collapse. A second effect is that the turbulent velocities in the
cloud medium are substantial during the collapse and during
periods of large star formation rate, so that the stars made from
these clouds inherit significant initial velocities. Thus all
eccentricity distributions shown in Fig. 15 are fairly
broad. When the various distributions shown in that figure are
added with the appropriate mass weighting, a broad distribution
results.
.
As is
apparent from Fig. 14, there is a large dispersion
around the mean value except in the disk components. Figure 18 shows the mean orbital eccentricity and a sample of
individual stellar eccentricities (defined in Sect. 5.1) as a function of metallicity. It is clear that
at any metallicity, there is a large scatter in the orbital
shapes. One of the causes of this is the very substantial
deepening of the gravitational potential during the prolonged
infall, which also affect orbits of stars formed early in the
collapse. A second effect is that the turbulent velocities in the
cloud medium are substantial during the collapse and during
periods of large star formation rate, so that the stars made from
these clouds inherit significant initial velocities. Thus all
eccentricity distributions shown in Fig. 15 are fairly
broad. When the various distributions shown in that figure are
added with the appropriate mass weighting, a broad distribution
results.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f17.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg210.gif) |
Figure 17:
Mean stellar rotation velocity as a function of [Fe/H]
for all model stars. |
| Open with DEXTER |
Both the dependence of
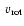 on metallicity in
Fig. 17 and that of eccentricity on [Fe/H] in
Fig. 18 are similar to those observed in the Milky Way
near the Sun (Chiba & Beers 2000), even though our model was not made
to match the Milky Way and does not in detail describe the Milky
Way. The main conclusion we draw from diagrams like
Figs. 17 and 18 is that realistic dissipative
collapses are much more complicated than the simple model put
forward by Eggen et al. (1962) forty years ago. Therefore, inferring
a merger history from the lack of rotation gradient with
metallicity and a broad eccentricity distribution in the Milky Way
halo is premature, irrespective of the fact that a fraction of the
halo is likely to have been formed out of merging fragments
(Ibata et al. 2001; Helmi et al. 1999; Chiba & Beers 2000). The important question,
about the relative importance of the disruption of small scale
stellar fragments, merging of gaseous fragments, and star
formation in smooth dissipative accretion, all within their dark
matter halos, will need more detailed modelling and more data to
answer. All of these processes are expected in current CDM galaxy
formation theories. The present simulations show that feedback is
important for the final properties of the stars formed.
on metallicity in
Fig. 17 and that of eccentricity on [Fe/H] in
Fig. 18 are similar to those observed in the Milky Way
near the Sun (Chiba & Beers 2000), even though our model was not made
to match the Milky Way and does not in detail describe the Milky
Way. The main conclusion we draw from diagrams like
Figs. 17 and 18 is that realistic dissipative
collapses are much more complicated than the simple model put
forward by Eggen et al. (1962) forty years ago. Therefore, inferring
a merger history from the lack of rotation gradient with
metallicity and a broad eccentricity distribution in the Milky Way
halo is premature, irrespective of the fact that a fraction of the
halo is likely to have been formed out of merging fragments
(Ibata et al. 2001; Helmi et al. 1999; Chiba & Beers 2000). The important question,
about the relative importance of the disruption of small scale
stellar fragments, merging of gaseous fragments, and star
formation in smooth dissipative accretion, all within their dark
matter halos, will need more detailed modelling and more data to
answer. All of these processes are expected in current CDM galaxy
formation theories. The present simulations show that feedback is
important for the final properties of the stars formed.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f18.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg211.gif) |
Figure 18:
Sample of stellar orbital eccentricities and mean
eccentricity of all stars in the model, as a function
of metallicity. |
| Open with DEXTER |
6 Conclusions
We have presented a model for the dissipative formation of a large
disk galaxy, inside a growing dark matter halo according to the
currently favoured  CDM cosmology with
CDM cosmology with
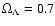 ,
,
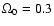 ,
,
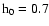 .
The dark halo mass accretion
history is taken from the large-scale structure formation
simulations of the GIF-VIRGO consortium (Kauffmann et al. 1999). We
use a total dark matter mass of
.
The dark halo mass accretion
history is taken from the large-scale structure formation
simulations of the GIF-VIRGO consortium (Kauffmann et al. 1999). We
use a total dark matter mass of
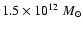 ,
a
total baryonic mass of
,
a
total baryonic mass of
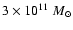 ,
a spin parameter
,
a spin parameter
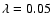 ,
and an angular momentum profile similar to the
universal profile found by Bullock et al. (2001).
,
and an angular momentum profile similar to the
universal profile found by Bullock et al. (2001).
We model the dynamics of stars and of two phases of the
interstellar medium, including a phenomenological description of
star formation, the most important interaction processes between
stars and the ISM, and the feedback from massive stars and
SNe. The dynamical evolution of the stars is treated with a
particle-mesh code. For the dynamical description of the cold
molecular and hot ionized gas components we use a
three-dimensional hydrodynamical grid code. Linked to the N-body
and hydrodynamical code is a Poisson solver for the self-gravity
and an interaction network, including a description of star
formation, the heating and enrichment of type Ia and II SNe, mass
return by intermediate mass stars, the heating and cooling by
radiation, dissipation in the cloudy medium, formation and
evaporation of cold clouds in the hot intercloud medium. We
discuss the range of uncertainty in the parameters that enter this
description. Because of the self-regulation of these processes
that is quickly established, even large changes in these
parameters only lead to moderate changes, about a factor of 2, in
the cloud velocity dispersion, hot gas temperature and ratio of
hot to cold gas density.
The simulation starts at a redshift of z = 4.85 with a dark halo
of
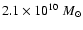 .
Inside the growing dark halo a disk
galaxy forms, whose star formation rate reaches a maximum of
.
Inside the growing dark halo a disk
galaxy forms, whose star formation rate reaches a maximum of
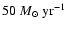 at redshift
at redshift
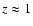 .
Our main results can be
summarized as follows:
.
Our main results can be
summarized as follows:
1. The formation and evolution of a galaxy in a dissipative
collapse scenario is much more complex than predicted by simple
models. The energy release by SNe and massive stars (feedback)
prevents the protogalaxy from a rapid collapse and delays the peak
in the star formation to a redshift of
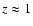 .
The
prolonged formation time causes fundamental changes in the
galactic shape, the kinematics of the stars, and the distribution
of the heavy elements.
.
The
prolonged formation time causes fundamental changes in the
galactic shape, the kinematics of the stars, and the distribution
of the heavy elements.
2. The galaxy forms radially from inside-out and vertically from
halo-to-disk. The dynamics of the collapse strongly influences the
star formation and chemical enrichment history, by modifying the
gas density, cooling time, and thus star formation rate. The on
average youngest and oldest stellar populations are found in the
outer disk and in the halo near the galactic rotation axis,
respectively. As a function of metallicity, we have described a
sequence of populations, reminiscent of the extreme halo, inner
halo, metal-poor thick disk, thick disk, thin disk and inner bulge
in the Milky Way. The first galactic component that forms is the
halo, followed by the bulge and the disk-halo transition region,
and as the last component the disk forms.
3. An interesting feature of this model is the formation of a
gaseous ring at a redshift of
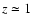 which collapses and
forms a galactic bar. The bar induces numerous changes of the
galaxy's properties. It alters the density structure of the disk,
induces spiral arms, enhances the mixing of ISM, and flattens
metallicity gradients in the disk. It also channels gas into the
centre, leading to prolonged star formation in the bulge region.
which collapses and
forms a galactic bar. The bar induces numerous changes of the
galaxy's properties. It alters the density structure of the disk,
induces spiral arms, enhances the mixing of ISM, and flattens
metallicity gradients in the disk. It also channels gas into the
centre, leading to prolonged star formation in the bulge region.
4. The bulge thus contains at least two stellar populations: An
old population that formed during the proto-galactic collapse and
a younger bar population. The distinguishing feature between these
populations is the [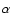 /Fe] ratio, with the bar population
reaching [
/Fe] ratio, with the bar population
reaching [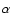 /Fe] < 0.
/Fe] < 0.
5. The disk is the youngest galactic component, characterized by
an approximately uniform star formation rate at late times. Its
metallicity is approximately solar and its stellar metallicity
distribution shows a pronounced lack of low-metallicity stars
compared to simple closed-box models, due to pre-enrichment of the
disk ISM.
6. Early in the collapse an approximately spherical halo forms.
As the collapse proceeds, the dissipation leads to spin-up of the
gas, and newly formed stars acquire increasing rotation speeds, as
expected. However, the distribution of orbital eccentricities as a
function of metallicity for halo stars has large scatter. As a
result, this distribution and the mean rotation rate as a function
of metallicity are not very different from those observed in the
solar neighbourhood. This shows that early homogeneous collapse
models are oversimplified, and that conclusions based on these
models about the degree of merging involved in the formation of
the Milky Way halo can be misleading.
7. The metal enrichment history in this model is broadly
consistent with the evolution of [Zn/H] metallicity in damped
Ly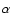 systems.
systems.
8. The most metal-rich stars form approximately
 after the
peak of the star formation, when the SN Ia rate is at its maximum.
These stars have the lowest [
after the
peak of the star formation, when the SN Ia rate is at its maximum.
These stars have the lowest [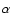 /Fe] ratios and, on average,
an age of
/Fe] ratios and, on average,
an age of 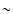
 in this model. The infall of gas and the
mass return from old stars decreases the average metallicity in
the inner galaxy at later times.
in this model. The infall of gas and the
mass return from old stars decreases the average metallicity in
the inner galaxy at later times.
This chemo-dynamical model provides kinematics and metallicities of
individual stars, but also can be used to obtain colours,
metallicities and velocity dispersions of integrated stellar
populations. It can therefore be used as a tool to understand
observations of distant spiral galaxies, and connect them with
stellar data in the Milky Way. In addition, it provides gas phase
metallicities and temperatures, and star formation rates, as a
function of time or redshift. Westera et al. (2002) have already used
this information to predict the colour evolution of large spiral
galaxies, and have compared with bulge colours in the Hubble Deep
Field. Further "observing'' of such models and comparing with
distant galaxy observations may lead to valuable insights on the
galaxy formation process.
A table of the positions, velocities, and metallicities for all
stars in the model can be obtained by request from the authors.
Acknowledgements
Most of this work was supported by the Swiss Nationalfond. We
thank M. Pettini for sending us the updated list of Zn abundances
in Ly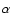 systems, and M. Steinmetz for a careful referee
report. The simulations were performed at the Swiss Centre for
Scientific Computing (CSCS) and the Computer Centre of the
University of Basel.
systems, and M. Steinmetz for a careful referee
report. The simulations were performed at the Swiss Centre for
Scientific Computing (CSCS) and the Computer Centre of the
University of Basel.
- Abraham, R. G.,
Merrifield, M. R., Ellis, R. S., Tanvir, N. R., & Brinchmann,
J. 1999, MNRAS, 308, 569
In the text
NASA ADS
- Avila-Reese, V.,
Colín, P., Valenzuela, O., D'Onghia, E., & Firmani, C. 2001,
ApJ, 559, 516
In the text
NASA ADS
- Barnes, J., &
Efstathiou, G. 1987, ApJ, 319, 575
In the text
NASA ADS
- Begelman, M. C., &
McKee, C. F. 1990, ApJ, 358, 375
In the text
NASA ADS
- Bekki, K., & Chiba,
M. 2001, ApJ, 558, 666
In the text
NASA ADS
- Bekki, K., & Shioya,
Y. 1998, ApJ, 497, 108
In the text
NASA ADS
- Bell, E. F., Barnaby, D.,
Bower, R. G., et al. 2000, MNRAS, 312, 470
In the text
NASA ADS
- Berczik, P. 1999, A&A, 348,
371
In the text
NASA ADS
- Best, P. N., Longair, M. S., &
Röttgering, H. J. A. 1998, MNRAS, 295, 549
In the text
NASA ADS
- Blais-Ouellette,
S., Amram, P., & Carignan, C. 2001, AJ, 121, 1952
In the text
NASA ADS
- Boissier, S., &
Prantzos, N. 2000, MNRAS, 312, 398
In the text
NASA ADS
- Borriello, A.,
& Salucci, P. 2001, MNRAS, 323, 285
In the text
NASA ADS
- Brinchmann, J.,
& Ellis, R. S. 2000, ApJ, 536, L77
In the text
NASA ADS
- Bullock, J. S., Dekel,
A., Kolatt, T. S., et al. 2001, ApJ, 555, 240
In the text
NASA ADS
- Chiba, M., & Beers,
T. C. 2000, AJ, 119, 2843
In the text
NASA ADS
- Clements, D. L., &
Couch, W. J. 1996, MNRAS, 280, L43
In the text
NASA ADS
- Cole, S., & Lacey,
C. G. 1996, MNRAS, 281, 716
In the text
NASA ADS
- Cole, S., Lacey, C. G., Baugh,
C. M., & Frenk, C. S. 2000, MNRAS, 319, 168
In the text
NASA ADS
- Colín, P.,
Avila-Reese, V., & Valenzuela, O. 2000, ApJ, 542, 622
In the text
NASA ADS
- Dalgarno, A., &
McCray, R. A. 1972, ARA&A, 10, 375
In the text
NASA ADS
- Dame, T. M., Elmegreem, B. G.,
Cohen, R. S., & Thaddeus, P. 1986, ApJ, 305, 892
In the text
NASA ADS
- de Blok, W. J. G.,
McGaugh, S. S., Bosma, A., & Rubin, V. C. 2001, ApJ, 552, L23
In the text
NASA ADS
- Del Popolo, A. 2001,
MNRAS, 325, 1190
In the text
NASA ADS
- Dey, A., Spinrad, H., Stern,
D., Graham, J. R., & Chaffee, F. H. 1998, ApJ, 498, L93
In the text
NASA ADS
- Eggen, O. J., Lynden-Bell,
D., & Sandage, A. R. 1962, ApJ, 136, 748
In the text
NASA ADS
- Ellis, R. S., Abraham, R. G.,
& Dickinson, M. 2001, ApJ, 551, 111
In the text
NASA ADS
- Elmegreen, B. G. 1989,
ApJ, 338, 178
In the text
NASA ADS
- Fall, S. M., &
Efstathiou, G. 1980, MNRAS, 193, 189
In the text
NASA ADS
- Fukushige, T.,
& Makino, J. 2001, ApJ, 557, 533
In the text
NASA ADS
- Gardner, J. P. 2001, ApJ, 557,
616
In the text
NASA ADS
- Guiderdoni, B.,
Hivon, E., Bouchet, F. R., & Maffei, B. 1998, MNRAS, 295, 877
In the text
NASA ADS
- Helmi, A., White, S. D. M.,
de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53
In the text
NASA ADS
- Hernandez, X.,
Gilmore, G., & Valls-Gabaud, D. 2000, MNRAS, 317, 831
In the text
NASA ADS
- Hockney, R. W., &
Eastwood, J. W. 1988, in Computer simulations using particles,
(Bristol and Philadelphia: Institute of Physics Publishing)
In the text
- Hultman, J., &
Pharasyn, A. 1999, A&A, 347, 769
In the text
NASA ADS
- Ibata, R., Irwin, M.,
Lewis, G., Ferguson, A. M. N. & Tanvir, N. 2001, Nature, 412, 49I
In the text
NASA ADS
- Jenkins, A., Frenk,
C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372
In the text
NASA ADS
- Kajisawa, M., &
Yamada, T. 2001, PASJ, 53, 833
In the text
NASA ADS
- Kauffmann, G.,
& Haehnelt, M. 2000, MNRAS, 311, 576
In the text
NASA ADS
- Kauffmann, G.,
Colberg, J. M., Diaferio, A., & White, S. D. M. 1999, MNRAS, 303,
188
In the text
NASA ADS
- Kay, S. T., Pearce, F. R.,
Jenkins, A., et al. 2000, MNRAS, 316, 374
In the text
NASA ADS
- Kennicutt, R. C. 1998,
ApJ, 498, 541
In the text
NASA ADS
- Klypin, A., Kravtsov,
A. V., Bullock, J. S., & Primack, J. R. 2001, ApJ, 554, 903
In the text
NASA ADS
- Köppen, J., Theis,
C. P., & Hensler, G. 1995, A&A, 296, 99
In the text
NASA ADS
- Larson, R. B. 1969, MNRAS, 145,
405
In the text
NASA ADS
- Levine, S. E., &
Sparke, L. S. 1998, ApJ, 496, L13
In the text
NASA ADS
- Lilly, S., Schade, D.,
Ellis, R., et al. 1998, ApJ, 500, 75
In the text
NASA ADS
- Maeder, A., & Meynet,
G. 1989, A&A, 210, 155
In the text
NASA ADS
- Manning, C., Stern, D.,
Spinrad, H., & Bunker, A. 2000, ApJ, 537, 65
In the text
NASA ADS
- Martinet, L., &
Friedli, D. 1997, A&A, 323, 363
In the text
NASA ADS
- McKee, C. F., &
Ostriker, J. P. 1977, ApJ, 218, 148
In the text
NASA ADS
- McKee, C. F., &
Begelman, M. C. 1990, ApJ, 358, 392
In the text
NASA ADS
- McKee, C. F. 1990, in The
evolution of the interstellar medium, ASP Conf. Proc.
(San Francisco), 3
In the text
- Menanteau, F.,
Abraham, R. G., & Ellis, R. S. 2001, MNRAS, 322, 1
In the text
NASA ADS
- Mestel, L. 1963, MNRAS, 126,
553
In the text
NASA ADS
- Mo, H. J., Mao, S., & White,
S. D. M. 1998, MNRAS, 295, 319
In the text
NASA ADS
- Moore, B., Governato, F.,
Quinn, T., Stadel, J., & Lake, G. 1998, ApJ, 499, L5
In the text
NASA ADS
- Moore, B., Ghigna, S.,
Governato, F., et al. 1999,
ApJ, 524, L19
In the text
NASA ADS
- Mosconi, M. B., Tissera,
P. B., Lambas, D. G., & Cora, S. A. 2001, MNRAS, 325, 34
In the text
NASA ADS
- Navarro, J. F., &
Benz, W. 1991, ApJ, 380, 320
In the text
NASA ADS
- Navarro, J. F., Frenk,
C. S., & White, S. D. M. 1995, MNRAS, 275, 56
In the text
NASA ADS
- Navarro, J. F., Frenk,
C. S., & White, S. D. M. 1996, ApJ, 462, 563
In the text
NASA ADS
- Navarro, J. F.,
& Steinmetz, M. 1997, ApJ, 478, 13
In the text
NASA ADS
- Navarro, J. F., Frenk,
C. S., & White, S. D. M. 1997, ApJ, 490, 493
In the text
NASA ADS
- Navarro, J. F.,
& Steinmetz, M. 2000a, ApJ, 528, 607
In the text
NASA ADS
- Navarro, J. F.,
& Steinmetz, M. 2000b, ApJ, 538, 477
In the text
NASA ADS
- Nomoto, K., Thielemann,
F.-K., & Yokoi, K. 1984, ApJ, 286, 644
In the text
NASA ADS
- Norman, M. L., Wilson,
J. R., & Barton, R. T. 1980, ApJ, 239, 968
In the text
NASA ADS
- Pearce, F. R., Jenkins,
A., Frenk, C. S., et al. (The Virgo
Consortium), 1999, ApJ, 521, L99
In the text
NASA ADS
- Pearce, F. R., Jenkins,
A., Frenk, C. S., et al. 2001, MNRAS, 326, 649
In the text
NASA ADS
- Pentericci, L.,
McCarthy, P. J., Röttgering, H. J. A., et al. 2001, ApJS, 135, 63
In the text
NASA ADS
- Pettini, M., Ellison,
S. L., Steidel, C. C., & Bowen, D. V. 1999, ApJ, 510, 576
In the text
NASA ADS
- Prochaska, J. X.,
Wolfe, A. M., Tytler, D., et al. 2001, ApJS,
137, 21
In the text
NASA ADS
- Prugniel, Ph.,
Maubon, G., & Simien, F. 2001, A&A, 366, 68
In the text
NASA ADS
- Reed, B. C. 2001, PASP, 113, 537
In the text
NASA ADS
- Rocha-Pinto,
H. J., Scalo, J., Maciel, W. J., & Flynn, C. 2000, ApJ, 531, L11
In the text
- Salucci, P., &
Burkert, A. 2000, ApJ, 537, L9
In the text
NASA ADS
- Samland, M., &
Hensler, G. 1996, in Rev. Mod. Astron., vol. 9, ed. R. E. Schielicke (Hamburg: Astronomische Gesellschaft), 277
In the text
- Samland, M., Hensler,
G., & Theis, C. P. 1997, ApJ, 476, 544
In the text
NASA ADS
- Samland, M. 1998, ApJ, 496,
155
In the text
NASA ADS
- Sandage, A. 1986, A&A, 161,
89
In the text
NASA ADS
- Sandage, A. 1990, JRASC, 84,
70
In the text
NASA ADS
- Schaerer, D., Meynet,
G., Maeder, A., & Schaller, G. 1993, A&AS, 98, 523
In the text
NASA ADS
- Schaerer, D., &
Vacca, W. D. 1998, ApJ, 497, 618
In the text
NASA ADS
- Schaller, G.,
Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269
In the text
NASA ADS
- Schmidt, M. 1959, ApJ, 129,
243
In the text
NASA ADS
- Searle, L., & Zinn,
R. 1978, ApJ, 225, 357
In the text
NASA ADS
- Somerville,
R. S., & Primack, J. R. 1999, MNRAS, 310, 1087
In the text
NASA ADS
-
Sommer-Larsen, J., Gelato, S., & Vedel, H. 1999, ApJ, 519, 501
In the text
NASA ADS
- Steidel, C. C.,
Adelberger, K. L., Giavalisco, M., Dickinson, M., & Pettini,
M. 1999, ApJ, 519, 1
In the text
NASA ADS
- Steinmetz, M.,
& Müller, E. 1994, A&A, 281, L79
In the text
- Steinmetz,
M., & Müller, E. 1995, MNRAS, 276, 549
In the text
NASA ADS
- Steinmetz,
M., & Bartelmann, M. 1995, MNRAS, 272, 570
In the text
NASA ADS
- Steinmetz, M.,
& Navarro, J. F. 2002, New Astron., 7(4), 155
In the text
NASA ADS
- Strang, G. 1968, SIAM
J. Num. Anal., 5, 506
In the text
- Sutherland,
R. S., & Dopita, M. A. 1993, ApJS, 88, 253
In the text
NASA ADS
- Swaters, R. A.,
Schoenmakers, R. H. M., Sancisi, R., & van Albada, T. S. 1999,
MNRAS, 304, 330
In the text
NASA ADS
- Tammann, G. A.,
Löffler, W., & Schröder, A. 1994, ApJS, 92, 487
In the text
NASA ADS
- Thacker, R. J., &
Couchman, H. M. P. 2001, ApJ, 555, L17
In the text
NASA ADS
- Theis, Ch., Burkert, A., &
Hensler, G. 1992, A&A, 265, 465
In the text
NASA ADS
- Thielemann, F.-K.,
Nomoto, K., & Hashimoto, M. 1996, ApJ, 460, 408
In the text
NASA ADS
- Timmes, F. X., Woosley,
S. E., & Weaver, T. A. 1995, ApJS, 98, 617
In the text
NASA ADS
- Unavane, M., Wyse,
R. F. G., & Gilmore, G. 1996, MNRAS, 278, 727
In the text
NASA ADS
- van den
Bergh, S., Cohen, J. G., Hogg, D. W., & Blandford, R. 2000, AJ,
120, 2190
In the text
NASA ADS
- van den Bosch,
F. C. 1998, ApJ, 507, 601
In the text
NASA ADS
- van den Bosch,
F. C. 2002, MNRAS, 331, 98
In the text
NASA ADS
- van den
Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305
In the text
NASA ADS
- van Dokkum, P. G.,
Franx, M., Fabricant, D., Kelson, D. D., & Illingworth, G. D., ApJ,
520, L95
In the text
NASA ADS
- Van Leer B. 1977,
J. Comp. Phys., 23, 276
In the text
NASA ADS
- Wechsler, R. H.,
Bullock, J. S., Primack, J. R., Kravtsov, A. V., & Dekel, A. 2002,
ApJ, 568, 52
In the text
NASA ADS
- Westera, P., Samland,
M., Buser, R., & Gerhard, O. E. 2002, A&A, 389, 761
In the text
NASA ADS
- Williams, P. R., &
Nelson, A. H. 2001, A&A, 374, 839
In the text
NASA ADS
- Woosley, S. E., &
Weaver, T. A. 1995, ApJS, 101, 181
In the text
NASA ADS
- Yoshida, N., Springel,
V., White, S. D. M., & Tormen, G. 2000, ApJ, 535, L103
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f1.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg29.gif)
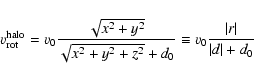
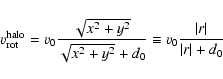
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f2.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg42.gif)
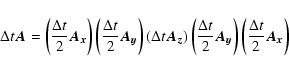
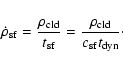
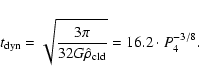
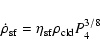
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f3.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg87.gif)
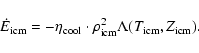
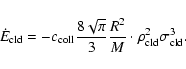
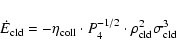
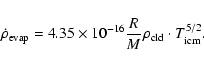
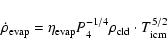
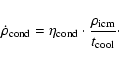
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f4.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg126.gif)
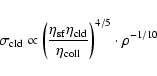
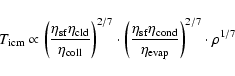
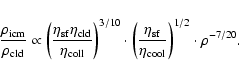
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f5.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg149.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f6.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg163.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS2866f7.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg166.gif)
![\begin{figure}
\par\includegraphics[width=18cm,clip]{MS2866f8.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg167.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f9.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg175.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f10.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg176.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f11.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg178.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f12.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg182.gif)
![\begin{figure}
\par\includegraphics[width=17.1cm,clip]{MS2866f13.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg188.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f14.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg193.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{MS2866f15a.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg198.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{MS2866f15b.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg199.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f16.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg206.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f17.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg210.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2866f18.eps} \end{figure}](/articles/aa/full/2003/09/aa2866/Timg211.gif)