A&A 399, 723-730 (2003)
DOI: 10.1051/0004-6361:20021815
Towards an explanation of features in
the diagnostic diagram of a model atmosphere
I. Linear wave equations with convenient invariants
F. Schmitz1 - B. Fleck2
1 - Institut für Theoretische Physik und Astrophysik
der Universität Würzburg, Am Hubland, 97074 Würzburg, Germany
2 -
ESA Research and Scientific Support Department, NASA/GSFC,
Mailcode 682.3, Greenbelt, MD 20771, USA
Received 4 November 2002 / Accepted 6 December 2002
Abstract
New standard forms of the time-independent linear adiabatic wave equation
of plane atmospheres are presented. The main objective is to obtain
equations with invariants as simple as possible so that oscillation
theorems can be applied effectively.
By transformations of both the independent and the dependent
variables, equations with simple invariants are formulated. We present a
standard form of the wave equation the invariant of which depends only on the first derivative
of the equilibrium density, as opposed to the common standard form the
invariant of which depends also on second derivatives.
Further, we discuss a procedure which replaces the wave equation by
a system of two simple second order differential equations.
In this case we try to draw conclusions on the general behavior of solutions
by use of oscillation theorems.
In addition, a re-formulation of the wave equation is presented, which eliminates
terms with
first derivatives of atmospheric quantities. The independent variable
of the resulting equation depends not only on the geometrical height but
also on the ratio 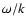 .
In this case, it is necessary to use a diagnostic
diagram the axes of which are given by
.
In this case, it is necessary to use a diagnostic
diagram the axes of which are given by 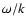 and
and 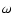 instead of
the common
instead of
the common 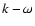 diagram.
Therefore we discuss the meaning of the parameter
diagram.
Therefore we discuss the meaning of the parameter 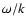 for
the representation of dispersion curves.
Finally, for the VAL-atmosphere (Vernazza et al. 1981),
regions of certainly nonoscillatory waves
are considered.
for
the representation of dispersion curves.
Finally, for the VAL-atmosphere (Vernazza et al. 1981),
regions of certainly nonoscillatory waves
are considered.
Key words: Sun: atmosphere - Sun: oscillations - stars: atmospheres
The present paper is a continuation of a paper by Schmitz & Fleck
(1998), called Paper I, which considered vertically
propagating adiabatic waves in a plane atmosphere.
There, common standard forms of the 1-dimensional wave equation are discussed
critically and a
wave equation with a very simple invariant is presented.
We now have performed extensions of the strategy of Paper I to
the three-dimensional propagation of linear adiabatic waves
in plane atmospheres.
Here, the problem of the reformulation of the time-independent
wave equation is significantly more
complex than in the one-dimensional case.
To solve the wave equation numerically, one takes a
corresponding system of two first order equations.
In general, one uses the two linearized hydrodynamical equations
from which the wave equation is formed. If we take
appropriate dependent variables
(vertical displacement and Lagrangian pressure perturbation),
then this system is uncomplicated,
and can easily be integrated numerically.
To obtain solutions in closed
form for simple analytical model atmospheres,
the representation of the wave equation and the choice of the variables
are crucial. In that case one tries to transform the wave equation to known
second order equations, in particular equations of special functions
(e.g. Schmitz & Steffens 1999).
To understand the behavior of waves without solving the wave equation
explicitely or to interprete results of numerical calculations,
one writes the wave equation in standard form and studies the behavior
of the invariant.
Besides, the standard form is also used for a numerical integration, as
there are particular numerical integration methods for
so-called Schoedinger-type equations.
It is clear that a simple invariant is convenient.
Further, a simple invariant is useful in connection with approximation
methods of solutions as the WKB-approximation (e.g. Mathews & Walker 1970).
Recent investigations of resonances of standing waves in the VAL-atmosphere
and modifications (cool chromosphere or shifted transition layer)
of this atmosphere by Steffens et al. (1997)
have yielded a wealth of features in the diagnostic diagram.
Further, investigations of the influence of atmospheric layers
(VAL-atmosphere and modifications)
on the p-modes of the sun by Steffens (1998),
and Steffens & Schmitz (2000) have led to
complicated dispersion curves.
The corresponding ridges in the diagnostic diagram show
strong bending or indicate avoided crossing.
For the VAL-atmosphere, the frequency range where such effects
occur is
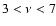 mHz.
The results are not yet interpreted and understood.
mHz.
The results are not yet interpreted and understood.
A frequently discussed, but not commonly accepted phenomenon is that of
a chromospheric mode, presumably due to an acoustic cavity between the
temperature minimum and the transition region (cf. e.g. Leibacher &
Stein 1981). For a detailed discussion refer to
Steffens et al. (1985), who report on signatures of a
chromospheric mode at 6 mHz in their observations. However, Steffens & Schmitz
(2000) demonstrated that the corresponding features can appear in a
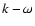 diagram even without a chromosphere, i.e. without a
temperature minimum and a chromospheric temperature increase. It
therefore does not necessarily require invoking a chromospheric mode to
explain these features. Further, their results show that, in order to
understand the diagnostic diagram of the Sun, it is useful to consider
modifications and variations of the outer layers. It remains open,
however, how to best explain certain features in diagnostic diagrams
- by physical systems (e.g. cavities) or by a discussion of the equations.
A nice example can be found in Aizenman et al. (1977).
They have investigated the behavior of l=2-modes
of stars "evolving away from the main sequence''. There, in a frequency-age diagram
mode bending (bumping) similar to that in the solar
diagram even without a chromosphere, i.e. without a
temperature minimum and a chromospheric temperature increase. It
therefore does not necessarily require invoking a chromospheric mode to
explain these features. Further, their results show that, in order to
understand the diagnostic diagram of the Sun, it is useful to consider
modifications and variations of the outer layers. It remains open,
however, how to best explain certain features in diagnostic diagrams
- by physical systems (e.g. cavities) or by a discussion of the equations.
A nice example can be found in Aizenman et al. (1977).
They have investigated the behavior of l=2-modes
of stars "evolving away from the main sequence''. There, in a frequency-age diagram
mode bending (bumping) similar to that in the solar
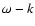 diagram occurs.
The authors have shown that the bending of the ridges can be explained by avoided
crossing of the ridges of two single systems. These systems however, are
fictitious systems defined by equations which are obtained by simplifying
the full equations.
diagram occurs.
The authors have shown that the bending of the ridges can be explained by avoided
crossing of the ridges of two single systems. These systems however, are
fictitious systems defined by equations which are obtained by simplifying
the full equations.
However that may be, the common standard form of the adiabatic
wave equation is not suitable to explain and understand the features.
Further, it is not clear which combinations of the wave number k
and the frequency 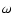 should be taken to understand the behavior
of structures and ridges in the
diagnostic diagram: the pairs (
should be taken to understand the behavior
of structures and ridges in the
diagnostic diagram: the pairs (
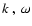 )
or
(
)
or
(
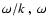 )
or (
)
or (
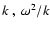 )
etc.?
)
etc.?
Paper I was closed by the presentation of a simple
standard form of the equation of vertically propagating waves.
In the case of the VAL-atmosphere, the numerical behavior
of the invariant of this equation is very simple.
The three-dimensional case is
much more complicated and the optimal standard form of the equation is not
unique. Thus, in the present paper we concentrate on the mathematical tools.
A subsequent paper by co-workers will deal with
features and ridges in diagnostic diagrams.
The present paper is organized as follows: in Sect. 2 we present the
linearized hydrodynamic equations and the resulting wave equation.
Section 3 deals with the common standard form of the wave equation.
This form is critized in Sect. 4 where also oscillation theorems are
given. In Sect. 5, we present and discuss some new standard forms
of the wave equations. The equation given in Sect. 5.1 is obtained
by introducing the logarithmic mass as the independent variable.
In Sect. 5.2 we separate the wave equation
into two second order differential equations and apply oscillation
theorems to obtain general statements on the behavior of solutions.
A standard form of the wave equation the invariant of which is
free of first derivatives of atmospheric quantities is presented
in Sect. 6. In Sect. 7 we discuss criteria for nonoscillatory waves
with applications to the VAL-atmosphere.
Let z be the vertical, outwards directed geometrical coordinate
and g the constant gravity.
Let p(z) and 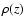 be the pressure and the density of the equilibrium
atmosphere, c(z) the adiabatic sound speed,
be the pressure and the density of the equilibrium
atmosphere, c(z) the adiabatic sound speed,
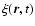 the vertical component of the Lagrangian
displacement and
the vertical component of the Lagrangian
displacement and
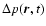 the Lagrangian
pressure perturbation.
The horizontal position
the Lagrangian
pressure perturbation.
The horizontal position
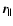 and the time t are
separated by
and the time t are
separated by
![$\exp[~i~(\omega~ t - \vec k~\vec r_\parallel)]$](/articles/aa/full/2003/08/aah4082/img13.gif) ,
where
,
where
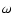 is the real frequency, and
is the real frequency, and 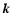 the horizontal
wave vector.
the horizontal
wave vector.
From the linearized hydrodynamic equations we obtain two first
order differential equations (cf. e.g. Schmitz & Fleck 1994)
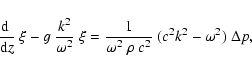 |
(1) |
![\begin{displaymath}\frac{{\rm d}\;}{{\rm d} z}~\Delta p + g~\frac{k^2}{\omega^2}...
...a p =
\rho~\left[\omega^2-\frac{k^2 g^2}{\omega^2}\right]~\xi
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img16.gif) |
(2) |
where now
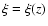 ,
,
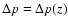 ,
and
,
and
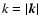 .
We use the variables
.
We use the variables 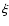 and
and 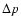 as only these perturbations are
continuous at a contact discontinuity where
as only these perturbations are
continuous at a contact discontinuity where 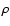 and c are
discontinuous.
Because of the continuity of
and c are
discontinuous.
Because of the continuity of 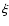 and
and 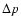 ,
the coefficients of the
equations cannot contain derivatives of
,
the coefficients of the
equations cannot contain derivatives of 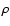 and c.
In the case of other variables as the Eulerian pressure perturbation or the
Lagrangian density perturbation the coefficients of the corresponding
equations contain first order derivatives of atmospheric quantities like
c and
and c.
In the case of other variables as the Eulerian pressure perturbation or the
Lagrangian density perturbation the coefficients of the corresponding
equations contain first order derivatives of atmospheric quantities like
c and 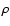 .
.
From Eqs. (1) and (2) we obtain the
time-independent wave
equation of the Lagrangian pressure perturbation 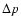 :
:
![\begin{displaymath}\omega^2~c^2~\left[~{ {\rm d}^2~\Delta p\over {\rm d} z^2\;~}...
...ght)
+ \omega^2~(~c^2~k^2 - \omega^2~)~\right]~\Delta p = 0\;.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img23.gif) |
(3) |
The Lagrangian pressure perturbation 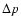 is a scalar,
the vertical displacement
is a scalar,
the vertical displacement 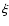 a component of a vector.
The corresponding wave equation of
a component of a vector.
The corresponding wave equation of 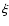 has a critical level
at
has a critical level
at
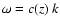 .
Hence, it is more complicated than the equation of
.
Hence, it is more complicated than the equation of 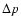 .
.
For this form (see e.g. Deubner & Gough 1984),
the independent variable is the geometrical height z.
With the transformation
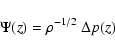 |
(4) |
the wave Eq. (3) turns into the standard form
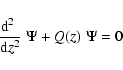 |
(5) |
where the invariant Q(z) is given by
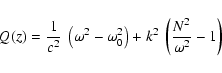 |
(6) |
with
![\begin{displaymath}\omega_0^2 = {c^2\over 4}~\left[{3\over\rho^2}
\left({{\rm d}...
...ht )^2 - {2\over\rho}\;{{\rm d}^2\rho\over {\rm d} z^2}\right]
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img28.gif) |
(7) |
and
![\begin{displaymath}N^2 = g~\left[ -~{1\over\rho}~{{\rm d}\rho\over {\rm d} z} - {g\over c^2}\right ]\cdot
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img29.gif) |
(8) |
In the case of the isothermal atmosphere, 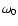 is the constant acoustic cut-off
frequency and N the constant Brunt-Vaisala frequency.
The factorized form of the invariant Q(z) reads:
is the constant acoustic cut-off
frequency and N the constant Brunt-Vaisala frequency.
The factorized form of the invariant Q(z) reads:
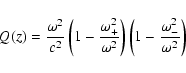 |
(9) |
where
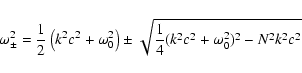 |
(10) |
(cf. Deubner & Gough 1984).
The standard form given here is the most common.
Occasionally, other forms of the wave equation are used.
Mihalas & Toomre (1981) used a standard form which was obtained
by the wave equation of the vertical displacement 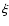 .
.
The common standard form of the wave equation is not suitable, as
it requires the calculation of the second derivative of the density, which is
nearly impossible to do in the case of an empirical atmosphere.
The invariant used by Mihalas & Toomre (1981)
contains the second derivative of the adiabatic sound speed
(comparable to the second derivative of the density in Eq. (7)).
The authors write:
"however, it was found to be essential to smooth the model in order
to obtain continuos derivatives of the sound speed and density scale height.
Otherwise small scale fluctuations in the vertical wave number produce numerous
partial reflections which are artifacts of the model and have no physical basis''.
Numerical differentiation is usually a difficult operation,
particularly in the case of empirical data.
In Paper I we calculated the second
derivative of the adiabatic sound speed of the VAL-atmosphere.
There, small deviations from the VAL-data strongly influenced the second derivative.
Besides, the numerical behavior of the invariant is far too complicated
to draw conclusions to the form of the solutions.
In Paper I we have extensively discussed this problem for the vertical case k=0.
The so-called invariant of a second order differential equation is not a physical
invariant, i.e. a scalar field, but it changes when the variables are
transformed. In Paper I we have compared some different representations of the wave
equation. We have seen how the invariants undergo strong changes when the
variables are transformed.
It was shown that the behavior of waves can be described by
a wave equation, the invariant of which contains only one coefficient,
which is the quantity 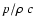 .
In the VAL atmosphere, and there in particular in the chromosphere,
the behavior of this quantity
differs markedly from the behavior of the temperature or the adiabatic sound speed.
.
In the VAL atmosphere, and there in particular in the chromosphere,
the behavior of this quantity
differs markedly from the behavior of the temperature or the adiabatic sound speed.
An uncomplicated and computationally simple invariant plays a role also in the following
case:
for a numerical integration, a differential equation of higher order
is replaced by a system of first order equations.
There is an exception to this rule.
For the numerical integration of second order differential
equations whithout the first derivative,
there are particular methods.
Mihalas & Toomre (1981) have used such a method
to solve the wave equation.
Oscillation and nonoscillation theorems for second order equations
are given in Gradshteyn & Ryzhik (1980).
Only a few oscillation theorems for the solutions of second order
differential equations are really useful.
Most of such theorems concern infinite
intervals. (Mathematically, solutions are said to be
oscillatory if they possess
an infinite number of zeros in the interval
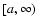 ,
nonoscillatory, if they possess only a finite number of zeros.)
,
nonoscillatory, if they possess only a finite number of zeros.)
For this paper, we need only the following two nonoscillating theorems
for a differential equation
y'' + f(x) y = 0:
1. If 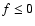 on
an interval (a,b) or on
on
an interval (a,b) or on
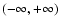 ,
then y(x) has not more
than one zero in this interval.
In this paper, we call this case nonoscillatory.
,
then y(x) has not more
than one zero in this interval.
In this paper, we call this case nonoscillatory.
2. There are strictly increasing and decreasing linearly independent
positive solutions if f < 0 is continuous in
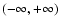 and if
x f(x) is not integrable on
and if
x f(x) is not integrable on
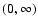 .
This property corresponds to the existence of the solutions e-x and
e+x of the equation
y'' - y = 0 where only these solutions, apart of
constant factors, are strictly
monotonous and positive as opposed to the solutions
.
This property corresponds to the existence of the solutions e-x and
e+x of the equation
y'' - y = 0 where only these solutions, apart of
constant factors, are strictly
monotonous and positive as opposed to the solutions 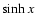 or
or 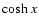 .
As we shall consider atmospheric layers with finite extension
the integrability of the function x f(x) is unimportant.
For f < 0 we can always find a monotonic and positive solution.
.
As we shall consider atmospheric layers with finite extension
the integrability of the function x f(x) is unimportant.
For f < 0 we can always find a monotonic and positive solution.
When the invariant is negative, the solutions are nonoscillatory.
This statement is sufficient, but not necessary. So, f(x)=0does not separate exponential and oscillatory behavior as it is often
claimed. Only criteria for certainly nonoscillatory behavior
can be given.
Using the column mass m given by
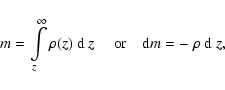 |
(11) |
we obtain:
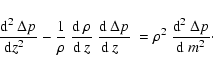 |
(12) |
Then, the wave Eq. (3) reads:
![\begin{displaymath}{{\rm d}^2\Delta p\over {\rm d} m^2\;~}+
{1\over \omega^2 c^2...
...d}~m} -g)
+ \omega^2 (\omega^2 - c^2 k^2)\right]\Delta p = 0 .
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img42.gif) |
(13) |
For
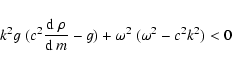 |
(14) |
solutions are certainly nonoscillatory.
This condition, however, is weak:
in the case of an isentropic stratification it reduces to
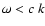 ,
in the case k=0 to
,
in the case k=0 to
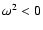 .
It is not of advantage to replace the density
.
It is not of advantage to replace the density 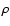 by the
temperature T, as
by the
temperature T, as 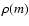 increases monotonously,
whereas T(m) is not monotonous.
Because of the Schwarzschild criterion for convective stability,
increases monotonously,
whereas T(m) is not monotonous.
Because of the Schwarzschild criterion for convective stability,
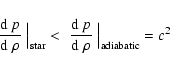 |
(15) |
and because of p=m g, we have
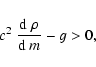 |
(16) |
so that the corresponding term of the invariant of the wave Eq. (13)
is positive.
For k=0, the wave equation reduces to:
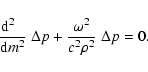 |
(17) |
As regards the representation of the propagation characteristics of a wave,
the mass is a somewhat disadvantegeous coordinate.
A wave equation which in the case of the isothermal atmosphere reduces
to a differential equation with constant coefficients is more familiar.
So instead of
the mass we should use a geometrical coordinate.
First, however, we present a more general form of the wave equation.
We define a new independent variable x by
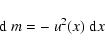 |
(18) |
with arbitrary u(x). The coordinate x is outwards directed.
By this transformation,
we obtain an equation which contains the first
derivative of 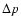 .
To eliminate this derivative,
we have to put
.
To eliminate this derivative,
we have to put
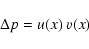 |
(19) |
with v(x) as a new dependent variable.
We obtain
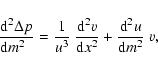 |
(20) |
so that the wave Eq. (13) takes the form
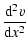 + +![$\displaystyle v\;u^3 {{\rm d}^2 u\over {\rm d} m^2} +{u^4\over\omega^2~c^2~\rho...
...m d}~\rho\over {\rm d}~m}-g\right)+
\omega^2~(\omega^2 - c^2 k^2)\right]~v = 0.$](/articles/aa/full/2003/08/aah4082/img54.gif) |
(21) |
Here, the function u(m) is arbitrary.
In the following sections we try to choose the function u(m) so that
the differential equation simplifies.
We discuss two possibilities: we set u(m) or we
define u(m) by a linear second order differential equation.
We proceed as in the case k=0 in Paper I.
Let H be an arbitrary scale height. Putting
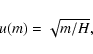 |
(22) |
we obtain
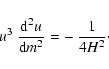 |
(23) |
Further, we get
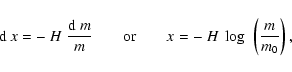 |
(24) |
so that the coordinate x has the dimension of a length.
Finally, we obtain the equation
![\begin{displaymath}\hspace*{1cm}\left(~k^2~g~\left(c^2~{{\rm d}~\rho\over {\rm d...
...omega^2~(\omega^2 - c^2~k^2)~\right)-{1\over 4}~\bigg]\;v = 0,
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img59.gif) |
(25) |
where we have put m=p/g.
For k=0, this equation reduces to the equation recommended in Paper I
as the basic equation of vertically propagating waves:
![\begin{displaymath}{{\rm d}^2 v\over {\rm d} x^2} + {1\over H^2}\;\left[~{\omega^2~p^2\over g^2~c^2~\rho^2}
- {1\over 4}\right]\;v = 0.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img60.gif) |
(26) |
By Eqs. (24), we have introduced a quasi-geometrical coordinate x.
The dependent variable becomes
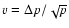 .
For constant adiabatic sound speed c, Eq. (25)
reduces to the usual wave equation of the isothermal atmosphere and xbecomes the real geometrical coordinate z.
As p = m g and
.
For constant adiabatic sound speed c, Eq. (25)
reduces to the usual wave equation of the isothermal atmosphere and xbecomes the real geometrical coordinate z.
As p = m g and
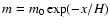 the pressure perturbation is given by
the pressure perturbation is given by
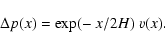 |
(27) |
When
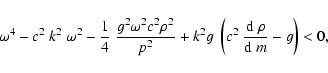 |
(28) |
the solutions v(x) of Eq. (25) are certainly nonoscillatory.
We put
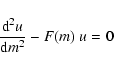 |
(29) |
where F(m) must be a positive function which is composed of parts of the third term
of Eq. (21). Then, the solutions u(m) of Eq. (29)
are nonoscillatory functions. Corresponding to
theorem 2 of Sect. 4 there exists a monotonous positive
solution. Let u0(m) be such a solution. Then, integration of
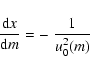 |
(30) |
yields a monotonous function x(m).
Finally, we obtain a monotonous positive function u0(x).
As the function F(m) contains parts of the third term of Eq. (21),
this equation simplifies.
We consider only two cases. First, we put
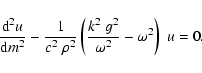 |
(31) |
In this case, the solutions u(m) are certainly nonoscillatory only for
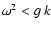 so that this case applies to gravity waves. Let u0(m) be a positive monotonous
solution. Then, also u0(x) is positive and monotonous.
The wave Eq. (21) reduces to:
so that this case applies to gravity waves. Let u0(m) be a positive monotonous
solution. Then, also u0(x) is positive and monotonous.
The wave Eq. (21) reduces to:
![\begin{displaymath}{{\rm d}^2 v\over {\rm d} x^2} +
{u_0^4~k^2\over\rho^2~\omeg...
...left[g~
{{\rm d}~\rho\over {\rm d}~m}- \omega^2\right]\;v = 0.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img69.gif) |
(32) |
The invariant of this equation is negative for
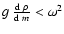 ,
and hence, the solutions v(x) are certainly
nonoscillatory if
,
and hence, the solutions v(x) are certainly
nonoscillatory if
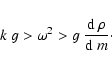 |
(33) |
This condition holds for extremely high values of k, and is therefore
unimportant.
For
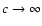 ,
a trivial solution of Eq. (31) is u=1.
For
u= u0 = 1, Eq. (32) becomes
,
a trivial solution of Eq. (31) is u=1.
For
u= u0 = 1, Eq. (32) becomes
![\begin{displaymath}{{\rm d}^2 v\over {\rm d} m^2} +
{k^2\over\rho^2~\omega^2}\le...
...}~m}- \omega^2\right]\;v = 0\quad{\rm with}\quad v = \Delta p.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img73.gif) |
(34) |
This is the wave equation of the so-called "heterogeneous
incompressible model'' (Ledoux & Walraven 1958)
in the plane layer approximation.
By this model, gravity waves are described approximately,
acoustic waves are suppressed.
Hence, the function u0(x) describes deviations of incompressibility.
It is evident, that the form of the invariant
of Eq. (32)
is relativly simple. Hence, for gravity waves with
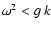 no particular effects should occur.
In fact, the ridges of gravity modes of the sun
(Cowling's and plane layer approximation, Steffens & Schmitz 2000)
show no particular features.
no particular effects should occur.
In fact, the ridges of gravity modes of the sun
(Cowling's and plane layer approximation, Steffens & Schmitz 2000)
show no particular features.
More important than gravity waves are acoustic waves. In this case, we put
![\begin{displaymath}{{\rm d}^2 u\over {\rm d} m^2} +
{k^2\over\rho^2~\omega^2}
\left[g~
{{\rm d}~\rho\over {\rm d}~m}- \omega^2\right]
\;u = 0.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img74.gif) |
(35) |
The solutions u(m) of this equation are nonoscillatory for
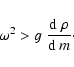 |
(36) |
From the maximum of
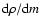 shown in Fig. 1
we can infer that this
condition is fulfilled for frequencies
shown in Fig. 1
we can infer that this
condition is fulfilled for frequencies 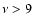 mHz, i.e. above the range
mHz, i.e. above the range
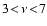 mHz, mentioned in the introduction.
There is a monotonic solution u0(m) and hence a function
u0(x), which is monotonic and positive.
For v(x) we obtain the equation
mHz, mentioned in the introduction.
There is a monotonic solution u0(m) and hence a function
u0(x), which is monotonic and positive.
For v(x) we obtain the equation
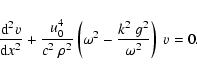 |
(37) |
The solution v(x) is certainly nonoscillatory for
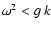 ,
so that
we again obtain the condition (33).
The invariant of Eq. (37) is simple.
For sound waves where
,
so that
we again obtain the condition (33).
The invariant of Eq. (37) is simple.
For sound waves where
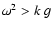 it does not change the sign.
Hence we may infer that no pecularities will occur for frequencies
it does not change the sign.
Hence we may infer that no pecularities will occur for frequencies
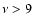 mHz.
Results of the investigations of Steffens & Schmitz
(2000) and of Steffens et al. (1997)
confirm this conclusion.
mHz.
Results of the investigations of Steffens & Schmitz
(2000) and of Steffens et al. (1997)
confirm this conclusion.
Therefore, for a given atmospheric stratification,
only waves with frequencies
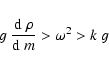 |
(38) |
should show striking features.
In this frequency range,
it is not possible to separate Eq. (21) conveniently.
Thus, to discuss acoustic waves with
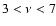 mHz
we have to use Eq. (25). However, there is another possibility.
mHz
we have to use Eq. (25). However, there is another possibility.
In the following we combine Eqs. (1) und (2) to a
wave equation the invariant of which does not contain the
derivative of the density. As the coefficients of these equations
are free of derivatives, such a procedure should be possible.
We found that only one way is practicable.
We may assume that
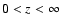 .
By the transformations of the displacement
and the pressure perturbation
.
By the transformations of the displacement
and the pressure perturbation
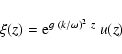 |
(39) |
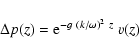 |
(40) |
we obtain the equations
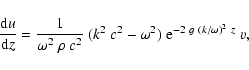 |
(41) |
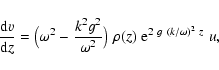 |
(42) |
for continuous functions u(z) und v(z).
Now we introduce a new independent variable y by
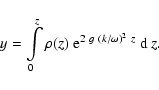 |
(43) |
The ratio 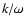 is assumed to be given.
The physical dimension of the variable y is that of a column mass.
As the integrand is positiv, the function y(z) increases monotonously with z.
Therefore, also the inverse z(y) is a monotonous function.
The above differential equations read:
is assumed to be given.
The physical dimension of the variable y is that of a column mass.
As the integrand is positiv, the function y(z) increases monotonously with z.
Therefore, also the inverse z(y) is a monotonous function.
The above differential equations read:
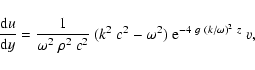 |
(44) |
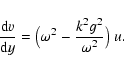 |
(45) |
Eliminating u(y), we obtain the second-order
equation
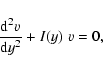 |
(46) |
with the invariant
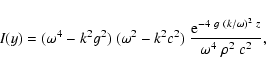 |
(47) |
where z=z(y).
The function z(y) can be obtained by a differential equation which
corresponds to the integral (43). For
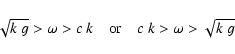 |
(48) |
solutions are certainly nonoscillatory.
In the vertical case with k=0, the integral (43) reduces to
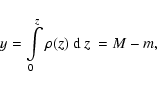 |
(49) |
where M is the total mass of the layer and m the complement (11).
Then, the invariant is
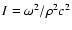 ,
so that Eq. (46)
reduces to Eq. (17) if k=0.
We shall now transform Eq. (46)
by introducing a new independent variable. The strategy is to obtain Eq.
(26) when k=0 and, in the limit of a constant sound speed,
the wave equation of the isothermal atmosphere.
,
so that Eq. (46)
reduces to Eq. (17) if k=0.
We shall now transform Eq. (46)
by introducing a new independent variable. The strategy is to obtain Eq.
(26) when k=0 and, in the limit of a constant sound speed,
the wave equation of the isothermal atmosphere.
First, we introduce a new dependent variable w and an new coordinate x by
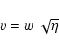 |
(50) |
and
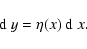 |
(51) |
With these transformations, Eq. (46) reads:
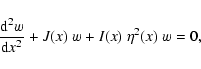 |
(52) |
with
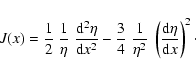 |
(53) |
In principle, the form of 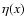 is free. However,
J(x) should be a simple function.
Now, if
is free. However,
J(x) should be a simple function.
Now, if 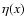 is an exponential,
J becomes constant.
For this reason, we put
is an exponential,
J becomes constant.
For this reason, we put
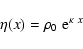 |
(54) |
where 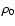 is a constant density and
is a constant density and
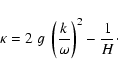 |
(55) |
Then, we have
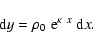 |
(56) |
We obtain
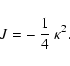 |
(57) |
Finally, Eq. (52) reduces to
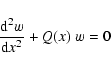 |
(58) |
with the invariant
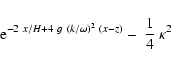 |
(59) |
with 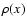 ,
c(x), and z(x). The independent variable x has the
physical dimension of a length. Hence, it is a quasi-geometrical
coordinate.
We can obtain the function z(x) by the numerical integration of the simple
and uncomplicated differential equation
,
c(x), and z(x). The independent variable x has the
physical dimension of a length. Hence, it is a quasi-geometrical
coordinate.
We can obtain the function z(x) by the numerical integration of the simple
and uncomplicated differential equation
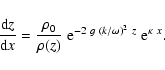 |
(60) |
It depends on the ratio 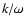 .
.
In the case of the isothermal atmosphere we have:
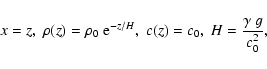 |
(61) |
where 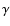 is the adiabatic exponent.
In this case, the invariant (59) becomes constant:
is the adiabatic exponent.
In this case, the invariant (59) becomes constant:
 |
(62) |
This invariant yields the familiar dispersion relation of the isothermal atmosphere.
Finally, for k=0 the wave equation reduces to Eq. (26), the
equation recommended in Paper I. The pressure perturbation is given by
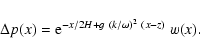 |
(63) |
Usually, corresponding to the axes k and 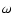 of the
familiar diagnostic diagram, one discusses how solutions of the wave equation
depend on the frequency
of the
familiar diagnostic diagram, one discusses how solutions of the wave equation
depend on the frequency 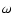 for given k.
In the case of the wave
Eq. (58), however, the parameter
for given k.
In the case of the wave
Eq. (58), however, the parameter 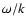 takes the place of k.
This is a little inconvenient. However,
takes the place of k.
This is a little inconvenient. However, 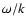 is a physical quantity,
the phase velocity.
Further, for the ridges of solar p-modes,
Duvall (1982) found empirically, that
is a physical quantity,
the phase velocity.
Further, for the ridges of solar p-modes,
Duvall (1982) found empirically, that
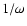 is a simple function of
is a simple function of 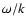 alone (Duvall's law,
see also Deubner & Gough 1984, Fig. 3).
Also the dispersion curves of the modes of a polytropic layer
(a convection zone without an overlaying atmosphere)
can be written in the form (Lamb 1932):
alone (Duvall's law,
see also Deubner & Gough 1984, Fig. 3).
Also the dispersion curves of the modes of a polytropic layer
(a convection zone without an overlaying atmosphere)
can be written in the form (Lamb 1932):
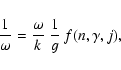 |
(64) |
where f is an algebraic function of the polytropic index n,
the adiabatic exponent 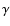 ,
and the vertical wave number
j=0, 1, 2, ...
Schmitz & Steffens (1999) have calculated the modes
of an asymptotically polytropic convection zone with a
smoothly matched, asymptotically isothermal atmosphere.
In the case of an asymptotically isentropic stratification of
the convection zone (i.e.
,
and the vertical wave number
j=0, 1, 2, ...
Schmitz & Steffens (1999) have calculated the modes
of an asymptotically polytropic convection zone with a
smoothly matched, asymptotically isothermal atmosphere.
In the case of an asymptotically isentropic stratification of
the convection zone (i.e.
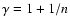 )
the frequency of the p1-mode is
given by a quadratic equation for
)
the frequency of the p1-mode is
given by a quadratic equation for 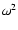 :
:
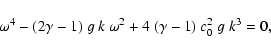 |
(65) |
where c0 is the asymptotic, adiabatic
sound speed of the atmosphere. We can reduce this equation to the
simple form
![\begin{displaymath}{1\over\omega} = \left(\displaystyle{\omega\over k}\right)^3\...
...\right)^2 g~(2\gamma-1) -
4~(\gamma-1)~c_0^2~g\;\right]^{-1}.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img120.gif) |
(66) |
Also for the other p-modes, the relation
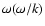 is simpler than the relation
is simpler than the relation 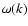 .
These findings are in agreement with Duvall's law.
We thus think that the use of
.
These findings are in agreement with Duvall's law.
We thus think that the use of 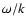 instead of k as a parameter of
the invariant Q(x) and the geometrical coordinate z(x)makes sense.
instead of k as a parameter of
the invariant Q(x) and the geometrical coordinate z(x)makes sense.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4082F1.eps}\end{figure}](/articles/aa/full/2003/08/aah4082/Timg123.gif) |
Figure 1:
The adiabatic sound speed and the derivative of the density as
functions of the height z. |
| Open with DEXTER |
We now give inequalities which hold for realistic frequencies and wave numbers.
In regions, where these inequalities hold, waves are certainly nonoscillatory.
In Sect. 6, we obtained:
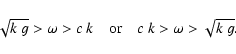 |
(67) |
These conditions, however, are weak as they define
only small regions of the diagnostic diagram.
The condition given in Sect. 5.1 is more important:
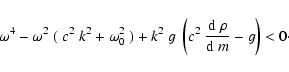 |
(68) |
with
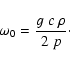 |
(69) |
The curves
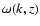 given by the square-roots of
given by the square-roots of
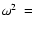
![\begin{displaymath}{1\over 2}\;\left[\left(c^2 k^2 + \omega_0^2\right)
\pm~\left...
...^2~{{\rm d}~\rho\over {\rm d}~m} -g\right)\right]^{1/2}\right]
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img129.gif) |
(70) |
define regions with certainly nonoscillatory waves.
Let us now consider the VAL-atmosphere (Vernazza et al. 1981).
We take the temperature stratification T(z) and the pressure p(z)of this atmosphere.
We calculate the density 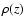 and the adiabatic
sound speed c(z) including dissociation and ionization of hydrogen
and ionization of helium: H
and the adiabatic
sound speed c(z) including dissociation and ionization of hydrogen
and ionization of helium: H
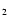 ,
H, H+, He, He+, He++, e-. We
have used the LTE-code described by Wolf (1983).
The calculated densities coincide with the tabulated densities of
the VAL-atmosphere. Only in the upper chromosphere (z > 1500 km) there are deviations,
because of the NLTE-effects of the VAL-atmosphere.
We therefore may assume that also the calculated adiabatic
sound speed is correct.
In the paper of Steffens & Schmitz (2000), the VAL-
atmosphere was matched to the convection zone of Spruit (1977).
There an equidistant data set was generated
from the tabulated points of the convection zone and the VAL-atmosphere.
This set, which was used to interpolate the coefficients of
Eqs. (1) and (2) for the numerical integration,
is not suitable to calculate the derivative of the density.
We have therefore calculated the derivative of the density at the tabulated
points of the VAL-atmosphere using a simple second order formula
for non-equidistant points.
Figure 1 shows the adiabatic sound speed and the derivative of the density
as functions of the geometrical height.
At the four lowest points of the VAL-atmosphere, the stratification is
superadiabatic so that Eq. (70) yields complex frequencies.
Also the HSRA-atmosphere (Gingerich et al. 1971)
has this property, and even a density inversion.
In the following we omit the first four points of the VAL-atmosphere.
,
H, H+, He, He+, He++, e-. We
have used the LTE-code described by Wolf (1983).
The calculated densities coincide with the tabulated densities of
the VAL-atmosphere. Only in the upper chromosphere (z > 1500 km) there are deviations,
because of the NLTE-effects of the VAL-atmosphere.
We therefore may assume that also the calculated adiabatic
sound speed is correct.
In the paper of Steffens & Schmitz (2000), the VAL-
atmosphere was matched to the convection zone of Spruit (1977).
There an equidistant data set was generated
from the tabulated points of the convection zone and the VAL-atmosphere.
This set, which was used to interpolate the coefficients of
Eqs. (1) and (2) for the numerical integration,
is not suitable to calculate the derivative of the density.
We have therefore calculated the derivative of the density at the tabulated
points of the VAL-atmosphere using a simple second order formula
for non-equidistant points.
Figure 1 shows the adiabatic sound speed and the derivative of the density
as functions of the geometrical height.
At the four lowest points of the VAL-atmosphere, the stratification is
superadiabatic so that Eq. (70) yields complex frequencies.
Also the HSRA-atmosphere (Gingerich et al. 1971)
has this property, and even a density inversion.
In the following we omit the first four points of the VAL-atmosphere.
For different wave numbers k, we now consider
frequencies with certainly nonoscillatory solutions.
Figure 2 shows boundary curves
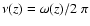 defined by Eq. (70)
for
k= 0, 1, 2, 2.485, and 3.
In the range
2.485 < k < 7.6085, where the regions are not connected,
instead of the inequality (68) the inequalities (67)
can be used. Therefore, the figures show the atmospheric f-mode with
defined by Eq. (70)
for
k= 0, 1, 2, 2.485, and 3.
In the range
2.485 < k < 7.6085, where the regions are not connected,
instead of the inequality (68) the inequalities (67)
can be used. Therefore, the figures show the atmospheric f-mode with
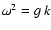 and the so called "Lamb-mode''
and the so called "Lamb-mode''
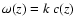 ,
denoted by f and L.
In the limit
,
denoted by f and L.
In the limit
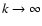 we have:
we have:
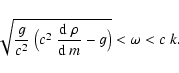 |
(71) |
This result is familiar:
for the isothermal atmosphere, the square-root reduces to the constant
Brunt-Vaisala-frequency.
Between the Lamb-mode and the Brunt-Vaisala-frequency,
waves are evanescent. As theorem 1 of Sect. 4 is only sufficient,
the complementary regions of Fig. 2 may contain
solutions with both oscillatory or nonoscillatory behavior.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{H4082F2.eps}\par\includegr...
...ip]{H4082F5.eps}\par\includegraphics[width=6.2cm,clip]{H4082F6.eps}
\end{figure}](/articles/aa/full/2003/08/aah4082/Timg136.gif) |
Figure 2:
The VAL-atmosphere: regions with certainly nonoscillatory waves.
The solid curves limit the regions where Eq. (68) holds.
The dotted curves are the f-mode and the "Lamb-mode''
and limit the regions
given by Eqs. (67). |
| Open with DEXTER |
Studies of the propagation behavior of linear adiabatic
waves in empirical or theoretical model atmospheres usually
comprise two steps:
the numerical integration of the wave equation and the
interpretation of the results. The first order Eqs. (1) and (2)
are well suited for numerical integration.
They are simple and the coefficients can be calculated without
complications. However, to understand the results
and get a deeper insight into
the underlying physical effects, it is necessary to use a
standard form of the wave equation. For standard forms, oscillation
theorems and comparison theorems are powerful tools.
The invariant of the common standard form of the 3-dimensional
wave equation of plane atmospheres, given in Sect. 3
depends on second derivatives. This makes
the wave equation too complicated for heuristic or interpretative
studies. Even first derivatives
of atmospheric quantities in the invariant
can cause complications. It is for these reasons that we have sought
suitable transformations that yield new standard forms of the wave equation
with simple invariants.
The standard form (25) is still conventional. It offers the advantage
that the independent variable, the logarithmic mass, is a very simple quantity.
The invariant of this equation contains only the first derivative of the density,
which makes this equation superior to previous standard forms of the wave
equation.
In Sect. 5.2 we have adopted an unconventional approach and
have replaced the wave equation by a non-linearly coupled system of
two linear second order differential equations.
The behavior of the invariants of these equations
indicates an uncomplicated behavior of
high frequency acoustic waves and of gravity waves.
It is worth pointing out, that, for the latter,
this includes the whole range
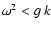 of gravity waves.
of gravity waves.
In Sect. 6, by some unconventional transformations,
we were able to find a wave equation the invariant of
which does not even contain the first derivative of the density.
The disadvantage of this wave equation, however, is that the independent
variable is no longer a function only of the geometrical height, but also
a function of the parameter 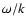 .
One thus has to discuss the invariant
for a given
.
One thus has to discuss the invariant
for a given 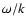 .
We have therefore given some arguments for
such a procedure which are related to Duvall's law. Like the wave equation
given in Sect. 5.1, this wave equation, too, offers
the advantage that, in the isothermal case, it reduces directly
to the familiar wave equation of the isothermal atmosphere.
.
We have therefore given some arguments for
such a procedure which are related to Duvall's law. Like the wave equation
given in Sect. 5.1, this wave equation, too, offers
the advantage that, in the isothermal case, it reduces directly
to the familiar wave equation of the isothermal atmosphere.
The invariant of the wave equation presented in Sect. 5.1
defines
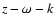 regions with certainly nonoscillatory solutions.
For selected values of the horizontal wave
number k we have presented such regions in the
regions with certainly nonoscillatory solutions.
For selected values of the horizontal wave
number k we have presented such regions in the 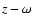 plane.
plane.
A future paper will address specific features in the diagnostic diagram
such as the p-mode ridges. We also hope that future studies in this area
will clarify which of the two wave equations is the most effective.
- Aizenman, M., Smeyers, P., & Weigert, A. 1977, A&A, 58, 41
NASA ADS
- Deubner, F.-L., & Gough, D. O. 1984, ARA&A, 22, 593
In the text
NASA ADS
- Duvall, T. L. Jr. 1982, Nature, 300, 242
In the text
NASA ADS
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971,
Sol. Phys., 18, 347
In the text
NASA ADS
- Gradshteyn, I. S., & Ryzhik, I. M. 1980, Tables of Integrals,
Series, and Products (Academic Press, New York)
In the text
- Lamb, H. 1932, Hydrodynamics (University Press, Cambridge)
In the text
- Ledoux, P., & Walraven, Th. 1958, in Handbuch der Physik, 51,
ed. S. Flügge (Springer-Verlag, Berlin), 526
In the text
- Leibacher, J. W., & Stein, R. F. 1981, in the Sun as a Star,
ed. J. Stuart, NASA SP-450, 263
In the text
- Mathews, J., & Walker, R. L. 1970,
Mathematical Methods of Physics (W. A. Benjamin Inc., New York)
In the text
- Mihalas, B. W., & Toomre, J. 1981, ApJ, 249, 349
In the text
NASA ADS
- Schmitz, F., & Fleck, B. 1994, A&AS, 106, 129
In the text
NASA ADS
- Schmitz, F., & Fleck, B. 1998, A&A, 337, 487
In the text
NASA ADS
- Schmitz, F., & Steffens, S. 1999, A&A, 344, 973
In the text
NASA ADS
- Spruit, H. 1977, Thesis, University of Utrecht
In the text
- Steffens, S. 1998, Thesis, University of Würzburg
In the text
- Steffens, S., Deubner, F.-L., Hofmann, J., & Fleck, B.
1995, A&A, 302, 277
NASA ADS
- Steffens, S., & Schmitz, F. 2000, A&A, 354, 280
In the text
NASA ADS
- Steffens, S., Schmitz, F., & Deubner, F.-L.
1997, Sol. Phys., 172, 85
In the text
NASA ADS
- Vernazza, J., Avrett, E., & Loeser, R. 1981, ApJS, 45, 635
In the text
NASA ADS
- Wolf, B. E. 1983, A&A, 127, 93
In the text
NASA ADS
Copyright ESO 2003
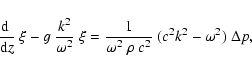
![\begin{displaymath}\frac{{\rm d}\;}{{\rm d} z}~\Delta p + g~\frac{k^2}{\omega^2}...
...a p =
\rho~\left[\omega^2-\frac{k^2 g^2}{\omega^2}\right]~\xi
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img16.gif)
![\begin{displaymath}\omega^2~c^2~\left[~{ {\rm d}^2~\Delta p\over {\rm d} z^2\;~}...
...ght)
+ \omega^2~(~c^2~k^2 - \omega^2~)~\right]~\Delta p = 0\;.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img23.gif)
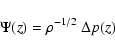
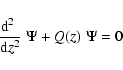
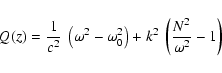
![\begin{displaymath}\omega_0^2 = {c^2\over 4}~\left[{3\over\rho^2}
\left({{\rm d}...
...ht )^2 - {2\over\rho}\;{{\rm d}^2\rho\over {\rm d} z^2}\right]
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img28.gif)
![\begin{displaymath}N^2 = g~\left[ -~{1\over\rho}~{{\rm d}\rho\over {\rm d} z} - {g\over c^2}\right ]\cdot
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img29.gif)
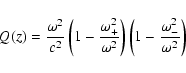
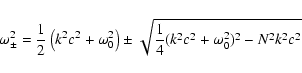
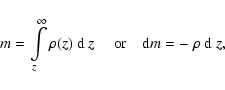
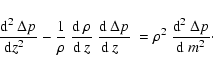
![\begin{displaymath}{{\rm d}^2\Delta p\over {\rm d} m^2\;~}+
{1\over \omega^2 c^2...
...d}~m} -g)
+ \omega^2 (\omega^2 - c^2 k^2)\right]\Delta p = 0 .
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img42.gif)
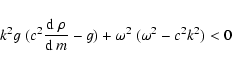
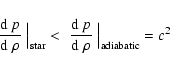
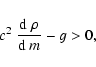
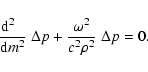
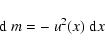
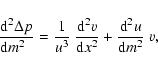
![$\displaystyle v\;u^3 {{\rm d}^2 u\over {\rm d} m^2} +{u^4\over\omega^2~c^2~\rho...
...m d}~\rho\over {\rm d}~m}-g\right)+
\omega^2~(\omega^2 - c^2 k^2)\right]~v = 0.$](/articles/aa/full/2003/08/aah4082/img54.gif)
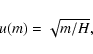
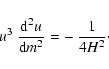
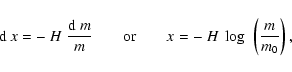
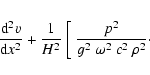
![\begin{displaymath}\hspace*{1cm}\left(~k^2~g~\left(c^2~{{\rm d}~\rho\over {\rm d...
...omega^2~(\omega^2 - c^2~k^2)~\right)-{1\over 4}~\bigg]\;v = 0,
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img59.gif)
![\begin{displaymath}{{\rm d}^2 v\over {\rm d} x^2} + {1\over H^2}\;\left[~{\omega^2~p^2\over g^2~c^2~\rho^2}
- {1\over 4}\right]\;v = 0.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img60.gif)
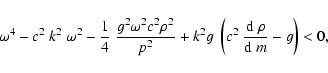
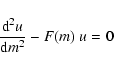
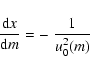
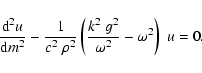
![\begin{displaymath}{{\rm d}^2 v\over {\rm d} x^2} +
{u_0^4~k^2\over\rho^2~\omeg...
...left[g~
{{\rm d}~\rho\over {\rm d}~m}- \omega^2\right]\;v = 0.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img69.gif)
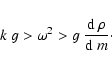
![\begin{displaymath}{{\rm d}^2 v\over {\rm d} m^2} +
{k^2\over\rho^2~\omega^2}\le...
...}~m}- \omega^2\right]\;v = 0\quad{\rm with}\quad v = \Delta p.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img73.gif)
![\begin{displaymath}{{\rm d}^2 u\over {\rm d} m^2} +
{k^2\over\rho^2~\omega^2}
\left[g~
{{\rm d}~\rho\over {\rm d}~m}- \omega^2\right]
\;u = 0.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img74.gif)
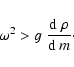
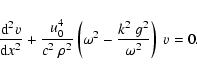
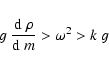
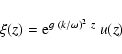
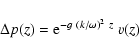
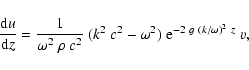
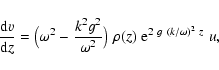
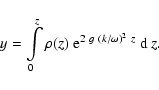
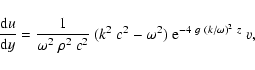
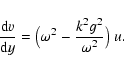
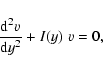
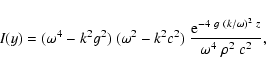
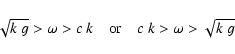
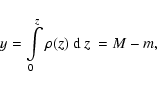
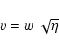
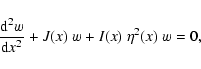
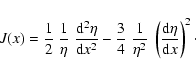
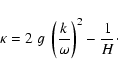
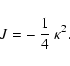
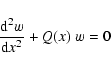
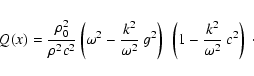
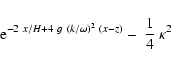
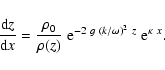
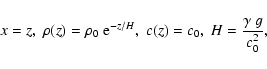

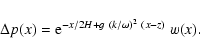
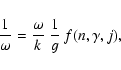
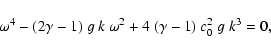
![\begin{displaymath}{1\over\omega} = \left(\displaystyle{\omega\over k}\right)^3\...
...\right)^2 g~(2\gamma-1) -
4~(\gamma-1)~c_0^2~g\;\right]^{-1}.
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img120.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H4082F1.eps}\end{figure}](/articles/aa/full/2003/08/aah4082/Timg123.gif)
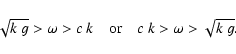
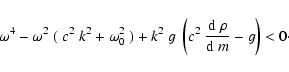
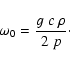
![\begin{displaymath}{1\over 2}\;\left[\left(c^2 k^2 + \omega_0^2\right)
\pm~\left...
...^2~{{\rm d}~\rho\over {\rm d}~m} -g\right)\right]^{1/2}\right]
\end{displaymath}](/articles/aa/full/2003/08/aah4082/img129.gif)
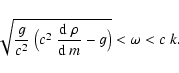
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{H4082F2.eps}\par\includegr...
...ip]{H4082F5.eps}\par\includegraphics[width=6.2cm,clip]{H4082F6.eps}
\end{figure}](/articles/aa/full/2003/08/aah4082/Timg136.gif)