

Up: On the precession of
Subsections
2 The precession
Consider a rigid, biaxial rotating star with
the principle axes
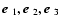 and corresponding principle
moment of inertia
and corresponding principle
moment of inertia
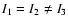 .
The star's angular momentum
.
The star's angular momentum  is
misaligned to the symmetry axis
is
misaligned to the symmetry axis
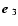 by a wobble angle
by a wobble angle 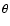 ,
i.e.
,
i.e.
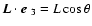 .
In general, we assume that the stellar
magnetic field is
dipolar and changes with time as
.
In general, we assume that the stellar
magnetic field is
dipolar and changes with time as
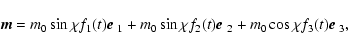 |
(1) |
where m0 is the
average
value of 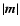 over a period
over a period
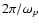 and
and 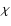 is the angle
between
is the angle
between 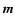 and
and
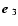 .
The functions
f1(t), f2(t) and f3(t) are arbitrary functions in time
and will be determined later by
using the data.
The equations of
motion in the corotating frame are
.
The functions
f1(t), f2(t) and f3(t) are arbitrary functions in time
and will be determined later by
using the data.
The equations of
motion in the corotating frame are
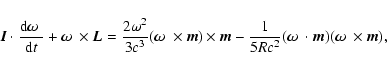 |
(2) |
where R is the average radius of the star.
The first term of the magnetic torque,
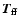 ,
is due to the
far-field radiation and has components both parallel and perpendicular
to the
spin axis. It is responsible for spinning down the star. The second term,
,
is due to the
far-field radiation and has components both parallel and perpendicular
to the
spin axis. It is responsible for spinning down the star. The second term,
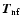 ,
represents the near-field radiation torque and is exactly
perpendicular to the spin axis. It has no contribution to the energy/angular
momentum transfer from the star. This torque does affect the wobble angle
and spin
rate of a freely
precessing star.
Following Link & Epstein (2001), for small wobble angle
,
represents the near-field radiation torque and is exactly
perpendicular to the spin axis. It has no contribution to the energy/angular
momentum transfer from the star. This torque does affect the wobble angle
and spin
rate of a freely
precessing star.
Following Link & Epstein (2001), for small wobble angle
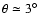 ,
suggested by
the observed pulse shape variations of PSR B1828-11 over one precession
period, and for small
oblateness
,
suggested by
the observed pulse shape variations of PSR B1828-11 over one precession
period, and for small
oblateness
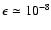 ,
we have
,
we have
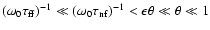 .
Here
.
Here 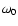 is the angular frequency of the star,
is the angular frequency of the star,
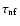 (
(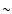 104 yr), and
104 yr), and
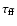 (
(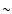 108 yr) are the corresponding near- and far-field
radiation torque time scales, respectively.
So up to the first
order of
108 yr) are the corresponding near- and far-field
radiation torque time scales, respectively.
So up to the first
order of 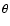 ,
the magnetic torques in the RHS of Eq. (2) can be neglected.
Therefore in this order, the angular velocity vector
,
the magnetic torques in the RHS of Eq. (2) can be neglected.
Therefore in this order, the angular velocity vector
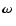 precesses freely around the star's symmetry axis as
precesses freely around the star's symmetry axis as
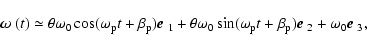 |
(3) |
with the precession frequency
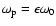 ,
and a constant phase
,
and a constant phase
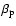 .
For the case of PSR B1828-11, observations
suggest that
.
For the case of PSR B1828-11, observations
suggest that
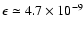 (Stairs et al. 2000).
Then
(Stairs et al. 2000).
Then
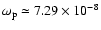 Hz or equivalently
Hz or equivalently
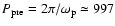 d.
d.
The observed timing behavior can be understood by considering the
contribution
of other torque's components in the variations of the spin rate.
By multiplying
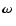 in Eqs. (2) we have
in Eqs. (2) we have
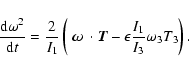 |
(4) |
Equation (4) shows the torque-induced variations in the spin rate of
star.
From Eq. (2) it is clear that the
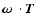 term
does not
depend on the near-field torque. It contributes to the spin rate change
only through the negligible final term.
Using Eqs. (1) and (2), by calculating
term
does not
depend on the near-field torque. It contributes to the spin rate change
only through the negligible final term.
Using Eqs. (1) and (2), by calculating
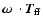 and subtracting Eq. (4) from the secular spin down of the
star (in the absence of precession),
and subtracting Eq. (4) from the secular spin down of the
star (in the absence of precession),
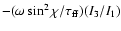 ,
one can find the spin rate due to the far-field torque as
(dropping constant terms)
,
one can find the spin rate due to the far-field torque as
(dropping constant terms)
Using Fourier expansion, we expand the functions
f1(t), f2(t), and
f3(t) as follow
| f1(t) |
= |
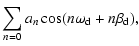 |
|
| f2(t) |
= |
 |
|
| f3(t) |
= |
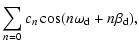 |
(5a) |
where
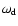 is frequency of the magnetic field's variation and
is frequency of the magnetic field's variation and
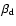 is constant. The coefficients an, bn, and cn will be
determined by fitting the data.
Equation (5) shows that the spin rate variations depend
on both the precession frequency and the variation frequency of the dipole
field.
For the case a0=c0=1 and
an=bn-1=cn=0 for
is constant. The coefficients an, bn, and cn will be
determined by fitting the data.
Equation (5) shows that the spin rate variations depend
on both the precession frequency and the variation frequency of the dipole
field.
For the case a0=c0=1 and
an=bn-1=cn=0 for 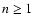 ,
Eq. (5) reduces to one obtained by
Link & Epstein (2001)
(except by a factor I3/I1).
,
Eq. (5) reduces to one obtained by
Link & Epstein (2001)
(except by a factor I3/I1).
To obtain the reported spectrum of PSR B1828-11, it is enough to consider
n=0 and 1 terms in Eq. (5) only.
The 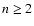 terms will produce
the higher harmonics which will be discussed later. Simply a correct
behavior of the spin rate can be found by setting c1=0, c0=1, and
b1=-a1.
Therefore Eq. (5) reduces to (dropping constant terms)
terms will produce
the higher harmonics which will be discussed later. Simply a correct
behavior of the spin rate can be found by setting c1=0, c0=1, and
b1=-a1.
Therefore Eq. (5) reduces to (dropping constant terms)
As one expected, the expression for observable variations in period
derivative,
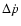 ,
will be modified as well.
The star's residual in
,
will be modified as well.
The star's residual in 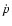 is owing to both
torque variation, Eq. (5), and the geometrical
effect.
The later is due to the orientation of the star's angular velocity vector
is owing to both
torque variation, Eq. (5), and the geometrical
effect.
The later is due to the orientation of the star's angular velocity vector
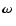 relative to the observer. As expected, the torque
effects dominate the geometrical effects by a factor
relative to the observer. As expected, the torque
effects dominate the geometrical effects by a factor
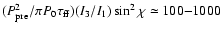 for the precession
period
for the precession
period
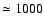 d, and so we neglected it here. Therefore
d, and so we neglected it here. Therefore
where
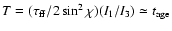 is
approximately equal to the characteristic spin-down age and P0 is the
spin period of star. Equation (7) gives the period derivative
residual due to far-field torque variations.
Now let us set
is
approximately equal to the characteristic spin-down age and P0 is the
spin period of star. Equation (7) gives the period derivative
residual due to far-field torque variations.
Now let us set
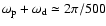 d-1
(equivalently
d-1
(equivalently
 d-1)
in Eq. (7). By assuming the fundumental precession
frequency is
d-1)
in Eq. (7). By assuming the fundumental precession
frequency is
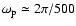 d-1, i.e.
d-1, i.e.
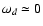 ,
only the 500 d and 250 d components
will survive in Eq. (7), as obtained by Link & Epstein
(2001), and all other harmonics are forbidden.
Although, as shown by observations, both 500 d and 250 d
Fourier components are dominant and have comparable amplitudes,
the other Fourier components, especially the 1000 d-component, have
nonzero amplitudes (Stairs et al. 2000).
To get the 1000 d-component
we choose
,
only the 500 d and 250 d components
will survive in Eq. (7), as obtained by Link & Epstein
(2001), and all other harmonics are forbidden.
Although, as shown by observations, both 500 d and 250 d
Fourier components are dominant and have comparable amplitudes,
the other Fourier components, especially the 1000 d-component, have
nonzero amplitudes (Stairs et al. 2000).
To get the 1000 d-component
we choose
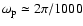 d-1corresponding to the fundamental Fourier frequency seen in the data,
so we have
d-1corresponding to the fundamental Fourier frequency seen in the data,
so we have
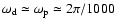 d-1. As is clear
from Eq. (7), the fundamental period
d-1. As is clear
from Eq. (7), the fundamental period 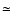 1000 d
and its first three harmonics,
1000 d
and its first three harmonics, 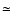 500, 333, and 250 d are present
in period derivative residual variations.
We note that the latter assumption requires
the magnetic field of the star changes in time with period
500, 333, and 250 d are present
in period derivative residual variations.
We note that the latter assumption requires
the magnetic field of the star changes in time with period
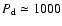 d close to the precession period
d close to the precession period
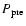 .
We will get back to this point later.
Therefore, Eq. (7)
reduces to (for
.
We will get back to this point later.
Therefore, Eq. (7)
reduces to (for
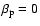 and
and
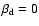 )
)
where t measured in days. Here we ignore the 1000 d and 500 d
contributions to the 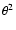 order.
For
order.
For
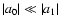 ,
the 250 d-component will be comparable to the
500 d-component if we have
,
the 250 d-component will be comparable to the
500 d-component if we have
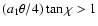 ,
or
,
or
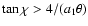 .
For a small
.
For a small 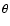 (
(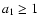 ), one finds that the magnetic dipole
moment must be nearly
orthogonal to the symmetry axis
), one finds that the magnetic dipole
moment must be nearly
orthogonal to the symmetry axis
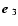 .
Hence for
.
Hence for
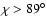 and
and
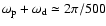 d-1,
the most dominant terms are the second and fourth harmonics, 500 d and
250 d, in good agreement with the observed data.
Since the proposed inclination angle between the star's spin axis and
the magnetic
field's symmetry axis is nearly a right angle,
d-1,
the most dominant terms are the second and fourth harmonics, 500 d and
250 d, in good agreement with the observed data.
Since the proposed inclination angle between the star's spin axis and
the magnetic
field's symmetry axis is nearly a right angle,
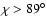 ,
one may consider the rotation of dipole vector as a magnetic poles reversal,
see Sect. 3 for more discussion.
,
one may consider the rotation of dipole vector as a magnetic poles reversal,
see Sect. 3 for more discussion.
In Fig. 1, by using Eq. (8) we fit the
observed 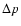 and
and
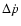 data (Stairs et al. 2000)
with a precession period of
data (Stairs et al. 2000)
with a precession period of
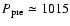 d,
a wobble angle
d,
a wobble angle
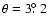 ,
and the inclination angle
,
and the inclination angle
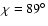 between the magnetic dipole and star's symmetry axis. The
Fourier expansion coefficients are a0=.01 and a1=1. We
note that our
fit is indistinguishable from the one obtained by Link & Epstein
(2001).
between the magnetic dipole and star's symmetry axis. The
Fourier expansion coefficients are a0=.01 and a1=1. We
note that our
fit is indistinguishable from the one obtained by Link & Epstein
(2001).
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3968F1.eps}
\end{figure}](/articles/aa/full/2003/08/aah3968/Timg102.gif) |
Figure 1:
Timing data for PSR B1828-11 (from Stairs et al. 2000). The top panel shows period residual 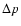 (in ns)
relative to the star's secular spin-down. The bottom panel
gives the time derivative
(in ns)
relative to the star's secular spin-down. The bottom panel
gives the time derivative
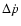 (in units of 10-15). The
solid curves are the fit explained in the text.
(in units of 10-15). The
solid curves are the fit explained in the text. |
It is interesting to note that Eq. (8) includes
1000,
500, 333, and 250 d
Fourier components. Further, by considering 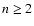 terms in Eq. (5),
one can find the
higher harmonics in
terms in Eq. (5),
one can find the
higher harmonics in
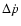 .
These terms were missing in the Link & Epstein's model.
In Table 1 we compare the time-varying magnetic field model with
one suggested by
Link & Epstein (2001),
and the observations made by Stairs et al. (2000).
.
These terms were missing in the Link & Epstein's model.
In Table 1 we compare the time-varying magnetic field model with
one suggested by
Link & Epstein (2001),
and the observations made by Stairs et al. (2000).
Table 1:
In this table we compare the
time-varying magnetic field model for PSR B1828-11
with one suggested by
Link & Epstein (2001) and the observed data reported by Stairs et al. (2000).
P0,
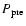 ,
,
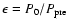 ,
,
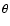 ,
and
,
and 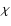 are the star's period,
precession period,
star's oblateness, wobble angle, and field's inclination angle,
respectively.
are the star's period,
precession period,
star's oblateness, wobble angle, and field's inclination angle,
respectively.
| Data/Model |
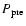 (d)
(d) |
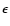 |
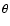 |
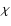 |
| Data |
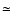 1000, 500, 250, 167
1000, 500, 250, 167 |
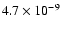 |
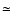 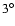 |
>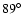 |
| Time-varying mag. model |
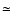 1000a, all harmonics 1000a, all harmonics |
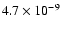 |
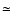 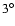 |
>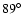 |
| Link & Epstein's model |
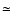 500a, 500a,
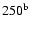 |
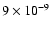 |
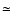 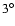 |
>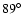 |


Up: On the precession of
Copyright ESO 2003
![]() and corresponding principle
moment of inertia
and corresponding principle
moment of inertia
![]() .
The star's angular momentum
.
The star's angular momentum ![]() is
misaligned to the symmetry axis
is
misaligned to the symmetry axis
![]() by a wobble angle
by a wobble angle ![]() ,
i.e.
,
i.e.
![]() .
In general, we assume that the stellar
magnetic field is
dipolar and changes with time as
.
In general, we assume that the stellar
magnetic field is
dipolar and changes with time as
![]() terms will produce
the higher harmonics which will be discussed later. Simply a correct
behavior of the spin rate can be found by setting c1=0, c0=1, and
b1=-a1.
Therefore Eq. (5) reduces to (dropping constant terms)
terms will produce
the higher harmonics which will be discussed later. Simply a correct
behavior of the spin rate can be found by setting c1=0, c0=1, and
b1=-a1.
Therefore Eq. (5) reduces to (dropping constant terms)
![]() and
and
![]() data (Stairs et al. 2000)
with a precession period of
data (Stairs et al. 2000)
with a precession period of
![]() d,
a wobble angle
d,
a wobble angle
![]() ,
and the inclination angle
,
and the inclination angle
![]() between the magnetic dipole and star's symmetry axis. The
Fourier expansion coefficients are a0=.01 and a1=1. We
note that our
fit is indistinguishable from the one obtained by Link & Epstein
(2001).
between the magnetic dipole and star's symmetry axis. The
Fourier expansion coefficients are a0=.01 and a1=1. We
note that our
fit is indistinguishable from the one obtained by Link & Epstein
(2001).
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3968F1.eps}
\end{figure}](/articles/aa/full/2003/08/aah3968/Timg102.gif)
![]() terms in Eq. (5),
one can find the
higher harmonics in
terms in Eq. (5),
one can find the
higher harmonics in
![]() .
These terms were missing in the Link & Epstein's model.
In Table 1 we compare the time-varying magnetic field model with
one suggested by
Link & Epstein (2001),
and the observations made by Stairs et al. (2000).
.
These terms were missing in the Link & Epstein's model.
In Table 1 we compare the time-varying magnetic field model with
one suggested by
Link & Epstein (2001),
and the observations made by Stairs et al. (2000).