A&A 399, 421-431 (2003)
DOI: 10.1051/0004-6361:20021753

Swirling astrophysical flows - efficient amplifiers of Alfvén waves!?

A. D. Rogava1,2,3,[*] - S. M. Mahajan4 - G. Bodo2 - S. Massaglia1


1 - Dipartimento di Fisica Generale, Universitá degli Studi di Torino, Via Pietro Giuria 1, Torino 10125, Italy
2 - Osservatorio Astronomico di Torino, Strada dell'Osservatorio 20, 10025 Pino Torinese, Italy
3 - Abdus Salam International Centre for Theoretical Physics, Strada Costiera 11, Trieste 34014, Italy
4 - Institute for Fusion Studies, The University of Texas at Austin, Texas 78712, USA

Received 27 November 2001 / Accepted 25 November 2002

Abstract
We show that a helical shear flow of a magnetized plasma may serve as an efficient amplifier of Alfvén waves. We find that even when the flow is purely ejectional (i.e., when no rotation is present) Alfvén waves are amplified through the transient, shear-induced, algebraic amplification process. Series of transient amplifications, taking place sequentially along the flow, may result in a cascade amplification of these waves. However, when a flow is swirling or helical (i.e., some rotation is imposed on the plasma motion), Alfvén waves become subject to new, much more powerful shear instabilities. In this case, depending on the type of differential rotation, both usual and parametric instabilities may appear. We claim that these phenomena may lead to the generation of large amplitude Alfvén waves and the mechanism may account for the appearance of such waves in the solar atmosphere, in accretion-ejection flows and in accretion columns. These processes may also serve as an important initial (linear and nonmodal) phase in the ultimate subcritical transition to MHD Alfvénic turbulence in various kinds of astrophysical shear flows.

Key words: magnetohydrodynamics (MHD) - waves


1 Introduction

Most of astrophysical objects involve different kinds of plasma flows. Recently it was fully realized that collective phenomena in flows with spatially inhomogeneous velocities (shear flows hereafter referred as SF) are characterized by remarkable, so called "nonmodal" processes, related with non-self-adjointness of linear dynamics of perturbations. Namely, it was found that SF: exchange energy with sound waves (Butler & Farrell 1992); couple different collective modes with one another and lead to their mutual transformations (Chagelishvili et al. 1996); generate nonperiodic, vortical modes of collective behaviour (so called "shear vortices" Rogava et al. 1998) - which eventually may or may not acquire wave-like features; excite beat wave phenomena both in neutral fluids (Rogava & Mahajan 1997) and plasmas (Poedts et al. 1998).

These processes take place not only in neutral fluids (Butler & Farrell 1992; Rogava & Mahajan 1997), standard MHD (Chagelishvili et al. 1996; Rogava et al. 1996; Tatsuno et al. 2001) and electrostatic plasmas (Rogava et al. 1998; Volponi et al. 2000; Mikhailenko et al. 2000), but also in strongly magnetized plasmas with anisotropic pressure (Chagelishvili et al. 1997), electron-positron plasmas (Mahajan et al. 1997) and dusty plasmas (Poedts et al. 2000). The possible role of these phenomena in astrophysical context was immediately realized and a number of astrophysical applications, including pulsar magnetospheric plasmas (Mahajan et al. 1997), solar atmospheric phenomena (Poedts et al. 1998; Rogava et al. 2000) and galactic gaseous disk dynamics (Rogava et al. 1999) appeared within a span of years.

One of the main shortcomings of all these studies, stemming from the very design of nonmodal schemes, is that the description is given in the wave number space (k-space), the knowledge about the appearance of shear-induced phenomena in the real, physical space is lacking. Two more serious limitations of these investigations are related with the neglect of the back reaction of perturbations on the mean flow and with the omission of viscous dissipation effects. However recently a successful effort was made in the direction of spatial visualization of the shear-induced wave transformations (Bodo et al. 2001), became clear that shear-induced processes in SF are quite robust and easily recognizable, even in the presence of quite heavy dissipation.

All these processes were studied predominantly for simple, plane-parallel flow geometries with linear velocity shear profiles. However, recently, a new method was developed (Mahajan & Rogava 1999), which allows a local analysis of the dynamics of linearized perturbations in SF with arbitrarily complex geometry and kinematics ${\vec U}(x,y,z)$. It was found that a slight deviation from the plane-parallel mode of motion brings into the game a variety of new, exotic and asymptotically persistent modes of collective behavior. Still the systematic investigation of shear-induced processes in kinematically complex SF is a challenging task in a state of infancy. The original study has been limited to two-dimensional flow patterns of neutral fluids (Mahajan & Rogava 1999).

One begins to wonder whether those astrophysical systems, where kinematically complex modes of plasma motion are definitely present - e.g., astrophysical jets (Ferrari 1998) or solar tornados (Pike & Mason 1998; Velli & Liewer 1999) - might sustain these collective phenomena and what kind of observational consequences could they lead to.

In this paper we consider interaction of a helical flow with Alfvén waves generated within the flow. This problem is actual in plasma physics and plasma astrophysics from experimental/observational, theoretical and numerical points of view.

We are used to observe Alfvén waves, being in interaction with plasma flows, in different astrophysical situations. For example, for the long time it is known that the Sun radiates Alfvén waves: outward propagating Alfvén waves are routinely observed in the solar wind flow at r>0.3 AU (Hollweg 1990). The observations of quasiperiodic pulsed ionospheric flows (PIF) have shown that the PIF are driven and correlated with Alfvénic fluctuations observed in the upstream solar wind (Prikryl et al. 2002). While the observations of the solar transition region (Peter 2001) imply that structuring of the transition region involves closed loops and coronal funnels showing unambiguous evidence for the presence of passing Alfvén waves.

In the theoretical domain the problem of the interaction between Alfvén waves and ambient flows is quite popular topic of studies in the wide range of applications including different kinds of laboratory, geophysical and astrophysical plasma flows. Recent studies of toroidal flows in axisymmetric tokamaks (van der Holst et al. 2000), for instance, revealed that these flows generate low-frequency Alfvén waves. The problem of Alfvén waves sustained by plasma flows is especially popular in the context of solar physics. It is argued that chromosphere and transition region flows are primary energy sources for the fast solar wind; while Alfvén waves, generated by post-reconnection processes, are continuously interacting with these flows (Ryutova et al. 2001). In accretion disks Alfvén waves also seem to be actively interacting with the disk flow - they are found to be unstable both in high-$\beta$(Balbus & Hawley 1991) and low-$\beta$ (Tagger et al. 1992) disks. Most recently it was claimed that the Accretion-Ejection Instability (Tagger & Pellat 1999) can extract accretion energy and angular momentum from magnetized disk, generate Alfvén waves and "feed" the disk corona with them (Varnièr & Tagger 2002).

Currently sophisticated numerical codes are developed, which allow to study the propagation of Alfvén waves along an open magnetic flux tube (Saito et al. 2001). These simulations are aimed to clarify mechanisms of the coronal heating and of the formation of solar plasma flow patterns: viz. solar spicules, macrospicules and solar tornadoes. More general numerical tools, like FINESSE and PHOENIX, aimed to study waves and instabilities in different kinds of flows, were very recently developed (Belien et al. 2002). We assume that all these numerical tools could also be used in a number of astrophysical applications involving "parent" flows and "inborn" Alfvén waves interacting with each other.

Most of above-cited studies considered simple (plane-parallel or locally plane-parallel) kinds of flows and the processes were treated by means of usual normal-mode analysis. The purpose of this paper (Paper I) is to study "nonmodal'' evolution of Alfvén waves in swirling flows and to show that these flows may operate as efficient "amplifiers" of Alfvén waves.

In the next section we develop the mathematical formalism and derive general equations governing the evolution of Alfvén waves in helical flows. However, the third section is dedicated to the study of the simpler example of a parallel SF ("pure outflow"). Still, even in this simple case, we find that the amplification of Alfvén waves takes place. The amplification mechanism is linear, transient and can be described by appealingly simple mathematics. The amplification occurs within a relatively brief time interval and it appears as an abrupt, burst-like increase of the wave amplitude. It is tempting to argue that individual acts of wave amplifications, occurring sequentially, may ignite the "chain reaction" of nonmodal cascade amplification of Alfvén waves.

The fourth section of the paper is dedicated to fully helical SF. We show that when SF are helical ("outflow + rotation") there appear new classes of shear instabilities capable of generating high-amplitude Alfvén waves. The presence of differential rotation is crucial for these instabilities and in certain cases the instability is of parametric nature. These instabilities are powerful, often have a "resonant'' nature and are exclusively related with the kinematic complexity of "parent'' shear flows.

The fifth section of the paper contains discussion of the obtained results and of their possible astrophysical applications. We argue that such wave amplification processes may have various astrophysical manifestations including large amplitude Alfvén waves actually observed in the solar atmosphere (Balogh et al. 1995). They could provide the necessary seeding for the development of MHD turbulence in hydromagnetic shear flows. These processes may be present and may lead to perceptible morphological variety and diverse observational appearances in various kinds of "accretion-ejection'' flows: innermost regions of accretion disks, disk-jet transition regions, accretion columns in X-ray pulsars and cataclysmic variables, inner regions of galactic gaseous disks, etc.

This paper will be followed by the second one (Paper II), where we will consider the same flow structure but allow the perturbations to be fully compressible, bringing on-stage another two additional linear MHD wave modes - the slow and fast magnetosonic waves.

2 Main consideration

Our aim is to develop a theory of collective phenomena in helical flows of magnetized plasmas. We adopt the standard MHD model and consider incompressible perturbations in an axisymmetric, cylindrical, steady flow of a plasma with uniform density ( ${\rho}_0={\rm const.}$), embedded in a vertical, homogeneous ${\vec B}_0=(0,~0,~B_0)$ magnetic field. With $\rho = {\rho}_0+ \varrho$, P=P0+p, ${\vec V}={\vec U}+{\bf u}$, ${\vec B}={\vec B}_0+ {\vec B}^{'}$, the basic set of MHD equations for linearized perturbations is:

                                 $\displaystyle \nabla {\vec u}=0,$ (1)
    $\displaystyle D_t {\vec u}+({\vec u} \cdot {\nabla}){\vec U}=-{1 \over {\rho}_0... ...a}p-{{{\vec B}_0}\over {4{\pi}{\rho}_0}}{\times}({\nabla}{\times}{\vec B}^{'}),$ (2)
    $\displaystyle D_t{\vec B}^{'}=({\vec B}^{'} \cdot {\nabla}){\vec U} + ({\vec B}_0 \cdot {\nabla}){\vec u},$ (3)
    $\displaystyle \nabla {\vec B}^{'}=0,$ (4)

where $D_t\equiv{\partial}_t+({\vec U} \cdot {\nabla})$ is the convective derivative operator and ${\vec U}(r)$is the vector field of the steady state flow. Unfortunately the actual kinematic portrait of astrophysical helical flows is largely unknown. There is no credible data for recently discovered solar macrospicules with helical plasma motion (solar tornados), for accretion columns related to X-ray pulsars and cataclysmic variables, for accretion-ejection flows and galactic and extragalactic jets. Therefore, we need to adopt a phenomenological model for ${\vec U}$, that has to be general enough to encompass different possible sorts of real helical flows. Preferably the model must be three-dimensional and it should include a possibility of both outflowing/inflowing and rotational modes of motion. The model we choose is (Rogava & Poedts 1999):
$\displaystyle {\vec U}(r)\equiv[0,~r{\Omega}(r),~U(r)],$     (5)

where r=(x2+y2)1/2 is a distance from the rotation axis. For the angular velocity we take:
$\displaystyle {\Omega}(r)={\cal A}/r^n,$     (6)

with ${\cal A}$ and n as constants. This model implies the following two limiting cases: The corresponding Cartesian components of the linear azimuthal velocity $U_{\phi}=r{\Omega}(r)$ are:
    $\displaystyle U_x(x,y)=-{\cal A}y/r^n,$ (7a)
    $\displaystyle U_y(x,y)={\cal A}x/r^n.$ (7b)

The basic role in our analysis is played by the shear matrix ${\cal S}_{ik} \equiv{\partial}U_i/{\partial}x_k$. Evidently rotational part of the flow velocity generates the following four nonzero components of the shear matrix:
                            $\displaystyle {\sigma}\equiv{\cal S}_{xx}=2{\cal A}nx_0y_0/r_0^{n+2},$ (8a)
    $\displaystyle {\cal S}_{yy}=-{\sigma},$ (8b)
    $\displaystyle A_1\equiv{\cal S}_{xy}=-{\cal A}\left[x_0^2+(1-n)y_0^2\right]/r_0^{n+2},$ (8c)
    $\displaystyle A_2\equiv{\cal S}_{yx}={\cal A}\left[(1-n)x_0^2+y_0^2\right]/r_0^{n+2}.$ (8d)

As regards the outflow component of the velocity we can use the model (Rogava et al. 2000):

\begin{displaymath}U_z(x,y)=U_m\left[1-(r/R)^2\right], \end{displaymath} (9a)

comprising a parabolically sheared "outflow" along the Z-axis, being similar to the well-known Hagen-Poiseuille flow. The outflow model may be modeled also in a number of other ways. In astrophysical jet literature, for instance, the model (Ferrari 1998):

\begin{displaymath}U_z=U_m/{\rm cosh}[r^m], \end{displaymath} (9b)

is often used. One can easily see that the outflow component, given by (9), generates the following two components of the shear matrix:
$\displaystyle C_1\equiv{\cal S}_{zx}=-2U_mx_0/R^2,$     (10a)
$\displaystyle C_2\equiv{\cal S}_{zy}=-2U_my_0/R^2.$     (10b)

Therefore, the resulting helical flow is the superposition of a cylindrical outflow along the Z-axis with a differential motion in the transverse cross-section of the jet. The complete $3 \times 3$traceless shear matrix is:
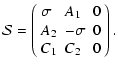$\displaystyle {\cal S}=\left(\begin{array}{lll} {\sigma}&A_1&0\cr A_2&-{\sigma}&0 \cr C_1&C_2&0\cr\end{array}\right).$     (11)

This shear matrix has a number of interesting properties. Its square is equal to:
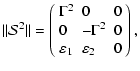$\displaystyle \vert\vert{\cal S}^2\vert\vert=\left(\begin{array}{lll} {\Gamma}^... ...-{\Gamma}^2 & 0 \cr {\varepsilon}_1& {\varepsilon}_2 &0 \cr \end{array}\right),$     (12)

where we use the notation:
                             $\displaystyle {\varepsilon}_1\equiv A_2C_2+{\sigma}C_1,$ (13a)
    $\displaystyle {\varepsilon}_2\equiv A_1C_1-{\sigma}C_2;$ (13b)
    $\displaystyle {\Gamma}\equiv\left({\sigma}^2+A_1A_2\right)^{1/2}=\sqrt{n-1}~{\Omega}(r),$ (13c)

and its cube is: $\vert\vert{\cal S}^3\vert\vert={\Gamma}^2\vert\vert{\cal S}\vert\vert$.

The nonmodal local method for studying the dynamics of linearized perturbations in kinematically complex flows (Lagnado et al. 1984; Craik & Criminale 1986; Mahajan & Rogava 1999) allows to reduce the initial set of partial differential equations for perturbation variables $F({\vec r},t)$, defined in the real physical space, to the initial value problem formulated for the perturbation variable amplitudes ${\hat F}({\vec k},t)$, defined in the space of wave numbers (k-space). The key element of this approach is the time variability of ${\vec k}$'s, imposed by the presence of the shear flow! This variability is governed by the following set of equations:

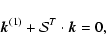\begin{displaymath}{\vec k}^{(1)}+{\cal S}^T\cdot{\vec k}=0, \end{displaymath} (14)

henceforth for an arbitrary function f we use the notation: ${\partial}_t^nf\equiv f^{(n)}$.

For the helical flow we find that ${\vec k}^{(3)}={\Gamma}^2{\vec k}^{(1)}$. The corresponding characteristic equation ${\rm det}[{\cal S}^T-{\lambda}{\times} {\cal I}]=0$ (with ${\cal I}$ being a unit matrix) yields the equation for the eigenvalues:

\begin{displaymath}{\lambda}({\lambda}-{\Gamma})({\lambda}+{\Gamma})=0, \end{displaymath} (15a)

with the solutions:

\begin{displaymath}{\lambda}_1=0,~~~~{\lambda}_{2,3}={\pm}{\Gamma}. \end{displaymath} (15b)

We see that the differential rotation parameter nplays a decisive role in determining the evolution scenario for the wave number vector ${\vec k}(t)$: when n<1 (including the rigid rotation case) $\Gamma$ is imaginary and the time evolution of ${\vec k}(t)$ is periodic, while when n>1 (including the Keplerian rotation regime), $\Gamma$ is real and makes the time behavior of ${\vec k}(t)$ exponential.

In the dimensionless notation $v_{x,y,z}\equiv{\hat u}_{x,y,z}$, ${\cal P}\equiv i{\hat p}/{\rho}_0$, $b_{x,y,z}\equiv i{\hat B}^{'}_{x,y,z}/B_0$, perturbation amplitudes evolve as:

                         $\displaystyle ({\vec k}{\cdot}{\vec v})=0,$ (16)
    $\displaystyle {\vec v}^{(1)}+{\cal S}{\cdot}{\vec v}=-{\vec k}{\cal P}-C_{\rm A}^2[{\vec k}b_z-k_z {\vec b}],$ (17)
    $\displaystyle {\vec b}^{(1)}={\cal S}{\cdot}{\vec b}-k_z{\vec v}, (i=x,y)$ (18)
    $\displaystyle ({\vec k}{\cdot}{\vec b})=0.$ (19)

In the next two sections we separately consider the problem of a purely ejectional/injectional flow, and a flow with helical motion of plasma particles. We shall see that in both cases the Alfvén waves sustained by the flow are amplified. For the former case the amplification is transient (algebraic instability), while for the latter case the velocity shear makes Alfvén waves exponentially unstable.

3 Ejectional flow

This case corresponds to $\sigma=A_1=A_2=0$. We can introduce a vector ${\vec C}\equiv[C_x \equiv C_1,C_y \equiv C_2,C_z=0]$, which is proportional to the position vector ${\vec r}_0= (x_0, y_0, 0)$ connecting the point A(x0,y0,z0) (the centre of our local frame) with the Z-axis in a z=z0 plane. Its absolute value is equal to ${\rm d}U_z/{\rm d}r$. The wave number dynamics is given by simple linear solutions: ki(t)=ki(0)-Cikzt, with i=x, y, while the vertical component kz stays constant. The symmetry of the flow implies that the vector product of ${\vec C}$ and ${\vec k}$ has a constant vertical component ${\Delta}\equiv- ({\vec C}{\times}{\vec k})_z=C_yk_x(t)-C_xk_y(t)={\rm const}(t)$, which, in its turn, is a linear combination of transverse components of the wave number vector. This fact suggests the decomposition $k_{\parallel}(t)\equiv({\vec C} \cdot {\vec k})/\vert{\vec C}\vert$, $k_{\perp}\equiv({\vec C} \times {\vec k})_z/\vert{\vec C}\vert$, i.e.,

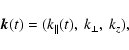\begin{displaymath}{\vec k}(t)=(k_{\parallel}(t),~k_{\perp},~k_z), \end{displaymath} (20)

with the entire time dependence of ${\vec k}(t)$ contained in

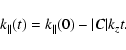\begin{displaymath}k_{\parallel}(t)=k_{\parallel}(0)-\vert{\vec C}\vert k_zt. \end{displaymath} (21)

The system admits a surprisingly efficient and complete analytic description if we introduce, first, vectors of hydrodynamic ( ${\vec{\Omega}_h}\equiv{\vec k}{\times}{\vec v}$) and magnetic ( ${\vec{\Omega}_m}\equiv{\vec k}{\times}{\vec b}$) vorticity and consider the following scalar products: $V\equiv({\vec C}{\cdot}{\vec v}) $, ${\cal V}\equiv({\vec C}{\cdot}{\vec{\Omega}}_h)$, $B\equiv({\vec C} {\cdot}{\vec b})$, and ${\cal B}\equiv({\vec C}{\cdot}{\vec{\Omega}}_m)$. The usefulness of these variables becomes apparent when we check that they obey the following set of first-order equations:
                            $\displaystyle V^{(1)}=-\left[ln\left(\vert{\vec k}(t)\vert^2\right)\right]^{(1)}V+C_{\rm A}^2k_zB,$ (22a)
    $\displaystyle {\cal V}^{(1)}={\Delta}V+C_{\rm A}^2k_z{\cal B},$ (22b)
    B(1)=-kzV, (23a)
    $\displaystyle {\cal B}^{(1)}=-{\Delta}B-k_z{\cal V},$ (23b)

which is remarkably simple with only one time-dependent coefficient (time dependence exclusively due to shear) in Eq. (22a).

These variables give complete description of the system, because "physical" variables ${\vec v}$ and ${\vec b}$ are readily expressed by means of V, $\cal V$, B, and $\cal B$ via the following vector identities:

                               $\displaystyle {\vec v}={1 \over{\vert{\vec C}{\times}{\vec k}\vert^2}}{\biggl[{... ...vec C}{\times} {\vec k})+V({\vec k}{\times}({\vec C}{\times}{\vec k}))\biggr]},$ (24a)
    $\displaystyle {\vec b}={1 \over{\vert{\vec C}{\times}{\vec k}\vert^2}}{\biggl[{... ...vec C}{\times} {\vec k})+B({\vec k}{\times}({\vec C}{\times}{\vec k}))\biggr]}.$ (24b)

While for the kinetic and magnetic energies of the system we also have rather transparent expressions:
                                 $\displaystyle E_{\rm k}={1 \over 2}\vert{\vec v}\vert^2={1 \over{2\vert{\vec C}{\times}{\vec k}\vert^2}} {\biggl[{\cal V}^2+V^2\vert{\vec k}\vert^2\biggr]},$ (25a)
    $\displaystyle E_{\rm m}={C_{\rm A}^2 \over 2}\vert{\vec b}\vert^2={C_{\rm A}^2 ... ...C}{\times} {\vec k}\vert^2}}{\biggl[{\cal B}^2+B^2\vert{\vec k}\vert^2\biggr]},$ (25b)
    $\displaystyle E_{\rm tot}\equiv E_{\rm k} + E_{\rm m}.$ (25c)

From (22) and (23) we can further notice that the Alfvén waves, sustained by this system are "splitted" by the presence of the velocity shear. Note that the symmetry of (31) implies that its solutions must be invariant with respect to the inversion operation. Namely, if a pair of initial values ${\Psi}_a(-T_0)$ and ${\Psi}^{(1)}_a(-T_0)$gives a certain solution then ${\Psi}_a(T_0)$ and $-{\Psi}^{(1)}_a(T_0)$ gives inversion-symmetric solution.


  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{plot1.ps}\end{figure} Figure 1: The plots of the function ${\Omega }^2_{\rm eff}(T)$ for different values of the a parameter. Solid line corresponds to the case a=0.9, dashed line to a=0.7, dotted one to a=0.5, and dashed-dotted to a=0.3.
Open with DEXTER

Analysis of (31) begins by studying the temporal behavior of the "effective frequency"

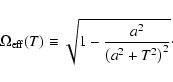\begin{displaymath}{\Omega}_{\rm eff}(T)\equiv{\sqrt { 1-{{a^2}\over{{\left(a^2+T^2 \right)}^2}}}}\cdot \end{displaymath} (32)

For sufficiently large absolute values of T, ${\Omega}_{\rm eff}(T)\simeq 1$, implying that at the corresponding periods of time, the system supports just the usual constant frequency and constant amplitude Alfvén waves. However, when |a|<1 there are two moments of time $T_{\pm}\equiv\pm {\sqrt {a(1-a)}}$ when the "effective frequency of shear-modified Alfvén waves" becomes zero and in the interval T-<T< T+it stays imaginary. Therefore, within this time interval (with the width determined by $\Delta T\equiv 2T_{+}$), swift and sudden changes in the temporal evolution of Alfvén waves may be expected.

Quantitative picture of this behavior is illustrated by Fig. 1 where we plotted the ${\Omega }^2_{\rm eff}(T)$ for different (but all |a|<1) values of a. One sees that with the decrease of a the minimum of ${\Omega }^2_{\rm eff}(T)$ becomes sharper: the depth of the minimum in Fig. 1 (which accounts for maximum increments of the transient instability) steadily increases with the decreasing a. The width of the time interval, in which this function stays negative (and, correspondingly, ${\Omega}_{\rm eff}(T)$ is imaginary) is maximum for a=1/2 and tends to zero when $a\simeq 1$ and $a \ll 1$.

At a first glance, from (31), it seems that decreasing a we would have the continuous increase of the transient amplification rate. However decreasing a we also make smaller the scaling factor between the physical time t and the variable T, which appears in (31). Besides, the small values of a imply smaller values of the Alfvén speed and the vertical component of the wavenumber vector kz. Therefore, we can conclude that transient amplification factor for lower frequency Alfvén waves is higher, but for the amplification to occur the system needs a longer time interval. This means, in turn, that outflows with shorter/longer lifetime values are expected to amplify higher/lower frequency Alfvén waves.


  \begin{figure} \par\includegraphics[angle=90,width=8.1cm,clip]{plot2.ps}\end{figure} Figure 2: The numerical solution of Eq. (31) featuring the function ${\Psi }_a(T)$ for a=0.1 case. The initial values are: ${\Psi }_a(-100)=0.01$ and ${\Psi }_a^{(1)}(-100)=0$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.1cm,clip]{plot3.ps} \end{figure} Figure 3: The numerical solution of Eq. (31), which is inversion-symmetric to the one given in Fig. 2. Initial values here are: ${\hat{\Psi}}_a(-100)=-0.1354$ and ${\hat{\Psi}}_a^{(1)}(-100)=-0.2186$.
Open with DEXTER

The presence of the imaginary effective frequency for a limited time interval means that Alfvén waves excited and maintained by the shear flow become subject to a certain, velocity shear induced instability, which is present only within the limited time interval. That is why we specify this phenomenon by the term "transient instability". Since the time interval is rather brief one can expect that the appearance of this instability will have a burst-like, explosive nature: initially at times T < T- waves stay almost unaffected by the presence of the shear flow. However, as soon as the system will enter the transient instability interval T-<T< T+, the Alfvén waves undergo drastic and abrupt change in their amplitudes. Depending on the initial values, the mode of evolution will be a certain mixture of swiftly decaying and/or increasing modes within the $\Delta T$instability domain. But as soon as T > T+ the waves become stable again and their amplitudes do not change anymore The resulting wave amplitude is enhanced/diminished in comparison with the initial amplitude depending whether transiently increasing/decreasing component was dominant for the initially excited wave.


  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{plot4.ps}\end{figure} Figure 4: The numerical solution of Eq. (28) presented for all components of ${\vec v}$ (solid lines on first three plots) and ${\vec b}$ (dashed lines on first three plots) vectors. Last plot shows time evolution of $E_{\rm tot}(t)/E_{\rm tot}(0)$. The values of parameters are: $C_{\rm A}=0.2$, kx=20, ky=10, kz=0.1, Cx=0.1, Cy=0.05, a=0.1789. Initial values are: ${\Psi }(0) =0.01$ and ${\Psi }^{(1)}(0)=0$.
Open with DEXTER

Numerical results, represented by Figs. 2-5, fully confirm these qualitative expectations. Figures 2 and 3 illustrate the inversion symmetry of the functions  ${\Psi }_a(T)$. The first of these two plots shows the temporal evolution for a=0.1 and with initial conditions ${\Psi }_a(-100)=0.01$ and ${\Psi }_a^{(1)}(-100)=0$. The figure is plotted for the interval -100<T<100. Evidently the inversion symmetry implies that an another solution of this equation for the same value of a but with the initial values ${\hat{\Psi}}_a(-100)={\Psi}_a(100)$ and ${\hat{\Psi}}_a^{(1)}(-100)=-{\Psi}_a^{(1)}(100)$ will be exactly inverse-symmetric. In this particular example these initial values are ${\hat{\Psi}}_a(-100)=-0.1354$ and ${\hat{\Psi}}_a^{(1)}(-100)=-0.2186$. The inversion symmetry of these solutions is apparent. Physically this fact implies that the presence of the shear flow ensures burst-like and robust increase of amplitudes (energy) of some Alfvén waves, while there are always other waves which, on the contrary, sharply loose their energy under the influence of the shear flow.

Momentary appearance of the transient instability on the presented graphs is related to the narrowness of the transient instability interval, which is apparent from Fig. 1. Note that the plotting time interval in Fig. 1 is taken very narrow in order to give magnified portrait of the behavior of ${\Omega}_{\rm eff}$, while Figs. 2 and 3 are deliberately drawn for the much wider range in order to illustrate the behavior of waves on a large time span.

The family of solutions ${\Psi }_a(T)$ of (31) does not represent a physical variable of the problem, so in order to recover information about the temporal evolution of perturbations for physical variables it is more convenient to solve numerically (22-23) and to recover components of vectors ${\vec v}$ and ${\vec b}$ from (24). Besides, it is instructive to calculate the kinetic energy, the magnetic energy and the total energy of perturbations as given by (25). In order to track the temporal evolution of the shear-modified wave branch as such we set the amplitude of the unmodified component ${\cal B}(t)$ to be zero ${\cal C}=0$. Alternatively our numerical task was, first, to solve Eq. (28) in order to get functions ${\Psi}(t)$ and ${\Psi}^{(1)}(t)$. Second step was to calculate the physical variables by means of Eqs. (22)-(25).

This set of calculations was performed for different values of the system parameters and some representative examples are given in Figs. 4 and 5. Note that they are plotted as functions of the real time variable t and not the variable T used in (31). From these figures we readily see that when $\Delta = 0$( $k_{\perp}=0$), the shear flow efficiently "pumps" energy into the longitudinal components of the velocity and the magnetic field perturbations, while the transverse components stay basically unchanged aside from the transitory, "burst-like" increase of their amplitudes in the brief, transient amplification phase. This is another indication of the above-mentioned fact that the velocity shear primarily affects the incompressible limit of the fast magnetosonic waves. The asymptotic increase of the total energy, as shown in Fig. 4, being entirely due to the increase in vz and bz, is quite substantial (about two orders of magnitude for the given example).


  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{plot5.ps} \end{figure} Figure 5: The numerical solution of Eqs. (22)-(23) with the same parameters as in Fig. 4 except ky=10.1.
Open with DEXTER

This is a typical mode of behavior for perturbations with $\Delta = 0$ and it is quite similar with the behavior of hydromagnetic waves in plane shear flows (Chagelishvili et al. 1993). By imparting a small but nonzero ${\Delta}$ (see Fig. 5), we can make all perturbation components grow. However, the overall increase of the total energy of perturbations in the latter case is somewhat smaller than in the former case.

4 Helical flow

For more complicated MHD flows, the time evolution of the wavenumber vector  ${\vec k}(t)$, governed by Eqs. (14), becomes nonlinear and it makes the temporal behavior of linear perturbations much more complex. A relatively simple, 2-D hydrodynamic system of such complexity was recently investigated (Mahajan & Rogava 1999). For the MHD helical flow, specified by the shear matrix (11) and considered in this section, we may deduce from (15) and (13c) that the perturbations may grow either exponentially (when differential rotation rate n>1), or vary in time in a periodic way (when n<1). Below we develop the mathematical formalism for the study of perturbation evolution for these two classes of solutions.

4.1 General formalism

The starting set of equations is again (16)-(19). Taking time derivative of (16) we find out that

$\displaystyle ({\vec k}{\cdot}{\vec v})^{(1)}=-({\cal S}^T{\cdot}{\vec k}){\cdo... ...c k}{\cdot} ({\cal S}{\cdot}{\vec v})-\vert{\vec k}\vert^2(P+C_{\rm A}^2b_z)=0,$      

which after noticing that $({\cal S}^T{\cdot}{\vec k}){\cdot}{\vec v}= {\vec k}{\cdot}({\cal S}{\cdot}{\vec v})$ implies that the following algebraic relation holds:
$\displaystyle P+C_{\rm A}^2b_z=-2{\vec k}{\cdot}({\cal S}{\cdot}{\vec V})/\vert{\vec k}\vert^2=2{\vec k}^{(1)} {\cdot}{\vec v}/\vert{\vec k}\vert^2.$     (33)

Note that this relation follows from (16), which, in turn, is direct consequence of the "incompressibility'' condition. The relation (33), applied to (17), helps to reduce the initial system to the following pair of the first-order ODE's:
                            $\displaystyle {\vec v}^{(1)}+{\cal S}{\cdot}{\vec v}=C_{\rm A}^2k_z{\vec b}-2\left({\vec k}^{(1)}{\cdot}{\vec v}\right) {\vec k}/\vert{\vec k}\vert^2,$ (34)
    $\displaystyle {\vec b}^{(1)}={\cal S}{\cdot}{\vec b}-k_z{\vec v}.$ (35)

It is worthwhile also to note that $ {\vec k}({\vec k}^{(1)}{\cdot}{\vec v})={\vec v}{\times}({\vec k}{\times}{\vec k}^{(1)})$, which allows to rewrite (34) in the following form:
$\displaystyle {\vec v}^{(1)}+{\cal S}{\cdot}{\vec v}=C_{\rm A}^2k_z{\vec b} +{\vec R}{\times}{\vec v},$     (36)

with ${\vec R}$ defined as:
$\displaystyle {\vec R}(t)\equiv\left({\vec k}{\times}{\vec k}^{(1)}\right)/\vert{\vec k}\vert^2.$     (37)

The interesting property of this form of the Eq. (34) is that the only time-dependent coefficient is just represented by one vector R(t)!

We can reduce (34) and (35) to the following explicit second-order equation for the magnetic field:

$\displaystyle {\vec b}^{(2)}+{\left[{\omega}_{\rm A}^2-{\cal S}^2 \right]}{\vec... ...t[{\vec k}^{(1)}{\cdot}{\vec b}^{(1)}+{\vec k}^{(2)}{\cdot}{\vec b} \right]}=0.$     (38)

This equation is quite informative, because it shows explicitly the effects of the helical flow imposed upon the evolution of perturbations. Note that the term containing ${\vec k}^{(1)}{\cdot}{\vec b}^{(1)}$is also present in the pure outflow case (see for comparison Eq. (27)). While terms containing ${\cal S}^2{\vec b}$ and ${\vec k}^{(2)} \cdot {\vec b}$ are characteristic to the case of helical flow and they reflect different aspects of shear-induced processes in helical flows.

Obviously (38) is a general equation and we can base our analysis on it. However a different approach may also be useful. Let us introduce "projection variables":

                      $\displaystyle U\equiv{\cal S}_{ij}k_iv_j=-{\vec k}^{(1)}{\cdot}{\vec v},$ (39a)
    $\displaystyle H\equiv{\cal S}_{ij}k_ib_j=-{\vec k}^{(1)}{\cdot}{\vec b},$ (39b)
    $\displaystyle V\equiv{\cal S}^2_{ij}k_iv_j={\vec k}^{(2)}{\cdot}{\vec v},$ (39c)
    $\displaystyle B\equiv{\cal S}^2_{ij}k_ib_j={\vec k}^{(2)}{\cdot}{\vec b}.$ (39d)

Using these definitions and our basic set of equations we find:
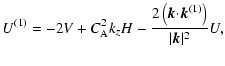                               $\displaystyle U^{(1)}=-2V+C_{\rm A}^2k_zH-{{2\left({\vec k}{\cdot}{\vec k}^{(1)}\right)}\over{\vert{\vec k}\vert^2}}U,$ (40)
    H(1)=-kzU, (41)
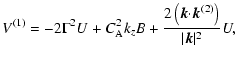    $\displaystyle V^{(1)}=-2{\Gamma}^2U+C_{\rm A}^2k_zB+{{2\left({\vec k}{\cdot}{\vec k}^{(2)}\right)}\over{\vert{\vec k}\vert^2}}U,$ (42)
    B(1)=-kzV. (43)

From this set we can derive the following two second-order equations for H and B:
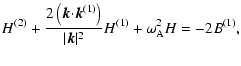                                      $\displaystyle H^{(2)}+{{2\left({\vec k}{\cdot}{\vec k}^{(1)}\right)}\over{\vert{\vec k}\vert^2}}H^{(1)}+{\omega}_{\rm A}^2H= -2B^{(1)},$ (44)
    $\displaystyle B^{(2)}+{\omega}_{\rm A}^2B=f(t)H^{(1)},$ (45)

where
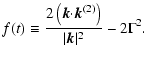$\displaystyle f(t)\equiv{{2\left({\vec k}{\cdot}{\vec k}^{(2)}\right)}\over{\vert{\vec k}\vert^2}}-2{\Gamma}^2.$     (46)

Moreover, if we define
$\displaystyle {\Psi}\equiv\vert{\vec k}\vert H,$     (47)

we can rewrite (44) also as:
$\displaystyle {\Psi}^{(2)}+{\left[{\omega}_{\rm A}^2-\vert\vec R\vert^2-{{\left... ...ight)}\over {\vert{\vec k}\vert^2}}\right]}{\Psi}=-2\vert{\vec k}\vert B^{(1)}.$     (48)

Note the appearance of the vector ${\vec R}$ in this equation. Overall, (45) and (48) give rather transparent analytic presentation, which can be used for the analysis of interesting classes of solutions. Note also that in the absence of rotation f(t)=0 these equations become decoupled and they reduce to the "pure outflow" case. In that case, we had a splitting of the mode into the usual Alfvén and shear-modified ("hybrid" as we can also call it) Alfvén mode. Below we shall see that rotation not only gives birth to new instabilities but it couples these two branches of the Alfvén mode!

4.2 Exponential k(t) case

Depending on the actual type of the motion in the plane normal to Z there will be different regimes of the time variation of ${\vec k}(t)$ (see for details Mahajan & Rogava 1999). Instabilities are present both when the wavenumber varies exponentially and periodically.

In the former case, i.e., when the absolute value of ${\vec k}(t)$increases exponentially, the dissipation effects will eventually start to be important and try to damp the mode (Mahajan & Rogava 1999) despite the presence of the shear instability. The same argument is valid for those cases, too, when the temporal growth of the wavenumber is linear. Therefore, considering shear-induced nonmodal effects in inviscid fluids in cases when $\vert{\vec k}\vert$ is monotonously increasing, we should realize that the description is physically meaningful only for initial (finite) times.


  \begin{figure} \par\includegraphics[angle=90,width=8.1cm,clip]{plot6.ps}\end{figure} Figure 6: The numerical solution for the case when temporal evolution of ${\vec k}$'s is exponential. The values of parameters are: kx=5, ky=10, kz=1, $\sigma = 10^{-2}$, A1=0.3, A2=10-2, C1=0.8, C2=0.9, $C_{\rm A}=0.5$.
Open with DEXTER

It is worthwhile to make a look at some of these solutions. In Fig. 6 we present the results of numerical calculations, taken for the case, when kx=5, ky=10, kz=1, $\sigma = 10^{-2}$, A1=0.3, A2=10-2, C1=0.8, C2=0.9, $C_{\rm A}=0.5$. The value of ${\Gamma}^2=3.1{\times}10^{-3}$ is positive and the value of $\vert{\vec k}(t)\vert$ is exponentially increasing (see Fig. 6a). The characteristic amplification time scale ${\cal T}\simeq{\Omega}^{-1}$ is of the order of the period of rotation. The resulting wave evolves accordingly, which is clearly visible from the figures. It is noteworthy to see that, analogous to the pure outflow case, shear flow energy is most efficiently absorbed by the longitudinal components of the velocity and the magnetic field perturbations. Still, now, the energy growth, plotted again for the $E_{\rm tot}(t)/E_{\rm tot}(0)$, is not algebraic but exponential and is entirely due to the exponential evolution of the perturbation wave number vector.

4.3 Periodic k(t) case

When values of ${\Gamma}^2$ are negative, the temporal evolution of ${\vec k}(t)$'s is periodic, which means that the absolute value of the wavenumber vector stays bounded within certain limits. It means that in this case shear-induced effects have potentially much wider durability and may potentially lead to strongly perceptible effects. The limits of this paper does not allow us to present full analysis of all possible classes of solutions. The most interesting feature of this case is that Alfvén waves become parametrically unstable in a helical flow. Figures 7-9 demonstrate this noteworthy fact. All figures are drawn for the case when A1=-A2=0.3, and ${\sigma }=0.01$, so that $W\equiv(-{\Gamma}^2)^{1/2}\simeq 0.2998$. Figure 7 shows the case when Alfvén frequency is ${\omega }_{\rm A}=0.29$. The system is still out of the parametric resonance and the system, therefore, exhibits just Alfvén waves, modulated by the periodic shear. The picture is drastically different when ${\omega }_{\rm A}=0.3$- Fig. 8 shows that there appears a robust instability of parametric (resonant) nature that leads to the strong exponential increase of the system energy in the same span of time as in Fig. 7. The resonance is quite sharp, because as soon as Alfvén frequency slightly exceeds the value of W the system becomes stable again, as it is visible from the Fig. 9, which is drawn for the case when ${\omega }_{\rm A}=0.31$.


  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{plot7.ps}\end{figure} Figure 7: The numerical solution for the case when A1=-A2=0.3, ${\sigma }=0.01$, C1=0.8, C2=0.9, $W\simeq 0.2998$ and ${\omega }_{\rm A}=0.29$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.2cm,clip]{plot8.ps} \end{figure} Figure 8: The numerical solution for the case when $W\simeq 0.2998$ (the same set of parameters as in Fig. 7) but with ${\omega }_{\rm A}=0.3$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8.3cm,clip]{plot9.ps} \end{figure} Figure 9: The numerical solution for the case when $W\simeq 0.2998$ (the same set of parameters as in Fig. 7) but with ${\omega }_{\rm A}=0.31$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{plot10.ps}\end{figure} Figure 10: The numerical solution for total energy of perturbations normalized on their initial values. The values of parameters are: kx=20, ky=5, kz=1, $\sigma = 0.6$, A1=0.5, A2=-0.9, Cx=0.01, Cy=0.05. In this case W=0.3, while ${\omega }_{\rm A}=0.3, 0.5, 0.6,$ and 0.8 on the plots labeled (a), (b), (c), and (d), respectively.
Open with DEXTER

Further study shows that actually there are several isolated regions of instability, which happen to be centered around the values ${\omega}_{\rm A}=nW, n=1,2,...$ and usually first resonance $W={\omega}_{\rm A}$ is the most efficient one. This is a strong indication in favor of the resonant and parametric nature of this instability. Figures 10 and 11 illustrate this interesting property of the system. The plots are drawn for the total energy of a perturbation, normalized on its initial value: $E_{\rm tot}(t)/E_{\rm tot}(0)$. The simulation is made for the case when kx=20, ky=5, kz=1, $\sigma = 0.6$, A1=0.5, A2=-0.9, Cx=0.01, Cy=0.05. Note that in this case W=0.3. Making simulations for different values of the Alfvén velocity we see that perturbations are strongly unstable when ${\omega}_{\rm A}\simeq nW$. Namely the instability is present in Figs. 10a, c and Figs. 11a, c, where the values of ${\omega}_{\rm A}$ are 0.3, 0.6, 0.9, and 1.2, respectively. At the same time we see that for intermediate values of ${\omega}_{\rm A}$, when $nW<{\omega}_{\rm A}<(n+1)W$, the Alfvén waves stay stable. Unfortunately the complexity of the system does not allow us to perform strict analytic analysis and locate the actual width and size of instability regions. However, our results do show that there are several such regions and presumably the efficiency of the instability decreases with the increase of n.


  \begin{figure} \par\includegraphics[angle=90,width=8cm,clip]{plot11.ps}\end{figure} Figure 11: The numerical solution for the total energy of perturbations. The values of parameters are the same as in Fig. 10. while ${\omega }_{\rm A}=0.9, 1.1, 1.2,$ and 1.4 on the plots labeled (a), (b), (c), and (d), respectively.
Open with DEXTER

5 Discussion

The results of the present study clearly show that both helical and purely ejectional flows of MHD plasmas could serve as efficient "amplifiers" of Alfvén waves. In alliance with other shear-induced phenomena (such as shear-induced wave transformations and/or generation of shear vortices), these processes could lead to the cascade amplification of hydromagnetic waves leading to MHD turbulence in these flows (Rogava et al. 2000). In more general terms it could be stated that the presence of the velocity shear strongly modifies the nature of Alfvén waves such that they can extract energy from the mean flow.

Certainly, while talking about these processes, we should bear in mind that due to the limitation of the "nonmodal approach'' we are not able to describe quantitatively the onset of these processes in the real physical space. Besides the linearized nature of our calculations prevents us from taking into account of the back reaction of shear-modified Alfvén waves on the mean flow. The last but not the least limitation is related with the neglect of the dissipation in the flow.

Can Alfvénic perturbations still extract energy from the background flow when dissipation is present? For magnetoacoustic modes sustained by a simple, linearly sheared two-dimensional flow it was recently found (Bodo et al. 2001) that the presence of dissipation doesn't prevent a shear-modified MHD mode from the energy extraction. For the case of helical dissipative flows until now no numerical studies were done. Numerical study of these processes in the swirling flows requires 3-dimensional MHD simulations over large time intervals, which is quite a tough challenge. We expect that the outcome of the "competition" between the increase of the energy due to the presence of the shear flow and viscous damping due to the presence of the dissipation will depend on the time scales of both processes and initial conditions. Relevant numerical studies are planned to be started in the near future.

However, basing on our results about "nonmodal'' temporal evolution of Alfvénic perturbations, we can give qualitative picture of the physical appearance of these Alfvén waves in the presence of viscous dissipation for all those three subclasses of flows - viz: (a) ejectional outflows with no rotation; (b) helical flows with exponentially increasing $\vert{\vec k}(t)\vert$; (c) helical flows with periodically changing $\vert{\vec k}(t)\vert$) - which were considered.

For an ejectional outflow, with linear temporal growth of the $\vert{\vec k}(t)\vert$, a monochromatic Alfvénic disturbance would undergo one act of transient, "burst-like'' amplification followed by the viscous decay. For the package, containing harmonics of different $\vert{\vec k}(0)\vert$, one could expect a sequence ("cascade'') of their transient amplifications mixed with their viscous damping. This sort of the Alfvén wave, while passing through the flow, would slowly decay but repeatedly regain its energy via the chain-sequence of amplification events.

For helical flows, where the temporal increase of the $\vert{\vec k}(t)\vert$ is exponential, the Alfvén waves could be less fortunate. It is true that their energy might grow exponentially, but the increase of the $\vert{\vec k}(t)\vert$ seems to be a more rapid process than the increase of the total energy of the Alfvén wave (see Fig. 6). Therefore, even if initially the Alfvén waves could extract some energy from the background flow, the powerful viscous damping would sooner or later prevail and return the energy back to the flow in the form of heat. It means that in this situation, perhaps, one could not see any high amplitude Alfvén waves, but one would rather witness an efficient heating of the flow due to this "self-heating'' process: when Alfvén waves serve as energy transmitters, extract a part of the flow's regular kinetic energy and returning the energy back to the flow in the form of the heat.

For helical flows, where the variability of the $\vert{\vec k}(t)\vert$ is periodic, the situation can be the most exotic. The strength of the viscous damping in such flows is limited, because the value of the $\vert{\vec k}(t)\vert$ is kept finite: it doesn't increase neither algebraically nor exponentially. At the same time, Alfvén waves are modulated by the presence of the flow and there exist separate regions of parametric instability, which implies that under favourable conditions the Alfvén waves propagating through this kind of flow can be unstable. Therefore, flow patterns of this gender might serve as efficient amplifiers of Alfvén waves.

In all these cases the ultimate "fate'' of any individual Alfvén wave would depend on the time- and length-scales of their propagation and the flow geometry, as well as, of course, on the actual strength of the viscous dissipation in the flow.

The shear-modified Alfvén waves seem to be the hybrids of the usual Alfvén waves and the so called "Kelvin modes'' (Marcus & Press 1977; Rogava et al. 1998). The latter are nonperiodic, transiently growing modes inherent to the incompressible neutral shear flows. In the absence of the equilibrium magnetic field, the Kelvin Transients are the only modes of collective behaviour exhibited by the flow. The shear-modified Alfvén waves are formed by combining the features of the usual waves with the transient shear vortices; their ability to extract/give energy from/to the mean flow follows from the latter.

Within the framework of the nonmodal approach we are able to track and study properties of these shear-modified Alfvén waves in the space of wave numbers (${\vec k}$-space). The orientation and magnitude of a wave number vector, being variable in time and governed by Eq. (14), varies because of the local straining of the background flow. The evolution of the ${\vec k}(t)$ field, in its turn, exercises influence on the temporal behaviour of physical variables: density and pressure perturbations, components of the magnetic field and the velocity vectors. In terms of the usual physical coordinates (space and time) these variables are periodic in each space coordinate. However, these modes are "non-normal'' (Butler & Farrell 1992) because both wavenumbers and amplitudes associated with each disturbance are functions of time, implying that the solutions are not separable in space and time. The latter, nonexponential time-dependence of the solutions is disclosed through the nonmodal approach and it helps to "smoke-out" new classes of modes hardly accessible through traditional normal mode analysis. In order to have complete real-space physical picture of the evolution of these Alfvénic perturbations we need, therefore, to develop phenomenological approach and try to understand the dynamics in terms of vorticity dynamics (Craik & Criminale 1986). Alternatively one might approach the problem through direct numerical simulations, generalizing the very first attempts of numerical studies of much simpler MHD velocity patterns (Bodo et al. 2001).

Turning our attention back to astrophysics, we might argue that the role of the shear-modified hybrid Alfvén waves could be quite important in a number of astrophysical situations. Let us first assess the relevance these waves could have to the solar plasma flows. It is known that higher layers of the solar chromosphere consist of long, vertical columns (spicules) rising above the general background (Athay 1986) and well-visible at the extreme limb of the Sun, where the overall structure of the chromosphere resembles a "burning prairie". The spicules rise vertically, like slender magnetic flux tubes (filaments) out of the network beginning in the chromosphere and threading through the solar transition region into the low corona. Their average lifetime is 10-15 min, characteristic length scale 10 000 km, and characteristic diameter 700-1000 km. Often the spicules appear to have an "Eifel tower" shape with vertical flow velocities in the range 20-25 km s-1. There is also some evidence for plasma rotation in spicules (Kudoh & Shibata 1999). It means that the plasma motion within spicules may easily be of helical nature. The recent discovery of swirling macrospicules, called solar tornados (Pike & Mason 1998) provides additional evidence in this direction.

If we imagine flow patterns, like spicules or solar tornadoes, with moderate storage of total (quasi)equilibrium energy it may happen that transiently amplified Alfvén waves, bred within these structures, could efficiently "suck out'' much of their energy and lead to eventual exhaustion and disappearance of the flow patterns. The shear-induced cascade of Alfvén waves could take away much of the available energy of the "parent" flow. The observational consequences may be dramatic; we could imagine individual spicules acting as short-lived plasma cannons firing away heavy blasts of large-amplitude Alfvén waves and disappearing after the wave package has drained most of the energy from the "parent" flow.

It is quite fascinating to surmise that cascade of transient amplifications of Alfvén waves within spicules, together with other kinds of shear-induced wave processes (like, e.g., "MHD wave oscillations" Rogava et al. 2000) may account for the quasisteady appearance of spicules in the solar atmosphere. Taking the "burning prairie" metaphor a little further, we may speculate that shear induced processes, "burning" individual "grass blades", could be responsible for the overall conflagration of the spicule network which, in turn, provides an efficient mechanism for the transfer of energy from the quasisteady motions of solar plasmas into the flux of large-amplitude Alfvén waves. These waves are able to penetrate through the solar transition region and reach the lower layers of the solar corona. Here the processes of the shear-induced "MHD wave oscillations" (Rogava et al. 2000) may contribute to the appearance of compressible MHD modes (slow and/or fast magnetosonic waves) which, in turn, are effectively damped giving back their energy to the solar plasma particles, accelerating them and providing initial launch of the solar wind flows. This highly speculative picture must be carefully developed and tested in order to make it convincing. We are in the process of developing a numerical model for an individual helical solar flow pattern, and hope to see the above-described processes in real physical space through numerical simulations.

The parametric Alfvén instability may be effective in flows, where conditions are favorable for the correlation between the rate of rotation and stretching of the flow lines (which determines the value of the characteristic frequency W) and the strength of the equilibrium magnetic field (which determines the magnitude of the Alfvén frequency ${\omega}_{\rm A}$). Such a correlation may easily happen within solar jet flows, where both the ejectional and rotational modes of motion are present. Any time such correlation takes place it will lead to a burst-like generation of high-amplitude Alfvén waves with corresponding "exhaustion" (and, maybe, even disappearance) of the "parent" helical flow pattern. Since the modern apparatus used on the last generation solar satellites enables one to measure both the strength of magnetic fields and the rate of rotation, one can assume that it will be fairly realistic to verify whether the appearance of high-amplitude Alfvén waves is really related to shear-induced resonant parametric instability of helical flows.

We think that shear-induced instabilities of this nature may be also present in accretion-ejection flows. The differential rotation parameter n controls the ${\vec k}(t)$ dynamics which, in turn, specifies the nature of fluctuations in a given flow. When n<1(including the rigid rotation case) $\Gamma$ is imaginary and ${\vec k}(t)$ is periodic. In such cases (e.g., innermost regions of galactic gaseous disk, believed to have almost constant rotation rates) the system may sustain parametrically unstable Alfvén waves. While when n>1 (including the Keplerian rotation regime), $\Gamma$ is real and makes the time behavior of ${\vec k}(t)$ exponential. This regime can be realized in different kinds of quasi Keplerian accretion disks. Note that the characteristic amplification time scale ${\cal T}\simeq{\Omega}^{-1}$ is of the order of the inverse period of rotation, being at least of the same order as the "Magnetorotational instability" growth rate (Balbus & Hawley 1998). Since the latter instability is thought to be the strongest one, accounting for the turbulence in accretion disks, we could surmise that the shear-induced instability discussed in this paper could also play a role in the onset of turbulence in accretion-ejection flows.

Finally, considering our results in the context of galactic gaseous disks and their large-scale magnetic fields, we might envisage a possible relation between the shear-induced amplification of Alfvén waves and standard dynamo action in swirling flows. Within galactic disks algebraic and/or usual instabilities of the nonmodal origin might provide the important mechanism for the initial amplification of the magnetic energy and this process could compete with the omnipresent Ohmic diffusion. This is a challenging task to see what is the role of nonmodal, shear-induced processes in the framework of the general theory of dynamo generation of galactic magnetic fields.

Acknowledgements
G. Bodo, S. Massaglia and A. Rogava were supported, in part, by the INTAS grant No. 97-0504. A. Rogava is grateful to the Abdus Salam ICTP and Universitá degli Studi di Torino for supporting him, in part, through the Regular Associate Membership Award and the Assegno di Ricerca, respectively.

References

 

Copyright ESO 2003