| (A.1) |
In Dutrey et al. (1994), we use the following parametrizations for the
physical laws in the type 0 model:
Kinetic temperature:
| (A.3) |
| n(r) | = | (A.4) | |
| = | (A.5) | ||
| s | = | h + p = 1 + v +p - q/2 | (A.6) |
| n(r,z) | = | (A.7) |
| H(r) | = | 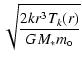 |
(A.8) |
| = | 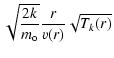 |
(A.9) | |
| = | (A.10) | ||
| h | = | 1 + v -q/2. | (A.11) |
For the ![]() ,
we take the value of
,
we take the value of
![]() where
where ![]() is the hydrogen mass (Beckwith &
Sargent 1993).
is the hydrogen mass (Beckwith &
Sargent 1993).
Note that other groups (in particular those working on theoretical dust disk
modelling) usually use the following definition for
![]() ,
which leads to:
,
which leads to:
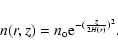
Copyright ESO 2003