6 Discussion

6.1 Line widths: Warp or turbulence

We note that the non-thermal component of the linewidth, dV, increases from d $V = 0.07 \pm 0.02$ km s^-1 measured with $^{12}{\rm CO}$ to values around $0.15\pm0.02$ km s^-1 from the $^{13}{\rm CO}$ and ${\rm C}^{18}{\rm O}$ isotopes. A straightforward interpretation would be that the turbulence is higher in the disk mid-plane, sampled by the CO isotopomers, than in the disk atmosphere, sampled by $^{12}{\rm CO}$.

However, Table 3 also shows that the derived disk inclination differs from one isotopomer to the other. Higher inclinations are found from the rarer isotopomers than from $^{12}{\rm CO}$. Systematic bias resulting from the analysis by a type 0 model of a more complex disk structure would result in the opposite effect (lower inclination for $^{13}{\rm CO}$ and ${\rm C}^{18}{\rm O}$, see Sect. 4.2), suggesting that the difference in inclination is real. Since $^{13}{\rm CO}$ and ${\rm C}^{18}{\rm O}$ preferentially sample the inner part of the disk ( $r \leq 200$ AU), while $^{12}{\rm CO}$ is sensitive to the whole disk ( $r \simeq 800$ AU), this could be indicative of a warped disk. Continuum emission also provides a measurement of the inner disk inclination: a value of $36 \pm 4^\circ$ is found from the 1.4 mm measurements. Unfortunately, this is only a lower limit, since it should be corrected from seeing effects. If the disk is warped, the change of inclination with radius will result in enhanced projected velocity gradients, which will mimic an increase in linewidth near the disk center. The magnitude of the effect depends on the warp intensity, and is difficult to estimate. However, one should remember that the apparent inclinations we measure are lower limits to the inclination variations, since they are averaged values over large areas of the disk.

Note that inclination and line widths are well de-coupled parameters. Inclination is determined from the shape of the individual channel images, while the line width is constrained by the total flux (see Beckwith & Sargent 1993; Guilloteau & Dutrey 1994, 1998). Hence, with the present observations, the two alternatives (warp or enhanced turbulence in the disk plane) remain plausible.

6.2 Dynamical mass

Analysing the data with an inappropriate model could lead to inconsistent inclination determination, and hence to errors on the stellar mass derived from Keplerian motions. Table 3 shows some possible effects at the level of a few degrees, leading to errors of $\sim$9% on the stellar mass, but with ${\rm C}^{18}{\rm O}$ and $^{13}{\rm CO}$  $J=1\!\rightarrow\! 0$ data being the least affected. These errors are at most comparable to the 1 $\sigma$error on real data.

6.3 Possible selective photodissociation of CO

The observed outer radius of DM Tau, in the $^{13}{\rm CO}$  $J=1\!\rightarrow\! 0$ and $J=2\!\rightarrow\! 1$ transitions ($\sim$640 AU) is significatively different from the $^{12}{\rm CO}$  $J=1\!\rightarrow\! 0$ and $J=2\!\rightarrow\! 1$ ones ($\sim$800 AU). The $^{12}{\rm CO}$ lines are optically thick. The observed radius in these transitions reveal a clear cut off in the radial density distribution, whereas the $^{13}{\rm CO}$ outer radius could be governed by its ability to photodissociate at higher extinction than its main isotope.

The behaviour of the photodissociation rates for both CO isotopes as a result of self-shielding, mutual shielding, other atoms and molecules absorption (mainly H and H₂) as well as dust screening are discussed in the interstellar cloud cases by e.g. van Dishoeck & Black (1988) and Glassgold et al. (1985).

If we look at the Fig. 8 of van Dishoeck & Black (1988), we see that the photodissociation of CO becomes effective as soon as the H₂ column density is lower than $1.4 \times 10^{21}$ cm^-2, for a model with $I_{{\rm UV}}\approx 1$, i.e. a normal interstellar radiation field (Draine 1974). In the DM Tau model of GD98, at 800 AU, the vertical column density above the disk mid-plane N is given by $\frac{\sqrt{\pi}}{2} \times H \times N(r=800~{\rm AU},z=0)$, i.e. $n_{{\rm H}_2}\approx 1.3 \times 10^{21}$ cm^-2, consistent with the fact this outer radius is governed by photodissociation.

We now use the relation $N_{{\rm H}}/A_{{\rm V}}= 1.59 \times 10^{21}$ cm^-2 mag^-1 to determine the minimum $A_{{\rm Vth}}$ required to protect $^{12}{\rm CO}$, which leads to $A_{{\rm Vth}}\approx 0.8$. The corresponding photodissociation rate at which $^{12}{\rm CO}$ is destroyed, using the Fig. 5 of van Dishoeck & Black (1998) is of 10^-13 s^-1. Assuming we need the same rate to dissociate ¹³CO, the corresponding $A_{{\rm V}}$ equals 1.15. The column density at the $^{13}{\rm CO}$ outer radius (640 AU) should therefore be 1.4 times the one at 800 AU. As the surface density law is given by $\Sigma(r)=\Sigma_0 \times (r/{\rm 100~AU})^{-p}$, we can derive that:

$$p=\frac{{\rm log}\left(\frac{\Sigma({\rm 640~AU})}{\Sigma({\r... ...40}\right)}=\frac{{\rm log}(1.4)}{{\rm log}(1.25)}\approx1.5.$$

As pointed out by van Dishoeck & Black (1988), the CO line widths being small as compared to the natural width of most lines, it should not affect the photodissociation rates and these models provide a good comparison to the case we are studying.

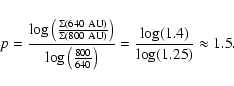
However, if we now take into account that in the T Tauri disks the grain coagulation and growth has started, we expect the $N_{{\rm H}}/A_{{\rm V}}$ ratio to be higher than in molecular clouds. The shielding by dust will become less important. It should not have a strong influence on the $^{12}{\rm CO}$ shielding as it is already effective at low dust extinction (see Fig. 5a of van Dishoeck & Black 1988 and Fig. 3 of Glassgold et al. 1985). However, it should have an influence on the $^{13}{\rm CO}$ photodissociation rates, which should raise. If we proceed in the same way as described above to determine the difference in A $_{{\rm Vth}}$ required to protect $^{12}{\rm CO}$ and $^{13}{\rm CO}$, it implies that $\Sigma({\rm 640~AU})/\Sigma({\rm 800~AU})\geq1.4$. Given that the uncertainty in the derivation of the observed $R_{\rm out}$ is of $\sim$20 AU, and assuming the $A_{{\rm Vth}}$ ratio determination is accurate at the 10% level, it is compatible with $p\ge 0.9$. This does not provide a strong constraint on the p index, but rather demonstrate that the photodissociation of CO is a reasonable process to explain the observations.

6.4 Temperature

Figure 9: Representation of the characteristic vertical scales and number densities in the DM Tau disk. The short dashed line represent the local hydrostatic scale height. The heights probed with the $^{12}{\rm CO}$  $J=2\!\rightarrow\! 1$ transition with $\tau =0.5$, 1 and 2 are given by the dot-dashed curves. The critical density $N_{\rm c}$ to reach LTE with this transition is given by the continuous line and shows CO is thermalized. Typical heights associated with the direct heating by stellar photons impinging on the dust (so-called "super-heated layer'') are outlined by the long dashed curves in two different models. For the definition of the local hydrostatic scale height H, see the appendix.

The temperature structure of protoplanetary disks has been modeled by CG97 and dA99, in view of analyzing the IR emission from disks. Both models concentrate on the dust temperature, while we are interested in the gas temperature. However, at the densities (>10⁶ cm^-3) and temperatures (10-50 K) where the CO emission arises, the gas cooling is very inefficient, so that the kinetic temperature is essentially identical to the dust temperature. On the other hand, the dust-gas coupling has negligible effect on the dust temperature, which is completely dominated by heating by the stellar light.

This results in two major effects on the temperature structure of the disk. The disk photosphere, defined as the surface where the optical depth of the dust to the stellar light is about unity is heated to high temperatures by stellar photons directly impinging on the disk surface. For T Tauri stars, it corresponds to $\tau_{{\rm dust}}({\rm IR}) \simeq 1$. This warm "super-heated'' layer reradiates at longer wavelengths to heat the disk interior.

To compare with models of super-heated layers, it is important to note that our definition of the hydrostatic scale height differs from that used in the models of CG97 and dA99 by $\sqrt{2}$, our scale height being larger (see Appendix for the details). Following our definition, the dust photosphere lies approximately at $h_{\rm phot} \approx 4H/\sqrt{2}$ in CG97. At the radius of 100 AU, the midplane temperature is of 20 K, whereas the surface is heated at $\sim$90 K. In the model developped by dA99, $h_{\rm phot} \approx 5H/\sqrt{2}$, and the temperature are of 15 K and 60 K at mid-plane and dust surface, respectively. Both models assume a 0.5 $M_\odot$ central star, with an effective temperature T_*=4000 K. The former takes $R_* = 2.5~R_\odot$, whereas for the later $R_* = 2~R_\odot$. Figure 9 summarizes the scale heights relevant for the comparison.

In addition to this "super-heated'' layer, there is a temperature "plateau'' in the disk mid-plane, resulting from a temperature gradient between the disk atmosphere and the disk plane. When the disk is optically thick to the illuminating radiation, but thin to its own emission, the disk plane is cooler than the disk atmosphere. This can happen in a well defined region of the disk with the appropriate surface density (see e.g. dA99, their Fig. 3). Closer to the star, when the surface density is higher, the mid plane temperature rises again with q = 0.5. At the outer edge, the mid-plane temperature asymptotically reaches the temperature of the disk atmosphere. Hence, in the disk plane, as a function of radius, there is a region where the temperature law flattens, while q becomes again of order 0.6 at larger distances.

Since, as shown in Fig. 9, the $^{12}{\rm CO}$  $J=2\!\rightarrow\! 1$ line probe a slightly lower layer than the dust photosphere, we cannot fully constrain the "super-heated'' layer from our observations. On the other hand, the temperature "plateau'' can be traced by the $^{13}{\rm CO}$ transitions.

The kinetic temperature distribution we deduce from the CO data in the DM Tau outer disk is shown Fig. 10.

Figure 10: Schematic representation of the gas and dust temperature in the disk mid-plane and disk atmosphere as probed with the $^{13}{\rm CO}$ and $^{12}{\rm CO}$ millimeter transitions. The estimate of the inner disk temperature distribution inferred from Far Infrared measurement is also reported (dotted line). The inner and outer boundary of the nearly constant temperature region are labeled $R_{\rm Thick}$ and $R_{\rm Thin}$ ( $R_{\rm Thin} = R_q$ in the formal description of type II model) respectively. The arrow delineates the part of the disk constrained by the PdBI observations.

While $q = 0.63 \pm 0.04$ from ¹²CO J=1-0 and J=2-1 data, with $T_0 = 32\pm 2$ K at 100 AU, the ¹³CO observations suggest lower values for both q ($\simeq 0$-0.4) and T₀ (13 K), although the later value depends on the assumption that the same density power law regime holds between 100 AU (sampled by J=1-0 line) and 300 AU (sampled by the J=2-1 line). The temperature law is thus steeper above the plane than near the disk mid-plane.

The outer edge of the "plateau'' ( $R_{\rm Thin}$ in Fig. 10) is determined from our data by the intersection of the $T_{\rm atm} = 32$ K, q = 0.63 law with the $T_{\rm plane} \simeq 13$ K, $q \approx 0$, i.e. about 400 AU. The inner edge cannot be determined directly by our observations, due to the lack of angular resolution. However, it can be reasonably estimated by assuming the dust and gas temperature are equal. The dust temperature distribution in the inner regions can be determined from the FIR flux densities around 60 $\mu$m. Beckwith et al. (1990) find for DM Tau T_k(1 AU $) \approx 110$ K and $q \approx 0.51$ from the IRAS data. This temperature law intersects that of the "plateau'' around $R_{\rm Thick} \approx 70$ AU. The direct observation of a temperature "plateau'' allows to resolve the apparent inconsistencies between the low temperatures derived from the mid and FIR and the higher values derived from ¹²CO observations at larger radius. The measurement of the inner radius would require better angular resolution at mm wavelengths (e.g. ALMA).

6.5 Depletion

Using the results on the continuum and the CO lines, we can estimate X(CO) and the CO depletion factor f(CO). The CO abundance is given by the ratio (see Fig. 7 for the values)

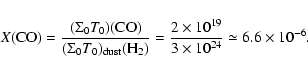$$X({\rm CO}) = \frac{(\Sigma_0 T_0)({\rm CO})}{(\Sigma_0 T_0)_... ...{2 \times 10^{19}}{3 \times 10^{24}} \simeq 6.6\times 10^{-6}.$$ (9)

For $X_{\rm ref} =7\times 10^{-5}$, we get $f({\rm CO}) \sim 10$. If we take into account the uncertainties at 3$\sigma$ on $(\Sigma_0 T_0)({\rm CO})$ and $(\Sigma_0 T_0)_{\rm dust}$, $f({\rm CO})$ is ranging from $\sim$7 to 15. Assuming a depletion of 10, as a mean value over the disk, is therefore reasonable.

In the type II model, we determine $n_0({\rm CO}) \simeq 4200$ cm^-3, from which, using a scale height of $H\simeq 10$ AU at 100 AU, consistent with the T₀=13 K mid-plane temperature, gives $\Sigma_0({\rm CO}) T_0 \simeq 2.2\times 10^{19}$ cm² K, as for the type 0 models.

Using standard isotopic abundances, we derive identical depletion factors from $^{13}{\rm CO}$  $J=2\!\rightarrow\! 1$ and the optically thinner transition ${\rm C}^{18}{\rm O}$  $J=2\!\rightarrow\! 1$, although they do not sample the same volume in the disk. This suggests that the depletion does not vary by huge factors within the disk. Note that the depletion is not sufficient to significantly deplete CO, which is optically thick up to 800 AU, whereas the grain temperature is below the freezing point at radii above 200 AU. Except for the external region, which can be affected by other effects like photodissociation, this high opacity is ubiquitous in observed disks (GG Tau, Dutrey et al. 1994; GM Auriga, Dutrey et al. 1998; Simon et al. 2000). Hence, there is still a sufficient amount of CO at the temperature of the "plateau'' (13 K) even if it is well below the CO freeze out point.

6.6 Density

The existence of a temperature "plateau'' can place indirect constraints on the disk mass, because the "plateau'' appears within a defined surface density range. In the dA99 models, this temperature plateau happens when $\Sigma_{\rm d}$ is about 0.1 g cm^-2. When the disk becomes more massive (see Fig. 3 dA99), the opacity is such that the plateau never exist. The observation of a plateau therefore sets an upper limit on the disk mass. However, the precise position of this plateau depends both on the slope and the absolute value of the dust opacity function between 50 and 300 $\mu$m, related to the temperature range of reemission concerned (10-60 K).

With the dust properties adopted by dA99 (Draine & Lee (1984) optical constants and Mathis et al. (1977) size distribution), the existence of the "plateau'' implies $M_{\rm disk} < 4\times 10^{-3} ~{M}_{\odot}$. However, this combination of dust opacity and disk mass fails to reproduce the observed mm flux densities by a factor $\simeq$10. The discrepancy can be resolved if significant grain growth has occurred. In this case, the millimeter opacities are increased, but the shorter wavelengths opacities decrease (see for example Kruegel & Siebenmorgen 1994, their Fig. 12), thereby moving inward the position of the plateau for a given disk mass. From $\Sigma_0 T_0$ derived from the dust, and using $T_0 \simeq 15$ K for the dust temperature (or equivalently, using an average depletion of 10 for CO relative to standard Taurus abundances), our measurement indicates $\Sigma_0 \sim 2\times 10^{23}$ H₂ cm^-2 at 100 AU or $\Sigma_{\rm d} \sim 0.8$ g cm^-2. Although this goes in the expected direction more detailed disk models with more appropriate dust parameters are required to predict quantitatively the position and extent of the temperature "plateau''.

Finally, let us note that the density exponent, $p \simeq 1.5$, agrees with the ratio of the outer radii for ¹²CO and ¹³CO, when the CO distribution is truncated by photodissociation.