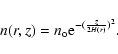We use high angular and spectral resolution (
A&A 399, 773-787 (2003)
DOI: 10.1051/0004-6361:20021638
E. Dartois 1 - A. Dutrey 2 - S. Guilloteau 3
1 - Institut d'Astrophysique Spatiale, UMR 8617,
Bât. 121, Campus Paris XI,
91405 Orsay, France
2 -
Laboratoire d'Astrophysique de l'Observatoire de Grenoble,
BP 53, 38041 Grenoble Cedex 9, France
3 -
Institut de Radio Astronomie Millimétrique,
300 Rue de la Piscine, 38406 Saint Martin d'Hères, France
Received 20 August 2002 / Accepted 6 November 2002
Abstract
We use high angular and spectral resolution (
![]() &
0.1 km s-1) images in
&
0.1 km s-1) images in
![]() ,
,
![]()
![]() ,
,
![]() and
and
![]()
![]() coming from
the IRAM interferometer to probe the vertical temperature distribution
in the disk of DM Tau. We investigate here a new method based on the
different opacities of the CO isotopomers to sample the temperature
disk structure at various vertical scales inside the disk. Typically,
the
coming from
the IRAM interferometer to probe the vertical temperature distribution
in the disk of DM Tau. We investigate here a new method based on the
different opacities of the CO isotopomers to sample the temperature
disk structure at various vertical scales inside the disk. Typically,
the
![]() transitions are sampling at 2-4 scale heights, while the
transitions are sampling at 2-4 scale heights, while the
![]() data are more likely tracing 1 scale height for the J=2-1, and
the disk mid-plane for the J=1-0 line. At the disk scale at which the
IRAM observations are sensitive (
data are more likely tracing 1 scale height for the J=2-1, and
the disk mid-plane for the J=1-0 line. At the disk scale at which the
IRAM observations are sensitive (![]() -60 AU), the analysis
reveals a vertical temperature gradient. The outer layers
where
-60 AU), the analysis
reveals a vertical temperature gradient. The outer layers
where ![]() (
(
![]()
![]()
![]() are warmer
(
are warmer
(![]() K) than the inner layers probed by
K) than the inner layers probed by
![]() and
and
![]() data
(
data
(![]() -20 K). These findings are consistent with the structure
expected for flared irradiated disks around TTauri stars. We also observe that
the outer radius of the disk is smaller in
-20 K). These findings are consistent with the structure
expected for flared irradiated disks around TTauri stars. We also observe that
the outer radius of the disk is smaller in
![]() and
and
![]() than in
than in
![]() .
These differences in truncation radius are in agreement with photodissociation effects. We also note that the dynamical mass determination from CO is weakly affected by the temperature gradient.
.
These differences in truncation radius are in agreement with photodissociation effects. We also note that the dynamical mass determination from CO is weakly affected by the temperature gradient.
Key words: stars: individual: DM Tauri - stars: circumstellar matter - stars: pre-main sequence - radio-lines: stars
CO line observations of low-mass Pre-Main-Sequence (PMS) stars in
Taurus-Auriga (![]() 140 pc, Elias 1978) provide now strong evidence
that many of them are surrounded by large (
140 pc, Elias 1978) provide now strong evidence
that many of them are surrounded by large (
![]() -800 AU) Keplerian disks (GM Aur, Koerner et al. 1993; GG Tau:
Dutrey et al. 1994; MWC 480: Mannings et al. 1997). Guilloteau & Dutrey
1998 (hereafter GD98) have shown that a simple ray tracing code
assuming LTE conditions applied on CO images allows one to retrieve the
physical parameters of disks if the quality of the CO data is high
enough to perform reliable
-800 AU) Keplerian disks (GM Aur, Koerner et al. 1993; GG Tau:
Dutrey et al. 1994; MWC 480: Mannings et al. 1997). Guilloteau & Dutrey
1998 (hereafter GD98) have shown that a simple ray tracing code
assuming LTE conditions applied on CO images allows one to retrieve the
physical parameters of disks if the quality of the CO data is high
enough to perform reliable ![]() minimisation on disk
parameters. Using
minimisation on disk
parameters. Using
![]()
![]() data from the IRAM interferometer, the
method was first applied to the DM Tau CO disk (GD98). One of the key
parameters determined from such an analysis is the stellar mass: the
initial work on DM Tau was followed by more systematic measurements
for a dozen stars (Simon
et al. 2000).
data from the IRAM interferometer, the
method was first applied to the DM Tau CO disk (GD98). One of the key
parameters determined from such an analysis is the stellar mass: the
initial work on DM Tau was followed by more systematic measurements
for a dozen stars (Simon
et al. 2000).
Another important result is the determination of the kinetic
temperature law. For DM Tau, GD98 found
![]() K. Since the
K. Since the
![]()
![]() transition is
optically thick, this measurement is relevant to the region where
transition is
optically thick, this measurement is relevant to the region where
![]() is around 1. The CO column density is still very
high in such objects, therefore
is around 1. The CO column density is still very
high in such objects, therefore
![]() is easily
reached and traces the "CO disk surface''. This determination assumes
a purely radial gradient of the temperature, and no vertical
gradient. Yet, vertical gradients are expected in proto-planetary
disks. Because of the frequency dependence of the dust absorption
coefficient, heating by the stellar light is expected to produce an
inverse green-house effect which results in a cold disk plane
surrounded by a warmer disk photosphere. Detailed models have been
performed by Chiang & Goldreich (1997, hereafter CG97) and d'Alessio
et al. (1999, hereafter dA99). Viscous heating resulting from accretion
in the disk plane could result in the opposite effect. Imprints of
such temperature gradients in the inner disk (<10 AU) can be found
in the IR SED of the disk. However, the outer disk parts are so cold
that only the mm domain can probe them.
is easily
reached and traces the "CO disk surface''. This determination assumes
a purely radial gradient of the temperature, and no vertical
gradient. Yet, vertical gradients are expected in proto-planetary
disks. Because of the frequency dependence of the dust absorption
coefficient, heating by the stellar light is expected to produce an
inverse green-house effect which results in a cold disk plane
surrounded by a warmer disk photosphere. Detailed models have been
performed by Chiang & Goldreich (1997, hereafter CG97) and d'Alessio
et al. (1999, hereafter dA99). Viscous heating resulting from accretion
in the disk plane could result in the opposite effect. Imprints of
such temperature gradients in the inner disk (<10 AU) can be found
in the IR SED of the disk. However, the outer disk parts are so cold
that only the mm domain can probe them.
This paper provides a first attempt to measure the vertical temperature gradient in the outer parts of a proto-planetary disk. The goal is two-fold: i) to test the validity of the disk models, and ii) to assess the possible influence of such a gradient on the determination of other disk parameters (like density, inclination or dynamical stellar mass). We take advantage of the varying opacities of the lowest transitions of CO and its isotopes to probe different disk layers, and constrain a possible vertical temperature gradient inside the outer disk (at r > 50-100 AU). Such multi-transition, multi-isotope techniques were used in the past to sample temperature profiles of molecular cores. The extension of this "old'' technique to proto-planetary disks is particularly attractive, since the known geometry of the disk allows more accurate modeling.
We describe here the method, its current limitations and give
estimates of the vertical temperature gradient. We also assess the
reliability of the determination of other disk parameters when the
temperature gradient cannot be completely constrained. The
presentation of the observations and the data reduction (in Sect. 2) is followed by a description of the method (Sect. 3). We apply it to
![]() and
and
![]()
![]() transitions in
Sect. 4. The best temperature gradient is determined by
transitions in
Sect. 4. The best temperature gradient is determined by
![]() minimization performed on 6 different spectral lines (3 isotopes, 2 transitions). In Sect. 5, we discuss our
results and compare them in Sect. 6 to temperature
models existing in the literature.
minimization performed on 6 different spectral lines (3 isotopes, 2 transitions). In Sect. 5, we discuss our
results and compare them in Sect. 6 to temperature
models existing in the literature.
![\begin{figure}
\par\includegraphics[width=18cm,clip]{ms3027f1.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg45.gif) |
Figure 1:
Channel maps of the
|
| Open with DEXTER | |
All observations were performed with the IRAM interferometer on
Plateau de Bure. The DM Tau millimeter center is located at
![]() (2000)= 04h33m48.73s;
(2000)= 04h33m48.73s; ![]() (2000
(2000
![]()
The
![]()
![]() data where obtained in Sep. 1995 under good weather
conditions. A precise description of the observing conditions and
data reduction is given in GD98. These observations provided an
angular resolution of
data where obtained in Sep. 1995 under good weather
conditions. A precise description of the observing conditions and
data reduction is given in GD98. These observations provided an
angular resolution of
![]() with a 0.17 km s-1velocity resolution. The
with a 0.17 km s-1velocity resolution. The
![]()
![]() data were obtained during the
winter 1996/1997 and summer 1997. The observations were performed in
snapshot mode. The observational conditions and the data reduction is
described in Simon et al. (2000). The resultant angular
resolution obtained is of the order of 0.7'' with a 0.18 km s-1 velocity
resolution. In one transit, 4 T Tauri disks where observed. The
total integration time on the DM Tau disk is about 4 hours.
data were obtained during the
winter 1996/1997 and summer 1997. The observations were performed in
snapshot mode. The observational conditions and the data reduction is
described in Simon et al. (2000). The resultant angular
resolution obtained is of the order of 0.7'' with a 0.18 km s-1 velocity
resolution. In one transit, 4 T Tauri disks where observed. The
total integration time on the DM Tau disk is about 4 hours.
The
![]()
![]() line was observed in C2, B2 and A configurations
between Feb. 1999 and March 1999. This provides baselines up to 400 m,
and an angular resolution of
line was observed in C2, B2 and A configurations
between Feb. 1999 and March 1999. This provides baselines up to 400 m,
and an angular resolution of
![]() at PA
at PA ![]() at
2.7 mm, after tapering to adjust to the same resolution as the
at
2.7 mm, after tapering to adjust to the same resolution as the
![]() line. We observed simultaneously at 110 GHz to cover the
line. We observed simultaneously at 110 GHz to cover the
![]()
![]() and
and
![]()
![]() lines, and at 220 GHz to cover the
lines, and at 220 GHz to cover the
![]()
![]() line. At 1.3 mm, the tuning was double-side-band (DSB)
while at 2.7 mm, the tuning offered 6 dB rejection. The rms phase
were up to 40
line. At 1.3 mm, the tuning was double-side-band (DSB)
while at 2.7 mm, the tuning offered 6 dB rejection. The rms phase
were up to 40
![]() at 2.7 mm on the longest baseline, offering a
seeing better than 0.7''. The backend correlator of 10 MHz
bandwidth provided a velocity resolution of 0.11 km s-1
at 2.7 mm on the longest baseline, offering a
seeing better than 0.7''. The backend correlator of 10 MHz
bandwidth provided a velocity resolution of 0.11 km s-1
The
![]()
![]() line was observed in C2, B2 and A configurations
between Feb. 1999 and March 1999, simultaneously with the
line was observed in C2, B2 and A configurations
between Feb. 1999 and March 1999, simultaneously with the
![]()
![]() and
and
![]()
![]() lines. The data was heavily tapered to produce an image
with an angular resolution of
lines. The data was heavily tapered to produce an image
with an angular resolution of
![]() at PA
at PA ![]() .
We also applied Hanning smoothing in velocity to obtain
0.23 km s-1 resolution, with 0.11 km s-1 channel
spacing. The
.
We also applied Hanning smoothing in velocity to obtain
0.23 km s-1 resolution, with 0.11 km s-1 channel
spacing. The
![]()
![]() line was also detected during these
observations, but does not bring any new significant constraint due to
the low signal to noise of this detection.
line was also detected during these
observations, but does not bring any new significant constraint due to
the low signal to noise of this detection.
The
![]()
![]() line was observed in D configuration on Nov. 28, 1999
and in C2 configurations on Jan. 29 and Feb. 11, 2001. This provides
baselines up to 180 m, and an angular resolution of
line was observed in D configuration on Nov. 28, 1999
and in C2 configurations on Jan. 29 and Feb. 11, 2001. This provides
baselines up to 180 m, and an angular resolution of
![]() at PA
at PA ![]() ,
nearly identical to that of the
,
nearly identical to that of the
![]()
![]() data. We observed simultaneously at 88 GHz (HCN
data. We observed simultaneously at 88 GHz (HCN
![]() )
and 220.4 GHz
(
)
and 220.4 GHz
(
![]()
![]() ). At 1.3 mm, the tuning was double-side-band (DSB) while
at 3.4 mm, the tuning was purely single-side band (LSB). The backend
was a correlator with one band of 10 MHz (spectral resolution 0.13
). At 1.3 mm, the tuning was double-side-band (DSB) while
at 3.4 mm, the tuning was purely single-side band (LSB). The backend
was a correlator with one band of 10 MHz (spectral resolution 0.13
![]() )
centered on the HCN
)
centered on the HCN
![]() line, and one band of 20 MHz
(spectral resolution 0.13
line, and one band of 20 MHz
(spectral resolution 0.13
![]() )
centered on the
)
centered on the
![]()
![]() line
respectively. The remaining bands were used to provide continuum
observations. The phase and flux calibrators were 0415+379, 0430+052
and 0528+134, and the absolute flux scale was set using MWC 349 as a
reference. The rms phase noise was 7
line
respectively. The remaining bands were used to provide continuum
observations. The phase and flux calibrators were 0415+379, 0430+052
and 0528+134, and the absolute flux scale was set using MWC 349 as a
reference. The rms phase noise was 7
![]() to 20
to 20
![]() and 15
and 15
![]() to 50
to 50
![]() at 3.4 mm and 1.3 mm, respectively, resulting in an
effective seeing about 0.7''.
at 3.4 mm and 1.3 mm, respectively, resulting in an
effective seeing about 0.7''.
We used the GILDAS software package to reduce the data. Images were
produced using various tapers, to match all images to similar angular
resolution. However, in the model fitting, the original, untapered
uv distributions were used. We did not subtract the continuum
emission from the line maps. The
![]()
![]() ,
,
![]()
![]() and
and
![]()
![]() maps are presented in Fig. 1.
maps are presented in Fig. 1.
The total line flux is an important parameter to constrain the
temperature of the disk (see Sect. 3). Therefore having a
coherent absolute calibration scale for every line observed is
fundamental. Although our original calibration is expected to be
accurate to the 15% level or better, in order to optimize the flux
calibration, we proceed as follows. We calibrate the flux density by
the standard method using MWC 349 (IRAM flux report 13) and the
quasars 0415+379, 0528+134 or 3C 273 as secondary references. We then
measured the total flux density of the dust disk at the various
observing wavelengths: 3.5, 3.4, 2.7, 2.6, 1.35, 1.3 mm. We find that
the best spectral index for the dust disk is
![]() .
Then assuming
.
Then assuming
![]() and using the
and using the
![]()
![]() frequency for
the absolute flux reference (
frequency for
the absolute flux reference (![]() mJy), we fix the continuum
flux (hence the line flux) to the fitted values. No correction higher
than 15% was found in this process. This flux density scale is
accurately transferred to the line observations due to the high
precision of the bandpass calibrations (
mJy), we fix the continuum
flux (hence the line flux) to the fitted values. No correction higher
than 15% was found in this process. This flux density scale is
accurately transferred to the line observations due to the high
precision of the bandpass calibrations (![]() 1%). By this
method, we obtain a reliable relative calibration from one frequency
to another, thereby allowing direct comparison of the temperatures and
molecular abundances determined by the various observations. Note also
that the flux scale obtained with this method agrees within one
1%). By this
method, we obtain a reliable relative calibration from one frequency
to another, thereby allowing direct comparison of the temperatures and
molecular abundances determined by the various observations. Note also
that the flux scale obtained with this method agrees within one
![]() with the bolometer flux determination at 1 mm from Beckwith
et al. (1990) (
with the bolometer flux determination at 1 mm from Beckwith
et al. (1990) (![]() mJy).
mJy).
CO presents the advantage to possess 4 isotopomers:
![]() ,
,
![]() ,
,
![]() and C17O, whose relative abundances in disks span a large
range. The various transitions of each species, each one having
different line strengths, provide an access to different depth levels
inside the disk. The analysis of the
and C17O, whose relative abundances in disks span a large
range. The various transitions of each species, each one having
different line strengths, provide an access to different depth levels
inside the disk. The analysis of the
![]() and
and
![]() rotational lines
of CO are also simplified by the fact that they have low critical
densities and are therefore thermalized at the densities encountered
in protoplanetary disks (this can be seen in Fig. 9 where we
plot
rotational lines
of CO are also simplified by the fact that they have low critical
densities and are therefore thermalized at the densities encountered
in protoplanetary disks (this can be seen in Fig. 9 where we
plot ![]() for the
for the
![]() transition of CO). Based on these ideas,
using the LTE excitation radiative transfer model by Dutrey
et al. (1994), we can determine the surface at which
transition of CO). Based on these ideas,
using the LTE excitation radiative transfer model by Dutrey
et al. (1994), we can determine the surface at which ![]() is
reached along the line-of-sight, for the various CO isotopomers and
transitions
is
reached along the line-of-sight, for the various CO isotopomers and
transitions
![]() and
and
![]() .
More details about this model can be found in the appendix.
.
More details about this model can be found in the appendix.
In a first step, following GD98, we assumes that there is no dependency of
Tk with z, the vertical scale of the disk. In this model, the kinetic
temperature only varies as a power law with radius r like
![]() .
For convenience, we call Type 0 this isothermal model.
The input parameters of the model are given by the
.
For convenience, we call Type 0 this isothermal model.
The input parameters of the model are given by the ![]() minimization on
minimization on
![]()
![]() channel maps presented by GD98 (their Table 1).
channel maps presented by GD98 (their Table 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3027f2.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg65.gif) |
Figure 2:
Iso-opacity surfaces for various CO and
|
| Open with DEXTER | |
Let us assume first that the disk is seen pole-on (the inclination
angle i=0). Figure 2 displays the vertical scale z at
which ![]() ,
1 and 2 are reached for the observed transitions
(
,
1 and 2 are reached for the observed transitions
(
![]()
![]() ,
,
![]()
![]() and
and
![]()
![]() )
as a function of r. The
physical parameters used to derive these curves are appropriate for a
disk like that of DM Tau (including the CO abundance). The surfaces
at
)
as a function of r. The
physical parameters used to derive these curves are appropriate for a
disk like that of DM Tau (including the CO abundance). The surfaces
at ![]() and 2, are given in order to indicate the narrowness
of the emitting region. By comparison to typical planetary
atmospheres, this is equivalent to estimate how wide is the
atmospheric weight function in the disk.
and 2, are given in order to indicate the narrowness
of the emitting region. By comparison to typical planetary
atmospheres, this is equivalent to estimate how wide is the
atmospheric weight function in the disk.
Figure 2 clearly shows that the
![]()
![]() and
and
![]() emissions originate from a narrow region in the very upper part of the
disk. It is then not surprising that the best models of
emissions originate from a narrow region in the very upper part of the
disk. It is then not surprising that the best models of
![]()
![]() and
and
![]() maps give exactly the same disk parameters (see Simon
et al. 2000): both transitions of
maps give exactly the same disk parameters (see Simon
et al. 2000): both transitions of
![]() are sampling the same
vertical scale. In the central regions (r < 200 AU), the
are sampling the same
vertical scale. In the central regions (r < 200 AU), the
![]() surface is located well above the hydrodynamic scale height H (thick
point line), at which
surface is located well above the hydrodynamic scale height H (thick
point line), at which
![]() (see also
appendix).
(see also
appendix).
Contrary to
![]() ,
the main contribution to the
,
the main contribution to the
![]()
![]() emission
arises near the disk plane. The
emission
arises near the disk plane. The
![]() transition starts to be almost
optically thin as the surface at
transition starts to be almost
optically thin as the surface at ![]() crosses the mid-plane, and
the density then falls exponentially. Both transitions sample a much
thicker part of the disk than the
crosses the mid-plane, and
the density then falls exponentially. Both transitions sample a much
thicker part of the disk than the
![]() lines.
lines.
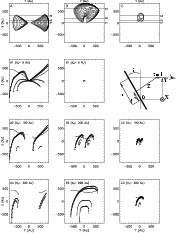 |
Figure 3:
Representation of the calculated iso-opacity surfaces in
three characteristic velocity channels of the
|
| Open with DEXTER | |
For ![]() ,
as it is usually the case, the existence of gradients
in density allows us to sample various vertical scales z in the disk
depending which velocity is observed. The density gradients
encountered in the disk imply that at a given velocity and projected
distance d to the star, one does not penetrate through the disk
atmosphere symmetrically. This implies that, even in the case of an
isothermal vertical atmosphere, the emission from the surface at
,
as it is usually the case, the existence of gradients
in density allows us to sample various vertical scales z in the disk
depending which velocity is observed. The density gradients
encountered in the disk imply that at a given velocity and projected
distance d to the star, one does not penetrate through the disk
atmosphere symmetrically. This implies that, even in the case of an
isothermal vertical atmosphere, the emission from the surface at ![]() in the two symmetric lines-of-sight associated to d does not
come from the same height z in the disk.
in the two symmetric lines-of-sight associated to d does not
come from the same height z in the disk.
This property is illustrated in Fig. 3, where we performed
the same calculations as above with
![]() ,
the inclination
measured in DM Tau by GD98. The surfaces at
,
the inclination
measured in DM Tau by GD98. The surfaces at ![]() 1 are shown for
the main transitions of
1 are shown for
the main transitions of
![]() and
and
![]() in various cuts through the
more representative velocity channels. We chose three main channels:
(a) the systemic velocity of the disk; (b) an intermediate channel;
(c) an extreme channel probing the inner part of the disk. Therefore a
wealth of information on the vertical temperature distribution can
come from the observation of a single transition. Indeed, the
comparison between a model and the data, based on a
in various cuts through the
more representative velocity channels. We chose three main channels:
(a) the systemic velocity of the disk; (b) an intermediate channel;
(c) an extreme channel probing the inner part of the disk. Therefore a
wealth of information on the vertical temperature distribution can
come from the observation of a single transition. Indeed, the
comparison between a model and the data, based on a ![]() minimization (as done by GD98) use all the spectral and spatial
information originating in various parts of the disk to constrain the
temperature model. GD98 measure that the temperature follows
minimization (as done by GD98) use all the spectral and spatial
information originating in various parts of the disk to constrain the
temperature model. GD98 measure that the temperature follows
![]() .
The curves presented in
Fig. 3 show that this measurement corresponds to scales
between 50 and 200 AU above the disk plane.
.
The curves presented in
Fig. 3 show that this measurement corresponds to scales
between 50 and 200 AU above the disk plane.
While
![]() samples at
samples at ![]() 2-4 scale heights from the disk
midplane, with the CO isotopes, in particular through the
2-4 scale heights from the disk
midplane, with the CO isotopes, in particular through the
![]()
![]() line, one can sample the disk properties much closer to the disk plane
(see Figs. 2 and 3). However, part of the
emission becomes optically thin, so that not only the temperature, but
also the surface density (and chemical abundance) governs the
brightness temperature. On one hand, this gives a chance to constrain
the surface density, on another hand, the analysis becomes more
complex since parameters like (p,q) are coupled, as are
line, one can sample the disk properties much closer to the disk plane
(see Figs. 2 and 3). However, part of the
emission becomes optically thin, so that not only the temperature, but
also the surface density (and chemical abundance) governs the
brightness temperature. On one hand, this gives a chance to constrain
the surface density, on another hand, the analysis becomes more
complex since parameters like (p,q) are coupled, as are
![]() ,
,
![]() and T0.
and T0.
In the case of the
![]()
![]() transition, this coupling takes a
particularly simple form, because, to first order, the line is
optically thin throughout most of the disk. For a face on disk, the
brightness temperature is
transition, this coupling takes a
particularly simple form, because, to first order, the line is
optically thin throughout most of the disk. For a face on disk, the
brightness temperature is
| Tb(r) | |||
| (6) | |||
| (7) |
This is not the case for the
![]() line because 1) of the exponential
dependence on the temperature Tk(r) of the population of the
lower level, but also because 2) this transition is optically thick
out to about 400 AU. The
line because 1) of the exponential
dependence on the temperature Tk(r) of the population of the
lower level, but also because 2) this transition is optically thick
out to about 400 AU. The
![]()
![]() data only constrain p-q and
data only constrain p-q and
![]() ,
while the
,
while the
![]()
![]() data offer a more complex dependence
on the parameters.
data offer a more complex dependence
on the parameters.
These behaviors are shown in Fig. 4 where are displayed the
exact and high temperature limit calculations, for the three first
transitions of CO as a function of the gas kinetic temperature. Note
that in the 10-20 K range the CO
![]() line brightness temperature
only varies by 10%, as does the
line brightness temperature
only varies by 10%, as does the
![]() one in the 15-40 K range.
one in the 15-40 K range.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms3027f15.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg87.gif) |
Figure 4: Dependence of the brightness temperature (arbitrary units) versus kinetic temperature for the J=1-0, 2-1 and 3-2 CO transitions in the constant linewidth and optically thin cases. Thick lines use the exact calculation. Dashed lines correspond to the high temperature approximation limit, where the brightness follows a 1/T dependence. |
| Open with DEXTER | |
The parametric disk model used by GD98 does not take into account a possible
vertical variation of the temperature. The dA99 model shows that the
temperature distribution of disks as a function of radius is quite complex (see
their Fig. 3). A parametric approach to such a complex variation is not simple,
and would require a significant number of new free parameters. Rather than
following such an approach, we shall first show that information on a vertical
temperature gradient can be recovered from parametric disk models which assume
only radial gradients. This is feasible because vertical temperature gradients
imply different radial temperature distributions as function of scale height in
the disk (see for example Fig. 5).
We would then expect that the analysis of the various CO isotopes and
transitions will result in different values for ![]() and q (and perhaps some
other disk parameters).
and q (and perhaps some
other disk parameters).
To illustrate this property, and to find out which are the relevant observable parameters for a possible temperature variation, we generated two disk models with different vertical temperature gradients.
The first one (type I) is a very simple modification of the type 0
temperature distribution
![]() by adding a single parameter
by adding a single parameter ![]() :
:
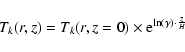 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms3027f16.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg95.gif) |
Figure 5:
Representation of the isothermal curves in the case
of a purely radial dependence of the temperature distribution ( |
| Open with DEXTER | |
Although it does not necessarily bear any physical justification, this simple
model can simulate either positive gradients (hotter disk atmosphere,
like in CG97, see also Sect. 6) or negative gradients (hotter disk
midplane, coming from local viscous dissipation at the disk mid-plane, like in
Shakura & Sunayev 1973; Lynden-bell & Pringle 1974). Figure 5
shows the distribution of the kinetic temperature for two values of ![]() .
As Tk will vary both in r and z, the resulting iso-temperature surfaces
will make an angle with the disk plane (case
.
As Tk will vary both in r and z, the resulting iso-temperature surfaces
will make an angle with the disk plane (case
![]() )
instead of being
perpendicular to it in the isothermal model (
)
instead of being
perpendicular to it in the isothermal model (
![]() ). They will
asymptotically tend to be parallel to the disk plane as the gradient is steeper
in the z direction.
). They will
asymptotically tend to be parallel to the disk plane as the gradient is steeper
in the z direction.
We also generated another disk model (type II), with a different radial and
vertical temperature distribution. In this model, the disk "atmosphere'' (z >
zq) follows a power law temperature distribution with radius, while the
temperature in the disk midplane is constant below some radius Rq.
For ![]() :
:
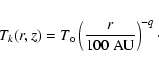
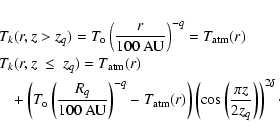
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{ms3027f17.eps}\end{figure}](/articles/aa/full/2003/08/aa3027/Timg102.gif) |
Figure 6:
Comparison of the behavior of the kinetic temperature laws for type I
and type II models versus the vertical scale z:
|
| Open with DEXTER | |
Figure 6 describes the kinetic temperature laws versus z for both
models when r=100 AU (
![]() for type II).
for type II).
Note that a vertical temperature gradient can have a strong influence
on the disk images in spectral lines. This can be understood in
Fig. 3. With a positive gradient, at the systemic velocity,
the CO line brightness will increase around the spatial position
defined by the plane X0=0 AU;
![]() /-200 AU
(Fig. 3, frame A1) where CO probes scales up to a few times
above the local hydrodynamic scale height.
/-200 AU
(Fig. 3, frame A1) where CO probes scales up to a few times
above the local hydrodynamic scale height.
Before analyzing the data, we investigate how much
the derived type 0 parameters are affected by the presence of a type I or type II
temperature gradient. We proceed as follows. We generate disks models
in
![]() and
and
![]()
![]() with vertical gradients of types I and II and minimize them
assuming that there is no vertical gradient inside the disk. The aim
of such minimizations is to determine what are the most important
parameters that influence the minimizations and if any secure
criterion can be used to constrain a gradient. Except for vertical
gradients, the generated models use disk parameters relatively close
to those inferred from
with vertical gradients of types I and II and minimize them
assuming that there is no vertical gradient inside the disk. The aim
of such minimizations is to determine what are the most important
parameters that influence the minimizations and if any secure
criterion can be used to constrain a gradient. Except for vertical
gradients, the generated models use disk parameters relatively close
to those inferred from
![]()
![]() in the DM Tau disk by GD98 (see
Tables 1 and 2).
in the DM Tau disk by GD98 (see
Tables 1 and 2).
| Parameter | Type I | minimization | minimization | minimization | minimization |
| model | 13CO(1-0) | 13CO(2-1) | 12CO(2-1) | C18O(2-1) | |
| 1200 | 1200 | 1200 | 1200 | 1200 | |
| s=1.5+p-q/2 | 2.75 | 2.75 | 2.75 | 2.75 | 2.75 |
| 25 | 32.9 | 29.3 | 42.2 | 37 | |
| q | 0.60 | 0.63 | 0.44 | 0.48 | 0.58 |
| 2.10 | 2.24 | 2.12 | 2.30 | 2.35 | |
| i ( |
-40 | -37.1 | -39.6 | -34.9 | -34.5 |
| PA ( |
63 | 62.7 | 62.7 | 62.5 | 62.7 |
|
|
650 | 643 | 648 | 643 | 610 |
| 1.5 | 1 | 1 | 1 | 1 | |
| 2 | 9 | 490 | 4 | ||
Table 1 presents the test models with a type I gradient, with
![]() to be consistent with CG97, and the best minimization without
gradient. Note that the
to be consistent with CG97, and the best minimization without
gradient. Note that the ![]() (last line) is slightly different to
standard definition because there is no noise added to the model. This
should be equal to "zero'' if the fit of the model would perfectly
represent the model itself. In other words, this
(last line) is slightly different to
standard definition because there is no noise added to the model. This
should be equal to "zero'' if the fit of the model would perfectly
represent the model itself. In other words, this ![]() indicates the
departure of the model.
The
indicates the
departure of the model.
The
![]() and
and
![]() analysis shows significant differences on the absolute
intensity (given by
analysis shows significant differences on the absolute
intensity (given by ![]() )
and the index of the temperature power law (q).
The index appears smaller for the
)
and the index of the temperature power law (q).
The index appears smaller for the
![]()
![]() than for the
than for the
![]()
![]() and for
which it is close to the input value at the mid-plane. From
Fig. 2, there is a relatively straightforward explanation. With the
and for
which it is close to the input value at the mid-plane. From
Fig. 2, there is a relatively straightforward explanation. With the
![]()
![]() isotope, we probe the disk mid-plane whose temperature distribution
with radius follows the same distribution as obtained with no vertical gradient. The
difference appears strongly with the
isotope, we probe the disk mid-plane whose temperature distribution
with radius follows the same distribution as obtained with no vertical gradient. The
difference appears strongly with the
![]()
![]() transition. As previously seen, this
transition probes a much higher height (
transition. As previously seen, this
transition probes a much higher height (![]() 200-300 AU above the plane, see
Fig. 2), thus giving access to the radial variation of the
temperature at this height in the disk atmosphere, which possesses a different
radial behavior as can be seen in Fig. 5. Iso-temperature lines
separate out with height in the disk, thus leading to a flatter radial
dependence of the temperature (i.e. smaller q).
200-300 AU above the plane, see
Fig. 2), thus giving access to the radial variation of the
temperature at this height in the disk atmosphere, which possesses a different
radial behavior as can be seen in Fig. 5. Iso-temperature lines
separate out with height in the disk, thus leading to a flatter radial
dependence of the temperature (i.e. smaller q).
| Parameter | Type II | minimization | minimization | minimization | minimization |
| model | 13CO(1-0) | 13CO(2-1) | 12CO(2-1) | C18O(2-1) | |
|
|
1200 | 1200 | 1200 | 1200 | 1200 |
| s=1.5+p-q/2 | 2.75 | 2.75 | 2.75 | 2.75 | 2.75 |
| 35 | 20.6 | 25.9 | 30.2 | 28.5 | |
| q | 0.60 | 0.27 | 0.35 | 0.51 | 0.26 |
| 2.10 | 2.09 | 2.19 | 2.09 | 2.30 | |
| i ( |
-40 | -40.3 | -38.9 | -39.9 | -35.4 |
| PA ( |
63 | 62.6 | 62.7 | 62.3 | 62.7 |
|
|
650 | 650.4 | 631 | 644 | 590 |
| Rq* | 250 | - | - | - | - |
| zq and |
2 H and 2 | - | - | - | - |
|
|
1 | 19 | 40 | 5 | |
* Rq,zq and ![]() are not defined and have no meaning for the type 0 model.
are not defined and have no meaning for the type 0 model.
Table 2 presents the test models with a type II gradient, with
Rq = 180 AU and zq = 2 H, which is representative of the dA99 dust
temperature distribution, and the best minimization without gradient.
In this case, the
![]() data closely represents the outer disk atmosphere, while
data closely represents the outer disk atmosphere, while
![]()
![]() and
and
![]()
![]() find a lower value for q, as expected since they probe
closer to the disk mid-plane.
find a lower value for q, as expected since they probe
closer to the disk mid-plane.
The minimization on type II gradient models (
![]()
![]() )
with type 0 model leads
to an inclination less than the value in input. The type II gradient possesses
a pivotal point (Rq in AU).
The type 0 models might in fact try to compensate the differences with
the type II models in opacity and surface emission by lowering the
inclination in the comparison. This is because using a single power
law for the temperature dependence in the entire disk, the fitted type 0 temperature in the outer part lies above the real temperature, so
that the brightness is reproduced by lowering the opacity along the
line of sight, obtained by lowering the inclination. In the inner part
(below Rq), the type 0 fitted temperature is below the real
temperature, and the flux is reproduced by increasing the emission
area, which can only be done by lowering again the inclination. The
effect will be particularly pronounced when the line opacity is about 1 at Rq, such as for example
)
with type 0 model leads
to an inclination less than the value in input. The type II gradient possesses
a pivotal point (Rq in AU).
The type 0 models might in fact try to compensate the differences with
the type II models in opacity and surface emission by lowering the
inclination in the comparison. This is because using a single power
law for the temperature dependence in the entire disk, the fitted type 0 temperature in the outer part lies above the real temperature, so
that the brightness is reproduced by lowering the opacity along the
line of sight, obtained by lowering the inclination. In the inner part
(below Rq), the type 0 fitted temperature is below the real
temperature, and the flux is reproduced by increasing the emission
area, which can only be done by lowering again the inclination. The
effect will be particularly pronounced when the line opacity is about 1 at Rq, such as for example
![]()
![]() or
or
![]() in the DM Tau case.
Note that we also checked the reversibility of the type II modelling by performing
a
in the DM Tau case.
Note that we also checked the reversibility of the type II modelling by performing
a
![]() parameter minimization of a type II model using the type II
model itself. The
parameter minimization of a type II model using the type II
model itself. The ![]() converge on all the input values within one
converge on all the input values within one ![]() .
.
We present in Table 3, the ![]() minimization
performed on 2-parameter fits with a type 0 model as described in GD98.
Table 4 summarizes the 4-parameter
minimization
performed on 2-parameter fits with a type 0 model as described in GD98.
Table 4 summarizes the 4-parameter
![]() minimization obtained with the same model.
We caution that, since only
2 or 4-parameter fits were used, the error bars are underestimates of the true
errors, although not by a large amount since the parameter couplings we have
neglected should be small. The results of the type II minimization of
the
minimization obtained with the same model.
We caution that, since only
2 or 4-parameter fits were used, the error bars are underestimates of the true
errors, although not by a large amount since the parameter couplings we have
neglected should be small. The results of the type II minimization of
the
![]() data are given in Table 5.
The results are shown in Figs. 7 and 8. Note that
the volume density
data are given in Table 5.
The results are shown in Figs. 7 and 8. Note that
the volume density
![]() and the surface density
and the surface density
![]() are always referenced to the abundance of
12CO, the main isotope of CO.
are always referenced to the abundance of
12CO, the main isotope of CO.
As shown in Figs. 2 and 3, both the
![]()
![]() and
and
![]() transitions are optically thick and almost probe the same
region of the disks. The 2-parameter minimization therefore gives the same
results. The results obtained on the minimization of both transitions
are presented in Table 3, and are adapted from Simon et al. (2000).
transitions are optically thick and almost probe the same
region of the disks. The 2-parameter minimization therefore gives the same
results. The results obtained on the minimization of both transitions
are presented in Table 3, and are adapted from Simon et al. (2000).
We also present in Table 3 the results of the best
2-parameter
![]()
![]() fits. Since these observations
have the lowest signal to noise, they do not bring more
precise constraints on the disk parameters than the
fits. Since these observations
have the lowest signal to noise, they do not bring more
precise constraints on the disk parameters than the
![]() results
presented below. However, they indicate that the abundance ratio
results
presented below. However, they indicate that the abundance ratio
![]() /
/
![]() is compatible with the standard isotopic ratio of 70 and 550. They also
confirm the large local line width,
is compatible with the standard isotopic ratio of 70 and 550. They also
confirm the large local line width, ![]()
![]() ,
found with
,
found with
![]() and
the outer radius.
and
the outer radius.
Following GD98, there are a priori 14 parameters relevant for
the images of the 13CO line: x0,y0, ![]() ,
,
![]() ,
V0, v, i,
,
V0, v, i,
![]() ,
T0, q,
,
T0, q, ![]() ,
p, dV,
,
p, dV,
![]() .
PA and
.
PA and
![]() are geometrical
parameters which are well constrained independently of the assumed
physical parameters. x0,y0 are determined from the continuum data,
and v = 0.5 for Keplerian motions. The turbulent linewidth dV is
also fitted and appears larger than for CO lines. The abundance
appears as a scale factor for the surface density
are geometrical
parameters which are well constrained independently of the assumed
physical parameters. x0,y0 are determined from the continuum data,
and v = 0.5 for Keplerian motions. The turbulent linewidth dV is
also fitted and appears larger than for CO lines. The abundance
appears as a scale factor for the surface density ![]() ,
which
can only be set by comparing with other mass determination (e.g. from
dust emission, see Sect. 5.4).
Although, in principle, the remaining parameters are all coupled, the
pair (
,
which
can only be set by comparing with other mass determination (e.g. from
dust emission, see Sect. 5.4).
Although, in principle, the remaining parameters are all coupled, the
pair (
![]() )
should not depend significantly on temperature
or density distribution (see GD98), and a separate fit was done for
this pair of parameters. We further neglect the coupling between
)
should not depend significantly on temperature
or density distribution (see GD98), and a separate fit was done for
this pair of parameters. We further neglect the coupling between
![]() and the remaining parameters T0, q,
and the remaining parameters T0, q, ![]() , p,
since it is only due to limited angular resolution.
, p,
since it is only due to limited angular resolution.
Table 3 presents the disk parameters derived with the
above procedures. The outer radius is well defined,
![]() AU from both
AU from both
![]() transitions. We note clear differences
for T0 from
transitions. We note clear differences
for T0 from
![]() and
and
![]() ,
,
![]() and
and
![]() with values of q decreasing from 0.63 to -0.3, although
the latter is only at 2 sigmas from q=0. We conclude from this
analysis that a simple radial temperature variation seems unable to
provide a satisfactory fit for all the transitions simultaneously, as
expected in the case of a vertical temperature gradient does exist in
the disk.
with values of q decreasing from 0.63 to -0.3, although
the latter is only at 2 sigmas from q=0. We conclude from this
analysis that a simple radial temperature variation seems unable to
provide a satisfactory fit for all the transitions simultaneously, as
expected in the case of a vertical temperature gradient does exist in
the disk.
However, the previous 2-parameter analysis arbitrarily separates
![]() and T, whereas these parameters are coupled because the
and T, whereas these parameters are coupled because the
![]() transitions involved are partly optically thin. Therefore, we
investigate a global fit taking into account the presence of this
coupling. The calculations presented in Sect. 3.3 show that the
natural analysis to perform is a minimisation using the 4 parameters
{
transitions involved are partly optically thin. Therefore, we
investigate a global fit taking into account the presence of this
coupling. The calculations presented in Sect. 3.3 show that the
natural analysis to perform is a minimisation using the 4 parameters
{
![]() ,
,
![]() ,p+q,p-q}, since, in the
optically thin LTE and constant abundance case, the brightness
temperature for the
,p+q,p-q}, since, in the
optically thin LTE and constant abundance case, the brightness
temperature for the
![]()
![]() transition should depend only on
transition should depend only on
![]() and p-q, whereas the brightness dependence of the
and p-q, whereas the brightness dependence of the
![]()
![]() transition is more complex, but mostly depend on
transition is more complex, but mostly depend on
![]() and p+q.
The other fixed parameters are presented in Table 4. From this 4-parameter
and p+q.
The other fixed parameters are presented in Table 4. From this 4-parameter ![]() cube, we extract the
2-parameter
cube, we extract the
2-parameter ![]() surfaces presented in Fig. 7 for both
surfaces presented in Fig. 7 for both
![]() transitions observed.
transitions observed.
![]()
![]() ,
which was expected from
Sect. 3.3 to constrain essentially p-q, in fact allows a broad
range of values for (p,q).
,
which was expected from
Sect. 3.3 to constrain essentially p-q, in fact allows a broad
range of values for (p,q).
![]()
![]() ,
being thicker, constrains
p+q. In the {
,
being thicker, constrains
p+q. In the {
![]() ,
,
![]() }
} ![]() planes, we
overplotted the slopes corresponding to constant excitation
temperatures of 10, 20 and 30 K. A constant temperature of
planes, we
overplotted the slopes corresponding to constant excitation
temperatures of 10, 20 and 30 K. A constant temperature of ![]() 13 K provides an appropriate fit to the
13 K provides an appropriate fit to the
![]()
![]() data, while temperatures of order 20 K are required for
data, while temperatures of order 20 K are required for
![]()
![]() .
Hence, the left and middle panels of Fig. 7 indicate that different
temperatures are required to represent both lines. This is emphasized
in the rightmost panels, which present the projected
.
Hence, the left and middle panels of Fig. 7 indicate that different
temperatures are required to represent both lines. This is emphasized
in the rightmost panels, which present the projected ![]() surfaces
resulting from the combination of both
transitions (note that the rightmost panels are not just the sum of the left
and middle ones since all 4 parameters are coupled).
The best combination lies near the 4 to 6
surfaces
resulting from the combination of both
transitions (note that the rightmost panels are not just the sum of the left
and middle ones since all 4 parameters are coupled).
The best combination lies near the 4 to 6 ![]() contours
from the best independent solutions.
contours
from the best independent solutions.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms3027f18.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg121.gif) |
Figure 7:
Analysis with the type 0 model (top) |
| Open with DEXTER | |
| Parameter | minimization | minimization | minimization | minimization | minimization |
| C18O(2-1) | 13CO(2-1) | 13CO(1-0) | 12CO(2-1) | 12CO(1-0) | |
|
|
1400 | 1400 |
1800 |
1400 | 1400 |
| s=1.5+p-q/2 | 2.75 |
2.75 |
2.7 |
2.75 | 2.75 |
| 35 |
22 |
14 |
32.5 |
31 |
|
| q | 0.30 |
0.30 |
-0.30 |
0.63 |
0.63 |
| 2.15 |
2.25 |
2.01 |
2.18 |
2.15 |
|
| i ( |
-34 |
-31 |
-38 |
-32 |
33 |
| PA ( |
66 |
65 |
65 |
67 |
66 |
|
|
6.01 |
6.03 |
6.09 |
6.05 |
6.05 |
|
|
600 |
640 |
650 |
800 |
790 |
| dV (km s-1) | 0.14 |
0.16 |
0.16 |
0.07 |
0.07 |
|
|
1. | 1. | 1. | 1. | 1. |
The
![]() and
and
![]() type 0 analysis presented above clearly
demonstrates that a simple power law for the temperature cannot fit
all transitions. Since, following Sect. 3, each line is sensitive to a
different depth in the disk, the increase in temperature found from
type 0 analysis presented above clearly
demonstrates that a simple power law for the temperature cannot fit
all transitions. Since, following Sect. 3, each line is sensitive to a
different depth in the disk, the increase in temperature found from
![]()
![]() to
to
![]()
![]() and
and
![]() suggest a vertical temperature gradient
with temperatures above the disk plane.
suggest a vertical temperature gradient
with temperatures above the disk plane.
We therefore decided to go deeper in the analysis by performing a type II minimization, which explicitely takes into account the presence of
a vertical gradient in the inner disk. Following the description of
this model in Sect. 4.1, it implies minimization on the four coupled
parameters
{Rq, zq/H,
![]() ,
s}.
Rq defines the articulation point of the law, at which there
is a separation between the vertically isothermal behavior and the
beginning of a temperature vertical gradient. zq/H defines the
steepness of the gradient as compared to the local hydrostatic scale
height.
,
s}.
Rq defines the articulation point of the law, at which there
is a separation between the vertically isothermal behavior and the
beginning of a temperature vertical gradient. zq/H defines the
steepness of the gradient as compared to the local hydrostatic scale
height.
![]() defines the absolute CO volume density
value at the reference point (100 AU) and s its radial variation.
All these parameters fully describe a type II model. Rq and zqare fully defined in Sect. 4.1, type II model, whereas
defines the absolute CO volume density
value at the reference point (100 AU) and s its radial variation.
All these parameters fully describe a type II model. Rq and zqare fully defined in Sect. 4.1, type II model, whereas
![]() ,
s and H are defined in the Appendix. We use
T0 = 32 K, and q=0.63, the law derived from the observation
of the "CO atmosphere'' of the disk with the
,
s and H are defined in the Appendix. We use
T0 = 32 K, and q=0.63, the law derived from the observation
of the "CO atmosphere'' of the disk with the
![]() transitions, and
all other parameters were taken from the type 0 model fit. The
transitions, and
all other parameters were taken from the type 0 model fit. The
![]()
![]() {Rq, zq/H}
{Rq, zq/H} ![]() plane indicates a rather well defined value
of
plane indicates a rather well defined value
of
![]() AU, but high values of zq/H (
AU, but high values of zq/H (
![]() ). Since the bulk of the
). Since the bulk of the
![]()
![]() emission is from low values of z/H, this is consistent
with a constant temperature; this temperature is defined by Rq:
emission is from low values of z/H, this is consistent
with a constant temperature; this temperature is defined by Rq:
![]() -13 K. As expected,
these results are in complete agreement with those of
Fig. 7.
The
-13 K. As expected,
these results are in complete agreement with those of
Fig. 7.
The
![]()
![]() line, which traces slightly upper
layers in the disk can better probe the vertical gradient and
constrains zq/H. The combined {Rq, zq/H}
line, which traces slightly upper
layers in the disk can better probe the vertical gradient and
constrains zq/H. The combined {Rq, zq/H} ![]() plane
allows a common solution to be found within
plane
allows a common solution to be found within ![]() of each
individual fit. This is more consistent than in the type 0 model, but
still indicates that the type II model is not a perfect representation
of the disk structure (in temperature and/or density). The agreement
with the data could be improved by using a hotter, steeper temperature
law
Tk(r,z>zq), as suggested by the results of Table 2, since it
appears that even
of each
individual fit. This is more consistent than in the type 0 model, but
still indicates that the type II model is not a perfect representation
of the disk structure (in temperature and/or density). The agreement
with the data could be improved by using a hotter, steeper temperature
law
Tk(r,z>zq), as suggested by the results of Table 2, since it
appears that even
![]() does not exactly represent the upper layers
(z>zq).
does not exactly represent the upper layers
(z>zq).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{ms3027f19.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg127.gif) |
Figure 8:
Analysis with type II model (top) |
| Open with DEXTER | |
| Parameter | Type 0 |
|
|
2.03 |
| i ( |
-37 |
| PA ( |
66 |
|
|
6.05 |
|
|
650 |
| dV (km s-1) | 0.15 |
| Parameter | Type II |
|
|
32 |
| q | 0.63 |
| 2.03 | |
| i ( |
-37 |
| PA ( |
66 |
|
|
6.05 |
|
|
650 |
| dV (km s-1) | 0.15 |
A detailed analysis of the continuum data is beyond the scope of this paper. However, it is important to note at this stage how we use the dust continuum emission in order to determine the CO depletion factor because the disk mass is best estimated from the mostly optically thin continuum flux at 1.3 mm.
Following Beckwith et al. (1990), we assume for the absorption coefficient
![]() (cm2 g-1).
For DM Tau, we use
(cm2 g-1).
For DM Tau, we use
![]() because this value gives the best fits of the
continuum interferometric maps. It leads to
because this value gives the best fits of the
continuum interferometric maps. It leads to
![]() and
and
![]() cm2 g-1.
This dust absorption coefficient takes into account the gas by
assuming a gas-to-dust ratio of
cm2 g-1.
This dust absorption coefficient takes into account the gas by
assuming a gas-to-dust ratio of
![]() and the mass is the total dust+gas mass
of the disk. Using this dust absorption coefficient, we fit the continuum
emission at all wavelengths. Taking
and the mass is the total dust+gas mass
of the disk. Using this dust absorption coefficient, we fit the continuum
emission at all wavelengths. Taking
![]() ,
we
performed a 4-parameter
,
we
performed a 4-parameter ![]() minimization on
{p+q, p-q,
minimization on
{p+q, p-q,
![]() ,
,
![]() } as described in Pietu et al. (2002).
As expected, since the dust emission is mostly optically thin,
the minimization contrains
} as described in Pietu et al. (2002).
As expected, since the dust emission is mostly optically thin,
the minimization contrains
![]() cm-2 K,
and
cm-2 K,
and
![]() .
These values will be used in Sect. 6
where we discuss the density distribution and the CO depletion.
The disk mass can then be estimated provided T0 and q are known.
Because of the evidence for vertical temperature gradients, the appropriate
values for T0,q are however unclear.
.
These values will be used in Sect. 6
where we discuss the density distribution and the CO depletion.
The disk mass can then be estimated provided T0 and q are known.
Because of the evidence for vertical temperature gradients, the appropriate
values for T0,q are however unclear.
If the dust and CO sample the same region, the CO abundance is directly
given by:
To avoid using these extra parameters, we have chosen to present all
CO results in the measured quantity which is the
![]() surface density
surface density
![]() (or the volume density
(or the volume density
![]() ), using the
standard isotopomer ratios of 70 and 550 to convert from
), using the
standard isotopomer ratios of 70 and 550 to convert from
![]() and
and
![]() measurements.
measurements.
We note that the non-thermal component of the linewidth, dV, increases from
d
![]() km s-1 measured with
km s-1 measured with
![]() to values around
to values around
![]() km s-1 from the
km s-1 from the
![]() and
and
![]() isotopes. A straightforward
interpretation would be that the turbulence is higher in the disk mid-plane,
sampled by the CO isotopomers, than in the disk atmosphere, sampled by
isotopes. A straightforward
interpretation would be that the turbulence is higher in the disk mid-plane,
sampled by the CO isotopomers, than in the disk atmosphere, sampled by
![]() .
.
However, Table 3 also shows that the derived disk
inclination differs from one isotopomer to the other. Higher
inclinations are found from the rarer isotopomers than from
![]() .
Systematic bias resulting from the analysis by a type 0 model of
a more complex disk structure would result in the opposite effect
(lower inclination for
.
Systematic bias resulting from the analysis by a type 0 model of
a more complex disk structure would result in the opposite effect
(lower inclination for
![]() and
and
![]() ,
see Sect. 4.2), suggesting
that the difference in inclination is real. Since
,
see Sect. 4.2), suggesting
that the difference in inclination is real. Since
![]() and
and
![]() preferentially sample the inner part of the disk (
preferentially sample the inner part of the disk (
![]() AU),
while
AU),
while
![]() is sensitive to the whole disk (
is sensitive to the whole disk (
![]() AU), this
could be indicative of a warped disk. Continuum emission also provides
a measurement of the inner disk inclination: a value of
AU), this
could be indicative of a warped disk. Continuum emission also provides
a measurement of the inner disk inclination: a value of
![]() is found from the 1.4 mm measurements. Unfortunately, this
is only a lower limit, since it should be corrected from seeing
effects. If the disk is warped, the change of inclination with radius
will result in enhanced projected velocity gradients, which will mimic
an increase in linewidth near the disk center. The magnitude of
the effect depends on the warp intensity, and is difficult to
estimate. However, one should remember that the apparent inclinations
we measure are lower limits to the inclination variations, since they
are averaged values over large areas of the disk.
is found from the 1.4 mm measurements. Unfortunately, this
is only a lower limit, since it should be corrected from seeing
effects. If the disk is warped, the change of inclination with radius
will result in enhanced projected velocity gradients, which will mimic
an increase in linewidth near the disk center. The magnitude of
the effect depends on the warp intensity, and is difficult to
estimate. However, one should remember that the apparent inclinations
we measure are lower limits to the inclination variations, since they
are averaged values over large areas of the disk.
Note that inclination and line widths are well de-coupled parameters. Inclination is determined from the shape of the individual channel images, while the line width is constrained by the total flux (see Beckwith & Sargent 1993; Guilloteau & Dutrey 1994, 1998). Hence, with the present observations, the two alternatives (warp or enhanced turbulence in the disk plane) remain plausible.
Analysing the data with an inappropriate model could lead to inconsistent inclination
determination, and hence to errors on the stellar mass derived from Keplerian
motions. Table 3 shows some possible effects at the level of a few degrees, leading
to errors of ![]() 9% on the stellar mass, but with
9% on the stellar mass, but with
![]() and
and
![]()
![]() data
being the least affected. These errors are at most comparable to the 1
data
being the least affected. These errors are at most comparable to the 1 ![]() error on real data.
error on real data.
The observed outer radius of DM Tau, in the
![]()
![]() and
and
![]() transitions
(
transitions
(![]() 640 AU) is significatively different from the
640 AU) is significatively different from the
![]()
![]() and
and
![]() ones (
ones (![]() 800 AU). The
800 AU). The
![]() lines are optically thick. The observed radius in
these transitions reveal a clear cut off in the radial density distribution,
whereas the
lines are optically thick. The observed radius in
these transitions reveal a clear cut off in the radial density distribution,
whereas the
![]() outer radius could be governed by its ability to
photodissociate at higher extinction than its main isotope.
outer radius could be governed by its ability to
photodissociate at higher extinction than its main isotope.
The behaviour of the photodissociation rates for both CO isotopes as a result of self-shielding, mutual shielding, other atoms and molecules absorption (mainly H and H2) as well as dust screening are discussed in the interstellar cloud cases by e.g. van Dishoeck & Black (1988) and Glassgold et al. (1985).
If we look at the Fig. 8 of van Dishoeck & Black (1988), we see that the
photodissociation of CO becomes effective as soon as the H2 column density
is lower than
![]() cm-2, for a model with
cm-2, for a model with
![]() ,
i.e. a normal interstellar radiation field (Draine
1974). In the DM Tau model of GD98, at 800 AU, the vertical column density above the disk mid-plane N
is given by
,
i.e. a normal interstellar radiation field (Draine
1974). In the DM Tau model of GD98, at 800 AU, the vertical column density above the disk mid-plane N
is given by
![]() ,
i.e.
,
i.e.
![]() cm-2, consistent with the fact
this outer radius is governed by photodissociation.
cm-2, consistent with the fact
this outer radius is governed by photodissociation.
We now use the relation
![]() cm-2 mag-1 to determine the minimum
cm-2 mag-1 to determine the minimum
![]() required to protect
required to protect
![]() ,
which leads to
,
which leads to
![]() .
The
corresponding photodissociation rate at which
.
The
corresponding photodissociation rate at which
![]() is destroyed, using the Fig. 5 of van Dishoeck & Black (1998) is of 10-13 s-1. Assuming we need the same
rate to dissociate 13CO, the corresponding
is destroyed, using the Fig. 5 of van Dishoeck & Black (1998) is of 10-13 s-1. Assuming we need the same
rate to dissociate 13CO, the corresponding
![]() equals 1.15.
The column density at the
equals 1.15.
The column density at the
![]() outer radius (640 AU) should therefore be 1.4 times the one at 800 AU. As the surface density law is given by
outer radius (640 AU) should therefore be 1.4 times the one at 800 AU. As the surface density law is given by
![]() ,
we can derive that:
,
we can derive that:
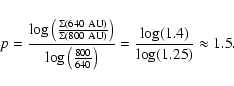
However, if we now take into account that in the T Tauri disks the grain
coagulation and growth has started, we expect the
![]() ratio to be higher than in molecular clouds.
The shielding by dust will become less important. It should not have a strong
influence on the
ratio to be higher than in molecular clouds.
The shielding by dust will become less important. It should not have a strong
influence on the
![]() shielding as it is already effective at low dust
extinction (see Fig. 5a of van Dishoeck & Black 1988 and Fig. 3 of Glassgold et al.
1985). However, it should have an influence on the
shielding as it is already effective at low dust
extinction (see Fig. 5a of van Dishoeck & Black 1988 and Fig. 3 of Glassgold et al.
1985). However, it should have an influence on the
![]() photodissociation
rates, which should raise. If we proceed in the same way as described above to
determine the difference in A
photodissociation
rates, which should raise. If we proceed in the same way as described above to
determine the difference in A
![]() required to protect
required to protect
![]() and
and
![]() ,
it implies that
,
it implies that
![]() .
Given that the uncertainty in the derivation of the observed
.
Given that the uncertainty in the derivation of the observed
![]() is of
is of ![]() 20 AU, and assuming the
20 AU, and assuming the
![]() ratio determination is
accurate at the 10% level, it is compatible with
ratio determination is
accurate at the 10% level, it is compatible with ![]() .
This does not
provide a strong constraint on the p index, but rather demonstrate that the
photodissociation of CO is a reasonable process to explain the observations.
.
This does not
provide a strong constraint on the p index, but rather demonstrate that the
photodissociation of CO is a reasonable process to explain the observations.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{ms3027f20.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg165.gif) |
Figure 9:
Representation of the characteristic vertical scales and
number densities in the DM Tau disk. The short dashed line represent
the local hydrostatic scale height. The heights probed with the
|
| Open with DEXTER | |
The temperature structure of protoplanetary disks has been modeled by CG97 and dA99, in view of analyzing the IR emission from disks. Both models concentrate on the dust temperature, while we are interested in the gas temperature. However, at the densities (>106 cm-3) and temperatures (10-50 K) where the CO emission arises, the gas cooling is very inefficient, so that the kinetic temperature is essentially identical to the dust temperature. On the other hand, the dust-gas coupling has negligible effect on the dust temperature, which is completely dominated by heating by the stellar light.
This results in two major effects on the temperature structure of the
disk. The disk photosphere, defined as the surface where the optical depth
of the dust to the stellar light is about unity is heated to high temperatures by stellar photons directly impinging on the disk surface. For T Tauri stars,
it corresponds to
![]() .
This warm
"super-heated'' layer reradiates at longer wavelengths to heat the
disk interior.
.
This warm
"super-heated'' layer reradiates at longer wavelengths to heat the
disk interior.
To compare with models of super-heated layers, it is important to note
that our definition of the
hydrostatic scale height differs from that used in the models of CG97 and
dA99 by ![]() ,
our scale height being larger (see Appendix for the
details). Following our definition, the dust photosphere lies approximately
at
,
our scale height being larger (see Appendix for the
details). Following our definition, the dust photosphere lies approximately
at
![]() in CG97. At the radius of 100 AU, the
midplane temperature is of 20 K, whereas the surface
is heated at
in CG97. At the radius of 100 AU, the
midplane temperature is of 20 K, whereas the surface
is heated at ![]() 90 K. In the model developped by dA99,
90 K. In the model developped by dA99,
![]() ,
and the temperature are of 15 K
and 60 K at mid-plane and dust surface, respectively. Both models
assume a 0.5
,
and the temperature are of 15 K
and 60 K at mid-plane and dust surface, respectively. Both models
assume a 0.5 ![]() central star, with an effective temperature
T*=4000 K. The former takes
central star, with an effective temperature
T*=4000 K. The former takes
![]() ,
whereas for the
later
,
whereas for the
later
![]() .
Figure 9 summarizes the scale heights relevant for the comparison.
.
Figure 9 summarizes the scale heights relevant for the comparison.
In addition to this "super-heated'' layer, there is a temperature "plateau'' in the disk mid-plane, resulting from a temperature gradient between the disk atmosphere and the disk plane. When the disk is optically thick to the illuminating radiation, but thin to its own emission, the disk plane is cooler than the disk atmosphere. This can happen in a well defined region of the disk with the appropriate surface density (see e.g. dA99, their Fig. 3). Closer to the star, when the surface density is higher, the mid plane temperature rises again with q = 0.5. At the outer edge, the mid-plane temperature asymptotically reaches the temperature of the disk atmosphere. Hence, in the disk plane, as a function of radius, there is a region where the temperature law flattens, while q becomes again of order 0.6 at larger distances.
Since, as shown in Fig. 9, the
![]()
![]() line probe a
slightly lower layer than the dust photosphere, we cannot fully constrain the
"super-heated'' layer from our observations. On the other hand,
the temperature "plateau'' can be traced by the
line probe a
slightly lower layer than the dust photosphere, we cannot fully constrain the
"super-heated'' layer from our observations. On the other hand,
the temperature "plateau'' can be traced by the
![]() transitions.
transitions.
The kinetic temperature distribution we deduce from the CO data in the
DM Tau outer disk is shown Fig. 10.
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{ms3027f21.eps}
\end{figure}](/articles/aa/full/2003/08/aa3027/Timg173.gif) |
Figure 10:
Schematic representation of the gas and dust
temperature in the disk mid-plane and disk atmosphere as probed with the
|
| Open with DEXTER | |
The outer edge of the "plateau'' (
![]() in Fig. 10) is
determined from our data by the intersection of the
in Fig. 10) is
determined from our data by the intersection of the
![]() K, q = 0.63
law with the
K, q = 0.63
law with the
![]() K,
K,
![]() ,
i.e. about 400 AU. The inner edge
cannot be determined directly by our observations, due to the lack of angular
resolution. However, it can be reasonably estimated by assuming the dust and
gas temperature are equal. The dust temperature distribution in the inner
regions can be determined from the FIR flux densities around 60
,
i.e. about 400 AU. The inner edge
cannot be determined directly by our observations, due to the lack of angular
resolution. However, it can be reasonably estimated by assuming the dust and
gas temperature are equal. The dust temperature distribution in the inner
regions can be determined from the FIR flux densities around 60 ![]() m.
Beckwith et al. (1990) find for DM Tau Tk(1 AU
m.
Beckwith et al. (1990) find for DM Tau Tk(1 AU
![]() K and
K and
![]() from the IRAS data. This temperature law intersects that of the
"plateau'' around
from the IRAS data. This temperature law intersects that of the
"plateau'' around
![]() AU. The direct observation of a
temperature "plateau'' allows to resolve the apparent inconsistencies between
the low temperatures derived from the mid and FIR and the higher values derived
from 12CO observations at larger radius. The measurement of the inner
radius would require better angular resolution at mm wavelengths (e.g. ALMA).
AU. The direct observation of a
temperature "plateau'' allows to resolve the apparent inconsistencies between
the low temperatures derived from the mid and FIR and the higher values derived
from 12CO observations at larger radius. The measurement of the inner
radius would require better angular resolution at mm wavelengths (e.g. ALMA).
Using the results on the continuum and the CO lines, we can estimate X(CO)
and the CO depletion factor f(CO). The CO abundance is given by the ratio
(see Fig. 7 for the values)
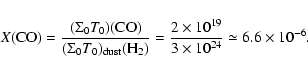 |
(9) |
In the type II model, we determine
![]() cm-3, from which, using
a scale height of
cm-3, from which, using
a scale height of
![]() AU at 100 AU, consistent with the T0=13 K mid-plane temperature,
gives
AU at 100 AU, consistent with the T0=13 K mid-plane temperature,
gives
![]() cm2 K, as for the
type 0 models.
cm2 K, as for the
type 0 models.
Using standard isotopic abundances, we derive identical depletion factors from
![]()
![]() and the optically thinner transition
and the optically thinner transition
![]()
![]() ,
although they do not sample
the same volume in the disk. This suggests that the depletion does not
vary by huge factors within the disk. Note that the depletion is
not sufficient to significantly deplete CO, which is optically thick
up to 800 AU, whereas the grain temperature is below the freezing
point at radii above 200 AU. Except for the external region, which can
be affected by other effects like photodissociation, this high opacity
is ubiquitous in observed disks (GG Tau, Dutrey et al. 1994; GM Auriga,
Dutrey et al. 1998; Simon et al. 2000). Hence, there is still a sufficient
amount of CO at the temperature of the "plateau'' (13 K) even if it is
well below the CO freeze out point.
,
although they do not sample
the same volume in the disk. This suggests that the depletion does not
vary by huge factors within the disk. Note that the depletion is
not sufficient to significantly deplete CO, which is optically thick
up to 800 AU, whereas the grain temperature is below the freezing
point at radii above 200 AU. Except for the external region, which can
be affected by other effects like photodissociation, this high opacity
is ubiquitous in observed disks (GG Tau, Dutrey et al. 1994; GM Auriga,
Dutrey et al. 1998; Simon et al. 2000). Hence, there is still a sufficient
amount of CO at the temperature of the "plateau'' (13 K) even if it is
well below the CO freeze out point.
The existence of a temperature "plateau'' can place indirect constraints on
the disk mass, because the "plateau'' appears within a defined surface density
range. In the dA99 models, this temperature plateau happens when
![]() is
about 0.1 g cm-2. When the disk becomes more massive (see Fig. 3 dA99),
the opacity is such that the plateau never exist. The observation of a plateau
therefore sets an upper limit on the disk mass. However, the precise position
of this plateau depends both on the slope and the absolute value of the dust
opacity function between 50 and 300
is
about 0.1 g cm-2. When the disk becomes more massive (see Fig. 3 dA99),
the opacity is such that the plateau never exist. The observation of a plateau
therefore sets an upper limit on the disk mass. However, the precise position
of this plateau depends both on the slope and the absolute value of the dust
opacity function between 50 and 300 ![]() m, related to the temperature range of
reemission concerned (10-60 K).
m, related to the temperature range of
reemission concerned (10-60 K).
With the dust properties adopted by dA99
(Draine & Lee (1984) optical constants and Mathis et al. (1977)
size distribution), the existence of the "plateau'' implies
![]() .
However, this combination of dust opacity and disk mass fails
to reproduce the observed mm flux densities by a factor
.
However, this combination of dust opacity and disk mass fails
to reproduce the observed mm flux densities by a factor ![]() 10. The
discrepancy can be resolved if significant grain growth has occurred. In this
case, the millimeter opacities are increased, but the shorter wavelengths
opacities decrease (see for example Kruegel & Siebenmorgen 1994, their Fig. 12),
thereby moving inward the position of the plateau for a given disk mass.
From
10. The
discrepancy can be resolved if significant grain growth has occurred. In this
case, the millimeter opacities are increased, but the shorter wavelengths
opacities decrease (see for example Kruegel & Siebenmorgen 1994, their Fig. 12),
thereby moving inward the position of the plateau for a given disk mass.
From
![]() derived from the dust, and using
derived from the dust, and using
![]() K for
the dust temperature (or equivalently, using an average depletion of 10
for CO relative to standard Taurus abundances), our measurement indicates
K for
the dust temperature (or equivalently, using an average depletion of 10
for CO relative to standard Taurus abundances), our measurement indicates
![]() H2 cm-2 at 100 AU or
H2 cm-2 at 100 AU or
![]() g cm-2. Although this goes in the expected direction
more detailed disk models with more appropriate
dust parameters are required to predict quantitatively the position and
extent of the temperature "plateau''.
g cm-2. Although this goes in the expected direction
more detailed disk models with more appropriate
dust parameters are required to predict quantitatively the position and
extent of the temperature "plateau''.
Finally, let us note that the density exponent,
![]() ,
agrees with the ratio of the outer radii for 12CO and
13CO, when the CO distribution is truncated by
photodissociation.
,
agrees with the ratio of the outer radii for 12CO and
13CO, when the CO distribution is truncated by
photodissociation.
Using high angular (1'') resolution PdBI millimeter interferometry we have
mapped the circumstellar disk of the T Tauri star DM Tau in
![]() ,
,
![]() and
and
![]() in their
in their
![]() and
and
![]() transitions. The combination of isotopes imaging
allows to sample the entire line opacity range in the disk and therefore to
separate and constrain the parameters describing its physical state. The
analysis of the data allow to draw several conclusions:
transitions. The combination of isotopes imaging
allows to sample the entire line opacity range in the disk and therefore to
separate and constrain the parameters describing its physical state. The
analysis of the data allow to draw several conclusions:
Acknowledgements
We acknowledge all the PdBI IRAM staff for their help during the observations. Particular thanks to D. Nürnberger who pointed out a spurious problem. Most of the calculations were performed using the LAOG computer facilities we thank Ginette Buisson for assisting us in the installation of the software.
In Dutrey et al. (1994), we use the following parametrizations for the
physical laws in the type 0 model:
Kinetic temperature:
| (A.3) |
| n(r) | = | (A.4) | |
| = | (A.5) | ||
| s | = | h + p = 1 + v +p - q/2 | (A.6) |
| n(r,z) | = | (A.7) |
| H(r) | = | 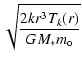 |
(A.8) |
| = | 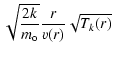 |
(A.9) | |
| = | (A.10) | ||
| h | = | 1 + v -q/2. | (A.11) |
For the ![]() ,
we take the value of
,
we take the value of
![]() where
where ![]() is the hydrogen mass (Beckwith &
Sargent 1993).
is the hydrogen mass (Beckwith &
Sargent 1993).
Note that other groups (in particular those working on theoretical dust disk
modelling) usually use the following definition for
![]() ,
which leads to:
,
which leads to: