A&A 399, 583-587 (2003)
DOI: 10.1051/0004-6361:20021533

Complex bifurcations in interstellar chemistry?

S. B. Charnley1 - A. J. Markwick2


1 - Space Science Division, NASA Ames Research Center, MS 245-3, Moffett Field, CA 94035, USA
2 - Department of Physics, UMIST, PO Box 88, Manchester M60 1QD, UK

Received 6 November 2001 / Accepted 21 October 2002

Abstract
Bifurcation diagrams for the steady-state chemical abundances of dense molecular gas have been computed in the region of parameter space where bistable solutions are known to occur. Despite the appearance of many exotic bifurcations, which could be interpreted as sections though higher dimensional catastrophes, we show that they are fundamentally projection effects of the same basic bifurcation, which is an hysteresis loop.

Key words: ISM: abundances - ISM: molecules - molecular processes


1 Introduction

Astrochemical models of dense molecular clouds typically involve the simultaneous solution of many coupled, nonlinear, ordinary differential equations of the form

\begin{displaymath}\vec{\dot {y}} = \vec{F} (\vec{y}, t; {\bf\epsilon} ) \end{displaymath} (1)

where $\vec{y}$ is a vector of chemical fractional abundances or concentrations and $\vec{F}$ is a nonlinear function expressing the production and loss rates of each species. Equation (1) is analogous to that describing any dynamical system (Drazin 1992) and is solved subject to some prescribed set of initial conditions $\vec{y}(0)=\vec{y}^0$. The elements of the vector ${\bf\epsilon}$ are the bifurcation or control parameters whose variation essentially determines the nature and stability of the fixed-point solution, and hence the evolution of the dynamical system.

An important theoretical advance was made by Le Bourlot et al. (1993) who demonstrated that bistable solutions exist for the fixed-point solutions of Eq. (1). For N chemical species, these are the solutions of the system

\begin{displaymath}{ {\vec{F} _i}(\vec{y}; {\bf\epsilon} ) = 0 ~~~~~~i=1,...,N}. \end{displaymath} (2)

The characterisation of any dynamical system first involves the determination of the loci and stability of its fixed points in phase space. For interstellar chemistry these reside in a multidimensional phase space and are the solutions of the system

\begin{displaymath}{ {\vec{F} _i}(\vec{y}; \zeta/n_{\rm H}, T, \beta, \delta_{C}, \delta_{O}, \delta_{S}, \delta_{M} ) = 0~~~~~~i=1,...,N} \end{displaymath} (3)

where the control parameters are: the cosmic ray ionization rate $\zeta$, the particle density $n_{\rm H}$, the gas temperature T, the secondary photodissociation rate due to cosmic rays $\beta$, the depletion factors for the major elements $\delta_{j}$ ($j=\rm C$, O, N, S), and the depletion factor for the refractory metals $\delta_{\rm M}$. In this paper it is assumed that the reaction rate coefficients remain fixed and are not therefore control parameters (see Le Bourlot et al. 1995).

The bistable loci found previously are hysteresis or reverse-hysteresis loops (Le Bourlot et al. 1993, 1995; Shalabiea & Greenberg 1995; Lee et al. 1998). Hysteresis loops are cross-sections through higher dimensional objects, such as the cusp catastrope in three dimensions. As part of an extensive investigation into the dynamical structure of astrochemical kinetics, we have investigated the solutions of Eq. (3), we have computed the bifurcation diagrams for Eq. (3) with $n_{\rm H}$ and $\delta_{\rm S}$ as control parameters. In this paper we report the analysis of the observed bifurcation phenomena.


 

 
Table 1: Parameters of the model.
Temperature T 10 K
Visual extinction Av 15 mag
Cosmic ray ionization rate $\zeta$ $5\times 10^{-17}$ s-1
Prasad-Tarafdar photons? $\beta$ Yes



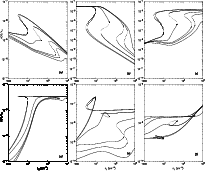  \begin{figure} { \psfig{file=10437fig1.ps,height=15cm,angle=-90,width=18cm,clip=} } \end{figure} Figure 1: Bifurcation diagrams for selected CHO-bearing species. Unstable loci are shown as broken lines. The full curves correspond to $\delta _{\rm S}=1$ and no bifurcation; other curves correspond to $\delta_{\rm S}=0.5, 0.3, 0.1, 0.01 \rm ~and~ 0.001$. The species shown are a) $\rm H_3^+$, b) $\rm C^0$, c) $\rm O_2$, d) $\rm CO$, e) $\rm CH_4$, f) $\rm Na^0$.
Open with DEXTER

2 Steady-state model

We used a static, isothermal, model containing 66 gas phase chemical species linked by 708 reactions (see Charnley 1998). The chemical network is based on the UMIST reaction database (Millar et al. 1997) and includes cosmic ray-induced photoreactions (Prasad & Tarafdar 1983). The relevant physical and chemical parameters were taken from Le Bourlot et al. (1993) and are summarised in Tables 1 and 2. As we wish to compute both the stable and unstable fixed points, the system of (3) was solved by Newton-Raphson iteration.


 

 
Table 2: Elemental abundances (relative to total hydrogen nuclei).

Element		 Abundance Element Abundance

O		 $8.53\times 10^{-5}$ C $3.62\times 10^{-5}$
Na $1.5\times 10^{-8}$ He 0.1
S$^\dagger$ $1.85\times 10^{-5}$ $\delta_{\rm S}$    
$^\dagger$ See text.


3 Bifurcation diagrams

Figures 1 and 2 show the way in which bifurcations "evolve'' (or unfold) when $\delta_{\rm S}$ is reduced through values of 1.0, 0.5, 0.3, 0.1, 0.01 and 0.001. The temperature in each case was 10 K. Figures 1a-c show the loci of fixed points for $\rm H_3^+$, atomic carbon, and O2. These curves are the well-known hysteresis loops reported in previous studies of astrochemical bistability. Figures 1d-f appear to show that other, fundamentally distinct, bifurcations are present in interstellar chemistry. The steady-state CO abundances (Fig. 1d) exhibit fixed point loci that appear to be sections through a higher-dimensional catastrophe, such as the butterfly (Poston & Stewart 1978; Saunders 1980; Arnol'd 1992). Figure 1f shows that atomic abundances of the representative metal in this model, Na, exhibit hysteresis loops which seem to evolve into a "bubble'' for intermediate values of $\delta_{\rm S}$ and thereafter into a more complex form with the unstable solution branch crossing and lying above the stable ones. The exotic nature of bifurcations in the CHO-chemistry is most evident for CH4. The methane fixed point loci in Fig. 1e evolve from simple hysteresis loops into a bubble. At intermediate values of $\delta_{\rm S}$ the loci are extremely complex.

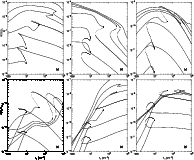  \begin{figure} { \psfig{file=10437fig2.ps,height=14cm,angle=-90,width=17cm,clip=} } \end{figure} Figure 2: As Fig. 1 but for selected S-bearing species: a) $\rm S^0 $, b) $\rm S^+ $, c) $\rm SH$, d) $\rm HCS^+$, e) $\rm OCS$, f) $\rm H_2CS$.
Open with DEXTER

Figures 2a-f display the bifurcation diagrams for the abundances of the some major S-bearing species when $\delta_{\rm S}$ and $n_{\rm H}$ are varied. All the bifurcation phenomena described above are present in these figures, as well as even more complicated forms. S0 begins as a simple hysteresis loop and evolves through a bubble to a structure similar to sections through the butterfly catastrophe (Saunders 1980, Fig. 4.11). S+ evolves from a hysteresis loop to the ``breaking wave'' (e.g. Gray & Scott 1990) at the lowest values of $\delta_{\rm S}$; this is also evident in the diagrams of C/CO versus $\zeta$ presented by Le Bourlot et al. (1995). OCS initially exhibits hysteresis then develops a bubble which is deformed but subsequently reappears. The H2CS bifurcation immediately opens out into a bubble and retains this basic form for all values of $\delta_{\rm S}$. HCS+ evolves from a simple hysteresis loop to a bubble but, for intermediate values of $\delta_{\rm S}$, apparently displays a peculiar "figure-of-eight'' bifurcation in which the unstable state threads one of the stable ones.


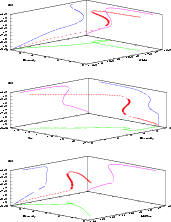  \begin{figure} {\psfig{file=10437fig3i.eps,height=5.8cm,width=15cm} }\vspace*{1... ...ce*{1cm} {\psfig{file=10437fig3iii.eps,height=5.8cm,width=15cm} } \end{figure} Figure 3: Two-dimensional projections of 3-dimensional hysteresis loops. The phase space is defined by $n_{\rm H}$, y($\rm O_2$) and a) y($\rm CH_4$) with $\delta _{\rm S}=0.001$ b) y($\rm S^+ $) with $\delta _{\rm S}=0.001$ c) y($\rm HCS^+$) with $\delta _{\rm S}=0.01$.
Open with DEXTER

4 Discussion

Apart from the existence of hysteresis loops, the most common bifurcation feature found is the formation of a "bubble''. The form of these bubbles is reminiscent of various degenerate loci found, in bifurcation diagrams, which appear as intermediate between the disappearance of an isola and the formation of a mushroom (see Gray & Scott 1990, Fig. 7.4). We were unable to find isola or mushroom bifurcations. The presence of exotic bifurcation phenomena led us to speculate (as in Sect. 3) that, just as sections through the cusp catastrophe yield the hysteresis loops, these bifurcations could be sections through the multidimensional phase space defined by the solutions of Eq. (3). This is similar to what is found in catastrophe theory. For example, the butterfly catastrophe has a 5-dimensional equilibrium surface and four control parameters; sections through it for various pairs of control parameters bear resemblance to some of the curves in Figs. 1 and 2 (Saunders 1980, Fig. 4.11). However, as we now show, these bifurcation phenomena can simply be understood as projection effects.

Figures 3a-c show plots of the 3-dimensional phase space defined by the fixed points of the number density, the $\rm O_2$ abundance, and the abundances of each of $\rm CH_4$, $\rm S^+ $ and $\rm HCS^+$. Figure 3 clearly illustrates that three apparently complex bifurcations evident in Figs. 1 and 2: "bubble'' (or "degenerate isola'') ($\rm CH_4$); ``breaking wave'' ($\rm S^+ $); and "figure-of-eight'' ($\rm HCS^+$), are simply projections of 3D hysteresis loops on to the 2D bifurcation diagram.

5 Conclusions

We have computed bifurcation diagrams in the bistable regime of interstellar chemistry. These diagrams show many apparently complex bifurcations. In fact, these bifurcations can be shown to be 2D projections of 3D hysteresis loops. The multidimensional phase space of dense cloud chemistry is defined by solutions of Eq. (3). Sections through higher-dimensional elementary catastrophes can yield complex bifurcation diagrams (Poston & Stewart 1978; Saunders 1980) and, since we have only touched on a small region of the solution space, it is quite possible that more bifurcation phenomena await discovery. However, it is clear that one must be cautious in interpreting 2D bifurcation diagrams.

Only a few chemical species are important for allowing multistability in interstellar chemistry, and simple models of can provide insight into the type of nonlinear kinetics expected (Charnley et al. 2002). A relevant example is the model of Oppenheimer & Dalgarno (1974) for the ionisation fraction in molecular clouds. Here the steady-state electron density obeys a cubic equation in which the number density of refractory metal atoms, $n(\rm M)$ say, appears in the coefficients (Oppenheimer & Dalgarno 1974). The steady-state model is completed by an equation in $n(\rm M)$ which is quadratic. Hence, in this case the electron fraction, having three possible roots, could in principle exhibit bistability, whereas the refractory metal could not. This shows analytically that the "bubble'' in the Na abundance of Fig. 1f cannot truly be a multistable region.

The content of this paper is largely mathematical and a widespread role for astrochemical instabilities remains to be confirmed observationally. However, perhaps the most intriguing aspect of the existence of bifurcations in models of molecular cloud chemistry is that they occur for values of the physical and chemical control parameters that are within the range suggested by observations.

Acknowledgements
We are especially grateful to the Referee, Jacques Le Bourlot, for a detailed report and for demonstrating to us that some bifurcation phenomena could be understood as projection effects. Part of this work was completed during a workshop at the Lorentz Centre of Leiden University and we thank the organisers for their hospitality. Theoretical astrochemistry at NASA Ames is supported by NASA's Origins of Solar Systems and Exobiology Programs through NASA Ames Interchange NCC2-1162. AJM is supported by a PPARC postdoctoral research associateship.

References

 

Copyright ESO 2003