A&A 399, 409-420 (2003)
DOI: 10.1051/0004-6361:20021827
T. A. Enßlin
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str.1, 85740 Garching, Germany
Department of Physics, University of Toronto, 60 St. George Street,
Toronto M5S1A7, Canada
Received 2 November 2000 / Accepted 12 November 2002
Abstract
The escape rate of cosmic ray (CR) particles from radio
galaxy cocoons is a problem of high astrophysical relevance: e.g. if
CR electrons are stored for long times in the dilute relativistic
medium filling the radio cocoons (radio plasma in the following)
they are protected against Coulomb losses and thus are able to produce
a significant non-thermal Comptonisation signature on the CMB. On the
other hand, CR protons and positrons which leak out of radio plasma
can interact with the ambient medium, leading to characteristic gamma
ray radiation by pion decay and pair annihilation. In order better
understand such problems a model for the escape of CR particles from
radio galaxy cocoons is presented here. It is assumed that the radio
cocoon is poorly magnetically connected to the environment. An extreme
case of this kind is an insulating boundary layer of magnetic fields,
which can efficiently suppress particle escape. More likely, magnetic
field lines are less organised and allow the transport of CR particles
from the source interior to the surface region. For such a scenario
two transport regimes are analysed: diffusion of particles along
inter-phase magnetic flux tubes (leaving the cocoon) and cross field
transport of particles in flux tubes touching the cocoon surface. The
cross field diffusion is likely the dominate escape path, unless a
significant fraction of the surface is magnetically connected to the
environment. Major cluster merger should strongly enhance the
particle escape by two complementary mechanisms. i) The merger shock
waves shred radio cocoons into filamentary structures, allowing the
CRs to easily reach the radio plasma boundary due to the changed
morphology. ii) Also efficient particle losses can be expected for
radio cocoons not compressed in shock waves. There, for a short period
after the sudden injection of large scale turbulence, the (anomalous)
cross field diffusion can be enhanced by several orders of
magnitude. This lasts until the turbulent energy cascade has reached
the microscopic scales, which determine the value of the microscopic
diffusion coefficients.
Key words: ISM: cosmic rays - diffusion - magnetic fields - galaxies: intergalactic medium - galaxies: active
The outflows of radio galaxies fill large regions in the intergalactic space with relativistic, magnetised plasma. The fate of this radio plasma is unclear, since it rapidly becomes undetectable for radio telescopes due to the radiative energy losses of the higher energy electrons, which emit the observable synchrotron emission at radio bands. Lower energy electrons, and any possible present relativistic proton population, may reside for cosmological times, unless they are able to escape by spatial diffusion.
The escape of CRs out of radio plasma is of high astrophysical relevance. If CR electrons are able to leak out of the cocoon, they are possible seed particles for the Mpc-sized radio halos in clusters of galaxies if they are re-accelerated in the cluster turbulence to radio-observable energies (Giovannini et al. 1993; Brunetti et al. 2001). If radio cocoons release CR protons into the intra-cluster medium, secondary CR electrons are produced in hadronic interactions with the background gas, which also could explain the existence of cluster radio halos (Dennison 1980). If radio plasma contains a significant fraction of positrons, they could lead to a detectable annihilation line, if they would be able to leave the radio cocoon and interact with a dense ambient intra-cluster medium (Furlanetto & Loeb 2002).
On the other hand, if the relativistic electrons are efficiently confined for cosmological time-scales in radio cocoons, they are shielded from severe energy losses by Coulomb interaction with the environmental gas. In such a case they would be long-lived and would therefore be able to produce a non-thermal Comptonisation signature in the cosmic microwave background (Enßlin & Kaiser 2000; Enßlin & Sunyaev 2002). Further, if old, invisible radio plasma with confined relativistic electrons is dragged into a shock wave of the large-scale structure formation, its radio emission is possibly revived and forms the observed cluster radio relics (Enßlin & Brüggen 2002, and references therein).
The recent detections of several ghost cavities in galaxy clusters (for lists of recent detections e.g. Enßlin & Heinz 2002; Soker et al. 2002), which are often but not always radio-emitting, support the assumption that the environmental gas and the bulk of the relativistic plasma stays separated on a timescale of 100 Myr. However, leakage of higher energy particles is not excluded by these observations.
CR escape from radio plasma can also play a role in our galaxy. Microquasars are proposed to contribute characteristic spectral features to the galactic CR spectrum, if CRs are able to leave the ejected plasma (Heinz & Sunyaev 2002).
The usual description of CR escape from systems like our Galaxy is
done in terms of leaky box models, where the CR particles
trapped in some region are attributed a characteristic escape time or
frequency (
![]() ). This escape time is often
empirically determined (e.g. for the CR escape from the Galaxy by
radioactive CR clocks (e.g. Cesarsky 1980)). It is
the goal of this work to provide an estimate of this escape time and
its dependency on the geometrical and plasma parameters of the system
under investigation. The focus of this work is cocoons of radio
galaxies, but the presented model may have other applications.
). This escape time is often
empirically determined (e.g. for the CR escape from the Galaxy by
radioactive CR clocks (e.g. Cesarsky 1980)). It is
the goal of this work to provide an estimate of this escape time and
its dependency on the geometrical and plasma parameters of the system
under investigation. The focus of this work is cocoons of radio
galaxies, but the presented model may have other applications.
In many applications, the physical parameters will not be sufficiently constrained to allow an accurate calculation of the escape time. Nevertheless, insight into the dependencies on parameters such as turbulence, fraction of the magnetically open surface etc. allows statements of the relative CR escape rates in different situations to be made. This should help to formulate hypotheses about the conditions in which CR escape is efficient, which may be tested observationally. Examples of such tests were given in Sect. 1.1.
The following simplifications are used to compile the CR escape model:
The structure of this article is the following: in Sect. 2 the theoretical tools for the description of the CR propagation in inhomogeneous media are compiled. The inter-phase CR transport is analysed in Sect. 3. Three escape routes are considered: the penetration of an isolating boundary layer (Sect. 3.1), the parallel diffusion along inter-phase magnetic flux tubes (Sect. 3.2), and the cross field escape (Sect. 3.3). In Sect. 4 the CR escape from radio plasma cocoons is investigated and in Sect. 5 the main findings of the paper are listed. In Appendix A the spatially homogenised transport equation of CRs in a small-scale inhomogeneous medium is derived. Appendix B contains a glossary of the frequently used symbols and abbreviations.
Since the magnetic field topology dominates the mobility of CR
particles, adapted coordinates are chosen. The length x is measured
along the (local) mean direction ![]() of a field bundle with
local field strength
of a field bundle with
local field strength
![]() .
Although
individual field lines may leave the flux tubes, due to magnetic
fluctuations
.
Although
individual field lines may leave the flux tubes, due to magnetic
fluctuations
![]() ,
this mean field flux tube is well
defined and gives an appropriate local coordinate system.
,
this mean field flux tube is well
defined and gives an appropriate local coordinate system.
The analysis is restricted to particles with gyro-radii much smaller
than the length-scale of the magnetic fields. In this case the cross
field diffusion is orders of magnitude slower than the diffusion along
the field lines. Particles can be regarded as being confined in a
flux tube. Since the diameter and the field strength of the tube can
change as a function of x, it is convenient to work with the number
of particles F per flux tube length ![]() and magnetic flux
and magnetic flux
![]() ,
instead of the
usual volume normalisation
,
instead of the
usual volume normalisation
![]() .
The
particle phase space distribution function is
.
The
particle phase space distribution function is
![]() ,
and its source density is
,
and its source density is
![]() .
.
![]() is
the momentum of the particle, v its velocity, m is its mass, and
c is the speed of light.
is
the momentum of the particle, v its velocity, m is its mass, and
c is the speed of light.
![]() is the
cosine of the pitch angle between
is the
cosine of the pitch angle between ![]() (or
(or ![]() )
and
)
and
![]() .
The particle distribution is assumed to be rotationally
symmetric with respect to
.
The particle distribution is assumed to be rotationally
symmetric with respect to ![]() ,
therefore the azimuthal angle has
been integrated out. The particles entering or leaving the flux tube
are included in the source term Q and in the loss term
,
therefore the azimuthal angle has
been integrated out. The particles entering or leaving the flux tube
are included in the source term Q and in the loss term
![]() in the Fokker-Planck equation for F:
in the Fokker-Planck equation for F:
The continuous pitch angle changes can be calculated from the
adiabatic invariants of a particle with charge
Z moving in spatially slowly
varying, and temporally constant magnetic fields. Specifically, these
are the linear momentum p and the magnetic flux within a gyro-radius
![]() ,
where
,
where
![]() is the gyro-radius. One gets
is the gyro-radius. One gets
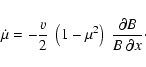 |
(2) |
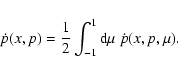 |
(7) |
The parallel diffusion coefficient depends on the pitch angle
diffusion coefficient according to Eq. (6). By defining
the particle-wave scattering frequency ![]()
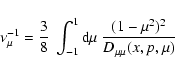 |
(9) |
The scattering frequency ![]() depends on details of the
underlying plasma turbulence on scales comparable to the gyro-radius
of the particle. There are two contributions important to this
small-scale turbulence: the first is the Kolmogorov (or Kraichnan)
cascade of large-scale turbulent kinetic energy to smaller
length-scale, and the second is turbulence induced by CR streaming
(Wentzel 1968, 1969; Skilling 1975a).
Since the focus of this work is on the transport of poorly connected
regions, the amount of CR streaming is expected to be low. In the
following numerical examples, only external Kolmogorov-like
turbulence is assumed. In other cases, the theory of this article can
still be applied if the appropriate diffusion coefficients are used.
depends on details of the
underlying plasma turbulence on scales comparable to the gyro-radius
of the particle. There are two contributions important to this
small-scale turbulence: the first is the Kolmogorov (or Kraichnan)
cascade of large-scale turbulent kinetic energy to smaller
length-scale, and the second is turbulence induced by CR streaming
(Wentzel 1968, 1969; Skilling 1975a).
Since the focus of this work is on the transport of poorly connected
regions, the amount of CR streaming is expected to be low. In the
following numerical examples, only external Kolmogorov-like
turbulence is assumed. In other cases, the theory of this article can
still be applied if the appropriate diffusion coefficients are used.
A simplified parameterisation of the scattering frequency is adopted
here. It is assumed that
The parameter ![]() and
and
![]() play an important role for
many of the addressed questions and their expected values should
briefly be discussed here, although our knowledge of these quantities
is still very limited.
play an important role for
many of the addressed questions and their expected values should
briefly be discussed here, although our knowledge of these quantities
is still very limited. ![]() is roughly speaking the ratio of the
magnetic power on the largest length-scale, on which the power-law
spectrum of the inertia range of the turbulence is valid, to the total
magnetic energy density. For a sharply peaked, single power-law
magnetic spectrum it is
is roughly speaking the ratio of the
magnetic power on the largest length-scale, on which the power-law
spectrum of the inertia range of the turbulence is valid, to the total
magnetic energy density. For a sharply peaked, single power-law
magnetic spectrum it is
![]() .
For a broken power-law
spectrum, or a very broad maximum above the inertia-range
length-scales, we expect
.
For a broken power-law
spectrum, or a very broad maximum above the inertia-range
length-scales, we expect
![]() .
.
![]() gives the
efficiency of CR scattering per magnetic power on length-scales of the
order of the particle gyro-radius, thus the power on scales which can
resonate with the particle gyro-orbit. For an Alfvén wave spectrum
with slab-like geometry (waves-vectors are mainly parallel to the
magnetic main direction) one expects
gives the
efficiency of CR scattering per magnetic power on length-scales of the
order of the particle gyro-radius, thus the power on scales which can
resonate with the particle gyro-orbit. For an Alfvén wave spectrum
with slab-like geometry (waves-vectors are mainly parallel to the
magnetic main direction) one expects
![]() .
.![]() However, the nature of MHD turbulence might be anisotropic on small
scales in the sense that mainly wave-modes with wave-vectors
perpendicular to the main field are populated
(Sridhar & Goldreich 1994; Goldreich & Sridhar 1997). In that case a strong
reduction of the scattering frequency can be expected (
However, the nature of MHD turbulence might be anisotropic on small
scales in the sense that mainly wave-modes with wave-vectors
perpendicular to the main field are populated
(Sridhar & Goldreich 1994; Goldreich & Sridhar 1997). In that case a strong
reduction of the scattering frequency can be expected (
![]() )
(a quasi-linear estimate is provided by Chandran 2000b, however it is also
noted there that the quasi-linear approximation is not fully applicable in this case).
)
(a quasi-linear estimate is provided by Chandran 2000b, however it is also
noted there that the quasi-linear approximation is not fully applicable in this case).
In order that the propagation of CRs is diffusive the pitch angle
distribution should be sufficiently isotropic. This is given if the
scattering length
![]() is small compared to any CR density
scale-length (
is small compared to any CR density
scale-length (
![]() ). Within the above
parametrisation we get
). Within the above
parametrisation we get
| |
= | 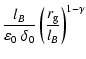 |
|
| = | 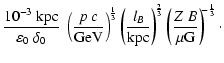 |
(14) |
The resulting diffusion coefficients for CR particles are then
Cross field diffusion is strongly inhibited. The small mobility of
particles perpendicular to the field lines can be amplified by rapid
parallel diffusion along diverging field lines
(Rechester & Rosenbluth 1978). A particle's microscopic displacement
from its original field line of the order of the gyro-radius by
microscopic cross-field diffusion grows exponentially while it follows
its new field line. This can be described in terms of a Liapunov
length
![]() ,
which depends on the behaviour of the
magnetic field autocorrelation function at small displacements, since
the old and new field lines will be strongly correlated. As soon the
particle is sufficiently far from its original field line, it can be
regarded as de-correlated from it. During the time needed for the
particle to de-correlate from its present field line, the particle is
tied to it and follows its stochastic wandering while diffusing along
it. The stochastic field line wandering can be described as a
diffusion process, with a diffusion coefficient DB which gives the
perpendicular displacement (squared) per unit length travelled along
the field line. Thus, during a de-correlation time the particle is
doing perpendicular steps of the length given by the field line
wandering times the typical diffusion length along the field line
(during this time). Since this leads to a stochastic displacement, the
combined propagation can be described as a macroscopic diffusion
process, which is called anomalous diffusions. This anomalous
diffusion allows the CRs to use the usually more powerful large-scale
magnetic fluctuations for their transverse propagation. A
mathematical description of this can be found in
Duffy et al. (1995), which should be consulted for
details. In their formalism the anomalous diffusion depends strongly
on the parameter
,
which depends on the behaviour of the
magnetic field autocorrelation function at small displacements, since
the old and new field lines will be strongly correlated. As soon the
particle is sufficiently far from its original field line, it can be
regarded as de-correlated from it. During the time needed for the
particle to de-correlate from its present field line, the particle is
tied to it and follows its stochastic wandering while diffusing along
it. The stochastic field line wandering can be described as a
diffusion process, with a diffusion coefficient DB which gives the
perpendicular displacement (squared) per unit length travelled along
the field line. Thus, during a de-correlation time the particle is
doing perpendicular steps of the length given by the field line
wandering times the typical diffusion length along the field line
(during this time). Since this leads to a stochastic displacement, the
combined propagation can be described as a macroscopic diffusion
process, which is called anomalous diffusions. This anomalous
diffusion allows the CRs to use the usually more powerful large-scale
magnetic fluctuations for their transverse propagation. A
mathematical description of this can be found in
Duffy et al. (1995), which should be consulted for
details. In their formalism the anomalous diffusion depends strongly
on the parameter
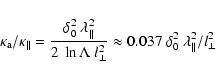 |
(22) |
Under certain circumstances the anomalous cross field diffusion is
extremely efficient. The anomalous diffusion coefficient
![]() depends quadratically on
depends quadratically on ![]() (Eq. (20)),
which is mainly the ratio of large-scale to small scale turbulence
(Eq. (18)).
(Eq. (20)),
which is mainly the ratio of large-scale to small scale turbulence
(Eq. (18)). ![]() is therefore independent of the level
of the turbulence, as long as the spectral shape of the turbulence
energy spectrum is not changed. Increasing the turbulence energy
density of a system by a factor
is therefore independent of the level
of the turbulence, as long as the spectral shape of the turbulence
energy spectrum is not changed. Increasing the turbulence energy
density of a system by a factor ![]() increases
increases
![]() also
by
also
by ![]() ,
due to the dependence of
,
due to the dependence of
![]() (or
(or
![]() )
on the small scale
turbulence.
)
on the small scale
turbulence.
If the slope of the turbulence is changed, drastic changes in
![]() can result. If e.g. large-scale kinetic energy is
suddenly injected into a system, it may need a period on the order of
the eddy turnover time
can result. If e.g. large-scale kinetic energy is
suddenly injected into a system, it may need a period on the order of
the eddy turnover time
![]() before the
turbulent cascade has also raised the small-scale turbulence
level. During this
period the microscopic diffusion coefficients
before the
turbulent cascade has also raised the small-scale turbulence
level. During this
period the microscopic diffusion coefficients
![]() and
and
![]() stay unchanged, but
stay unchanged, but
![]() is increased by
a factor of
is increased by
a factor of
![]() .
.
If a boundary layer of insulating magnetic fields (without any flux leaving the boundary layer regions) separates the interior from the surrounding of the source region the escape of cosmic ray particles is strongly inhibited. Although radio polarization observations of radio cocoons indicate that magnetic fields are well aligned with the cocoon surface (e.g. Laing 1980, 1981; Spangler et al. 1984), it is far from obvious if this implies an insulating boundary layer. The origin of such a hypothetical layer may be due to mixing of radio plasma with the ambient gas in a thin surface mixing layer, which is then dynamically decoupled from the turbulent interior due to its much higher inertia. The expected shear between the interior and the mixing layer may amplify and align magnetic fields into such an insulating boundary layer.
As a simplified model we assume the source region to be spherical with
radius ![]() ,
the boundary layer to have a thickness
,
the boundary layer to have a thickness
![]() .
The layer, which
extends from radius
.
The layer, which
extends from radius
![]() to
to ![]() ,
is assumed to be filled with magnetic fields which are mainly
tangential to the source surface at
,
is assumed to be filled with magnetic fields which are mainly
tangential to the source surface at ![]() .
Therefore the radial
diffusion coefficient is that of the macroscopic cross field diffusion
.
Therefore the radial
diffusion coefficient is that of the macroscopic cross field diffusion
![]() .
In a quasi-stationary situation (slow particle
escape) the space density of particles is given by
.
In a quasi-stationary situation (slow particle
escape) the space density of particles is given by
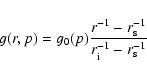 |
(23) |
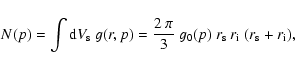 |
(24) |
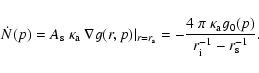 |
(25) |
| |
= | 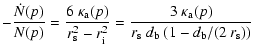 |
(26) |
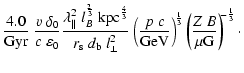 |
It should be noted that enhanced anomalous diffusion due to a sudden
raise of the large-scale turbulence level by a factor ![]() increases the particle escape rate through a boundary layer by a
factor
increases the particle escape rate through a boundary layer by a
factor
![]() during the period of not fully developed
turbulence, and
during the period of not fully developed
turbulence, and ![]() afterwards (see Sect. 2.3).
afterwards (see Sect. 2.3).
If some magnetic flux ![]() leaks from the source to the loss
region, the CR can escape following the field lines. A possible
situation is sketched in Fig. 1. The leakage requires that
the particles of the source region enter the inter-phase flux tube
either by perpendicular diffusion from disconnected regions, or by
travelling along the flux tube from a distant reservoir. Then they
diffuse through a transition zone between the two phases and finally
leave the tube in the loss region by cross field diffusion (or
escape to infinity along the field line).
leaks from the source to the loss
region, the CR can escape following the field lines. A possible
situation is sketched in Fig. 1. The leakage requires that
the particles of the source region enter the inter-phase flux tube
either by perpendicular diffusion from disconnected regions, or by
travelling along the flux tube from a distant reservoir. Then they
diffuse through a transition zone between the two phases and finally
leave the tube in the loss region by cross field diffusion (or
escape to infinity along the field line).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{geometry.eps}
\end{figure}](/articles/aa/full/2003/08/aa10429/Timg124.gif) |
Figure 1:
Geometry of the inter-phase region. The
left (
|
| Open with DEXTER | |
For simplicity it is assumed that within the source and the loss
regions all parameters of Eq. (5) are spatially
constant. The source function q is given by ![]() ,
which is
the average density of particles within the source (per magnetic flux)
divided by the time
,
which is
the average density of particles within the source (per magnetic flux)
divided by the time
![]() a particle needs to cross-field
diffuse over the distance given by the diameter of the flux
tube. The typical time a particle requires to enter
or leave a flux tube with flux
a particle needs to cross-field
diffuse over the distance given by the diameter of the flux
tube. The typical time a particle requires to enter
or leave a flux tube with flux
![]() and radius
and radius
![]() is given by
is given by
![]() .
In the loss region q=0.
In the transition zone
.
In the loss region q=0.
In the transition zone ![]() and B might be functions of the
position, but no particle losses or sources are assumed
there. Furthermore, any energy loss processes are ignored. These
conditions lead to the following parameters:
and B might be functions of the
position, but no particle losses or sources are assumed
there. Furthermore, any energy loss processes are ignored. These
conditions lead to the following parameters:
| (27) | |||
| (28) | |||
| (29) | |||
| (30) | |||
| (31) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{profile1.ps}
\end{figure}](/articles/aa/full/2003/08/aa10429/Timg151.gif) |
Figure 2:
Profiles of f(x),
g(x) = B(x) f(x),
B(x), and
|
| Open with DEXTER | |
An example density profile is shown in Fig. 2 for strong fields in the source and weak field in the loss region, and in Fig. 3 for the reversed geometry.
If one introduces the spatial average within the transition zone by
![]() ,
where
,
where
![]() ,
one can write
,
one can write
| (37) | |||
| (38) |
The total particle loss of the source into the loss region is given by
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{profile2.ps}
\end{figure}](/articles/aa/full/2003/08/aa10429/Timg171.gif) |
Figure 3:
As Fig. 2, but
|
| Open with DEXTER | |
In the following it is assumed that the source field region has the
strongest magnetic fields and therefore Eq. (41) is used.
If a number of ![]() flux-tubes with diameter
flux-tubes with diameter
![]() each
leave the source region the total magnetic flux leaving the source is
each
leave the source region the total magnetic flux leaving the source is
![]() .
Applying the identity
.
Applying the identity
![]() one
finds that the particle loss frequency is then given by
one
finds that the particle loss frequency is then given by
If the CRs escape rapidly from the source region, they can excite
plasma waves which again scatter the CRs. This limits the escape
velocity to approximately the Alfvén- or thermal velocity, or
whichever is larger (Tademaru 1969; Holman et al. 1979). For the high energy part of the CR spectrum the
limiting velocity can be even larger, since the small number density
of high energy CRs in typical power-law distributions does not lead to
an efficient excitation of the scattering waves
(e.g. Felice & Kulsrud 2001). However, an important quantity is
the CR escape velocity at the surface of the source region:
In order to model the cross field escape frequency an individual flux tube
of diameter
![]() is investigate first, which touches the
inter phase surface on a length-scale
is investigate first, which touches the
inter phase surface on a length-scale
![]() (see
Fig. 4). The particle distribution function along this
tube is governed by Eq. (5) if one adopts the following
parameters:
(see
Fig. 4). The particle distribution function along this
tube is governed by Eq. (5) if one adopts the following
parameters:
| (47) | |||
| (48) | |||
| (49) | |||
| (50) | |||
![\begin{displaymath}%
f(x) = f_{\rm s} ~\left[ 1 - \frac{1}{2~ l_{\rm s}}
\int_{x...
...~
\sigma_\perp (x') ~ \exp(-\vert x-x'\vert/l_{\rm s})\right].
\end{displaymath}](/articles/aa/full/2003/08/aa10429/img188.gif) |
(51) |
![$\displaystyle f(x) = f_{\rm s} \left[ 1- \frac{\sigma_\perp}{2}~ \left( h\left(...
...}
\right) + h\left(\frac{x_2-x}{l_{\rm s}} \right) \right) \right],~\mbox{with}$](/articles/aa/full/2003/08/aa10429/img191.gif) |
|||
| (52) |
![\begin{displaymath}%
- \dot{N}_\perp = \frac{f_{\rm s} ~ \lambda_\Vert~ \sigma_\...
...}
\left[ 1 - \frac{\sigma_\perp}{y} ~(y + e^{- y} -1) \right],
\end{displaymath}](/articles/aa/full/2003/08/aa10429/img193.gif) |
(53) |
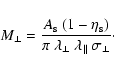 |
(55) |
It should be noted that enhanced anomalous diffusion due to a sudden raise of the
large-scale turbulence level by a factor ![]() increases the cross
field particle escape rate by a factor
increases the cross
field particle escape rate by a factor
![]() during the period of
not fully developed turbulence, and
during the period of
not fully developed turbulence, and ![]() afterwards (see
Sect. 2.3).
afterwards (see
Sect. 2.3).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{geoperp.eps}
\end{figure}](/articles/aa/full/2003/08/aa10429/Timg203.gif) |
Figure 4:
Geometry of a flux tube which is part of
the source boundary. The
left (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fperp.ps}
\end{figure}](/articles/aa/full/2003/08/aa10429/Timg205.gif) |
Figure 5:
Profile of f(x) for
|
| Open with DEXTER | |
The most efficient escape route can be found by comparing the escape
frequencies for the flux tube and the cross field escape route:
The old radio plasma cocoon of a small radio galaxy in the central IGM of
a galaxy cluster might be of approximately spherical shape. Here the
following parameters are assumed:
![]() G,
G,
![]() kpc,
kpc,
![]() kpc, and a cocoon diameter of 50 kpc.
The turbulence inside old radio plasma is likely the turbulence
induced by the environment, and therefore assumed to be
Kolmogorov-like. The diffusion coefficients of 10 GeV CR particles are
then
kpc, and a cocoon diameter of 50 kpc.
The turbulence inside old radio plasma is likely the turbulence
induced by the environment, and therefore assumed to be
Kolmogorov-like. The diffusion coefficients of 10 GeV CR particles are
then
![]() ,
,
![]() ,
and
,
and
![]() .
If the radio cocoon
has a boundary layer of thickness
.
If the radio cocoon
has a boundary layer of thickness
![]() kpc, which is
isolating the interior from the exterior due to the lack of any
magnetic flux exchange, then the escape frequency of these CRs is
kpc, which is
isolating the interior from the exterior due to the lack of any
magnetic flux exchange, then the escape frequency of these CRs is
![]() .
This is
extremely slow for a low level of magnetic turbulence (
.
This is
extremely slow for a low level of magnetic turbulence (
![]() ).
).
If such a isolating layer does not exist, CR particles can
reach the surface much easier and leave by cross field diffusion (over a short
distance) or by following open field lines. Since only reconnection
events of the fossil fields with the much weaker environmental fields
could have opened the magnetic topology,
![]() is
assumed due to the possible rarity of such events. Under such
conditions the escape frequencies of 10 GeV particles are
is
assumed due to the possible rarity of such events. Under such
conditions the escape frequencies of 10 GeV particles are
![]() ,
and
,
and
![]() .
The CR streaming velocity
along open flux tubes is 460 km s-1
.
The CR streaming velocity
along open flux tubes is 460 km s-1
![]() and therefore likely
much below the cluster sound speed, so that CR self-confinement is not
important for these particles. For a low level of magnetic turbulence
(
and therefore likely
much below the cluster sound speed, so that CR self-confinement is not
important for these particles. For a low level of magnetic turbulence
(
![]() )
and a mostly closed field topology (
)
and a mostly closed field topology (
![]() )
the escape of 10 GeV particles requires several Gyr. If one
considers further that such radio plasma is buoyant and therefore
leaves the cluster centre within a few 100 Myr
(Churazov et al. 2001; Enßlin & Heinz 2002), the fraction of CRs
injected into a cluster core is expected to be small under such
circumstances. This can impose constraints on several of the
theoretical considerations listed in Sect. 1.1, which rely
on an efficient escape of CR electrons, positrons or protons from
radio cocoons into the centre of galaxy clusters.
)
the escape of 10 GeV particles requires several Gyr. If one
considers further that such radio plasma is buoyant and therefore
leaves the cluster centre within a few 100 Myr
(Churazov et al. 2001; Enßlin & Heinz 2002), the fraction of CRs
injected into a cluster core is expected to be small under such
circumstances. This can impose constraints on several of the
theoretical considerations listed in Sect. 1.1, which rely
on an efficient escape of CR electrons, positrons or protons from
radio cocoons into the centre of galaxy clusters.
Further, during the buoyant rise of a radio cocoon through a
cluster atmosphere, the cocoon expands adiabatically. If all magnetic
length-scales scale linearly with the cocoon size ![]() ,
and the
magnetic field strength decreases adiabatically as
,
and the
magnetic field strength decreases adiabatically as
![]() then all escape frequencies discussed here (
then all escape frequencies discussed here (
![]() ,
,
![]() ,
,
![]() )
decrease according to
)
decrease according to
![]() .
This implies that CRs are better confined in a
larger cocoon, or that CR escape is most rapidly at an early stage of
the cocoon's buoyant voyage through the intra-cluster medium.
.
This implies that CRs are better confined in a
larger cocoon, or that CR escape is most rapidly at an early stage of
the cocoon's buoyant voyage through the intra-cluster medium.
If a cluster merger event suddenly injects large-scale turbulence the radio plasma can
become transparent even for low energy CR particles. The merger might
produce turbulent flows with velocities of
![]() km s-1 on a scale of
km s-1 on a scale of
![]() kpc which increase
the turbulent magnetic energy density on large-scales by a factor of
kpc which increase
the turbulent magnetic energy density on large-scales by a factor of
![]() from initially
from initially
![]() for example. For
roughly an eddy turnover time
for example. For
roughly an eddy turnover time
![]() Myr the small scale turbulence is not increased in
regions far from shock waves. During only a tenth of this period (10 Myr, which is of the order the turbulent cascades needs to transfer
energy from the scales of the radio cocoon (10 kpc) down to the CR
gyro-radius length scales) an enhanced anomalous cross field escape
should allow roughly 30%
Myr the small scale turbulence is not increased in
regions far from shock waves. During only a tenth of this period (10 Myr, which is of the order the turbulent cascades needs to transfer
energy from the scales of the radio cocoon (10 kpc) down to the CR
gyro-radius length scales) an enhanced anomalous cross field escape
should allow roughly 30%
![]() of the 10 GeV CR particles
initially confined in the radio cocoon to escape. A similar number of
the CRs would escape in the remaining 90 Myr of fully developed
turbulence. Significant losses would occur on even shorter timescales
in the case that the pitch angle scattering efficiency is low (
of the 10 GeV CR particles
initially confined in the radio cocoon to escape. A similar number of
the CRs would escape in the remaining 90 Myr of fully developed
turbulence. Significant losses would occur on even shorter timescales
in the case that the pitch angle scattering efficiency is low (
![]() ). The total loss of particles escaping along inter phase flux
tubes is roughly 6%
). The total loss of particles escaping along inter phase flux
tubes is roughly 6%
![]() during
during
![]() ,
and likely negligible if only a few kpc2 of
the cocoons surface is opened (
,
and likely negligible if only a few kpc2 of
the cocoons surface is opened (
![]() ). If the cocoon
would have an isolating boundary layer of thickness 5 kpc, then only 1.7% of the CR particles would be released during
). If the cocoon
would have an isolating boundary layer of thickness 5 kpc, then only 1.7% of the CR particles would be released during
![]() .
.
Cluster mergers happen frequently (Mohr et al. 1995; Jones & Forman 1999; Schuecker et al. 2001) so that shock waves appear
often in clusters (Quilis et al. 1998; Miniati et al. 2000),
which should raise the turbulence level on all length scales during
their passage. Therefore the strongly enhanced anomalous diffusivity
discussed above is not expected to appear in this case. However, the
turbulence level should increase substantially, leading to some
enhancement of the particle escape rate, and the typical lengthscale
![]() the particles have to travel before leaving the source
also decreases substantially. Both effects in combination should lead
to efficient particle escape.
the particles have to travel before leaving the source
also decreases substantially. Both effects in combination should lead
to efficient particle escape.
The escape length
![]() decreases due to
two effects: first, the radio plasma volume shrinks by a factor
C=V2/V1 = (P1/P2)3/4 for radio plasma with a
relativistic equation of state which is adiabatically (due to the high
internal sound speed) compressed in an environmental shock wave
with pressure jump P2/P1. Second, the shock wave should disrupt
the radio plasma into filamentary or torus-like morphologies, as seen
in numerical simulations (Enßlin & Brüggen 2002) and in high
resolution radio maps of some cluster radio relics
(Slee et al. 2001). The numerical simulations show that a
spherical radio cocoon transforms into a torus with major radius equal
to the radius of the original sphere (the torus diameter is roughly
that of the former sphere). Using the dimensions of the torus
given by this observation and the above given volume shrinking factor
C one finds that the characteristic length-scale
decreases due to
two effects: first, the radio plasma volume shrinks by a factor
C=V2/V1 = (P1/P2)3/4 for radio plasma with a
relativistic equation of state which is adiabatically (due to the high
internal sound speed) compressed in an environmental shock wave
with pressure jump P2/P1. Second, the shock wave should disrupt
the radio plasma into filamentary or torus-like morphologies, as seen
in numerical simulations (Enßlin & Brüggen 2002) and in high
resolution radio maps of some cluster radio relics
(Slee et al. 2001). The numerical simulations show that a
spherical radio cocoon transforms into a torus with major radius equal
to the radius of the original sphere (the torus diameter is roughly
that of the former sphere). Using the dimensions of the torus
given by this observation and the above given volume shrinking factor
C one finds that the characteristic length-scale
![]() decreases due to shock compression and change of the
morphology by a factor
decreases due to shock compression and change of the
morphology by a factor
![\begin{displaymath}%
\frac{L_{\rm s,2}}{L_{\rm s,1}} = \sqrt{\frac{3~C}{4~\pi}} ...
...rac{4~C}{3~\pi^2}} \right]^{-1} \approx \frac{1}{2} ~\sqrt{C}.
\end{displaymath}](/articles/aa/full/2003/08/aa10429/img241.gif) |
(61) |
A model has been presented describing the escape of CR particles from regions which are poorly magnetically connected to the environment. The main application of this theoryis to cocoons of radio galaxies.
In order to apply this model quantitatively to astrophysical systems,
several poorly known parameters have to be determined, like the
geometry of the source (![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ), the field fluctuation length-scales
(
), the field fluctuation length-scales
(
![]() ,
,
![]() ,
,
![]() ,
lB), the nature and the
level of the turbulence (
,
lB), the nature and the
level of the turbulence (![]() ), and the coupling strength
between small-scale magnetic turbulence and the gyro-motion of charged
particles (
), and the coupling strength
between small-scale magnetic turbulence and the gyro-motion of charged
particles (
![]() ). Several of these parameters are closely related
and can roughly be estimated (e.g. the characteristic turbulence
length-scales). Other parameters will remain unknown until a truly
detailed knowledge of radio plasma is available.
). Several of these parameters are closely related
and can roughly be estimated (e.g. the characteristic turbulence
length-scales). Other parameters will remain unknown until a truly
detailed knowledge of radio plasma is available.
However, even without detailed knowledge of these parameters, insight into the qualitative behaviour of CR transport between different phases is provided:
Acknowledgements
I thank Benjamin Chandran, Eugene Churazov, Sebastian Heinz, Philipp P. Kronberg, and Kandu Subramanian for discussions and comments on the manuscript. This work was done in the framework of the EC Research and Training Network The Physics of the Intergalactic Medium.
It is instructive to derive the macroscopic transport equation in the
case that the spatial fluctuations in the parameters of
Eq. (5) can be described by a large-scale x' and a much
smaller scale ![]() ,
so that
,
so that
![]() and
and ![]() is
the ratio of the small to the large-scale. A quantity
is
the ratio of the small to the large-scale. A quantity
![]() is averaged over the smaller scale by
is averaged over the smaller scale by
![]() .
.
The evolution of the distribution function can be expressed as an
asymptotic series in the small parameter ![]() .
To lowest order
in
.
To lowest order
in ![]() this method of homogenisation gives
this method of homogenisation gives