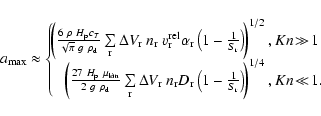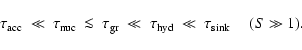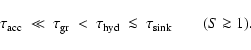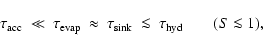A&A 399, 297-313 (2003)
DOI: 10.1051/0004-6361:20021734
Dust in brown dwarfs
II. The coupled problem of dust formation and sedimentation
P. Woitke1 -
Ch. Helling1,2
1 - Zentrum für Astronomie und Astrophysik, Technische
Universität Berlin, Hardenbergstraße 36, 10623 Berlin, Germany
2 -
Konrad-Zuse-Zenrum für Informationstechnik Berlin,
Takustraße 7, 14195 Berlin, Germany
Received 9 August 2002 / Accepted 19 November 2002
Abstract
In this paper, we quantify and discuss the physical and
surface chemical processes leading to the formation, temporal
evolution and sedimentation of dust grains in brown dwarf and giant gas
planet atmospheres: nucleation, growth, evaporation and gravitational
settling. Considering dust particles of arbitrary sizes in the
different hydrodynamical regimes (free molecular flow, laminar flow,
turbulent flow), we evaluate the equilibrium drift velocities (final
fall speeds) and the growth rates of the particles due to accretion
of molecules. We show that a depth-dependent maximum size of the
order of
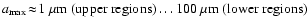 exists, which depends on
the condensate and the stellar parameters, beyond which
gravitational settling is faster than growth. Larger particles can
probably not be formed and sustained in brown dwarf atmospheres. We
furthermore argue that the acceleration towards equilibrium drift is
always very fast and that the temperature increase of the grains due
to the release of latent heat during the growth process is
negligible. Based on these findings, we formulate the problem of
dust formation coupled to the local element depletion/enrichment of
the gas in brown dwarf atmospheres by means of a system of partial
differential equations. These equations state an extension of
the moment method developed by Gail
exists, which depends on
the condensate and the stellar parameters, beyond which
gravitational settling is faster than growth. Larger particles can
probably not be formed and sustained in brown dwarf atmospheres. We
furthermore argue that the acceleration towards equilibrium drift is
always very fast and that the temperature increase of the grains due
to the release of latent heat during the growth process is
negligible. Based on these findings, we formulate the problem of
dust formation coupled to the local element depletion/enrichment of
the gas in brown dwarf atmospheres by means of a system of partial
differential equations. These equations state an extension of
the moment method developed by Gail
 Sedlmayr (1988) with an
additional advective term to account for the effect of
size-dependent drift velocities of the grains. A dimensionless
analysis of the new equations reveals a hierarchy of nucleation
Sedlmayr (1988) with an
additional advective term to account for the effect of
size-dependent drift velocities of the grains. A dimensionless
analysis of the new equations reveals a hierarchy of nucleation
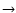 growth
growth 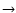 drift
drift 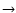 evaporation, which characterises the
life cycle of dust grains in brown dwarf atmospheres. The developed
moment equations can be included into hydrodynamics or classical
stellar atmosphere models. Applications of this description will be
presented in a forthcoming paper of this series.
evaporation, which characterises the
life cycle of dust grains in brown dwarf atmospheres. The developed
moment equations can be included into hydrodynamics or classical
stellar atmosphere models. Applications of this description will be
presented in a forthcoming paper of this series.
Key words: stars: atmospheres -
stars: low-mass, brown dwarfs -
dust, extinction -
molecular processes -
methods: numerical
1 Introduction
Brown dwarfs are the only stars known so far that are cool enough to
host small solid particles or fluid droplets (henceforth called dust or dust grains) in their atmospheres. The dust has a
strong influence on the opacity and hence on the structure of the
atmosphere as well as on the spectral appearance of brown dwarfs
(Allard
 2001; Marley
2001; Marley
 2002; Tsuji 2002; Cooper
2002; Tsuji 2002; Cooper
 2002), e.g.by
smoothing out molecular bands and thermalising the radiation, by
increasing the temperature below optically thick cloud layers, and in
particular, by affecting the element composition of the gas
depth-dependently.
2002), e.g.by
smoothing out molecular bands and thermalising the radiation, by
increasing the temperature below optically thick cloud layers, and in
particular, by affecting the element composition of the gas
depth-dependently.
Furthermore, the dust component seems to be responsible for a wealth
of variability phenomena recently observed (Bailer-Jones
 Mundt 2001a,b; Bailer-Jones 2002; Martín
Mundt 2001a,b; Bailer-Jones 2002; Martín
 2001;
Eislöffel
2001;
Eislöffel
 Scholz 2001). The observed light variations are partly
non-periodic and, thus, cannot be explained solely by rotation and
magnetic spots.
Scholz 2001). The observed light variations are partly
non-periodic and, thus, cannot be explained solely by rotation and
magnetic spots.
In order to study the atmospheres of these ultra-cool stars and giant
gas planets, a consistent physical description of the formation,
temporal evolution and gravitational settling of dust grains is
required, which states a new fundamental problem to the classical
theory of stellar atmospheres. A better physical description of the
dust component is likely to provide the key not only to understand the
variability of brown dwarfs, but also the structure of their
atmospheres and the observations of brown dwarfs in general.
In comparison to other astronomical sites of effective dust formation
(Sedlmayr 1994), the atmospheres of brown dwarfs provide special
conditions for the dust formation process. The convection replenishes
the gas in the upper layers with fresh uncondensed gas from the deep
interior, probably in a non-continuous and spatially inhomogeneous
way. The convection energises turbulence which creates strongly
varying thermodynamical conditions on small scales, causing an
inhomogeneous and time-dependent distribution of the dust
(Helling
 2001, henceforth called Paper I).
Three further points are to be mentioned:
2001, henceforth called Paper I).
Three further points are to be mentioned:
(i) The stellar gravity (
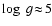 )
is about a hundred
times larger than in the earth's atmosphere and roughly 104 to
105 times larger than in the circumstellar envelopes of red giants.
This strong gravity puts severe physical constraints on the dynamical
behaviour of the forming dust component. Once formed from the gas
phase, dust grains are immediately forced to sink downwards. The
atmosphere can be expected to clean up from dust grains via
gravitational settling on time-scales ranging in minutes to months,
depending on the dust grain size. This is just the opposite as encountered
in the circumstellar envelopes of red giants, where the forming dust grains
are accelerated outwards due to radiation pressure.
)
is about a hundred
times larger than in the earth's atmosphere and roughly 104 to
105 times larger than in the circumstellar envelopes of red giants.
This strong gravity puts severe physical constraints on the dynamical
behaviour of the forming dust component. Once formed from the gas
phase, dust grains are immediately forced to sink downwards. The
atmosphere can be expected to clean up from dust grains via
gravitational settling on time-scales ranging in minutes to months,
depending on the dust grain size. This is just the opposite as encountered
in the circumstellar envelopes of red giants, where the forming dust grains
are accelerated outwards due to radiation pressure.
(ii) The dust forming gas in brown dwarf atmospheres is very dense,
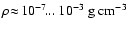 .
On the one hand
side, these high densities simplify a physical description of the dust
formation process, since chemical equilibrium in the gas phase can be
assumed. On the other hand side, the large densities lead to a quite
different molecular composition of the gas (for example a simultaneous
occurrence of CH4, H2O and CO2, i.e.no CO-blocking), like in
planetary atmospheres (e.g.Lodders
.
On the one hand
side, these high densities simplify a physical description of the dust
formation process, since chemical equilibrium in the gas phase can be
assumed. On the other hand side, the large densities lead to a quite
different molecular composition of the gas (for example a simultaneous
occurrence of CH4, H2O and CO2, i.e.no CO-blocking), like in
planetary atmospheres (e.g.Lodders
 Fegley 1994).
Consequently, different chemical preconditions for the dust formation
process are present as e.g.in M-type giants (Gail
Fegley 1994).
Consequently, different chemical preconditions for the dust formation
process are present as e.g.in M-type giants (Gail
 Sedlmayr 1998). Other nucleation species and other
surface chemical reactions can be important for the dust growth
process. Other solid compounds and even fluid phases can be stable in
a brown dwarf atmosphere.
Sedlmayr 1998). Other nucleation species and other
surface chemical reactions can be important for the dust growth
process. Other solid compounds and even fluid phases can be stable in
a brown dwarf atmosphere.
(iii) The high densities lead furthermore to a qualitatively different
dynamical behaviour of the gas flow around a dust grain. The mean free
path lengths of the gas particles can be smaller than a typical
diameter of a grain, leading to small Knudsen numbers
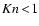 .
This affects the range of applicability of certain
physical descriptions at hand, concerning for example the drag force
or the growth of a dust grain due to accretion of molecules from the
gas phase, which may be limited by the diffusion of the molecules
toward the grain's surface.
.
This affects the range of applicability of certain
physical descriptions at hand, concerning for example the drag force
or the growth of a dust grain due to accretion of molecules from the
gas phase, which may be limited by the diffusion of the molecules
toward the grain's surface.
One of the key processes to understand the structure of planetary and
brown dwarf atmospheres - including element depletion and
weather-like features - is the dust sedimentation, which means a
non-zero relative motion between the dust particles and the
surrounding gas, known as the drift problem. Various
approaches have been carried out to simulate the dynamics of
dust/gas mixtures, e.g.in the circumstellar envelopes of late-type stars
(Gilman 1972; Berruyer
 Frisch 1983; MacGregor
Frisch 1983; MacGregor
 Stencel 1992; Krüger
Stencel 1992; Krüger
 1994, 1997). Mostly, two-fluid
approaches have been applied, assuming a constant dust grain size,
where nucleation is disregarded or assumed to be followed by an
instantaneous growth to the mean particle size. Simis
1994, 1997). Mostly, two-fluid
approaches have been applied, assuming a constant dust grain size,
where nucleation is disregarded or assumed to be followed by an
instantaneous growth to the mean particle size. Simis
 (2001) and Sandin
(2001) and Sandin
 Höfner (2003) have relaxed this approach by
allowing for a varying mean grain size, according to the results of a
time-dependent treatment of the dust nucleation and growth according
to (Gail
Höfner (2003) have relaxed this approach by
allowing for a varying mean grain size, according to the results of a
time-dependent treatment of the dust nucleation and growth according
to (Gail
 1984; Gail
1984; Gail
 Sedlmayr 1988).
However, an unique velocity of the dust component is assumed. Assuming
stationarity, Krüger
Sedlmayr 1988).
However, an unique velocity of the dust component is assumed. Assuming
stationarity, Krüger
 (1995) have developed a bin
method for the 1D drift problem in stellar winds including a full
time-dependent description of the dust component, which explicitly
allows for a size-dependent drift velocity. This powerful approach
has inspired Lüttke (2002) to develop an
adaptive bin tracking algorithm where the evolution of each bin is
followed in time and space, using the multi-grid method of
Nowak (1993).
(1995) have developed a bin
method for the 1D drift problem in stellar winds including a full
time-dependent description of the dust component, which explicitly
allows for a size-dependent drift velocity. This powerful approach
has inspired Lüttke (2002) to develop an
adaptive bin tracking algorithm where the evolution of each bin is
followed in time and space, using the multi-grid method of
Nowak (1993).
In the business of fitting the spectra of brown dwarfs and extra-solar
gas planets, much simpler approaches have been adopted so far in order
to study the effects of element depletion and dust sedimentation by
gravitational settling. In the frame of static model atmospheres with
frequency-dependent radiative transfer, the usual procedure is to
remove heavy elements like Ti, Fe, Mg, 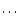 from the object's
atmosphere, assuming that these elements have been consumed by dust
formation guided by stability arguments (Burrows
from the object's
atmosphere, assuming that these elements have been consumed by dust
formation guided by stability arguments (Burrows
 1997;
Burrows
1997;
Burrows
 Sharp 1999; Saegers
Sharp 1999; Saegers
 Sasselow 2000). Depending on the purpose of the model, dust
formation is either simply disregarded, the dust is assumed to be
fully present or to have rained out completely, leaving behind a
saturated gas. An extensive time-scale study of dust formation and
sedimentation for the atmospheres of Jupiter, Venus, and Mars has been
presented by Rossow (1978). Ackermann
Sasselow 2000). Depending on the purpose of the model, dust
formation is either simply disregarded, the dust is assumed to be
fully present or to have rained out completely, leaving behind a
saturated gas. An extensive time-scale study of dust formation and
sedimentation for the atmospheres of Jupiter, Venus, and Mars has been
presented by Rossow (1978). Ackermann
 Marley (2001) have extended these time-scale
considerations to the turbulent regime for large dust Reynolds numbers
by adopting various data fits. Cooper
Marley (2001) have extended these time-scale
considerations to the turbulent regime for large dust Reynolds numbers
by adopting various data fits. Cooper
 (2002) have presented
further time-scale arguments in consideration of an atmosphere
with prescribed supersaturation to arrive at a maximum size of dust
particles as function of depth, emphasising the influence of
particles sizes on the resulting spectra. However, usually much
simpler ad-hoc assumptions about the grain size distribution are
made, e.g.relying on the size distribution function known from the
interstellar medium (e.g.Allard
(2002) have presented
further time-scale arguments in consideration of an atmosphere
with prescribed supersaturation to arrive at a maximum size of dust
particles as function of depth, emphasising the influence of
particles sizes on the resulting spectra. However, usually much
simpler ad-hoc assumptions about the grain size distribution are
made, e.g.relying on the size distribution function known from the
interstellar medium (e.g.Allard
 2001). Very
recently, Tsuji (2002) has published photospheric models based on the
assumption that the dust particles remain very small (smaller than the
critical cluster size) such that the particles are continuously
evaporating and re-forming. In this case, the problem of the
gravitational settling does not occur. All these simple approaches
allow for an easy use of up-to-date solid opacity data in the
simulations, but a consistent theoretical description of the dust
component is still not at hand.
2001). Very
recently, Tsuji (2002) has published photospheric models based on the
assumption that the dust particles remain very small (smaller than the
critical cluster size) such that the particles are continuously
evaporating and re-forming. In this case, the problem of the
gravitational settling does not occur. All these simple approaches
allow for an easy use of up-to-date solid opacity data in the
simulations, but a consistent theoretical description of the dust
component is still not at hand.
In this paper, we aim at a solution of this new problem in stellar
atmospheres. We formulate a physical description of the formation, the
temporal evolution and the gravitational settling of dust grains in brown
dwarf atmospheres, consistently coupled to the element consumption from the
gas phase, by modifying and extending the moment method developed by
Gail
 Sedlmayr (1988). This description is based on partial differential
equations for the moments of the dust grain size distribution function in
conservation form, which avoids an elaborate and time-consuming binning of the
size distribution function, thus making a straightforward inclusion into
hydrodynamics and classical stellar atmosphere calculations possible.
Sedlmayr (1988). This description is based on partial differential
equations for the moments of the dust grain size distribution function in
conservation form, which avoids an elaborate and time-consuming binning of the
size distribution function, thus making a straightforward inclusion into
hydrodynamics and classical stellar atmosphere calculations possible.
After the outline of the forces in the equation of motion, the concept
of equilibrium drift is discussed in Sect. 2.
Section 3 contains a physical description of the dust
growth by accretion of molecules in the free molecular flow (
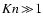 )
and in the viscous case (
)
and in the viscous case (
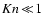 ).
Section 4 investigates the influence of the latent
heat of condensation and the frictional heating due to particle
drift on the growth process. In Sect. 5, our new
description of the dust component by means of moment equations is
developed. The character of these equations is discussed by analysing the
corresponding dimensionless equations and characteristic numbers
in Sect. 6. Section 7 comprises our
conclusions and future aims.
).
Section 4 investigates the influence of the latent
heat of condensation and the frictional heating due to particle
drift on the growth process. In Sect. 5, our new
description of the dust component by means of moment equations is
developed. The character of these equations is discussed by analysing the
corresponding dimensionless equations and characteristic numbers
in Sect. 6. Section 7 comprises our
conclusions and future aims.
2 The equation of motion
The trajectory
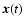 of a spherical dust particle of radius a and
mass
of a spherical dust particle of radius a and
mass
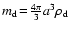 ,
floating in a gaseous
environment like a stellar atmosphere, is determined by Newton's law
,
floating in a gaseous
environment like a stellar atmosphere, is determined by Newton's law
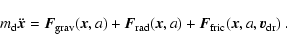 |
(1) |
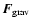 is the gravitational force,
is the gravitational force,
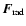 the radiative force due
to absorption and scattering of photons, and
the radiative force due
to absorption and scattering of photons, and
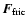 the frictional
force exerted by the surrounding gas via collisions. The frictional
force depends on the relative velocity (drift velocity) between the
dust particle and the gas
the frictional
force exerted by the surrounding gas via collisions. The frictional
force depends on the relative velocity (drift velocity) between the
dust particle and the gas
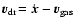 .
The gas is hereby
considered as a hydrodynamic ensemble with velocity
.
The gas is hereby
considered as a hydrodynamic ensemble with velocity
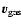 .
.
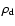 is the density of the dust grain material.
is the density of the dust grain material.
2.1 Force of gravity
The gravitational force on the grain is given by
 |
(2) |
where
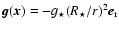 is the gravitational
acceleration and
is the gravitational
acceleration and
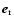 the unit vector in radial direction. Because of
the small extension of the atmospheres of brown dwarfs
(
the unit vector in radial direction. Because of
the small extension of the atmospheres of brown dwarfs
(
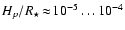 ), the radial distance r is about
equal to the stellar radius
), the radial distance r is about
equal to the stellar radius 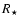 ,
and
,
and 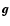 becomes a constant.
becomes a constant.
2.2 Force of radiation
The radiative force is given by the momentum transfer from the ambient
radiation field to the grain due to absorption and scattering of photons
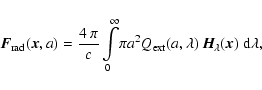 |
(3) |
where
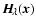 is the Eddington flux of the radiation field
at wavelength
is the Eddington flux of the radiation field
at wavelength 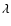 and site
and site 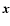 .
.
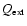 is a dimensionless
extinction efficiency of the grain, which can be calculated from the optical
properties of the grain material (real and imaginary part of the refractory
index) by applying Mie theory, see e.g.Bohren
is a dimensionless
extinction efficiency of the grain, which can be calculated from the optical
properties of the grain material (real and imaginary part of the refractory
index) by applying Mie theory, see e.g.Bohren
 Huffman (1983).
Huffman (1983).
However, as the following rough estimation will demonstrate, the radiative
force is small compared to the other forces in brown dwarf atmospheres and can
be neglected. We simplify the integral in Eq. (3) by pulling out
the flux mean extinction efficiency
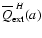 .
The
wavelength integrated Eddington flux is given by
.
The
wavelength integrated Eddington flux is given by
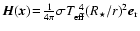 ,
where
,
where
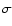 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and
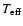 is the effective
temperature of the star. Considering furthermore the small particle limit
(SPL) of Mie theory
is the effective
temperature of the star. Considering furthermore the small particle limit
(SPL) of Mie theory
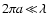 (Rayleigh limit), the extinction
efficiency is proportional to the grain size
(Rayleigh limit), the extinction
efficiency is proportional to the grain size
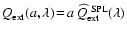 ,
and Eq. (3) results in
,
and Eq. (3) results in
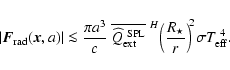 |
(4) |
For large grains, the radiative force is smaller than in the small
particle limit and asymptotically scales as 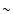 a2. Therefore,
we put the relation sign "
a2. Therefore,
we put the relation sign "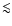 '' in Eq. (4). The
flux mean extinction coefficient is roughly given by a typical value
of
'' in Eq. (4). The
flux mean extinction coefficient is roughly given by a typical value
of
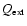 around the maximum of the stellar flux (see
Table 1). Considering a wavelength interval from
around the maximum of the stellar flux (see
Table 1). Considering a wavelength interval from
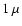 m to
m to 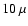 m, typical values of the extinction efficiency
m, typical values of the extinction efficiency
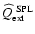 are found to vary between
are found to vary between
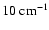 (crystalline, glassy materials like
(crystalline, glassy materials like
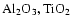 )
and
)
and
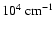 (e.g.amorphous carbon, iron bearing solid
materials like
(e.g.amorphous carbon, iron bearing solid
materials like
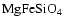 ), see Mutschke
), see Mutschke
 (1998), Tamanai
(1998), Andersen
(1998), Tamanai
(1998), Andersen
 (1999), Posch
(1999), Posch
 (1999) or, for an overview,
see Woitke (1999).
(1999) or, for an overview,
see Woitke (1999).
Table 1 demonstrates that the radiative force on dust
grains in brown dwarf atmospheres is always much smaller than the
gravity, even in case of light but opaque grains![[*]](/icons/foot_motif.gif) . Consequently, the radiative force can be
neglected, and the dust grain's equation of motion
(Eq. (1)) simplifies to
. Consequently, the radiative force can be
neglected, and the dust grain's equation of motion
(Eq. (1)) simplifies to
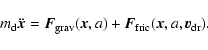 |
(5) |
2.3 Force of friction
An unique description of the frictional force (drag force) is
difficult to obtain for brown dwarf atmospheres. These difficulties
arise from the fact that the behaviour of the gas flow around the
moving dust grain changes qualitatively with changing grain size,
changing drift velocity and/or changing thermodynamic state of the
gas. There are transitions from freely impinging gas particles to a
viscous flow, from a subsonic to a supersonic behaviour, and from a
laminar flow to turbulence. The physical conditions in brown dwarf
atmospheres are such that all transitions may possibly occur.
Reliable physical descriptions of the drag force are only available in
certain limited regimes and an unique description must be compiled from
these special cases.
In order to quantify the behaviour of the streaming gas flow, the
following characteristic numbers are introduced: the Knudsen number Kn and
the dust Reynolds number
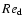 .
The Knudsen number Kn is
defined by the ratio of the mean free path length of the gas particles
.
The Knudsen number Kn is
defined by the ratio of the mean free path length of the gas particles
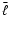 to a typical dimension
to a typical dimension
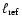 of the gas flow
under consideration, here given by the diameter of the grain
of the gas flow
under consideration, here given by the diameter of the grain
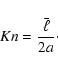 |
(6) |
Kn expresses the influence of inter-molecular collisions.
In case 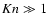 (e.g.small gas densities), inter-molecular
collisions are rare in the streaming flow. Consequently, the drag
force results from a simple superposition of independent, elementary
collisions where the velocity distribution of the impinging gas
particles resembles a Maxwellian distribution characterised by the gas
temperature T which is shifted in velocity space by
(e.g.small gas densities), inter-molecular
collisions are rare in the streaming flow. Consequently, the drag
force results from a simple superposition of independent, elementary
collisions where the velocity distribution of the impinging gas
particles resembles a Maxwellian distribution characterised by the gas
temperature T which is shifted in velocity space by
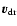 ( free molecular flow).
( free molecular flow).
In contrast, if
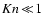 ,
inter-molecular collisions are
frequent and the stream of gas particles colliding with the dust grain
becomes viscous. In this case, the drag force cannot be obtained via
reduction to elementary collisions. This is the regime of continuum
theory for which well-tested empirical formulae are available, e.g.
from engineering science (viscous case or slip flow), depending
on whether the gas flow around the dust grain is laminar or turbulent.
In order to characterise the transition from laminar (Stokes) friction
to turbulent (Newtonian) friction, the dust grain's Reynolds number
,
inter-molecular collisions are
frequent and the stream of gas particles colliding with the dust grain
becomes viscous. In this case, the drag force cannot be obtained via
reduction to elementary collisions. This is the regime of continuum
theory for which well-tested empirical formulae are available, e.g.
from engineering science (viscous case or slip flow), depending
on whether the gas flow around the dust grain is laminar or turbulent.
In order to characterise the transition from laminar (Stokes) friction
to turbulent (Newtonian) friction, the dust grain's Reynolds number
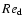 is introduced
is introduced
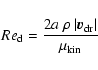 |
(7) |
with the characteristic properties
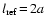 ,
,
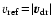 ,
and
,
and
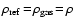 .
For large Reynolds numbers (
.
For large Reynolds numbers (
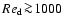 )
the flow around a dust particle is turbulent, whereas for small
Reynolds numbers (
)
the flow around a dust particle is turbulent, whereas for small
Reynolds numbers (
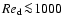 )
the flow is laminar (for a
discussion on these limits see e.g.Großmann 1995).
)
the flow is laminar (for a
discussion on these limits see e.g.Großmann 1995).
In order to evaluate the kinematic viscosity of the gas
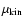 we follow the considerations of Jeans
(1967) for a mixture of ideal gases
we follow the considerations of Jeans
(1967) for a mixture of ideal gases
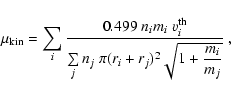 |
(8) |
where ni, mi, ri and
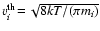 are
the gas particle densities, masses, radii and thermal velocities,
respectively. Assuming a mixture of H2 and He with particle ratio
5:1 and particle radii derived from friction experiments (
are
the gas particle densities, masses, radii and thermal velocities,
respectively. Assuming a mixture of H2 and He with particle ratio
5:1 and particle radii derived from friction experiments (
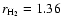 Å and
Å and
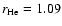 Å; Jeans 1967), we find
the viscosity to be
Å; Jeans 1967), we find
the viscosity to be
![\begin{displaymath}\mu_{\rm kin}= 5.877 \times 10^{-6} \frac{\rm g}{\rm cm\;s}
~ \sqrt{T\rm [K]} .
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img118.gif) |
(9) |
The mean free path
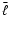 entering into Eq. (6) is
calculated backwards from Eq. (9), using the general
relation
entering into Eq. (6) is
calculated backwards from Eq. (9), using the general
relation
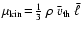 in consideration of mean gas particles
only
in consideration of mean gas particles
only![[*]](/icons/foot_motif.gif) , where
, where
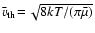 is the mean thermal
velocity and
is the mean thermal
velocity and
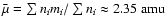 is the mean molecular weight
is the mean molecular weight
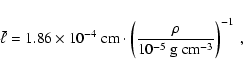 |
(10) |
which corresponds to a value of the mean collisional cross section of the
H2/He-mixture defined by
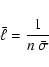 |
(11) |
of
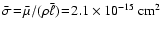 ,
which is more than three times larger as
,
which is more than three times larger as
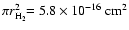 .
.
Considering the mechanics of rarefied gases, Schaaf (1963)
derives a formula for the drag force by freely impinging gas particles due to
elastic collisions, equally applicable in the subsonic as well as in the
supersonic range,
![$\displaystyle \vec{F}^{\rm Sch}_{\rm fric} =
-\pi a^2 \rho~\vert\vec{v}_{\rm dr...
...t(\frac{1}{s}+\frac{1}{2s^3}\right)
\frac{{\rm e}^{-s^2}}{\sqrt{\pi}} \right] ,$](/articles/aa/full/2003/07/aah3912/img127.gif) |
|
|
(12) |
with abbreviations
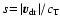 and
and
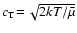 .
The error function
is defined by
.
The error function
is defined by
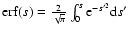 .
Equation (12) has the following asymptotic behaviour
.
Equation (12) has the following asymptotic behaviour
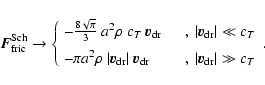 |
(13) |
In this regime, continuum theory is valid for which well-tested
empirical formulae exist. Lain
 (1999), carrying out
experimental studies on bubbly flows, arrive at the following
empirical expression for the drag force
(1999), carrying out
experimental studies on bubbly flows, arrive at the following
empirical expression for the drag force
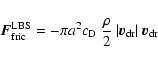 |
(14) |
where the drag coefficient 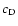 is given by
is given by
![\begin{displaymath}c_{\rm D} = \left\{ \begin{array}{ll}
\displaystyle{\frac{24...
...\\ [1.2ex]
2.61 & , Re_{\rm d} > 1500 .
\end{array} \right.
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img134.gif) |
(15) |
Comparable formulae can be found in (Huber
 Sommerfeld 1998), studying spherical coal particles in
pipes, and in (Macek
Sommerfeld 1998), studying spherical coal particles in
pipes, and in (Macek
 Polasek 2000), modelling the
inverse problem of porous media in combustion engineering for
elliptical particles
Polasek 2000), modelling the
inverse problem of porous media in combustion engineering for
elliptical particles![[*]](/icons/foot_motif.gif) . We note that Eqs. (12)
and (14) are strictly valid only for
perfectly rigid, spherical particles. Deviations from this ideal
case, e.g.shape distortions of liquid grains, porosity and
non-spherical shapes of solid grains, generally lead to an increase of the effective surface area and hence to a decrease of the gravitational fall speed as defined in Sect. 2.4
(for further details see Rossow 1978, p. 14). Such second order
effects might roughly be accounted for by reducing the dust material
density
. We note that Eqs. (12)
and (14) are strictly valid only for
perfectly rigid, spherical particles. Deviations from this ideal
case, e.g.shape distortions of liquid grains, porosity and
non-spherical shapes of solid grains, generally lead to an increase of the effective surface area and hence to a decrease of the gravitational fall speed as defined in Sect. 2.4
(for further details see Rossow 1978, p. 14). Such second order
effects might roughly be accounted for by reducing the dust material
density
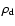 .
.
Using Eq. (7), the drag force in the viscous case according to
Eq. (14) is found to have the following
asymptotic behaviour
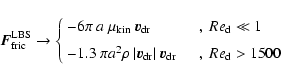 |
(16) |
which reveals the classical formulae for Stokes friction (laminar flow)
and Newtonian friction (turbulent flow), respectively.
For flows with an intermediate Knudsen number (
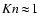 ), so-called transitions flows, reliable expressions
for the drag force are difficult to obtain. We therefore define a
critical Knudsen number
), so-called transitions flows, reliable expressions
for the drag force are difficult to obtain. We therefore define a
critical Knudsen number
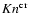 where
where
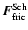 equals
equals
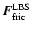 .
Considering the limiting cases of subsonic drift velocities and small
.
Considering the limiting cases of subsonic drift velocities and small
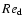 in Eqs. (13) and (16),
respectively, the result is exactly
in Eqs. (13) and (16),
respectively, the result is exactly
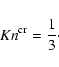 |
(17) |
In order to arrive at a general formula for arbitrary Knudsen numbers
we adopt a simple interpolation scheme![[*]](/icons/foot_motif.gif)
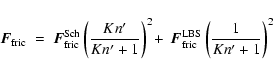 |
(18) |
where
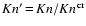 .
We note that a Cunningham factor
.
We note that a Cunningham factor
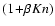 has been introduced in the literature (see e.g.
Rossow 1978) in order to extrapolate the resulting formula for the
final fall speed valid in the
has been introduced in the literature (see e.g.
Rossow 1978) in order to extrapolate the resulting formula for the
final fall speed valid in the
 case (see
Eq. (72)) into the
case (see
Eq. (72)) into the
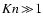 regime. The constant
regime. The constant
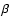 is usually fixed by measurements. However, it is
questionable whether the theoretically known friction law for the
limiting case
is usually fixed by measurements. However, it is
questionable whether the theoretically known friction law for the
limiting case
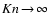 is revealed in this way. Our
finding is consistent with
is revealed in this way. Our
finding is consistent with
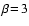 (or
(or
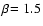 if the Knudsen number is defined as
if the Knudsen number is defined as
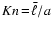 ,
compare Eqs. (6) and (63)).
,
compare Eqs. (6) and (63)).
2.4 Equilibrium drift
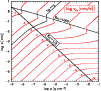 |
Figure 1:
Contour plot of the equilibrium drift velocity
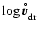 [cm s-1]
as function of grain radius a and gas density [cm s-1]
as function of grain radius a and gas density 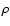 at constant
temperature
at constant
temperature
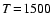 K and gravitational acceleration
g=105cm s-2. A mass density of the dust grain material of K and gravitational acceleration
g=105cm s-2. A mass density of the dust grain material of
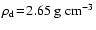 (quartz - SiO2) is assumed.
(quartz - SiO2) is assumed. |
| Open with DEXTER |
Considering a dust particle of constant radius a floating in a gas at
constant thermodynamical conditions (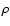 ,
T) and a constant
velocity
,
T) and a constant
velocity
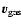 ,
the particle will be accelerated until a
force equilibrium is reached, where the gravitational acceleration is
balanced by frictional deceleration
,
the particle will be accelerated until a
force equilibrium is reached, where the gravitational acceleration is
balanced by frictional deceleration
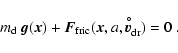 |
(19) |
Equation (19) states an implicit definition for the
gravitational fall speed (or, more precisely, the equilibrium drift
velocity![[*]](/icons/foot_motif.gif) )
)
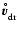 .
The equilibrium drift
velocity is determined by
.
The equilibrium drift
velocity is determined by  ,
a,
,
a, 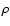 and T, and is always
directed towards the centre of gravity, even
within a horizontal gas flow. Whether or not this equilibrium state is
reached in a realistic situation will be discussed in Sect. 2.5. In
the general case,
and T, and is always
directed towards the centre of gravity, even
within a horizontal gas flow. Whether or not this equilibrium state is
reached in a realistic situation will be discussed in Sect. 2.5. In
the general case,
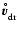 cannot be obtained from an analytical inversion of
Eq. (19), but must be calculated by finding the root of
Eq. (19) numerically, applying iterative methods.
cannot be obtained from an analytical inversion of
Eq. (19), but must be calculated by finding the root of
Eq. (19) numerically, applying iterative methods.
Figure 1 shows the resulting values of
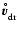 in a brown
dwarf's atmosphere with
in a brown
dwarf's atmosphere with
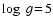 .
The equilibrium drift velocities
roughly range in
[10-4,10+6] cm s-1 and are generally smaller
for small particles and large densities. The small bendings of the contour
lines around
.
The equilibrium drift velocities
roughly range in
[10-4,10+6] cm s-1 and are generally smaller
for small particles and large densities. The small bendings of the contour
lines around
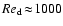 are no numerical artifacts but result
from the measured re-increase of the drag coefficient of spherical particles
are no numerical artifacts but result
from the measured re-increase of the drag coefficient of spherical particles
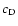 between
between
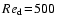 and
and
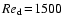 (Eq. (15)), associated with the transition from laminar to
turbulent friction.
(Eq. (15)), associated with the transition from laminar to
turbulent friction.
Small dust particles can sustain longer in the respective atmospheric
layers, whereas large grains will "rain out'' sooner. Only dust
particles 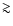 100
100 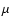 m at gas densities
m at gas densities 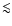 10
10
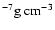 can hereby reach a drift velocity beyond the local
velocity of sound
can hereby reach a drift velocity beyond the local
velocity of sound
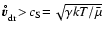 .
However, such particles will remove themselves so
quickly from the respective atmospheric layers (
.
However, such particles will remove themselves so
quickly from the respective atmospheric layers (
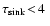 s) that this case seems very unlikely to be relevant
for any part of the atmosphere, unless there exists a physical process
(convective streams or atmospheric winds) which is capable to produce
supersonic upwinds. The time-scale for gravitational
settling is hereby defined as
s) that this case seems very unlikely to be relevant
for any part of the atmosphere, unless there exists a physical process
(convective streams or atmospheric winds) which is capable to produce
supersonic upwinds. The time-scale for gravitational
settling is hereby defined as
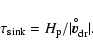 |
(20) |
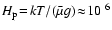 cm is the pressure
scale height of the brown dwarf's atmosphere.
cm is the pressure
scale height of the brown dwarf's atmosphere.
Figure 1 demonstrates furthermore that even the
smallest dust particles cannot sustain forever but will slowly sink
into deeper layers. Assuming that the dust particles do not grow
along their way down the atmosphere (which would increase their drift
velocity), a 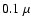 m-particle starting in an atmospheric layer
with
m-particle starting in an atmospheric layer
with
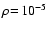 g cm-3 needs about
g cm-3 needs about
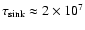 s (8 months) to pass one
scale height. A dust particle with
s (8 months) to pass one
scale height. A dust particle with
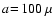 m needs only
m needs only
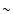 1/4 hour
1/4 hour![[*]](/icons/foot_motif.gif) .
.
The destiny of those particles drifting inward is to finally reach an
atmospheric layer where the temperature is high enough to evaporate
them thermally. This sets free the elements the dust grains are
composed off and thereby enriches the surrounding gas in this
layer. Hence, the rain-out will tend to saturate the gas below the
cloud base, where the "cloud base'' is identified with the level in
the atmosphere where the dust grains are just thermodynamically stable
(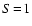 ,
see Sect. 3).
,
see Sect. 3).
2.5 Accelerated drift
The actual relative velocity of the dust particle with respect to the
gas,
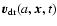 ,
can of course deviate from its equilibrium value
defined in Sect. 2.4. It will only asymptotically reach
,
can of course deviate from its equilibrium value
defined in Sect. 2.4. It will only asymptotically reach
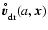 for
for
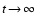 ,
if the parameters a,
,
if the parameters a,
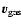 ,
,
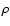 and T are constant. However, considering a dust particle
created in a brown dwarf atmosphere, the particle may grow by
accretion of molecules (
and T are constant. However, considering a dust particle
created in a brown dwarf atmosphere, the particle may grow by
accretion of molecules (
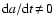 ,
see Sect. 3)
and the physical state of the surrounding gas may change with time
(e.g.
,
see Sect. 3)
and the physical state of the surrounding gas may change with time
(e.g.
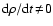 )
as the particle sinks into deeper layers of
the atmosphere. Turbulence may furthermore create a time-dependent
velocity field (
)
as the particle sinks into deeper layers of
the atmosphere. Turbulence may furthermore create a time-dependent
velocity field (
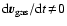 ), which provides an additional
cause for temporal deviations between
), which provides an additional
cause for temporal deviations between
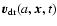 and
and
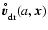 .
.
Thus, an important question for the discussion of the dynamical
behaviour of the dust component in brown dwarf atmosphere is, whether
or not
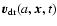 can be replaced by
can be replaced by
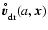 ,
at least
approximately.
,
at least
approximately.
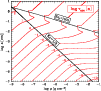 |
Figure 2:
Contour plot of the acceleration time-scale towards equilibrium
drift
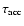 [s] as function of grain radius a and gas
densities [s] as function of grain radius a and gas
densities 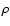 .
Other parameters are the same as in
Fig. 1. .
Other parameters are the same as in
Fig. 1. |
| Open with DEXTER |
In order to discuss this question, we consider the dust particle
acceleration time-scale
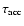 towards equilibrium drift. Expressing
the dust particle's equation of motion (Eq. (5)) in terms
of the first-order differential equation
towards equilibrium drift. Expressing
the dust particle's equation of motion (Eq. (5)) in terms
of the first-order differential equation
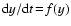 with
with
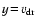 and
and
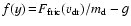 ,
and
assuming small deviations
,
and
assuming small deviations 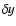 from the stability point
from the stability point
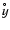 (where
(where
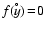 ), the temporal change of y is
), the temporal change of y is
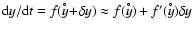 .
Accordingly, the acceleration time-scale is given by
.
Accordingly, the acceleration time-scale is given by
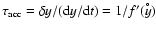 ,
or
,
or
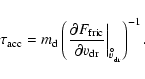 |
(21) |
This time-scale is to be compared with the other characteristical time-scales
inherent in the ambient medium. A hydrodynamical time-scale
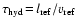 results to be
results to be
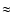 10 s when the so-called micro-turbulence velocity
10 s when the so-called micro-turbulence velocity
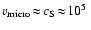 cm s-1, introduced to fit
otherwise unidentified line broadening effects, is considered on macroscopic
scales
cm s-1, introduced to fit
otherwise unidentified line broadening effects, is considered on macroscopic
scales
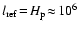 cm. About the same value is
found when mean convective velocities derived from mixing length theory
cm. About the same value is
found when mean convective velocities derived from mixing length theory
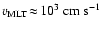 are considered on microscopic
scales
are considered on microscopic
scales
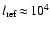 cm. Comparison to Fig. 2
shows that usually
cm. Comparison to Fig. 2
shows that usually
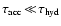 in brown dwarf
atmospheres, unless very large grains with supersonic fall speeds are
considered. This implies that the dust particles will reach their equilibrium
drift velocity much faster than usual hydrodynamical changes occur.
in brown dwarf
atmospheres, unless very large grains with supersonic fall speeds are
considered. This implies that the dust particles will reach their equilibrium
drift velocity much faster than usual hydrodynamical changes occur.
For a powerlaw dependence
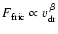 ,
Eqs. (20) and (21) result in
,
Eqs. (20) and (21) result in
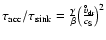 ,
i.e.we find
,
i.e.we find
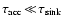 for
for
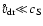 .
Since
Sect. 3 will demonstrate that also the growth of the
dust particles is slow in comparison to
.
Since
Sect. 3 will demonstrate that also the growth of the
dust particles is slow in comparison to
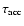 ,
we may conclude that
the concept of equilibrium drift provides a good approximation for the
description of the size-dependent relative velocities between dust and
gas in brown dwarf atmospheres.
,
we may conclude that
the concept of equilibrium drift provides a good approximation for the
description of the size-dependent relative velocities between dust and
gas in brown dwarf atmospheres.
3 Dust growth and evaporation
A fundamental process for the consideration of the time-dependent
behaviour of the dust component in brown dwarf atmospheres is the
growth of the dust particles by accretion of molecules. The
respective reverse process (thermal evaporation, in view of more
complex surface reactions also sometimes denoted by chemical
sputtering) is important at high temperatures![[*]](/icons/foot_motif.gif) . Considering the thermodynamical conditions
in brown dwarf atmospheres, we are again faced with the problem of
qualitative changes of the dynamical behaviour of the gas component
due to different Knudsen numbers.
. Considering the thermodynamical conditions
in brown dwarf atmospheres, we are again faced with the problem of
qualitative changes of the dynamical behaviour of the gas component
due to different Knudsen numbers.
For large Knudsen numbers (lKn), gas molecules of all kinds are freely
impinging onto the surface of the grain. Some of these dust-molecule
collisions (sometimes a certain sequence of them) will initiate a chemical
surface reaction which causes a growth step (or an evaporation step) of the
dust particle. This case has been extensively studied in the circumstellar
envelopes of AGB stars (Gail
 Sedlmayr 1988; Gauger
Sedlmayr 1988; Gauger
 1990;
Dominik
1990;
Dominik
 1993).
1993).
The accretion rate, expressed in terms of the increase of the
particle's volume
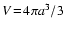 due to chemical surface
reactions for large Knudsen numbers is given by
due to chemical surface
reactions for large Knudsen numbers is given by
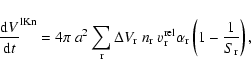 |
(22) |
where "r'' is a general surface reaction index,
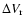 is the increase of
the dust particle's volume V caused by one reaction "r''.
is the increase of
the dust particle's volume V caused by one reaction "r''. 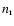 is the particle density of a key gas species whose collision rate
limits the rate of the surface reactions of index "r''. This gas species
has to be identified by considering the particle densities present in the
ambient gas and stoichiometric constraints.
Equation (22) explicitly allows for the consideration of
heterogeneous growth, where different solid phases can
grow simultaneously on the same surface, resulting in "dirty''
grains. The relative velocity is here defined as
is the particle density of a key gas species whose collision rate
limits the rate of the surface reactions of index "r''. This gas species
has to be identified by considering the particle densities present in the
ambient gas and stoichiometric constraints.
Equation (22) explicitly allows for the consideration of
heterogeneous growth, where different solid phases can
grow simultaneously on the same surface, resulting in "dirty''
grains. The relative velocity is here defined as
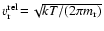 where
where 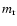 is the mass of
the key species.
is the mass of
the key species.
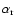 is a sticking coefficient which
contains more detailed knowledge about the surface chemical process,
if available.
is a sticking coefficient which
contains more detailed knowledge about the surface chemical process,
if available.
The last term on the r.h.s. of Eq. (22) takes into
account the reverse chemical processes, namely the thermal evaporation
rates. It determines the sign of
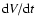 and hence decides whether
the dust particle grows or shrinks.
and hence decides whether
the dust particle grows or shrinks.
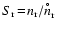 is
a generalised supersaturation ratio of the surface reaction "r''
(Dominik
is
a generalised supersaturation ratio of the surface reaction "r''
(Dominik
 1993) where
1993) where
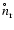 is the particle density of the key
species in phase-equilibrium over the condensed dust material.
is the particle density of the key
species in phase-equilibrium over the condensed dust material.
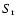 is not known a priori. In the case of simple surface
reactions, which transform
is not known a priori. In the case of simple surface
reactions, which transform 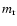 units of the solid material
units of the solid material 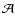 from the gaseous into the condensed phase (and vice versa), e.g.
from the gaseous into the condensed phase (and vice versa), e.g.
![$~\rm
[TiO_2]_N(s) + TiO_2 \rightleftharpoons [TiO_2]_{N+1}(s)$](/articles/aa/full/2003/07/aah3912/img213.gif) (
(
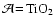 ,
,
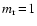 )
or
)
or
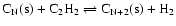 (
(
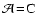 ,
,
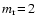 ), the generalised
supersaturation ratio
), the generalised
supersaturation ratio 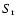 is related to the usual supersaturation ratio
is related to the usual supersaturation ratio
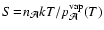 of the dust grain
material
of the dust grain
material 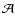 (Gauger
(Gauger
 1990) by
1990) by
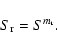 |
(23) |
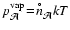 denotes the saturation vapour
pressure of the molecule
denotes the saturation vapour
pressure of the molecule 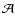 over a flat surface of the
condensed state, which is a pure temperature function determined by
the Gibbs free energies of the solid and the gaseous species
over a flat surface of the
condensed state, which is a pure temperature function determined by
the Gibbs free energies of the solid and the gaseous species
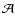 .
The supersaturation ratio S is well-defined even if
.
The supersaturation ratio S is well-defined even if 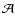 is not stable as a free molecule (Woitke 1999).
It is principally possible to account for additional effects caused by
a fast relative motion of the grain within the scope of this
description for grain growth and evaporation. These effects comprise
an enlargement of
is not stable as a free molecule (Woitke 1999).
It is principally possible to account for additional effects caused by
a fast relative motion of the grain within the scope of this
description for grain growth and evaporation. These effects comprise
an enlargement of
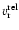 as well as a decrease of
as well as a decrease of
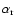 in the case of super-thermal collisions (see
Krüger et al. 1996). However, such
effects become only relevant for supersonic drift velocities which,
following the discussion in Sect. 2.4, are not very
likely to be relevant for brown dwarf atmospheres due to the fast
self-removal of the respective dust particles.
in the case of super-thermal collisions (see
Krüger et al. 1996). However, such
effects become only relevant for supersonic drift velocities which,
following the discussion in Sect. 2.4, are not very
likely to be relevant for brown dwarf atmospheres due to the fast
self-removal of the respective dust particles.
Viscous case (
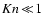 ):
):
For small Knudsen numbers (sKn), the transport of gas molecules to the
surface of the grain (or the transport of evaporating molecules away
from the grain's surface) is not a simple free flight with thermal
velocity as assumed in Eq. (22), but is hindered by
inter-molecular collisions. Consequently, the grain growth and
evaporation is limited by the diffusion of molecules towards or away
from the grain's surface, considering growth or evaporation in the
laminar case, respectively (we disregard here convection as transport
process for the molecules, expected to occur in the turbulent case).
We consider the following particle conservation equation with a
diffusive transport term (see Landau & Lifschitz 1987, Eq. (38.2)
ff)
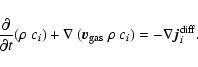 |
(24) |
![$c_i\!=\!n_i/\rho\;\rm [g^{-1}]$](/articles/aa/full/2003/07/aah3912/img224.gif) is the concentration of gaseous
molecules of kind i in the gas with mass density
is the concentration of gaseous
molecules of kind i in the gas with mass density 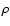 and velocity
and velocity
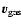 .
The diffusive particle flux is given by
.
The diffusive particle flux is given by
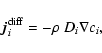 |
(25) |
where Di is the diffusion constant of gas particles of the kind i in the
gas mainly composed of H2 molecules (we neglect He atoms here), as given by
Jeans (1967, Eq. (260))
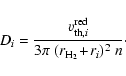 |
(26) |
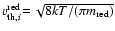 is the
thermal velocity of a gas particle of kind i with reduced mass
is the
thermal velocity of a gas particle of kind i with reduced mass
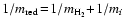 ,
where
,
where
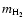 and
mi are the masses of H2 and i, respectively.
and
mi are the masses of H2 and i, respectively.
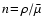 is the total gas particle density. The
particle radii ri can be derived from friction experiments (see Jeans
1967, p. 183) and vary between the values for hydrogen
is the total gas particle density. The
particle radii ri can be derived from friction experiments (see Jeans
1967, p. 183) and vary between the values for hydrogen
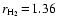 Å, carbon monoxide
Å, carbon monoxide
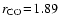 Å,
water and carbon dioxide
Å,
water and carbon dioxide
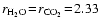 Å to benzene
Å to benzene
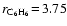 Å.
Å.
Considering the static case (
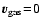 )
and assuming stationary
(
)
and assuming stationary
(
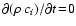 )
and spherical symmetry,
Eq. (24) results in
)
and spherical symmetry,
Eq. (24) results in
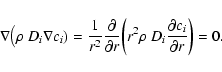 |
(27) |
Assuming furthermore constant 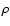 and Di, we find
and Di, we find
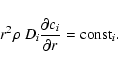 |
(28) |
In order to solve the second order diffusion equation (27),
two boundary conditions must be specified. First, considering the asymptotic
behaviour for
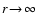 ,
we assume that the concentration ciapproaches the undisturbed value
,
we assume that the concentration ciapproaches the undisturbed value 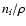 in the distant gas.
Second, at the lower integration boundary
in the distant gas.
Second, at the lower integration boundary 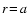 ,
we assume phase
equilibrium
,
we assume phase
equilibrium
i.e.we assume that the chemical surface reactions responsible for the
growth and evaporation of the dust particle are sufficiently effective
to completely exhaust or enrich the gas in the boundary layer with
molecules of kind i for growth and evaporation, respectively. As in
the last paragraph,
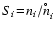 is the supersaturation ratio.
is the supersaturation ratio.
The solution of Eq. (28) with the boundary
conditions (29) and (30) is
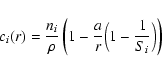 |
(31) |
and the the total volume accretion rate of the grain for small Knudsen
numbers, summing up the contributions of several surface reactions
of index r (like in Eq. (22)) with net rate
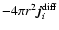 ,
according to Eqs. (25) and
(31), is
,
according to Eqs. (25) and
(31), is
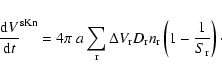 |
(32) |
The description of the volume accretion rate according to
Eq. (32) again allows for the simultaneous growth of
different solid materials on the same surface, resulting in "dirty''
grains (heterogeneous growth).
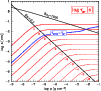 |
Figure 3:
Contour plot of the growth time-scale
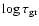 [s]
as function of the grain radius a and the gas density [s]
as function of the grain radius a and the gas density 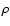 at
constant temperature
at
constant temperature
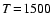 K for quartz (SiO2, K for quartz (SiO2,
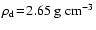 ). We assume growth by accretion of
the key species SiO with solar particle density ). We assume growth by accretion of
the key species SiO with solar particle density
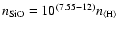 and extreme
supersaturation (
and extreme
supersaturation (
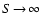 ). ).
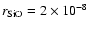 cm is estimated. cm is estimated. |
| Open with DEXTER |
For arbitrary Knudsen numbers we apply the same interpolation scheme
as outlined in Sect. 2.3. We define a critical Knudsen
number
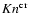 by equating Eqs. (22) with (32)
by equating Eqs. (22) with (32)
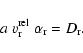 |
(33) |
Using Eqs. (26) and (11), the result is
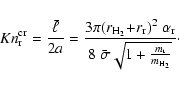 |
(34) |
Assuming perfect sticking (
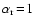 )
and considering
typical molecular radii and masses between
)
and considering
typical molecular radii and masses between
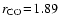 Å
and
Å
and
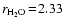 Å, and between
Å, and between
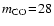 amu
and
amu
and
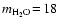 amu, respectively, the resulting critical
Knudsen numbers for growth
amu, respectively, the resulting critical
Knudsen numbers for growth
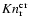 are found to range in 0.15
to 0.24, independent of density and temperature. Thus, we simply
adopt an unique critical Knudsen number for all growth and evaporation
species
are found to range in 0.15
to 0.24, independent of density and temperature. Thus, we simply
adopt an unique critical Knudsen number for all growth and evaporation
species
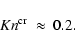 |
(35) |
Our ansatz of the general volume accretion rate for arbitrary
Knudsen numbers with
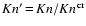 is
is
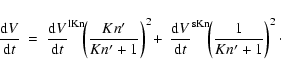 |
(36) |
Figure 3 shows the resulting growth time-scale
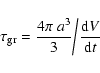 |
(37) |
as function of particle size a and gas density  for the
example of quartz grains in an extremely supersaturated gas
(
for the
example of quartz grains in an extremely supersaturated gas
(
 )
of solar abundances, where all Si is bound to SiO.
We consider the explicit growth reaction
)
of solar abundances, where all Si is bound to SiO.
We consider the explicit growth reaction
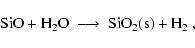 |
(38) |
where SiO is identified as the key educt.
The particle growth is found to be typically 3 orders of magnitude
slower than the acceleration which allows us to assume instantaneous
acceleration (equilibrium drift). For large Knudsen numbers, we find
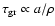 whereas for small Knudsen numbers
the growth time-scale increases faster for larger grains and becomes
density-independent,
whereas for small Knudsen numbers
the growth time-scale increases faster for larger grains and becomes
density-independent,
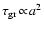 .
Note that the
influence of the drift velocities on the particle growth has not been
considered in Eqs. (22) and (32) such
that for supersonic drift velocities or large dust Reynolds numbers, the
presented physical description is not valid.
.
Note that the
influence of the drift velocities on the particle growth has not been
considered in Eqs. (22) and (32) such
that for supersonic drift velocities or large dust Reynolds numbers, the
presented physical description is not valid.
3.1 Maximum grain size
An additional dashed line is depicted in Fig. 3, where
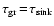 .
This line defines a maximum dust
grain size
.
This line defines a maximum dust
grain size
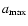 in a brown dwarf atmosphere. For larger
particles (
in a brown dwarf atmosphere. For larger
particles (
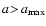 above the dashed line), the growth
time-scale exceeds the time-scale for gravitational settling
(
above the dashed line), the growth
time-scale exceeds the time-scale for gravitational settling
(
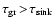 )
which means that such particles
are already removed from the atmosphere before they can be formed.
Consequently, such particles cannot exist. The maximum grain size
)
which means that such particles
are already removed from the atmosphere before they can be formed.
Consequently, such particles cannot exist. The maximum grain size
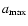 varies between
varies between 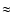 1
1 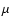 m in the thin, outer
atmospheric regions (
m in the thin, outer
atmospheric regions (
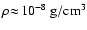 )
and
)
and
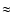 100
100 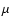 m in the dense, inner regions
(
m in the dense, inner regions
(
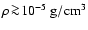 ). These values depend on the stellar
parameters and the considered dust material density.
). These values depend on the stellar
parameters and the considered dust material density.
Note, that an absolute minimum of
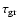 has been
considered in Fig. 3 since extreme supersaturation
(
has been
considered in Fig. 3 since extreme supersaturation
(
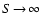 )
and solar abundance of silicon in the gas phase
have been assumed. In the case of an Si-depleted or nearly saturated
gas (
)
and solar abundance of silicon in the gas phase
have been assumed. In the case of an Si-depleted or nearly saturated
gas (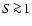 ),
),
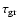 becomes larger and the maximum
particle radius
becomes larger and the maximum
particle radius
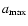 becomes smaller. Furthermore, the
values for
becomes smaller. Furthermore, the
values for
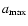 are relatively independent of temperature,
but will shift as
are relatively independent of temperature,
but will shift as
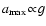 in the free molecular flow
case and
in the free molecular flow
case and
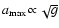 in the laminar viscous case,
remembering that
in the laminar viscous case,
remembering that
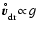 in both cases and that
in both cases and that
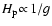 (see also Eq. (81)).
(see also Eq. (81)).
Figure 3 demonstrates furthermore that dust particles
moving with supersonic drift velocities cannot be expected in brown
dwarf atmospheres. Similarly, the turbulent flow regime with dust
Reynolds numbers
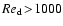 is barely reached at
very large densities. Therefore, we can conclude that for dust grains in
brown dwarf atmospheres the subsonic free molecular flow and the
laminar viscous flow are the important cases to be investigated.
is barely reached at
very large densities. Therefore, we can conclude that for dust grains in
brown dwarf atmospheres the subsonic free molecular flow and the
laminar viscous flow are the important cases to be investigated.
4 Energy balance of dust grains
The surface chemical reactions responsible for the growth of a dust
particle liberate the latent heat of condensation
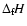 [erg/g] which
causes a heating of the grain as
[erg/g] which
causes a heating of the grain as
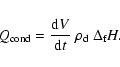 |
(39) |
It has been proposed (Cooper
 2002) that this heating can increase
the internal dust temperature
2002) that this heating can increase
the internal dust temperature 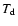 substantially, until the
sublimation temperature is reached (where
substantially, until the
sublimation temperature is reached (where 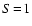 ). In that case,
the growth rate is limited by the need to remove the latent heat
of condensation from the grain and Eqs. (22) and
(32) are not valid.
). In that case,
the growth rate is limited by the need to remove the latent heat
of condensation from the grain and Eqs. (22) and
(32) are not valid.
A further heating process of the dust particle is given by the
friction caused by the motion relative to the gas,
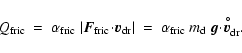 |
(40) |
Hereby, we assume that the total work done by the frictional force per
time,
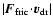 ,
is converted into heat, from
which the fraction
,
is converted into heat, from
which the fraction
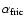 is delivered to the grain. For
the r.h.s. expression, the condition of equilibrium drift
is delivered to the grain. For
the r.h.s. expression, the condition of equilibrium drift
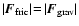 is used
(Eq. (5)). Since elastic collisions do not transfer any
energy, we assume
is used
(Eq. (5)). Since elastic collisions do not transfer any
energy, we assume
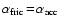 (see
Eq. (43))
(see
Eq. (43))![[*]](/icons/foot_motif.gif) .
.
In order to determine the dust temperature increase, we balance these heating
processes with the net energy losses due to radiation and due to inelastic
collisions. The net radiative cooling rate of a single dust grain is given by
![\begin{displaymath}Q_{\rm rad} = 4\pi\!\!\int\!\!\pi a^2 Q_{\rm abs}(a,\lambda) ...
...ig[B_{\lambda}(T_{\rm d})-J_{\lambda}\big] ~{\rm d}\lambda \ ,
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img288.gif) |
(41) |
where
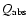 is the absorption efficiency,
is the absorption efficiency,
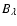 the Planck function
and
the Planck function
and
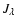 the mean intensity of the radiation field.
the mean intensity of the radiation field.
The cooling due to inelastic collisions with gas particles, in particular with
H2, depends again on the Knudsen number. For large Knudsen numbers (
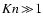 )
the collisional cooling rate is given by
)
the collisional cooling rate is given by
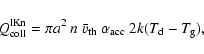 |
(42) |
where 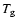 is the gas temperature,
is the gas temperature,
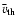 the mean thermal velocity introduced on page 300 and
the mean thermal velocity introduced on page 300 and
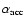 the efficiency for thermal accommodation,
given by Burke
the efficiency for thermal accommodation,
given by Burke
 Hollenbach (1983)
Hollenbach (1983)
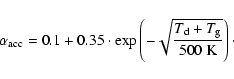 |
(43) |
For small Knudsen numbers (
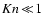 ), the removal
of heat from the grain's surface in the laminar
case
), the removal
of heat from the grain's surface in the laminar
case![[*]](/icons/foot_motif.gif) is limited by the heat
conductivity of the ambient gas. We consider the energy equation of an
ideal fluid
is limited by the heat
conductivity of the ambient gas. We consider the energy equation of an
ideal fluid
![\begin{displaymath}\frac{{\rm\partial} }{{\rm\partial} t}(\rho~e) + \nabla \big(\vec{v}_{\rm gas}[\rho~e+P]\big) = - \nabla \vec{j}_{\rm HC}
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img297.gif) |
(44) |
where e is the internal energy of the gas including kinetic and
gravitational potential energies (Paper I) and P the
thermal gas pressure. The energy flux by heat conduction is given by
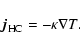 |
(45) |
![$\kappa\;\rm [erg~K^{-1}cm^{-1}s^{-1}]$](/articles/aa/full/2003/07/aah3912/img299.gif) is the heat conductivity
of the gas which according to Jeans (1967) equals
is the heat conductivity
of the gas which according to Jeans (1967) equals
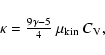 |
(46) |
where
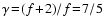 is the adiabatic index, f the
number of degrees of freedom,
is the adiabatic index, f the
number of degrees of freedom,
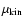 the kinematic viscosity
(Eq. (9)) and
the kinematic viscosity
(Eq. (9)) and
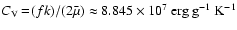 the isochoric heat capacity of the gas, resulting in
the isochoric heat capacity of the gas, resulting in
![\begin{displaymath}\kappa = 988~{\rm\frac{erg}{\rm K~cm~s}}~\sqrt{T_{\rm g}\rm [K]} .
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img303.gif) |
(47) |
The further derivation of the cooling rate by heat conduction is
analogous to the derivation of the viscous growth rate on
page 303. We consider the static case
(
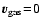 )
and assume stationary (
)
and assume stationary (
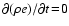 )
and spherical symmetry, such that
Eq. (44) becomes
)
and spherical symmetry, such that
Eq. (44) becomes
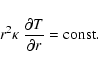 |
(48) |
Regarding 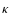 as a constant, the solution of
Eq. (48) with boundary conditions
as a constant, the solution of
Eq. (48) with boundary conditions
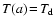 and
and
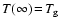 is
is
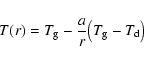 |
(49) |
and the collisional cooling rate
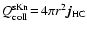 ,
according to Eqs. (45) and (49),
results in
,
according to Eqs. (45) and (49),
results in
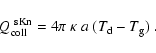 |
(50) |
The general collisional cooling rate with
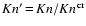 is
again approximated by
is
again approximated by
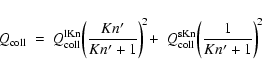 |
(51) |
where
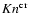 results from equating Eqs. (42)
with (50). We find a value of 0.023 at 1000 K
and a value of 0.019 at 2000 K. For simplicity, we apply a constant
value for the critical Knudsen number as
results from equating Eqs. (42)
with (50). We find a value of 0.023 at 1000 K
and a value of 0.019 at 2000 K. For simplicity, we apply a constant
value for the critical Knudsen number as
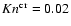 in
the following.
in
the following.
The energy balance of a single dust grain is finally given by
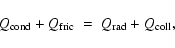 |
(52) |
which states an implicit equation for the temperature increase
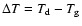 due to the liberation of latent heat during grain growth
and frictional heating.
due to the liberation of latent heat during grain growth
and frictional heating.
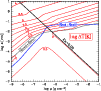 |
Figure 4:
Contour plot of the temperature increase
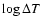 [K],
due to the liberation of latent heat during grain growth and
frictional heating, as function of the grain radius a and gas
density [K],
due to the liberation of latent heat during grain growth and
frictional heating, as function of the grain radius a and gas
density  at constant gas temperature
at constant gas temperature
 K for
quartz grains with the same parameters as in
Fig. 3. We assume growth by accretion of the key
species SiO with maximum particle density K for
quartz grains with the same parameters as in
Fig. 3. We assume growth by accretion of the key
species SiO with maximum particle density
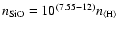 and extreme
supersaturation (
and extreme
supersaturation (
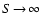 ). The two dashed lines indicate
where the two considered heating and cooling rates are equal.
Above these lines, ). The two dashed lines indicate
where the two considered heating and cooling rates are equal.
Above these lines,
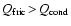 and
and
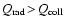 ,
respectively. ,
respectively. |
| Open with DEXTER |
Figure 4 shows an example for the resulting temperature
increase 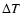 of quartz grains. We assume
of quartz grains. We assume
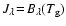 and again consider the explicit
growth reaction (Eq. (38)) with a release of latent
heat of
and again consider the explicit
growth reaction (Eq. (38)) with a release of latent
heat of
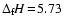 eV per reaction at 1000 K, 5.61 eV at
1500 K and 5.49 eV at 2000 K (data reduced from the
enthalpies of formation of the involved molecules and the solid,
source: JANAF-tables, electronic version, Chase
eV per reaction at 1000 K, 5.61 eV at
1500 K and 5.49 eV at 2000 K (data reduced from the
enthalpies of formation of the involved molecules and the solid,
source: JANAF-tables, electronic version, Chase
 1985).
1985).
For the sake of simplicity, we furthermore assume
 |
(53) |
for this calculation, where the extinction efficiency over a in the
small particle limit of Mie theory is given by
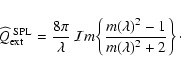 |
(54) |
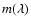 is the complex refractory index of the dust
grain material and
is the complex refractory index of the dust
grain material and  the imaginary part. The optical
constants for amorphous SiO2 (quartz glass) are taken from
H. R. Philipp's section in (Palik 1985) and the
resulting
the imaginary part. The optical
constants for amorphous SiO2 (quartz glass) are taken from
H. R. Philipp's section in (Palik 1985) and the
resulting
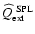 -values are
log-log-interpolated between the measured wavelengths points.
-values are
log-log-interpolated between the measured wavelengths points.
Despite these simplifications, Fig. 4 clearly indicates
that the warming of the dust grains due to the release of latent heat
is negligible, being less than 3.5 K all over the relevant parts of
the size-density-plane, where
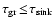 (compare Fig. 3). Here, we find that this heating is
balanced by collisional cooling
(compare Fig. 3). Here, we find that this heating is
balanced by collisional cooling
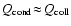 .
Since both heating/cooling rates scale as
.
Since both heating/cooling rates scale as
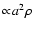 for large
Knudsen numbers and as
for large
Knudsen numbers and as
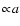 for small Knudsen numbers, a
constant value for
for small Knudsen numbers, a
constant value for 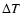 tunes in for both cases,
tunes in for both cases,
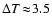 K for large Kn, and
K for large Kn, and
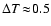 K for
small Kn. Note that the calculated temperature differences are always
an upper estimate. The actual temperature differences may be much
smaller because we have assumed solar, undepleted abundances of Si in
the gas phase and
K for
small Kn. Note that the calculated temperature differences are always
an upper estimate. The actual temperature differences may be much
smaller because we have assumed solar, undepleted abundances of Si in
the gas phase and
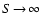 for the calculation of
for the calculation of
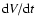 .
.
For larger particles (roughly at
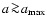 as defined in
Sect. 3.1), the character of the energy balance of the dust
particles changes. Here, the frictional heating due to the rapid
relative motion and the radiative cooling dominate, i.e.
as defined in
Sect. 3.1), the character of the energy balance of the dust
particles changes. Here, the frictional heating due to the rapid
relative motion and the radiative cooling dominate, i.e.
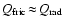 .
Much larger temperature deviations up
to 10 000 K result in this case. However, as argued before, such
large grains cannot be formed in brown dwarf atmospheres.
.
Much larger temperature deviations up
to 10 000 K result in this case. However, as argued before, such
large grains cannot be formed in brown dwarf atmospheres.
Thus, the resulting increase of the dust temperature 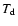 is by far
too small to reach the sublimation temperature
is by far
too small to reach the sublimation temperature
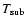 ,
unless
gas temperatures very close to
,
unless
gas temperatures very close to
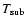 are considered and,
therefore, Eqs. (22) and (32) remain
valid.
are considered and,
therefore, Eqs. (22) and (32) remain
valid.
5 Moment method for nucleation, growth, evaporation and
equilibrium drift
The physical and chemical processes discussed so far (nucleation,
growth, evaporation, gravitational settling and element
depletion/enrichment) occur simultaneously in the atmosphere and may
be strongly coupled. Therefore, our aim in this section is to derive a
consistent time-dependent description of the dust component in
brown dwarf or giant gas planet atmospheres. We will
derive a system of partial differential equations which describes the
evolution of the dust component by means of the moments of its size
distribution function. This idea was originally developed by
Gail
 Sedlmayr (1988) and extended by Dominik
Sedlmayr (1988) and extended by Dominik
 (1993) to core-mantle and dirty grains. The
resulting differential equations are supposed to be simple and
includable into hydrodynamics or classical stellar atmosphere
calculations. In contrast, we want to avoid an elaborate and
time-consuming multi-component treatment of the dust component, e.g.by
using discrete bins for the dust size distribution function with
individual drift velocities in this paper.
(1993) to core-mantle and dirty grains. The
resulting differential equations are supposed to be simple and
includable into hydrodynamics or classical stellar atmosphere
calculations. In contrast, we want to avoid an elaborate and
time-consuming multi-component treatment of the dust component, e.g.by
using discrete bins for the dust size distribution function with
individual drift velocities in this paper.
 |
Figure 5:
Two surface chemical processes ( and
and  )
populating or depopulating an infinitesimal dust grain volume
interval )
populating or depopulating an infinitesimal dust grain volume
interval
![$[V,V\!+\!{\rm d}V]$](/articles/aa/full/2003/07/aah3912/img338.gif) . . |
| Open with DEXTER |
The master equation for dust particles
![$\in\![V,V\!+\!{\rm d}V]$](/articles/aa/full/2003/07/aah3912/img340.gif) ,
,
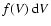 ,
where
,
where
![$f(V)~\rm [cm^{-6}]$](/articles/aa/full/2003/07/aah3912/img342.gif) is the distribution function of
dust particles in volume space, is given by
is the distribution function of
dust particles in volume space, is given by
![\begin{displaymath}\frac{{\rm\partial} }{{\rm\partial} t}\big(f(V)~{\rm d}V\big)...
...rc}}(V)\big]f(V)~{\rm d}V\!\Big) = \sum\limits_k R_k~{\rm d}V.
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img343.gif) |
(55) |
The r.h.s. of Eq. (55) expresses the population and depopulation
of the considered volume interval
![$[V,V\!+\!{\rm d}V]$](/articles/aa/full/2003/07/aah3912/img338.gif) with dust particles which
are changing their size due to accretion or evaporation of molecules
(see Fig. 5),
with dust particles which
are changing their size due to accretion or evaporation of molecules
(see Fig. 5),
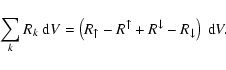 |
(56) |
Multiplication of Eq. (55) with Vj/3 (
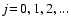 )
and integration over V from a lower integration boundary
)
and integration over V from a lower integration boundary
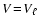 to
to
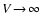 results in
results in
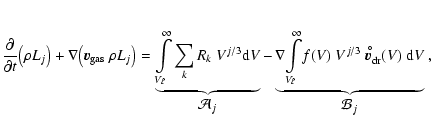 |
|
|
(57) |
where the jth moment of the dust size distribution function
![$L_
j~{\rm [cm}^j\!/{\rm g]}$](/articles/aa/full/2003/07/aah3912/img349.gif) is defined by
is defined by
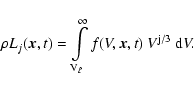 |
(58) |
The source term
 expresses the effects of surface chemical
reactions on the dust moments and
expresses the effects of surface chemical
reactions on the dust moments and
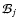 is an additional, advective
term in the dust moment equations which comprises the effects
caused by a size-dependent drift motion of the grains, e.g.due to gravity.
is an additional, advective
term in the dust moment equations which comprises the effects
caused by a size-dependent drift motion of the grains, e.g.due to gravity.
The maximum grain sizes to be expected in brown dwarf atmospheres
(Fig. 3) allow us to concentrate on two major cases in
the following, namely the subsonic free molecular flow and the
laminar viscous flow.
5.1 Subsonic free molecular flow
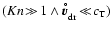
For large Knudsen numbers, the chemical rates depicted in
Fig. 5 can be expressed according to Eq. (22):
 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V)~{\rm d}V~4\pi[a(V)]^2~
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r}$](/articles/aa/full/2003/07/aah3912/img355.gif) |
(59) |
 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V\!-\!\Delta V_{\rm r})~{\rm d}V~4\pi\!
\le...
...V\!-\!\Delta V_{\rm r})\right]^2\!
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r}$](/articles/aa/full/2003/07/aah3912/img357.gif) |
(60) |
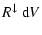 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V\!+\!\Delta V_{\rm r})~{\rm d}V~4\pi [a(V)]^2~
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r} \frac{1}{S_{\rm r}}$](/articles/aa/full/2003/07/aah3912/img359.gif) |
(61) |
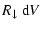 |
= |
![$\displaystyle \sum\limits_{\rm r} f(V)~{\rm d}V~
4\pi\!\left[a(V\!-\!\Delta V_{...
...\right]^2
n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r} \frac{1}{S_{\rm r}}\cdot$](/articles/aa/full/2003/07/aah3912/img361.gif) |
(62) |
Applying detailed balance considerations (Milne relations),
Gauger
 (1990) and Patzer
(1990) and Patzer
 (1998) have
shown that for simple types of surface reactions, denoted by
homogeneous and heterogeneous growth, the (inverse) evaporation rates
can be expressed by the related (forward) growth rates and the
supersaturation ratio in the way written in Eqs. (61) and
(62). For Eqs. (59) and (60), we
have neglected a possible influence of a fast drift motion on the
growth rates and for Eqs. (61) to (62), we
have assumed thermal equilibrium (dust temperature
(1998) have
shown that for simple types of surface reactions, denoted by
homogeneous and heterogeneous growth, the (inverse) evaporation rates
can be expressed by the related (forward) growth rates and the
supersaturation ratio in the way written in Eqs. (61) and
(62). For Eqs. (59) and (60), we
have neglected a possible influence of a fast drift motion on the
growth rates and for Eqs. (61) to (62), we
have assumed thermal equilibrium (dust temperature  gas
temperature) and chemical equilibrium among the molecules in the gas
phase.
gas
temperature) and chemical equilibrium among the molecules in the gas
phase.
Solving Eq. (19) with the frictional force according
to Eq. (13, subsonic case) the equilibrium drift
velocity is
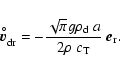 |
(63) |
By means of the Eqs. (59) to (63), the
integrals on the r.h.s. of Eq. (57) can be evaluated as
shown in more detail concerning the term
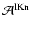 in
(Gail
in
(Gail
 Sedlmayr 1988). After some algebraic manipulations,
including
Sedlmayr 1988). After some algebraic manipulations,
including
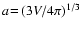 ,
the approximation
,
the approximation
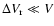 and
partial integration, the results are
and
partial integration, the results are
where
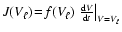 is the
current of dust particles in volume space at the lower integration
boundary. In case of net growth,
is the
current of dust particles in volume space at the lower integration
boundary. In case of net growth,
![$J({V_{\ell}})~\rm [cm^{-3}s^{-1}]$](/articles/aa/full/2003/07/aah3912/img372.gif) can be
identified with the stationary nucleation rate
can be
identified with the stationary nucleation rate 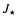 (Gail
(Gail
 Sedlmayr 1988). The characteristic growth speed
Sedlmayr 1988). The characteristic growth speed
![$\chi_{\rm lKn}^{\rm
net}~\rm [cm/s]$](/articles/aa/full/2003/07/aah3912/img374.gif) (an increase of radius per time) and the
characteristic gravitational force density
(an increase of radius per time) and the
characteristic gravitational force density
![$\xi_{\rm lKn}~\rm
[{\rm d}yn/cm^3]$](/articles/aa/full/2003/07/aah3912/img375.gif) are given by
are given by
5.2 Laminar viscous flow
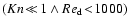
The derivation of the moment equations for the case of small Knudsen numbers
is analogous to the previous subsection. We express the surface chemical
rates according to Eq. (32) by
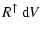 |
= |
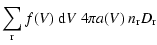 |
(68) |
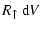 |
= |
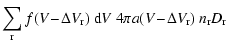 |
(69) |
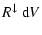 |
= |
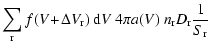 |
(70) |
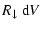 |
= |
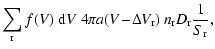 |
(71) |
again neglecting the influence of drift on growth and assuming
thermal and chemical equilibrium. The equilibrium drift velocity results
from Eq. (19) with the frictional force according to
Eq. (16, small
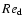 case)
case)
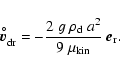 |
(72) |
By repeating the procedure of the last subsection, the r.h.s. terms
of the dust moment equations are
The characteristic growth speed
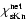 has now the
unit [cm2 s-1] (an increase of surface per time) whereas the
characteristic gravitational force density
has now the
unit [cm2 s-1] (an increase of surface per time) whereas the
characteristic gravitational force density
 remains the same
except for a different geometry factor.
remains the same
except for a different geometry factor.
6 Discussion
6.1 Dimensionless analysis
For the sake of analysis and discussion, we transform the dust moment
equations derived in Sects. 5.1 and 5.2
into their dimensionless form by introducing reference values as
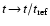 ,
,
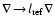 ,
,
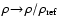 ,
,
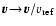 ,
,
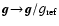 ,
,
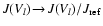 ,
,
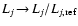 ,
,
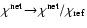 ,
,
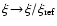 ,
,
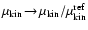 following the procedure described in Paper I. The reference values are to be
chosen according to the expected order of magnitude of the respective
quantities and the length and time-scales under investigation. After this
substitution, all quantities are dimensionless and can be compared by number.
following the procedure described in Paper I. The reference values are to be
chosen according to the expected order of magnitude of the respective
quantities and the length and time-scales under investigation. After this
substitution, all quantities are dimensionless and can be compared by number.
This allows us to identify the leading terms in the equations, e.g.in
the inner and outer regions of a brown dwarf atmosphere. The remaining
constants (products of the reference values) can be summarised into
characteristic numbers which provide an efficient way to describe the
qualitative behaviour of the dust component.
The dimensionless dust moment equations for nucleation, growth,
evaporation, and equilibrium drift write for a subsonic free
molecular flow (
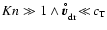 )
)
and for a laminar viscous flow (
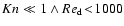 )
)
The equations are valid for
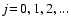 . The constants
in squared brackets are written in terms of characteristic numbers,
which are further explained in Table 2. All other
quantities and terms in Eqs. (77) and (78)
are of the order of unity for an appropriate choice of the reference
values.
. The constants
in squared brackets are written in terms of characteristic numbers,
which are further explained in Table 2. All other
quantities and terms in Eqs. (77) and (78)
are of the order of unity for an appropriate choice of the reference
values.
The following discussion is based on a typical structure of a brown
dwarf atmosphere with solar abundances in the gas phase, i.e.
neglecting the possible depletion due to dust formation (see
Table 2). As underlying (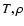 )-structure we refer to a
brown dwarf model atmosphere with
)-structure we refer to a
brown dwarf model atmosphere with
 K and
K and
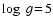 which has been kindly provided by
T. Tsuji (2002)
which has been kindly provided by
T. Tsuji (2002)![[*]](/icons/foot_motif.gif) . As exemplary dust species we consider solid SiO2(amorphous quartz), growing by the accretion of SiO and H2O
(Eq. (38)). Since the nucleation of SiO2 seems
dubious (the monomer is rather unstable as a free molecule and hence
not very abundant in the gas phase) we consider nucleation of TiO2instead
. As exemplary dust species we consider solid SiO2(amorphous quartz), growing by the accretion of SiO and H2O
(Eq. (38)). Since the nucleation of SiO2 seems
dubious (the monomer is rather unstable as a free molecule and hence
not very abundant in the gas phase) we consider nucleation of TiO2instead![[*]](/icons/foot_motif.gif) .
.
An analysis of the characteristic numbers in front of the source terms
in Eqs. (77) and (78) (see
Table 2) reveals a hierarchy of nucleation
 growth
growth  drift:
drift:
- 1)
- In the cool outer layers, the gas is strongly
supersaturated (
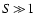 )
and nucleation is effective
(
)
and nucleation is effective
(
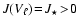 ). The products of the Damköhler number of
nucleation
). The products of the Damköhler number of
nucleation
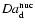 with the Strouhal number
with the Strouhal number 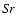 and the Sedlmaÿr
numbers
and the Sedlmaÿr
numbers 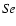 are as large as the products of the Damköhler numbers of growth
are as large as the products of the Damköhler numbers of growth
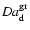 with the Strouhal number
with the Strouhal number 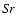 (even larger for small j) and
much larger than the combined drift numbers, indicating that the nucleation
provides an important source term in Eqs. (77) and
(78). Consequently, the condensable elements will be quickly
consumed by the process of nucleation before the particles can grow much
further. Hence, the dust particles remain very small in this layer of
effective nucleation.
(even larger for small j) and
much larger than the combined drift numbers, indicating that the nucleation
provides an important source term in Eqs. (77) and
(78). Consequently, the condensable elements will be quickly
consumed by the process of nucleation before the particles can grow much
further. Hence, the dust particles remain very small in this layer of
effective nucleation.
- 2)
- In the warmer layers, the gas is almost
saturated (
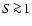 )
and nucleation is not effective
(
)
and nucleation is not effective
(
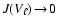 ). The products of the Damköhler numbers of growth
). The products of the Damköhler numbers of growth
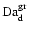 with the Strouhal number
with the Strouhal number 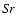 are large and the growth
term (the second term on the r.h.s.) is the leading source term in
the dust moment Eqs. (77) and (78).
In comparison, the influence of the drift term is small as
quantified by the combined drift numbers in
Table 2. Consequently, the dust growth process
will substantially be completed before the dust grains start to
settle gravitationally. In these growth-dominated layers,
a few existing particles will quickly consume all condensable
elements from the gas phase and, thus, will reach much larger
particle sizes. Since these particles cannot be created via
nucleation here, they must have been formed elsewhere and
transported into these layers by winds or drift. The growth will
either be terminated by element consumption or by the loss due to
gravitational settling when the particles reach their maximum size
as introduced in Sect. 3.1.
are large and the growth
term (the second term on the r.h.s.) is the leading source term in
the dust moment Eqs. (77) and (78).
In comparison, the influence of the drift term is small as
quantified by the combined drift numbers in
Table 2. Consequently, the dust growth process
will substantially be completed before the dust grains start to
settle gravitationally. In these growth-dominated layers,
a few existing particles will quickly consume all condensable
elements from the gas phase and, thus, will reach much larger
particle sizes. Since these particles cannot be created via
nucleation here, they must have been formed elsewhere and
transported into these layers by winds or drift. The growth will
either be terminated by element consumption or by the loss due to
gravitational settling when the particles reach their maximum size
as introduced in Sect. 3.1.
- 3)
- At the cloud base, the gas is hot and
saturated (
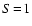 ). Consequently, nucleation and growth vanish
and the only remaining source term on the r.h.s. of
Eqs. (77) and (78) is the additional
advection of the particles due to their drift motion (drift term).
The combined drift numbers, however, are small indicating that the
drift term has a smaller influence than the hydrodynamical advection term.
). Consequently, nucleation and growth vanish
and the only remaining source term on the r.h.s. of
Eqs. (77) and (78) is the additional
advection of the particles due to their drift motion (drift term).
The combined drift numbers, however, are small indicating that the
drift term has a smaller influence than the hydrodynamical advection term.
Table 4 shows some dependencies of the combined
characteristic numbers (the squared brackets in
Eqs. (77), (78)), which provides
scaling laws for the importance of the different processes in the
different regimes:
- 1)
- The drift term scales as
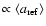 (
(
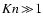 )
or
)
or
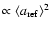 (
(
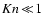 )
whereas the growth term scales as
)
whereas the growth term scales as
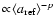 with different
with different
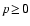 for the different cases (Table 4). This
means that at a certain large mean particle size, the drift term
will start to dominate over growth, which in fact just occurs at
the maximum particle size
for the different cases (Table 4). This
means that at a certain large mean particle size, the drift term
will start to dominate over growth, which in fact just occurs at
the maximum particle size
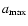 introduced in
Sect. 3.1.
introduced in
Sect. 3.1.
- 2)
- Nucleation (always) and growth (
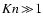 )
become increasingly important with increasing gas density
)
become increasingly important with increasing gas density
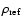 (note that typically
(note that typically
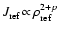 with
with 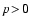 ), whereas the drift term (
), whereas the drift term (
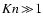 )
diminishes for increasing
)
diminishes for increasing
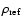 ,
i.e.the drift is
generally more important in a thin gas. However, the particles are
expected to remain smaller in such a thin gas situated in the upper
layers, which has a stronger, opposite effect on the
drift term.
,
i.e.the drift is
generally more important in a thin gas. However, the particles are
expected to remain smaller in such a thin gas situated in the upper
layers, which has a stronger, opposite effect on the
drift term.
- 3)
- The larger the considered length scale
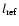 ,
the more stiff the dust moment equations become because of
the increasingly large nucleation and growth terms. This may
actually cause some numerical difficulties for models on macroscopic
scales. In comparison, the advective and the drift term are
independent on
,
the more stiff the dust moment equations become because of
the increasingly large nucleation and growth terms. This may
actually cause some numerical difficulties for models on macroscopic
scales. In comparison, the advective and the drift term are
independent on
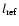 ,
which means that these terms gain
importance on small scales in relation to the other terms.
,
which means that these terms gain
importance on small scales in relation to the other terms.
- 4)
- The drift term scales as
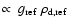 ,
i.e.the drift is naturally
more important for heavy grains in a strong gravitational field.
,
i.e.the drift is naturally
more important for heavy grains in a strong gravitational field.
In Table 2, we have assumed
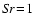 ,
i.e.we have
considered time-scales
,
i.e.we have
considered time-scales
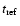 of the order of
of the order of
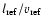 ,
appropriate for disordered (e.g.turbulent)
velocity fields, where the l.h.s. terms of Eqs. (77) and
(78) are of comparable importance. However, if
large-scale systematic motions are stable for a long time (e.g.a
circulating thunderstorm or a stable convection roll), the system may
reach a quasi-stationary situation where
,
appropriate for disordered (e.g.turbulent)
velocity fields, where the l.h.s. terms of Eqs. (77) and
(78) are of comparable importance. However, if
large-scale systematic motions are stable for a long time (e.g.a
circulating thunderstorm or a stable convection roll), the system may
reach a quasi-stationary situation where
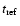 becomes much
larger and hence
becomes much
larger and hence
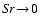 .
In this case, the first
term on the l.h.s. of Eqs. (77) and (78)
vanishes (see Table 4) whereas all other terms remain
unaffected.
.
In this case, the first
term on the l.h.s. of Eqs. (77) and (78)
vanishes (see Table 4) whereas all other terms remain
unaffected.
An interesting special case occurs if additionally
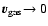 ,
i.e.when the dust-forming system reaches the static
case. In this case, also the advective terms in
Eqs. (77) and (78) vanish and the source
terms must balance each other. In the
,
i.e.when the dust-forming system reaches the static
case. In this case, also the advective terms in
Eqs. (77) and (78) vanish and the source
terms must balance each other. In the 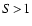 case, this means that
the gain of dust by nucleation and growth must be balanced by the loss
of dust due to rain-out, which means that the gas will be depleted. In
the
case, this means that
the gain of dust by nucleation and growth must be balanced by the loss
of dust due to rain-out, which means that the gas will be depleted. In
the 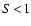 case, just the opposite is true, i.e.the loss by
evaporation must be balanced by the gain of dust particles raining in
from above. Consequently, the gas in such undersaturated layers will
be enriched by the condensable elements liberated by the evaporating
grains.
case, just the opposite is true, i.e.the loss by
evaporation must be balanced by the gain of dust particles raining in
from above. Consequently, the gas in such undersaturated layers will
be enriched by the condensable elements liberated by the evaporating
grains.
However, both control mechanisms (in the static limit) result in an
efficient transport of condensable elements from the cool upper layers
into the warm inner layers, which cannot last forever. We may conclude
that if the brown dwarf's atmosphere is truly static for a long time,
there is no other than the trivial solution for
Eqs. (77) and (78) where the gas is
saturated (
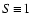 )
and dust-free (
)
and dust-free (
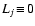 ). This situation
changes, however, if the brown dwarf's atmosphere is turbulent or, in
particular, when it is convective. In that case, the replenishment of
the atmosphere with fresh uncondensed gas from the deep interior will
counteract the downward transport of condensable elements by the
formation and gravitationally settling of dust grains. Simulations of
this quasi-static balance will be the subject of the forthcoming paper
in this series.
). This situation
changes, however, if the brown dwarf's atmosphere is turbulent or, in
particular, when it is convective. In that case, the replenishment of
the atmosphere with fresh uncondensed gas from the deep interior will
counteract the downward transport of condensable elements by the
formation and gravitationally settling of dust grains. Simulations of
this quasi-static balance will be the subject of the forthcoming paper
in this series.
A dynamical modelling of the dust component in brown dwarf atmospheres
by means of a moment method as proposed in this paper - consistently
coupled to hydrodynamics, radiative transfer and element depletion in
the scope of hydrodynamical or classical stellar atmosphere
calculations - seems straightforward as soon as two major problems can
be solved:
The structure of the dust moment Eqs. (77) / (78) changes with changing
Knudsen number. The size distribution function f(V), however, will
generally include small and large grains simultaneously, which may possess
large and small Knudsen numbers, respectively. A proper treatment
of all dust grains by means of a moment method is hence possible only in
one of the limiting cases
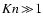 or
or
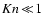 ,
where all grains fall into one particular case. This situation may be
relevant for the cool upper regions of a brown dwarf atmosphere, where
the densities are small and the dust particles remain tiny. In
general, however, a solution of this problem by means of a moment
method can only be approximate in nature and will require additional
numerical tricks, e.g.switching the case as soon as the Knudsen number
according to the mean size of the particles reaches unity.
,
where all grains fall into one particular case. This situation may be
relevant for the cool upper regions of a brown dwarf atmosphere, where
the densities are small and the dust particles remain tiny. In
general, however, a solution of this problem by means of a moment
method can only be approximate in nature and will require additional
numerical tricks, e.g.switching the case as soon as the Knudsen number
according to the mean size of the particles reaches unity.
The number of unknowns in
Eqs. (77) / (78) exceeds the number of
equations, since the drift term on the r.h.s. involves a higher dust
moment Lj+1 (for
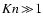 )
or even Lj+2 (for
)
or even Lj+2 (for
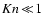 ). Therefore, in order to benefit from the moment Eqs. (77) / (78), we require a physically
reliable closure condition, as e.g.
). Therefore, in order to benefit from the moment Eqs. (77) / (78), we require a physically
reliable closure condition, as e.g.
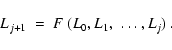 |
(79) |
Such closure conditions are fastidious problems. We are optimistic,
nevertheless, to find such a closure term, because the size
distribution f(V) is usually a very smooth function and the dust
moments Lj often reveal a very simple functional dependency on the
index j, indicating that the true number of the degrees of freedom
for a parametric description of f(V) is actually quite small.
One idea to construct such a closure condition has been developed by
Deufelhard
 Wulkow (1989) and Wulkow (1992),
studying the kinetics of polyreaction systems. The size distribution
function f(V) is here approximated by a weight function
Wulkow (1989) and Wulkow (1992),
studying the kinetics of polyreaction systems. The size distribution
function f(V) is here approximated by a weight function
 ,
which describes the basic shape of f(V), and
modified by a sum of orthogonal polynomials
,
which describes the basic shape of f(V), and
modified by a sum of orthogonal polynomials
 (k=0,1,2, ... ,n) as
(k=0,1,2, ... ,n) as
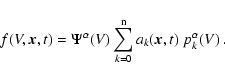 |
(80) |
 is an additional parameter (dependent on
is an additional parameter (dependent on  )
of the
weight function and ak are polynomial coefficients. The parameters
)
of the
weight function and ak are polynomial coefficients. The parameters
 and ak
and ak
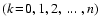 are stepwise adjusted in
order to fit the known moments Lj
are stepwise adjusted in
order to fit the known moments Lj
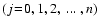 exactly, using the orthogonality relation
exactly, using the orthogonality relation
 .
Once
these coefficients are known, all missing moments of the size
distribution function can be reconstructed from
Eq. (80), again utilising the orthogonality relation.
This procedure leads to reliable results, if the weight function
.
Once
these coefficients are known, all missing moments of the size
distribution function can be reconstructed from
Eq. (80), again utilising the orthogonality relation.
This procedure leads to reliable results, if the weight function
 is already close to the actual size distribution
function f(V), such that the polynomials only provide small
corrections and the sum in Eq. (80) converges
rapidly.
is already close to the actual size distribution
function f(V), such that the polynomials only provide small
corrections and the sum in Eq. (80) converges
rapidly.
7 Conclusions
In this paper, we have investigated the basic physical and chemical
processes which are responsible for the formation, the temporal
evolution and the precipitation of dust grains in brown dwarf
atmospheres.
In contrast to other astronomical sites of effective dust formation,
the dust particles are embedded in such a dense gas that the Knudsen
numbers may fall short of unity. This requires a careful fall
differentiation for the different hydrodynamical regimes: free
molecular flow (subsonic and supersonic) and slip flow (laminar and
turbulent case).
Compiling a general formula for the drag force from the different
special cases, we have shown that the large gravity in brown dwarf
atmospheres forces the dust particles to move with a considerably high
downward drift velocity relative to the gas. The acceleration of the
dust particles (on a time-scale
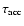 )
towards the
equilibrium drift velocity (final fall speed) results to be always
much faster than any other considered process (nucleation, growth,
hydrodynamical acceleration and sedimentation) such that an instantaneous acceleration of the particles to equilibrium
drift can be assumed. In contrast, the outward acceleration
of dust grains due to radiation pressure is completely negligible
in brown dwarf atmospheres.
)
towards the
equilibrium drift velocity (final fall speed) results to be always
much faster than any other considered process (nucleation, growth,
hydrodynamical acceleration and sedimentation) such that an instantaneous acceleration of the particles to equilibrium
drift can be assumed. In contrast, the outward acceleration
of dust grains due to radiation pressure is completely negligible
in brown dwarf atmospheres.
The large drift velocities are found to limit the residence time of the
forming dust grains and hence their maximum size
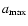 as
as
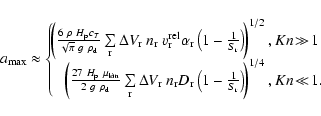 |
(81) |
Typical values for
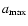 vary between
vary between 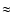 1
1 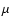 m in the
thin outermost atmospheric layers and
m in the
thin outermost atmospheric layers and  100
100 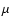 m in the
dense innermost layers. As soon as the particles come close to this
limiting size, they rain out quickly. This maximum size does not allow
for the existence of supersonic dust particles or dust particles with
very high Reynolds numbers, such that the subsonic free
molecular flow and the laminar viscous flow are the important
main cases to be discussed for dust grains in brown dwarf atmospheres.
m in the
dense innermost layers. As soon as the particles come close to this
limiting size, they rain out quickly. This maximum size does not allow
for the existence of supersonic dust particles or dust particles with
very high Reynolds numbers, such that the subsonic free
molecular flow and the laminar viscous flow are the important
main cases to be discussed for dust grains in brown dwarf atmospheres.
For small Knudsen numbers, the growth of the particles by accretion of
molecules is limited by the diffusion of the molecules towards the
grain surface, and the energy exchange with the surrounding
gas is limited by heat conduction. The latter process co-works
with the radiative gains and losses of the hot grains.
According to our results, the release of latent heat during the growth
does only lead to a small increase of the grain temperature
(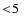 K) and has no particular influence on the growth rates.
K) and has no particular influence on the growth rates.
Based on these findings, we have formulated a system of partial
differential equations for the consistent physical description of the
dust component in brown dwarf and giant gas planet atmospheres. These
moment equations represent an unique tool to model the nucleation, growth and size-dependent equilibrium drift of the dust
particles, and the element depletion/enrichment of the gas. We consider
such a description as essential, because these processes occur
simultaneously and are strongly coupled. The description allows for an
inclusion into hydrodynamics or classical stellar atmosphere
calculations, although a few unsolved questions still remain, e.g.a
reliable closure condition and a clean Knudsen number fall
differentiation.
A dimensionless analysis of the moment equations reveals the existence
of the following three regimes associated with the formation of a
cloud layer:
- 1)
- At high altitudes the temperatures are much
lower than the sublimation temperatures of the various solid
materials and the gas is highly supersaturated. Consequently,
nucleation is effective and we find the following relation between
the time-scales inherent in the different physical processes:
This means that the dust particles are mainly created here (by
nucleation) as consequence of hydrodynamical enrichment events, e.g.
due to the mixing caused by the convection. The particles in this
region of efficient nucleation remain much smaller than
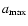 .
The gravitational settling of the grains is very
slow such that they form a rather passive component, subject to
hydrodynamical streams (e.g.winds).
.
The gravitational settling of the grains is very
slow such that they form a rather passive component, subject to
hydrodynamical streams (e.g.winds).
- 2)
- At lower altitudes where the temperatures are
close to the sublimation temperatures (the cloud layer is expected
to reach its maximum opacity here), nucleation is inefficient and
the particle growth is the leading physical process
In this growth-dominated region, the dust particles may
reach much larger sizes, only limited by element consumption or,
eventually, by gravitational settling when they even reach
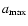 .
Anyway, the dust growth will be essentially completed
before the particles are influenced by drift. The dust grains are
not created here (by nucleation) but are transported into these
layers by winds or rain in from above. The efficient growth will
consume most of the condensable elements from these layers and
thereby bring the supersaturation ratio close to unity in this region.
.
Anyway, the dust growth will be essentially completed
before the particles are influenced by drift. The dust grains are
not created here (by nucleation) but are transported into these
layers by winds or rain in from above. The efficient growth will
consume most of the condensable elements from these layers and
thereby bring the supersaturation ratio close to unity in this region.
- 3)
- Below the cloud base, the temperatures
are higher than the sublimation temperatures, and the dust grains
that rain in from above will quickly evaporate
thereby releasing the condensable elements of the grains and enriching
the surrounding gas.
It remains to be pointed out, however, that in a turbulent fluid field
considerable variations of the thermodynamical conditions may occur.
For example, the nucleation of dust particles may take place even in a
dust-hostile environment, if interfering expansion waves
temporarily cause low temperatures, i.e.high supersaturation ratios
(Paper I). In such turbulent environments, the correlation between the
supersaturation ratio S and the atmospheric height (as assumed in
the upper item list) is loosened. Thus, the regimes are
characterised by S rather than by the atmospheric height, and may
possibly occur also on small scales.
The life cycle of dust grains in brown dwarf atmospheres is
finally completed by convective streams which mix up gas from the deep
interior into the upper layers. On a large scale, we expect an intricate
balance of this upward mixing of condensable elements by convection
with the downward gravitational settling of the condensing dust
grains, which will determine the large-scale structure of the element
abundances in the atmosphere related to the observation of the various
molecular features.
This work will be continued in the next paper of this series by
solving the dust moment equations for the special case of a static
atmosphere.
Acknowledgements
We thank T. Tsuji for contributing the hydrostatic reference model
atmosphere and Akemi Tamanai for providing us with an electronic
version of the optical constants of amorphous quartz. The anonymous
referee is thanked for helpful comments, in particular concerning
the fricional heating. We thank R. Klein for pointing out the work
of Deufelhard
 Wulkow. This work has been supported by the
DFG (Sonderforschungsbereich 555, Teilprojekt B8, and grand
Se 420/19-1 and 19-2). Most of the literature search has been
performed with the ADS system.
Wulkow. This work has been supported by the
DFG (Sonderforschungsbereich 555, Teilprojekt B8, and grand
Se 420/19-1 and 19-2). Most of the literature search has been
performed with the ADS system.
-
Ackermann, S., & Marley, M. 2001, ApJ, 556, 872
In the text
NASA ADS
-
Allard, F., Hauschildt, P., Alexander, D., Tamanai, A., & Schweitzer, A. 2001,
ApJ, 556, 357
In the text
NASA ADS
-
Andersen, A., Jäger, C., Mutschke, H., et al. 1999, A&A, 343, 933
In the text
NASA ADS
-
Bailer-Jones, C. A. L. 2002, A&A, 389, 963
In the text
NASA ADS
-
Bailer-Jones, C. A. L., & Mundt, R. 2001a, A&A, 374, 1071
In the text
NASA ADS
-
Bailer-Jones, C. A. L., & Mundt, R. 2001b, A&A, 367, 218
NASA ADS
-
Berruyer, N., & Frisch, H. 1983, A&A, 126, 269
In the text
NASA ADS
-
Bohren, C. F., & Huffman, D. R. 1983, Absorption and Scattering of Light by
Small Particles (John Wiley & Sons, New York)
In the text
-
Burke, J. R., & Hollenbach, D. J. 1983, ApJ, 265, 223
In the text
NASA ADS
-
Burrows, A., Marley, M., Hubbard, W. B., et al. 1997, ApJ, 491, 856
In the text
NASA ADS
-
Burrows, A., & Sharp, C. M. 1999, ApJ, 512, 843
In the text
NASA ADS
-
Chase Jr., M. W., Davies, C. A., Downey Jr., J. R., et al. 1985, JANAF
Thermochemical Tables (National Bureau of Standards)
In the text
-
Cooper, C. S., Sudarsky, D., Milsom, J. A., Lunine, J. I., & Burrows, A. 2002,
ApJ, accepted
In the text
-
Deufelhard, P., & Wulkow, M. 1989, IMPACT Comp. Sci. Eng., 1, 269
In the text
-
Dominik, C., Sedlmayr, E., & Gail, H.-P. 1993, A&A, 277, 578
In the text
NASA ADS
-
Eislöffel, J., & Scholz, A. 2001, in The Origins of Stars and Planets: The
VLT View, ed. J. Alves, 216
In the text
-
Gail, H.-P., Keller, R., & Sedlmayr, E. 1984, A&A, 133, 320
In the text
NASA ADS
-
Gail, H.-P., & Sedlmayr, E. 1988, A&A, 206, 153
In the text
NASA ADS
-
Gail, H.-P., & Sedlmayr, E. 1998, in Chemistry and physics of molecules and
grains in space, Faraday Discussion no. 109, ed. P. Sarre, London, GB, 303
In the text
-
Gail, H.-P., & Sedlmayr, E. 1999, A&A, 347, 594
In the text
NASA ADS
-
Gauger, A., Gail, H.-P., & Sedlmayr, E. 1990, A&A, 235, 345
In the text
NASA ADS
-
Gilman, R. C. 1972, ApJ, 178, 423
In the text
NASA ADS
-
Großmann, P. 1995, Physikalische Blätter, 51, 641
In the text
-
Helling, Ch., Oevermann, M., Lüttke, M., Klein, R., & Sedlmayr, E. 2001,
A&A, 376, 194 (Paper I)
In the text
NASA ADS
-
Huber, N., & Sommerfeld, M. 1998, Powder Technology, 99, 90
-
Jeans, J. 1967, An introduction to the kinetic theory of gases (Cambridge
University Press)
In the text
-
Krüger, D., Gauger, A., & Sedlmayr, E. 1994, A&A, 290, 573
In the text
NASA ADS
-
Krüger, D., Patzer, A. B. C., & Sedlmayr, E. 1996, A&A, 313, 891
In the text
NASA ADS
-
Krüger, D., & Sedlmayr, E. 1997, A&A, 321, 557
In the text
NASA ADS
-
Krüger, D., Woitke, P., & Sedlmayr, E. 1995, A&AS, 113, 593
In the text
NASA ADS
-
Lain, S., Bröder, D., & Sommerfeld, M. 1999, Chem. Eng. Sc., 54, 4913
In the text
-
Landau, L. D., & Lifshitz, E. M. 1987, Course of Theoretical Physics, Vol. VI,
Fluid Mechanics, 2nd edn. (Pergamon Press)
In the text
-
Lodders, K., & Fegley, B. 1994, Icarus, 110, 117
In the text
-
Lüttke, M. J. H. 2002, Ph.D. Thesis, Techmische Universität, Berlin,
Germany
In the text
-
Macek, J., & Polasek, M. 2000, in Colloquium Fluid Dynamics 2000, ed. P. Jonas,
& V. Uruba (Institute of Thermomechanics AS CR, Prague), 79
In the text
-
MacGregor, K. B., & Stencel, R. E. 1992, ApJ, 397, 644
In the text
NASA ADS
-
Marley, M., Seager, S., Saumon, D., et al. 2002, ApJ, 568, 335
In the text
NASA ADS
-
Martín, E., Zapatero Osorio, M., & Lehto, H. 2001, ApJ, 557, 822
In the text
NASA ADS
-
Mutschke, H., Begemann, B., Dorschner, J., et al. 1998, A&A, 333, 188
In the text
NASA ADS
-
Nowak, U. 1993, Ph.D. Thesis, Freie Universität, Berlin, Germany
In the text
-
Palik, E. D. 1985, Handbook of Optical Constants of Solid (Academic Press Inc.)
In the text
-
Patzer, A. B. C., Gauger, A., & Sedlmayr, E. 1998, A&A, 337, 847
In the text
NASA ADS
-
Posch, T., Kerschbaum, F., Mutschke, H., et al. 1999, A&A, 352, 609
In the text
NASA ADS
-
Rossow, W. V. 1978, Icarus, 36, 1
In the text
NASA ADS
-
Sandin, C., & Höfner, S. 2003, A&A, 398, 253
In the text
NASA ADS
-
Schaaf, S. A. 1963,
Handbuch der Physik, volume VIII/2, chapter:
Mechanics of Rarefied Gases
(Springer Verlag, Berlin, Göttingen, Heidelberg), 591
In the text
-
Seager, S., & Sasselov, D. 2000, A&A, 537, 916
In the text
-
Sedlmayr, E. 1976, Dynamische Entwicklung von HII-Gebieten: Globale
Entwicklung und Transportprozesse, Habilitationsschrift (Universität
Heidelberg)
-
Sedlmayr, E. 1994,
In Jørgensen U. G., IAU Colloq 146, Molecules in the
Stellar Environment (Springer Verlag, Berlin), 163
In the text
-
Simis, Y. J. W., Icke, V., & Dominik, C. 2001, A&A, 371, 205
In the text
NASA ADS
-
Tamanai, A. 1998, Master's thesis, Wichita State University, KS, USA
In the text
-
Tsuji, T. 2002, ApJ, 575, 264
In the text
NASA ADS
-
Woitke, P. 1999, in Astronomy with Radioactivities, ed. R. Diehl, &
D. Hartmann, Schloß Ringberg, Germany, MPE Report 274, 163
In the text
-
Wulkow, M. 1992, IMPACT Comp. Sci. Eng., 4, 153
In the text
Copyright ESO 2003
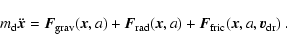

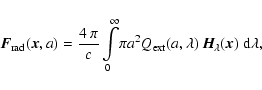
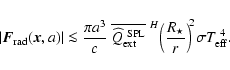
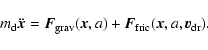
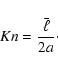
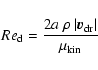
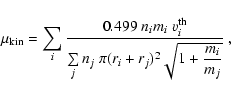
![\begin{displaymath}\mu_{\rm kin}= 5.877 \times 10^{-6} \frac{\rm g}{\rm cm\;s}
~ \sqrt{T\rm [K]} .
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img118.gif)
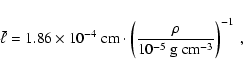
![$\displaystyle \vec{F}^{\rm Sch}_{\rm fric} =
-\pi a^2 \rho~\vert\vec{v}_{\rm dr...
...t(\frac{1}{s}+\frac{1}{2s^3}\right)
\frac{{\rm e}^{-s^2}}{\sqrt{\pi}} \right] ,$](/articles/aa/full/2003/07/aah3912/img127.gif)
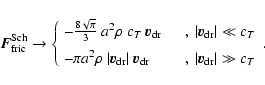
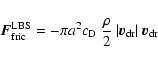
![\begin{displaymath}c_{\rm D} = \left\{ \begin{array}{ll}
\displaystyle{\frac{24...
...\\ [1.2ex]
2.61 & , Re_{\rm d} > 1500 .
\end{array} \right.
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img134.gif)
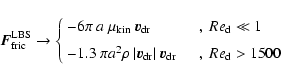
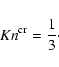
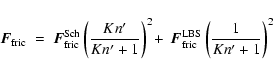

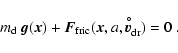
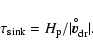

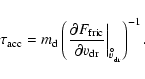
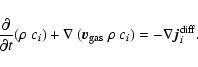
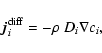
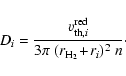
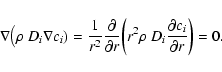
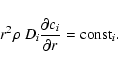
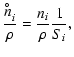
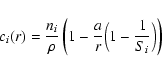
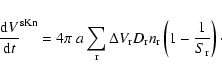

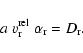
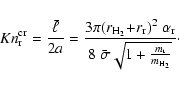
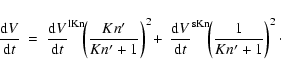
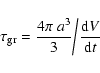
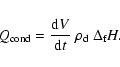
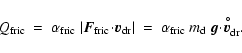
![\begin{displaymath}Q_{\rm rad} = 4\pi\!\!\int\!\!\pi a^2 Q_{\rm abs}(a,\lambda) ...
...ig[B_{\lambda}(T_{\rm d})-J_{\lambda}\big] ~{\rm d}\lambda \ ,
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img288.gif)
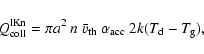
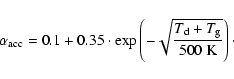
![\begin{displaymath}\frac{{\rm\partial} }{{\rm\partial} t}(\rho~e) + \nabla \big(\vec{v}_{\rm gas}[\rho~e+P]\big) = - \nabla \vec{j}_{\rm HC}
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img297.gif)
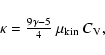
![\begin{displaymath}\kappa = 988~{\rm\frac{erg}{\rm K~cm~s}}~\sqrt{T_{\rm g}\rm [K]} .
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img303.gif)
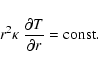
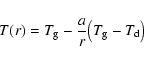
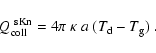
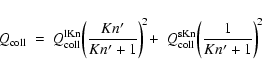


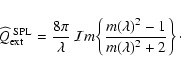

![\begin{displaymath}\frac{{\rm\partial} }{{\rm\partial} t}\big(f(V)~{\rm d}V\big)...
...rc}}(V)\big]f(V)~{\rm d}V\!\Big) = \sum\limits_k R_k~{\rm d}V.
\end{displaymath}](/articles/aa/full/2003/07/aah3912/img343.gif)
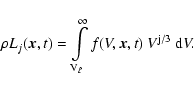
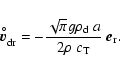
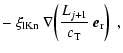
![$\displaystyle \sqrt[3]{36\pi}~\sum\limits_{\rm r}
\Delta V_{\rm r}~n_{\rm r} v^{\rm rel}_{\rm r} \alpha_{\rm r}
\left(1-\frac{1}{S_{\rm r}}\right)$](/articles/aa/full/2003/07/aah3912/img377.gif)
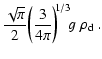
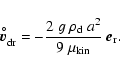
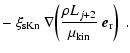
![$\displaystyle \sqrt[3]{48\pi^2}~\sum\limits_{\rm r}
\Delta V_{\rm r}~n_{\rm r}~D_{\rm r}
\left(1-\frac{1}{S_{\rm r}}\right)$](/articles/aa/full/2003/07/aah3912/img393.gif)
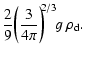
![$\displaystyle \big[{S\!r}\big]\frac{{\rm\partial} }{{\rm\partial} t}\big(\rho L_j\big)$](/articles/aa/full/2003/07/aah3912/img407.gif)