A&A 399, 169-175 (2003)
DOI: 10.1051/0004-6361:20021798
I. M. Taban1 - W. A. Schutte1 - K. M. Pontoppidan2 - E. F. van Dishoeck1,2
1 - Raymond and Beverly Sackler Laboratory for Astrophysics,
Leiden Observatory, PO Box 9513, 2300 RA Leiden, The Netherlands
2 - Leiden Observatory, PO Box 9513, 2300 RA Leiden, The Netherlands
Received 19 September 2002 / Accepted 14 November 2002
Abstract
We obtained near-infrared spectroscopy of the high mass young stellar
object W 33A between 1.9-2.5 ![]() m in search of absorption features
of circumstellar ices. The 2.27
m in search of absorption features
of circumstellar ices. The 2.27 ![]() m band of
m band of
![]() is positively
identified in the spectrum, its intensity being fully consistent with
the column density derived earlier from the methanol bands at 3.54 and
3.91
is positively
identified in the spectrum, its intensity being fully consistent with
the column density derived earlier from the methanol bands at 3.54 and
3.91 ![]() m. The 2.21
m. The 2.21 ![]() m band of solid
m band of solid ![]() ,
on the other hand,
was not detected. This shows that the quantity of solid
,
on the other hand,
was not detected. This shows that the quantity of solid ![]() towards
W 33A is at least 3 times lower than earlier estimates based on the
towards
W 33A is at least 3 times lower than earlier estimates based on the
![]() umbrella mode at 9
umbrella mode at 9 ![]() m.
m.
Key words: methods: laboratory - stars: individual: W 33A - ISM: abundances - ISM: molecules - infrared: ISM - ISM: lines and bands
While, at least for the general dense medium, the total oxygen and
carbon budget seems to be rather well accounted for (Schutte 1999),
the nature of the gaseous and icy carriers of the nitrogen is still
quite unclear. Ammonia (![]() )
could be an important nitrogen
carrying component of interstellar ices. It forms when atomic nitrogen
is reduced by atomic hydrogen on the surfaces of dust particles
(Hiraoka et al. 1995). Furthermore,
)
could be an important nitrogen
carrying component of interstellar ices. It forms when atomic nitrogen
is reduced by atomic hydrogen on the surfaces of dust particles
(Hiraoka et al. 1995). Furthermore, ![]() could accrete from the
gas phase after it is formed by ion-molecule reactions (Scott et al. 1997). In hot core regions where elevated grain temperatures cause
sublimation of the icy mantles, large gas phase abundances of ammonia
have been found ((1-10)
could accrete from the
gas phase after it is formed by ion-molecule reactions (Scott et al. 1997). In hot core regions where elevated grain temperatures cause
sublimation of the icy mantles, large gas phase abundances of ammonia
have been found ((1-10) ![]() 10-6 relative to hydrogen;
Genzel et al. 1982; Blake et al. 1987; Heaton et al. 1989; Cesaroni et al. 1994). This considerably exceeds the abundance of
10-6 relative to hydrogen;
Genzel et al. 1982; Blake et al. 1987; Heaton et al. 1989; Cesaroni et al. 1994). This considerably exceeds the abundance of ![]() in
cold dense regions (
in
cold dense regions (
![]() /
/
![]()
![]() 10-7;
Federman et al. 1990), indicating that the ices indeed form an
important reservoir of
10-7;
Federman et al. 1990), indicating that the ices indeed form an
important reservoir of ![]() .
.
The presence (or absence) of solid ![]() has important
implications for the chemistry of star forming regions. Whether in
dense quiescent regions gaseous nitrogen will reside in its molecular
or atomic form depends on the depletion of oxygen, since the reactions
of atomic nitrogen with OH are an essential step towards
has important
implications for the chemistry of star forming regions. Whether in
dense quiescent regions gaseous nitrogen will reside in its molecular
or atomic form depends on the depletion of oxygen, since the reactions
of atomic nitrogen with OH are an essential step towards ![]() formation (Charnley & Rodgers 2002). Thus the quantity of
formation (Charnley & Rodgers 2002). Thus the quantity of ![]() that is present in the ices could give important information on the
gas phase conditions of condensation. In addition,
that is present in the ices could give important information on the
gas phase conditions of condensation. In addition, ![]() can
produce ions through acid-base chemistry under cryogenic conditions.
This process likely explains the presence of OCN- and probably
HCOO- in interstellar ices (Grim & Greenberg 1987; Demyk et al. 1998; Novozamsky et al. 2002; Hudson et al. 2001; Keane et al. 2002). Finally, in the presence of
can
produce ions through acid-base chemistry under cryogenic conditions.
This process likely explains the presence of OCN- and probably
HCOO- in interstellar ices (Grim & Greenberg 1987; Demyk et al. 1998; Novozamsky et al. 2002; Hudson et al. 2001; Keane et al. 2002). Finally, in the presence of ![]() ,
energetic
processing of the ices by the ambient UV field could give rise to
complex organic molecules, some of which could be of pre-biological
significance, e.g., amino acids (Bernstein et al. 1995; Muñoz Caro
et al. 2002; Bernstein et al. 2002; Muñoz Caro & Schutte 2003).
,
energetic
processing of the ices by the ambient UV field could give rise to
complex organic molecules, some of which could be of pre-biological
significance, e.g., amino acids (Bernstein et al. 1995; Muñoz Caro
et al. 2002; Bernstein et al. 2002; Muñoz Caro & Schutte 2003).
The main mid-infrared signatures of solid ![]() are the umbrella
mode at 9.0
are the umbrella
mode at 9.0 ![]() m, the NH stretching mode at 2.96
m, the NH stretching mode at 2.96 ![]() m and the
ammonium hydrate (
m and the
ammonium hydrate (![]() .
.![]() )
feature at 3.48
)
feature at 3.48 ![]() m.
Searches for these bands are hampered by overlap with considerably
stronger bands of other dust constituents. The 2.96
m.
Searches for these bands are hampered by overlap with considerably
stronger bands of other dust constituents. The 2.96 ![]() m band
overlaps with the strong 3
m band
overlaps with the strong 3 ![]() m band of
m band of ![]() ice, the 9
ice, the 9 ![]() m
band falls in the wing of the intense 9.7
m
band falls in the wing of the intense 9.7 ![]() m silicate absorption,
and the 3.48
m silicate absorption,
and the 3.48 ![]() m feature is superimposed on the long wavelength
shoulder of the 3
m feature is superimposed on the long wavelength
shoulder of the 3 ![]() m band. The non-detection of the 2.96
m band. The non-detection of the 2.96 ![]() m
band as a substructure on the 3
m
band as a substructure on the 3 ![]() m feature mildly constrains the
m feature mildly constrains the
![]() abundance to
abundance to ![]() 10% of
10% of ![]() when the ice in the
line of sight is unannealed (Dartois et al. 2001; Smith et al. 1989;
Gibb et al. 2001). However, for a considerable fraction of objects
the ices in the line of sight are partially crystalline. In this case
the upper limit is even less stringent, since crystalline
when the ice in the
line of sight is unannealed (Dartois et al. 2001; Smith et al. 1989;
Gibb et al. 2001). However, for a considerable fraction of objects
the ices in the line of sight are partially crystalline. In this case
the upper limit is even less stringent, since crystalline ![]() ice produces a feature at 2.96
ice produces a feature at 2.96 ![]() m which is indistinguishable from
the ammonia band (Gibb et al. 2001). In addition, the strength of the
2.96
m which is indistinguishable from
the ammonia band (Gibb et al. 2001). In addition, the strength of the
2.96 ![]() m band is considerably reduced when provisions are made for
the effects of particle shapes (van der Bult et al. 1985; Smith et al.
1989).
m band is considerably reduced when provisions are made for
the effects of particle shapes (van der Bult et al. 1985; Smith et al.
1989).
Recently there have been a number of papers claiming the detection of
the 9.0 ![]() m umbrella mode of
m umbrella mode of ![]() .
Abundances of up to 15%
rel. to solid
.
Abundances of up to 15%
rel. to solid ![]() were inferred (Lacy et al. 1998; Gibb et al.
2000, 2001; Gürtler et al. 2002). However, such a detection is
difficult, since it requires a reliable matching of the very strong
underlying silicate feature. The profile of the silicate band varies
between objects and so far no class of silicate materials has been
found that consistently reproduces the 9.7
were inferred (Lacy et al. 1998; Gibb et al.
2000, 2001; Gürtler et al. 2002). However, such a detection is
difficult, since it requires a reliable matching of the very strong
underlying silicate feature. The profile of the silicate band varies
between objects and so far no class of silicate materials has been
found that consistently reproduces the 9.7 ![]() m feature for embedded
YSO's. Therefore, these studies relied on polynomial fitting of the
silicate band. This technique has the clear drawback that it offers no
guarantee for a robust match of the band profile underlying the broad
m feature for embedded
YSO's. Therefore, these studies relied on polynomial fitting of the
silicate band. This technique has the clear drawback that it offers no
guarantee for a robust match of the band profile underlying the broad
![]() feature and therefore introduces the risk of a spurious
detection. In addition, a comprehensive paper on this subject (Gibb et al. 2001) invoked a second, unidentified, feature centered at 9.2
feature and therefore introduces the risk of a spurious
detection. In addition, a comprehensive paper on this subject (Gibb et al. 2001) invoked a second, unidentified, feature centered at 9.2 ![]() m to compensate for the poor match by the ammonia band of the
absorption feature obtained after subtraction of the polynomial
baseline. Clearly, independent confirmation of these detections is
highly desirable.
m to compensate for the poor match by the ammonia band of the
absorption feature obtained after subtraction of the polynomial
baseline. Clearly, independent confirmation of these detections is
highly desirable.
Dartois & d'Hendecourt (2001) and Dartois et al. (2002), based on the
weakness of the 3.48 ![]() m feature of ammonium hydrate
m feature of ammonium hydrate
![]() towards YSO's, derived
towards YSO's, derived ![]() upper limits of less than 5%. Gibb et al. (2001) however argued that the
upper limits of less than 5%. Gibb et al. (2001) however argued that the
![]() feature is much broader than the observed 3.48
feature is much broader than the observed 3.48 ![]() m band and
concluded that it could be part of the strong long wavelength shoulder
of the 3
m band and
concluded that it could be part of the strong long wavelength shoulder
of the 3 ![]() m band, preventing significant constraints.
m band, preventing significant constraints.
Traditionally observations of interstellar ices have been limited to
the absorption features due to fundamental intramolecular vibrational
transitions in the mid-IR region (2.5-20 ![]() m). The vibrational
overtones and combination bands fall in the near-IR (1-2.5
m). The vibrational
overtones and combination bands fall in the near-IR (1-2.5 ![]() m). These features are quite weak, with peak intensities of at
most
m). These features are quite weak, with peak intensities of at
most ![]() 5% of those of the fundamentals. Observations of the
near-IR bands of frozen molecules have been used for a long time to
study the composition of the planets and satellites of the outer-solar
system which are covered by thick layers of ice (e.g., Quirico et al.
1999). However, observations of interstellar ices are constrained by
the amount of ice in the line of sight and the band strength therefore
becomes a crucial factor. In addition, the near-IR region falls in the
short wavelength tail of the emission by hot circumstellar dust where
the flux drops very rapidly. Therefore, a meaningful search for
interstellar ice features in the near-IR had to await the advent of 8 meter class telescopes like the Very Large Telescope (VLT).
5% of those of the fundamentals. Observations of the
near-IR bands of frozen molecules have been used for a long time to
study the composition of the planets and satellites of the outer-solar
system which are covered by thick layers of ice (e.g., Quirico et al.
1999). However, observations of interstellar ices are constrained by
the amount of ice in the line of sight and the band strength therefore
becomes a crucial factor. In addition, the near-IR region falls in the
short wavelength tail of the emission by hot circumstellar dust where
the flux drops very rapidly. Therefore, a meaningful search for
interstellar ice features in the near-IR had to await the advent of 8 meter class telescopes like the Very Large Telescope (VLT).
The spectroscopic K-band which covers the 1.9-2.6 ![]() region provides a window for a number of near-IR features of ice
components. First,
region provides a window for a number of near-IR features of ice
components. First, ![]() has a feature near 2.21
has a feature near 2.21 ![]() m (Trotta
& Schmidt 1994). Unlike its mid-IR features, this band is not
overwhelmed by strong absorptions of other solids. Furthermore
m (Trotta
& Schmidt 1994). Unlike its mid-IR features, this band is not
overwhelmed by strong absorptions of other solids. Furthermore
![]() has a feature at 2.27
has a feature at 2.27 ![]() m (Sect. 4.1 below). The presence
of
m (Sect. 4.1 below). The presence
of
![]() in the ices towards high mass YSO's has been firmly
established from observations of a number of mid-IR absorption
features (e.g., Dartois et al. 1999). Detection of the 2.27
in the ices towards high mass YSO's has been firmly
established from observations of a number of mid-IR absorption
features (e.g., Dartois et al. 1999). Detection of the 2.27 ![]() m
band would therefore be an important test for the feasibility of
observing interstellar ices in the near-IR and the consistency of the
near-IR and mid-IR lines of sight. Finally
m
band would therefore be an important test for the feasibility of
observing interstellar ices in the near-IR and the consistency of the
near-IR and mid-IR lines of sight. Finally ![]() ice gives two
broad structures at 2 and 2.45
ice gives two
broad structures at 2 and 2.45 ![]() m (e.g., Schmitt et al. 1998).
m (e.g., Schmitt et al. 1998).
Due to its exceptionally high ice column density, the high mass
embedded YSO W 33A has classically been the prime target to search for
weak ice bands. This paper reports a search for the 2.21 and 2.27 ![]() m bands towards W 33A with the the Infrared Spectrometer And Array
Camera (ISAAC) at the Very Large Telescope (VLT) at Paranal,
Chile. From these observations, in combination with laboratory
experiments, we obtain stringent constraints on the abundance of solid
m bands towards W 33A with the the Infrared Spectrometer And Array
Camera (ISAAC) at the Very Large Telescope (VLT) at Paranal,
Chile. From these observations, in combination with laboratory
experiments, we obtain stringent constraints on the abundance of solid
![]() which contradict earlier estimates based on mid-IR
observations.
which contradict earlier estimates based on mid-IR
observations.
W 33A was observed on July 28 and September 22, 2001 with a
total on-source integration time of
![]() evenly distributed
among the two nights. A 0
evenly distributed
among the two nights. A 0
![]() 6 slit was used, which together with
the low resolution grating on ISAAC gives an average resolution of
R=750. All spectra were obtained using a 15
6 slit was used, which together with
the low resolution grating on ISAAC gives an average resolution of
R=750. All spectra were obtained using a 15
![]() nod throw
along the slit in a standard ABBA scheme with
nod throw
along the slit in a standard ABBA scheme with ![]() of
integration time per frame. Each night a telluric standard star was
observed before and after the observation of W 33A with an airmass
difference of less than 0.05 in order to get the best cancellation of
telluric lines. On the first night the telluric standards used were
HD 91713 (K1III) and HD 175876 (O7V) while
HD 154066 (B8V) and HD 161961 (B0.5III) were
observed as standards during the second night. In the final spectrum
HD 91713 was not used, since it did not have sufficiently high S/Nand would thus only add noise to the combined spectrum of W 33A.
of
integration time per frame. Each night a telluric standard star was
observed before and after the observation of W 33A with an airmass
difference of less than 0.05 in order to get the best cancellation of
telluric lines. On the first night the telluric standards used were
HD 91713 (K1III) and HD 175876 (O7V) while
HD 154066 (B8V) and HD 161961 (B0.5III) were
observed as standards during the second night. In the final spectrum
HD 91713 was not used, since it did not have sufficiently high S/Nand would thus only add noise to the combined spectrum of W 33A.
The frames were dark subtracted, flat fielded, distortion corrected and combined using the standard eclipse library. The spectra were then wavelength calibrated relative to a xenon arc lamp and flux calibrated relative to the standard stars.
Due to a strong reflection nebulosity around the primary source in
W 33A, the extraction of a 1D spectrum has to be done with care. A
pointlike source is clearly visible a few arcseconds to the south of the
reflection nebula, which as expected is significantly more blue than
the point source. The 1-dimensional spectrum of W 33A was extracted
from a cross dispersion
region centered on the point source with a width that maximizes the
S/N ratio on the continuum of the extracted spectrum. The final
spectrum has a S/N ratio of 150-200 at
![]() .
.
The final spectrum was obtained by dividing each spectrum of W 33A by a
standard star spectrum and combining the spectra from the two
nights. A small shift of a fraction of a pixel was applied to the
standard star spectra in order to optimize the telluric division.
A very good cancellation of telluric features was achieved except in
the
![]() region, where residuals from strong
telluric absorption are still visible.
region, where residuals from strong
telluric absorption are still visible.
Figure 1 shows the observations. It can be seen that the spectrum is
dominated by the exponentally rising continuum emission originating
from the hot dust (![]() 800-1000 K) close to the star
while a number of relatively
faint emission lines of circumstellar origin are superposed (see below).
To enable a better search for minor absorption bands at the % level
we divided by the indicated continuum. The continuum is given by
a second order polynomial in the log(F) vs.
800-1000 K) close to the star
while a number of relatively
faint emission lines of circumstellar origin are superposed (see below).
To enable a better search for minor absorption bands at the % level
we divided by the indicated continuum. The continuum is given by
a second order polynomial in the log(F) vs. ![]() plane which deviates
only marginally from a straight line. The polynomial
was defined by fitting the regions 4530-4500
plane which deviates
only marginally from a straight line. The polynomial
was defined by fitting the regions 4530-4500
![]() and
4040-4000
and
4040-4000
![]() .
Other spectral regions either
contain circumstellar emission features, or contain absorption bands of the
various ice components towards W 33A (see Sect. 4 below).
.
Other spectral regions either
contain circumstellar emission features, or contain absorption bands of the
various ice components towards W 33A (see Sect. 4 below).
The resulting optical depth spectrum is shown in Fig. 2. For
comparison the atmospheric transmission in this region is also shown.
The spectrum is dominated by a number of emission
lines. Most prominent are the CO vibrational overtones
between 2.3 and
![]() ,
vibrational transitions of molecular
hydrogen and the
,
vibrational transitions of molecular
hydrogen and the
![]() and
and
![]() hydrogen
recombination lines at
hydrogen
recombination lines at
![]() and
and
![]() ,
respectively. The presence of a significant population of
,
respectively. The presence of a significant population of ![]() in the second vibrational level and the CO bandheads indicate that the
gas is hot (>
in the second vibrational level and the CO bandheads indicate that the
gas is hot (>
![]() ), although the molecular hydrogen
lines may be shock excited. Also, the fact that the CO lines are
seen in emission shows that the gas is not placed in front of the
infrared continuum source, but may be part of a nearly face-on
circumstellar disk (e.g. Najita et al. 1996; Carr et al. 2001).
), although the molecular hydrogen
lines may be shock excited. Also, the fact that the CO lines are
seen in emission shows that the gas is not placed in front of the
infrared continuum source, but may be part of a nearly face-on
circumstellar disk (e.g. Najita et al. 1996; Carr et al. 2001).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f1.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg34.gif) |
Figure 1: K band spectrum of W 33A. The dashed line indicates the adopted continuum (see text). |
| Open with DEXTER | |
The hydrogen recombination lines are often interpreted as being a sign
of accretion activity and in the case of high mass young stars they
may originate in an ionized wind (e.g. Nisini et al. 1995).
In this case the lines are formed within a few
stellar radii of the star itself. In the case of a massive star like
W 33A the lines may also be formed in the associated HII region, since
the line-to-continuum ratio varies with more than an order of
magnitude throughout the nebulosity in the cross dispersion
direction. This clearly indicates that the hydrogen emission is not
scattered from the inner regions of the source along with the
continuum emission, but is rather produced where it is observed. On
the other hand the line-to-continuum ratio of the CO lines seems to be
constant on all positions along the slit, indicating that this
emission is indeed scattered along with the continuum emission and is
thus produced close to the source. The ![]() lines are
unfortunately too weak to be clearly detected in the reflection
nebulosity.
lines are
unfortunately too weak to be clearly detected in the reflection
nebulosity.
It can be seen that a shallow absorption band appears at 2.27 ![]() m. In addition a broad absorption feature may be present between
1.92-2.12
m. In addition a broad absorption feature may be present between
1.92-2.12 ![]() m. An apparent absorption structure at 2
m. An apparent absorption structure at 2 ![]() m is
caused by residual telluric structure.
m is
caused by residual telluric structure.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f2.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg35.gif) |
Figure 2:
Bottom curve: Optical depth spectrum of W 33A in the K band
obtained by division with the adopted continuum
(Fig. 1). The nature of the various emission bands is indicated.
The arrows give the location of the 2.21 |
| Open with DEXTER | |
It can be argued that if the emission towards W 33A in the K-band is
due to scattered light, a different line of sight may be probed than at
mid-infrared wavelengths.
We have tested this possible difficulty by comparing our K-band
acquisition image to a
![]() image which was obtained during
the same observation run.
Astrometry relative to 4 nearby stars constrain the positions of the W 33A
point source at
image which was obtained during
the same observation run.
Astrometry relative to 4 nearby stars constrain the positions of the W 33A
point source at
![]() and
and
![]() to differ by
less than 0
to differ by
less than 0
![]() 3.
This indicates that the lines of sight probed are identical within 1100 AU, assuming a distance of 3.7 kpc (Wynn-Williams 1982). This distance
may still be enough
to cause significant differences in observed abundances, since the small
scale distribution
of ices around young stars is largely unknown. E.g. adaptive optics
K-band spectroscopy is necessary to further constrain the effects of
differing lines of sight due to scattering. However, as will be
discussed in Sects. 5 and 6, column densities of tracer species such
as
3.
This indicates that the lines of sight probed are identical within 1100 AU, assuming a distance of 3.7 kpc (Wynn-Williams 1982). This distance
may still be enough
to cause significant differences in observed abundances, since the small
scale distribution
of ices around young stars is largely unknown. E.g. adaptive optics
K-band spectroscopy is necessary to further constrain the effects of
differing lines of sight due to scattering. However, as will be
discussed in Sects. 5 and 6, column densities of tracer species such
as
![]() and
and ![]() appear to be invariant between the
near- and mid-IR, indicating that such line of sight effects are likely
negligible.
appear to be invariant between the
near- and mid-IR, indicating that such line of sight effects are likely
negligible.
A detailed description of the procedure used for the creation and analysis by infrared spectroscopy of simulated interstellar ice samples was published earlier (Gerakines et al. 1995). The samples were deposited at 12 K followed by a step-wise warm-up while monitoring the evolution of the infrared spectrum.
The reagents used in these experiments were ![]() liquid
(purified by three freeze-thaw cycles),
liquid
(purified by three freeze-thaw cycles), ![]() gas (Praxair,
99.996% purity),
gas (Praxair,
99.996% purity), ![]() gas (Praxair, 99.99% purity) and
gas (Praxair, 99.99% purity) and
![]() liquid (Janssen Chimica, 99.9% purity).
For samples containing both
liquid (Janssen Chimica, 99.9% purity).
For samples containing both ![]() and
and ![]() ,
,
![]() was deposited through a separate tube, to prevent
reactions prior to deposition.
was deposited through a separate tube, to prevent
reactions prior to deposition.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f3.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg39.gif) |
Figure 3:
Near-IR spectra of 1. |
| Open with DEXTER | |
Figure 3 gives the spectra of solid ![]() ,
,
![]() and
and ![]() over
the entire near-IR region. It can be seen that
over
the entire near-IR region. It can be seen that ![]() produces two
sharp features, near 2.00 and 2.21
produces two
sharp features, near 2.00 and 2.21 ![]() m. However, the stronger
2.00
m. However, the stronger
2.00 ![]() m feature falls in a region of very poor atmospheric transmission
(Fig. 2).
m feature falls in a region of very poor atmospheric transmission
(Fig. 2).
![]() shows
a variety of structures. Apart from the 2.27
shows
a variety of structures. Apart from the 2.27 ![]() m band,
these are shallow and fall in regions that are crowded with
atmospheric lines or circumstellar emission bands (Fig. 2).
m band,
these are shallow and fall in regions that are crowded with
atmospheric lines or circumstellar emission bands (Fig. 2).
![]() gives 2 broad features, at 2.0 and 2.45
gives 2 broad features, at 2.0 and 2.45 ![]() m, where the
latter is quite weak.
m, where the
latter is quite weak.
We studied the spectra of the 2.27 ![]() m
m
![]() and 2.21
and 2.21 ![]() m
m ![]() bands as well as the broad feature of amorphous
bands as well as the broad feature of amorphous ![]() ice
around 2
ice
around 2 ![]() m in a variety of ice mixtures.
Three different kind of mixtures were used: ices dominated by
m in a variety of ice mixtures.
Three different kind of mixtures were used: ices dominated by
![]() ,
ices in which
,
ices in which ![]() ,
,
![]() and
and
![]() are present in similar abundances, and finally the pure ices.
The mixtures are thought to be
representative of the composition of interstellar ices
in various dense regions (Dartois et al. 1999; Gerakines et al. 1999;
Ehrenfreund et al. 1999). The pure samples were studied for comparison.
are present in similar abundances, and finally the pure ices.
The mixtures are thought to be
representative of the composition of interstellar ices
in various dense regions (Dartois et al. 1999; Gerakines et al. 1999;
Ehrenfreund et al. 1999). The pure samples were studied for comparison.
Figure 4 presents 4800-4300
![]() spectra of the ice
mixtures
spectra of the ice
mixtures
![]() ,
,
![]() as well as pure
as well as pure
![]() at 12 K and 120 K showing the 2.27
at 12 K and 120 K showing the 2.27 ![]() m feature of
m feature of
![]() .
The width and position of this band depends somewhat
on temperature and composition (Fig. 4).
The position varies between 4410 and 4395
.
The width and position of this band depends somewhat
on temperature and composition (Fig. 4).
The position varies between 4410 and 4395
![]() ,
and
FWHM varies between 55-65
,
and
FWHM varies between 55-65
![]() .
Besides the
.
Besides the
![]() feature, the spectra also show the
feature, the spectra also show the ![]() band at 2.21
band at 2.21 ![]() m
(Sect. 4.2) and a feature at 2.13
m
(Sect. 4.2) and a feature at 2.13 ![]() m caused by
m caused by ![]() .
.
We measured the band strengths of the 2.27 ![]() m band at different
temperatures (see Table 1). These were obtained
by comparison with mid-IR features of known intensity, using:
m band at different
temperatures (see Table 1). These were obtained
by comparison with mid-IR features of known intensity, using:
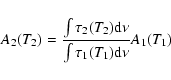 |
(1) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f4.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg43.gif) |
Figure 4:
The 2.27 1. 2. 3. 4. 5. 6. The spectra have been offset for clarity. |
| Open with DEXTER | |
Figure 5 shows the 2.21 ![]() m ammonia feature for a number of
mixtures,
m ammonia feature for a number of
mixtures,
![]() ,
,
![]() and pure
and pure ![]() .
The position is almost the same for all mixtures, around
4525
.
The position is almost the same for all mixtures, around
4525
![]() ,
while the pure ammonia feature falls at
4480
,
while the pure ammonia feature falls at
4480
![]() .
The FWHMvaries between 45-70
.
The FWHMvaries between 45-70
![]() for the matrices.
For pure ammonia, the width is
for the matrices.
For pure ammonia, the width is ![]() 85
85
![]() .
The band strength for the 2.21
.
The band strength for the 2.21 ![]() m feature was calculated
with the procedure described in Sect. 4.1 (see Table 1).
m feature was calculated
with the procedure described in Sect. 4.1 (see Table 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f5.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg45.gif) |
Figure 5:
The 2.21 1. 2. 3. 4. 5. 6. The spectra have been offset for clarity. |
| Open with DEXTER | |
The near-IR spectrum of pure ![]() ice after deposition at 12 K and
warm-up to 50 and 120 K is shown in Fig. 4.
The band strength was derived following the method described
in Sect. 4.1 (see Table 1).
ice after deposition at 12 K and
warm-up to 50 and 120 K is shown in Fig. 4.
The band strength was derived following the method described
in Sect. 4.1 (see Table 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f6.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg47.gif) |
Figure 6:
Spectra of pure |
| Open with DEXTER | |
| Ice Mixture | Molecule | T | A(near-IR) | mid-IR mode | A(mid-IRa) | |||||
|
|
K | cm-1 | |
cm molecule-1 | cm molecule-1 | |||||
| 1 | 0.8 | 1 | 0.3 |
|
12 | 4404 | 2.271 |
|
C-O stretching |
|
| 120 | 4398 | 2.274 |
|
|||||||
| 12 | 4517 | 2.214 |
|
umbrella |
|
|||||
| 120 | 4521 | 2.212 |
|
|||||||
| 1 | 0.7 | 1 |
|
12 | 4410 | 2.268 |
|
C-O stretching |
|
|
| 120 | 4407 | 2.269 |
|
|||||||
| 10 | 1.4 | 12 | 4528 | 2.208 |
|
umbrella |
|
|||
| 50 | 4527 | 2.209 |
|
|||||||
| 1 | 12 | 4478 | 2.233 |
|
umbrella |
|
||||
| 50 | 4481 | 2.232 |
|
|||||||
| 1 |
|
12 | 4395 | 2.275 |
|
C-O stretching |
|
|||
| 50 | 4394 | 2.276 |
|
|||||||
| 1 | 12 | 4998 | 2.001 |
|
O-H stretching |
|
||||
| 50 | 4998 | 2.001 |
|
|||||||
| Ice mixture | Molecule |
|
N | N/N( |
Temperature | |||
|
|
(cm-1) | (cm-2) | % | (K) | ||||
| 1 | 0.8 | 1 | 0.3 | <0.60 | <
|
<3.6 | 120 | |
| 10 | 1.4 | <0.31 | <
|
<5.0 | 50 | |||
| 1 | <0.60 | <
|
<5.9 | 50 | ||||
| 1 | 0.7 | 1 |
|
0.8 |
|
15 | 120 | |
| 1 | 0.8 | 1 | 0.3 |
|
1.5 |
|
16 | 120 |
| 1 |
|
1.2 |
|
14 | 50 | |||
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f7.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg76.gif) |
Figure 7:
The optical depth spectrum of W 33A
compared with
|
| Open with DEXTER | |
Figure 7 compares the W 33A spectrum to
![]() (at 120 K) and
(at 120 K) and
![]() (at 50 K). Temperatures were selected according to the temperatures which
have been derived from the ice features in the mid-IR, e.g.,
solid
(at 50 K). Temperatures were selected according to the temperatures which
have been derived from the ice features in the mid-IR, e.g.,
solid
![]() shows T
shows T ![]() 116 K (Gerakines et al. 1999;
Ehrenfreund et al. 1999). No direct observations are available
for the water 3
116 K (Gerakines et al. 1999;
Ehrenfreund et al. 1999). No direct observations are available
for the water 3 ![]() m feature, because it is saturated for W 33A. However, observations of this feature towards other high
mass young stellar objects give temperatures in the range 20-70 K
(Smith et al. 1989). Therefore, we used 50 K for water-dominated
ices when matching these to the W 33A spectrum.
m feature, because it is saturated for W 33A. However, observations of this feature towards other high
mass young stellar objects give temperatures in the range 20-70 K
(Smith et al. 1989). Therefore, we used 50 K for water-dominated
ices when matching these to the W 33A spectrum.
The methanol feature in Fig. 7 gives a good match to the
shallow 2.27 ![]() m absorption band in the W 33A spectrum. Table 2
lists the implied
m absorption band in the W 33A spectrum. Table 2
lists the implied
![]() column density. The value of
1.8
column density. The value of
1.8 ![]() 1018 cm-2 is in excellent agreement with the
column density of 1.85
1018 cm-2 is in excellent agreement with the
column density of 1.85 ![]() 1018 cm-2 obtained from the
methanol features at 3.54 and 3.91
1018 cm-2 obtained from the
methanol features at 3.54 and 3.91 ![]() m (Dartois et al. 1999). To
assess the robustness of this result, we also list the column
densities which were obtained by matching the observations to the
methanol feature in the other laboratory mixtures, giving similar
results. The match was less favorable for these other mixtures. This
agrees well with the results from the mid-IR, which showed that ices
containing similar abundances of
m (Dartois et al. 1999). To
assess the robustness of this result, we also list the column
densities which were obtained by matching the observations to the
methanol feature in the other laboratory mixtures, giving similar
results. The match was less favorable for these other mixtures. This
agrees well with the results from the mid-IR, which showed that ices
containing similar abundances of
![]() ,
,
![]() and
and ![]() give the best matches to the methanol features
(Dartois et al. 1999; Ehrenfreund et al. 1999).
give the best matches to the methanol features
(Dartois et al. 1999; Ehrenfreund et al. 1999).
Figure 7 shows that there is no indication of the presence
of the 2.21 ![]() m
m ![]() feature in the W 33A spectrum.
Using the
feature in the W 33A spectrum.
Using the
![]() ice spectrum, we estimate an upper limit
of
ice spectrum, we estimate an upper limit
of ![]() (2.21)
(2.21) ![]() 0.004 (Fig. 6). This band depth
is constrained by the 3
0.004 (Fig. 6). This band depth
is constrained by the 3 ![]() noise level from
2.220-2.227
noise level from
2.220-2.227 ![]() m (4505-4490
m (4505-4490
![]() ), a clear
spectral region free of emission and absorption bands. With the band
strength from Table 1, the upper limit yields
N(
), a clear
spectral region free of emission and absorption bands. With the band
strength from Table 1, the upper limit yields
N(![]() ) < 6.1
) < 6.1 ![]() 1017 cm-2.
Comparison with the spectra of the other two mixtures gave similar upper
limits (Table 2), showing that the amount of solid
1017 cm-2.
Comparison with the spectra of the other two mixtures gave similar upper
limits (Table 2), showing that the amount of solid ![]() is <5% of
is <5% of ![]() .
.
While theoretically it is possible that there would be an emission
band in the 2.220-2.227 ![]() m region which would exactly cancel
out an absorption band due to
m region which would exactly cancel
out an absorption band due to ![]() ,
the likelihood of such
a phenomenon seems small. Indeed there are 10 data points in this
interval, and none shows a non-statistical deviation from the smooth
overall spectral behaviour in this region. Higher resolution
spectroscopy could provide a decisive test of this issue.
,
the likelihood of such
a phenomenon seems small. Indeed there are 10 data points in this
interval, and none shows a non-statistical deviation from the smooth
overall spectral behaviour in this region. Higher resolution
spectroscopy could provide a decisive test of this issue.
It is unlikely that the 2.13 ![]() m feature of
m feature of ![]() can be detected
towards W 33A. While in the laboratory sample in Fig. 6
can be detected
towards W 33A. While in the laboratory sample in Fig. 6 ![]() :
:
![]() = 0.7:1, the relative column densities towards W 33A give
= 0.7:1, the relative column densities towards W 33A give
![]() :
:
![]() = 1:0.7 (Gibb et al. 2001). Therefore it is
expected that for W 33A, relative to the
= 1:0.7 (Gibb et al. 2001). Therefore it is
expected that for W 33A, relative to the
![]() 2.27
2.27 ![]() m feature,
the 2.13
m feature,
the 2.13 ![]() m band would be 2 times weaker than in the laboratory sample.
Figure 6 indicates that such a band would be undetectable.
m band would be 2 times weaker than in the laboratory sample.
Figure 6 indicates that such a band would be undetectable.
Finally, Fig. 8 compares the 2 ![]() m water
feature to the W 33A spectrum. The laboratory feature has been
scaled to the column density derived from the mid-IR spectrum
(1.2
m water
feature to the W 33A spectrum. The laboratory feature has been
scaled to the column density derived from the mid-IR spectrum
(1.2 ![]() 1019 cm-2; Gibb et al. 2000; Schutte
et al. 2002). It is clear that, while the observed spectrum
is consistent with the presence of the 2
1019 cm-2; Gibb et al. 2000; Schutte
et al. 2002). It is clear that, while the observed spectrum
is consistent with the presence of the 2 ![]() m feature,
a positive detection of this feature is hampered by the strong telluric
structure between 5200-4800
m feature,
a positive detection of this feature is hampered by the strong telluric
structure between 5200-4800
![]() .
.
The column density of
![]() derived from the 2.27
derived from the 2.27 ![]() m
feature agrees with that derived from the mid-IR absorption
bands. The same kind of agreement was also observed for the 2.7, 4.2
and 15.2
m
feature agrees with that derived from the mid-IR absorption
bands. The same kind of agreement was also observed for the 2.7, 4.2
and 15.2 ![]() m features of
m features of ![]() towards various other sources
(Gerakines et al. 1999; Keane
et al. 2001). This indicates that the mid- and near-IR photons trace
the same line of sight.
towards various other sources
(Gerakines et al. 1999; Keane
et al. 2001). This indicates that the mid- and near-IR photons trace
the same line of sight.
On the other hand, the ![]() upper limit of 5.9
upper limit of 5.9 ![]() 1017 cm-2 (<5% of solid
1017 cm-2 (<5% of solid ![]() )
derived
from the absence of the 2.21
)
derived
from the absence of the 2.21 ![]() m feature is a factor 3 lower than
the previously reported column density N(NH3) = 1.7
m feature is a factor 3 lower than
the previously reported column density N(NH3) = 1.7 ![]() 1018 cm-2 (Gibb et al. 2000, 2001; Gürtler et al. 2002). It agrees with the general upper limit of
1018 cm-2 (Gibb et al. 2000, 2001; Gürtler et al. 2002). It agrees with the general upper limit of ![]() 5%
derived by Dartois & d'Hendecourt (2001) and Dartois et al. (2002) from the
3.47
5%
derived by Dartois & d'Hendecourt (2001) and Dartois et al. (2002) from the
3.47 ![]() m
ammonium hydrate feature. We note that the current determination is more direct
and does not suffer from any baseline ambiguities which could
have influenced this earlier determination (Gibb et al. 2001). We
attribute the discrepancy between the present upper limit and the
column density from Gibb et al. to the large uncertainty in the
baseline definition in the region of the 9
m
ammonium hydrate feature. We note that the current determination is more direct
and does not suffer from any baseline ambiguities which could
have influenced this earlier determination (Gibb et al. 2001). We
attribute the discrepancy between the present upper limit and the
column density from Gibb et al. to the large uncertainty in the
baseline definition in the region of the 9 ![]() m umbrella mode which
falls inside the intense silicate absorption feature (see discussion
Sect. 1). While our result reveals such a
discrepancy only for W 33A, similar problems may apply to all
prior determinations of the
m umbrella mode which
falls inside the intense silicate absorption feature (see discussion
Sect. 1). While our result reveals such a
discrepancy only for W 33A, similar problems may apply to all
prior determinations of the ![]() abundance towards YSO's based on the umbrella mode. We thus conclude
that the abundance of solid
abundance towards YSO's based on the umbrella mode. We thus conclude
that the abundance of solid ![]() may have been considerably
overestimated in general, and that, except for W 33A, no stringent
limits to its abundance are available at this time.
may have been considerably
overestimated in general, and that, except for W 33A, no stringent
limits to its abundance are available at this time.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3102f8.eps}\end{figure}](/articles/aa/full/2003/07/aa3102/Timg80.gif) |
Figure 8:
The optical depth spectrum of W 33A
compared to pure water ice at 50 K. The laboratory spectrum was scaled
to correspond to the |
| Open with DEXTER | |
Further observations of the ![]() 2.21
2.21 ![]() m band are essential to
investigate the role of
m band are essential to
investigate the role of ![]() in interstellar ices.
Another object which is a prime target for observing the 2.21
in interstellar ices.
Another object which is a prime target for observing the 2.21 ![]() m
feature is NGC 7538:IRS9, for which an
m
feature is NGC 7538:IRS9, for which an ![]() abundance
of
abundance
of ![]() 10% has been reported based on the possible detection of the
umbrella mode (Lacy et al. 1998; Gibb et al. 2001; Gürtler et al. 2002).
10% has been reported based on the possible detection of the
umbrella mode (Lacy et al. 1998; Gibb et al. 2001; Gürtler et al. 2002).
In view of the stringent upper limit for ![]() ,
other species
must contain most of the nitrogen in the ices towards W 33A. A good
candidate is the infrared inactive molecule
,
other species
must contain most of the nitrogen in the ices towards W 33A. A good
candidate is the infrared inactive molecule ![]() .
On the other
hand,
.
On the other
hand, ![]() could have initially accreted, but may have been converted
to other species by subsequent chemistry. Such a species could
be the
could have initially accreted, but may have been converted
to other species by subsequent chemistry. Such a species could
be the
![]() ion, whose presence seems to be indicated
by the 6.85
ion, whose presence seems to be indicated
by the 6.85 ![]() m ice absorption band observed towards embedded
YSO's (Grim et al. 1989; Schutte & Khanna 2003). In any case,
the present result gives
essential new insight in the form in which nitrogen is included
in the icy grain mantles near young stellar objects and therefore
gives important constraints to our understanding of the chemical
conditions of star formation.
m ice absorption band observed towards embedded
YSO's (Grim et al. 1989; Schutte & Khanna 2003). In any case,
the present result gives
essential new insight in the form in which nitrogen is included
in the icy grain mantles near young stellar objects and therefore
gives important constraints to our understanding of the chemical
conditions of star formation.
Acknowledgements
We thank Louis d'Hendecourt and Emmanuel Dartois for their scientific advice and stimulating discussions.