A&A 399, 9-17 (2003)
DOI: 10.1051/0004-6361:20021738
Starburst galaxies and the X-ray background
M. Persic1 -
Y. Rephaeli2,3
1 - INAF/Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131
Trieste, Italy
2 -
School of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978,
Israel
3 -
CASS, University of California, San Diego, La Jolla, CA 92093, USA
Received 5 September 2002 / Accepted 14 November 2002
Abstract
Integrated X-ray spectra of an evolving population of
starburst galaxies (SBGs) are determined based on the observed
spectra of local SBGs. In addition to emission from hot gas and
binary systems, our model SBG spectrum includes a nonthermal
component from Compton scattering of relativistic electrons by the
intense ambient far-IR and the (steeply evolving) CMB radiation
fields. We use these integrated spectra to calculate the levels of
contribution of SBGs to the cosmic X-ray background assuming that
their density evolves as (1+z)q up to a maximal redshift of 5.
We find that at energies
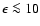 keV this contribution is
at a level of few percent for
keV this contribution is
at a level of few percent for 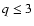 ,
and in the range of
,
and in the range of
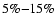 for
for
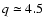 .
The Compton component is predicted
to be the main SBG emission at high energies, and its relative
contribution gets progressively higher for increasing redshift.
.
The Compton component is predicted
to be the main SBG emission at high energies, and its relative
contribution gets progressively higher for increasing redshift.
Key words: X-ray: galaxies - galaxies: spiral - stars:
formation
In starburst galaxies (SBGs) enhanced star formation activity
(lasting typically 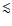 108 yr) drives a chain of coupled
stellar and interstellar phenomena that are manifested
by intense far-infrared (FIR) emission. The SBG spectrum shows
a distinctive large bump of thermal FIR dust emission which
is correlated with optical emission (e.g., Silva et al. 1998),
a result of the fact that
dust emission is reprocessed starlight from a population of
hot OB stars. Such stars are short-lived (106-7 years) and
end up as supernovae. The subsequent radio emission from synchrotron
radiation in supernova remnants (SNRs) is tightly correlated with
the IR emission (e.g., Condon 1992). Interest in SBGs stems also from
the realization that these resemble young galaxies in the earlier
universe. Indeed, a starburst phase was very common then, as a result of
both astrophysical processes (baryonic infall and early star
formation) and dynamical processes (close encounters and mergers
which, in turn, trigger star formation). Consequently, the cosmic
star formation rate (SFR) was substantially higher at epochs
corresponding to
108 yr) drives a chain of coupled
stellar and interstellar phenomena that are manifested
by intense far-infrared (FIR) emission. The SBG spectrum shows
a distinctive large bump of thermal FIR dust emission which
is correlated with optical emission (e.g., Silva et al. 1998),
a result of the fact that
dust emission is reprocessed starlight from a population of
hot OB stars. Such stars are short-lived (106-7 years) and
end up as supernovae. The subsequent radio emission from synchrotron
radiation in supernova remnants (SNRs) is tightly correlated with
the IR emission (e.g., Condon 1992). Interest in SBGs stems also from
the realization that these resemble young galaxies in the earlier
universe. Indeed, a starburst phase was very common then, as a result of
both astrophysical processes (baryonic infall and early star
formation) and dynamical processes (close encounters and mergers
which, in turn, trigger star formation). Consequently, the cosmic
star formation rate (SFR) was substantially higher at epochs
corresponding to 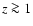 ,
with the SFR having either a peak
at
,
with the SFR having either a peak
at
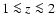 (Madau et al. 1996), or a plateau out to
(Madau et al. 1996), or a plateau out to
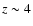 (Thompson et al. 2001).
(Thompson et al. 2001).
A primary manifestation of the starburst activity is X-ray emission. Given
the greatly enhanced SFR, energetic phenomena related to stellar
evolution - OB stars, X-ray binaries, SNRs, galactic winds, and
Compton scattering of ambient FIR and CMB photons off relativistic
electrons that are accelerated by SN shocks - clearly suggest that
SBGs are typically more powerful X-ray emitters than normal galaxies
of comparable stellar mass (e.g., Rephaeli et al. 1991; Schmitt et al.
1997). The mean X-ray spectrum of SBGs reflects the diverse nature of
high energy activity in these galaxies (Persic & Rephaeli 2002;
Rephaeli et al. 1991, 1995).
The link between SBGs and the cosmic X-ray background (CXB) was made
early on (Bookbinder et al. 1980; Stewart et al. 1982; Weedman
1987; Griffiths & Padovani 1990; Rephaeli et al. 1991, 1995;
David et al. 1982; Ricker & Meszaros 1993; Moran et al. 1999).
Most previous estimates of the SBG contribution to the CXB were
essentially based on the SBG emission at 2 keV, with either no source
evolution (Weedman 1987), or with some assumed degree of evolution
(Griffiths & Padovani 1990; Ricker & Meszaros 1993). Clearly, the
use of the 2 keV emission as baseline is unjustified given the wide
spectral range (3-100 keV) over which the CXB seems to have been well
determined (e.g., Gruber et al. 1999). The SBG contribution was also
evaluated based on the emission over a wider spectral range, either
in the context of an assumed spectral model (Ricker & Meszaros 1993),
or from a statistically deduced mean spectrum (determined from the
HEAO-1 A2+A4 datasets: Rephaeli et al. 1991, 1995).
In this paper we compute the contribution of SBGs to the CXB incorporating
recent results in the study of SBGs. In particular, we
use the knowledge of SBG spectral properties gained from direct ASCA, BeppoSAX, and RXTE observations of local galaxies.
This, complemented with an assumed form for the cosmic evolution of the
SBG X-ray luminosity density, enables us to compute the component of
the CXB spectrum which originates in SBGs. We first (Sect. 2)
review the spectral properties of (local) SBGs, and proceed
to discuss the local SBG luminosity density and its cosmic evolution
in Sects. 3 and 4. The predicted CXB spectrum is then calculated
in Sect. 5, followed by a discussion (Sect. 6), and a summary
(Sect. 7). Our calculations are carried out in the context of the
Einstein-de Sitter (
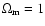 ,
,
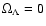 ;
hereafter EdS) and
(currently favoured) flat
;
hereafter EdS) and
(currently favoured) flat 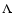 (
(
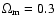 ,
,
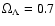 )
cosmological
models, with H0=50 km s-1 Mpc-1.
)
cosmological
models, with H0=50 km s-1 Mpc-1.
Local SBGs have been repeatedly observed in X-rays (see Fabbiano
1989; Rephaeli et al. 1995; Dahlem et al. 1998; Persic & Rephaeli
2002; and references therein). In
most of these (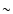 10) galaxies the 0.5-10 keV spectra can be well
fit by a combination of thermal, low-temperature (
10) galaxies the 0.5-10 keV spectra can be well
fit by a combination of thermal, low-temperature (
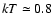 keV)
emission, and photoelectrically self-absorbed emission that can be
represented by an exponentially cutoff power law (CPL) of the form
keV)
emission, and photoelectrically self-absorbed emission that can be
represented by an exponentially cutoff power law (CPL) of the form
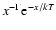 ,
where x is the energy in the source frame,
,
where x is the energy in the source frame,
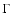 is the photon index and kT is the cutoff energy
is the photon index and kT is the cutoff energy![[*]](/icons/foot_motif.gif) (Persic & Rephaeli 2002; Persic et al. 2002; see Fig. 1).
(Persic & Rephaeli 2002; Persic et al. 2002; see Fig. 1).
The low-temperature and CPL components can be interpreted as due to
emission from galactic winds and X-ray binaries, respectively.
From a detailed discussion of a synthetic X-ray spectrum of SBGs,
based on an evolutionary model of galactic stellar populations and on
the X-ray spectra of the relevant emission processes, Persic &
Rephaeli (2002) have suggested that X-ray binaries contribute most
of the 2-15 keV emission. Both types of X-ray binaries, high- and
low-mass systems, have spectra that can be described as variously
cutoff power laws (White et al. 1983; Christian & Swank 1997). In
general, the population-averaged spectrum emitted by a realistic
mix of X-ray binaries (high- and low-mass systems of various
luminosities in Galactic proportions) can be described as a CPL
with
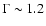 and
and 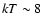 keV (Persic & Rephaeli 2002).
keV (Persic & Rephaeli 2002).
The enhanced SFR activity in SBGs results in a high SN rate and
consequently - among other effects - in a higher rate of electron
acceleration to relativistic energies. This prospect, coupled with
the higher energy density in the enhanced FIR radiation field,
almost certainly implies that Compton scattering of the electrons
by both the FIR and CMB fields yields a substantially higher level
of nonthermal X-ray emission than in normal galaxies (Schaaf et al.
1989; Rephaeli et al. 1991). A quantitative assessment of this
process in NGC 253 was given by Goldshmidt & Rephaeli (1995).
Substantial PL X-ray emission may also be produced in the galactic
nucleus, especially if the SB-driven turbulence of the gas increases
the mass inflow rate onto a central black hole (e.g., Veilleux 2001).
Such spectral components can be described as 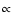
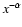 with
the photon index in the range
with
the photon index in the range
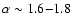 over a broad energy
range (e.g., Goldshmidt & Rephaeli 1995; Rothschild et al. 1983).
over a broad energy
range (e.g., Goldshmidt & Rephaeli 1995; Rothschild et al. 1983).
The spectral similarity shown by the local SBGs (see also Roberts
et al. 2001) provides a reasonably good basis for a first
approximation at modelling the population as a whole. We therefore
assume that a typical starburst spectrum consists of a 0.8
keV thermal component (i.e., a thermal bremsstrahlung spectrum, with the
Gaunt factor numerically calculated as prescribed by Itoh et al.
2000), plus a CPL with photon spectral index
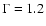 and cutoff
energy kT=7.5 keV. This second component is photoelectrically
absorbed in situ through a HI gas of column density
and cutoff
energy kT=7.5 keV. This second component is photoelectrically
absorbed in situ through a HI gas of column density 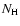 .
The two components are normalized such that the thermal-to-CPL
energy flux ratio in the 2-10 keV band is 0.03.
.
The two components are normalized such that the thermal-to-CPL
energy flux ratio in the 2-10 keV band is 0.03.
In addition to the wind and binary emission, we include also two
emission components originating from Compton scattering of
relativistic electrons by the FIR and CMB radiation fields. While
the full calculation of the respective fluxes requires a detailed,
self-consistent solution of the kinetic equation for the electrons
(taking into account their varius energy loss mechanisms and their
propagation mode in the disk and halo - see, e.g., Rephaeli 1979),
we greatly simplify the treatment by keeping only the most salient
features pertinent to our discussion here. Assuming the typical
value of 0.8 for the radio (spectral energy) index of the radio
synchrotron flux in the disk, and estimating typical energy loss
times of the electrons by synchrotron emission and Compton scattering
off the FIR and CMB radiation fields, we can roughly represent the
latter two Compton components as follows: A primarily inner-disk
FIR-scattered component with a (photon) flux that is 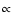 x-1.8, and a (primarily) outer-disk and halo CMB-scattered
component
x-1.8, and a (primarily) outer-disk and halo CMB-scattered
component 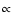 x-2.3 due to electrons from the higher-energy
region of the (electron) spectrum that is steepened by radiative losses.
x-2.3 due to electrons from the higher-energy
region of the (electron) spectrum that is steepened by radiative losses.
The relative contribution of the Compton fluxes is substantially
uncertain since this emission has not yet been unequivocally detected
in SBGs (see, e.g., Goldshmidt & Rephaeli 1995; Rephaeli & Gruber
2002). However, the expectation that Compton scattering of the
enhanced relativistic electron population by the intense ambient FIR
radiation field provides strong motivation for inclusion of this
emission in our modelling of SBG X-ray emission. Our modelling of the
Compton fluxes is based on the radio properties of the nearby SBGs
M 82 and NGC 253, and well known Compton-synchrotron relations (e.g.,
Tucker 1975) between the radio luminosity and deduced mean magnetic
field in the disk (typically, 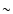 10
10 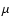 G, but with appreciable
uncertainty) and the predicted X-ray flux from Compton scattering of
the radio producing electrons by the FIR and CMB fields. The relative
strength of these two radiation fields largely determines (under
typical conditions in local SBGs) the normalization between their
respective fluxes. The energy density of the FIR radiation field,
G, but with appreciable
uncertainty) and the predicted X-ray flux from Compton scattering of
the radio producing electrons by the FIR and CMB fields. The relative
strength of these two radiation fields largely determines (under
typical conditions in local SBGs) the normalization between their
respective fluxes. The energy density of the FIR radiation field,
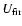 ,
was estimated by Goldshmidt & Rephaeli (1995) in the
context of a quantitative model for the emission from warm dust. We
adopt their result,
,
was estimated by Goldshmidt & Rephaeli (1995) in the
context of a quantitative model for the emission from warm dust. We
adopt their result,
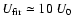 where
where 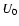 is the energy density in the CMB, as roughly typical in the inner
region of a SBG disk. Doing so, and using the usual Compton-synchrotron
relations, we obtain that in local SBGs we might expect that the FIR
and CMB Compton contributions to the overall 2-10 keV (energy)
flux are roughly at a level of
is the energy density in the CMB, as roughly typical in the inner
region of a SBG disk. Doing so, and using the usual Compton-synchrotron
relations, we obtain that in local SBGs we might expect that the FIR
and CMB Compton contributions to the overall 2-10 keV (energy)
flux are roughly at a level of 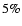 and
and 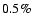 ,
respectively.
We do not yet have unequivocal evidence for nonthermal Compton X-ray
emission in SBGs. Power-law fits to both ASCA and RXTE data on M 82 and NGC 253
were found to be formally acceptable (e.g. Matsumoto & Tsuru 1999;
Rephaeli & Gruber 2002), but a closer assessment of the residuals of such
fits over the wider energy range afforded by RXTE leads only to what are
essentially upper limits to nonthermal contribution. With the higher
spatial resolution of the Chandra satellite it was clearly
established that some of the 2-10 keV emission in M 82 is diffuse,
emanating from a central elliptical region,
,
respectively.
We do not yet have unequivocal evidence for nonthermal Compton X-ray
emission in SBGs. Power-law fits to both ASCA and RXTE data on M 82 and NGC 253
were found to be formally acceptable (e.g. Matsumoto & Tsuru 1999;
Rephaeli & Gruber 2002), but a closer assessment of the residuals of such
fits over the wider energy range afforded by RXTE leads only to what are
essentially upper limits to nonthermal contribution. With the higher
spatial resolution of the Chandra satellite it was clearly
established that some of the 2-10 keV emission in M 82 is diffuse,
emanating from a central elliptical region,
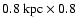 kpc,
that is coplanar and coaligned with the galactic disk (Griffith
et al. 2000). According to these authors the spectral fits to these
measurements make a Compton origin of most of the emission quite likely.
The luminosity of the extended emission region is
kpc,
that is coplanar and coaligned with the galactic disk (Griffith
et al. 2000). According to these authors the spectral fits to these
measurements make a Compton origin of most of the emission quite likely.
The luminosity of the extended emission region is
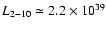 erg s-1 (for an assumed distance D=3.6 Mpc);
this value constitutes
erg s-1 (for an assumed distance D=3.6 Mpc);
this value constitutes 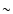
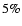 of the total 2-10 keV luminosity
(
of the total 2-10 keV luminosity
(
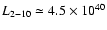 erg s-1) measured by
BeppoSAX (Persic & Rephaeli 2002).
Given that some or most of this diffuse hard component in M 82 is thermal
as suggested by the presence of a substantial 6.7 keV Fe-K emission, the
figure of
erg s-1) measured by
BeppoSAX (Persic & Rephaeli 2002).
Given that some or most of this diffuse hard component in M 82 is thermal
as suggested by the presence of a substantial 6.7 keV Fe-K emission, the
figure of 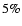 is actually a strong upper limit on the Compton contribution
in M 82
is actually a strong upper limit on the Compton contribution
in M 82![[*]](/icons/foot_motif.gif) .
.
Finally, let f(x) be the spectral profile (in the source frame),
normalized in the band relative to which the surface brightness is
being computed. In accord with our discussion above, the X-ray photon spectral
profile of a SBG is a superposition of components that can be written
as
| f(x) |
= |
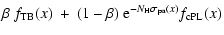 |
|
| |
|
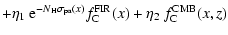 |
(1) |
where
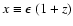 is the energy (in keV) in the source
frame (and z is the redshift;
is the energy (in keV) in the source
frame (and z is the redshift; 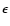 is the energy in the observer's
frame),
is the energy in the observer's
frame),
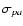 is the cross section for photoelectric
absorption per unit hydrogen column density
is the cross section for photoelectric
absorption per unit hydrogen column density 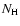 within the source
(in the calculations we have adopted the analytic expression for
within the source
(in the calculations we have adopted the analytic expression for
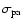 given by Morrison & McCammon 1983;
given by Morrison & McCammon 1983; 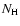 is taken
at a nominal level of 1022 cm-2), and
is taken
at a nominal level of 1022 cm-2), and 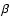 ,
,
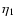 ,
and
,
and 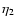 are constants of normalization that are estimated as
described above. Note that the CMB scattered flux is z-dependent,
an important fact that will be elaborated upon in Sect. 5.
are constants of normalization that are estimated as
described above. Note that the CMB scattered flux is z-dependent,
an important fact that will be elaborated upon in Sect. 5.
In order to calculate the contribution of SBGs to the CXB we
need to model the population at all z, beginning - of course -
with the local source density which can be deduced from the FIR
luminosity function. This has been determined from the 60 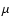 m
flux-limited IRAS samples (Saunders et al. 1990),
m
flux-limited IRAS samples (Saunders et al. 1990),
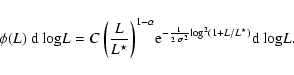 |
(2a) |
Sources in the IRAS Point Source Catalog with fluxes measured in all
four IRAS bands and with individual, identifiable galaxy types inhabit
distinct and well-defined areas in color-color diagrams (Rowan-Robinson
& Crawford 1989). Each one of these distinct components of the IRAS
point-source population largely produces most of the emission at
specific wavelengths, and is characterized by a specific set of
parameters for Eq. (2a). For the warm-source component that peaks
at 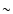 60
60 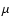 m which is thought to be attributable to a dusty SBG
population, the parameters in Eq. (2a) take the values:
m which is thought to be attributable to a dusty SBG
population, the parameters in Eq. (2a) take the values:
![\begin{figure}
\par\mbox{\includegraphics[width=4.5cm]{papAA3067_fig1a.eps}\hspace*{3mm}
\includegraphics[width=4.5cm]{papAA3067_fig1b.eps}}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg50.gif) |
Figure 1:
The best-fit thermal + CPL models for M 82 (left) and NGC253 (right),
based on BeppoSAX data (see Persic & Rephaeli 2002). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm]{papAA3067_fig2.eps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg51.gif) |
Figure 2:
The template photon SBG spectrum assumed in the present calculations.
It consists of:
(i) an unabsorbed 0.8 keV thermal bremsstrahlung component,
(ii) an exponentially cutoff PL with photon index
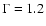 and
cutoff energy kT=7.5 keV, absorbed through
and
cutoff energy kT=7.5 keV, absorbed through
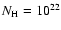 cm-2,
and (iii) a similarly absorbed PL with photon index cm-2,
and (iii) a similarly absorbed PL with photon index
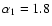 .
(The much fainter unabsorbed PL with photon index .
(The much fainter unabsorbed PL with photon index
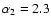 is not shown here.) The flux normalizations are as
specified in the text.
is not shown here.) The flux normalizations are as
specified in the text. |
| Open with DEXTER |
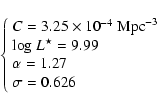 |
(2b) |
for luminosities in the range
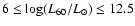 .
Pearson & Rowan-Robinson (1996) modeled the (sub-mm, IR,
optical) number-flux relation for extragalactic sources by including
a SBG population described by a local luminosity function as in Eq. (2).
The local 60
.
Pearson & Rowan-Robinson (1996) modeled the (sub-mm, IR,
optical) number-flux relation for extragalactic sources by including
a SBG population described by a local luminosity function as in Eq. (2).
The local 60 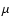 m luminosity density implied by Eq. (2) is:
m luminosity density implied by Eq. (2) is:
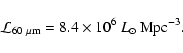 |
(3) |
For a sample of local SBGs observed with ASCA, the ratio of
2-10 keV flux to 60 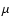 m flux
m flux![[*]](/icons/foot_motif.gif) is
is
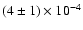 .
Assuming this to be the mean value for
the whole SBG population, we have for the 2-10 keV luminosity density
.
Assuming this to be the mean value for
the whole SBG population, we have for the 2-10 keV luminosity density
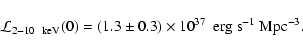 |
(4) |
Note that in our previous estimates of the SBG contribution to the CXB
(Rephaeli et al. 1991, 1995) we did consider only the high end (
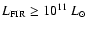 )
of the FIR luminosity function as
representative of the SBG population. Adopting the current more inclusive
luminosity function (Pearson & Rowan-Robinson 1996) allows a more realistic
estimate that accounts also for the emission from fainter SBGs.
By integrating the FIR luminosity function over the above (logarithmic)
range ([6, 12.5]), we compute a density of
)
of the FIR luminosity function as
representative of the SBG population. Adopting the current more inclusive
luminosity function (Pearson & Rowan-Robinson 1996) allows a more realistic
estimate that accounts also for the emission from fainter SBGs.
By integrating the FIR luminosity function over the above (logarithmic)
range ([6, 12.5]), we compute a density of 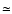
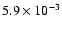 Mpc-3 for galaxies that are identified here as members of the
broader SBG population. (Obviously, this value of the density is much
higher than that of the more luminous galaxies, but this difference is
largely compensated for by the much lower mean FIR luminosity,
Mpc-3 for galaxies that are identified here as members of the
broader SBG population. (Obviously, this value of the density is much
higher than that of the more luminous galaxies, but this difference is
largely compensated for by the much lower mean FIR luminosity,
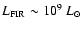 ,
of the SBGs that we include in this work.)
,
of the SBGs that we include in this work.)
Galactic evolution may generally be reflected in density and luminosity
variations over cosmic time due to the continued formation, interaction
and merging, and through intrinsic changes of the luminosity due to
dynamical and thermal evolution of stars and interstellar gas. The
evolution of SBGs is likely to be particularly pronounced as the SB
phase is thought to be triggered by galactic interactions and is
relatively short lived. These imply that SBGs were more abundant at
earlier times than would be expected based solely on pure density
evolution of sources in an expanding background (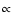 (1+z)3).
(1+z)3).
Observationally, the evolution of SBGs is inferred from radio, IR, and
optical measurements. At radio frequencies, two distinct populations are
identified at 1.4 GHz (Benn et al. 1993): radio-loud, and radio-faint,
the first consisting of giant ellipticals and QSOs, and the second
mainly of spirals (SBGs and radio-quiet QSOs). This latter faint
population is responsible for the low-flux upturn in the differential
counts, and is indistinguishable from the SBG-dominated 60  m
population (e.g., Danese et al. 1987; Franceschini et al. 1988),
which can be fit by a model using pure luminosity evolution of the
form
L(z)=L(0) (1+z)q with q=3.1 (Rowan-Robinson et al. 1993).
At IR wavelengths, Lonsdale et al. (1990) concluded that the dominant
population in the faint 60
m
population (e.g., Danese et al. 1987; Franceschini et al. 1988),
which can be fit by a model using pure luminosity evolution of the
form
L(z)=L(0) (1+z)q with q=3.1 (Rowan-Robinson et al. 1993).
At IR wavelengths, Lonsdale et al. (1990) concluded that the dominant
population in the faint 60  m counts from the IRAS Faint Source
Survey consists of strongly evolving SBGs
m counts from the IRAS Faint Source
Survey consists of strongly evolving SBGs![[*]](/icons/foot_motif.gif) .
Thus, it appears that from 60
.
Thus, it appears that from 60 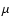 m to radio wavelengths what is mainly
sampled is starburst activity.
SBG evolution, either of the pure luminosity type (Lilly et al. 1995;
Ellis et al. 1996; Fried et al. 2001), or of the pure density type (Lin
et al. 1999), is deduced also from optical surveys.
m to radio wavelengths what is mainly
sampled is starburst activity.
SBG evolution, either of the pure luminosity type (Lilly et al. 1995;
Ellis et al. 1996; Fried et al. 2001), or of the pure density type (Lin
et al. 1999), is deduced also from optical surveys.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{papAA3067_fig3a.ps}
\par\vspace*{3.5mm}
\includegraphics[width=7.6cm,clip]{papAA3067_fig3b.ps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg64.gif) |
Figure 3:
The spectrum of the integrated background light arising from SBGs
evolving out to
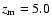 ,
for different values of the evolution
parameter. For each of the three values q=0, 3, 4.5, indicated by
solid, long-dashed, and dotted curves, the lighter curve represents
the unabsorbed bremsstrahlung emission plus absorbed CPL,
and the heavy curve
shows the sum of these two components plus Comptonized
emission (which consists of an absorbed ,
for different values of the evolution
parameter. For each of the three values q=0, 3, 4.5, indicated by
solid, long-dashed, and dotted curves, the lighter curve represents
the unabsorbed bremsstrahlung emission plus absorbed CPL,
and the heavy curve
shows the sum of these two components plus Comptonized
emission (which consists of an absorbed
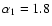 PL and unabsorbed
PL and unabsorbed
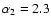 PL).
The local SBG X-ray luminosity density is given in Eq. (4), its cosmic
evolution is given in Eq. (5), and the template SBG spectrum is shown
in Fig. 2. The solid black curve on top represents the observed CXB
(see Eq. (12)). PL).
The local SBG X-ray luminosity density is given in Eq. (4), its cosmic
evolution is given in Eq. (5), and the template SBG spectrum is shown
in Fig. 2. The solid black curve on top represents the observed CXB
(see Eq. (12)). |
| Open with DEXTER |
The luminosity density of SBGs evolves mainly as result of their
steeply varying density, and - to a smaller extent, as discussed
below - the changes in the relative strength of the spectral
components. Density evolution is represented by the factor (1+z)q,
with 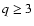 after the process of galaxy formation began in ernest
at some early redshift,
after the process of galaxy formation began in ernest
at some early redshift, 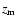 .
Since we do not know when exactly
galaxies began forming, the modelling the starburst phase of early galaxies
necessitates viewing both q and
.
Since we do not know when exactly
galaxies began forming, the modelling the starburst phase of early galaxies
necessitates viewing both q and 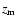 as essentially free parameters
as essentially free parameters![[*]](/icons/foot_motif.gif) .
We factor out the dominant redshift dependence of the luminosity
density:
.
We factor out the dominant redshift dependence of the luminosity
density:
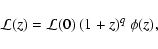 |
(5) |
with all the spectral dependence on z collected in the function 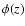 ;
this function will be specified below. The evolution of SBGs
is then largely gauged by the index q
;
this function will be specified below. The evolution of SBGs
is then largely gauged by the index q ![[*]](/icons/foot_motif.gif) ;
an estimate for
;
an estimate for
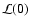 is given in Eq. (4).
is given in Eq. (4).
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{papAA3067_fig4a.ps}
\par\vspace*{2mm}
\includegraphics[width=7.4cm,clip]{papAA3067_fig4b.ps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg81.gif) |
Figure 4:
The fraction of the CXB arising from SBGs as a function of energy, for
various strengths of cosmological evolution. Models, parameter values,
and symbols are as in Fig. 3. |
| Open with DEXTER |
The surface brightness due to a population of unresolved sources is
given by (e.g., Boldt 1987)
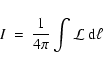 |
(6) |
where
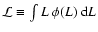 is the comoving
volume emissivity, and d
is the comoving
volume emissivity, and d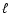 is the line element. Since d
is the line element. Since d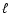 is
related to the look-back time
is
related to the look-back time 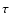 and the redshift z by d
and the redshift z by d
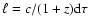 ,
we obtain
,
we obtain
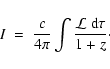 |
(7) |
The ensuing spectral density is then given by
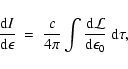 |
(8) |
where 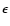 is the energy measured in the observer frame and
is the energy measured in the observer frame and
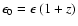 the energy measured in source rest frame.
the energy measured in source rest frame.
The look-back time 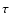 is related to the cosmic time t by
is related to the cosmic time t by
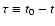 (with t0 the present age of the universe), and t is related
to the redshift z by
(with t0 the present age of the universe), and t is related
to the redshift z by
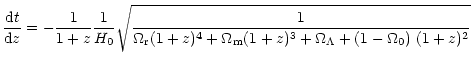 |
(9) |
|
where
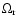 ,
,
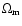 ,
,
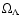 ,
and
,
and 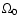 are the current density
parameters for radiation, matter,
are the current density
parameters for radiation, matter, 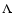 ,
and their sum, respectively.
In the matter dominated era,
,
and their sum, respectively.
In the matter dominated era,
![$\displaystyle { {\rm d} \tau \over {\rm d} z} = {1 \over H_0}
\times
\left\{
\b...
...z)^3 + 0.7} ~\bigr]^{-1}
& \mbox{${\rm flat}~\Lambda$ }
\end{array}\right.\cdot$](/articles/aa/full/2003/07/aa3067/img98.gif) |
|
|
(10) |
The SBG photon spectrum we have used in our calculations is given in
Eq. (1). Whereas the first two spectral components in Eq. (1) have been
adequately discussed in many previous works, the Compton CMB component
needs to be further elaborated upon here because of its enhanced role
in early SBGs. Most of the X-ray emission from a SBG is triggered by
stellar activity and involves the internal properties of the galaxy
during a starburst phase of its evolution. As such, the emission is largely
independent of redshift, if the main characteristics of this phase have
not changed over cosmic time. The Compton component of the emission has
evolved significantly, however, due to the much higher energy density
of the CMB at z>1. As we have noted in Sect. 2, in a local SBG
the FIR energy density is typically much higher than that of the CMB,
by as much as a factor of 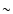 10 (Goldshmidt & Rephaeli 1995),
so the Compton CMB component begins to dominate already at
10 (Goldshmidt & Rephaeli 1995),
so the Compton CMB component begins to dominate already at
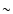 1. This, and the fast evolving SBG density, result in a very
steep combined spectral and density evolution of the emission from SBGs at high X-ray energies where Compton scattering is the main
emission component in SBGs. Due to the steep (1+z)4 dependence
of the CMB energy density,
1. This, and the fast evolving SBG density, result in a very
steep combined spectral and density evolution of the emission from SBGs at high X-ray energies where Compton scattering is the main
emission component in SBGs. Due to the steep (1+z)4 dependence
of the CMB energy density,
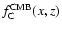 has an explicit
dependence on z in addition to the implicit dependence through x.
has an explicit
dependence on z in addition to the implicit dependence through x.
With
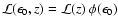 ,
where
,
where
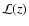 is given in Eq. (5) and
is given in Eq. (5) and
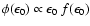 is the SBG energy spectrum (source frame) normalized by the 2-10 keV
flux, we have for the total intensity at an observed energy
is the SBG energy spectrum (source frame) normalized by the 2-10 keV
flux, we have for the total intensity at an observed energy 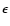 due
to a population of SBGs undergoing cosmic evolution according to
Eq. (5) out to a maximal redshift
due
to a population of SBGs undergoing cosmic evolution according to
Eq. (5) out to a maximal redshift 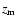
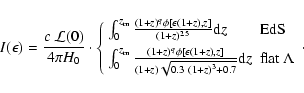 |
(11) |
The integrated intensity from SBGs was calculated at (the source frame)
energies
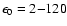 keV, for values of the evolutionary index q in
the range
keV, for values of the evolutionary index q in
the range
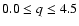 ,
and adopting
,
and adopting
 .
In Fig. 3 we
show the integrated background light arising from an evolving population
of SBGs as a function of the (observed) energy,
.
In Fig. 3 we
show the integrated background light arising from an evolving population
of SBGs as a function of the (observed) energy, 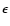 .
To determine the
fractional contribution of SBGs to the CXB intensity in the 2-20 keV
band, for the latter we use the analytic fit:
.
To determine the
fractional contribution of SBGs to the CXB intensity in the 2-20 keV
band, for the latter we use the analytic fit:
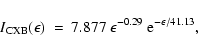 |
(12) |
with
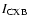 measured in
measured in
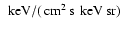 and
and 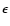 measured
in keV, given by Gruber et al. (1999) in the 3-60 keV band (based on
HEAO-1/A2+A4 all-sky data: dominated by A2 proportional-counter data for
measured
in keV, given by Gruber et al. (1999) in the 3-60 keV band (based on
HEAO-1/A2+A4 all-sky data: dominated by A2 proportional-counter data for
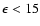 keV, and by A4 scintillator-experiment data for
keV, and by A4 scintillator-experiment data for
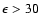 keV) and
shown by Gendreau et al. (1995) and Chen et al. (1997) to hold down to
1 keV (from ASCA data, based on a composite sample of the sky
corresponding to less than a square degree and therefore limited by by
sky surface brightness fluctuations)
keV) and
shown by Gendreau et al. (1995) and Chen et al. (1997) to hold down to
1 keV (from ASCA data, based on a composite sample of the sky
corresponding to less than a square degree and therefore limited by by
sky surface brightness fluctuations)![[*]](/icons/foot_motif.gif) .
In Fig. 4 we plot the SBG fractional contribution to the CXB as a function
of (observed) energy.
.
In Fig. 4 we plot the SBG fractional contribution to the CXB as a function
of (observed) energy.
Looking at Fig. 3 we see that for energies
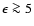 keV the shape of
the SBG background light gets progressively steeper than that of the CXB,
for the range of values of q considered here. (The steep rise of the
Comptonized CMB contribution moderates the decline somewhat.) From Fig. 4
it is seen that for no cosmic evolution (q=0) the contribution of SBGs
to the CXB is <
keV the shape of
the SBG background light gets progressively steeper than that of the CXB,
for the range of values of q considered here. (The steep rise of the
Comptonized CMB contribution moderates the decline somewhat.) From Fig. 4
it is seen that for no cosmic evolution (q=0) the contribution of SBGs
to the CXB is <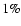 at all energies; while for an evolution as steep as
the maximum permitted by IR data (
at all energies; while for an evolution as steep as
the maximum permitted by IR data (
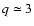 )
the contribution is
)
the contribution is 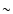
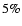 at 5 keV,
at 5 keV, 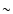
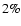 at 10 keV,
at 10 keV, 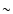
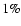 at 15 keV, and vanishing
at higher energies. This is so for the EdS model; the corresponding results
are even lower for the flat
at 15 keV, and vanishing
at higher energies. This is so for the EdS model; the corresponding results
are even lower for the flat 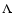 model.
model.
Also of interest is to determine the z dependence of the superposed SBG
emission (at a given energy) in order to assess when the contribution is
maximal. This can be readily found from the integrand of the z-integrated
spectral intensity in Eq. (10). Representing the main part of the spectral
energy flux of a SBG as
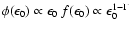 ,
with
,
with
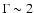 in the 1-200 keV band (see Fig. 2), we see that in the EdS
model the integrand in Eq. (10) is
in the 1-200 keV band (see Fig. 2), we see that in the EdS
model the integrand in Eq. (10) is 
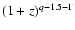 .
Thus, in
evolving models the relative contribution of SBGs increases with z if q
> 3.5, and decreases if q < 3.5. While the critical value of q for which
this transition occurs is different in the flat-
.
Thus, in
evolving models the relative contribution of SBGs increases with z if q
> 3.5, and decreases if q < 3.5. While the critical value of q for which
this transition occurs is different in the flat-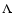 model, the behavior
is qualitatively similar. Note that, as emphasized already, the contribution
of the Compton component of the flux grows much more steeply due to the fact
that the CMB energy density is
model, the behavior
is qualitatively similar. Note that, as emphasized already, the contribution
of the Compton component of the flux grows much more steeply due to the fact
that the CMB energy density is 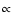 (1+z)4.
(1+z)4.
The starting point in our treatment and previous similar works
is the identification of SBGs based on their spectral properties
at 60 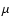 m, particularly the use of the same estimate for the
local 60
m, particularly the use of the same estimate for the
local 60 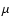 m luminosity density,
m luminosity density,
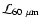 .
However, most previous studies were limited to the consideration
of only the low-energy (
.
However, most previous studies were limited to the consideration
of only the low-energy (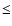 2 keV) contribution of SBGs to the CXB.
Weedman (1987), Griffiths & Padovani (1990), and Ricker & Meszaros
(1993), having based their estimates on Einstein data,
evaluated the SBG contribution at 2 keV. More recently, Moran et al. (1999) estimated the SBG contribution to the 5 keV CXB from ASCA data, based on the assumption that the 5 GHz radio emission
from galaxies lacking a radio-loud AGN can serve as a gauge of
star-formation activity, and that the value measured in NGC 3256
for the 5 keV to 5 GHz flux ratio is universal. They used the 5 GHz
number-count-flux relation, log N-log
2 keV) contribution of SBGs to the CXB.
Weedman (1987), Griffiths & Padovani (1990), and Ricker & Meszaros
(1993), having based their estimates on Einstein data,
evaluated the SBG contribution at 2 keV. More recently, Moran et al. (1999) estimated the SBG contribution to the 5 keV CXB from ASCA data, based on the assumption that the 5 GHz radio emission
from galaxies lacking a radio-loud AGN can serve as a gauge of
star-formation activity, and that the value measured in NGC 3256
for the 5 keV to 5 GHz flux ratio is universal. They used the 5 GHz
number-count-flux relation, log N-log
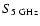 ,
in the
sub-mJy regime, and estimated that SBGs contribute
,
in the
sub-mJy regime, and estimated that SBGs contribute 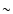
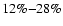 of the 5 keV CXB.
A less limited assessment of the SBG contribution was implemented
(Rephaeli et al. 1991, 1995) by considering the SBG emission in the
2-30 keV band. However, due to lack of observational data, our
previous works were based on a very preliminary statistical analysis
of stacked (low-exposure HEAO-1 A2+A4) data. Here, on the other
hand, we have estimated the 2-10 keV luminosity density using the
detailed 60
of the 5 keV CXB.
A less limited assessment of the SBG contribution was implemented
(Rephaeli et al. 1991, 1995) by considering the SBG emission in the
2-30 keV band. However, due to lack of observational data, our
previous works were based on a very preliminary statistical analysis
of stacked (low-exposure HEAO-1 A2+A4) data. Here, on the other
hand, we have estimated the 2-10 keV luminosity density using the
detailed 60 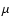 m and 2-10 keV luminosities measured for essentially
the same sample of local SBGs whose X-ray spectra have been adequately
measured (though not yet at the desired level of precision).
m and 2-10 keV luminosities measured for essentially
the same sample of local SBGs whose X-ray spectra have been adequately
measured (though not yet at the desired level of precision).
Inclusion of nonthermal emission due to Compton scattering of
relativistic electrons by the FIR and CMB fields is an important
new ingredient in the modeling
of the high energy emission in an evolving population of
SBGs. Although the level of this emission is still unknown, our
explicit accounting for this emission and its expected rapid rise with
redshift (which makes its relative contribution very
significant at z>1) provide further motivation for a more detailed
description than given here. (The occurrence of low-luminosity AGNs in
the nuclei of SBGs is a controversial issue (e.g., Veilleux 2001), so
we chose not to include such a component in the current treatment.)
Our main result that the evolving population of SBGs contributes
appreciably to the CXB in the 2-10 keV band is quite consistent with
our previous estimates (Rephaeli et al. 1991, 1995), and a similar
result by Griffiths & Padovani (1990). It was argued in the latter
paper that since the spectrum of X-ray binaries is quite hard and
comparable in shape to that of the residual CXB in the 2-30 keV range,
evolving SBGs in the redshift range
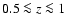 could
make an important contribution to the 2-10 keV CXB. In the use of a
quantitative spectral form and evolutionary function, our treatment
is similar in spirit to that of Ricker & Meszaros (1993, hereafter
RM93). The main improvement with respect to the work of RM93 is the
use of spectral results from individual SBGs observed with ASCA
and BeppoSAX and the inclusion of the two Compton components,
in contrast to their use of essentially an assumed theoretical model.
(We have included also the observed warm (
could
make an important contribution to the 2-10 keV CXB. In the use of a
quantitative spectral form and evolutionary function, our treatment
is similar in spirit to that of Ricker & Meszaros (1993, hereafter
RM93). The main improvement with respect to the work of RM93 is the
use of spectral results from individual SBGs observed with ASCA
and BeppoSAX and the inclusion of the two Compton components,
in contrast to their use of essentially an assumed theoretical model.
(We have included also the observed warm (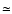 0.8 keV) component,
but its contribution to the emission at
0.8 keV) component,
but its contribution to the emission at
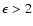 keV is relatively
minor.)
keV is relatively
minor.)
In order to check the stability of our results vs. the characteristics of
the FIR-selected SBG population, we have repeated the calculation using
the SBG population parameters of Franceschini et al. (2001), who fitted
the 12 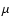 m number counts invoking the presence of a starbursting
population whose volume emissivity increases steeply out to z=0.8, and
remains constant at higher z (in a flat
m number counts invoking the presence of a starbursting
population whose volume emissivity increases steeply out to z=0.8, and
remains constant at higher z (in a flat 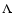 (
(
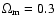 ,
,
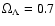 )
cosmological model). The contribution of Franceschini et al.'s SBG
population
)
cosmological model). The contribution of Franceschini et al.'s SBG
population![[*]](/icons/foot_motif.gif) turns out to be only marginally higher than that computed for the SBG
population of Pearson & Rowan-Robinson (1996) used in our main calculation
and described by Eqs. (2)-(5) (with q=3). On the whole, then, the results
of this variant calculation are qualitatively consistent with our main
results (see Fig. 5, where the "wind+binaries'' spectral model is used).
turns out to be only marginally higher than that computed for the SBG
population of Pearson & Rowan-Robinson (1996) used in our main calculation
and described by Eqs. (2)-(5) (with q=3). On the whole, then, the results
of this variant calculation are qualitatively consistent with our main
results (see Fig. 5, where the "wind+binaries'' spectral model is used).
Recent results from the Chandra deep surveys provide direct
estimates of the SBG contribution to the CXB. Using the 1 Ms Chandra
Deep Field North (Brandt et al. 2001a) and 15  m ISOCAM Hubble
Deep Field North (Aussel et al. 1999) surveys, Alexander et al. (2002)
found a tight correlation between the population of strongly evolving SBGs
at
m ISOCAM Hubble
Deep Field North (Aussel et al. 1999) surveys, Alexander et al. (2002)
found a tight correlation between the population of strongly evolving SBGs
at 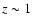 discovered in faint 15
discovered in faint 15 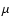 m ISOCAM surveys (e.g., Aussel et al. 1999; Elbaz et al. 1999, 2002) - whose space density is an order of
magnitude higher than that of local SBGs - and the apparently normal galaxies
detected at faint fluxes in X-ray surveys (Giacconi et al. 2001; Hornschemeier
et al. 2001; Brandt et al. 2001b). The characteristics (
m ISOCAM surveys (e.g., Aussel et al. 1999; Elbaz et al. 1999, 2002) - whose space density is an order of
magnitude higher than that of local SBGs - and the apparently normal galaxies
detected at faint fluxes in X-ray surveys (Giacconi et al. 2001; Hornschemeier
et al. 2001; Brandt et al. 2001b). The characteristics (
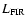 ,
Lx,
2-10 keV spectral slope) of the population of the X-ray detected galaxies,
whose redshifts are in the range
,
Lx,
2-10 keV spectral slope) of the population of the X-ray detected galaxies,
whose redshifts are in the range
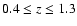 (based mainly on
Keck data; see Alexander et al. 2002 and references therein), are consistent
with those expected for SBGs resembling local objects such as M 82 and
NGC 3256. In particular, their stacked average 2-10 keV spectral slope,
(based mainly on
Keck data; see Alexander et al. 2002 and references therein), are consistent
with those expected for SBGs resembling local objects such as M 82 and
NGC 3256. In particular, their stacked average 2-10 keV spectral slope,
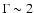 ,
is steep enough to suggest a low fraction of obscured AGN activity within
the population. The contribution of this population to the 0.5-8 keV CXB,
estimated to be
,
is steep enough to suggest a low fraction of obscured AGN activity within
the population. The contribution of this population to the 0.5-8 keV CXB,
estimated to be 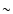
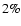 (Alexander et al. 2002), marginally agrees (on
the low side) with our result for q=3 (see Fig. 4). A contribution to the CXB will also come from the 1 Ms Chandra Deep Field North sources
identified as Lyman-break galaxies at
(Alexander et al. 2002), marginally agrees (on
the low side) with our result for q=3 (see Fig. 4). A contribution to the CXB will also come from the 1 Ms Chandra Deep Field North sources
identified as Lyman-break galaxies at
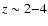 :
these star-forming
sources have rest-frame 2-8 keV luminosities and X-ray/B-band luminosity
ratios that are comparable to
those of local SBGs (Brandt et al. 2001c). Based on the above, there is
no evidence for a substantial change in the
:
these star-forming
sources have rest-frame 2-8 keV luminosities and X-ray/B-band luminosity
ratios that are comparable to
those of local SBGs (Brandt et al. 2001c). Based on the above, there is
no evidence for a substantial change in the 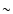 2-10 keV luminosity
and spectral slope of these X-ray-selected, star-forming galaxies. On the
other hand, their IR (15
2-10 keV luminosity
and spectral slope of these X-ray-selected, star-forming galaxies. On the
other hand, their IR (15 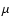 m ISOCAM) counterparts do show a strong
density evolution with redshift (e.g., Aussel et al. 1999; Elbaz et al.
1999, 2002). All this clearly supports our adopted scheme of cosmic
evolution, which is essentially of the density type (see Sect. 4).
m ISOCAM) counterparts do show a strong
density evolution with redshift (e.g., Aussel et al. 1999; Elbaz et al.
1999, 2002). All this clearly supports our adopted scheme of cosmic
evolution, which is essentially of the density type (see Sect. 4).
Finally, it is commonly thought that AGNs are the prime sources of the CXB
(e.g.: Comastri et al. 1995; Setti & Woltjer 1989; Boldt & Leiter 1981; Leiter & Boldt 1982), and that additional contributions from other sources
are typically estimated to be 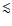
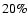 in the 2-10 keV range (Giacconi
et al. 2001; Tozzi et al. 2001; Mushotzky et al. 2000). Based on our results,
SBGs may possibly be the second most important contributors to the CXB.
(Clusters of galaxies also contribute a few percent: e.g., Piccinotti et al.
1982.) The importance of determining the level of the SBG contribution to the
2-10 keV CXB lies not only in the implications for the evolution of SBGs
themselves, but also in the ramifications for galaxy evolution in general,
and as an additional input on the evolution of the AGN phenomenon in
particular (e.g.: Fabian et al. 1998; Gilli et al. 1999).
in the 2-10 keV range (Giacconi
et al. 2001; Tozzi et al. 2001; Mushotzky et al. 2000). Based on our results,
SBGs may possibly be the second most important contributors to the CXB.
(Clusters of galaxies also contribute a few percent: e.g., Piccinotti et al.
1982.) The importance of determining the level of the SBG contribution to the
2-10 keV CXB lies not only in the implications for the evolution of SBGs
themselves, but also in the ramifications for galaxy evolution in general,
and as an additional input on the evolution of the AGN phenomenon in
particular (e.g.: Fabian et al. 1998; Gilli et al. 1999).
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{papAA3067_fig5a.ps}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{papAA3067_fig5b.ps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg143.gif) |
Figure 5:
The spectrum of the integrated background light (left), and the
corresponding contribution to the CXB (right), arising from the
SBG population of Franceschini et al. (2001), assuming a "starburst
only'' model for the spectrum.
See the text for more details. |
| Open with DEXTER |
Acknowledgements
We are glad to thank Elihu Boldt for enlightening exchanges on
the CXB normalization. We also thank the n anonymous referee for useful
suggestions.
M.P. acknowledges financial support from the Italian Space Agency
(ASI) through grant No. ASI RS 99 I/R/098/00, as well as the warm
and stimulating environment of the Center for Astrophysics and Space
Sciences (CASS) of the University of California at San Diego (UCSD),
where part of this work was carried out.
Y.R. acknowledges NASA for supporting his work at UCSD.
This research has made use of the NASA/IPAC Extragalactic Database
(NED) which is operated by the Jet Propulsion Laboratory, California
Institute of Technology, under contract with NASA.
- Alexander, D. M., Aussel, H., Bauer, F. E., et al. 2002, ApJ, 568, L85
In the text
NASA ADS
- Aussel, H., Cesarsky, C. J., Ebaz, D., & Starck, J. L. 1999, A&A, 342, 313
In the text
NASA ADS
- Benn, C. R., Rowan-Robinson, M., McMahon, R. G., Broadhurst, T. J., &
Lawrence, A. 1993, MNRAS, 263, 98
In the text
NASA ADS
- Boldt, E. 1987, Phys. Rep., 146, 215
In the text
- Boldt, E., & Leiter, D. 1981, Nature, 290, 483
In the text
NASA ADS
- Bookbinder, J., Cowie, L. L., Krolik, J. H., & Rees, M. 1980, ApJ, 237, 647
In the text
NASA ADS
- Brandt, W. N., Alexander, D. M., Hornschemeier, A. E., et al. 2001a, AJ, 122, 2810
In the text
NASA ADS
- Brandt, W. N., Hornschemeier, A. E., Alexander, D. M., et al. 2001b, AJ, 122, 1
NASA ADS
- Brandt, W. N., Hornschemeier, A. E., Schneider, D. P., et al. 2001c, ApJ, 558, L5
NASA ADS
- Cappi, M., Persic, M., Bassani, L., et al. 1999, A&A,
350, 777
NASA ADS
- Chen, L.-W., Fabian, A. C., & Gendreau, K. C. 1997, MNRAS, 285, 449
In the text
NASA ADS
- Christian, D. J, & Swank, J. H. 1997, ApJS, 109, 177
In the text
NASA ADS
- Comastri, A., Setti, G., Zamorani, G., & Hasinger, G. 1995, A&A, 296, 1
In the text
NASA ADS
- Condon, J. J. 1992, ARA&A, 30, 575
In the text
NASA ADS
- Dahlem, M., Weaver, K. A., & Heckman, T. M. 1998, ApJS, 118, 401
In the text
NASA ADS
- Danese, L., De Zotti, G., Franceschini, A., & Toffolatti, L. 1987, ApJ,
318, L15
In the text
NASA ADS
- David, L. P., Jones, C., & Forman, W. 1992, ApJ, 338, 82
- Della Ceca, R., Griffiths, R. E., Heckman, T. M., Lehnert, M. D., &
Weaver, K. A. 1999, ApJ, 514, 772
NASA ADS
- Della Ceca, R., Griffiths, R. E., Heckman, T. M., & MacKenty, J. W.
1996, ApJ, 469, 662
NASA ADS
- Elbaz, D., Cesarsky, C. J., Chanial, P., et al. 2002, A&A, 384, 848
In the text
NASA ADS
- Elbaz, D., Cesarsky, C. J., Fadda, D., et al. 1999, A&A, 351, L37
In the text
NASA ADS
- Ellis, R. S., Colless, M., Broadhurst, T., Heyl, J., & Glazebrook, K.
1996, MNRAS, 280, 235
In the text
NASA ADS
- Fabbiano, G. 1989, ARA&A, 27, 87
In the text
NASA ADS
- Fabian, A. C., Barcons, X., Almaini, O., & Iwasawa, K. 1998, MNRAS, 297, L11
In the text
NASA ADS
- Franceschini, A., Aussel, H., Cesarsky, C. J., Elbaz, D., & Fadda,
D. 2001, A&A, 378, 1
In the text
NASA ADS
- Franceschini, A., Danese, L., De Zotti, G., & Xu, C. 1988, MNRAS, 233,
175
In the text
NASA ADS
- Franceschini, A., Braito, V., Persic, M., et al. 2002, MNRAS, submitted
- Fried, J. W., von Kuhlmann, B., Meisenheimer, K., et al. 2001, A&A, 367, 788
In the text
NASA ADS
- Gendreau, K. C., Mushotzky, R., Fabian, A.C., et al. 1995, PASJ, 47, L5
In the text
NASA ADS
- Giacconi, R., Rosati, P., Tozzi, P., et al. 2001, ApJ, 551, 624
In the text
NASA ADS
- Gilli, R., Risaliti, G., & Salvati, M. 1999, A&A, 347, 424
In the text
NASA ADS
- Goldshmidt, O., & Rephaeli, Y. 1995, ApJ, 444, 113
In the text
NASA ADS
- Griffiths, R., & Padovani, P. 1990, ApJ, 360, 483
In the text
NASA ADS
- Griffiths, R. E., Ptak, A., Feigelson, E. D., et al. 2000, Science, 290, 1325
In the text
NASA ADS
- Gruber, D. E., Matteson, J. L., Peterson, L. E., & Jung, G. V. 1999,
ApJ, 520, 124
In the text
NASA ADS
- Hornschemeier, A. E., Brandt, W. N., Garmire, G. P., et al. 2001, ApJ, 554, 742
In the text
NASA ADS
- Itoh, N., Sakamoto, T., Kusano, S., Nozawa, S., & Koyama, Y. 2000, ApJS,
128, 125
In the text
NASA ADS
- Kim, D.-C., & Sanders, D. B. 1998a, ApJ, 508, 627
NASA ADS
- Kim, D.-C., & Sanders, D. B. 1998b, ApJS, 119, 41
NASA ADS
- Leiter, D., & Boldt, E. 1982, ApJ, 260, 1
In the text
NASA ADS
- Lilly, S. J., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1
NASA ADS
- Lilly, S. J., Tresse, L., Hammer, F., Crampton, D., & Le Fevre, O. 1995,
ApJ, 455, 108
In the text
NASA ADS
- Lin, H., Yee, H. K. C., Carlberg, R. G., et al. 1999, ApJ, 518, 523
In the text
- Lonsdale, C. J., Hacking, P. B., Conrow, T. P., & Rowan-Robinson, M. 1990,
ApJ, 358, 60
In the text
NASA ADS
- Lonsdale, C. J., Helou, G., Good, J. C., & Rice, W. 1985, Cataloged
Galaxies and Quasars Observed in the IRAS Survey (JPL, Pasadena, CA)
- Madau, P., Ferguson, H. C., Dickinson, M. E., et al. 1996, MNRAS, 283, 1388
In the text
NASA ADS
- Marshall, F. E., Boldt, E. A., Holt, S. S., et al. 1980, ApJ, 235, 4
NASA ADS
- Matsumoto, H., & Tsuru, T. G. 1999, PASJ, 51, 321
In the text
NASA ADS
- Miyaji, T., Ishisaki, Y., Ogasaka, Y., et al. 1998, A&A, 334, L13
NASA ADS
- Mizuno, T., Ohbayashi, H., Iyomoto, N., & Makishima, K. 1998,
in The Hot Universe, ed. K. Koyama, S. Kitamoto, & M. Itoh, IAU Symp., 188, 284
- Moran, E. C., Lehnert, M. D., & Helfand, D. J. 1999, ApJ, 526, 649
In the text
NASA ADS
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119
In the text
NASA ADS
- Mushotzky, R. F., Cowie, L. L., Barger, A. J., & Arnaud, K. A. 2000, Nature, 404, 459
In the text
NASA ADS
- Okada, K., Mitsuda, K., & Dotani, T. 1997, PASJ, 49, 653
NASA ADS
- Pearson, C., & Rowan-Robinson, M. 1996, MNRAS, 283, 174
In the text
NASA ADS
- Persic, M., Gruber, D. E., & Rephaeli, Y. 2002, in preparation
In the text
- Persic, M., & Rephaeli, Y. 2002, A&A, 382, 843
NASA ADS
- Piccinotti, G., Mushotzky, R. F., Boldt, E. A., et al. 1982, ApJ, 253, 485
In the text
NASA ADS
- Ptak, A., Serlemitsos, P. J., Yaqoob, T., Mushotzky, R., & Tsuru, T. 1997,
AJ, 113, 1286
NASA ADS
- Rephaeli, Y. 1979, ApJ, 227, 364
In the text
NASA ADS
- Rephaeli, Y., & Gruber, D. 2002, A&A, 389, 752
In the text
NASA ADS
- Rephaeli, Y., Gruber, D., & Persic, M. 1995, A&A, 300, 91
In the text
NASA ADS
- Rephaeli, Y., Gruber, D., Persic, M., & McDonald, D. 1991, ApJ, 380, L59
In the text
NASA ADS
- Ricker, P. M., & Meszaros, P. 1993, ApJ, 418, 49
In the text
NASA ADS
- Roberts, T. P., Schurch, N. J., & Warwick, R. S. 2001, MNRAS, 324, 737
In the text
NASA ADS
- Rothschild, R. E., Baity, W. A., Gruber, D. E., et al. 1983, ApJ, 269, 423
In the text
NASA ADS
- Rowan-Robinson, M., & Crawford, J. 1989, MNRAS, 238, 523
In the text
NASA ADS
- Rowan-Robinson, M., Benn, C. R., Lawrence, A., McMahon, R. G., &
Broadhurst, T. J. 1993, MNRAS, 263, 123
In the text
NASA ADS
- Saunders, W., Rowan-Robinson, M., Lawrence, A., et al. 1990, MNRAS, 242, 318
In the text
NASA ADS
- Schaaf, R., Pietsch, W., Biermann, P. L., Kronberg, P. P., & Schmutzler, T.
1989, ApJ, 336, 722
In the text
NASA ADS
- Schmitt, H. R., Kinney, A. L., Calzetti, D., & Storchi Bergmann, T. 1997, AJ, 114, 592
In the text
NASA ADS
- Setti, G., & Woltjer, L. 1989, A&A, 224, L21
In the text
NASA ADS
- Shapley, A., Fabbiano, G., & Eskridge, P. B. 2001, ApJS, 137, 139
NASA ADS
- Silva, L., Granato, G. L., Bressan, A., & Danese, L. 1998, ApJ, 509, 103
In the text
NASA ADS
- Stewart, G. C., Fabian, A. C., Terlevich, R. J., & Hazard, C. 1982, MNRAS, 200, 61P In the text
- Thompson, R. I., Weymann, R. J., & Storrie-Lombardi, L. J. 2001, ApJ, 546, 694
In the text
NASA ADS
- Tozzi, P., Rosati, P., Nonino, M., et al. 2001, ApJ, 562, 42
In the text
NASA ADS
- Tucker, W. A. 1975, Radiation Processes in Astrophysics (Cambridge: MIT Press), 169
In the text
- Veilleux, S. 2001, in Starburst Galaxies: Near and Far, ed. L.Tacconi, &
D. Lutz (Heidelberg: Springer-Verlag), 88
In the text
- Weedman, D. W. 1987, in Star Formation in Galaxies, ed. C. J. Lonsdale
(NASA CP-2466), 351
In the text
- White, N. E., Swank, J. H., & Holt, S. S. 1983, ApJ, 270, 711
In the text
NASA ADS
- Wilson, G., Cowie, L., Barger, A. J., & Burke, D. J. 2002, AJ, 124, 1258
NASA ADS
- Zezas, A. L., Georgantopoulos, I., & Ward, M. J. 1998, MNRAS, 301, 915
NASA ADS
Copyright ESO 2003
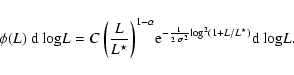
![\begin{figure}
\par\includegraphics[width=8.8cm]{papAA3067_fig2.eps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg51.gif)
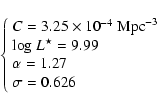
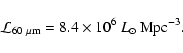
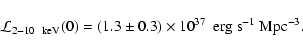
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{papAA3067_fig3a.ps}
\par\vspace*{3.5mm}
\includegraphics[width=7.6cm,clip]{papAA3067_fig3b.ps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{papAA3067_fig4a.ps}
\par\vspace*{2mm}
\includegraphics[width=7.4cm,clip]{papAA3067_fig4b.ps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg81.gif)
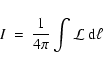
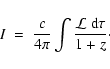
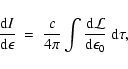
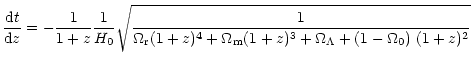
![$\displaystyle { {\rm d} \tau \over {\rm d} z} = {1 \over H_0}
\times
\left\{
\b...
...z)^3 + 0.7} ~\bigr]^{-1}
& \mbox{${\rm flat}~\Lambda$ }
\end{array}\right.\cdot$](/articles/aa/full/2003/07/aa3067/img98.gif)
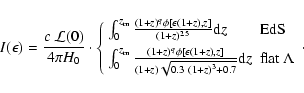
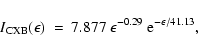
![\begin{figure}
\par\includegraphics[width=4.3cm,clip]{papAA3067_fig5a.ps}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{papAA3067_fig5b.ps}\end{figure}](/articles/aa/full/2003/07/aa3067/Timg143.gif)