A&A 399, 243-251 (2003)
DOI: 10.1051/0004-6361:20021771
J. Fernandes1 - M. J. P. F. G. Monteiro2,3
1 - Observatório Astronómico da Universidade de Coimbra e
Departamento de Matemática,
FCTUC, Portugal
2 -
Departamento de Matemática Aplicada,
Faculdade de Ciências da Universidade do Porto, Portugal
3 -
Centro de Astrofísica da Universidade do Porto,
Rua das Estrelas, 4150-762 Porto, Portugal
Received 29 April 2002 / Accepted 14 November 2002
Abstract
A detailed review of the models for the star
![]() is done
by adjusting the evolutionary sequences to the most recent
bolometric, spectroscopic and astrometric data.
The dependence of the solution on some of the relevant
modelling parameters is analysed and the degeneracy of the
solution using the HR diagram analysis discussed.
is done
by adjusting the evolutionary sequences to the most recent
bolometric, spectroscopic and astrometric data.
The dependence of the solution on some of the relevant
modelling parameters is analysed and the degeneracy of the
solution using the HR diagram analysis discussed.
Recent ground-based observations,
and the forthcoming asteroseismic missions,
can provide detailed oscillation spectra for this star.
The seismic data can be
used as a complementary constraint on the models.
We analyse the seismic properties of the star and discuss the
viability of using such complementary tests in order to clarify some
of the degeneracy of the model solutions.
Preliminary results on the fundamental parameters of
![]() are presented
and the expected seismic behaviour of the star is described.
are presented
and the expected seismic behaviour of the star is described.
Key words: stars: evolution - stars: fundamental parameters -
stars: individual: ![]() Hydri - stars: oscillations
Hydri - stars: oscillations
![]() ,
,
![]() (HD 2151, HR 98, HIP 2021), is a G2 IV
star in the neighbourhood of the Sun belonging to the old disc of
the Galaxy.
This evolved star is frequently seen as the distant future
of the Sun (Dravins et al. 1993).
So
(HD 2151, HR 98, HIP 2021), is a G2 IV
star in the neighbourhood of the Sun belonging to the old disc of
the Galaxy.
This evolved star is frequently seen as the distant future
of the Sun (Dravins et al. 1993).
So ![]() has been extensively studied
in different aspects placing it in a very interesting place among
the solar type stars: the tentative detection of extra-solar planets
(Skuljan et al. 2000), the abnormal high lithium
abundance for an evolved star - 10 times the solar value (cf. Randich et al. 1999),
atmospheric and chromospheric activity
(Chmielewski 2000), etc.
On the other hand, thanks to HIPPARCOS data and to recent
determinations of the observed bolometric flux, as well
as spectroscopic evaluations of the atmospheric parameters, the
position of this star in the Hertzsprung-Russel diagram (HRD)
is known to better than
has been extensively studied
in different aspects placing it in a very interesting place among
the solar type stars: the tentative detection of extra-solar planets
(Skuljan et al. 2000), the abnormal high lithium
abundance for an evolved star - 10 times the solar value (cf. Randich et al. 1999),
atmospheric and chromospheric activity
(Chmielewski 2000), etc.
On the other hand, thanks to HIPPARCOS data and to recent
determinations of the observed bolometric flux, as well
as spectroscopic evaluations of the atmospheric parameters, the
position of this star in the Hertzsprung-Russel diagram (HRD)
is known to better than ![]() .
It can, therefore, be used to test the stellar evolution theory
and constraints on the physical description of the stellar interiors.
Using modern stellar evolutionary models, Dravins et al. (1998)
concluded that the mass of the star should be around 1.05-1.22
of the solar mass, with an age of 6.7 Gyr.
This value is lower than the previous
determination of 8 to 10 Gyr, thanks to the new distance of 7.5 pc measured
by HIPPARCOS compared to the old 6.7 pc obtained from the ground
(van Altena et al. 1995).
.
It can, therefore, be used to test the stellar evolution theory
and constraints on the physical description of the stellar interiors.
Using modern stellar evolutionary models, Dravins et al. (1998)
concluded that the mass of the star should be around 1.05-1.22
of the solar mass, with an age of 6.7 Gyr.
This value is lower than the previous
determination of 8 to 10 Gyr, thanks to the new distance of 7.5 pc measured
by HIPPARCOS compared to the old 6.7 pc obtained from the ground
(van Altena et al. 1995).
However, Dravins et al. (1998) discuss the modelling in the HRD
of ![]() based on the lower value of the metallicity of
[Fe/H]=-0.2.
Further observations indicated that this value should be
slightly higher, near -0.1.
On the other hand it can be
expected that stars with mass higher than the solar value develop a
convective core during some part of their evolution
(cf. Guenther & Demarque 2000),
so the effect of the overshooting must be checked.
based on the lower value of the metallicity of
[Fe/H]=-0.2.
Further observations indicated that this value should be
slightly higher, near -0.1.
On the other hand it can be
expected that stars with mass higher than the solar value develop a
convective core during some part of their evolution
(cf. Guenther & Demarque 2000),
so the effect of the overshooting must be checked.
On the other hand it is well known that the analysis of the HRD position of a single star, other than the Sun, is inconclusive because the number of free parameters is higher that the observables. Models with different sets of free parameters can easily satisfy the observations.
Recently, Bedding et al. (2001) and
Carrier et al. (2001) confirmed the presence of
solar type oscillations in ![]() .
A clear excess power has been measured independently for this
star at about 1000
.
A clear excess power has been measured independently for this
star at about 1000 ![]() Hz.
An extensive seismic analysis can only be done if a significant number
of individual mode frequencies is measured, which has not been done yet.
However, information associated with the frequency separation, as detected in
this case, is already a useful observational test that can
complement the classical HRD analysis (eg. Morel et al. 2000
and references therein).
Hz.
An extensive seismic analysis can only be done if a significant number
of individual mode frequencies is measured, which has not been done yet.
However, information associated with the frequency separation, as detected in
this case, is already a useful observational test that can
complement the classical HRD analysis (eg. Morel et al. 2000
and references therein).
In this work we will revise the present models of ![]() by using the latest updates of the physics and adjusting the most
recent spectroscopic, photometric and astrometric data for this star.
We further aim at studying how seismic data for this star can be used to
solve some of the degeneracy associated with the model parameters
used to adjust the observed luminosity and effective temperature.
In order to do so we address the problem by considering
different sets of seismic data.
We start by simply using the large frequency separation, going up to
the best case of having a significant set of individual mode
frequencies which can be identified and whose frequency
is measured with high accuracy.
by using the latest updates of the physics and adjusting the most
recent spectroscopic, photometric and astrometric data for this star.
We further aim at studying how seismic data for this star can be used to
solve some of the degeneracy associated with the model parameters
used to adjust the observed luminosity and effective temperature.
In order to do so we address the problem by considering
different sets of seismic data.
We start by simply using the large frequency separation, going up to
the best case of having a significant set of individual mode
frequencies which can be identified and whose frequency
is measured with high accuracy.
With such an analysis we attempt to provide state of the art models for the star and how the seismic data, which we expect to have in the near future, can help to resolve some of the uncertainties that cannot be addressed with the "classical'' observational data.
A summary of the presently available data on ![]() is described here.
We have chosen to divide the observations by "classical''
(spectrometric, bolometric and astrometric) and seismic data, in order to
reflect the structure of the work presented in the following sections.
is described here.
We have chosen to divide the observations by "classical''
(spectrometric, bolometric and astrometric) and seismic data, in order to
reflect the structure of the work presented in the following sections.
The luminosity of a star can be determined through the knowledge of
the observed bolometric flux and the distance, so avoiding the
bolometric correction.
Recently Blackwell et al. (1998) and
DiBenedetto (1998) found the same value for the
bolometric flux for
![]() :
:
![]() W/m2,
using the Infra-Red Flux Method (IRFM).
The HIPPARCOS mission measured the parallax as being
W/m2,
using the Infra-Red Flux Method (IRFM).
The HIPPARCOS mission measured the parallax as being
![]() mas (Perryman et al. 1997).
By combining these values, a luminosity for
mas (Perryman et al. 1997).
By combining these values, a luminosity for ![]() of
of
![]() times the solar luminosity (
times the solar luminosity (![]() )
is found.
)
is found.
Many authors have claimed that the effective temperature of ![]() is identical to the solar value
(see Dravins et al. 1993 for details).
Recently DiBenedetto (1998),
using the IRFM method, found
is identical to the solar value
(see Dravins et al. 1993 for details).
Recently DiBenedetto (1998),
using the IRFM method, found ![]() K, confirming
the solar value of the temperature for this star.
We adopt this value, consistent with the above bolometric
flux and in excellent agreement with Favata et al. (1997),
who found 5775 K using the (R-I) colour index.
K, confirming
the solar value of the temperature for this star.
We adopt this value, consistent with the above bolometric
flux and in excellent agreement with Favata et al. (1997),
who found 5775 K using the (R-I) colour index.
In the last version of the Catalogue of [Fe/H] determinations,
the edition by Cayrel de Strobel et al. (2001),
we can find reference to eight metallicity values for ![]() .
This catalogue only includes determinations that have been submitted to
detailed spectroscopic analysis from the ground.
The two most recent determinations using high resolution spectra
give identical values:
.
This catalogue only includes determinations that have been submitted to
detailed spectroscopic analysis from the ground.
The two most recent determinations using high resolution spectra
give identical values:
![]() (Favata et al. 1997)
and
(Favata et al. 1997)
and
![]() (Castro et al. 1999).
We adopt the average of these determinations
(with a conservative error bar), [Fe/H]=-
(Castro et al. 1999).
We adopt the average of these determinations
(with a conservative error bar), [Fe/H]=-
![]() ,
a value slightly higher than
the -0.2 assumed previously (Dravins et al. 1998).
For Pop. I stars the abundance of metals Z is related to the Fe/H by
[Fe/H
,
a value slightly higher than
the -0.2 assumed previously (Dravins et al. 1998).
For Pop. I stars the abundance of metals Z is related to the Fe/H by
[Fe/H
![]() ,
where
,
where
![]() is the ratio of the solar mixture
(Grevesse & Noels 1993).
This gives
is the ratio of the solar mixture
(Grevesse & Noels 1993).
This gives
![]() for
for ![]() .
.
The rotation has also an influence on the HRD position
(e.g. Maeder & Meynet 2000).
Dravins and Nordlund (1990), by fitting line profiles
from hydrodynamic models of the atmosphere,
found
![]() km s-1.
Thus, we can expect this star to be a slow rotator - a non-rotating
and spherical stellar model seems to be appropriate.
km s-1.
Thus, we can expect this star to be a slow rotator - a non-rotating
and spherical stellar model seems to be appropriate.
Seismic data for this star has been found by
Bedding et al. (2001) and Carrier et al. (2001)
indicating a clear excess power around
![]()
![]() Hz,
corresponding to a signal of about 0.40 m s-1 peak amplitude.
Bedding et al. (2001) cite the value of 56.2
Hz,
corresponding to a signal of about 0.40 m s-1 peak amplitude.
Bedding et al. (2001) cite the value of 56.2 ![]() Hz as the most likely value of the large frequency separation.
Carrier et al. (2001) found a value of 58
Hz as the most likely value of the large frequency separation.
Carrier et al. (2001) found a value of 58 ![]() Hz (with an uncertainty of about 2
Hz (with an uncertainty of about 2 ![]() Hz) which
is compatible with the previous result.
Hz) which
is compatible with the previous result.
In order to illustrate how seismic data can be used to provide stringent
constraints on the models we will also consider here the possibility of
having accurate seismic data.
Such data will be available from scheduled
space missions like MONS (Kjeldsen et al. 2000),
MOST (Matthews et al. 2000) and
COROT (Baglin et al. 1998),
or missions like Eddington (Favata et al. 2002).
From these projects we expect to have a wide set (more than 20)
of individual mode frequencies for
l=0,1,2 (and eventually l=3), with an accuracy of
![]()
![]() Hz.
Here we address what such data will provide in terms of
complementing the already available classical data for this star.
Hz.
Here we address what such data will provide in terms of
complementing the already available classical data for this star.
| Observable |
|
|
|
|
|
Blackwell et al. (1998) |
| DiBenedetto (1998) | ||
|
|
|
DiBenedetto (1998) |
|
|
|
Favata et al. (1997) |
| Castro et al. (1999) | ||
|
|
|
Bedding et al. (2001) |
The stellar evolution calculations were computed with the CESAM code version 3. (Morel 1997), running at the Coimbra Observatory.
Details on the physics of these models can be found in
Lebreton et al. (1999).
Here we summarise:
the CEFF equation of state, including Coulomb corrections
to the pressure (Eggleton et al. 1973;
Christensen-Dalsgaard 1991);
nuclear reactions rates given by Caughlan & Fowler (1988);
solar mixture from Grevesse & Noels (1993);
OPAL opacities (Iglesias & Rogers 1996)
complemented at low temperatures by opacities data from
Alexander & Ferguson (1993) following a
prescription of Houdek & Rogl (1996);
the atmosphere is described with an Eddington ![]() -law;
convection is treated according to the mixing-length
theory from Bohm-Vitense (1958)
leaving the mixing-length (
-law;
convection is treated according to the mixing-length
theory from Bohm-Vitense (1958)
leaving the mixing-length (
![]() )
and
the amount of the core overshooting (
)
and
the amount of the core overshooting (
![]() )
as unknowns;
)
as unknowns;
![]() and
and
![]() are parameters
where
are parameters
where ![]() is the local pressure scale height.
is the local pressure scale height.
With this input physics the solar model fits the observed luminosity
and radius, in one part in 10000, with
![]() ,
helium abundance Y=0.268 and Z=0.0175for the common accepted solar age of
4.6 Gyr (Dziembowski et al. 1999)
and the ratio of the solar mixture from
Grevesse & Noels (1993).
,
helium abundance Y=0.268 and Z=0.0175for the common accepted solar age of
4.6 Gyr (Dziembowski et al. 1999)
and the ratio of the solar mixture from
Grevesse & Noels (1993).
It is well known that the knowledge of the HRD position -
L and
![]() - is not sufficient to define all stellar
parameters.
In fact, any point in the HRD depends on stellar
mass, helium, metallicity, age and some free parameters on the input
physics of stellar models.
This problem can be solved for the Sun, whose mass, metallicity and
age are known (e.g. Christensen-Dalsgaard 1982)
and for some binary systems where individual masses are available
(e.g. Noels et al. 1991; Fernandes et al. 1998).
For a single star, other than the Sun, commonly there are more
unknowns than observables.
For
- is not sufficient to define all stellar
parameters.
In fact, any point in the HRD depends on stellar
mass, helium, metallicity, age and some free parameters on the input
physics of stellar models.
This problem can be solved for the Sun, whose mass, metallicity and
age are known (e.g. Christensen-Dalsgaard 1982)
and for some binary systems where individual masses are available
(e.g. Noels et al. 1991; Fernandes et al. 1998).
For a single star, other than the Sun, commonly there are more
unknowns than observables.
For ![]() we take the
metallicity as an observable - we then have three observables
(Z/X, L,
we take the
metallicity as an observable - we then have three observables
(Z/X, L,
![]() )
-
for six unknowns (Y, Z, M,
)
-
for six unknowns (Y, Z, M, ![]() ,
,
![]() ,
,
![]() ).
).
We construct our reference model by tuning the parameters in
order to reproduce the observations on the HRD taking into account
some constraints:
mass - different authors have claimed that the
mass of ![]() should be around 1.0-1.2
should be around 1.0-1.2 ![]() (Dravins et al. 1998, and references therein);
age - for a long time that it has been known
that
(Dravins et al. 1998, and references therein);
age - for a long time that it has been known
that ![]() is an evolved star on the sub-giant stage, so
typically the age should be higher than the solar one;
overshooting - stellar models of stars with mass higher than
the solar value show the presence of a convective core, at
least at the beginning of their evolution.
This seems to be confirmed by observations
(Ribas et al. 2000).
is an evolved star on the sub-giant stage, so
typically the age should be higher than the solar one;
overshooting - stellar models of stars with mass higher than
the solar value show the presence of a convective core, at
least at the beginning of their evolution.
This seems to be confirmed by observations
(Ribas et al. 2000).
|
|
Y |
|
||
| S0 | 1.10 | 0.27 | 1.4 | 0.25 |
|
1.00 | - | - | - |
| Sa2 | 1.20 | - | - | - |
|
- | 0.24 | - | - |
| Sb2 | - | 0.30 | - | - |
|
- | - | 1.6 | - |
| Sc2 | - | - | 1.8 | - |
|
- | - | - | 0.00 |
| Sd2 | - | - | - | 0.15 |
Our reference model, hereafter S0, has the following
characteristics:
![]() ,
Y=0.27, Z=0.014,
,
Y=0.27, Z=0.014,
![]() and
and
![]() .
This model reproduces the observed quantities (L,
.
This model reproduces the observed quantities (L,
![]() )
as well as
)
as well as ![]() for an age of 6.82 Gyr.
for an age of 6.82 Gyr.
We have also studied the sensitivity of model S0 to the variation of the parameters. In Table 2 we list the computed models for different parameters (when it is not indicated, the model characteristics are the same as for S0). In Figs. 1 and 3 we plot the corresponding evolutionary tracks when each parameter is changed, relative to model S0, and the observational error box (see Sect. 2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f1.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg51.gif) |
Figure 1: Evolutionary tracks for the test models; S0 (full line), Sa1 and Sa2 (dotted lines), Sb1 and Sb2 (dashed lines), listed in Table 2, are shown in order to illustrate how sensitive the evolution is to stellar mass and helium. |
| Open with DEXTER | |
It is clear from Fig. 1 that the HRD position of the models is strongly dependent on mass and helium. As it is well known, both helium and mass have similar effects on the main-sequence and sub-giant phases: the increase of helium or mass produces an increase in luminosity and effective temperature.
However if we concentrate on the sub-giant phase,
for a fixed
![]() and leaving the age free,
we can infer that an increase in helium can be compensated by a
decrease of the mass in order to get the same position in the
HRD (e.g. Lebreton et al. 1993): a helium-mass degeneracy.
This is so because the evolution in this regime
is almost parallel to the
and leaving the age free,
we can infer that an increase in helium can be compensated by a
decrease of the mass in order to get the same position in the
HRD (e.g. Lebreton et al. 1993): a helium-mass degeneracy.
This is so because the evolution in this regime
is almost parallel to the
![]() -axis,
as expected for an evolution characterised almost solely by
the size of the central helium core.
So, we can find the pairs (M,Y)
that, for a fixed value of
-axis,
as expected for an evolution characterised almost solely by
the size of the central helium core.
So, we can find the pairs (M,Y)
that, for a fixed value of
![]() (e.g. the observed value), reproduce
the observed luminosity,
(e.g. the observed value), reproduce
the observed luminosity,
![]() ,
using a solar calibration-like
formula (Christensen-Dalsgaard 1982)
for Z=0.014:
,
using a solar calibration-like
formula (Christensen-Dalsgaard 1982)
for Z=0.014:
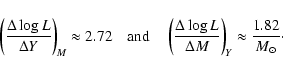 |
(2) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f2.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg60.gif) |
Figure 2: Mass-luminosity degeneracy - evolutionary tracks for the test models S0 (full line), S1 (dashed line) and S2 (dotted line) - see Table 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f3.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg61.gif) |
Figure 3:
Evolutionary tracks for the test models
Sc1 and Sc2 (different values of |
| Open with DEXTER | |
Concerning the sensitivity of the models to the convection parameters
(![]() ,
,
![]() ),
Fig. 3 shows a curious situation: the error box
of
),
Fig. 3 shows a curious situation: the error box
of ![]() is precisely in the region where all evolutionary tracks
intercept each other. No distinction is possible.
So by the simple analysis of the HRD, it is not
possible to decide about (i) the value of the mixing length parameter
and (ii) the value of the overshooting.
Eventual improvements on the error box of (L,
is precisely in the region where all evolutionary tracks
intercept each other. No distinction is possible.
So by the simple analysis of the HRD, it is not
possible to decide about (i) the value of the mixing length parameter
and (ii) the value of the overshooting.
Eventual improvements on the error box of (L,
![]() )
will not change the situation because the changes in
convection parameters produce mainly a horizontal variation in the HRD.
)
will not change the situation because the changes in
convection parameters produce mainly a horizontal variation in the HRD.
Similar conclusions can be obtained regarding mass and helium, as a result of the degeneracy between mass and helium that we have discussed above.
|
|
Y |
|
|
|
|
|||||
| S0 | 1.10 | 0.27 | 1.4 | 0.25 | 0.019(6) |
6.820 | 1.899 | 3.540 | 5751 | |
|
1.05 | 0.30 | 1.4 | 0.25 | 0.020(4) |
6.414 | 1.878 | 3.529 | 5778 | |
| S2 | 1.15 | 0.23 | 1.4 | 0.25 | 0.018(5) |
7.125 | 1.883 | 3.477 | 5749 | |
| S3 | 1.10 | 0.27 | 1.4 | 0.00 | 0.019(6) |
6.653 | 1.878 | 3.520 | 5775 | |
| S4 | 1.10 | 0.27 | 1.8 | 0.25 | 0.019(6) |
7.038 | 1.908 | 3.595 | 5760 | |
| S5 | 1.07 | 0.27 | 1.4 | 0.25 | 0.016(7) |
6.926 | 1.830 | 3.443 | 5818 | |
| S6 | 1.10 | 0.28 | 1.4 | 0.25 | 0.022(7) |
0.000 | 1.036 | 1.239 | 5984 |
|
| S6 | 1.10 | 0.23 | 1.4 | 0.25 | 0.018(8) |
6.881 | 1.878 | 3.477 | 5757 |
As indicated above, old metallicity determinations give a value lower
than the one used in the calculation of S0,
so we tested our models for a
metallicity equal to the lower extreme of the error bar;
[Fe/H]=-0.19 or Z/X=0.016.
Using the same S0 helium value it follows that Z=0.012.
We compute a model with the same
characteristics of S0 but using a different Z.
Figure 4 shows the effect of a change in metal abundance.
The variation in the HRD is similar to an increase in helium or mass.
A lower value of about
![]() in mass (or 0.02 in helium)
is sufficient to return the evolutionary track to agreement with the
observations (model S5, see Table 3).
in mass (or 0.02 in helium)
is sufficient to return the evolutionary track to agreement with the
observations (model S5, see Table 3).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f4.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg72.gif) |
Figure 4:
Evolutionary track for a test model calculated with
the same parameters as S0, except for
Z/X=0.016 (dashed line).
In order to compare, both the reference model S0, and
the evolutionary sequence for model S5 (with mass
|
| Open with DEXTER | |
The solar standard model can be put in closer agreement with Helioseismology if the efficiency of the microscopic diffusion of helium and metals is considered (e.g. Bahcall & Pinsonneault 1995). The classical formalism for the treatment of the gravitational settling of chemical elements seems also to put in agreement observations and theory for nearby low mass stars of Population II (Lebreton et al. 1999) and for old globular clusters (e.g. Castellani et al. 1997). On the other hand the present formalism fails to explain the depletion of light elements in the surface of the Sun and stars, such as the lithium (e.g. Morel et al. 2000), as well as to explain the photospheric abundances in stars more massive than the Sun (Richer et al. 2000). Other descriptions are strongly needed; for example the turbulent mixing just under the convection zone (Montalban & Schatzman 2000).
Because ![]() has a mass close to the solar value and it
is a evolved star,
we choose to test the effect of diffusion using the
same formalism that has been tested and well
established for the Sun (Morel et al. 1997).
has a mass close to the solar value and it
is a evolved star,
we choose to test the effect of diffusion using the
same formalism that has been tested and well
established for the Sun (Morel et al. 1997).
We start by computing a model with the exact characteristics of
S0 but including the diffusion of helium and metals
(Fig. 5).
As expected, due to the increase of the hydrogen opacity
in the external layers of the star, the evolutionary
track with diffusion becomes cooler than S0.
Thanks to the depletion of the helium and metals,
when the evolutionary track crosses the error box,
around an age of 6.9 Gyr, the Z/X at the surface is no longer
the observed value 0.019, but instead 0.016.
This can still be considered consistent with the observations as
this value is the lower extreme of the Z/X error bar.
However, in order to try to find the best model, we recomputed a new
evolutionary track that reproduces
the observed Z/X, as well as (L,
![]() )
- this is model S6.
)
- this is model S6.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f5.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg73.gif) |
Figure 5:
Evolutionary track for a test model calculated
including the diffusion of chemical elements (dashed line).
The reference model S0 is also shown (full line).
The model S6 (dotted line) also includes diffusion, and reproduces
the observed (Z/X,
|
| Open with DEXTER | |
By considering different sets of seismic data that are (or may become) available for this star we discuss here the constraints that we may impose on the models for this star. With such set of tests we aim at defining what aspects of the physics discussed above can be separated, lifting some of the degeneracy we have found with the HRD analysis.
Table 3 lists the properties of the models we consider here. They all have the observed value of the luminosity and effective temperature (within the error bars), but use different combinations of the stellar mass and initial helium abundance, and other modelling parameters.
We will now apply some of the seismic tests available and consider the analysis for different sets of seismic data that have been or will be measured for this star.
![]() is an evolved star of a mass slightly higher than the solar value.
By calculating the linear adiabatic oscillations with degree l=0,1,2 for
our reference model S0 we find that modes with mode order 8<n<24have frequencies between
is an evolved star of a mass slightly higher than the solar value.
By calculating the linear adiabatic oscillations with degree l=0,1,2 for
our reference model S0 we find that modes with mode order 8<n<24have frequencies between
![]()
![]() Hz.
Because the expected age for this star places it after the end of
the main-sequence evolution the model exhibits the characteristic
avoided crossings (Aizenman et al. 1977) in its p-mode spectra.
Such behaviour corresponds to modes changing nature as
a consequence of the evolution in this
advanced evolutionary stage of the core.
This behaviour is expected for these stars
(see for example Christensen-Dalsgaard et al. 1995
and Morel et al. 2001),
making the analysis of their seismic spectra much more difficult.
Hz.
Because the expected age for this star places it after the end of
the main-sequence evolution the model exhibits the characteristic
avoided crossings (Aizenman et al. 1977) in its p-mode spectra.
Such behaviour corresponds to modes changing nature as
a consequence of the evolution in this
advanced evolutionary stage of the core.
This behaviour is expected for these stars
(see for example Christensen-Dalsgaard et al. 1995
and Morel et al. 2001),
making the analysis of their seismic spectra much more difficult.
|
|
|
|||
| Sx7 | 1.051 | 1.301 | 0200.0 | 0.704 |
| Sx5 | 1.200 | 1.776 | 3000.0 | 0.490 |
| Sx2 | 1.477 | 2.378 | 5759.1 | 0.174 |
|
1.899 | 3.540 | 6819.6 | 0.000 |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f6.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg78.gif) |
Figure 6: Large frequency separations (Eq. (4)) for models with the same properties as our reference model but with different ages (from the ZAMS up to the age of model S0). The open circles are the values of the separation for modes of degree l=1, while the closed circles are for l=0. |
| Open with DEXTER | |
Radial modes are not expected to be affected, but the frequencies
found for l=1 and l=2 show this characteristic behaviour.
It is illustrated in Fig. 6 where the
large frequency separation is shown for models of different ages
corresponding to the evolutionary sequence that produces
our reference model S0.
Only at the end of the main-sequence, as the central helium core is formed,
does the effect of avoided crossings for modes of l=1(and
![]() )
show up as a strong deviation of the
separations from its expected asymptotic behaviour.
)
show up as a strong deviation of the
separations from its expected asymptotic behaviour.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f7.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg80.gif) |
Figure 7: Differences between the large frequency separations for modes with l=1 and modes with l=0. The differences are shown for models of different ages: S0 (full line) and a younger model (dashed line), as indicated for each curve by the age. Also shown are the differences calculated after scaling the frequencies by a factor as given in Eq. (5) (dotted line) - it illustrates the contribution to the diferences due to the change of the radius of the star with age. |
| Open with DEXTER | |
Figure 7 illustrates how the large
frequency separations for modes of degree ![]() change with time as the mass of the helium core increases.
A change in age of about 0.07 Gyr moves the strongest
deviation of the separation from the asymptotic behaviour by about 50
change with time as the mass of the helium core increases.
A change in age of about 0.07 Gyr moves the strongest
deviation of the separation from the asymptotic behaviour by about 50 ![]() Hz.
Part of this shift (
Hz.
Part of this shift (![]()
![]() )
is due to the change of the
radius of the star with age.
The remaining component results from the change of the relative
mass of the helium-core with age.
)
is due to the change of the
radius of the star with age.
The remaining component results from the change of the relative
mass of the helium-core with age.
The seismic information that can more easily be identified in
the power spectrum of the oscillations is the large separation.
It is a regular spacing between frequencies of consecutive mode
order n and the same mode degree l.
Asymptotically this value is expected to scale with
(M/R3)1/2,
where M is the mass of the star and R its radius.
Here we calculate the separation
(Monteiro et al. 2002)
as being its value at a fixed frequency after removing the periodic
component present due to the helium ionization zone
(Monteiro & Thompson 1998).
Figure 8 illustrates how the separations have
been calculated using the modes with degree l=0 from the values
of
The values found for the large frequency separation of the models
considered in Table 3 are given
in Table 5.
There is a clear difference between models that
can be as large as 2 ![]() Hz.
Part of that difference is a simple homologous scaling for
frequency, resulting from the differences in mass M and radius R.
Considering that from the observations we can only estimate the radius,
the best way to compare the models with the observed seismic data
is by considering a "reduced'' separation;
Hz.
Part of that difference is a simple homologous scaling for
frequency, resulting from the differences in mass M and radius R.
Considering that from the observations we can only estimate the radius,
the best way to compare the models with the observed seismic data
is by considering a "reduced'' separation;
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f8.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg91.gif) |
Figure 8:
Large frequency separations (Eq. (4))
for three of the models listed in Table 3.
Only modes with |
| Open with DEXTER | |
|
|
|
|
| S0 | 55.47 | - |
| S1 | 55.17 | 54.27 |
| S2 | 57.45 | 56.74 |
| S3 | 56.44 | 55.50 |
| S4 | 55.37 | 55.75 |
| S5 | 57.82 | 54.69 |
| S6 | 56.40 | 55.47 |
|
|
56.2 | 55.2 |
The method developed by Monteiro & Thompson (1998) can,
in principle, be used to resolve the stellar mass-helium abundance
degeneracy of the HRD.
Such a method isolates from the frequencies a periodic component produced
at the second helium ionization zone.
The characteristics of the signature are a direct function of the
helium abundance near the surface and therefore can be used to
provide a complementary constraint when both the mass and the
helium abundance are not accurately known.
Such a method can be used for low-degree modes of main-sequence stars.
However, for evolved stars, as is the case of ![]() ,
we can only take
radial modes (see for example Fig. 8)
which places strong limitations on the precision with which we may
determine the value of Y.
,
we can only take
radial modes (see for example Fig. 8)
which places strong limitations on the precision with which we may
determine the value of Y.
We also note that the behaviour of the ![]() modes, as represented
in Figs. 6 and 7,
for the case of an evolved star is strongly dependent on age.
Therefore it may be used to constrain the age, providing a complementary
test on what a fitting parameter is in the HRD analysis.
Such a dependence is a direct consequence of the direct dependence of
the evolution of the star in this post-main sequence phase on the
size of its helium core, when the star evolves almost at constant
effective temperatures.
modes, as represented
in Figs. 6 and 7,
for the case of an evolved star is strongly dependent on age.
Therefore it may be used to constrain the age, providing a complementary
test on what a fitting parameter is in the HRD analysis.
Such a dependence is a direct consequence of the direct dependence of
the evolution of the star in this post-main sequence phase on the
size of its helium core, when the star evolves almost at constant
effective temperatures.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2636f9.eps} \end{figure}](/articles/aa/full/2003/07/aa2636/Timg94.gif) |
Figure 9: Reduced large frequency separations (Eq. (5)) for all models listed in Table 3. The continuous line is a least squares fit to all points (see Eq. (6)) while the dotted line illustrates the change introduced in the scaling law by changes in the treatment of convection. The dashed line corresponds to the observational value found by Bedding et al. (2001). |
| Open with DEXTER | |
Figure 9 shows the reduced large frequency separation
for all models that adjust ![]() in the HRD.
The differences between S0, S3, S4 and S6 are a measure
of the deviation from the scaling law used to define
in the HRD.
The differences between S0, S3, S4 and S6 are a measure
of the deviation from the scaling law used to define
![]() (Eq. (5)).
The change in the mixing length parameter is the strongest.
The homology scaling is not directly dependent on the initial
helium abundance Y(see model S6) making the large frequency separation
an important indicator of stellar mass, when the helium abundance
is not known.
(Eq. (5)).
The change in the mixing length parameter is the strongest.
The homology scaling is not directly dependent on the initial
helium abundance Y(see model S6) making the large frequency separation
an important indicator of stellar mass, when the helium abundance
is not known.
The fact that the reduced large frequency separation is mainly dependent
on the mass of the star can be used to infer this quantity from
the seismic observations.
As an example we consider the local dependence of
![]() on
on ![]() ,
estimated from the properties of all models
listed in Table 3.
In order to do so, and taking into account the relation given in
Eq. (4), we consider that
,
estimated from the properties of all models
listed in Table 3.
In order to do so, and taking into account the relation given in
Eq. (4), we consider that
The local estimation of this relation is also affected by systematic
contributions due to deviations from the scaling law resulting
from changes in the physics.
Figure 9 shows that the change of the mixing length
introduces a deviation from the scaling, giving an error of
less than 0.01 ![]() for the estimation of the stellar mass.
for the estimation of the stellar mass.
We presented a detailed HRD analysis of ![]() by taking
the latest observational data for this stars.
If we assume that the helium abundance of
by taking
the latest observational data for this stars.
If we assume that the helium abundance of ![]() should
be higher than the primordial helium (
should
be higher than the primordial helium (
![]() ;
Peimbert et al. 2002 and references), and
lower than the highest value of the helium determined for
Population I stars with similar ages and masses as
;
Peimbert et al. 2002 and references), and
lower than the highest value of the helium determined for
Population I stars with similar ages and masses as
![]() (Guenther & Demarque 2000;
Morel et al. 2000), we can infer that the helium abundance
of
(Guenther & Demarque 2000;
Morel et al. 2000), we can infer that the helium abundance
of ![]() should be between 0.25 and 0.30.
By using the relation (3) we can estimate that,
for
should be between 0.25 and 0.30.
By using the relation (3) we can estimate that,
for ![]() ,
,
The use of the large frequency separation can
constrain the mass of the star if the radius is known
with high precision.
The present bolometric and spectroscopic observations give
the determination of the radius with an uncertainty of about 4%.
At present, the large frequency separation is
not known to better than 4.0%.
Consequently, the uncertainty on the value of the mass is still large, with
the preliminary result giving that
We note that the quoted error bars (Eqs. (7)
and (9)) for the mass of ![]() do not include the unknown uncertainties on the calculation
of the models used to estimate the mass from the observations.
This contribution is expected to be different for the determination
from the HRD analysis or for the result found with the seismic study
of the star.
Therefore, the fact that both values are
consistent is of great relevance.
We will need more detailed seismic data in order to confirm that this
consistency remains if the error bar in Eq. (9)
is reduced.
do not include the unknown uncertainties on the calculation
of the models used to estimate the mass from the observations.
This contribution is expected to be different for the determination
from the HRD analysis or for the result found with the seismic study
of the star.
Therefore, the fact that both values are
consistent is of great relevance.
We will need more detailed seismic data in order to confirm that this
consistency remains if the error bar in Eq. (9)
is reduced.
The seismic information we can have on a star is not limited to
the large frequency separation.
The signature from the region of the second ionization of helium
can be a valuable tool to constrain the value of Y.
Such a test will require all individual frequencies
(for n between 8 and 24) with an accuracy of about 0.1 ![]() Hz.
With such data we can also expect to be able to provide an estimate
of the mass/size (or equivalently - the age) for the helium core of the
star.
Hz.
With such data we can also expect to be able to provide an estimate
of the mass/size (or equivalently - the age) for the helium core of the
star.
In this work we have recalculated the best models for adjusting
![]() in the HR Diagram.
In doing so, a detailed study of the uncertainty in the adjusting
parameters has been done in order to evaluate the size of the
parameter space that holds compatible solutions for the observed
luminosity and effective temperature.
The modelling parameters which have been evaluated are the
helium abundance (Y), the stellar mass (M), the age (t),
the mixing length parameter (
in the HR Diagram.
In doing so, a detailed study of the uncertainty in the adjusting
parameters has been done in order to evaluate the size of the
parameter space that holds compatible solutions for the observed
luminosity and effective temperature.
The modelling parameters which have been evaluated are the
helium abundance (Y), the stellar mass (M), the age (t),
the mixing length parameter (![]() )
and
the overshooting parameter (
)
and
the overshooting parameter (
![]() ).
For the case of
).
For the case of ![]() ,
an evolved solar-type star, we have found
that the models are basically insensitive to convection parameters.
The HRD analysis does not allow us to determine these parameters.
Similar results were found for the helium abundance and
stellar mass as a result of the strong degeneracy in (Y, M).
,
an evolved solar-type star, we have found
that the models are basically insensitive to convection parameters.
The HRD analysis does not allow us to determine these parameters.
Similar results were found for the helium abundance and
stellar mass as a result of the strong degeneracy in (Y, M).
Given the recent seismic observations of this star, and the planned
missions in Asteroseismology, we have discussed the possibility
of using seismic observations to test some of the modelling parameters.
In particular we have aim at investigating the possibility of removing the (Y, M) degeneracy.
The use of the large frequency separation can provide that extra dimension
to the HRD, which, at least partially, will remove some of the
degeneracy by providing a direct determination of the mass.
In this work we have in particular focused on how the mass and the age, and
consequently the helium abundance, could be constrained by the observations.
By taking into consideration the seismic observations already
available for ![]() ,
and what we expect to have in the near future,
we have shown that with accurate seismic data for
,
and what we expect to have in the near future,
we have shown that with accurate seismic data for ![]() we may
provide an extremely important post-main sequence calibration point
on the evolution of a solar-type star.
we may
provide an extremely important post-main sequence calibration point
on the evolution of a solar-type star.
The fact that ![]() is an evolved star represents an extra
difficulty in applying the traditional seismic tools for the
analysis of the global parameters of the star.
But the different behaviour of the oscillations for such a type of stars
can also be used successfully to test the relevant aspects of their
interiors, namely the age, or equivalently, the size of the central
helium core as the star moves towards the red-giant phase.
is an evolved star represents an extra
difficulty in applying the traditional seismic tools for the
analysis of the global parameters of the star.
But the different behaviour of the oscillations for such a type of stars
can also be used successfully to test the relevant aspects of their
interiors, namely the age, or equivalently, the size of the central
helium core as the star moves towards the red-giant phase.
Acknowledgements
This work was supported in part by Fundação para a Ciência e a Tecnologia - Portugal, through projects PESO/P/PRO15128/1999, ESO/FNU/43658/2001 and POCTI/1999/FIS/34549. JF gratefully thanks Pierre Morel for making the CESAM code available and to David Valls-Gabaud who instaled it at the Coimbra Observatory.