| |
(1) |
A&A 398, 801-807 (2003)
DOI: 10.1051/0004-6361:20021691
M. Vandas1 - E. P. Romashets2
1 - Astronomical Institute, Academy of
Sciences, Bocní II 1401, 141 31 Praha 4, Czech Republic
2 -
Institute of Terrestrial
Magnetism, Ionosphere, and Radio Wave Propagation, Russian Academy of
Sciences, Troitsk, Moscow Region, 142190, Russia
Received 10 September 2002 / Accepted 30 October 2002
Abstract
A force-free magnetic field with constant alpha for a circular cylindrical
flux rope (Lundquist solution) is widely used to describe the magnetic field
configuration in interplanetary flux ropes. Observations as well as MHD
simulations indicate that interplanetary flux ropes are not circular but
have an oblate shape. Here we present an analytical solution for
a force-free magnetic field with constant alpha in an elliptic flux rope
which may be regarded as a direct generalization of the Lundquist solution.
An alternative simpler solution for a force-free magnetic field with constant
alpha in an oblate flux rope is discussed.
Key words: magnetic fields - Sun: coronal mass ejections (CMEs)
A magnetic force-free field with constant alpha fulfills the equation
Lundquist (1950) has found a solution of (1) in the
cylindrical geometry, which reads
We solve Eq. (1) in the elliptic cylindrical coordinates
u, v, and Z. These coordinates are defined by
Equation (1) in elliptic cylindrical coordinates has the components
A substitution for Bu and Bv from (9)-(10)
into (11) yields the equation for BZ
We shall assume that the flux rope has the shape of the generating
ellipse.
We shall solve (12) by a method of separation of variables
and denote
Let us examine the conditions (13)-(14). By in the x=0plane must fulfill
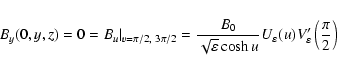
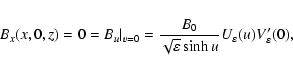
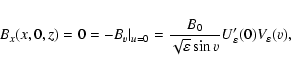
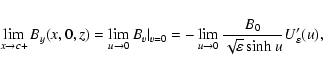
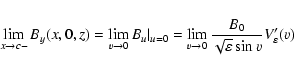
The substitution
![]() (i is an imaginary unit)
converts (26) exactly into the form of (27),
therefore the solution is
(i is an imaginary unit)
converts (26) exactly into the form of (27),
therefore the solution is
![]() for a given
for a given
![]() is expressed by an infinite
fraction (Kuznetsov 1965)
is expressed by an infinite
fraction (Kuznetsov 1965)
For calculation purposes we derive expressions
for the functions
![]() and
and
![]() in the form of a series.
The substitution
in the form of a series.
The substitution
![]() changes (27)
(the prime is now a derivative by w) into
changes (27)
(the prime is now a derivative by w) into
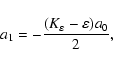
![\begin{displaymath}a_n = \frac{\left[4(n-1)^2 - K_\varepsilon + \varepsilon\right] a_{n-1} -
\varepsilon a_{n-2}}{2n(2n-1)}\cdot
\end{displaymath}](/articles/aa/full/2003/06/aah4052/img78.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f1.eps}\end{figure}](/articles/aa/full/2003/06/aah4052/Timg80.gif) |
Figure 1:
The function
|
| Open with DEXTER | |
Equation (26) will be solved in a similar way. The
substitution
![]() converts it (the prime is now a derivative by
s) into
converts it (the prime is now a derivative by
s) into
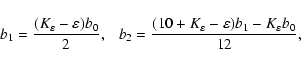
![\begin{eqnarray*}b_n & = & \{[2(n-1)(6n-7) + K_\varepsilon - \varepsilon] b_{n-1...
...\varepsilon] b_{n-2} \\
& & +2(n-3)(2n-5) b_{n-3}\}/[2n(2n-1)].
\end{eqnarray*}](/articles/aa/full/2003/06/aah4052/img85.gif)
A profile of the function
![]() is shown in Fig. 2
for
is shown in Fig. 2
for
![]() = 25; the same as used in Fig. 1, so the functions
= 25; the same as used in Fig. 1, so the functions
![]() and
and
![]() from Figs. 1, 2 determine
a particular solution of the magnetic field. The function
from Figs. 1, 2 determine
a particular solution of the magnetic field. The function
![]() has roots and its first root (labelled by u0 in Fig. 2) determines
an elliptic boundary of the flux rope (21), and hence its oblateness
by (8).
has roots and its first root (labelled by u0 in Fig. 2) determines
an elliptic boundary of the flux rope (21), and hence its oblateness
by (8).
Let us have a given ellipse with a and b; we shall construct
a solution for a flux rope having the shape of this ellipse. More
specifically, the boundary of the flux rope will be defined by BZ=0 and will coincide with this ellipse. The semiaxes a and b determine u0 by (8) and we must find an appropriate
function
![]() for which the first root is u0.
Equation (21) is an implicit equation for
for which the first root is u0.
Equation (21) is an implicit equation for
![]() and can
be solved by the method of bisections. A given
and can
be solved by the method of bisections. A given
![]() determines
determines
![]() by (30)-(31) and then
by (30)-(31) and then
![]() by (35). The condition (21) is checked
etc. The final
by (35). The condition (21) is checked
etc. The final
![]() defines
defines ![]() by (15).
For a numerical solution it is useful to use a table of
pre-calculated values:
by (15).
For a numerical solution it is useful to use a table of
pre-calculated values:
| a/b | u0 |
|
|
| 1.25 | 1.098612 | 2.663889 | 1.119968 |
| 1.5 | 0.804719 | 5.197484 | 1.869170 |
| 2 | 0.549306 | 10.700177 | 2.962558 |
| 3 | 0.346574 | 24.864983 | 4.719335 |
| 4 | 0.255413 | 43.797785 | 6.357117 |
| 5 | 0.202733 | 67.633761 | 7.965562 |
| 6 | 0.168236 | 96.386108 | 9.560726. |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{h4052f2.eps}\end{figure}](/articles/aa/full/2003/06/aah4052/Timg87.gif) |
Figure 2:
The function
|
| Open with DEXTER | |
| |
Figure 3: Magnetic field lines for case a/b=3. The flux rope boundary is the generating ellipse. |
| Open with DEXTER | |
Figure 3 shows magnetic field lines for our solution
when a/b=3. The largest oval is the boundary of the flux rope
and it is an ellipse, which coincides with the generating ellipse.
Because the magnetic field components do not depend on Z (i.e.,
z), magnetic field lines are defined by conditions
![]() ,
as can be demonstrated by the following calculation
,
as can be demonstrated by the following calculation
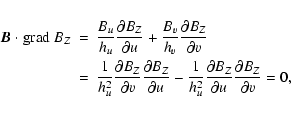
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f4.eps}\end{figure}](/articles/aa/full/2003/06/aah4052/Timg91.gif) |
Figure 4:
Deviation of inner magnetic field line projections (on the z=0 plane)
from ellipses.
Let the projection of a magnetic field line crosses the x axis at a' and
the y axis at b'. This determines the ellipse with semiaxes a' and b'and its deviation from the projection of the magnetic field line is shown;
|
| Open with DEXTER | |
The magnetic field magnitude distribution is shown in Fig. 5. While projections of magnetic field lines are oblate ovals, the contours of the field magnitude are prolate. A similar distribution can be found in flux ropes from MHD simulations (e.g., Vandas et al. 2002b).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f5.eps}\end{figure}](/articles/aa/full/2003/06/aah4052/Timg92.gif) |
Figure 5:
Magnetic field magnitude distribution inside and around an
elliptic flux rope (a/b=3).
The black oval shows the flux rope boundary (generating ellipse).
The magnetic field magnitude B is scaled by the central (maximum) magnitude
value |
| Open with DEXTER | |
The magnetic field strength falls off more slowly along the shorter semiaxis b than along the longer one a. A similar statement is true when comparing with the Lundquist solution for a circular cylinder (Fig. 6). The magnetic field strength falls off more slowly along the shorter semiaxis b than in a circular flux rope with radius b and the opposite is true for the longer semiaxis ain comparison with a circular flux rope with radius a (the boundary of a circular flux rope is also defined by BZ = 0). The differences are quite remarkable.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f6.eps}\end{figure}](/articles/aa/full/2003/06/aah4052/Timg93.gif) |
Figure 6:
Profiles of the magnetic field magnitude (labeled B, solid lines) along the
semiaxes a and b in an elliptic flux rope when
a/b=3 (case shown in Figs. 3 and 5).
For comparison
profiles of the magnetic field magnitude for the corresponding Lundquist
solution (labeled BL, dash-dotted lines) were added. The dashed lines
give profiles of the BZ component in the elliptic flux rope.
The magnetic field profiles are scaled by the central (maximum) magnitude
value |
| Open with DEXTER | |
A correspondence to the Lundquist solution can be demonstrated in
the following way. For a nearly circular
cylinder
![]() holds (
holds (
![]() ).
For x and y to have
).
For x and y to have
![]() values, u must be large, i.e.,
values, u must be large, i.e.,
![]() ,
,
![]() ,
,
![]() .
The cylindrical coordinates are approximately
.
The cylindrical coordinates are approximately
![]() ,
,
![]() .
The quantities
.
The quantities
![]() (Whittaker & Watson 1997),
(Whittaker & Watson 1997),
![]() (33), and
(33), and
![]() (a series in the Bessel functions Jn
for the function
(a series in the Bessel functions Jn
for the function
![]() was used, Kuznetsov 1965)
for small
was used, Kuznetsov 1965)
for small
![]() are
are
We also examined another solution which yields an oblate flux rope,
namely a sum of two Lundquist solutions with different centres.
If we have two force-free solutions with the same ![]() ,
then their sum
is a force-free solution with
,
then their sum
is a force-free solution with ![]() ,
too, due to the linearity of
Eq. (1). Formally this solution can be derived from (12).
Let us make a substitution of variables,
,
too, due to the linearity of
Eq. (1). Formally this solution can be derived from (12).
Let us make a substitution of variables,
![]() ,
and assume that BZ depends on
s only,
BZ = B0 q(s), where q(s) is an unknown function.
Equation (12) is very much simplified with such a BZ and one
gets a Bessel equation
,
and assume that BZ depends on
s only,
BZ = B0 q(s), where q(s) is an unknown function.
Equation (12) is very much simplified with such a BZ and one
gets a Bessel equation
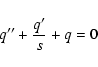 |
(39) |
The other magnetic field components follow from (9) and (10):
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f7.eps}\par\end{figure}](/articles/aa/full/2003/06/aah4052/Timg161.gif) |
Figure 7:
Magnetic field lines (thick lines) for three different values of the oblateness
a/b of flux ropes. The longest magnetic field lines are flux rope boundaries
where BZ=0. The thin dashed lines are generating ellipses
given by semiaxes a and b, the thin solid lines are ellipses
given by semiaxes |
| Open with DEXTER | |
The magnetic field lines of this solution are not strict ellipses, as can be
seen from Fig. 7. Their deviation from an elliptical shape is more
pronounced for larger oblateness (compare Figs. 7a and 7b).
As has been stated,
magnetic field lines were defined by conditions
![]() ,
therefore magnetic field lines in Fig. 7 are also contour lines of
BZ and the largest contours have BZ=0.
,
therefore magnetic field lines in Fig. 7 are also contour lines of
BZ and the largest contours have BZ=0.
As is usual for a cylindrical flux rope, we shall assume BZ = 0 on
our flux rope boundary. The boundary does not coincide with a
generating ellipse (nor another ellipse) and we shall determine
c for a given
"elliptical'' flux rope with semiaxes ![]() and
and ![]() in a sense that the rope boundary crosses the x axis at the
distance
in a sense that the rope boundary crosses the x axis at the
distance ![]() and the y axis at the distance
and the y axis at the distance ![]() .
We may set
.
We may set
![]() .
The denomination is illustrated in
Fig. 7a.
.
The denomination is illustrated in
Fig. 7a.
From BZ = 0 at the point
![]() in the xy plane,
i.e.,
in the xy plane,
i.e., ![]() ,
we have a condition
,
we have a condition
![]() ,
i.e.,
,
i.e.,
![]() ,
where r1 is the first root of J0(r) (
,
where r1 is the first root of J0(r) (
![]() ).
From BZ = 0 at the point
).
From BZ = 0 at the point
![]() in the xy plane,
i.e., v=0, we have a condition
in the xy plane,
i.e., v=0, we have a condition
We cannot get an arbitrary large oblateness for a single flux
rope; there is a limit above which magnetic field lines split
into two flux ropes embedded into a larger closed common
structure ("double flux rope'' - see Fig. 7c).
Such a behaviour is obvious, because the solution is the sum of two
Lundquist solutions; for larger oblatenesses the foci are sufficiently
distant for each Lundquist solution "to manifest its identity''.
The limiting oblateness can be found by examining the
BZ profile along the ![]() semiaxis. For smaller oblateness this
profile has a maximum at the centre, but for larger ones the
maximum is shifted and there is a local minimum (depression) at
the centre. We have u=0 and
semiaxis. For smaller oblateness this
profile has a maximum at the centre, but for larger ones the
maximum is shifted and there is a local minimum (depression) at
the centre. We have u=0 and
![]() near the centre
along the a semiaxis:
near the centre
along the a semiaxis:
![\begin{eqnarray*}B_Z(v) = \frac{B_0}{2}\left\{J_0\left[\alpha c \left(1 +
\cos v...
...] + J_0\left[\alpha c \left(1 - \cos v\right)
\right] \right\}.
\end{eqnarray*}](/articles/aa/full/2003/06/aah4052/img138.gif)
![\begin{eqnarray*}B_Z'(v) & = & \frac{B_0}{2} \alpha c \sin v \left\{J_1\left[\al...
...ft. J_1\left[\alpha c
\left(1 - \cos v\right) \right] \right\},
\end{eqnarray*}](/articles/aa/full/2003/06/aah4052/img139.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f8.eps}\end{figure}](/articles/aa/full/2003/06/aah4052/Timg152.gif) |
Figure 8:
Magnetic field magnitude distribution inside and around an oblate flux rope.
The black oval shows the flux rope boundary where BZ=0(
|
| Open with DEXTER | |
Figure 8 shows the magnetic field magnitude distribution inside and outside of a flux rope for the case displayed in Fig. 7a. The qualitative behaviour of this distribution is quite similar to that of the solution for an elliptic flux rope given above. This similarity is also demonstrated in Fig. 9, where the magnetic field profiles are given for the two presented solutions. Therefore the second solution can be used for moderate oblatenesses. Its advantage is its simplicity.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h4052f9.eps}\par\end{figure}](/articles/aa/full/2003/06/aah4052/Timg160.gif) |
Figure 9:
Profiles of the magnetic field magnitude (labeled B) and
the BZ component along the
semiaxes |
| Open with DEXTER | |
We have found an analytical solution of a force-free magnetic field with constant alpha in an elliptic cylindrical flux rope. Magnetic field lines inside the flux rope are not strict elliptic helices. They are ellipses only on the boundary. The obtained solution represents a generalization of the Lundquist solution for a circular cylinder. We have also presented another solution for an oblate cylindrical flux rope, which can be used for smaller oblatenesses and is simpler.
Acknowledgements
This work was supported by grant A3003003 and project S1003006 from the Academy of Sciences of the Czech Republic, and by EU/INTAS/ESA grant 99-00727 and CDRF grant TGP-848.