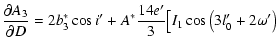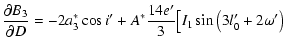A&A 398, 1091-1102 (2003)
DOI: 10.1051/0004-6361:20021688
On the detectability of long period perturbations in close
hierarchical triple stellar systems
T. Borkovits1 -
B. Érdi2 -
E. Forgács-Dajka2 -
T. Kovács2,![[*]](/icons/foot_motif.gif)
1 - Baja Astronomical Observatory of Bács-Kiskun County,
PO Box 766, 6500 Baja, Szegedi út, Hungary
2 -
Department of Astronomy, Eötvös Loránd University,
1117 Budapest, Pázmány P. sétány 1/A, Hungary
Received 26 September 2002 / Accepted 12 November 2002
Abstract
We study the possibility of the detection of the low amplitude long (P') period perturbative
effect of a distant third companion on the motion of a close binary. We give a new, more accurate analytical formula
for this kind of perturbation affecting the moments of the times of minima in eclipsing binaries. The accuracy of
this formula is tested by numerical integrations carried out for several
initial configurations. We also describe a numerical method based on a non-linear Levenberg-Marquardt
algorithm which makes it possible to separate this dynamical effect from the
pure geometrical light-time effect in the eclipsing O-C diagram. The
capabilities of this new method are demonstrated by the analysis of numerically
simulated O-Cs for test systems having physical parameters very similar to
Algol and IU Aur. The results show that the above mentioned
effect would be detectable in these systems nowadays, observing almost each
minima events in a 1-2 year-long interval.
Key words: methods: analytical - methods: numerical - celestial mechanics - binaries: close -
binaries: eclipsing
Several close binary stars have third, distant companion. Due to the presence
of this further component, the motion of the binary no longer will be purely
Keplerian, but different types of periodic and non-periodic (secular)
perturbations would occur. According to the classification of Brown (1936)
the periodic perturbations can be divided into the following three groups:
- Short period perturbations. The typical period is equal
to the orbital period P of the close binary, while the amplitude has the
order (P/P')2 (where P' denotes the period of the wide orbit);
- Long period perturbations. This group has a typical period of P', and magnitude of the
order (P/P');
- Apse-node terms. In this group the typical period is about P'2/P, and the order of the
amplitude reaches unity.
(We have to note that this classification differs from what is used in the classical planetary perturbation theories.
There the first two of our groups called together as "short period'' perturbations, while the "apse-node terms'' are
called as "long period'' ones. In the stellar three-body problem this latter classification was used by Harrington 1968, 1969.)
These effects can be most easily detected in those triple systems, where the close binary happens to be an eclipsing one.
This follows from different reasons. First, the usual orbital periods of the eclipsing binaries are several days,
so in favourable cases even the apse-node terms appear in a time-scale of some decades or centuries, which
for nowadays almost can be covered at least for a few systems. Furthermore, the variation of the orbital elements may
produce very spectacular effects in the characteristics of the eclipses. Here we refer to the
variable eclipse-depth at some eclipsing binaries in a time-scale of decades. The well-known examples are SS Lac
(Torres 2001, and further references therein), V907 Sco (Lacy et al. 1999),
SV Gem (Guilbault et al. 2001)![[*]](/icons/foot_motif.gif) ,
where the eclipses disappeared in the last decades, furthermore, the yet-eclipsing binary IU Aur
also shows fast inclination variations (Drechsel et al. 1994). Another important effect in eccentric binaries
is the precession of the line of the apsides caused by the third star. Nevertheless, this phenomenon is not so easily
observable in triple systems, since the main sources of the apsidal motion in the known cases are the tidal forces
arising from the close proximity of the members of such binaries. In the cases of some systems with abnormally slow
apsidal motion the superposition of the tide-generated and the third body-forced apsidal motion
might explain the discrepancies between the theory and the observations (see e.g. Khodykin & Vedeneyev 1997; Kozyreva et al. 1999
for the binary AS Cam).
,
where the eclipses disappeared in the last decades, furthermore, the yet-eclipsing binary IU Aur
also shows fast inclination variations (Drechsel et al. 1994). Another important effect in eccentric binaries
is the precession of the line of the apsides caused by the third star. Nevertheless, this phenomenon is not so easily
observable in triple systems, since the main sources of the apsidal motion in the known cases are the tidal forces
arising from the close proximity of the members of such binaries. In the cases of some systems with abnormally slow
apsidal motion the superposition of the tide-generated and the third body-forced apsidal motion
might explain the discrepancies between the theory and the observations (see e.g. Khodykin & Vedeneyev 1997; Kozyreva et al. 1999
for the binary AS Cam).
A further main advantage of dealing with eclipsing binaries is that all of the aforementioned phenomena (as well as further ones) affect the occurrence of eclipse events too.
Apart from several other physical mechanisms which can modify the observable eclipsing minima times (e.g. mass flow in/from the system,
tidal forces etc.), the effect of the third body on the eclipsing O-C diagram can be divided into a geometrical and a dynamical part.
The geometrical contribution is the well-known light-time effect. This reflects the motion of the eclipsing pair around the centre of
mass of the triple system. If its quasi-sinusoidal pattern can be separated from the other distortions of the O-C curve, some of
the orbital elements of the wide orbit (P', e', 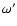 ,
,
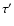 ,
,
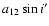 ,
where a12 denotes the semi-major axis of the
orbit of the eclipsing pair around the common centre of mass of the triple system) can be determined. (Perhaps the easiest
way of this calculation was introduced by Kopal 1978.)
,
where a12 denotes the semi-major axis of the
orbit of the eclipsing pair around the common centre of mass of the triple system) can be determined. (Perhaps the easiest
way of this calculation was introduced by Kopal 1978.)
The dynamical contributions arise from the different perturbations. The typical amplitudes of these terms are listed in Söderhjelm (1975).
During an apse-node cycle the magnitude of the O-C variations can reach even the order of days. Nevertheless, on a time-scale
which is significantly shorter than the apse-node period this variation can be manifested e.g. as a parabolic pattern in the
O-C curve, and its nature very easily can be misinterpreted (for an extended discussion see Borkovits et al. 2002).
Up to this moment we mainly concentrated only for the largest amplitude apse-node terms. Nevertheless, the O-C diagram might
give a unique possibility to detect some kinds of long periodic perturbations. Of course, the O-C curve reflects the
long, and even the short periodic variations of the orbital elements in the same way as in the case of the apse-node time-scale
perturbations, but the amplitude of such variations usually much smaller than the limit of observability. The only exception
(at least in some cases) arises from the direct (long period) perturbation in the mean motion of the close binary, which due to
its cumulative effect on the O-C diagram may exceed the limit of detectability.
In this paper we concentrate on this long period contribution of the O-C diagram. In Sect. 2 we give an analytical formula for
this term which is valid for arbitrary value of the mutual inclination, although only for nearly circular close orbits. We also
compare our result with the outputs of direct numerical integrations. In Sect. 3 we present a numerical process to
separate the dynamical and geometrical term of the O-C, and we examine whether and how this dynamical term can be
used to determine the real mutual spatial orientation of the orbits. We illustrate our results with numerically
generated O-C data. Finally in Sect. 4 we consider the chance of the separability in real triple systems.
By the use of the theory of Harrington (1968, 1969), based on the von Zeipel averaging method of the canonical equations,
Söderhjelm (1975, 1982) derived analytical formulae for the long period perturbations in the standard Delaunay variables.
Although these formulae are exact up to second order in the (a/a') ratio, their practical use is limited, at least in their original
forms. Mayer (1990) gave a simple, useful form with the assumptions that the elements of the wide orbit are constant, the close
orbit is circular, and the relative orientation of the two planes is invariant. Nevertheless, as it will be shown,
the expression of Mayer (1990) maybe somewhat inaccurate. More explanation will come later.
In the following we present a corrected new formula, which is valid for the same assumptions.
Such a solution could be get easily from the original formulae of Söderhjelm as it was done by Mayer. Despite
this fact we follow a different way. Instead of the perturbing potential we depart from the perturbing force, and we calculate directly
the perturbations in the eclipsing period in the function of the true anomaly of the eclipsing pair along the wide orbit. As it will be shown
this method is more effective and faster for this particular problem, than the usual methods, furthermore, this automatically helps
to avoid that kind of inaccuracies which occured in the former solution.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{h4008f1.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg7.gif) |
Figure 1:
The spatial orientation of the orbital planes. See text for details. |
| Open with DEXTER |
Using the mass-point approximation, the perturbing force acting upon the close binary is:
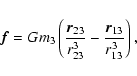 |
(1) |
where G denotes the gravitational constant, m3 is the mass of the tertiary, while
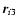 stands for
the position vector between the ith component of the binary and the third star.
The above expression, as it is well-known, can be expanded into a series of Lagrangian polynomials of the following form:
stands for
the position vector between the ith component of the binary and the third star.
The above expression, as it is well-known, can be expanded into a series of Lagrangian polynomials of the following form:
![$\displaystyle %
\vec{f}=\frac{Gm_3}{\rho_2^3}\left\{\left[\sum_{n=0}^\infty\lef...
...n\left(\frac{\rho_1}{\rho_2}\right)^nP_n(\lambda)\right]^3\vec{r}_{13}\right\},$](/articles/aa/full/2003/06/aah4008/img10.gif) |
|
|
(2) |
where M12 means the total mass of the binary, 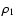 and
and 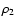 denote the absolute value of the first two Jacobian position-vectors,
(e.g.
denote the absolute value of the first two Jacobian position-vectors,
(e.g. 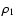 means the separation of the members of the eclipsing pair, while
means the separation of the members of the eclipsing pair, while 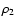 is the distance between the centre of mass of the binary and
the distant third companion), while
is the distance between the centre of mass of the binary and
the distant third companion), while 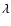 stands for the direction cosine between
stands for the direction cosine between
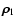 and
and
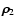 .
Let us define
a Cartesian coordinate system whose origin is at the centre of mass of the binary, and the three axes are parallel
with the vectors
.
Let us define
a Cartesian coordinate system whose origin is at the centre of mass of the binary, and the three axes are parallel
with the vectors
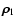 ,
,
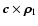 ,
,
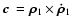 ,
respectively. The direction
cosines between the vector
,
respectively. The direction
cosines between the vector
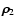 and the axes (as it can be seen in Fig. 1) are as follows:
and the axes (as it can be seen in Fig. 1) are as follows:
where w and w' denote the true longitude of the secondary and the tertiary measured from the intersection of the orbits,
and 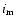 is the mutual inclination.
According to these the three (radial, transversal and normal) components of the perturbing force in the first order of the
ratio
is the mutual inclination.
According to these the three (radial, transversal and normal) components of the perturbing force in the first order of the
ratio
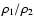 are
are
where
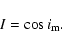 |
(10) |
(As it can be seen, the radial force component is divided into two parts. The first one contains terms depending on w, and very similar to
the 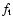 transversal component, while
transversal component, while
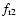 does not depend on the revolution of the eclipsing binary.)
does not depend on the revolution of the eclipsing binary.)
In what follows we will refer the orbital elements to a plane perpendicular to the line of sight of the observer,
and going accross the centre of mass of the binary. We will call it as the plane of the sky. It is clear that the
distance of this plane from the observer varies in time, according to the
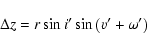 |
(11) |
function, where
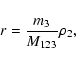 |
(12) |
furthermore v' denotes the true anomaly of the outer body, 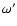 is the argument of the periastron of the binary's
orbit around the centre of mass of the triple system, and M123 stands for the total mass of the triple.
As it is well-known this motion is the source of the light-time effect detected in several triple systems.
is the argument of the periastron of the binary's
orbit around the centre of mass of the triple system, and M123 stands for the total mass of the triple.
As it is well-known this motion is the source of the light-time effect detected in several triple systems.
Using the above mentioned true anomaly, v', of the outer body, and the true longitude, u, of
the secondary measured from the plane of the sky, the force-components have the following forms:
where the phase angles are
(In the above expressions 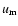 refers to the true longitude of the intersection of the two orbits
measured along the inner orbit, while
refers to the true longitude of the intersection of the two orbits
measured along the inner orbit, while
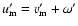 has the same meaning for the outer one.)
has the same meaning for the outer one.)
Using the expansions (13)-(16) the analytical form of the O-C can
be calculated very easily. To do that we depart from the well-known fact, that at the moment of a mid-minimum
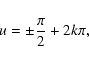 |
(19) |
where k is an integer. (Strictly speaking the above equation is valid exactly only if the eccentricity
of the eclipsing binary is zero, or the visible inclination is 90
 ,
nevertheless, in our treatment
the first condition is practically fulfilled.)
Let us define the so called instantaneous period of the binary in the following way:
,
nevertheless, in our treatment
the first condition is practically fulfilled.)
Let us define the so called instantaneous period of the binary in the following way:
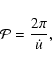 |
(20) |
where as it is well-known (see e.g. Milani et al. 1987, Chap. 3.2):
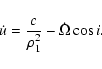 |
(21) |
Here we note an important fact. The first term on the rhs. is independent from the plane of reference, while
the second one has different values using different reference planes. (Please keep in your mind that in the
above expression, as well as in the following ones 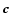 means the special angular momentum of the binary, e.g. the length of vector
means the special angular momentum of the binary, e.g. the length of vector 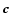 ,
and not the velocity of light.)
,
and not the velocity of light.)
Furthermore, let us denote by
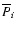 the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
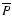 as eclipsing period.) Then it can be seen easily that
as eclipsing period.) Then it can be seen easily that
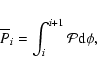 |
(22) |
where
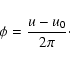 |
(23) |
According to this the eclipsing period is the average of the instantaneous period during a revolution.
Consequently the occurrence of the Nth primary minimum after a t0 epoch can be determined as
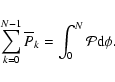 |
(24) |
Consequently, if the 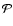 (or
(or 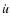 )
versus
)
versus 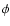 (or u) dependence is known, the theoretical form of the
O-C curve can be calculated formally by an integration. (Of course, the O-C curve is not a continuous
function, only at the integer values of the independent variable has physical meaning.)
(or u) dependence is known, the theoretical form of the
O-C curve can be calculated formally by an integration. (Of course, the O-C curve is not a continuous
function, only at the integer values of the independent variable has physical meaning.)
To get this relation we rewrite 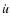 as
as
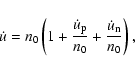 |
(25) |
where n0 stands for the mean motion of the unperturbed two-body revolution in a fixed (let's say t =t0) moment, and
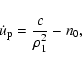 |
(26) |
while
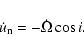 |
(27) |
As far as the perturbations are small
in the mean motion the relation between the instantaneous period 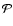 and the Keplerian period P0 of the unperturbed
motion can be written as
and the Keplerian period P0 of the unperturbed
motion can be written as
![\begin{displaymath}%
{\cal{P}}=P_0\left[1-\frac{P_0}{2\pi}(\dot{u}_{\rm p}+\dot{u}_{\rm n})\right]\cdot
\end{displaymath}](/articles/aa/full/2003/06/aah4008/img64.gif) |
(28) |
(In what follows we omit the "0'' subscripts from the initial values of the quantities referring to the unperturbed motion.)
First we calculate the effect of the
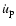 component on the instantaneous period. It can be easily seen, that
component on the instantaneous period. It can be easily seen, that
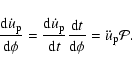 |
(29) |
The second derivative of the 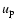 part of the true longitude has the following form (cf. Milani et al. 1987, Chap. 3.2):
part of the true longitude has the following form (cf. Milani et al. 1987, Chap. 3.2):
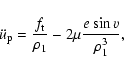 |
(30) |
where
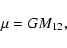 |
(31) |
and v denotes the true anomaly of the secondary component. Here we have to note an important fact. For the first sight
the presence of the second term in Eq. (30) contradicts our previous assumption, that the orbit of the binary is circular.
In fact it is not true.
Although the eccentricity is close to zero, it cannot be permanently exactly zero in perturbed systems. Even if at some moment the
close orbit was circular in the next moment due to the perturbing forces it would not be that. (For the possible
astrophysical importance of this small non-zero eccentricity especially for semi-detached systems see Eggleton et al. 1998.)
So in nearly circular systems the eccentricity oscillates between zero and a small value (typically some ten-hundredthousandths,
see e.g. our numerical integrations for the system IM Aur in Borkovits et al. 2002). In that case e approximately has
the same magnitude as 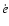 ,
and so it can be shown that the two terms on the rhs of (30) may have the
same order. Furthermore, since both
,
and so it can be shown that the two terms on the rhs of (30) may have the
same order. Furthermore, since both 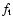 and
and 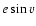 have the same order of magnitude as the small variation
in the
have the same order of magnitude as the small variation
in the 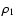 radius, the denominators in (30) can be replaced by a constant average
distance, which is the Keplerian semi-major axis a. On the other hand, we note that this is important only in the case
of the
radius, the denominators in (30) can be replaced by a constant average
distance, which is the Keplerian semi-major axis a. On the other hand, we note that this is important only in the case
of the 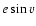 term of Eq. (30), as in the first expression the multiplicator
term of Eq. (30), as in the first expression the multiplicator 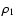 in the amplitude of
in the amplitude of
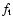 cancels the denominator.
cancels the denominator.
Let us define the expessions
| |
|
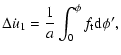 |
(32) |
| |
|
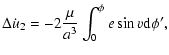 |
(33) |
respectively. Then
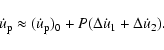 |
(34) |
For the evaluation of the first term we have to express the true anomaly of the third component by 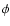 .
This can be done in two steps. First, we can change from the true anomaly to the mean anomaly by the use of the
expansions of Cayley (1861), and after that we approximate the mean anomaly l' by the following formula:
.
This can be done in two steps. First, we can change from the true anomaly to the mean anomaly by the use of the
expansions of Cayley (1861), and after that we approximate the mean anomaly l' by the following formula:
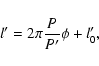 |
(35) |
where l'0 is the mean anomaly at the epoch t0. Now using the expressions
| |
|
![$\displaystyle \int_0^N\cos\left(jl'\pm{ku}\right){\rm d}\phi= \pm\frac{1}{2\pi}...
...\sin\left(jl'\pm{ku}\right)\left(1\mp\frac{j}{k}\frac{P}{P'}\right)\right]_0^N,$](/articles/aa/full/2003/06/aah4008/img76.gif) |
(36) |
| |
|
![$\displaystyle \int_0^N\sin\left(jl'\pm{ku}\right){\rm d}\phi=\mp\frac{1}{2\pi}\...
...[\cos\left(jl'\pm{ku}\right)\left(1\mp\frac{j}{k}\frac{P}{P'}\right)\right]_0^N$](/articles/aa/full/2003/06/aah4008/img77.gif) |
(37) |
the evaluation of (32) is trivial, and we get that
![\begin{displaymath}%
\Delta\dot{u}_1(\phi)=\frac{1}{4\pi}\left[\frac{f_{{\rm r1}}}{a}\right]^\phi_0\left[1+{\cal{O}}\left(P/P'\right)\right].
\end{displaymath}](/articles/aa/full/2003/06/aah4008/img78.gif) |
(38) |
Our next task is the calculation of (33). The dependence of the integrand on 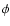 can be written as
can be written as
where the further integrands can be evaluated with good approximation as
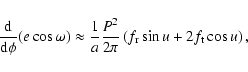 |
(40) |
and
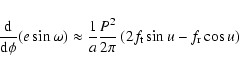 |
(41) |
(see e.g. Milani et al. 1987, Chap. 3.2).
Performing the integrations we obtain that
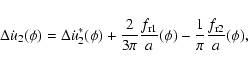 |
(42) |
where
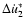 contains the constant terms and those depending upon only u (via some
trigonometric functions). These terms will not give any contribution to the values of the O-C, since they have
the same values in every minima, which fact is the direct consequence of (19).
contains the constant terms and those depending upon only u (via some
trigonometric functions). These terms will not give any contribution to the values of the O-C, since they have
the same values in every minima, which fact is the direct consequence of (19).
Finally we give the
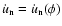 function.
As it is well known
function.
As it is well known
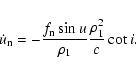 |
(43) |
Since
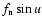 has itself the same order as the components of
has itself the same order as the components of
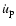 ,
the other quantities in (43) can be treated as constants.
Consequently, our approximation for
,
the other quantities in (43) can be treated as constants.
Consequently, our approximation for
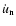 is the following:
is the following:
Let us turn back to the expression (28) of 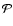 .
It can be seen easily that all
of the above calculated perturbative terms
have the order of (P/P')2, which is in the order of 10-2-10-4 even for the closest hierarchical
systems. So, our expansion is verified.
A further integration of (28) gives the analytical form of the effect of the long period perturbations on the
O-C curve. We keep only the terms which depend also on v'. (The constant terms will give a linear contribution
to the O-C, and so they will build up into the observed eclipsing period, while terms which contain pure trigonometric
functions of u will disappear.) First let's treat the terms which depend on only the true anomaly v' of the tertiary.
For these the integration can be carried out directly with respect to v', using the expression (cf. e.g. Roy 1988, p. 292)
.
It can be seen easily that all
of the above calculated perturbative terms
have the order of (P/P')2, which is in the order of 10-2-10-4 even for the closest hierarchical
systems. So, our expansion is verified.
A further integration of (28) gives the analytical form of the effect of the long period perturbations on the
O-C curve. We keep only the terms which depend also on v'. (The constant terms will give a linear contribution
to the O-C, and so they will build up into the observed eclipsing period, while terms which contain pure trigonometric
functions of u will disappear.) First let's treat the terms which depend on only the true anomaly v' of the tertiary.
For these the integration can be carried out directly with respect to v', using the expression (cf. e.g. Roy 1988, p. 292)
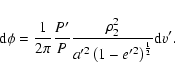 |
(45) |
Consequently, the amplitude of these integrated expressions is multiplied by
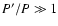 .
On the other hand, according to (36) and (37) terms which contain both v' and uafter the integration will have the same order of magnitude than before. Consequently, the terms which depend on purely
the orbital motion of the tertiary will be dominant. Keeping only these terms we obtain that
.
On the other hand, according to (36) and (37) terms which contain both v' and uafter the integration will have the same order of magnitude than before. Consequently, the terms which depend on purely
the orbital motion of the tertiary will be dominant. Keeping only these terms we obtain that
(Kepler's third law has been used for the transformation of the amplitude.)
For a comparison of our result with the formula of Mayer (1990) we enclose here his solution:
where
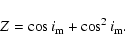 |
(48) |
(We used our notations instead of the original ones, furthermore, some obvious misprints were corrected here.)
The fundamental difference between (47) and (46) manifests in
the phase of the trigonometric terms. The phasing would be identical if 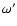 in Mayer's paper would
be measured from the intersection of the two orbital planes. Nevertheless, he used the same notation for
the argument of the periastron in the light-time contribution, where
in Mayer's paper would
be measured from the intersection of the two orbital planes. Nevertheless, he used the same notation for
the argument of the periastron in the light-time contribution, where 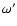 evidently has to be measured from
the plane of the sky. However, the two meanings of the
evidently has to be measured from
the plane of the sky. However, the two meanings of the 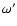 would be identical only if the observational
and the dynamical system of references were the same, or if the two orbital planes intersected each other
in the plane of the sky. As it is well-known the calculation of the perturbational
problems is usually carried out in the dynamical frame of reference, where the fundamental plane is the invariable
plane of the system. In the case of the hierarchical triple stellar systems the net angular momentum of the system
mainly concentrates in the wide orbit (see e.g. Eq. (26) of Söderhjelm 1975), consequently the plane of
the wide orbit is very close to the invariable plane, and in the immovable wide orbit approximation
(which was used by Mayer 1990) the two planes become identical.
The other discrepancies also arise from the same problem. If the plane of reference is the plane of the wide
orbit,
would be identical only if the observational
and the dynamical system of references were the same, or if the two orbital planes intersected each other
in the plane of the sky. As it is well-known the calculation of the perturbational
problems is usually carried out in the dynamical frame of reference, where the fundamental plane is the invariable
plane of the system. In the case of the hierarchical triple stellar systems the net angular momentum of the system
mainly concentrates in the wide orbit (see e.g. Eq. (26) of Söderhjelm 1975), consequently the plane of
the wide orbit is very close to the invariable plane, and in the immovable wide orbit approximation
(which was used by Mayer 1990) the two planes become identical.
The other discrepancies also arise from the same problem. If the plane of reference is the plane of the wide
orbit,
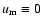 ,
consequently the terms multiplied by
,
consequently the terms multiplied by
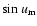 will disappear.
will disappear.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h4008f2a.eps}\hspace*{2mm}
\...
...e.eps}\hspace*{2mm}
\includegraphics[width=7.5cm,clip]{h4008f2f.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg113.gif) |
Figure 2:
The long period dinamical contribution of O-Cs calculated by numerical integration,
furthermore, with the analytical formulae presented in this paper, and in
Mayer (1990). Upper panels: low mutual inclinations. Middle panels: medium mutual inclinations.
Lower panels: high mutual inclinations. (For the exact input parameters see Tables 2, 3.) |
| Open with DEXTER |
In order to illustrate the accuracy of our result, and to compare it with the formula of
Mayer (1990) we carried out several numerical integrations with different initial conditions.
The description of the integrator can be found in Borkovits et al. (2002). The only alteration applied here is, that
the sampling of the Jacobian coordinates and velocities is done after the integration step closest to
the center of an eclipse, and not to the vicinity of the periastron. Only mass-point
approximation was applied. As initial parameters the physical properties and orbital elements of two
well-known close triple systems were chosen (see Tables 1-3).
As it can well be seen in Fig. 2, in the exact coplanar case (upper left panel), as well as in the case,
when the two orbital planes intersect each other on the plane of the sky (upper right panel) both Mayer's and our
results give similarly accurate approximations, while in the other cases the differences are significant.
Table 1:
The initial parameters of the close systems. (The masses are given in solar mass, the period in days, and the angular
orbital elements in degrees.)
The non-arbitrary parameters are taken from Söderhjelm (1980), Lestrade et al. (1993) for Algol,
and from Drechsel et al. (1994) for IU Aur.
| System |
m1 |
m2 |
P |
e |
i |
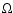 |
u |
| "Algol AB'' |
3.7 |
0.8 |
2.8673 |
0.0 |
82.3 |
52 |
60 |
| "IU Aur AB'' |
21.3 |
14.4 |
1.811474 |
0.0 |
88.0 |
60 |
90 |
Table 2:
The fixed initial parameters of the wide systems. The mass function f(m3) is calculated from the amplitude of the O-C curve, and is given in solar mass. The period P' is given in days, while the periastron passage 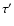 in HJD-2 400 000.
in HJD-2 400 000.
| System |
f(m3) |
P' |
e' |
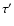 |
| "Algol AB-C'' |
0.125 |
679.9 |
0.23 |
50 000.0 |
| "IU Aur AB-C'' |
1.89 |
294 |
0.54a |
50 000.0 |
a In the (last) run I10 e'=0.24 was chosen. (See text for details.)
In this section first we show how the presence of the dynamical term can influence the usual
method of light-time solutions, and then, we give a numerical method to separate
the two terms, which can improve the accuracy of the light-time solution, and, furthermore,
may give additional information about the spatial orientation of the triple system.
A usual way of calculation of the light-time solution is based on the fact that there are
some very simple relations (at least in the first and second order in e') between the orbital
elements of the wide orbit and the first two or three pairs of coefficients of the Fourier-expansion
of the light-time curve, where the fundamental frequency is the period ratio, e.g. 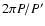 .
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
.
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
For the sake of completeness we describe here the most important formulae after Kopal (1978, Chap. V).
In the case of the pure light-time effect the mathematical form of the O-C curve is:
![\begin{displaymath}%
{\rm O}{-}{\rm C}=\sum_{k=1}^\infty\left[a_k\sin(k\nu N)+b_k\cos(k\nu N)\right]-\sum_{k=1}^\infty b_k,
\end{displaymath}](/articles/aa/full/2003/06/aah4008/img120.gif) |
(49) |
where N is the cycle number, and
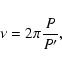 |
(50) |
while
| |
|
![$\displaystyle a_k=A\left[g_k\left(e'\right)\cos\omega'\cos{kl'_0}-h_k\left(e'\right)\sin\omega'\sin{kl'_0}\right],$](/articles/aa/full/2003/06/aah4008/img122.gif) |
(51) |
| |
|
![$\displaystyle b_k=A\left[g_k\left(e'\right)\cos\omega'\sin{kl'_0}+h_k\left(e'\right)\sin\omega'\cos{kl'_0}\right],$](/articles/aa/full/2003/06/aah4008/img123.gif) |
(52) |
where
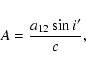 |
(53) |
furthermore,
| |
|
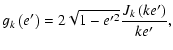 |
(54) |
| |
|
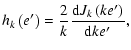 |
(55) |
and in the latter expressions Jk represents the Besselian function of the kth order. (We note, that in (53)
c stands for the velocity of light.) Considering
a quadratic approximation in the outer eccentricity the non-zero coefficients are as follows:
| |
|
![$\displaystyle a_1=A\left[\left(1-\frac{3e'^2}{8}\right)\cos\left(l'_0+\omega'\right)-\frac{e'^2}{4}\cos\omega'\cos{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img127.gif) |
(56) |
| |
|
![$\displaystyle b_1=A\left[\left(1-\frac{3e'^2}{8}\right)\sin\left(l'_0+\omega'\right)-\frac{e'^2}{4}\cos\omega'\sin{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img128.gif) |
(57) |
| |
|
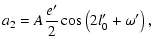 |
(58) |
| |
|
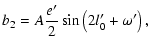 |
(59) |
| |
|
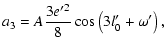 |
(60) |
| |
|
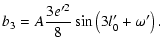 |
(61) |
Using the expansions of Cayley (1861) Eq. (46) also can be easily expanded into trigonometric series of the
mean anomaly l', as
where
We omitted terms which are multiplied by
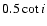 ,
as in eclipsing systems the observable inclination of the
binary is usually close to
,
as in eclipsing systems the observable inclination of the
binary is usually close to
 ,
consequently these terms give only a minor contribution. (E.g. even for
,
consequently these terms give only a minor contribution. (E.g. even for
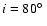 ,
,
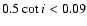 .)
A comparison between (62) and (49) reveals that in this case the coefficients are
as follows:
.)
A comparison between (62) and (49) reveals that in this case the coefficients are
as follows:
| |
|
![$\displaystyle a^*_1=A^*e'\left[{\cal{M}}\cos{l'_0}-{\cal{S}}\cos\left(l'_0+2\omega'\right)+{\cal{C}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img143.gif) |
(66) |
| |
|
![$\displaystyle b^*_1=A^*e'\left[{\cal{M}}\sin{l'_0}-{\cal{S}}\sin\left(l'_0+2\omega'\right)-{\cal{C}}\cos\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img144.gif) |
(67) |
| |
|
![$\displaystyle a_2^*=A^*\left[{\cal{S}}\cos2\left(l'_0+\omega'\right)-{\cal{C}}\sin2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img145.gif) |
(68) |
| |
|
![$\displaystyle b_2^*=A^*\left[{\cal{S}}\sin2\left(l'_0+\omega'\right)+{\cal{C}}\cos2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img146.gif) |
(69) |
| |
|
![$\displaystyle a_3^*=A^*\frac{7e'}{3}\left[{\cal{S}}\cos\left(3l'_0+2\omega'\right)-{\cal{C}}\sin\left(3l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img147.gif) |
(70) |
| |
|
![$\displaystyle b_3^*=A^*\frac{7e'}{3}\left[{\cal{S}}\sin\left(3l'_0+2\omega'\right)+{\cal{C}}\cos\left(3l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img148.gif) |
(71) |
where the amplitude A* is
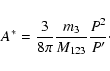 |
(72) |
(It will be seen in the next section, that in the case of systems interesting for us, for moderate
outer eccentricities, the order of A* is about Ae'. This is the reason why the quadratic
terms were held in (56)-(61).)
It is evident that a numerical modelling of the O-C curve in the form (49) yields to
coefficients which are the sums of the corresponding (56)-(61) and (66)-(71) terms.
Now some qualitative remarks can be easily done about the effect of the dynamical terms on a usual
light-time solution. First, if the third star revolves in a circular orbit, which is coplanar with the
orbit of the binary, the dynamical terms diminish, e.g. the geometrical terms are unaffected in that case.
Furthermore, for a non-coplanar, but circular outer orbit, the amplitude of the light-time solution remains
invariant, at least as far as the quadratic term is not counted. On the other hand, in the case of this configuration
the usual determination of the outer eccentricity (from the second Fourier-coefficients) may give
an error of several 10 percents. Finally, if the outer orbit is significantly eccentric, both the mass-function
(via the amplitude), and the outer eccentricity is affected.
The separation of the dynamical terms from the light-time curve may give two important advantages. The first
is the determination of more accurate orbital elements, mainly the "projected'' third-body mass. The second one is the possibility to determine the relative spatial orientation of the two orbital planes.
This latter arises from the fact, that the dynamical terms - through the orbital elements which determine
the light-time orbit - depend on the third body mass (m3), the observable inclination of the wide orbit
(i'), and the mutual inclination (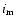 ). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
In order to make this separation we developed a computer code which is based on a non-linear
Levenberg-Marquardt algorithm (see Press et al. 1989, Chap. 14.4). In the present state the code adjusts the following eight parameters: c0 (a zero-point correction), P, A (the amplitude
of the light-time terms), e', 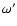 ,
l'0, i', and instead of the mutual inclination,
,
l'0, i', and instead of the mutual inclination,
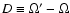 .
(Here we note, that although P is an adjusted parameter, de fundamental frequency
.
(Here we note, that although P is an adjusted parameter, de fundamental frequency 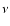 is constant during
the iteration.) The partial derivatives of the coefficients (56)-(71) are listed in the Appendix.
is constant during
the iteration.) The partial derivatives of the coefficients (56)-(71) are listed in the Appendix.
The method of the computation is the following. As a first step we determine the light-time solution from the O-C curve in the usual way. These orbital elements are used as input parameters for the Levenberg-Marquardt
method. For the remaining two parameters (i', D) several initial trial-values are applied automatically.
(Using the mass-function, the mass m3 and the amplitude A* are calculated in each iteration step.)
If a solution is convergent, the program saves the final parameters, and takes
the following set of the angular (i', D) parameters.
The results of our numerical fitting can be found in Tables 4, 5.
In the case of the "Algol-like'' system we deduced the following conclusions:
- In most cases more accurate orbital elements were gained for the elements e',
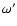 ,
,
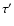 than
it was obtained from the simple light-time (L) fit. In these runs the
than
it was obtained from the simple light-time (L) fit. In these runs the 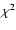 value also improved with respect to the corresponding L-fits;
value also improved with respect to the corresponding L-fits;
- Significant exceptions arise in fits A3, A6, A12, e.g. at those runs, where
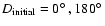 .
In these cases
.
In these cases
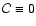 ,
while
,
while
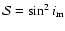 ,
which is also zero for run A3, while
,
which is also zero for run A3, while
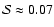 and
and
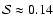 for runs A6 and A12, respectively.
Consequently, in these
cases only the
for runs A6 and A12, respectively.
Consequently, in these
cases only the 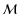 -term, and the coefficients a*1, b*1 have significant contributions.
On the other hand, in run A15, where
-term, and the coefficients a*1, b*1 have significant contributions.
On the other hand, in run A15, where
 was zero a good fit was also found. In this case
already the
was zero a good fit was also found. In this case
already the
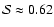 term is the dominant. (Here we note, that in this integration
the mutual inclination was
term is the dominant. (Here we note, that in this integration
the mutual inclination was
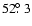 ,
which is very close to that "critical'' value where the
,
which is very close to that "critical'' value where the
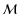 -term disappears.) It is interesting, that despite the weaker fits in these cases, the
-term disappears.) It is interesting, that despite the weaker fits in these cases, the
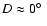 ,
,
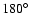 values were reproduced well;
values were reproduced well;
- The determination of the visible inclination of the outer orbit is less accurate. This is of course not
so surprising. We note that the dependence of the tertiary mass on the visible inclination (i') is very
weak in the high inclination region. A comparison of the upper or the middle panels in Fig. 2
shows this clearly. Nevertheless, for the last three runs (in the low visible inclination region), where a smaller variation in
the visible inclination i' results already significant
variation in m3, really a smaller inclination, and consequently larger third body mass was found;
- Finally, we can conclude that the better fits were reached when the mutual inclination had
a medium value.
Considering the "I'' runs with the parameters of the IU Aur system our results
are less satisfactory (see Table 5).
Although the light-time parameters were improved in more than the half of these runs, the accuracy is far from
that achieved in the "A'' runs. What could be the reason? There are three significant differences between the
configurations of the two systems. The first is the large outer eccentricity in the IU Aur system, while
the other two are the larger masses of the stars, and the smaller P'/P ratio, e.g. the closeness of this triple.
The effects of these properties for the behaviour of our solution are very complex. A purely mathematical
effect is that due to the larger eccentricity our expression gives a weaker approximation. On the other hand, we note,
as perhaps the most important physical effect, that because the latter system is more compact, the apse-node time scale
of the largest amplitude perturbations is significantly shorter, and these disturbances may manifest on the O-C
diagram within years. (E.g. according to Drechsel et al. 1994 the period of the nodal regression is about 300 years
in the IU Aur system.)
In order to study these two above mentioned phenomena we carried out the following two tests. In the last run (I10)
we changed the outer eccentricity for the value e'=0.24, while the other parameters had the same values as in
run I5. A significant improvement was found in most of the parameters (although a false result also occurred).
Furthermore, we calculated the O-C solution of run I1 for a shorter (about half of the original) time interval.
(These results are listed in the "I1S'' rows of Table 5.) We did not find significant discrepancy
with respect to the original "I1'' solutions. We can conclude, that the larger eccentricity plays a more important role in our weaker results in this case.
In this paper we examined the possibility of detecting certain kind of perturbations, which are manifesting
themselves on a very short time scale (even during a yearly observing window of the eclipsing variable),
but usually omitted due to their low amplitude. This question naturally has different aspects. These are as follows:
- There are only a few known systems where the amplitude of the dynamical term in the O-C exceeds
significantly the present observational accuracy. We can easily estimate the maximum-value
of the P'/P ratio which is necessary to fulfill this condition. Supposing that the three components have
equal masses, and the third body revolves in a circular orbit, according to Eq. (72) the amplitude may exceed the
10-3 day limit, if P'/P<40P, at least when the two orbits are perpendicular to each other. If the outer orbit
has significant eccentricity (say e'=0.50), or the system consists of stars with different masses, then this limit
in the function of the mutual inclination may even grow up to
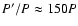 .
From that point of view
the two systems for which the numerical integrations were carried out in this paper are placed near the
limit of the detectability, as for Algol
.
From that point of view
the two systems for which the numerical integrations were carried out in this paper are placed near the
limit of the detectability, as for Algol
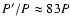 ,
while for IU Aur the same value is
,
while for IU Aur the same value is
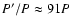 .
.
The three presently known closest eclipsing triple systems are 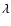 Tau (
Tau (
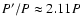 ),
DM Per (
),
DM Per (
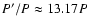 ), and VV Ori (
), and VV Ori (
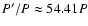 )
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of
)
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of 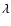 Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
- The second aspect is mainly a technical question. It refers to the observing strategy. This was written already
in the conclusion of Borkovits et al. (2002), but, for the sake of the completeness, we repeat it. In order to have any
chance for the detection of this phenomenon frequent and accurate timings are necessary. It is desirable to
cover a few revolutions of the distant object as densely as possible. The shorter the time interval of such coverage,
the smaller the apse-node time scale or secular variations in the orbital elements which could modify the results.
- Finally, the mathematical modelling of perturbations are necessary in order to extract all information
from the observations.
In this paper we concentrated mainly on this third item. We calculated a new analytical formula
which gives the long period perturbations of the times of minima in eclipsing binaries.
We found that this formula is very similar to the earlier expression of Mayer (1990), nevertheless, some
errors are corrected. Using this expression we developed a numerical method to separate this dynamical effect from
the pure geometrical light time effect. We tested the capabilities of our model by the analysis of numerically simulated
O-C curves. In the case of the test runs for outer orbits with moderate eccentricity, significantly better
solutions were found than in the larger eccentricity cases.
Naturally the next step would be the application of the method for observed O-C diagrams of real systems. Unfortunately,
up to now there are not any O-C diagrams with sufficient accuracy for the possible target systems. This is why
we plan to observe some of the few such systems in the near future to collect as many new times of minima as possible.
As it was mentioned in Sect. 3, the following eight parameters can be adjusted in our
non-linear Levenberg-Marquardt code: c0, P,
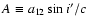 ,
e',
,
e', 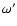 ,
l'0, i',
,
l'0, i',
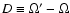 .
Here we list the analytical form of the partial derivatives of the Fourier-coefficients with respect to these parameters. The ak, bk symbols refer to the
coefficients of the geometrical light-time effect, while a*k, b*k denote the dynamical terms.
(We note that in the following:
.
Here we list the analytical form of the partial derivatives of the Fourier-coefficients with respect to these parameters. The ak, bk symbols refer to the
coefficients of the geometrical light-time effect, while a*k, b*k denote the dynamical terms.
(We note that in the following:
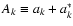 ,
,
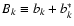 .)
.)
| |
|
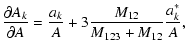 |
(A.1) |
| |
|
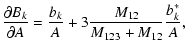 |
(A.2) |
| |
|
![$\displaystyle \frac{\partial{A_1}}{\partial{e'}}=-A\frac{e'}{2}\left[\frac{3}{2}\cos\left(l'_0+\omega'\right)+\cos\omega'\cos{l'_0}\right]+\frac{a^*_1}{e'},$](/articles/aa/full/2003/06/aah4008/img180.gif) |
(A.3) |
| |
|
![$\displaystyle \frac{\partial{B_1}}{\partial{e'}}=-A\frac{e'}{2}\left[\frac{3}{2}\sin\left(l'_0+\omega'\right)+\cos\omega'\sin{l'_0}\right]+\frac{b^*_1}{e'},$](/articles/aa/full/2003/06/aah4008/img181.gif) |
(A.4) |
| |
|
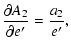 |
(A.5) |
| |
|
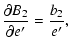 |
(A.6) |
| |
|
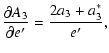 |
(A.7) |
| |
|
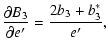 |
(A.8) |
| |
|
![$\displaystyle \frac{\partial a_1}{\partial\omega'}=A\left[\left(A.1-\frac{3e'^2}{8}\right)\sin\left(l'_0+\omega'\right)-\frac{e'^2}{4}\sin\omega'\cos{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img186.gif) |
(A.9) |
| |
|
![$\displaystyle \frac{\partial b_1}{\partial\omega'}=-A\left[\left(A.1-\frac{3e'^2}...
...right)\cos\left(l'_0+\omega'\right)+\frac{e'^2}{4}\sin\omega'\sin{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img187.gif) |
(A.10) |
| |
|
![$\displaystyle \frac{\partial a^*_1}{\partial\omega'}=-2A^*e'\left[{\cal{C}}\cos\left(l'_0+2\omega'\right)+{\cal{S}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img188.gif) |
(A.11) |
| |
|
![$\displaystyle \frac{\partial b^*_1}{\partial\omega'}=2A^*e'\left[{\cal{S}}\cos\left(l'_0+2\omega'\right)-{\cal{C}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img189.gif) |
(A.12) |
| |
|
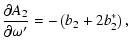 |
(A.13) |
| |
|
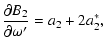 |
(A.14) |
| |
|
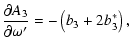 |
(A.15) |
| |
|
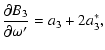 |
(A.16) |
| |
|
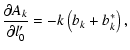 |
(A.17) |
| |
|
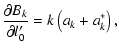 |
(A.18) |
| |
|
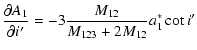 |
|
| |
|
![$\displaystyle \qquad\quad +A^*e'\sin2i_{\rm m}\big\{\cos{u'_{\rm m}}\left[6\cos{l'_0}+\cos\left(l'_0+2\omega'\right)\right]$](/articles/aa/full/2003/06/aah4008/img197.gif) |
|
| |
|
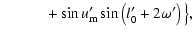 |
(A.19) |
| |
|
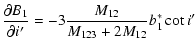 |
|
| |
|
![$\displaystyle \qquad\quad +A^*e'\sin2i_{\rm m}\big\{\cos{u'_{\rm m}}\left[6\sin{l'_0}+\sin\left(l'_0+2\omega'\right)\right]$](/articles/aa/full/2003/06/aah4008/img200.gif) |
|
| |
|
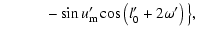 |
(A.20) |
| |
|
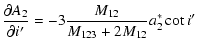 |
|
| |
|
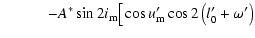 |
|
| |
|
![$\displaystyle \qquad\quad +\sin{u'_{\rm m}}\sin2\left(l'_0+\omega'\right)\big],$](/articles/aa/full/2003/06/aah4008/img204.gif) |
(A.21) |
| |
|
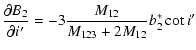 |
|
| |
|
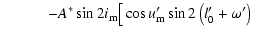 |
|
| |
|
![$\displaystyle \qquad\quad -\sin{u'_{\rm m}}\cos2\left(l'_0+\omega'\right)\big],$](/articles/aa/full/2003/06/aah4008/img207.gif) |
(A.22) |
| |
|
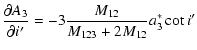 |
|
| |
|
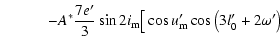 |
|
| |
|
![$\displaystyle \qquad\quad +\sin{u'_{\rm m}}\sin\left(3l'_0+2\omega'\right)\big],$](/articles/aa/full/2003/06/aah4008/img210.gif) |
(A.23) |
| |
|
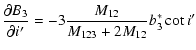 |
|
| |
|
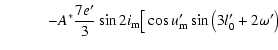 |
|
| |
|
![$\displaystyle \qquad\quad -\sin{u'_{\rm m}}\cos\left(3l'_0+2\omega'\right)\big],$](/articles/aa/full/2003/06/aah4008/img213.gif) |
(A.24) |
| |
|
|
|
| |
|
![$\displaystyle \frac{\partial A_1}{\partial D}=2A^*e'\big\{I_1\left[6\cos{l'_0}-\cos\left(l'_0+2\omega'\right)\right]-I_2\sin\left(l'_0+2\omega'\right)$](/articles/aa/full/2003/06/aah4008/img214.gif) |
|
| |
|
![$\displaystyle \qquad\quad -\cos{i'}\left[{\cal{C}}\cos\left(l'_0+2\omega'\right)+{\cal{S}}\sin\left(l'_0+2\omega'\right)\right]\big\},$](/articles/aa/full/2003/06/aah4008/img215.gif) |
(A.25) |
| |
|
![$\displaystyle \frac{\partial B_1}{\partial D}=2A^*e'\big\{I_1\left[6\sin{l'_0}-\sin\left(l'_0+2\omega'\right)\right]+I_2\cos\left(l'_0+2\omega'\right)$](/articles/aa/full/2003/06/aah4008/img216.gif) |
|
| |
|
![$\displaystyle \qquad\quad -\cos{i'}\left[{\cal{C}}\sin\left(l'_0+2\omega'\right)-{\cal{S}}\cos\left(l'_0+2\omega'\right)\right]\big\},$](/articles/aa/full/2003/06/aah4008/img217.gif) |
(A.26) |
| |
|
![$\displaystyle \frac{\partial A_2}{\partial D}=2b^*_2\cos{i'}+2A^*\left[I_1\cos2\left(l'_0+\omega'\right)+I_2\sin2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img218.gif) |
|
| |
|
|
(A.27) |
| |
|
![$\displaystyle \frac{\partial B_2}{\partial D}=-2a^*_2\cos{i'}+2A^*\left[I_1\sin2\left(l'_0+\omega'\right)-I_2\cos2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img219.gif) |
|
| |
|
|
(A.28) |
| |
|
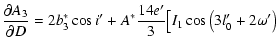 |
|
| |
|
![$\displaystyle \qquad\quad +I_2\sin\left(3l'_0+2\omega'\right)\big],$](/articles/aa/full/2003/06/aah4008/img221.gif) |
(A.29) |
| |
|
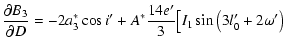 |
|
| |
|
![$\displaystyle \qquad\quad -I_2\cos\left(3l'_0+2\omega'\right)\big],$](/articles/aa/full/2003/06/aah4008/img223.gif) |
(A.30) |
where
| |
|
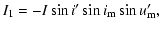 |
(A.31) |
| |
|
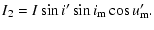 |
(A.32) |
Acknowledgements
We thank Dr. László Szabados and Mr. Szilárd Csizmadia for their comments on the manuscript,
as well as Mrs. Rita Borkovits-József and
Mr. Imre Barna Bíró for the linguistic corrections. This research has made use of NASA's
Astrophysics Data System Bibliographic Services.
-
Borkovits, T., Csizmadia, Sz., Hegedüs, T., et al. 2002, A&A, 392, 895
In the text
NASA ADS
-
Brown, E. W. 1936, MNRAS, 97, 62
In the text
NASA ADS
-
Cayley, A. 1861, Mem. Roy. Astron. Soc., 29
In the text
-
Chambliss, C. R. 1992, PASP, 104, 663
In the text
NASA ADS
-
Drechsel, H., Haas, S., Lorenz, R., & Mayer, P. 1994, A&A, 284, 853
In the text
NASA ADS
-
Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853
In the text
NASA ADS
-
Guilbault, P. R., Lloyd, C., & Paschke, A. 2001, IBVS, No. 5090
In the text
-
Harrington, R. S. 1968, AJ, 73, 190
In the text
NASA ADS
-
Harrington, R. S. 1969, Cel. Mech., 1, 200
In the text
NASA ADS
-
Khodykin, S. A., & Vedeneyev, V. G. 1997, ApJ, 475, 798
In the text
NASA ADS
-
Kopal, Z. 1978, Dynamics of Close Binary Systems (D. Reidel, Dordrecht)
In the text
-
Kozyreva, V. S., Zakharov, A. I., & Khaliullin, Kh. 1999, IBVS, No. 4690
In the text
-
Lacy, C. H. S., Helt, B. H., & Vaz, L. P. R. 1999, AJ, 117, 541
In the text
NASA ADS
-
Lestrade, J.-F., Phillips, R. B., Hodges, M. W., & Preston, R. A. 1993, ApJ, 410, 808
In the text
NASA ADS
-
Mayer, P. 1990, BAIC, 41, 231
In the text
-
Milani, A., Nobili, A. M., & Farinella, P. 1987, Non-gravitational perturbations and satellite geodesy (Adam Hilger, Bristol)
In the text
-
Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1989, Numerical Recipies in Pascal (Cambridge University Press, Cambridge)
In the text
-
Roy, A. E. 1988, Orbital Motion (Adam Hilger, Bristol)
In the text
-
Söderhjelm, S. 1975, A&A, 42, 229
In the text
NASA ADS
-
Söderhjelm, S. 1980, A&A, 89, 100
In the text
NASA ADS
-
Söderhjelm, S. 1982, A&A, 107, 54
In the text
NASA ADS
-
Torres, G. 2001, AJ, 121, 2227
In the text
NASA ADS
Copyright ESO 2003
![]()
![]() ,
,
![]() ,
,
![]() ,
where a12 denotes the semi-major axis of the
orbit of the eclipsing pair around the common centre of mass of the triple system) can be determined. (Perhaps the easiest
way of this calculation was introduced by Kopal 1978.)
,
where a12 denotes the semi-major axis of the
orbit of the eclipsing pair around the common centre of mass of the triple system) can be determined. (Perhaps the easiest
way of this calculation was introduced by Kopal 1978.)
![\begin{figure}
\par\includegraphics[width=12cm,clip]{h4008f1.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg7.gif)
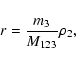
![]() the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
the elapsed time between the ith and the (i+1)th eclipsing
(let's say primary) minima. (Hereafter we refer to
![]() as eclipsing period.) Then it can be seen easily that
as eclipsing period.) Then it can be seen easily that
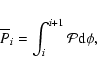
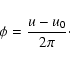
![]() as
as
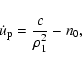
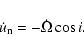
![]() component on the instantaneous period. It can be easily seen, that
component on the instantaneous period. It can be easily seen, that
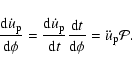
![$\displaystyle \left[(e\cos\omega)_0+\int_0^\phi\frac{{\rm d}}{{\rm d}\phi}(e\cos\omega){\rm d}\phi'\right]\sin{u}(\phi)$](/articles/aa/full/2003/06/aah4008/img80.gif)
![$\displaystyle -\left[(e\sin\omega)_0+\int_0^\phi\frac{{\rm d}}{{\rm d}\phi}(e\sin\omega){\rm d}\phi'\right]\cos{u}(\phi),$](/articles/aa/full/2003/06/aah4008/img81.gif)
![]() function.
As it is well known
function.
As it is well known
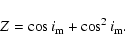
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h4008f2a.eps}\hspace*{2mm}
\...
...e.eps}\hspace*{2mm}
\includegraphics[width=7.5cm,clip]{h4008f2f.eps}\end{figure}](/articles/aa/full/2003/06/aah4008/Timg113.gif)
![]() .
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
.
Consequently, if the harmonic coefficients of the O-C were determined by some numerical methods (typically by
weighted least-squares fit), then the orbital elements could be calculated in a very simple way.
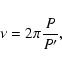
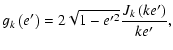
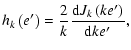
![]() ). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
). It is evident that the dependence on m3 appears in the
amplitude A*, while the effect of the inclinations manifests through the following equations of spherical triangles:
![]() Tau (
Tau (
![]() ),
DM Per (
),
DM Per (
![]() ), and VV Ori (
), and VV Ori (
![]() )
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of
)
(see e.g. the catalogue of Chambliss 1992). In the cases of the latter two binaries unfortunately only a very
few times of minima observations can be found in the literature, although we could expect the largest
effects at these stars. On the other hand, we have to note that as the amplitude of the light time-effect decreases with P'2/3,
at these stars already the detection of the pure geometrical effect is also a challenge. In the most interesting case
of ![]() Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
Tau, the amplitude of the perturbative terms may be larger with an order of magnitude than
that of the light-time terms. Furthermore, at this system due to the large amount of proximity our initial assumptions
may loose their validity.
![]() ,
e',
,
e', ![]() ,
l'0, i',
,
l'0, i',
![]() .
Here we list the analytical form of the partial derivatives of the Fourier-coefficients with respect to these parameters. The ak, bk symbols refer to the
coefficients of the geometrical light-time effect, while a*k, b*k denote the dynamical terms.
(We note that in the following:
.
Here we list the analytical form of the partial derivatives of the Fourier-coefficients with respect to these parameters. The ak, bk symbols refer to the
coefficients of the geometrical light-time effect, while a*k, b*k denote the dynamical terms.
(We note that in the following:
![]() ,
,
![]() .)
.)
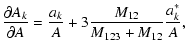
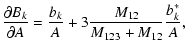
![$\displaystyle \frac{\partial{A_1}}{\partial{e'}}=-A\frac{e'}{2}\left[\frac{3}{2}\cos\left(l'_0+\omega'\right)+\cos\omega'\cos{l'_0}\right]+\frac{a^*_1}{e'},$](/articles/aa/full/2003/06/aah4008/img180.gif)
![$\displaystyle \frac{\partial{B_1}}{\partial{e'}}=-A\frac{e'}{2}\left[\frac{3}{2}\sin\left(l'_0+\omega'\right)+\cos\omega'\sin{l'_0}\right]+\frac{b^*_1}{e'},$](/articles/aa/full/2003/06/aah4008/img181.gif)
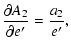
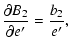
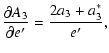
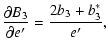
![$\displaystyle \frac{\partial a_1}{\partial\omega'}=A\left[\left(A.1-\frac{3e'^2}{8}\right)\sin\left(l'_0+\omega'\right)-\frac{e'^2}{4}\sin\omega'\cos{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img186.gif)
![$\displaystyle \frac{\partial b_1}{\partial\omega'}=-A\left[\left(A.1-\frac{3e'^2}...
...right)\cos\left(l'_0+\omega'\right)+\frac{e'^2}{4}\sin\omega'\sin{l'_0}\right],$](/articles/aa/full/2003/06/aah4008/img187.gif)
![$\displaystyle \frac{\partial a^*_1}{\partial\omega'}=-2A^*e'\left[{\cal{C}}\cos\left(l'_0+2\omega'\right)+{\cal{S}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img188.gif)
![$\displaystyle \frac{\partial b^*_1}{\partial\omega'}=2A^*e'\left[{\cal{S}}\cos\left(l'_0+2\omega'\right)-{\cal{C}}\sin\left(l'_0+2\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img189.gif)
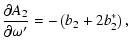
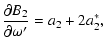
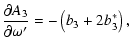
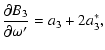
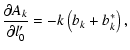
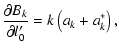
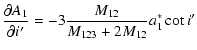
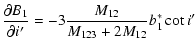
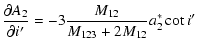
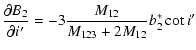
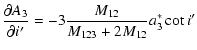
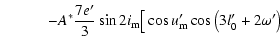
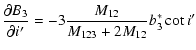
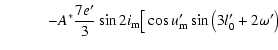
![$\displaystyle \frac{\partial A_1}{\partial D}=2A^*e'\big\{I_1\left[6\cos{l'_0}-\cos\left(l'_0+2\omega'\right)\right]-I_2\sin\left(l'_0+2\omega'\right)$](/articles/aa/full/2003/06/aah4008/img214.gif)
![$\displaystyle \frac{\partial B_1}{\partial D}=2A^*e'\big\{I_1\left[6\sin{l'_0}-\sin\left(l'_0+2\omega'\right)\right]+I_2\cos\left(l'_0+2\omega'\right)$](/articles/aa/full/2003/06/aah4008/img216.gif)
![$\displaystyle \frac{\partial A_2}{\partial D}=2b^*_2\cos{i'}+2A^*\left[I_1\cos2\left(l'_0+\omega'\right)+I_2\sin2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img218.gif)
![$\displaystyle \frac{\partial B_2}{\partial D}=-2a^*_2\cos{i'}+2A^*\left[I_1\sin2\left(l'_0+\omega'\right)-I_2\cos2\left(l'_0+\omega'\right)\right],$](/articles/aa/full/2003/06/aah4008/img219.gif)