A&A 398, 1151-1161 (2003)
DOI: 10.1051/0004-6361:20021713
Stability of the HD 12661 Planetary System
K. Gozdziewski
Torun Centre for Astronomy,
N. Copernicus University, Poland
Received 26 August 2002 / Accepted 14 November 2002
Abstract
In this paper we study the stability of the HD 12661 planetary
system in the framework of the N-body problem. Using the initial
conditions found and announced by the California & Carnegie Planet Search
Team, (http://exoplanets.org/almanacframe.html), we estimate the
dynamical limits on orbital parameters that provide stable (quasi-periodic)
motions of the system. We investigate the orbital stability by combining the
MEGNO indicator analysis with short-term integrations of the orbital
dynamics. The MEGNO technique, invented by Cincotta & Simó (2000), makes it
possible to distinguish efficiently between chaotic and regular dynamics of a
conservative dynamical system. The orbital evolution, derived simultaneously
with MEGNO, helps to identify sources of instability. The nominal initial
condition leads to a chaotic solution, with a Lyapunov time 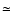 1300 yr.
In spite of this, the system motion seems to be bounded. This was examined
directly, by long-term, 1 Gyr integrations. During this time, the
eccentricities vary in the range (0.1, 0.4). The system is locked in apsidal
resonance with the critical argument librating about
1300 yr.
In spite of this, the system motion seems to be bounded. This was examined
directly, by long-term, 1 Gyr integrations. During this time, the
eccentricities vary in the range (0.1, 0.4). The system is locked in apsidal
resonance with the critical argument librating about
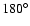 ,
with a
full amplitude varying typically between
,
with a
full amplitude varying typically between
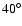 and
and
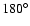 .
Using MEGNO, we found that the HD 12661 system evolves on a border of the 11:2
mean motion resonance. This resonance is stable and results in a
quasi-periodic evolution of the system. From the viewpoint of global
dynamics, the crucial factor for system stability is the presence of the
apsidal resonance. We detected this resonance in a wide neighborhood of the
initial condition in the space of orbital parameters of the system, and in
wide ranges of relative inclination and masses of the planets. The center of
libration can be
.
Using MEGNO, we found that the HD 12661 system evolves on a border of the 11:2
mean motion resonance. This resonance is stable and results in a
quasi-periodic evolution of the system. From the viewpoint of global
dynamics, the crucial factor for system stability is the presence of the
apsidal resonance. We detected this resonance in a wide neighborhood of the
initial condition in the space of orbital parameters of the system, and in
wide ranges of relative inclination and masses of the planets. The center of
libration can be
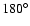 (as in the nominal system) or
(as in the nominal system) or 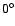 .
The regime depends on the initial values of the apsidal longitudes.
Statistically, the system prefers almost exclusively one of these two
resonance regimes. The HD 12661 system gives a very evident example of the
dynamical role of secular resonances, and their influence on the stability
of exosystems containing Jupiter-like planets. Data derived by numerical
experiments are compared with the results of Laplace-Lagrange secular theory.
The analytical theory gives a crude approximation of the secular dynamics,
because the eccentricities and masses of the planets are large, and the
nominal system is near the 11:2 mean motion resonance.
.
The regime depends on the initial values of the apsidal longitudes.
Statistically, the system prefers almost exclusively one of these two
resonance regimes. The HD 12661 system gives a very evident example of the
dynamical role of secular resonances, and their influence on the stability
of exosystems containing Jupiter-like planets. Data derived by numerical
experiments are compared with the results of Laplace-Lagrange secular theory.
The analytical theory gives a crude approximation of the secular dynamics,
because the eccentricities and masses of the planets are large, and the
nominal system is near the 11:2 mean motion resonance.
Key words: celestial mechanics, stellar dynamics - methods: numerical, N-body
simulations - planetary systems - stars: individual: HD 12661
The search for extrasolar planetary systems conducted in the past several
years by the California & Carnegie Planet Search Team has recently revealed
a number of new multi-planetary systems (Butler et al. 2002). This work is
devoted to a preliminary analysis of the orbital stability of the HD 12661 system, and its dependence on the orbital parameters that are unconstrained
by radial velocity observations. In our numerical experiments, we use the
2-Keplerian fit published by the California & Carnegie Planet Search Team on
their web site![[*]](/icons/foot_motif.gif) and
given in Table 1. Formally, we consider the orbital parameters as
osculating elements at the epoch of the periastron passage of the outer
planet. Because the orbital solution is uncertain, we try to recover some
qualitative dynamical properties of the HD 12661 planetary system.
and
given in Table 1. Formally, we consider the orbital parameters as
osculating elements at the epoch of the periastron passage of the outer
planet. Because the orbital solution is uncertain, we try to recover some
qualitative dynamical properties of the HD 12661 planetary system.
To explore the orbital parameters' space of the HD 12661 system, we use the
Mean Exponential Growth factor of Nearby Orbits (MEGNO), the fast indicator
invented by Cincotta & Simó (2000). This technique seems to be well designed
for studying the planetary dynamics in the framework of the N-body problem.
The basic idea of our approach relies on rapid determination whether an
investigated initial condition leads to quasi-periodic or irregular (chaotic)
motion of the planetary system. In Gozdziewski et al. (2001) we explain our
motivations and technical aspects of the calculations.
In this work, we generally follow Gozdziewski (2002). MEGNO is
utilized to construct one- and two-dimensional sections of the orbital
parameters' space in the neighborhood of the nominal initial condition. Such
maps make it possible to determine dynamical bounds on the orbital parameters
that are unconstrained by the fits, for instance, the inclination of the
system, the companions' masses, and the relative inclination of orbits.
Basically, we are not interested in studying the orbital stability with
long-term integrations. Instead, we search for regular motions that
constitute a skeleton of the phase space filled up with quasi-periodic,
stable evolutions. Simultaneously, we monitor the evolution of orbital
elements. The timescale of the integrations is about
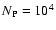 orbital periods of the outer companion. This time is long enough to derive
reliable estimates of both MEGNO as well as the Lyapunov Characteristic
Number (LCN,
orbital periods of the outer companion. This time is long enough to derive
reliable estimates of both MEGNO as well as the Lyapunov Characteristic
Number (LCN,
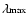 )
and to obtain valuable data that help to
identify the main sources of instabilities. The computational efficiency of
the method is a crucial factor that makes it possible to examine large sets
of initial conditions.
)
and to obtain valuable data that help to
identify the main sources of instabilities. The computational efficiency of
the method is a crucial factor that makes it possible to examine large sets
of initial conditions.
Most of the MEGNO integrations in this paper have been driven by a
Bulirsh-Stoer integrator. We used the ODEX code (Hairer & Wanner 1995). The
relative and absolute accuracies of the integrator have been set to
10-14 and
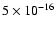 ,
respectively. The position of the nominal
condition is marked in contour plots by the intersection of two thin lines.
The stable areas are marked in MEGNO maps by light-gray (with value
,
respectively. The position of the nominal
condition is marked in contour plots by the intersection of two thin lines.
The stable areas are marked in MEGNO maps by light-gray (with value 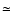 2), and chaotic zones are dark-shaded. (Colour versions of these maps are
published in the electronic edition of the Journal.)
2), and chaotic zones are dark-shaded. (Colour versions of these maps are
published in the electronic edition of the Journal.)
Using the initial condition given in Table 1 to examine the
evolution of the HD 12661 planetary system, the system immediately reveals its
inquiring nature. The results of a 300 Myr integration, performed with the
help of the ODEX integrator, are shown in Figs. 1a-f.
Apparently, the system behaves chaotically, and this can be clearly seen on
graphs representing the time-evolution of the semi-major axes and
eccentricities of the companions. This observation has a strong theoretical
confirmation. Using the method announced in (Gozdziewski 2003), we
calculated the orbital evolution of the system over 10 Myr, and we found
simultaneously its MEGNO and LCN signatures. The results are illustrated in
Figs. 1g, h. MEGNO grows linearly with time, at the rate
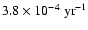 ,
obtained by the linear fit to the theoretical
asymptotic behaviour of MEGNO, described by
,
obtained by the linear fit to the theoretical
asymptotic behaviour of MEGNO, described by
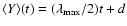 (Cincotta & Simó 2000). This fit provides a very good estimate of LCN
- using the direct variational algorithm, we obtained
(Cincotta & Simó 2000). This fit provides a very good estimate of LCN
- using the direct variational algorithm, we obtained
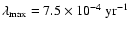 (see Fig. 1h). Thus, the
Lyapunov time scale of the HD 12661 system is very short,
(see Fig. 1h). Thus, the
Lyapunov time scale of the HD 12661 system is very short,  1300 yr.
This means that, integrating the equations of motion, one obtains the orbital
solution with 100% undeterminancy after
1300 yr.
This means that, integrating the equations of motion, one obtains the orbital
solution with 100% undeterminancy after  40 000 yr, assuming that
calculations are performed with a typical floating precision of 14-15
significant digits. In spite of the strong chaotic behaviour, the system
motion seems to be bounded. A dynamical mechanism, which certainly helps to
maintain the stability, is the secular apsidal resonance (SAR). This is
clearly illustrated in Fig. 1e. The apsidal lines remain
antialigned, and the critical argument of the SAR,
40 000 yr, assuming that
calculations are performed with a typical floating precision of 14-15
significant digits. In spite of the strong chaotic behaviour, the system
motion seems to be bounded. A dynamical mechanism, which certainly helps to
maintain the stability, is the secular apsidal resonance (SAR). This is
clearly illustrated in Fig. 1e. The apsidal lines remain
antialigned, and the critical argument of the SAR,
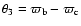 ,
librates with varying full
amplitude
,
librates with varying full
amplitude 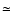 40-
40-
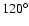 about
about
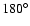 .
For comparison,
Fig. 1f shows the evolution of
.
For comparison,
Fig. 1f shows the evolution of 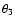 when the initial mean
anomaly of the inner planet is increased by
when the initial mean
anomaly of the inner planet is increased by
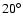 .
In this case, we
obtain perfectly regular oscillations of the critical argument. (This choice
will be clarified later.) The long term evolution of the HD 12661 system has
been further examined through a number of numerical integrations over
1 Gyr. The results of these experiments are illustrated in
Figs. 1i, j, showing variations of the critical argument of the
SAR. Panel 1i is for the Bulirsh-Stoer integrator and
panel 1j is for the RMVS integrator (Levison & Duncan 1994), used
with a time-step of 8 d. Actually, we found that
.
In this case, we
obtain perfectly regular oscillations of the critical argument. (This choice
will be clarified later.) The long term evolution of the HD 12661 system has
been further examined through a number of numerical integrations over
1 Gyr. The results of these experiments are illustrated in
Figs. 1i, j, showing variations of the critical argument of the
SAR. Panel 1i is for the Bulirsh-Stoer integrator and
panel 1j is for the RMVS integrator (Levison & Duncan 1994), used
with a time-step of 8 d. Actually, we found that 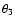 can
circulate, and the chaotic nature of the nominal HD 12661 system is very
evident.
can
circulate, and the chaotic nature of the nominal HD 12661 system is very
evident.
Possibly, in the case of the nominal HD 12661 system, we have convincing
evidence of the stability in the astronomical sense (Lissauer 1999).
This notion of stability implies that the system will remain bound, without
ejections or collisions, for a possibly long but finite period of time, and
this result is robust against sufficiently small perturbations. Although the
motion of the HD 12661 system is chaotic, its planets avoid close encounters
due to the protective dynamical mechanism of the secular resonance, and the
motion of planets can be bounded over a very long period of time.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{h3945f1.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg48.gif) |
Figure 1:
Orbital evolution of the HD 12661 system for the nominal initial condition
given in Table 1. Panels a), b) show changes of the
semi-major axes. Panels c), d) are for the eccentricities. Panel e)
shows the critical argument of the apsidal resonance
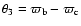 .
Panel f) shows the evolution of
the critical argument when the mean anomaly of the outer planet is increased
by .
Panel f) shows the evolution of
the critical argument when the mean anomaly of the outer planet is increased
by
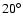 .
Panel g) is for the MEGNO .
Panel g) is for the MEGNO
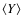 .
Panel h) is
for the Lyapunov Characteristic Number (LCN) calculated with the help of
the direct variational algorithm. Panels i) and j) illustrate
variations of .
Panel h) is
for the Lyapunov Characteristic Number (LCN) calculated with the help of
the direct variational algorithm. Panels i) and j) illustrate
variations of 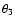 over 1 Gyr derived with the Bulirsh-Stoer
integrator, and with the RMVS integrator by Levison & Duncan (1994) from their
SWIFT package, respectively. Time is in Myr's.
over 1 Gyr derived with the Bulirsh-Stoer
integrator, and with the RMVS integrator by Levison & Duncan (1994) from their
SWIFT package, respectively. Time is in Myr's. |
| Open with DEXTER |
To examine where possible stable systems are located in the orbital
parameters' space, we computed a number of MEGNO sections of this space. A
one-dimensional scan of MEGNO, over the semi-major axis of the inner
planet, computed for the fixed, nominal value
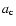 ,
is shown in
Fig. 2. We plotted both MEGNO (the upper graph), as well as the
maximal values of the eccentricities attained during the integration time
(equal to 104 periods of the outer companion). The later values are shown
in the two lower graphs. The MEGNO plot is accompanied by small triangles
that indicate the nominal positions of mean motion resonances (MMR). These
resonances are labeled by i:j, where
,
is shown in
Fig. 2. We plotted both MEGNO (the upper graph), as well as the
maximal values of the eccentricities attained during the integration time
(equal to 104 periods of the outer companion). The later values are shown
in the two lower graphs. The MEGNO plot is accompanied by small triangles
that indicate the nominal positions of mean motion resonances (MMR). These
resonances are labeled by i:j, where
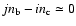 ,
and
,
and
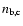 denote the mean motions of the planets,
respectively. This experiment reveals that the nominal initial condition is
located in a chaotic zone, which is very close to the 11:2 MMR. The
resonance can be characterized by librations of the critical argument
211360, with a full amplitude of
denote the mean motions of the planets,
respectively. This experiment reveals that the nominal initial condition is
located in a chaotic zone, which is very close to the 11:2 MMR. The
resonance can be characterized by librations of the critical argument
211360, with a full amplitude of 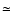
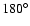 (see
Fig. 3a). It is accompanied by the SAR: its critical argument
librates with a full amplitude of
(see
Fig. 3a). It is accompanied by the SAR: its critical argument
librates with a full amplitude of 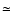
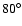 (Fig. 3a').
In this instance, MEGNO is close to 2, indicating a stable, quasi-periodic
system. In the vicinity of this stable MMR we see two symmetric peaks of
MEGNO, and the nominal system is located at one of these peaks
(Fig. 3a').
In this instance, MEGNO is close to 2, indicating a stable, quasi-periodic
system. In the vicinity of this stable MMR we see two symmetric peaks of
MEGNO, and the nominal system is located at one of these peaks![[*]](/icons/foot_motif.gif) . They can be identified with the components of the 11:2 MMR
separatrix.
. They can be identified with the components of the 11:2 MMR
separatrix.
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{h3945f2.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg56.gif) |
Figure 2:
A scan of MEGNO for the nominal initial condition of the HD 12661 system, over
the semi-major axis of the inner planet (in AU). The upper graph is for
MEGNO. Two graphs at the bottom (in the gray shaded area) are for the
maximal values of the eccentricity of the inner planet (thick line) and the
outer planet (thin line), attained during the integration time equal to
104 periods of the outer planet. The resolution of the plots is
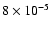 AU. Triangles at the level of 3.5 indicate the nominal positions of
mean motion resonances, and they are labeled. The nominal value of AU. Triangles at the level of 3.5 indicate the nominal positions of
mean motion resonances, and they are labeled. The nominal value of
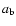 is marked with a thin vertical line at 0.82 AU. Regions of mean
motion resonances analyzed in Fig. 3 are shaded in light-gray.
is marked with a thin vertical line at 0.82 AU. Regions of mean
motion resonances analyzed in Fig. 3 are shaded in light-gray. |
| Open with DEXTER |
The nominal HD 12661 system lies on the border of a regular regime of motion.
This fact can provide another argument for the long-term, bounded behaviour
of the system, although without its confirmation by direct integrations, for
now it should be treated as speculative. Because the motion is close to a
separatrix (or takes place within it), it can be influenced by the
stickiness phenomenon. This effect was studied, e.g., by Murison et al. (1994),
and recently, by Tsiganis et al. (2000, 2002), for the models of
asteroid motion in the Solar system. The former authors found that the
long-term evolution of chaotic orbits initiated in the vicinity of some
high-order mean motion resonances with Jupiter is possible if there exist no
resonant periodic orbits in the framework of the elliptic-three body
problem. They showed that, in more complicated dynamical models, the
long-term evolution of chaotic orbits may also be governed by secular
resonances. The "stable-chaotic'' orbits found for some asteroids behave in a
way characteristic for trajectories being "sticky'' around an invariant
manifold of lower-than-full dimensionality in phase space. The dynamical
effects observed in the nominal HD 12661 system is reminiscent of the models
analyzed by Tsiganis et al. (2000, 2002). By analogy, the hypothesis
of the "stable-chaotic'' motion of the HD 12661 system can be supported by the
presence of the stickiness effect, which takes place in addition to the
secular resonance.
In the scan shown in Fig. 2, we can identify other MMR's which
are characterized by structures similar to that found in the case of the 11:2
MMR, i.e., a stable zone bounded by two symmetric spikes, indicating the
separatrix regions. This is clearly seen for the 8:1, 7:1, 6:1, 13:2, and 9:2
MMR. (Note that qualitatively similar structures, indicating the presence of
resonances, are observed in low-dimensional Hamiltonian systems
(Cincotta & Simó 2000).) The identification is illustrated by a few examples
shown in Fig. 3. This figure illustrates critical arguments of
the MMR's. In all these cases the apsidal resonance is also present. The
stabilizing influence of these resonances can be clearly recognized in the
evolution of the eccentricities (see the two graphs at the bottom of
Fig. 2). The maximal eccentricity of the outer, smaller planet,
is significantly lowered in the stable zones of the MMR's. The MEGNO scan
reveals a very interesting structure of the 5:1 MMR. In this instance, we
found an unstable zone in the middle of the resonance, together with
surrounding it, two unstable "wings''. The SAR is also present. The scan
makes it possible to estimate the width of the mean motion resonance as
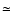 0.025 AU. In Fig. 2, a large number of other spikes
of MEGNO can be identified with high order resonances.
0.025 AU. In Fig. 2, a large number of other spikes
of MEGNO can be identified with high order resonances.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{h3945f3.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg57.gif) |
Figure 3:
Evolution of the critical arguments of mean motion resonances (the left
panels) and the critical argument of the apsidal resonance (the right
panels), calculated for a few initial conditions localized within the
resonances identified in Fig. 2. Panels a), a') are for the
stable 11:2 MMR. Panels b), b') and c), c') are for the middle
unstable and the left stable region of the 5:1 MMR, respectively. Note the
chaotic changes of 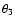 in panel b'). Panels d), d'), and
e), e') are for the stable center and for the unstable border of the
6:1 MMR, respectively.
in panel b'). Panels d), d'), and
e), e') are for the stable center and for the unstable border of the
6:1 MMR, respectively. |
| Open with DEXTER |
In the next experiment, we calculated 2D-MEGNO maps in the plane of
semi-major axes. The result is shown in the left panel of
Fig. 4. In this plot we can easily recognize MMR's already
identified in the one-dimensional scan. The middle panel of
Fig. 4 helps us to see the SAR and to estimate a
semi-amplitude of its critical argument 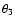 .
It has been derived by
the following simple method. In the program computing MEGNO, we evaluated
maximal value
.
It has been derived by
the following simple method. In the program computing MEGNO, we evaluated
maximal value
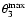 of
of 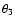 after every step of
renormalization of the variational equations. (The time step was equal to the
orbital period of the outer planet.) The maximal value of the critical
argument was taken relative to the center of libration
after every step of
renormalization of the variational equations. (The time step was equal to the
orbital period of the outer planet.) The maximal value of the critical
argument was taken relative to the center of libration
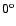 ,
or
,
or
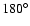 .
To avoid the effects of a possible transition into the apsidal
resonance, the determination of
.
To avoid the effects of a possible transition into the apsidal
resonance, the determination of
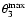 was started after the
first half of the integration period. Finally, if
was started after the
first half of the integration period. Finally, if
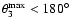 ,
then we treated this value as a
semi-amplitude of apsidal librations. Although the period of integrations is
relatively short, such an approximation of the semi-amplitude gives much
insight into the global dynamics of the system. One should be aware that the
apsidal resonance, in the sense considered here, can appear in chaotic zones
temporarily (for an illustration see Fig. 3b'). The result is
also false if the system is trapped into the secular resonance after a time
which is longer than the integration period. Moreover, a combination of
MEGNO- with
,
then we treated this value as a
semi-amplitude of apsidal librations. Although the period of integrations is
relatively short, such an approximation of the semi-amplitude gives much
insight into the global dynamics of the system. One should be aware that the
apsidal resonance, in the sense considered here, can appear in chaotic zones
temporarily (for an illustration see Fig. 3b'). The result is
also false if the system is trapped into the secular resonance after a time
which is longer than the integration period. Moreover, a combination of
MEGNO- with
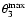 -maps still gives us much additional,
valuable information.
-maps still gives us much additional,
valuable information.
With this approach, we found that the signature of the apsidal resonance
covers a very wide neighborhood of the nominal initial condition in the
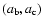 -plane and extends over 0.2 AU in
-plane and extends over 0.2 AU in
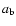 and
and
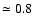 AU in
AU in
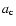 ,
respectively.
,
respectively.
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f4a.eps}\hspace*{4mm}
\in...
...f4b.eps}\hspace*{4mm}
\includegraphics[width=5.6cm]{h3945f4c.eps}
\end{figure}](/articles/aa/full/2003/06/aah3945/Timg63.gif) |
Figure 4:
Stability of the HD 12661 system in the semi-major axes plane. The left panel
is for MEGNO. The middle panel is for the semi-amplitude of apsidal librations,
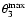 ,
relative to the libration center ,
relative to the libration center
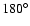 .
The
right panel shows the maximal eccentricity of the outer planet. The data
grid has the resolution .
The
right panel shows the maximal eccentricity of the outer planet. The data
grid has the resolution
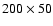 points.
points. |
| Open with DEXTER |
The stability map was also computed in the
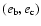 -plane
(see Fig. 5). The left panel is for MEGNO, and the middle
panel helps us to localize a region of the SAR. This simulation makes it
possible to determine the border of a global instability of the system. This
result is illustrated in the right panel of Fig. 5. In the zone
of apsidal resonance, the eccentricity of the outer planet can be as large
as
-plane
(see Fig. 5). The left panel is for MEGNO, and the middle
panel helps us to localize a region of the SAR. This simulation makes it
possible to determine the border of a global instability of the system. This
result is illustrated in the right panel of Fig. 5. In the zone
of apsidal resonance, the eccentricity of the outer planet can be as large
as 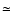 0.4 for small values of
0.4 for small values of
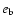 ,
and it cannot be larger
than
,
and it cannot be larger
than 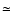 0.35 for
0.35 for
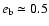 .
After this limit, global
instability occurs, leading to collisions between the companions or ejections
of a planet from the system. These limits are more extended than borders
determining quasi-periodic systems. Again, a fine correlation is evident
among the semi-amplitude of the apsidal resonance, the maximal eccentricity
of the outer planet, and structures seen in the MEGNO map. For example, let
us note an island of regular motions in the MEGNO plot around
(
.
After this limit, global
instability occurs, leading to collisions between the companions or ejections
of a planet from the system. These limits are more extended than borders
determining quasi-periodic systems. Again, a fine correlation is evident
among the semi-amplitude of the apsidal resonance, the maximal eccentricity
of the outer planet, and structures seen in the MEGNO map. For example, let
us note an island of regular motions in the MEGNO plot around
(
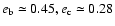 ), and its mirror images in
the
), and its mirror images in
the
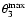 -, and
-, and
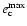 -plots. This is
even better seen in the
-plots. This is
even better seen in the
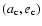 -plane, shown in
Fig. 6. In this case, the characteristic triangular -patterns,
which are present for both
-plane, shown in
Fig. 6. In this case, the characteristic triangular -patterns,
which are present for both
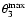 and
and
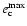 ,
have
their counterparts in the plot of MEGNO.
,
have
their counterparts in the plot of MEGNO.
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f5a.eps}\hspace*{4mm}
\in...
...b.eps}\hspace*{4mm}
\includegraphics[width=5.6cm]{h3945f5c.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg71.gif) |
Figure 5:
Stability of the HD 12661 system in the plane of the eccentricities. The left
panel if for MEGNO. The middle panel gives an estimation of the
semi-amplitude of apsidal librations,
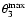 ,
about ,
about
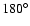 .
The right panel shows the maximal eccentricity of the outer
planet. The data grid has the resolution .
The right panel shows the maximal eccentricity of the outer
planet. The data grid has the resolution
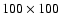 points.
points. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f6a.eps}\hspace*{4mm}
\in...
...b.eps}\hspace*{4mm}
\includegraphics[width=5.6cm]{h3945f6c.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg73.gif) |
Figure 6:
Stability of the HD 12661 system in the
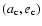 -plane. The
left panel is for MEGNO. The middle panel gives an estimation of the
semi-amplitude of apsidal librations, -plane. The
left panel is for MEGNO. The middle panel gives an estimation of the
semi-amplitude of apsidal librations,
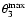 ,
about the line
of apsides antialignment. The right panel shows the maximal eccentricity of
the outer planet. The data grid has the resolution ,
about the line
of apsides antialignment. The right panel shows the maximal eccentricity of
the outer planet. The data grid has the resolution
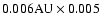 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f7a.eps}\hspace*{3mm}
\i...
...7b.eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f7c.eps}
\end{figure}](/articles/aa/full/2003/06/aah3945/Timg74.gif) |
Figure 7:
Stability map of the HD 12661 system in the plane of initial mean anomalies.
The left panel is for MEGNO, the middle panel shows the semi-amplitude of the
librations of 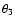 about the line of antialignment of apsides, the
right panel shows the maximal eccentricity of the outer planet. The data
grid has the resolution
about the line of antialignment of apsides, the
right panel shows the maximal eccentricity of the outer planet. The data
grid has the resolution
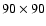 points.
points. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f8a.eps}\hspace*{3mm}
\i...
....eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f8f.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg77.gif) |
Figure 8:
Stability maps and zones of the apsidal resonance in the
(
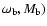 -plane (top), and in the
( -plane (top), and in the
(
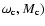 -plane (bottom). The left column is for
MEGNO. The middle columns give estimates of the semi-amplitude -plane (bottom). The left column is for
MEGNO. The middle columns give estimates of the semi-amplitude
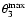 for the case of apsides aligned in the resonance. The
right column is for the semi-amplitude of the librations when the apsides are
antialigned in the exact resonance. The resolution of the plots is
for the case of apsides aligned in the resonance. The
right column is for the semi-amplitude of the librations when the apsides are
antialigned in the exact resonance. The resolution of the plots is
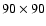 points.
points. |
| Open with DEXTER |
An inspection of stability maps calculated for different combinations of
orbital parameters, which are related to the initial orbital phase of the
planets, makes it possible to determine one more important characteristic of
the HD 12661 system. A map in the plane of the mean anomalies is shown in
Fig. 7. It uncovers an extremely complicated pattern of stable
and unstable zones. The nominal initial condition lies very close to a
relatively extended stable region. The signature of the apsidal resonance
covers the whole scan. The semi-amplitude of librations is 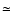
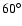 ,
with much lower values in areas correlated with stability zones
that are present in the MEGNO map. Also, the scan of the maximal eccentricity
of the outer planet is clearly correlated with this map.
,
with much lower values in areas correlated with stability zones
that are present in the MEGNO map. Also, the scan of the maximal eccentricity
of the outer planet is clearly correlated with this map.
This experiment shows that the HD 12661 system's dynamics are strongly
dependent on the orbital phases of the planets. A very small change of the
mean anomalies can lead to both stable and unstable motions. (For an
illustration, we changed the mean anomaly of the inner planet by
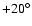 ,
with respect to the nominal data, and the resulting,
quasi-periodic evolution of
,
with respect to the nominal data, and the resulting,
quasi-periodic evolution of 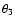 is shown in Fig. 1f.)
Because the fit errors of the mean anomalies are typically substantial, a
conclusion whether the system behaviour is quasi-periodic or chaotic,
actually seems to be very difficult to reach. Additionally, a small shift
of these initial parameters results in essential deformations of stability
maps in the planes of other orbital parameters. This is a consequence of
the sophisticated, multi-dimensional structure of the phase space in which
the HD 12661 system evolves.
is shown in Fig. 1f.)
Because the fit errors of the mean anomalies are typically substantial, a
conclusion whether the system behaviour is quasi-periodic or chaotic,
actually seems to be very difficult to reach. Additionally, a small shift
of these initial parameters results in essential deformations of stability
maps in the planes of other orbital parameters. This is a consequence of
the sophisticated, multi-dimensional structure of the phase space in which
the HD 12661 system evolves.
Another set of simulations, performed in the planes of
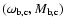 ,
is illustrated in Fig. 8
and helps us to determine a dependence of the width of the apsidal resonance
on the initial longitudes of the planets. This test reveals that the
librations of
,
is illustrated in Fig. 8
and helps us to determine a dependence of the width of the apsidal resonance
on the initial longitudes of the planets. This test reveals that the
librations of 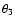 can take place not only about
can take place not only about
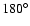 (semi-major axes are antialigned, as in the nominal system), but also about
(semi-major axes are antialigned, as in the nominal system), but also about
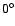 (semi-major axes are aligned). The apsidal resonance covers
almost all the scanned area. It can be seen more clearly in the
one-dimensional scan over
(semi-major axes are aligned). The apsidal resonance covers
almost all the scanned area. It can be seen more clearly in the
one-dimensional scan over
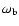 ,
calculated for the nominal
,
calculated for the nominal
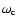 ,
and shown in Fig. 9. With the help of this
plot we discover that the zone of circulation is limited to narrow areas
around
,
and shown in Fig. 9. With the help of this
plot we discover that the zone of circulation is limited to narrow areas
around
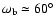 ,
and
,
and
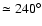 .
The
semi-amplitude of the librations can be as low as
.
The
semi-amplitude of the librations can be as low as
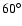 .
The MEGNO
scan, accompanying the
.
The MEGNO
scan, accompanying the
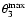 -graphs, helps us to predict
that configurations corresponding to an alignment of apsidal lines would be
mostly quasi-periodic and stable.
-graphs, helps us to predict
that configurations corresponding to an alignment of apsidal lines would be
mostly quasi-periodic and stable.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{h3945f9.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg87.gif) |
Figure 9:
An estimation of the semi-amplitude of the librations of 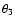 .
The scan
is over .
The scan
is over
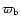 ,
with ,
with
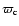 fixed at the nominal
value. The nominal
fixed at the nominal
value. The nominal
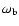 is marked by a thin vertical line. The
upper graphs correspond to libration centers
is marked by a thin vertical line. The
upper graphs correspond to libration centers 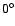 (thin line) and
(thin line) and
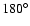 (thick line), respectively. (Note, that to make the figure more
clear, the plot for libration center
(thick line), respectively. (Note, that to make the figure more
clear, the plot for libration center 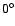 is artificially shifted by
is artificially shifted by
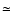
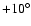 .) The graph at the bottom is for MEGNO. The resolution
of the scan is .) The graph at the bottom is for MEGNO. The resolution
of the scan is
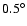 . . |
| Open with DEXTER |
In a recent paper, Malhotra (2002) analyzed a dynamical mechanism for
establishing apsidal resonance in a planetary system with two planets
initially in circular orbits. The author found that a perturbation (caused
by the ejection of a planet from the system, or by torques from a
protoplanetary disk), that changes the eccentricity of one planet's orbit,
causes the other planet's orbit to be eccentric as well. Such a mechanism can
explain the libration of the relative longitudes of apsides for a wide range
of initial conditions. The HD 12661 system seems to be a good candidate for
applying the model. The paper is based on the classical Laplace-Lagrange
secular theory (Murray & Dermott 2000). Assuming that the mean motion
resonances are absent, and the eccentricities and inclinations are small, we
can describe the secular variation of eccentricities and apsidal longitudes
by a set of first-order linear differential equations, in terms of the
quantities
called the
eccentricity vectors. The general solution for two planets is a superposition
of two eigenmodes (for each planet, j=1,2)
The amplitudes, eij, and fundamental frequencies,
gj, of the solution components are functions of the ratio of semi-major
axes,
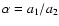 ,
and masses of the companions. The phases,
,
and masses of the companions. The phases,
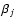 ,
are determined by the initial conditions (eccentricities and
apsidal longitudes). Using this theory, Laughlin et al. (2002) analyzed the
secular resonance in the 47 UMa system. They defined a quantity S
,
are determined by the initial conditions (eccentricities and
apsidal longitudes). Using this theory, Laughlin et al. (2002) analyzed the
secular resonance in the 47 UMa system. They defined a quantity S
which determines the behaviour of
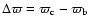 .
If S<1 then
.
If S<1 then
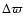 librates,
and if S>1 then
librates,
and if S>1 then
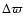 circulates. In the 47 UMa system the
eccentricities are moderately low, and the system is rather far from strong
resonances. These factors helped the authors to obtain remarkably good
qualitative agreement of the secular theory with the results of numerical
integrations.
circulates. In the 47 UMa system the
eccentricities are moderately low, and the system is rather far from strong
resonances. These factors helped the authors to obtain remarkably good
qualitative agreement of the secular theory with the results of numerical
integrations.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3945f10.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg95.gif) |
Figure 10:
Time evolution of the eccentricities as predicted by the secular theory of
Laplace-Lagrange (thin lines) and obtained by the numerical integration of
the equations of motion (thick lines), for the nominal HD 12661 system. |
| Open with DEXTER |
We performed the same test for the HD 12661 system. One should be aware that
in this case the validity of Laplace-Lagrange theory is very problematic,
because the eccentricities are large and the nominal system is near the 11:2
mean motion resonance. In fact, when applied to the nominal HD 12661 system,
the secular theory gives a very crude approximation of amplitudes and
modulation frequencies of the eccentricities (see Fig. 10). To
illustrate a comparison of the predictions of the secular theory with our
previous estimations of the zones of the SAR, we show in Fig. 11
scans of the quantity S. Formally, the initial condition is well located
within areas related to the apsidal resonance. The scan, presented in
Fig. 9, is surprisingly well reproduced in the middle panel of
Fig. 11. Both the width and the location of the secular
resonance coincide very well. However, the observed coincidence of the
results seems to be rather a matter of chance than a real value of the
secular theory. Possibly, a more elaborate secular theory, incorporating
higher terms in the masses and eccentricities, and terms related to the 11:2
mean motion resonance, will give a better analytical approximation of the
secular dynamics.
In the end, we return to the mechanism of establishing the apsidal resonance
investigated by Malhotra (2002). The author found that the amplitude of
secular variation of
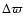 provides an observational constraint on
the dynamical history of planetary systems. Because in the HD 12661 system we
observe rather large full amplitudes of librations
provides an observational constraint on
the dynamical history of planetary systems. Because in the HD 12661 system we
observe rather large full amplitudes of librations 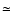
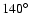 -
-
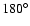 and relatively large values of
and relatively large values of
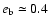 ,
the impulse mechanism could explain the eccentric orbits and
the presence of the apsidal resonance in the system. Another theory, which could
explain these features of the HD 12661 system is presented in a recent paper by
Chiang & Murray (2002).
,
the impulse mechanism could explain the eccentric orbits and
the presence of the apsidal resonance in the system. Another theory, which could
explain these features of the HD 12661 system is presented in a recent paper by
Chiang & Murray (2002).
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f11a.eps}\hspace*{3mm}
\...
...eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f11c.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg100.gif) |
Figure 11:
The quantity S calculated for the nominal HD 12661 system in the
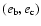 -, -,
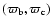 -, and -, and
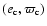 -planes. Values S<1 indicate the presence
of the apsidal resonance, as predicted by the secular theory of
Laplace-Lagrange. The data grids have the resolution -planes. Values S<1 indicate the presence
of the apsidal resonance, as predicted by the secular theory of
Laplace-Lagrange. The data grids have the resolution
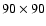 points.
points. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f12a.eps}\hspace*{3mm}
\...
...12b.eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f12c.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg101.gif) |
Figure 12:
Stability map of the HD 12661 system when the relative inclination of the
planets and the absolute inclination i are varied. The left panel is for
MEGNO. The middle panel shows the semi-amplitude of the librations of
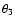 about
about
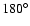 .
The right panel shows the maximal
eccentricity of the outer planet. The data grid has the resolution .
The right panel shows the maximal
eccentricity of the outer planet. The data grid has the resolution
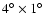 . . |
| Open with DEXTER |
The last series of numerical tests give some insight into the dependence of
system stability on planetary masses and the relative inclination of the
orbits. These parameters are unconstrained by the radial velocity
measurements. Not knowing even approximate values of these parameters, we can
only speculate on the system dynamics when they are changed within allowable
limits. We assumed in the tests that the inclinations of the orbits are
equal
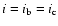 ,
and the relative inclination of the orbits
is primarily affected by the difference of nodal longitudes,
,
and the relative inclination of the orbits
is primarily affected by the difference of nodal longitudes,
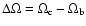 ,
according to the formula:
,
according to the formula:
We also assumed that both orbits are prograde. By changing i, we alter the
masses because the minimum masses,
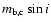 ,
corresponding to
edge-on orbits, must be preserved.
,
corresponding to
edge-on orbits, must be preserved.
The results are shown in Fig. 12. It is not surprising to find
the nominal system in a chaotic zone in the MEGNO scan. Moreover, within
this zone we detect an extended region of apsidal resonance. As in previously
analyzed scans, we can recognize a clear correlation of the
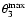 -,
-,
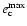 -, and MEGNO-plots in
extended ranges of inclinations. In the plot illustrating the maximal
eccentricity of the outer planet, we find a striking evidence that the
secular resonance is a crucial factor in system stability: without its
presence, the system can be strongly unstable. In chaotic zones related to
high relative inclinations and i confined to regions around
-, and MEGNO-plots in
extended ranges of inclinations. In the plot illustrating the maximal
eccentricity of the outer planet, we find a striking evidence that the
secular resonance is a crucial factor in system stability: without its
presence, the system can be strongly unstable. In chaotic zones related to
high relative inclinations and i confined to regions around
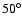 ,
the system disrupts on a timescale of a few thousands of years.
,
the system disrupts on a timescale of a few thousands of years.
Finally, we examined the stability and the width of the apsidal resonance in
(
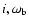 )-, and (
)-, and (
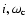 )-planes. The results of
this test are shown in Fig. 13. A clear correlation of MEGNO
maps with the maps showing
)-planes. The results of
this test are shown in Fig. 13. A clear correlation of MEGNO
maps with the maps showing
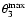 and
and
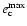 is evident. The apsidal resonance is present in
very extended ranges of the system inclination. Librations of
is evident. The apsidal resonance is present in
very extended ranges of the system inclination. Librations of 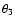 can
take place with the semi-major axes antialigned or aligned. The nominal
system seems to be deeply locked in the apsidal resonance, with
can
take place with the semi-major axes antialigned or aligned. The nominal
system seems to be deeply locked in the apsidal resonance, with 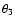 librating about
librating about
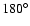 for a wide range of companion masses.
for a wide range of companion masses.
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f13a.eps}\hspace*{3mm}
\in...
....eps}\hspace*{3mm}
\includegraphics[width=5.6cm]{h3945f13f.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg111.gif) |
Figure 13:
Stability maps and zones of the apsidal resonance in the
(
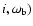 -plane (top), and in the ( -plane (top), and in the (
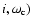 -plane
(bottom). The left column is for MEGNO. The plots in the middle column give
estimates of the semi-amplitude of the librations, -plane
(bottom). The left column is for MEGNO. The plots in the middle column give
estimates of the semi-amplitude of the librations,
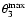 ,
for apsidal lines aligned in the exact resonance. The right column is for
the semi-amplitude of apsidal librations when the apsides are antialigned in
the resonance. Thin lines mark the initial values of the apsidal longitudes
in the nominal system. The resolution of the plots is ,
for apsidal lines aligned in the exact resonance. The right column is for
the semi-amplitude of apsidal librations when the apsides are antialigned in
the resonance. Thin lines mark the initial values of the apsidal longitudes
in the nominal system. The resolution of the plots is
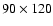 data
points.
data
points. |
| Open with DEXTER |
The dynamical analysis of the HD 12661 system provides some interesting
conclusions and raises a number of dynamical questions. The system
evolution, determined by the 2-Keplerian fit to the radial velocity
observations, is essentially chaotic, with a very short Lyapunov time of
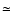 1300 yr. In spite of this strong chaotic behaviour, which can be
easily recognized in the evolution of the orbital elements, the system motion
seems to be bounded. This conclusion is supported by the 1 Gyr integrations
of the equations of motion. The stability of the system, in the astronomical
sense, is likely provided by the dynamical mechanism of the secular apsidal
resonance. It acts against the chaotic diffusion, and protects the planets
from an encounter. The secular resonance can be detected in wide ranges of
orbital elements. The current orbital fit implies that the apsidal lines
remain quite closely antialigned. By a change of initial apsidal
longitudes this configuration may be switched to librations of
1300 yr. In spite of this strong chaotic behaviour, which can be
easily recognized in the evolution of the orbital elements, the system motion
seems to be bounded. This conclusion is supported by the 1 Gyr integrations
of the equations of motion. The stability of the system, in the astronomical
sense, is likely provided by the dynamical mechanism of the secular apsidal
resonance. It acts against the chaotic diffusion, and protects the planets
from an encounter. The secular resonance can be detected in wide ranges of
orbital elements. The current orbital fit implies that the apsidal lines
remain quite closely antialigned. By a change of initial apsidal
longitudes this configuration may be switched to librations of 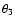 about
about 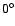 .
Statistically, the possibility of
.
Statistically, the possibility of
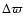 circulating is much less likely than librating about
circulating is much less likely than librating about 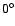 or
or
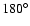 .
.
Applied to the system, the classical Laplace-Lagrange secular theory gives
only a crude description of planetary orbits calculated by numerical
integrations. Because the eccentricities of the HD 12661 planets are large and
the system is near the 11:2 mean motion resonance, this theory seems to be
not well suited for this case. Surprisingly, theoretical predictions of the
secular resonance's width and its localization in the parameters space agree
qualitatively very well with the results obtained by the numerical
integrations. Possibly, this agreement can be confirmed by a more elaborate
version of the secular theory, accounting for higher orders of masses and
eccentricities, and terms related to the 11:2 mean motion resonance.
Recently, Malhotra (2002) has shown that in a two planet-system, an
impulse perturbation on the eccentricity of the outer planet, caused, for
example, by planet-planet scattering, can excite the eccentricity of the
inner planet and will result in apsidal libration with 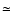 0.5
probability. In the opposite limit of a slow adiabatic perturbation (caused
for example by torques from the protoplanetary disk) that increases one
planet's eccentricity on a timescale much longer than the secular timescale
0.5
probability. In the opposite limit of a slow adiabatic perturbation (caused
for example by torques from the protoplanetary disk) that increases one
planet's eccentricity on a timescale much longer than the secular timescale
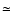 |g1-g2|-1, the apsidal resonance would occur with probability
nearly equal to 1. In this case, the resulting libration amplitude will be
small for nearly circular initial orbits. According to the theory, the
apsidal libration amplitude provides an observational diagnostic: large
amplitudes favour the impulse mechanism, whereas small amplitudes favour the
adiabatic mechanism for establishing the secular resonance. In the HD 12661 system, we observe large values of
|g1-g2|-1, the apsidal resonance would occur with probability
nearly equal to 1. In this case, the resulting libration amplitude will be
small for nearly circular initial orbits. According to the theory, the
apsidal libration amplitude provides an observational diagnostic: large
amplitudes favour the impulse mechanism, whereas small amplitudes favour the
adiabatic mechanism for establishing the secular resonance. In the HD 12661 system, we observe large values of
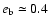 ,
and large full
libration amplitudes of
,
and large full
libration amplitudes of
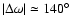 -
-
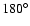 .
These factors would favour the impulse mechanism.
.
These factors would favour the impulse mechanism.
Using the combined MEGNO and short-term analysis of orbital elements, we
found that the system evolves on the border of the 11:2 mean motion
resonance. Within this resonance, the apsidal resonance acts simultaneously,
providing strictly stable, quasi-periodic configurations. A question of
whether the system may be captured into the 11:2 mean motion resonance, and
which dynamical mechanism can lead to this capture, needs a further study. We
can speculate that precise fits to the radial velocity observations, taking
into account the mutual gravitational interaction between the planets
(Laughlin & Chambers 2001), may provide systems that actually are locked in this
resonance.
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f14a.eps}\hspace*{3mm}
\in...
...5f14b.eps}\hspace*{3mm}
\includegraphics[width=5.6cm]{h3945f14c.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg113.gif) |
Figure 14:
Stability of the HD 12661 system for the revised initial condition by
Fischer et al. (2003). The left panel is for the
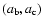 -plane.
The middle panel is for the -plane.
The middle panel is for the
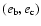 -plane. The right panel is
for the -plane. The right panel is
for the
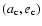 -plane. Compare with Figs. 4, 5, and 6, respectively. -plane. Compare with Figs. 4, 5, and 6, respectively. |
| Open with DEXTER |
The regime of the system motion appears to be extremely sensitive to small
changes in orbital elements. Thus, the determination of its real dynamical
state seems to be very difficult, unless we have a very precise fit to the
radial velocity data. In this case, the MEGNO stability maps change rapidly
with small changes in the initial conditions. The HD 12661 system seems to
give an example of a planetary configuration for which the formal distinction
into chaotic and quasi-periodic motion does not seem to be satisfactory for
deciding on the long-term stability in the astronomical sense. In such cases,
we propose to accompany MEGNO with simultaneous analysis of the orbital
elements, which are obtained as "a side effect'' of the MEGNO calculations.
This approach makes it possible to identify the main sources of
instabilities, and to determine dynamical factors that can stabilize the
motion. We stress that the distinct behaviours of the system, detected with
MEGNO, are definitely recognizable in the evolution of orbital elements. For
example, the MEGNO stability maps are very well correlated with maps of the
maximal eccentricities attained by the planets, in spite of a relatively
short period of integrations.
The secular apsidal resonance has been found as an important factor in
stabilizing the motion in a few newly discovered exosystems, e.g.,
 Andr (Chiang et al. 2001; Chiang & Murray 2002), Gliese 876 (Lee & Peale 2002),
possibly in HD 82943 (Gozdziewski & Maciejewski 2001), and in the 47 UMa system
(Laughlin et al. 2002; Gozdziewski 2002). The case of HD 12661 seems to give
one of the most evident examples of this resonance, and its protective role
for the dynamics of exosystems containing giant planets. We hope that when
the orbital fit for the HD 12661 system is more precise, the inquiring dynamics
of this system can be investigated more deeply.
Andr (Chiang et al. 2001; Chiang & Murray 2002), Gliese 876 (Lee & Peale 2002),
possibly in HD 82943 (Gozdziewski & Maciejewski 2001), and in the 47 UMa system
(Laughlin et al. 2002; Gozdziewski 2002). The case of HD 12661 seems to give
one of the most evident examples of this resonance, and its protective role
for the dynamics of exosystems containing giant planets. We hope that when
the orbital fit for the HD 12661 system is more precise, the inquiring dynamics
of this system can be investigated more deeply.
Recently, Fischer et al. (2003) published a revised fit to the HD 12661 radial
velocity curve. The new solution does not lead to qualitative changes of the
system dynamics. For a reference, we show scans of MEGNO in the plane of
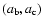 ,
,
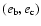 ,
and
,
and
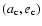 (see Fig. 14). The
orbital parameters are as follows:
(see Fig. 14). The
orbital parameters are as follows:
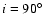 ,
,
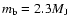 ,
,
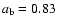 AU,
AU,
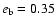 ,
,
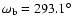 ,
,
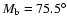 ,
,
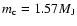 ,
,
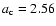 AU,
AU,
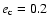 ,
,
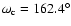 ,
,
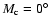 (see Table 5 in the paper cited).
(see Table 5 in the paper cited).
Note added in proofs:
Recently, we found a new, better orbital fit to the
radial velocity curve published in the preprint by
Fischer et al. (2003). This fit has
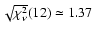 and RMS
and RMS 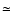 7.9 m-1. A preliminary dynamical analysis of this solution
reveals that the HD 12661 system can be locked in a stable
1:6 mean motion resonance (Gozdziewski & Maciejewski 2003,
in preparation).
7.9 m-1. A preliminary dynamical analysis of this solution
reveals that the HD 12661 system can be locked in a stable
1:6 mean motion resonance (Gozdziewski & Maciejewski 2003,
in preparation).
Acknowledgements
I am indebted to Dr. Eugenio J. Rivera for a detailed review of the
manuscript and vital remarks that improved the contents. I am very grateful
to Zbroja for corrections of the manuscript. Calculations in this paper have
been performed on the HYDRA computer-cluster, supported by the Polish
Committee for Scientific Research, Grants No. 5P03D 006 20 and
No. 2P03D 001 22. This work is supported by the Polish Committee for
Scientific Research, Grant No. 2P03D 001 22, and by the N. Copernicus
University Research Grant No. 362-A.
-
Butler, R. P., Marcy, G. W., Vogt, S. S., et al. 2002, ApJ,
submitted
In the text
-
Chiang, E. I., & Murray, N. 2002, ApJ, 576, 473
In the text
NASA ADS
-
Chiang, E. I., Tabachnik, S., & Tremaine, S. 2001, AJ, 122, 1607
In the text
NASA ADS
-
Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205
In the text
NASA ADS
-
Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2003, ApJ,
preprint, DOI: 10.1086/367889
In the text
-
Gozdziewski, K. 2002, A&A, 393, 997
In the text
NASA ADS
-
Gozdziewski, K. 2003, A&A, 398, 315
In the text
-
Gozdziewski, K., Bois, E., Maciejewski, A., & Kiseleva-Eggleton, L.
2001, A&A, 378, 569
In the text
NASA ADS
-
Gozdziewski, K., & Maciejewski, A. 2001, ApJ, 563, L81
In the text
NASA ADS
-
Hairer, E., & Wanner, G. 1995,
In the text
http://www.unige.ch/math/folks/hairer/
-
Laughlin, G., Chambers, J., & Fischer, D. 2002, ApJ, 579, 455
In the text
NASA ADS
-
Laughlin, G., & Chambers, J. E. 2001, ApJ, 551, L109
In the text
NASA ADS
-
Lee, M. H., & Peale, S. J. 2002, ApJ, 567, 596
In the text
NASA ADS
-
Levison, H. F., & Duncan, M. J. 1994, Icarus, 108, 18
In the text
NASA ADS
-
Lissauer, J. J. 1999, Rev. Mod. Phys., 71, 835
In the text
NASA ADS
-
Malhotra, R. 2002, ApJ, 575, L33
In the text
NASA ADS
-
Murison, M. A., Lecar, M., & Franklin, F. A. 1994, AJ, 108, 2323
In the text
NASA ADS
-
Murray, C. D., & Dermott, S. F. 2000, Solar System Dynamics (Cambridge
Univ. Press)
In the text
-
Tsiganis, K., Varvoglis, H., & Hadjidemetriou, J. D. 2000, Icarus, 146,
240
In the text
NASA ADS
-
Tsiganis, K., Varvoglis, H., & Hadjidemetriou, J. D. 2002, Icarus, 155, 454
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{h3945f1.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm,clip]{h3945f2.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{h3945f3.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f4a.eps}\hspace*{4mm}
\in...
...f4b.eps}\hspace*{4mm}
\includegraphics[width=5.6cm]{h3945f4c.eps}
\end{figure}](/articles/aa/full/2003/06/aah3945/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f5a.eps}\hspace*{4mm}
\in...
...b.eps}\hspace*{4mm}
\includegraphics[width=5.6cm]{h3945f5c.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f6a.eps}\hspace*{4mm}
\in...
...b.eps}\hspace*{4mm}
\includegraphics[width=5.6cm]{h3945f6c.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f7a.eps}\hspace*{3mm}
\i...
...7b.eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f7c.eps}
\end{figure}](/articles/aa/full/2003/06/aah3945/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f8a.eps}\hspace*{3mm}
\i...
....eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f8f.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg77.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{h3945f9.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg87.gif)
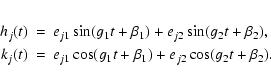
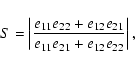
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3945f10.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg95.gif)
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f11a.eps}\hspace*{3mm}
\...
...eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f11c.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=5.75cm]{h3945f12a.eps}\hspace*{3mm}
\...
...12b.eps}\hspace*{3mm}
\includegraphics[width=5.75cm]{h3945f12c.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f13a.eps}\hspace*{3mm}
\in...
....eps}\hspace*{3mm}
\includegraphics[width=5.6cm]{h3945f13f.eps}\par\end{figure}](/articles/aa/full/2003/06/aah3945/Timg111.gif)
![\begin{figure}
\par\includegraphics[width=5.6cm]{h3945f14a.eps}\hspace*{3mm}
\in...
...5f14b.eps}\hspace*{3mm}
\includegraphics[width=5.6cm]{h3945f14c.eps}\end{figure}](/articles/aa/full/2003/06/aah3945/Timg113.gif)