

Up: From clouds to stars
A study with spherical symmetry can certainly not address all aspects of
the star formation process, as magnetic fields and angular momentum are
ignored, but it has the advantage that the process can be studied
by keeping close to basic physical principles-at least as close as stellar
evolution theory, with the notorious problem of the convection model.
Based on the concept of "maximum deduction at minimum assumptions'',
spherical symmetry provides a useful limiting and reference case.
With the symmetry assumption we are able to keep a close and
explicit relation to the fundamental conservation laws and other basic
physical principles. The essential modeling assumption that goes
into this work then is the ever present problem of the convection model.
But we have tried not to add further ambiguity that is not already present in
the modeling of stellar evolution.
As a consequence of our convection model the system
of equations we use represents the structure of the Sun correctly.
The number of free parameters
in any study of star formation cannot be made smaller than in ours unless
a parameter-free description of convection becomes available.
The energetics of the star formation process can be addressed
rather completely, most notably because all relevant energy transfer
processes, i.e., radiation, convection, advection and conduction can
be described accurately. Very likely star formation is most efficient
with zero angular momentum and hence a lower limit for star formation
time and upper limits for luminositites and accretion-rates are obtained.
Table 3:
Duration and averages
of accretion rates and luminosities for different accretion phases
of cloud fragments of
0.05, 0.1, 0.5, 1 and
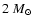 .
The phases are defined by ranges in optical thick mass
.
The phases are defined by ranges in optical thick mass
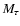 in units of the final mass
in units of the final mass
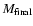 ,
in the second
column.
For each phase and fragment mass, M0,
duration,
,
in the second
column.
For each phase and fragment mass, M0,
duration,
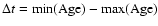 ,
mean mass-accretion rates,
,
mean mass-accretion rates,
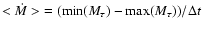 ,
and the median value for the luminosities, <L>, is given.
,
and the median value for the luminosities, <L>, is given.
Averages for 4 accretion phases separated by
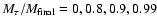 and 0.999 (cf. Fig. 4).
and 0.999 (cf. Fig. 4). |
|
M0 |
|
0.05  |
0.1  |
0.5 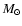 |
1 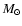 |
2 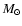 |
| |
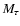 |
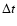 |
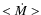 |
<L> |
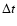 |
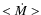 |
<L> |
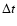 |
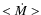 |
<L> |
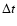 |
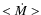 |
<L> |
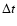 |
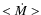 |
<L> |
| |
![$[M_{\rm final}]$](/articles/aa/full/2003/06/aa8963/img134.gif) |
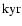 |
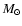 /yr /yr |
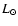 |
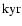 |
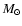 /yr /yr |
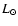 |
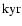 |
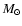 /yr /yr |
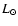 |
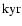 |
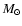 /yr /yr |
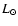 |
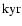 |
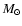 /yr /yr |
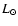 |
 |
 0.8 0.8 |
16 |
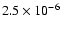 |
1.28 |
30 |
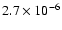 |
2.92 |
126 |
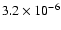 |
12.4 |
189 |
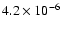 |
19.5 |
496 |
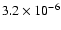 |
34.1 |
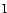 |
(0.8,0.9] |
6 |
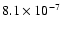 |
1.19 |
11 |
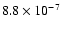 |
2.63 |
52 |
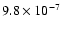 |
8.21 |
85 |
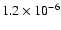 |
15.3 |
200 |
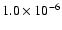 |
27.3 |
 |
(0.9,0.99] |
16 |
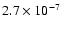 |
0.51 |
32 |
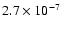 |
0.97 |
144 |
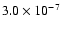 |
4.60 |
280 |
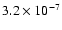 |
8.22 |
592 |
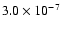 |
13.9 |
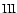 |
(0.99,0.999] |
15 |
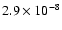 |
0.21 |
28 |
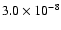 |
0.33 |
139 |
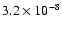 |
3.03 |
264 |
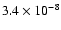 |
4.69 |
554 |
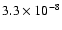 |
8.42 |
In particular spherical collapse provides quantitative
predictions for "stellar'' properties for the entire accretion process
starting with the formation of a photosphere-when a radiating
outer layer forms around an optically thick central cloud
region-to the quasi-hydrostatic pre-main sequence contraction. We have
shown that properties of stars with "initial thermal structures''
which result from the collapse of cloud fragments differ from those obtained
with simplifying assumptions like isentropic or polytropic radial structure.
The latter are commonly used as a starting point for the calculation of early
stellar evolution.
With our assumptions we can describe the pre-main sequence evolution as a
consequence of the star formation process, more precisely as a result of
the collapse of Bonnor-Ebert spheres. All "stellar'' masses appear at
locations
in the HRD that are different from the ones predicted by classical, fully
hydrostatic calculations. In particular, they do not start at the top of
a classical, initially fully convective track or at the birthline. Those
differences cannot be attributed to differences in energy transfer
treatment or differences in microphysics since we have constructed
our model equations in a way that assures a "stellar structure'' limit,
that is approached during pre-main sequence contraction and that coincides
with the assumptions made in our classical fully hydrostatic reference-study.
The ages obtained with collapse models differ significantly, i.e., up to 1 Myr,
from the ages derived from classical calculations. This is only in part due
to the fact that the time needed for collapse and accretion are not accounted
for in classical PMS calculations. The primary reason is that the contraction
behaviour of the young stars resulting from the collapse differs from
the one obtained for the usually assumed fully convective, isentropic, or
polytropic initial structures. The fact that deuterium is almost completely
burnt during the main accretion phase, i.e., before the PMS is reached for
all "truly'' stellar masses calculated here (the
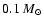 case is the
exception) also contributes to the difference.
Hence calculations of early stellar evolution depend
on the star formation process. Initial conditions are not forgotten in general.
Another way to summarize this is that the star formation time, in our study
about 3-4 free-fall times in all cases, is not sufficiently different from the
Kelvin-Helmholtz time-scale of young objects to separate initial energy
deposition into the star during the accretion phase from energy losses that
control the contraction to the main sequence. As a consequence,
protostellar collapse determines the PMS evolution.
case is the
exception) also contributes to the difference.
Hence calculations of early stellar evolution depend
on the star formation process. Initial conditions are not forgotten in general.
Another way to summarize this is that the star formation time, in our study
about 3-4 free-fall times in all cases, is not sufficiently different from the
Kelvin-Helmholtz time-scale of young objects to separate initial energy
deposition into the star during the accretion phase from energy losses that
control the contraction to the main sequence. As a consequence,
protostellar collapse determines the PMS evolution.
This effect is enhanced by the off-centre ingnition of D burning and its
interaction with
the thermal structure. Unlike during most of stellar evolution it is not only
controlled by the existing thermal structure but helps also to conserve the
global thermal structure
outside thermal equilibrium. This
differs from the usual behaviour close to complete equilibrium, e.g., of main
sequence stars, where nuclear reactions are adjusted to the thermal needs of
the star and re-establish global thermal equilibrium.
Our study re-emphasises the fact that star formation is an intrinsically time
dependent process, with variations in all flow quantities. We have tried to
tentatively group the young population into four different evolutionary phases
based on the fraction of the residual circumstellar mass around them.
We gave characteristic quantities for those phases showing that mass
accretion rates vary significantly over the main accretion phase.
Accretion rates are typically a few
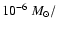 yr in the earliest
phase, a few
yr in the earliest
phase, a few
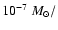 yr for the last 10% and
a few
yr for the last 10% and
a few
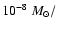 yr for the accretion of the last percent
of the final mass. Those values are not too far from what is currently inferred
from observations (e.g., Brown & Chandler 1999). Also our star formation times
of 0.07 to
yr for the accretion of the last percent
of the final mass. Those values are not too far from what is currently inferred
from observations (e.g., Brown & Chandler 1999). Also our star formation times
of 0.07 to
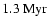 for 0.1 to
for 0.1 to
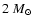 are consistent
with estimates from a comparison of T Tauri star- and embedded source
counts (Kenyon et al. 1990). Our median luminosities between about 0.3 to 10
are consistent
with estimates from a comparison of T Tauri star- and embedded source
counts (Kenyon et al. 1990). Our median luminosities between about 0.3 to 10 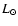 ,
depending on accretion phases, for cloud fragment masses from
0.01 to
,
depending on accretion phases, for cloud fragment masses from
0.01 to
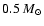 ,
make it much harder to construct a
"Class I luminosity problem'' than with the assumed constant, canonical mass
accretion rate of
,
make it much harder to construct a
"Class I luminosity problem'' than with the assumed constant, canonical mass
accretion rate of
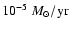 ,
that is in conflict with observations
(Brown & Chandler 1999).
Let us finally summarize our main points:
(1) the star formation processes, i.e., the protostellar collapse translates
initial cloud conditions into initial stellar thermal structure,
(2) pre-main sequence evolution depends qualitatively and
quantitatively on the collapse flows;
(3) D burning ignites and mostly occurs
during the accretion phase for cloud fragments of 0.5, 1, 2, and
,
that is in conflict with observations
(Brown & Chandler 1999).
Let us finally summarize our main points:
(1) the star formation processes, i.e., the protostellar collapse translates
initial cloud conditions into initial stellar thermal structure,
(2) pre-main sequence evolution depends qualitatively and
quantitatively on the collapse flows;
(3) D burning ignites and mostly occurs
during the accretion phase for cloud fragments of 0.5, 1, 2, and
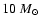 ;
(4) we confirm that protostars and PMS objects
have an outer convective shell and a
central radiative zone;
(5) the radiative core lasts at least to a (new) age of
1.5 Myr for cloud fragments of 0.5, 1, and
;
(4) we confirm that protostars and PMS objects
have an outer convective shell and a
central radiative zone;
(5) the radiative core lasts at least to a (new) age of
1.5 Myr for cloud fragments of 0.5, 1, and
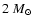 and we expect off-centre ignition of
hydrogen burning;
(6) collapse pre-main sequence tracks are initially cooler
than classical tracks. Later they cross the Hayashi
line rapidly and start their quasi-classical decent along a mixed
radiative/convective contraction track. After the final stellar
photosphere becomes visible they appear to the left of the
Hayashi lines. Typically at 0.05 dex hotter effective
temperatures than the corresponding classical, fully
hydrostatic pre-main sequence model;
(7) already during the early pre-main sequence phase the solar
mass case is roughly homologous to the Sun with its
radiative core rather
than to a fully convective star on the Hayashi track;
(8) collapse ages below 2 Myr are up to a Myr older than classical
ages for the same luminosity.
and we expect off-centre ignition of
hydrogen burning;
(6) collapse pre-main sequence tracks are initially cooler
than classical tracks. Later they cross the Hayashi
line rapidly and start their quasi-classical decent along a mixed
radiative/convective contraction track. After the final stellar
photosphere becomes visible they appear to the left of the
Hayashi lines. Typically at 0.05 dex hotter effective
temperatures than the corresponding classical, fully
hydrostatic pre-main sequence model;
(7) already during the early pre-main sequence phase the solar
mass case is roughly homologous to the Sun with its
radiative core rather
than to a fully convective star on the Hayashi track;
(8) collapse ages below 2 Myr are up to a Myr older than classical
ages for the same luminosity.
Acknowledgements
This work was supported by the Fonds
zur Förderung der wissenschaftlichen Forschung (FWF)
under
project numbers S7305-AST and S7307-AST and the
Deutsche
Forschungsgemeinschaft (DFG), SFB 359
(collaborative research center of the German national
science
foundation on "Reactive flows, diffusion and transport'').
GW thanks M. Feuchtinger for the collaboration on the convection
model and sharing the version of the VIP-code and the computational
environment that he developed, and H. Herndl for
providing a subroutine for the calculation of D reaction
rates.
We thank E. Dorfi for developing and
sharing the original version of the VIP-code and providing
substantial amounts of computational resources on
his VAX-cluster in Vienna where the computations were perfomed, and
for comments and discussion. We thank Christian Straka for
reading the manuscript.
We are indebted to Prof. H. Petersmann from the
Seminar für Klassische Philologie, University of Heidelberg,
for a most elucidated advice on the semantics and etymology of
the term isopleths.
from the
Seminar für Klassische Philologie, University of Heidelberg,
for a most elucidated advice on the semantics and etymology of
the term isopleths.


Up: From clouds to stars
Copyright ESO 2003