A&A 398, 1137-1149 (2003)
DOI: 10.1051/0004-6361:20021737

A study of coronal abundances in RS CVn binaries[*]

M. Audard1,[*] - M. Güdel1 - A. Sres2 - A. J. J. Raassen3,4 - R. Mewe3


1 - Paul Scherrer Institut, Würenlingen & Villigen, 5232 Villigen PSI, Switzerland
2 - Institute of Astronomy, ETH Zentrum, 8092 Zürich, Switzerland
3 - Space Research Organization of the Netherlands, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
4 - Astronomical Institute ``Anton Pannekoek'', Kruislaan 403, 1098 SJ Amsterdam, The Netherlands

Received 18 September 2002 / Accepted 21 November 2002

Abstract
We present XMM-Newton data of several RS CVn binary systems. High-resolution X-ray spectra obtained with the Reflection Grating Spectrometers have been interpreted simultaneously with the European Photon Imaging Camera spectra. Highly active stars show a depletion of elements with a low first ionization potential (FIP) relative to high-FIP elements, whereas intermediately active binaries show either no FIP bias or a possible solar-like FIP effect. We find that the low-FIP abundance ratios to oxygen vary with the coronal average temperature whereas the ratios for high-FIP elements stay constant. Since we observe that the absolute Fe (low-FIP) abundance increases with decreasing activity, this suggests that the abundances of elements with low FIP vary with the coronal activity level. Compared with laboratory measurements of the intensity ratios of the Fe XVII $\lambda\lambda$ 15.01 and 15.26 Å lines, the coronal plasmas are in the optically thin regime.

Key words: stars: abundances - stars: activity - stars: coronae - stars: flare - X-rays: stars


1 Introduction

The class of RS CVn binaries is loosely defined as a class of detached binary systems typically composed of a chromospherically active G or K star, usually evolved, with a late-type main-sequence or subgiant companion (Hall 1976). RS CVn binary systems generally rotate fast with typical orbital periods of a few days; tidal forces (Zahn 1966, 1975) between the two close components have locked their rotation periods to the orbital period ( $P_{\rm orb} = P_{\rm rot}$). These systems display a high level of activity with strong chromospheric line emissions and saturated coronal X-ray emission ( $L_{\rm X}/L_{\rm bol} \approx 10^{-3}$). High-resolution radio observations of RS CVn binary systems show extended magnetospheres (e.g., Mutel et al. 1985), consisting of a diffuse component ("halo'') and an unresolved compact component ("core''). Previous high-resolution data with EUVE showed that the emission measure (EM) distributions of active RS CVn binaries typically display hot plasma with peaks around $\log T_{\rm e} \approx 6.9$ and possibly at 7.35 (Griffiths & Jordan 1998; Griffiths 1999), although the latter peak could not be well constrained. Recent Chandra and XMM-Newton, with more extended spectral ranges, however suggest the presence of a broad EM distribution with local peaks around these temperatures (e.g., Drake et al. 2001; Audard et al. 2001a). Such systems often display powerful energetic flares, with very high temperatures (several tens of MK up to $\approx $100 MK, e.g., Güdel et al. 1999; Franciosini et al. 2001). EM distributions show a very hot (50-100 MK) plasma component that develops and dominates the X-ray emission during flares, although the cooler "quiescent'' part of the EM distribution remains unchanged (e.g., Güdel et al. 1999).

Recent X-ray spectral observations of magnetically active stars have renewed interest in the study of coronal composition. The elemental composition of the solar corona, of the solar wind, and of solar energetic particles (and even of galactic cosmic rays) shows a systematic pattern relative to solar photospheric abundances: elements with a low First Ionization Potential (FIP) are overabundant by factors of 4-6 relative to their respective photospheric abundances, whereas high-FIP elements are of photospheric composition (Meyer 1985; Feldman 1992; Laming et al. 1995). This effect implies the presence of a fractionation mechanism in the chromosphere which has the adequate temperature (5000-10 000 K) to ionize low-FIP elements and leave high-FIP elements mostly in a neutral state. Previous stellar analyses found abundance patterns sometimes at variance with the solar photospheric composition (e.g., Drake et al. 1994; White et al. 1994; Singh et al. 1996; Maggio et al. 1998). High-resolution spectroscopy in the extreme ultraviolet range with EUVE confirmed the overall deficiency of metal abundances (mostly Fe) in active RS CVn binaries (Schmitt et al. 1996a). Detailed studies with EUVE showed either the absence of any FIP-related bias (Drake et al. 1995), or the presence of a FIP effect in inactive stellar coronae (Drake et al. 1997; Laming & Drake 1999). The recent observations of active stars with XMM-Newton and Chandra have shown that an inverse FIP effect may be common in active stars (e.g., Brinkman et al. 2001; Audard et al. 2001a; Drake et al. 2001; Güdel et al. 2001a,b; Huenemoerder et al. 2001). The intermediately active binary star Capella, however, did not show evidence for either a FIP or an inverse FIP effect (Audard et al. 2001b). In contrast, significant increases of metal abundance have been found during flares in M stars, Algol-type and RS CVn-type binaries (e.g., Ottmann & Schmitt 1996; Mewe et al. 1997; Favata et al. 2000); medium-resolution spectra allowed to find complex patterns of abundance increases during a large flare in UX Ari (Güdel et al. 1999), where low-FIP elements increased to higher levels than the high-FIP elements. High-resolution spectroscopy of a flare in HR 1099 with XMM-Newton confirmed this pattern (Audard et al. 2001a). Recently, Güdel et al. (2002) brought up a broader view on the coronal composition in active stars. Their studies of solar-like spectra suggest that a transition from inverse FIP to a normal FIP effect occurs as the activity decreases. Note that their sample of stars have photospheres with abundances similar to the solar composition, hence it avoids any bias due to the uncertainty of the photospheric abundances. In this paper, we show that a similar transition is suggested in RS CVn binary stars; however, these systems are so active that only a transition from an inverse FIP effect to the absence of any FIP bias can be observed.

We present high-quality XMM-Newton data of five RS CVn binary systems with high to intermediate levels of activity: HR 1099 (=V711 Tauri), UX Arietis, $\lambda $ Andromedae, VY Arietis, and Capella (=$\alpha $ Aurigae). Some properties are given in Table 1. These non-eclipsing binaries are X-ray bright (Dempsey et al. 1993), with enhanced activity levels relative to single main-sequence solar-type stars. Despite their binarity, X-ray emission is believed to generally originate from the evolved star (e.g., Ayres et al. 2001; except for Capella, where both giants emit significantly in X-rays, Linsky et al. 1998).

In Sect. 2, we give details on the observations and data reduction; Sect. 3 describes the approach used to interpret the data. In Sect. 4, we discuss the results in terms of a FIP-biased abundance pattern (Sect. 4.1). We investigate the relevance of optical depths in stellar coronae (Sect. 4.2), and the importance of the use of solar (Sect. 4.3) and stellar (Sect. 4.4) photospheric abundances. In Sect. 4.5 we put our results for RS CVn binaries in relation with those in solar analogs. Finally, we present our conclusions in Sect. 5.

  
2 Observations and data reduction

The data presented here were obtained during the commissioning and the calibration phases of XMM-Newton, and as part of the Guaranteed Time of Reflection Grating Spectrometer Team. We present results based on the "quiescent'' X-ray spectra of the five targets. With the exception of HR 1099, their light curves showed no evidence for rapid flux variations as typical of flares; they were either constant or slowly varying within 25%. The binary HR 1099 displayed a strong flare at the end of the observation (Audard et al. 2001a); we have selected only the low-level pre-flare emission in this paper. Note that the HR 1099 and Capella data, previously published (Audard et al. 2001a,b), have been reanalyzed with a more recent and more accurate calibration. Table 2 gives the observation log for the five RS CVn binaries. We used only observations for which both EPIC and RGS observed our targets simultaneously (except for Capella).


 

 
Table 1: Properties of the targets; spectral types and orbital periods from Strassmeier et al. (1993), distances from Perryman et al. (1997).

Target		 Spectral Type $P_{\rm orb}$ (d) d (pc)

HR 1099		 K1 IV+G5 IV-V 2.84 28.97
UX Ari K0 IV+G5 V 6.44 50.23
$\lambda $ And G8 IV-III 20.52 25.81
VY Ari K3-4 IV-V 13.20 43.99
Capella G0 III+G8 III 104.02 12.94



   
Table 2: Observation log of the data presented in this paper. The revolution number and the observation identification number are given after the object's name. Dates are given in yyyy-mm-ddThh:mm:ss format. The exposures (in ksec) are corrected for deadtime.

INSTRUMENT		 FILTER MODE DATE-OBS (UT) DATE-END (UT) Exposure

HR 1099, rev 36, obsid 0117890901		  

MOS2$\dots$		 MEDIUM FULL FRAME 2000-02-18T14:26:07 2000-02-19T05:29:01a 40.3
RGS1$\dots$ NONE SPEC+Q 2000-02-18T13:24:45 2000-02-19T05:25:41a 43.9
RGS2$\dots$ NONE SPEC+Q 2000-02-18T13:24:45 2000-02-19T05:25:41a 43.9

UX Ari, rev 218, obsid 0111390301		  

MOS2$\dots$		 MEDIUM SMALL WINDOW 2001-02-15T19:39:30 2001-02-16T03:51:34 28.5
RGS1$\dots$ NONE SPEC+Q 2001-02-15T19:30:54 2001-02-16T04:08:30 30.9
RGS2$\dots$ NONE SPEC+Q 2001-02-15T19:30:54 2001-02-16T04:08:30 30.9

$\lambda $ And, rev 208, obsid 0099320101		  

MOS2$\dots$		 THICK SMALL WINDOW 2001-01-26T20:10:05 2001-01-27T04:08:49 27.7
RGS1$\dots$ NONE SPEC+Q 2001-01-26T19:21:29 2001-01-27T04:15:45 31.8
RGS2$\dots$ NONE SPEC+Q 2001-01-26T19:21:29 2001-01-27T04:15:45 31.8

VY Ari, rev 217, obsid 0111490401		  

MOS2$\dots$		 MEDIUM SMALL WINDOW 2001-02-13T19:33:30 2001-02-14T04:43:04 31.8
RGS1$\dots$ NONE SPEC+Q 2001-02-13T19:24:54 2001-02-14T04:50:50 33.8
RGS2$\dots$ NONE SPEC+Q 2001-02-13T19:24:54 2001-02-14T04:50:50 33.8

Capella, rev 54, obsid 0121920101		  

RGS1$\dots$		 NONE SPECTROSCOPY 2000-03-25T11:36:33 2000-03-26T02:54:09b 52.9
RGS2$\dots$ NONE SPECTROSCOPY 2000-03-25T11:36:33 2000-03-26T02:54:09b 52.9

a Quiescent data before 2000-02-19T01:46:40 UT only were used.		  
b Data from 00:30 to 00:50 UT on 2000 March 26 discarded due to attitude problems.  

The XMM-Newton Observatory (Jansen et al. 2001) carries three Wolter-type I X-ray telescopes which allow for simultaneous observations by five different detectors: two MOS-type (Turner et al. 2001) and one pn-type (Strüder et al. 2001) European Photon Imaging Cameras (EPIC), and two Reflection Grating Spectrometers (RGS; den Herder et al. 2001). An optical telescope, the Optical Monitor (OM; Mason et al. 2001), observes simultaneously as well. The EPIC instruments are sensitive from 0.1 to 15 keV, with a higher spectral resolution in the MOS than in the pn, although the sensitivity of the latter is higher. The RGS provide spectra at high resolution ( ${E/\Delta E} = 100{-}500$FWHM) in the soft X-ray range from 6 to 38 Å (0.3-2.1 keV; effective area $A_{\rm eff} \approx 140$ cm2 around 15 Å) and are optimized for the detection of H-like and He-like transitions of abundant elements (C, N, O, Ne, Mg, Si) and of a number of L-shell Fe transitions.

The XMM-Newton Science Analysis System (SAS) has been used to reduce the data, in conjunction with calibration files (June 2001). We used standard processing performed by the RGS metatask rgsproc and the EPIC MOS task emchain. The HR 1099 and Capella data were provided to us as part of the calibration phase; such data can be analyzed with the SAS in the same way as archival data. One of the main purposes of this analysis being the determination of coronal abundances, we have decided to give a larger weight to the high-resolution RGS data than to the EPIC data. Therefore, data from only one EPIC MOS have been used (MOS2 for practical reasons). It gives us access to the H-like and He-like transitions of Si, S, Ar, and Ca, and to the Fe K-shell transitions at 6.7 keV. The high-temperature component of the thermal bremsstrahlung continuum is also better constrained by the EPIC data. However, we did not use the full MOS spectrum in our fits, but only its information at energies above $\approx $1.33 keV (see below in Sect. 3.1 for more details). With the exception of HR 1099, EPIC MOS2 data were taken in the small window mode. In this mode, only the inner $100\times100$ pixels of the central CCD work (whereas the other 6 outer CCDs work nominally), with a smaller integration time, thus bright objects suffer less from pile-up. The disadvantage of this mode is that its window size is too small to extract a background region from the central CCD; therefore, we selected a source-free region on an outer CCD. No time-screening was applied since the background contamination due to solar flares was low during these observations.

We used the EPIC MOS instrument team response matrices (m2_medv9q19t5r5_all_15.rsp and m2_thickv9q19t5r5_all_15.rsp for the medium and thick filters, respectively). For VY Ari, UX Ari, and $\lambda $ And, we extracted the source data from a circle as large as the small window mode could allow ($\approx $1000 detector pixels = 50 $^{\prime\prime}$). Despite the brightness of the targets, the operating mode allowed us to obtain spectra with negligible pile-up for these stars. Indeed, the difference between spectra extracted with photon pattern 0 only and with patterns 0-12 (the default) proved to be insignificant. We additionally constructed images, divided the pixel values by the average exposure time, and multiplied it by the frame integration time to get units of counts per pixel per frame. We then confirmed that there were very few pixels with more than 0.01 counts per pixel per frame, a practical limit above which pile-up begins to be important (Jean Ballet, private communication). For HR 1099, despite the off-axis pointing (the source lies on CCD 6 on MOS2 and in CCD gaps for MOS1 and pn), the brightness of the source and the full frame mode produced severe pile-up; therefore, we used an annulus extraction region with inner and outer radii of 300 and 1800 detector pixels, respectively, to remove the piled-up central part of the XMM-Newton Point Spread Function (PSF). We used circular extraction regions on other CCD chips to obtain background information. Note that the sources were much brighter than the background, thus the former dominate the spectral features (except at the highest energies - typically above 8 keV - and possibly below 0.15 keV - but we always cut data below 1.33 keV, see Sect. 3.1). We did not apply corrections for vignetting, since the latter essentially has no influence on the contamination by soft protons (J. Ballet, private communication). Furthermore, the background spectra are consistent with the internal MOS detector background, thus the contribution by the vignetted cosmic X-ray background is negligible. Even if some correction factor should need to be applied, it would range between 20-30% and thus would essentially reduce slightly the high temperature component, however within the temperature uncertainties and with no essential influence on the abundances. For Capella, no EPIC data could be used due to severe optical contamination and pile-up.

For the RGS data reduction, we extracted the first order net spectra from a spatial cut including 90% of the cross-dispersion PSF (xpsfincl=90 in rgsproc) and an energy cut including 95% of the pulse-height distribution (pdistincl=95). The background spectra were extracted above and below the source spectra, by excluding 95% of the source's cross-dispersion PSF (xpsfexcl=95). The RGS matrices were created by rgsrmfgen 0.41 (except for VY Ari for which we used rgsrmfgen 0.44; the differences between the two versions are negligible and have virtually no impact), with 6000 energy bins and correcting for the background subtraction, and for the spatial and pulse-height cuts.

  
3 High-resolution X-ray spectra

We have interpreted the EPIC and RGS spectra using collisional ionization equilibrium (CIE) plasma models with variable cosmic abundances. To obtain reasonable estimates taking into account the uncertainties in the atomic parameters, we have used two different software packages that contain different atomic databases. The Utrecht software SPEX (Kaastra et al. 1996) uses an updated version of the MEKAL spectral code (Mewe et al. 1985; Mewe et al. 1995a; Phillips et al. 1999) with ionization balances from Arnaud & Rothenflug (1985) and Arnaud & Raymond (1992) for Fe. The XSPEC 11.0.1aj (Arnaud 1996) software uses the APEC 1.0.1 spectral code (Smith et al. 2001) with the self-consistent ionization balance from Mazzotta et al. (1998). The RGS spectra were grouped with a minimum of 30 to 80 counts per bin (depending on the source), whereas the EPIC MOS2 data were binned with a minimum of 25 counts per bin (100 for HR 1099).

  
3.1 Analysis approach

X-ray spectra have conventionally been interpreted either by measuring a number of selected lines above the continuum level and subsequently reconstructing the emission measure distribution and the abundances; or by fitting complete thermal models to the total spectrum. Each approach encounters severe limitations with our data. Extracting single line fluxes from RGS spectra is difficult in particular in the crucial but crowded region between 10-20 Å because of line blends and strongly overlapping line profiles and extended line wings. On the other hand, fits of the complete spectrum with pre-calculated thermal models are affected by numerous emission lines with poor atomic physics parameters in the codes (e.g., Audard et al. 2001b; Laming 2002; Raassen et al. 2002). We have chosen to apply a method half-way between the above two extremes that is ideally suited for RGS spectra. We selected a restricted number of individual, bright lines that are believed to be well known in the spectral codes and that cover a wide range of elements and ionization stages. Pieces of most likely line-free regions have been included for an accurate determination of the continuum level. By modeling the lines together and using the calibrated line spread function, we obtain an optimum determination of the fluxes of all overlapping lines. Since we still use a full thermal model including all catalogued lines and the continuum falling within the considered pieces of the spectrum, the method simultaneously takes care of possible ill-recognized weaker lines that may add a pseudo-continuum or that may blend with the selected line, thus altering their fluxes. Our method thus tries to maximize the information extraction from individual lines, and at the same time it approximately models additional flux contributions by weak lines in a self-consistent way.

The high signal-to-noise ratios of the spectra of our RS CVn binaries display a well-developed continuum emission, allowing us to put constraints on the EM from regions free of emission lines. The RGS and EPIC MOS2 spectra were interpreted simultaneously, with the exception of Capella (RGS only). We have introduced a free constant model to multiply the physical model for EPIC. This factor takes into account cross-calibration inaccuracies and especially corrects for the finite extraction radius used to obtain the source spectra. Indeed, the EPIC responses had been built under the assumption of an infinite extraction radius, hence overestimating the effective area. Note that the XMM-Newton on-axis PSF for the MOS cameras are almost energy-independent (Ehle et al. 2001); our 50 $^{\prime\prime}$ extraction regions include $\approx $90% of the fractional encircled energy. The best-fit values for the constant ranged between 0.90-0.95, except for HR 1099 (0.23-0.25) because we removed the central part of the PSF. To profit from the higher spectral resolution of the RGS, we have discarded the EPIC wavelength range longward of the Mg IX He$\alpha $ triplet ( $\lambda \ge 9.35$ Å, $E \le 1.33$ keV). Similarly, we eliminated the RGS wavelength range shortward of the Mg X Ly$\alpha $ line ( $\lambda \le 8.3$ Å, $E \ge 1.49$ keV) because of the small RGS effective area at high energies and the consequent limited quality of the calibration - with the exception of Capella, for which we included the range from 6.5 to 6.8 Å to account for the bright Si He-like triplet. Therefore, the RGS and EPIC spectra overlap around the Mg lines. The consistency between the two detector systems is additionally provided by the cross calibration, and by the broad-band continuum in both spectra.

  \begin{figure} \par\includegraphics[width=16.4cm,clip]{MS3099f1.eps} \end{figure} Figure 1: RGS first order spectra of the observed targets. The size of the wavelength bin is 25 mÅ. The spectra are ordered approximately with decreasing coronal activity (defined in this paper as the average coronal temperature) from top to bottom.
Open with DEXTER


 

 
Table 3: Spectral wavelength ranges excluded from the fitting procedure. Note that RGS stands for both RGS1 and RGS2.

Instrument		 $\lambda $ range (Å)

RGS ............................................		 $\leq $8.3a
RGS ............................................ 9.50-12.00
RGS ............................................ 13.95-14.15
RGS ............................................ 15.90-16.20
RGS ............................................ 17.15-17.80
RGS ............................................ 18.30-18.75
RGS ............................................ 19.20-20.80
RGS ............................................ 21.10-21.40
RGS1 .......................................... $\geq $22.40
RGS2 .......................................... 22.40-23.65
RGS2 .......................................... 24.00-24.50
RGS2 .......................................... 24.90-28.50
RGS2 .......................................... 30.10-31.10
RGS2 .......................................... 32.00-33.40
RGS2 .......................................... $\geq $33.85
MOS2 .......................................... $\leq $1.00
MOS2 .......................................... 6.80-7.80
MOS2 .......................................... $\geq $9.35

a For Capella, we included the range 6.5-6.8 Å.


The physical model was defined as a photoelectric absorption component with free atomic H column density (only for RGS1 and RGS2), and a combination of CIE models with free temperature, EM, and abundances (C, N, O, Ne, Mg, Si, S, Ar, Ca, Fe, Ni). In practice, a 4-T model proved adequate to fit the spectra, except for Capella for which a 3-T model was sufficient. The absorption components were left free to vary between RGS1 and RGS2 to account for cross-calibration uncertainties between the two instruments at the long wavelength end. The interstellar absorption is negligible for these nearby sources in the wavelength range of the RGS. Note that we have included an absorption edge model at 23.3 Å that was not yet included in the RGS effective areas generated by XMM-Newton SAS 5.2 (see, e.g., den Herder et al. 2002)[*].


  \begin{figure} \par\resizebox{\hsize}{!}{% \includegraphics[width=17cm]{MS3099f2.eps}} \end{figure} Figure 2: Extract of EPIC MOS2 spectra from 1 to 10 keV. The spectra have been shifted logarithmically along the vertical axis, for clarity (see labels). Some H-like and He-like transitions are indicated.
Open with DEXTER

  
3.2 Exclusion of lines with inaccurate atomic data

For this paper, we have decided to systematically exclude RGS spectral ranges where L-shell lines dominate (except those of Fe and Ni) because these lines are often inaccurately described in present spectral codes (Audard et al. 2001b). Eventually, most of the long wavelength range of the RGS spectra was eliminated. There remain however still some relatively bright low-Z L-shell lines in Capella's spectrum that we used to obtain the Si, S, Ar, and Ca abundances. These lines have atomic parameter uncertainties in the range 10-50%. The results, in particular for S, Ar, and Ca for Capella should therefore be treated with some caution. The Si He-like triplet was also included for this star; we caution, however, that the calibration of the effective area in this range is less reliable. A few Fe lines were discarded as well (e.g., Fe XVIII $\lambda $ 16.0 Å, Fe lines in the 9.5-12.0 Å range) as they were poorly fitted with both spectral codes. Table 3 summarizes the spectral ranges excluded from the fitting procedure.


  
Table 4: Elemental abundances relative to solar photospheric abundances from Anders & Grevesse (1989) except for Fe for which the solar photospheric value is taken from Grevesse & Sauval (1999). Temperatures are in keV, and EM in cm-3. Uncertainties refer to 90% confidence ranges for elemental abundances, but they are defined as 10% of the best-fit values for temperatures, and 0.1 dex for the EM (see text).

\begin{displaymath}\begin{tabular}{p{2cm}rrrrrrrr} \noalign{\smallskip }\hline\h... ... \noalign{\smallskip }\hline\noalign{\smallskip } \end{tabular}\end{displaymath}


  
3.3 Results

RGS fluxed spectra are shown in Fig. 1 ordered approximately in decreasing coronal activity (defined in this paper as the average coronal temperature - see below). Ne X, O VIII, and Fe L-shell lines dominate the RGS spectra. In contrast to the other RS CVn binaries in our sample, the Capella X-ray spectrum is softer and dominated by bright Fe XVII and Fe XVIII lines as previously observed (e.g., Brinkman et al. 2000; Canizares et al. 2000; Audard et al. 2001b; Behar et al. 2001; Mewe et al. 2001). We provide the high-energy EPIC MOS2 spectra in Fig. 2, except for Capella. The high quality of the spectra allows for the determination of Mg, Si, S, Ar, Ca, and Fe or upper limits thereof. Continuum emission is clearly detected in these bright X-ray sources, which provides constraints for the determination of the emission measure distributions. Although the X-ray spectra look similar (with the exception of Capella), each star shows different strengths of line fluxes and their ratios. For example, the strong N VII Ly$\alpha $line flux in UX Ari contrasts with that in, e.g., $\lambda $ And. However, in the former star, no significant N VI He-like triplet is detected, which points to an EM distribution dominated by high temperatures. Indeed, the formation of the N VI He-like triplet is constrained to a narrow range of (cool) temperatures (1.0-2.5 MK; e.g., Mewe et al. 1985). In contrast, the triplet is detected in Capella's spectrum. Note that the short wavelength range (5-10 Å) for the most active stars HR 1099 and UX Ari show weaker lines compared to the less active $\lambda $ And and Capella. In this range, H-like and He-like lines of Si and Mg should dominate together with transitions from highly ionized Fe. These elements have a low first ionization potential, which suggests that their coronal abundances are low. Also, the coronal temperature could be much lower than the maximum formation temperatures of these emission lines, but this is unlikely since the lines form at $\approx $10 MK, close to the average temperature of these coronae. In contrast, the 5-10 Å range in $\lambda $ And and Capella displays better developed emission lines, suggesting higher abundances of low-FIP elements in these stellar coronae.

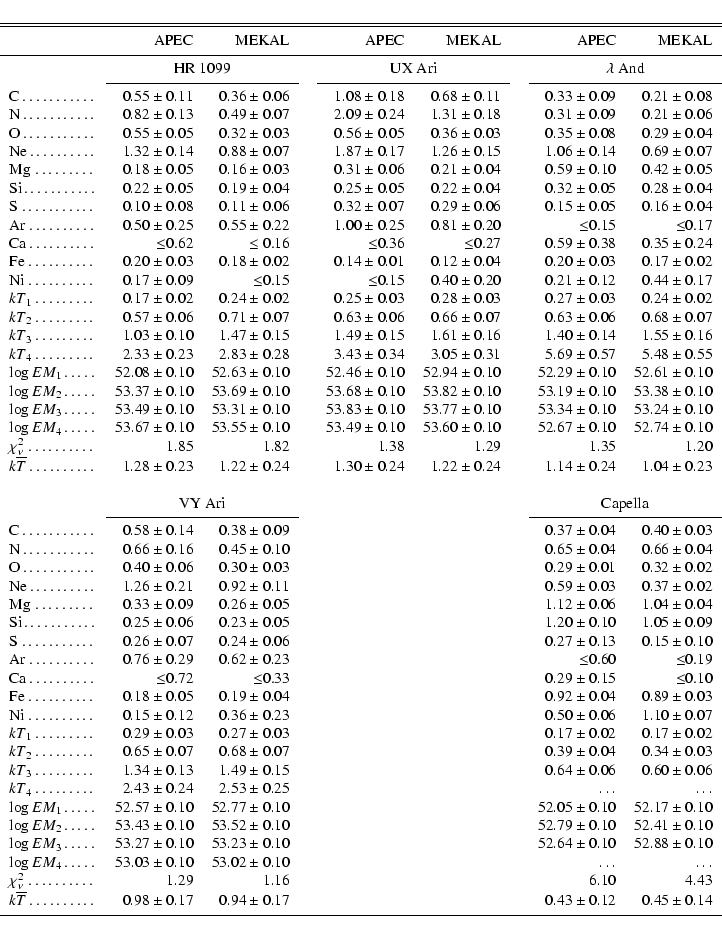
Coronal abundances obtained from the multi-temperature fits in SPEX and XSPEC are summarized in Table 4. As an example, Fig. 3 shows best fits and residuals for UX Ari. We provide reduced $\chi ^2$ values, although we emphasize that current uncertainties in the instrument calibration, in the atomic codes, and high signal-to-noise (S/N) ratios can produce systematic errors that cannot be described by $\chi ^2$. This is especially the case for Capella, for which its high S/N ratio produces $\chi ^2$ values exceeding 4. Inspection of the fit by eye shows, however, good agreement between the model fit and the data. The deviations are smaller than the typical uncertainties on the atomic physics parameters (order of 10%). Given the current uncertainties in the atomic parameters, our model description is thus satisfactory. Statistical 90% confidence ranges are given for each elemental abundance in Table 4. Since EM distributions are continuous, a 4-T model only provides an approximate discrete representation. Formal errors for T and EM are artificially underestimated, and are therefore of little use in this context. We adopt conservative estimates of the uncertainties for T as 10% of their values, whereas EM uncertainties are estimated to 0.1 dex. To characterize the global temperature average of the stellar corona, we hereafter assign an "average'' coronal temperature to each star (given in Table 4), obtained from the sum of logarithmic temperatures weighted by their EM,

 \begin{displaymath} \log \overline{T} = \frac{\sum_{i=1}^{N} \log T_i \times EM_i}{\sum_{i=1}^{N} EM_i}\cdot \end{displaymath} (1)

The error of the average temperature is obtained as
 
                     $\displaystyle \Delta ( \log \overline{T} )$ = $\displaystyle \sqrt{\frac{1}{N}\frac{\sum_{i=1}^{N} EM_i \times (\log T_i - \log \overline{T} )^2}% {(N - 1) \sum_{i=1}^{N} EM_i}},$ (2)
$\displaystyle \Delta ( \overline{T} )$ = $\displaystyle \sqrt{(\overline{T}_+ - \overline{T}) \times (\overline{T} - \overline{T}_-)},$ (3)

where
               $\displaystyle \overline{T}_+$ = $\displaystyle 10^{\log \overline{T} + \Delta ( \log \overline{T} )},$ (4)
$\displaystyle \overline{T}_-$ = $\displaystyle 10^{\log \overline{T} - \Delta ( \log \overline{T} )}.$ (5)

Such procedure has been applied to the XSPEC/APEC and SPEX/MEKAL results. For our subsequent discussion and the figures, we will use the derived coronal abundances and average coronal temperature from both spectral codes separately.


  \begin{figure} \par\includegraphics[width=16.1cm,clip]{MS3099f3a.eps}\\ [8.5mm] \includegraphics[width=16.1cm,clip]{MS3099f3b.eps} \end{figure} Figure 3: EPIC MOS2 (blue), RGS1 (red), and RGS2 (green) data of UX Ari with the 4-T best fits overlaid (thick black) for XSPEC/APEC (upper panel) and SPEX/MEKAL (lower panel). Error bars are plotted for MOS only, for clarity. Contributions to the $\chi ^2$ are also plotted; if the data bin is above the model, the $\chi ^2$ contribution is positive. Zoom-ins from 13 Å to 20 Å show the quality of the fits in the region from the Ne IX He-like triplet to O VIII Ly$\alpha $ and include bright Fe XVII and Fe XVIII lines. The wavelength ranges used for the fits (Table 3) are shown by horizontal bars for each instrument.
Open with DEXTER

  
4 Discussion

In this section, we will discuss the results in terms of a FIP-biased abundance pattern. We will also discuss potential problems, such as the relevance of optical depths, and the importance of the choice of solar and stellar photospheric abundances, that could influence the determination of coronal abundances or the abundance pattern.

  
4.1 A pattern for coronal abundances

Figure 4 shows elemental abundance ratios relative to O and to solar photospheric values for our star sample as a function of the first ionization potential. Although the determination of absolute abundances (relative to H) is subject to an accurate description of the underlying continuum, we have found that abundance ratios are robust and similar in the XSPEC and SPEX fits. Highly active stars show an inverse FIP effect, i.e., low-FIP elements are underabundant relative to high-FIP elements, as observed in an early analysis of the XMM-Newton RGS data of HR 1099 (Brinkman et al. 2001). $\lambda $ And however shows no particular FIP bias. For the intermediately active Capella, no clear trend is seen, although a possible overabundance of low-FIP elements compared to high-FIP elements is suggested, which is reminiscent of the solar FIP effect. Figure 4 therefore suggests the presence of a transition from an inverse FIP effect in the most active binaries toward the absence of FIP bias in intermediately active stars. This resembles the transition from an inverse FIP to a normal FIP effect in solar-like stars as a consequence of decreasing activity (Güdel et al. 2002). Similarly, Singh et al. (1999) have observed that the Fe abundance in active late-type dwarfs increases with decreasing activity.


  \begin{figure} \par\resizebox{\hsize}{!}{% \includegraphics[width=17cm]{MS3099f4.eps}} \end{figure} Figure 4: Abundance ratios relative to O and to solar photospheric values (Anders & Grevesse 1989) as a function of FIP. Ratios from XSPEC/APEC are shown as triangles, while ratios from SPEX/MEKAL are shown as squares. Activity/temperature decreases from top to bottom. Note the logarithmic scales.
Open with DEXTER

  
4.2 Optical depths


 

 
Table 5: Photon fluxes ( ${\rm 10^{-4}~photons~cm^{-2}~s^{-1}}$) for two Fe XVII 2p-3d lines and their flux ratio.

Star		 Fe XVII Flux ratio
  $\lambda $ 15.01 Å $\lambda $ 15.26 Å F(15.01)/F(15.26)

HR 1099 ...

 $5.91 \pm 0.20$ $2.04 \pm 0.21$ $2.90 \pm 0.32$
UX Ari ...... $2.06 \pm 0.13$ $0.66 \pm 0.11$ $3.14 \pm 0.58$
$\lambda $ And ...... $3.71 \pm 0.16$ $1.24 \pm 0.12$ $3.00 \pm 0.33$
VY Ari ...... $1.76 \pm 0.11$ $0.74 \pm 0.10$ $2.37 \pm 0.36$
Capella ..... $46.82 \pm 0.29$ $18.36 \pm 0.39$ $2.55 \pm 0.06$


Optical depths in stellar coronae can potentially have an impact on the determination of abundances. Since we interpret our data with optically thin models, we need to verify that the most critical lines seen in our spectra are indeed optically thin. We have therefore measured the fluxes in the Fe XVII $\lambda\lambda$ 15.014 and 15.261 Å lines. The ratio of these 2p6-2s2p53d lines is especially sensitive to the optical depth, since the former line has a very large oscillator strength, whereas the latter line does not (e.g., Rugge & McKenzie 1985; Mewe et al. 1995b; Kaastra & Mewe 1995). We used the best-fit models from XSPEC/APEC, then froze the fitting parameters, set the Fe and O abundances to zero, and added 6 emission lines. This procedure conserves the complete model including spectral lines and continuum from all elements except Fe and O, which we re-model separately to obtain explicit, accurately measured fluxes specifically for any one of the selected lines. The line photon fluxes were left free to vary, whereas their widths and their wavelengths were kept fixed. The additional four emission lines correspond to line blends from Fe XVII $\lambda $15.453 Å, Fe XIX $\lambda\lambda$ 15.079 and 15.198 Å, and O VIII Ly$\gamma$ at 15.176 Å. The RGS1 and RGS2 data have been fitted in the wavelength range from 14.8 to 15.5 Å simultaneously to increase the signal-to-noise ratio. Uncertainties for the line photon fluxes were obtained by averaging the 68% upper and lower limits for a single parameter of interest ( $\Delta\chi^2=1$). The observed flux ratios, F(15.01) / F(15.26), range from 2.4 to 3.1 (Table 5). Theoretical ratios range from 3.0-4.7 (e.g., Bhatia & Doschek 1992; also see Table 2 of Brown et al. 1998). Laboratory experiments, e.g., with electron beam ion traps (EBIT) have obtained lower ratios (2.8-3.2, Brown et al. 1998; Laming et al. 2000), suggesting that previous optical depths measurements based on theoretical ratios were overestimated. Using an EBIT ratio of $3.04 \pm 0.12$ measured at an electron energy of 1150 eV (Brown et al. 1998), and on the basis of the "escape-factor'' model (escape probability $P(\tau) \sim [1 + 0.43 \tau ]^{-1}$ for an optical depth $\tau \lesssim 50$) with a homogeneous mixture of emitters and absorbers in a slab geometry (Kaastra & Mewe 1995), we obtain optical depths no larger than $\tau \approx 0.66$, consistent with an optically thin plasma. Using the theoretical ratio of 3.53 from the APEC code, optical depths in $\lambda $ And and possibly Capella approach $\tau = 1$, although the other RS CVns still show $\tau \lesssim 0.5$.

  
4.3 Relation to solar photospheric abundances


  \begin{figure} \par\resizebox{\hsize}{!}{% \includegraphics[width=17cm]{MS3099f5.eps}} \end{figure} Figure 5: Similar to Fig. 4 for XSPEC/APEC, but using C, N, O, Ne, Mg, and Fe abundance of Holweger (2001, filled dots) and the C and O abundances of Allende Prieto et al. (2001, 2002, open squares).
Open with DEXTER

Solar photospheric abundances from Anders & Grevesse (1989) have been chosen except for Fe for which the more recent $A_{\rm Fe} = 7.50$ of Grevesse & Sauval (1999) has been adopted. Recent work has provided new estimates of solar photospheric abundances (e.g., Grevesse & Sauval 1998; Allende Prieto et al. 2001, 2002; Holweger 2001). In this section, we test the impact of choosing different solar photospheric abundances on the abundance pattern in RS CVn binaries; XSPEC/APEC results have been used. However, we emphasize that the SPEX/MEKAL abundance ratios were similar. Using new abundances from Holweger (2001), the observed trend (Fig. 4) is again found (albeit with slightly different ratios). Allende Prieto et al. (2001, 2002) propose new solar photospheric O and C abundances, respectively: $A_{\rm O} = 8.69$ and $A_{\rm C} = 8.39$, thus factors 1.74 and 1.48 smaller than in Anders & Grevesse (1989). The result is that abundance ratios to O in Fig. 4 should be reduced and get closer to the solar photospheric values for high-FIP elements. Although newer values of solar photospheric abundances can be useful for a direct comparison with the solar FIP effect, their adoption does not affect the suggested FIP bias in active stars. Figure 5 is similar to Fig. 4, except that it shows abundance ratios using Holweger (2001) abundances for C, N, O, Ne, Mg, Fe (filled dots), and using the C and O abundances of Allende Prieto et al. (2001, 2002, open squares). We note a possible two-plateau shape, as for the solar FIP effect but reversed: high-FIP abundance ratios are close to solar, whereas low-FIP ratios vary with the activity level. The separation lies around 10 eV, as in the Sun.

  
4.4 Relation to stellar photospheric abundances

Although it is practice to normalize stellar coronal abundances to the solar photospheric abundances, they should better be normalized to the stellar photospheric abundances. Some studies attempted to derive photospheric abundances of active binaries by modeling high-resolution optical spectra. In particular, RS CVn binaries have often been found to display large metallic abundance depletion (e.g., Randich et al. 1994). However, such systems are in general younger than the Sun, and thus nearby stars should show metallicities close to solar (Rocha-Pinto et al. 2000). For example, at an age of a few Gyrs, photospheres have [Fe/H] in the range -0.08 to -0.15 with uncertainties of about 0.12(Rocha-Pinto et al. 2000). The rare measured photospheric abundances are therefore probably biased by the enhanced chromospheric activity, high rotation rate, and the presence of spots. Previous abundance measurements are perhaps also biased by inaccurate determinations of fundamental stellar parameters, such as gravity and effective temperatures (Ottmann et al. 1998).


  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics[width=17cm]{MS3099f6.eps}} \end{figure} Figure 6: Abundance ratios to oxygen vs. FIP for $\lambda $ And using the XSPEC/APEC results. Stellar photospheric abundances from Donati et al. (1995, red open diamonds) and from Savanov & Berdyugina (1994, blue open squares) have been used. For comparison, we plot the ratios to solar photospheric values (Anders & Grevesse 1989; Grevesse & Sauval 1999, filled circles).
Open with DEXTER

On the other hand, photospheric abundances of $\lambda $ And, a slowly rotating giant, can be found in the literature. We have used abundances from Donati et al. (1995)[*] and Savanov & Berdyugina (1994)[*] since these authors provide estimates for several elements. Note that Ottmann et al. (1998) give values for Fe, Mg, and Si only, all of which are low-FIP elements with very similar FIP values. Figure 6 shows FIP-ordered abundance ratios to oxygen relative to stellar photospheric abundances (red open diamonds for Donati et al. 1995 and blue open squares for Savanov & Berdyugina 1994) in comparison with ratios relative to solar photospheric. Abundance ratios are slightly different, the overall shape of the coronal abundance pattern in $\lambda $ And stays similar, however: there is no apparent bias related to the first ionization potential. The Ca/O ratio using stellar abundances of Donati et al. (1995) is similar to the ratio relative to solar photospheric, but it is larger when abundances from Savanov & Berdyugina (1994) are used, although with larger uncertainties, thus formally compatible. Unfortunately, abundances of noble gases in stellar photospheres cannot be measured, preventing us from obtaining abundance ratios at ${\rm FIP} > 15$ eV.

$\lambda $ And may be regarded as an exceptional case where stellar photospheric abundances have been measured with some confidence. It would be interesting to obtain measurements for highly active stars, such as UX Ari and HR 1099, for which a clear inverse FIP effect is observed. However, abundance determinations are rare or often unclear (e.g., for the X-ray bright K star in HR 1099, ${\rm [Fe/H]} = 0$ from Savanov & Tuominen 1991 but ${\rm [Fe/H]} \approx -0.6$ for Randich et al. 1994; these authors used solar abundances from Anders & Grevesse 1989, thus a correction of +0.17 dex must be introduced for the Fe abundance).

  
4.5 Coronal abundances in stars

RS CVn binaries show enhanced magnetic activity thought to arise from the tidal interaction with their companions. Intermediately active binaries often correspond to loosely bound stars. Our sample thus investigates the upper range of coronal activity. In contrast, the solar-like stars sampled by Güdel et al. (2002) span all activity levels. Assuming that abundance ratios relative to solar photospheric in our sample approximately correspond to ratios relative to stellar photospheric abundances, we have compared the correlation between the FIP bias and the coronal activity, here characterized by the average coronal temperature, in RS CVn binaries and in solar analogs (Fig. 7). The average coronal temperature for the solar analogs were obtained with the same procedure as in Sect. 3.3. They are similar to those derived in previous studies, e.g., Güdel et al. (1997). Low-FIP abundance ratios (here exemplified by Fe) vary dramatically with the coronal temperature, whereas high-FIP abundance ratios (exemplified by Ne) show no variation. Note that ratios relative to Fe naturally show the inverse trend (low-FIP ratios constant, high-FIP ratios increasing with temperature). Together with the apparent increase of the absolute Fe abundance with decreasing activity level in RS CVn binaries, this suggests that abundances of elements with low first ionization potential vary with magnetic activity, whereas those of elements with high FIP stay constant.


  \begin{figure} \par\resizebox{\hsize}{!}{ \includegraphics[width=17cm]{MS3099f7.eps}} \end{figure} Figure 7: Fe/O and Ne/O abundance ratios relative to solar photospheric values (Anders & Grevesse 1989; Grevesse & Sauval 1999) for RS CVn and solar analogs using the XSPEC/APEC results (the SPEX/MEKAL results give similar relations) as a function of the average coronal temperature. Low-FIP abundance ratios follow an anticorrelation with $k\overline {T}$, whereas high-FIP elements show no correlation.
Open with DEXTER

  
5 Conclusions

Solar observations have shown a pattern of low-FIP material being overabundant relative to the high-FIP elements in the solar corona, in its wind, and also in solar energetic particles (Meyer 1985; Feldman 1992; Laming et al. 1995). Previous observations of stellar coronae have displayed a marked depletion of the metal abundance (essentially Fe) in active stars (e.g. Schmitt et al. 1996a), and either the absence of a FIP bias or a solar-like FIP effect in inactive stars (Drake et al. 1997). Recent results from XMM-Newton and Chandra have suggested the presence of a FIP bias at variance with the solar pattern; highly active stars appear to display a depletion of low-FIP elements relative to the high-FIP elements (Brinkman et al. 2001; Drake et al. 2001). In this paper, we have shown that a sample of RS CVn binary systems shows a FIP bias that appears to change from a marked inverse FIP effect in highly active binaries to an absence of a trend (or a possible solar-like FIP effect) in the intermediately active star Capella (Fig. 4). Although such a transition is only weakly suggested (since RS CVn binary systems often populate the highest levels of coronal activity), it resembles a similar transition found in solar-like stars (Güdel et al. 2002). The latter sample covers a wide range of activity levels and of ages. The highly active, young classical T Tauri star TW Hydrae displays a high depletion of the low-FIP Fe relative to O, whereas the high-FIP Ne is enhanced (Kastner et al. 2002). Preliminary results from the Chandra and XMM-Newton grating data of the extremely active YY Mensae show a similar marked depletion of low-FIP elements, with almost no emission lines and a well-developed continuum (Audard et al., in preparation). The above observations strongly suggest that the FIP bias in stellar coronae is correlated with the activity level. However, the absence of FIP bias in the inactive Procyon (Drake et al. 1995; Raassen et al. 2002) is a challenge. Procyon's coronal heating mechanism has been debated, with acoustic heating being a possibility, although this mechanism seems unlikely to play a major role in this star (Mullan & Cheng 1994; Schmitt et al. 1996b). A larger sample will eventually allow us to identify stars that may not fit into a simplistic activity-abundance correlation.

We have investigated whether currently used values of the solar photospheric abundances (Holweger 2001; Allende Prieto et al. 2001, 2002) have a significant effect on the observed FIP bias. Indeed, tables of solar abundance have changed significantly since the publication of the Anders & Grevesse (1989) standards. However, we have shown that their use does not remove the observed inverse FIP effect in highly active RS CVn binaries (Fig. 5). Although solar abundances are commonly used, it is preferential to use the stellar photospheric abundances to compare with the coronal abundances. In $\lambda $ And, we found no FIP bias either on the basis of solar or stellar photospheric abundances, suggesting that the absence of any FIP-related effect in this wide binary is real. However, $\lambda $ And may be a special case and a similar test would be more insightful if applied to a binary with a marked FIP bias, such UX Ari. However, the presently uncertain photospheric abundances in the most active stars does not allow such a procedure. Güdel et al. (2002) circumvented this problem for main-sequence stars by using solar analogs with known stellar photospheric abundances (similar to solar). Since their sample showed a transition from a solar FIP effect to an inverse FIP effect with decreasing age (or increasing activity level), the similar trend observed in RS CVn binaries at higher activity levels appears to be real.

The presence of the inverse FIP effect in highly active stars, and the suggested transition of the FIP bias as a function of the activity level could open up new views of the fractionation mechanisms in stellar atmospheres. Previous studies have focused on explaining the FIP effect in the Sun (see Hénoux 1995, for a review). One category of enrichment models suggests that the magnetic field plays no active role in the separation process. In these models, fractionation of ions from neutral species results from diffusion along the magnetic field lines, through collisions (e.g. Marsch et al. 1995; Peter 1996, 1998; Wang 1996). Another category of models proposes that the magnetic field does play an active role for the separation of elements. Fractionation occurs thanks to the difference between the drift velocities of ionized and neutral elements moving across the magnetic field (e.g. Vauclair & Meyer 1985; Vauclair 1996; von Steiger & Geiss 1989; Antiochos 1994; Hénoux & Somov 1997). Güdel et al. (2002) proposed to explain the inverse FIP effect seen in active stars by high-energy electrons detected by their gyrosynchrotron emission. The particles propagate downward and could prevent chromospheric ions - mostly low-FIP elements - from escaping along the magnetic field lines up into the corona by creating a downward-pointing electric field. In less active stars, the radio flux (therefore the density of high-energy electrons) is smaller, thus quenching the inverse FIP effect. This simplistic model could also account for the increase in the low-FIP abundances during large flares, as observed (Güdel et al. 1999; Audard et al. 2001a). However, more sophisticated models are timely to explain the inverse FIP effect in active stars.

Acknowledgements
We thank the XMM-Newton SOC team for allowing us to use data from the commissioning and calibration phases. We also thank the referee, Dr. A. Maggio, whose comments have improved the paper considerably. The PSI group acknowledges support from the Swiss National Science Foundation (grant 2000-058827 and fellowship 81EZ-67388). MA is grateful to Dr. S. White and the University of Maryland for their hospitality after the tragic events of 9/11, 2001. SRON is supported financially by NWO.

References

 
Copyright ESO 2003