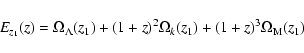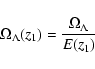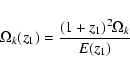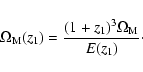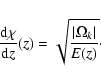Up: A hypothetical cosmological test:
2 Calculating
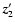
In the following I outline the method used to calculate the redshift
of an object as seen by another, distant observer. I use the notation
of L00 where I wrote the Robertson-Walker line
element as
![\begin{displaymath}
{\rm d}s^2 = -c^2 {\rm d}t^2 + a^2(t)\left[{\rm d}\chi^2 + \...
...chi)({\rm d}\theta^2 +
\sin^2\theta \: {\rm d}\phi^2)\right].
\end{displaymath}](/articles/aa/full/2003/05/aah3903/img21.gif) |
(1) |
The radial coordinate  is dimensionless and
is dimensionless and
 is
defined as
is
defined as 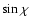 ,
,
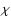 or
or
 if k = +1, 0 or
-1. Length dimensions are included in a(t) by setting a0 as the
curvature radius for
if k = +1, 0 or
-1. Length dimensions are included in a(t) by setting a0 as the
curvature radius for 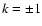 or
a0 = c H0-1 for k = 0.
or
a0 = c H0-1 for k = 0.
Consider an object 1 observed by us today at z1 and an object 2 at
z2 separated by an angle 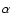 on the sky (cf. Fig. 1 of L00). Object 2 emits a photon towards object 1 which
is received by object 1 at the same time as object 1 emits the photon
we receive from it today. I denote the redshift of object 2 as
observed by object 1 as z2' and the comoving coordinate distance
between them as
on the sky (cf. Fig. 1 of L00). Object 2 emits a photon towards object 1 which
is received by object 1 at the same time as object 1 emits the photon
we receive from it today. I denote the redshift of object 2 as
observed by object 1 as z2' and the comoving coordinate distance
between them as 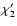 .
We have (L00)
.
We have (L00)
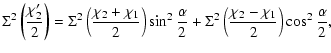 |
|
|
(2) |
where
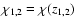 .
In L00 I set
.
In L00 I set
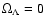 and derived analytic expressions for the right and left-hand
sides of Eq. (2) in terms of z1, z2 and z2'respectively. In the case
and derived analytic expressions for the right and left-hand
sides of Eq. (2) in terms of z1, z2 and z2'respectively. In the case
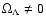 we relate the right-hand side
of Eq. (2) to z1 and z2 by using
we relate the right-hand side
of Eq. (2) to z1 and z2 by using
![\begin{displaymath}
\chi(z) = \sqrt{\vert\Omega_k\vert} \int_0^z \left[ E(x) \right]^{-1/2} {\rm d}x,
\end{displaymath}](/articles/aa/full/2003/05/aah3903/img32.gif) |
(3) |
where
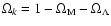 and
and
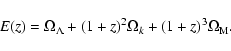 |
(4) |
When
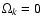 then
then 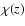 is given by just the integral (i.e. we
set
a0 = c H0-1). We relate the left-hand side of
Eq. (2) to z2' by noting that an observer at z1 would
write the above as
is given by just the integral (i.e. we
set
a0 = c H0-1). We relate the left-hand side of
Eq. (2) to z2' by noting that an observer at z1 would
write the above as
![\begin{displaymath}\chi_{z_1}(z) = \sqrt{\vert\Omega_k(z_1) \vert} \int_0^{z} \left[
E_{z_1}(x) \right]^{-1/2} {\rm d}x,
\end{displaymath}](/articles/aa/full/2003/05/aah3903/img37.gif) |
(5) |
where
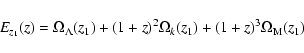 |
(6) |
and
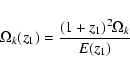 |
(7) |
Hence we have
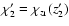 .
It is straightforward to
show that
.
It is straightforward to
show that
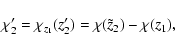 |
(8) |
where
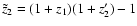 is today's redshift of the
photon emitted by object 2 and observed by object 1 to have a redshift
of z2'. Finally, to calculate z2' for a given z1, z2 and
is today's redshift of the
photon emitted by object 2 and observed by object 1 to have a redshift
of z2'. Finally, to calculate z2' for a given z1, z2 and
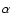 we substitute Eq. (8) into Eq. (2) and
numerically solve for
we substitute Eq. (8) into Eq. (2) and
numerically solve for
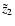 using the Newton-Raphson method
(Press et al. 2002), where the derivative of the function to be solved is
simply given by
using the Newton-Raphson method
(Press et al. 2002), where the derivative of the function to be solved is
simply given by
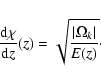 |
(9) |


Up: A hypothetical cosmological test:
Copyright ESO 2003
![]() on the sky (cf. Fig. 1 of L00). Object 2 emits a photon towards object 1 which
is received by object 1 at the same time as object 1 emits the photon
we receive from it today. I denote the redshift of object 2 as
observed by object 1 as z2' and the comoving coordinate distance
between them as
on the sky (cf. Fig. 1 of L00). Object 2 emits a photon towards object 1 which
is received by object 1 at the same time as object 1 emits the photon
we receive from it today. I denote the redshift of object 2 as
observed by object 1 as z2' and the comoving coordinate distance
between them as ![]() .
We have (L00)
.
We have (L00)
![\begin{displaymath}\chi_{z_1}(z) = \sqrt{\vert\Omega_k(z_1) \vert} \int_0^{z} \left[
E_{z_1}(x) \right]^{-1/2} {\rm d}x,
\end{displaymath}](/articles/aa/full/2003/05/aah3903/img37.gif)