In general, the radio continuum sources associated with YSOs are weak, and they are unresolved except with a subarcsecond resolution. It has been found that the shape of the SED at cm-wavelengths for YSOs is characteristic of thermal free-free emission. However, it is also known that this emission can not arise from a compact H II region which is ionized by stellar photons from the YSO. The required ionizing photon flux is that of an early B type star (Torrelles et al. 1985), which is orders of magnitude greater than the expected flux from the associated YSOs. Thus, there must be other mechanisms involved which contribute to the inferred ionization, unless YSOs produce much more Lyman continuum radiation than expected.
The different mechanisms can be distinguished by the shape of the radio spectrum, if observations over a large enough wavelength range are available. In the following we discuss some of them briefly. For a review of ionized winds from young stellar objects see André (1987) and Panagia (1991).
The accretion models are of special interest in this case, because there is evidence of mass infall towards the IRAS source, based on millimeter molecular line observations (Lehtinen 1997).
In Bertout's (1983) model of accretion onto a protostellar
core the radio-emitting region is photoionized by soft X-ray and EUV
radiation from an accretion shock around a protostellar core. In this
model the spectrum has roughly a
![]() shape.
shape.
Felli et al. (1982) have modelled thermal emission from an
extended, ionized circumstellar envelope which is in a state of
accretion. This model produces a non-power-law flat spectrum,
![]() (Felli et al. 1982; Panagia
1991; André 1987). The predicted flux density
is (Panagia 1988)
(Felli et al. 1982; Panagia
1991; André 1987). The predicted flux density
is (Panagia 1988)
| |
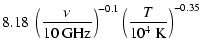 |
||
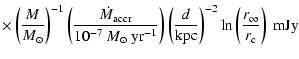 |
(1) |
Ionized stellar wind models have been presented which are either
spherically symmetric (Panagia & Felli 1975; Wright &
Barlow 1975; Felli et al. 1982; Panagia
1991) or nonsymmetric (Schmid-Burgk 1982;
Reynolds 1986). In the case of ionized stellar wind in
general, the frequency dependence has a large range from
![]() to
to
![]() (Reynolds
1986 and references therein). In the case of a spherical,
fully ionized, isothermal and constant-velocity flow, which is
considered as the "standard'' spherical wind, the 3 to 6 cm spectral
index is 0.6 for large opacity. Significant deviations from the
spectral index or flux predicted by the "standard'' spherical wind
occur only if the solid angle filled by the flow varies systematically
with radius or the wind is highly anisotropic (Schmid-Burgk
1982; Reynolds 1986).
(Reynolds
1986 and references therein). In the case of a spherical,
fully ionized, isothermal and constant-velocity flow, which is
considered as the "standard'' spherical wind, the 3 to 6 cm spectral
index is 0.6 for large opacity. Significant deviations from the
spectral index or flux predicted by the "standard'' spherical wind
occur only if the solid angle filled by the flow varies systematically
with radius or the wind is highly anisotropic (Schmid-Burgk
1982; Reynolds 1986).
Shock-induced ionized model was first proposed by Torrelles et al. (1985). The required ionizing photons are produced when a
powerful, high velocity neutral stellar wind is shocked by dense
matter surrounding the YSO. The now collimated wind produces a
molecular outflow. The shock-ionization model predicts a
![]() dependence for radio continuum emission (Curiel et
al. 1987, 1989) The predicted flux density in
the optically thin case is (Curiel et al. 1989)
dependence for radio continuum emission (Curiel et
al. 1987, 1989) The predicted flux density in
the optically thin case is (Curiel et al. 1989)
| |
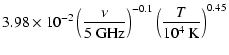 |
||
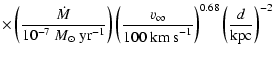 |
|||
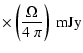 |
(2) |
Yet another possible source of emission is thermal emission from dust
grains, which has a positive spectral index. If we assume a ![]() frequency dependence for emission between 1.3 mm and 3 cm, typical
for optically thin dust emission, the 223 mJy flux at 1.3 mm
(Henning et al. 1993) can be used to predict a flux density
of 0.4
frequency dependence for emission between 1.3 mm and 3 cm, typical
for optically thin dust emission, the 223 mJy flux at 1.3 mm
(Henning et al. 1993) can be used to predict a flux density
of 0.4 ![]() Jy at 3 cm for the IRAS 13036-7644.
Jy at 3 cm for the IRAS 13036-7644.
A source that has a non-thermal spectrum (
![]() )
would
probably be a nonstellar background object. However, not every source
with
)
would
probably be a nonstellar background object. However, not every source
with
![]() is necessarily a nonstellar object; Abbot et al. (1984) have detected non-thermal emission from two O stars.
For YSOs the relevant non-thermal emission process is synchrotron
radiation.
is necessarily a nonstellar object; Abbot et al. (1984) have detected non-thermal emission from two O stars.
For YSOs the relevant non-thermal emission process is synchrotron
radiation.
Copyright ESO 2003