A&A 398, 687-696 (2003)
DOI: 10.1051/0004-6361:20021683

A new version of the moment method, optimized for mode identification in multiperiodic stars^,

M. Briquet ¹ - C. Aerts ²

1 - Institut d'Astrophysique et de Géophysique de Liège, Université de Liège, allée du Six Août 17, 4000 Liège, Belgium
2 - Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium

Received 26 September 2002 / Accepted 12 November 2002

Abstract
We present a numerical version of the moment method for the identification of non-radial pulsation modes. The new version requires less computation time than the previous one, allowing users to consider all the information contained in the first three moments of a multiperiodic star and to identify multiple modes simultaneously. This, together with the use of a new discriminant that considers the moments calculated at each time of observation, increases considerably the feasibility and the accuracy of the mode identification for multiperiodic stars. Moreover, the technique is extended to rotating pulsating stars. We apply the new version to three B stars showing multiperiodicity.

Key words: line: profiles - stars: oscillations - stars: individual: $\beta$ Crucis, 16 Lacertae, HD 74195

1 Introduction

Recent studies of multiple data-sets of non-radial oscillators have shown the need to improve current mode identification methods. In particular, the outcomes of mode identification based on photometric and spectroscopic data of the same star and for the same mode are often discrepant (e.g. De Cat 2001). This is very unsatisfactory if one wants to use the non-radial oscillations for detailed modelling of the internal structure of the stars. The current paper contributes to the improvement of one of the identification methods which is developed for the interpretation of time-series of high-resolution spectroscopic data.

The natural way of mode identification from line-profile variations is the method of line-profile fitting. By comparing the observed line-profile variations with theoretically calculated ones for many wavenumbers $(\ell,m)$and for a large grid of the other continuous parameters that occur in the velocity expression of a non-radial mode, one chooses the modes which best fit the observations. Unfortunately, this technique suffers from a major drawback: the unrealistic computation time for multiple modes.

The idea of the moment method is to replace each line profile by its first three moments, which describe respectively the centroid velocity of the line, the line width and the line skewness. The wavenumbers $(\ell,m)$ and the other continuous velocity parameters are then determined in such a way that the theoretically computed moment variations best fit the observed ones. The moment method was first introduced by Balona (1986a,b, 1987) and was further developed by Aerts et al. (1992) and Aerts (1996). They derived analytical expressions of the first three moment variations, which are valid for stars with a long rotational period compared to the pulsational periods ( $P_{\rm {rot}} > 10 P_{\rm {puls}}$). The major drawback of the moment method in the formulation by Aerts (1996) is the fact that all the modes are identified separately in the case of multiple modes. With such an approach, one cannot force there to be only one unique solution for the inclination angle of the star and the stellar rotational velocity. This is rather unsatisfactory, as conflicting values of these parameters are quite often encountered in practical applications of the method. The reason of Aerts (1996) for not performing one unified mode identification for all occurring modes simultaneously was of numerical origin, as it resulted in unrealistic computation times. This is no longer the case with the efficiency of current computers and with some clever re-arrangements of the theoretical moment expressions. In this paper, we present a numerical version of the moment method, which improves considerably the efficiency of the technique by performing the simultaneous identification of all the modes that are present in the data.

The paper is organized as follows. In Sect. 2, we describe the new version of the method. Tests on synthetic data are performed in Sect. 3. Section 4 provides a summary of the best optimal mode identification strategy. In Sect. 5, we apply our new method to three multiperiodic B-type stars: $\beta$ Crucis, 16 Lacertae and HD 74195. Finally, we give conclusions in Sect. 6.

2 A numerical version of the moment method

In order to be able to outline our new application of the moment method, we repeat here its basic ingredients, adapted to our numerical approach. The reader is referred to Aerts et al. (1992) and Aerts (1996) for a more in-depth description of the moment method.

2.1 The moments of a line profile

Let v be the observed velocity (in km s^-1) of a point on the stellar surface. The nth normalized moment of a line profile I(v,t) is defined as

$$\displaystyle <v^{n}>_I(t)=\frac{\displaystyle \int_{-\infty}... ...displaystyle \int_{-\infty}^{+\infty} \ I(v,t) \ {\rm d}v}\cdot$$

We note that the denominator in this formula is the equivalent width of the line.

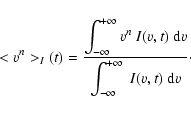
A line profile is the convolution of an intrinsic profile g and the component of the velocity field f. We assume that g is time-independent and symmetric, which is a good approximation. The first three moments can then be written as

$$\begin{eqnarray*}\lefteqn{ {<v>_I} = {<v>_f},}\\ \lefteqn{ {<v^2>_I} = {<v^2>_f... ...gma^2},}\\ \lefteqn{ {<v^3>_I} = {<v^3>_f + 3 \sigma^2 <v>_f},} \end{eqnarray*}$$

where the constant <v²>_g is denoted by $\sigma^2$.

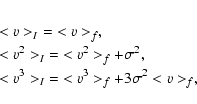
Let $v_{\rm {rot}}$ and $v_{\rm {puls}}$ be respectively the velocity in the line of sight due to rotation and pulsation. We use a system of spherical coordinates $(r,\theta,\phi)$ whose polar axis coincides with the axis of rotation and we consider a star which rotates uniformly. We assume also a constant intensity over the stellar surface and we use a limb-darkening law of the form $h_\lambda(\mu)=1-u_{\lambda}+u_{\lambda} \cos\mu$ where $\mu$ is the angle between the local radial vector and the line of sight. We divide the stellar surface into surface elements by taking steps of d$\theta$ in $\theta$ and d$\phi$ in $\phi$. One then has the following approximation

 

$${{<v^{n}>_f}=\frac{1}{m_0} \sum_{k=0}^{n} \frac{n!}{k! (n-k)!} \i... ...,\phi,t)} (1+ \beta \cos\mu) \cos\mu \ \sin\theta\ {\rm d}\theta \ {\rm d}\phi,$$ (1)

where the integral is taken over the visible stellar surface ( $\cos\mu > 0$). In this expression, $\beta \equiv u_{\lambda}/(1-u_{\lambda})$ and $m_0 \equiv \int \int (1+\beta \cos\mu) \cos\mu \ \sin\theta \$d$\theta$d$\phi$. The rotational velocity in the line of sight is given by $v_{\rm {rot}}= \Omega \ R \ \sin i \ \sin\theta \ \sin\phi \equiv v_\Omega\ \sin\theta \ \sin\phi$with $\Omega$ the angular frequency of rotation, R the radius of the star and i the angle of inclination of the star.

We note that we neglect temperature effects on moment variations. For pulsating B stars this is justified, as the moment variations are very well approximated with a pulsational velocity field only. Indeed, Dupret et al. (2002) and De Ridder et al. (2002a) showed that the line-profile variations of Silicon lines in slowly-rotating non-radially pulsating $\beta$ Cephei stars and SPB stars are very little affected by temperature variations at the surface of the star.

2.2 The pulsation velocity field

For linear theory, the general form for the temporal dependence of the projected pulsation velocity field due to N modes is given by

$$\displaystyle v_{\rm {puls}}=\sum_{j=1}^N A_{\ell_j}^{m_j} \c... ...ga_j t + \psi_j)+ B_{\ell_j}^{m_j} \sin(\omega_j t + \psi_j),$$ (2)

with

$$\displaystyle A_{\ell_j}^{m_j}=A_{\rm p}^j [C_{\ell_j}^{m_j}(i)+K_j D_{\ell_j}^{m_j}(i)],$$ (3)

and

$$\displaystyle B_{\ell_j}^{m_j}=A_{\rm p}^j [E_{\ell_j}^{m_j}(i)+K_j F_{\ell_j}^{m_j}(i)],$$ (4)

where the parameters $A_{\rm p}$ and K denote respectively the velocity amplitude and the ratio of the amplitude of the horizontal and of the vertical motion.

In Eqs. (3) and (4), the quantities $C_{\ell_j}^{m_j}$, $D_{\ell_j}^ {m_j}$, $E_{\ell_j}^{m_j}$ and $F_{\ell_j}^{m_j}$ are given by

$$\begin{eqnarray*}C_{\ell_j}^{m_j}&=&(\cos i \ \cos\theta + \sin i \ \sin\theta ... ... \\ &&- \sin i \ \sin\phi \ V_\phi^j(\theta) \ \cos(m_j \phi), \end{eqnarray*}$$

where

$$\begin{eqnarray*}V_{\rm r}(\theta)&=&N_{\ell_j}^{m_j} \ P_{\ell_j}^{m_j}(\cos\th... ..._j}{\sin\theta}N_{\ell_j}^{m_j} \ P_{\ell_j}^{m_j} (\cos\theta), \end{eqnarray*}$$

for a non-rotating pulsating star. In these latter expressions, $P_{\ell}^m$ is the associated Legendre polynomial and $N_{\ell}^m$ is a normalisation factor.

2.3 The first three moments

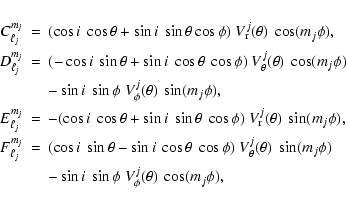
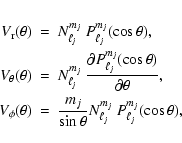
For the identification of the modes, we only use the first three moments <v>, <v²> and <v³> because the higher order observed moments are often too noisy. Moreover, the first three moments suffice to determine correctly the pulsation modes (Aerts et al. 1992).

From Eqs. (1) and (2) and after deleting the terms that equal zero due to symmetry properties, we have

$$\begin{eqnarray*}\lefteqn{ {<v>} = \sum_{j=1}^N A_1^{j} \cos(\omega_j t + \psi_j... ...\cos(( \omega_j + \omega_k - \omega_n) t +\psi_j+\psi_k-\psi_n), \end{eqnarray*}$$

where

$$\begin{eqnarray*}X^{j(kn)}=\frac{1}{m_0} \int \int x^{j(kn)} \ (1+\beta \cos\mu) \cos\mu \ \sin\theta \ {\rm d}\theta \ {\rm d}\phi \end{eqnarray*}$$

with

$$\begin{tabular}{cc} $X^{j\left(kn\right)}$ & $x^{j\left(kn\ri... ...^{m_j} \ A_{\ell_k}^{m_k} \ A_{\ell_n}^{m_n}.$\\ \end{tabular}$$

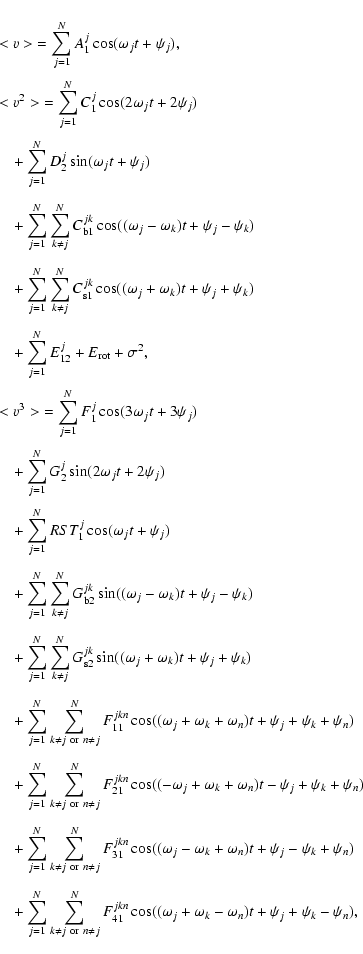
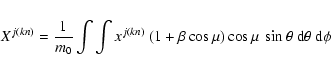
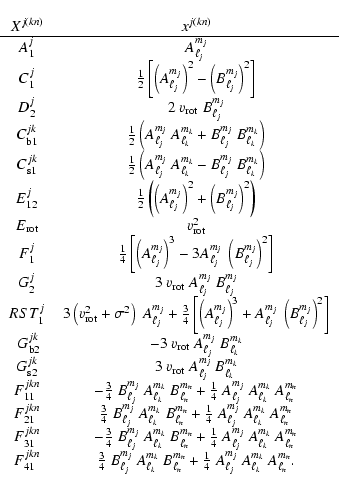
We point out that <v> varies with $\omega_j$; <v²> varies with $\omega_j$and $2\omega_j$ and also with the coupling frequencies $\omega_j + \omega_k$ and $\omega_j - \omega_k$; <v³> varies with $\omega_j$, $2\omega_j$, $3\omega_j$and also with coupling frequencies $\omega_j + \omega_k$, $\omega_j - \omega_k$, $\omega_j + \omega_k + \omega_n$, $- \omega_j + \omega_k + \omega_n$, $\omega_j - \omega_k + \omega_n$, $\omega_j + \omega_k - \omega_n$ for $j,k,n=1,\ldots,N$. All these coupling characteristics were also already given in Mathias et al. (1994), but were never implemented so far.

From Eqs. (3) and (4) and by denoting

$$I[x]\equiv\frac{1}{m_0}\int \int x \ (1+\beta \cos\mu) \cos\mu \ \sin\theta \ {\rm d}\theta \ {\rm d}\phi,$$

we have

$$A_1^j=A_{\rm p}^j \left\{ I[C_{\ell_j}^{m_j}] + K_j I[D_{\ell_j}^{m_j}] \right\} \cdot$$

The expressions for the amplitudes of the second and third moments are given in Appendix A in order to keep this section readable.

The great advantage of such a writing is that the integrals I[x] can be computed and memorized in files once and for all for chosen wavenumbers $(\ell,m)$ and inclinations i. This leads to an important gain of computation time in the computation of the moments for different values of the other parameters $A_{\rm p}$, K, $\sigma$ and the projected rotational velocity $v_{\Omega }$.

We point out that, for chosen $(\ell, \ m, \ K, \ i)$, the amplitude $A_{\rm p}$ is no longer a free parameter. We limit its range by imposing that the theoretical first moment amplitude $A_{\rm {th}}=A_{\rm p} \ A(\ell, \ m, \ K, \ i)$ must be equal to the observed one $A_{\rm {obs}}$. This condition, which was not considered by Aerts (1996), allows us to reduce greatly the grid of tested parameters. Such an approach is fully justified, as the relative standard error of $A_{\rm {obs}}$ is always much smaller than the ones of any of the other amplitudes of the higher-order moments.

2.4 A new discriminant

In the version of Aerts (1996), the mode identification is achieved by comparing the theoretically calculated amplitudes of <v>, <v²> and <v³> with the observed ones through a discriminant. In general, the observed amplitudes of the first moment as well as the constant term of the second moment are determined accurately. However, the other observed moment amplitudes can have large uncertainties. For this reason, we prefer using the moment values calculated at each time of observation t_k ( $k=1,...,N_{\rm {obs}}$) instead of the amplitudes of their fit.

We propose to choose the modes and the parameters for which the following new discriminant attains the lowest value

$$\begin{eqnarray*}\lefteqn{ \Sigma = \left\{ \frac{1}{N_{\rm {obs}}} \sum_{k=1}^{... ...>(t_k)-<v^3>_{\rm obs}(t_k) \right)^{2/3} \right] \Bigg\}^{1/2}, \end{eqnarray*}$$

where $<v^n>_{\rm obs}$denotes the nth observed moment.

2.5 An upper limit for the degree $\ell$

The moment method is particularly suited to identify modes whose frequency is clearly present in the observed moments. Consequently, the degrees of the modes corresponding to these frequencies are expected to be relatively low ( $\ell\leq 6$).

In what follows, we give a simple criterion allowing to derive an upper limit for $\ell$ using the observed first moment amplitude $A_{\rm {obs}}$ and the constant term of the observed second moment $C_{\rm {obs}}$, which can both be very accurately determined from the observed line-profile variations. By imposing the theoretical positive constant E₁₂ to be smaller than $C_{\rm {obs}}$, we have the following condition:

 

$${\left( a \ (A_{\rm {obs}})^2+b \ C_{\rm {obs}}\right) \ K^2 + \l... ...{obs}} \right) \ K} + \left( e \ (A_{\rm {obs}})^2+f \ C_{\rm {obs}}\right) < 0$$ (5)

with

$$\begin{eqnarray*}a&=&I \left[ (D_{\ell}^{m})^2 \right] +I \left[(F_{\ell}^{m})^2... ...t],\\ f&=&- 2 \left( I \left[ C_{\ell}^{m} \right] \right) ^2. \end{eqnarray*}$$

The quantities a, b, c, d, e and f are precomputed for several values of inclination i. Considering (5) as an inequation in K>0, one can exclude the modes with degree $\ell$ for which no solution is found. One then avoids to test useless modes, which again saves a considerable amount of computation time.

2.6 Generalization to rotating pulsating stars

The technique described above is no more restricted to slow rotators as was the case for the method by Aerts (1996). Here we extend the application to rotating pulsating stars by using the theory derived by Lee & Saio (1987). We remind that the velocity field depends on the ratio $$\eta=2 \Omega/\omega_{\rm c}$$between the angular frequency of rotation and the angular corotating frequency of pulsation. Note that taking $$\Omega=0$$ leads to the same description as the one of a non-rotating pulsating star.

We implemented this version of the moment method by using Townsend's code (1997) BRUCE, which computes the pulsation velocity field for this theory. A nice feature of our current version of the method is that this numerical version can be easily generalized to an improved formalism for the pulsational velocity, e.g. one that would take into account the effects of the centrifugal forces, should this become available.

3 Tests on synthetic data

We applied the moment method in our present new version to a large number of synthetic data sets in order to test its efficiency and our implemented version. Sets of artificial data were generated in such a way that they resemble real data as much as possible. For each set, we computed 254 line profiles at times of real observations. We added gaussian noise corresponding to a signal-to-noise of about 200 and finally we computed the first three moment variations.

We first tested the method for a monoperiodic star for all the sectoral, tesseral, and axisymmetric modes with $0 \le \ell \le$  3 ( $m=-\ell,\ldots,\ell$). It performs the identification without any problem, as it was already the case with the previous version (Aerts 1996). We note that, as expected, axisymmetric modes may be confused with axisymmetric modes of another degree for low values of the inclination, because of their very similar visible configuration.

We then tested 144 combinations of two modes including all kinds of modes until $\ell=3$. The value for $v_{\Omega }$ was randomly chosen between 10 and 30 km s^-1 and $\sigma$ was taken equal to 5.5 km s^-1. $A_{\rm p}$ was chosen so that the value of the radial velocity amplitude is compatible with observed values for $\beta$ Cephei stars and SPB stars. Each time, the velocity amplitude of the second mode was chosen so that its first moment amplitude is smaller than the one of the first dominant mode. The K-values were also taken according to typical values of these two kinds of B-type oscillators. In Tables 1-4, which are only available electronically, we show the values of the input parameters for several sets, together with the five best solutions of the mode identification. We can conclude that the method performs the identification very well. However, sometimes, the real combination of the two modes does not correspond to the lowest value of the discriminant but appears in the list of the few best solutions. In general, the estimates for the continuous parameters $(A_{\rm p}, K, i, v_\Omega, \sigma)$ are good, although large deviations do sometimes occur. Such failing of estimating these parameters well was already put forward by De Ridder et al. (2002b).

For evident computational reasons, we made less tests for three modes than for two. Some examples are given in Tables 5-8, which are again only available electronically. Also for these testcases the identifications are very conclusive, while the same remark as above for the continous parameters applies here.

We strongly encourage users of our mode identifcation method to study Tables 1-8 in order to obtain a feeling of the accuracy and the power, but also of the limitations, of the identification method.

A large number of tests indicates that the first three moments suffice to identify the modes correctly. In Appendix B, we show that it is indeed not necessary to add higher order moments. The computation time required to calculate the discriminant depends very much on the number of modes. It ranges from about half an hour for a monoperiodic star to several days for stars with three modes (with a Pentium 4, 2.4 GHz / 512 Mb RAM). We note that, with the previous version of the moment method, the identification of one mode required several days of computation, and the identification of three modes simultaneously would have required several months or more.

4 Mode identification strategy

It is evident from Tables 1-8 that, in many cases, one clear combination of different wavenumbers does not occur from the discriminant, as several solutions are almost equivalent in fitting the moment variations. This situation is inherent to the problem of mode identification, with whatever method, as several combinations of the velocity parameters result in almost the same line-profile variations. The strength of the moment method is precisely that it allows one to severely restrict the number of possible solutions.

One would hope that a statistically justified test would inform the user how many of the candidate modes can be rejected with safety from comparison of the different values of $\Sigma$. At present, such a significance test is still lacking. The main difficulty lies in defining a suitable test for the combination of discrete and continuous parameters. De Ridder et al. (2002b) have taken the first steps in this direction for a monoperiodic pulsation.

In view of the lack of a significance test, one needs to evaluate the "few'' best solutions resulting from the moment method, by constructing theoretical line-profile variations and by comparing these with the observed ones. One can do this for the profiles themselves, or else for their variation of amplitude and phase across the profile (for a definition of the latter diagnostic values, we refer to Schrijvers et al. 1997). The value of a "few'' depends on the complexity of the pulsation. We advise the user to look at at least the 5 best $(\ell,m)$for a monoperiodic star, the 10 best combinations of the wavenumbers for a biperiodic oscillator and so on. A recent example of such a procedure is provided in Aerts et al. (2002) for the $\beta~$Cep star EN Lac - see also below. We strongly urge users of our method not to omit this last step. We also stress, however, that, even after such an additional test, ambiguity among the solutions that survive the test will still remain, i.e. one single outcome will seldomly be reached. However, the number of possibilities will have decreased significantly, to such an extent that seismic modelling can be tried on the basis of the remaining accepted combinations of the wavenumbers.

5 Application to $\beta$ Ceps and SPBs

5.1 $\beta$ Crucis

Aerts et al. (1998) presented numerous high signal-to-noise spectroscopic data of the $\beta$ Cephei star $\beta$ Crucis with a total time span of 13 years. They found three frequencies in the moments of the Si III 4553 Å line: f₁=5.2305468 c/d, f₂=5.958666 c/d and f₃=5.472165 c/d. The corresponding observed first moment amplitudes are $A_{\rm {obs}}^1=1.41$ km s^-1, $A_{\rm {obs}}^2=0.62$ km s^-1 and $A_{\rm {obs}}^3=0.34$ km s^-1. Note that only the first frequency was known and detected in photometric observations before their study. A mode identification with the 1996-version of the moment method was performed. It pointed towards non-axisymmetric and non-radial modes. The mode corresponding to f₁ was found to be a low-degree sectoral mode with $\ell=1$ while f₂ and f₃ clearly correspond to higher degrees ($\ell=3$ or $\ell=4$), explaining why the two newly found frequencies were not detected photometrically. Meanwhile, these two additional modes have also been detected clearly in space photometry gathered by the WIRE satellite (Cuypers et al. 2002), as well as two additional candidates. It is then clear that this star exhibits multiple non-radial modes and is hence an interesting asteroseismic target.

 

 

Table 1: The ten best solutions of the mode identification through the discriminant $\Sigma$ for the $\beta$ Cephei star $\beta$ Crucis, using the Si III 4553 Å line for which the amplitudes of the first moment are $A_{\rm {obs}}^1=1.41$ km s^-1, $A_{\rm {obs}}^2=0.62$ km s^-1 and $A_{\rm {obs}}^3=0.34$ km s^-1. $A_{\rm p}$ is the amplitude of the radial part of the pulsation velocity, expressed in km s^-1; i is the inclination angle; $v_{\Omega }$ is the projected rotational velocity, expressed in km s^-1 and $\sigma$ is the intrinsic line-profile width, also expressed in km s^-1.

($\ell_1$, m1)	(1, 0)	(1, -1)	(0, 0)	(1, -1)	(0, 0)	(1, 0)	(0, 0)	(1, 0)	(0, 0)	(2, 0)
($\ell_2$, m2)	(4, 2)	(4, 3)	(4, 2)	(4, 2)	(3, 3)	(3, 3)	(3, 2)	(3, 2)	(4, 3)	(4, 2)
($\ell_3$, m3)	(3, 3)	(3, 3)	(3, 3)	(3, 2)	(2, 2)	(2, 2)	(3, 1)	(3, 1)	(3, 3)	(2, 2)
$A_{\rm p}^1$	6.51	8.32	7.24	10.66	7.24	5.88	7.24	5.41	7.24	11.21
$A_{\rm p}^2$	104.70	108.18	104.70	102.16	165.87	165.87	172.12	172.12	108.18	120.19
$A_{\rm p}^3$	36.35	9.21	36.35	7.93	15.92	15.92	13.25	13.25	9.21	11.39
i	35	65	35	45	25	25	10	10	65	30
$v_{\Omega }$	15	16	15	19	23	23	13	13	17	14
$\sigma$	19	19	19	19	19	19	11	11	19	17
$\Sigma$	5.43	5.43	5.44	5.44	5.45	5.45	5.45	5.46	5.46	5.47

In order to validate and/or improve the mode identification done by Aerts et al. (1998), we performed a mode identification by our new optimized version of the moment method, using the same K-values as adopted by Aerts et al. (1998): K₁=0.028, K₂=0.021 and K₃=0.025. In doing so, we force the amplitudes of the first moment to be equal to the observed values mentioned above. The outcome, which is given in Table 9, is compatible with the previous one. In particular, we recover the $\ell=1$ nature of the main mode and the higher-degree nature of the two lower-amplitude modes. While Aerts et al. (1998) found $\ell=3$ and 4 for respectively f₂ and f₃, we find the reverse here. This is not too surprising as these two modes resemble each other for a view at moderate inclination. The continuous parameter estimates $(i,v_\Omega, \sigma)$ we find here are intermittent to the three different values for the three modes in Aerts et al. (1998).

Note that we also performed a mode identification by using Lee & Saio's formalism (1987). As we could expect, we obtained the same outcome since the ratio $\eta$ is only about 0.015 for this star.

Data with a better time spread are needed to check the validity of the best solutions as outlined in Sect. 4, as the beating between the three modes is very badly covered. We therefore cannot yet perform seismic modelling of the star, but the studies by Aerts et al. (1998) and by Cuypers et al. (2002) have pushed this star upward in the list of potential asteroseismic targets for future space missions.

5.2 EN (16) Lacertae

EN (16) Lacertae is one of the most studied $\beta~$Cep stars ever. Lehmann et al. (2001) made for the first time a detailed spectroscopic study of EN (16) Lacertae, which is an eclipsing and spectroscopic binary. Besides providing accurate orbital parameters, they recovered and refined the three intrinsic frequencies known for this star from photometry in their radial-velocity data: f₁=5.91128 c/d, f₂=5.85290 c/d and f₃=5.50279 c/d. The corresponding observed first moment amplitudes are $A_{\rm {obs}}^1=2.57$ km s^-1, $A_{\rm {obs}}^2=2.71$ km s^-1 and $A_{\rm {obs}}^3=1.10$ km s^-1 (Aerts et al. 2002). Chapellier et al. (1995) summarized all photometric mode identification efforts so far and concluded that $\ell_1=0$, $\ell_2=2$ and $\ell_3=1$.

The first spectroscopic mode identification for this star was recently done by Aerts et al. (2002) who considered a subset of 940 high-resolution high S/Nspectra gathered by Lehmann et al. (2001). Our mode identification presented here, which was done using K₁=0.0824, K₂=0.0841 and K₃=0.0951, is one of the identification results adapted by Aerts et al. (2002), who considered also other spectroscopic diagnostics for identification. Our result is given in Table 10.

 

 

Table 2: The ten best solutions of the mode identification through the discriminant $\Sigma$ for the $\beta$ Cephei star 16 Lacertae, using the He I 6678 Å line for which the amplitudes of the first moment are $A_{\rm {obs}}^1=2.57$ km s^-1, $A_{\rm {obs}}^2=2.71$ km s^-1 and $A_{\rm {obs}}^3=1.10$ km s^-1. The meanings of the symbols are the same as in Table 9.

($\ell_1$, m1)	(0, 0)	(0, 0)	(0, 0)	(1, 0)	(0, 0)	(1, 0)	(0, 0)	(0, 0)	(0, 0)	(0, 0)
($\ell_2$, m2)	(2, 0)	(1, 0)	(2, 0)	(2, 0)	(2, 0)	(2, 0)	(2, 0)	(2, 0)	(1, 0)	(1, 0)
($\ell_3$, m3)	(1, 0)	(2, 0)	(2, -2)	(2, -2)	(2, 2)	(2, 2)	(2, -1)	(2, 1)	(1, -1)	(1, 1)
$A_{\rm p}^1$	13.45	13.45	12.10	8.38	12.10	8.38	12.10	12.10	13.45	13.45
$A_{\rm p}^2$	27.71	29.21	16.80	16.80	16.80	16.80	27.71	27.71	26.29	26.29
$A_{\rm p}^3$	12.38	11.98	39.99	39.99	39.99	39.99	12.69	12.69	4.82	4.82
i	75	70	25	25	25	25	75	75	70	70
$v_{\Omega }$	38	39	1	1	1	1	6	6	7	7
$\sigma$	5	2	19	19	19	19	19	19	19	19
$\Sigma$	3.86	3.86	3.87	3.87	3.87	3.87	3.88	3.89	3.90	3.90

It is compatible with the one resulting from the other method adapted by Aerts et al. (2002). We refer to Aerts et al. (2002) for an in-depth interpretation of the spectroscopic variability of this star and for a comparison of the moment method outcome with the observed line-profile variations as described in Sect. 4. We also note that a more recent and improved photometric mode identification by Dupret et al. (2002) leads to the same outcome.

Note that, as for $\beta$ Crucis, a mode identification with the rotating formalism does not change anything to the outcome.

5.3 HD 74195

De Cat (2001) studied the slowly pulsating B star HD 74195, among 12 other such stars. Based on multicolour Geneva photometry and high-resolution spectroscopy, he found four frequencies: f₁=0.35475 c/d, f₂=0.35033 c/d, f₃=0.34630 c/d and f₄=0.39864 c/d. The corresponding observed first moment amplitudes are $A_{\rm {obs}}^1=2.36$ km s^-1, $A_{\rm {obs}}^2=2.36$ km s^-1, $A_{\rm {obs}}^3=1.18$ km s^-1 and $A_{\rm {obs}}^4=1.43$ km s^-1. The mode identification from the moments of the 4128 Å Si II line based on the moment method in the version by Aerts (1996) attributed the first three frequencies to $\ell=2$ modes and f₄ to an $\ell=1$ mode. The identification from photometry, however, was found to be incompatible with this result by De Cat (2001) since it points towards $\ell=1$ modes for f₁, f₂ and f₃ and an $\ell=6$ mode for f₄.

In an attempt to resolve the issue, we performed a new identification with our version of the moment method. We point out that the values of the observed first moment amplitudes and of the observed constant term of the second moment clearly impose $\ell \le 3$ for the four frequencies, directly excluding a high degree mode for f₄. By eliminating degrees greater than 3 in the photometric outcome, the new candidate degree from Geneva data is also $\ell=1$ for the fourth frequency.

The result with the new moment method by taking K₁=41, K₂=42, K₃=43 and K₄=32 is given in the upper part of Table 11.

 

 

Table 3: The ten best solutions of the mode identification through the discriminant $\Sigma$ for the slowly pulsating B star HD 74195, using the Si II 4128 Å line for which the amplitudes of the first moment are $A_{\rm {obs}}^1=2.36$ km s^-1, $A_{\rm {obs}}^2=2.36$ km s^-1, $A_{\rm {obs}}^3=1.18$ km s^-1 and $A_{\rm {obs}}^4=1.43$ km s^-1. The meanings of the symbols are the same as in Table 9. The upper part of the table corresponds to an identification using the non-rotating formalism and fixing K-values. The middle one is the result by varying the K-values from 0.7 K to 1.3 K with a step of 0.1 K. The lower one is the outcome for an identification using Lee & Saio's formalism for the pulsational velocity of a rotating star.

($\ell_1$, m1)	(1, 0)	(1, 0)	(2, 0)	(2, 0)	(2, -1)	(2, 0)	(2, -1)	(1, 0)	(1, 0)	(2, 0)
($\ell_2$, m2)	(2, -2)	(2, -2)	(2, -2)	(3, -1)	(3, -1)	(2, -2)	(3, -1)	(3, -1)	(3, -1)	(3, -1)
($\ell_3$, m3)	(2, 1)	(2, 2)	(2, 2)	(2, 1)	(2, 2)	(2, 1)	(3, 1)	(2, 1)	(2, 2)	(2, 2)
($\ell_4$, m4)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)
$A_{\rm p}^1$	0.27	0.34	0.30	0.30	0.24	0.16	0.20	0.28	0.26	0.18
$A_{\rm p}^2$	1.04	0.36	0.44	0.25	0.23	1.04	0.23	0.23	0.23	0.22
$A_{\rm p}^3$	0.11	0.17	0.21	0.09	0.48	0.11	0.11	0.10	0.48	0.34
$A_{\rm p}^4$	0.62	0.37	0.41	0.41	0.62	0.62	0.46	0.53	0.62	0.52
i	25	45	40	40	25	25	35	30	25	30
$v_{\Omega }$	17	23	23	20	15	15	17	15	12	14
$\sigma$	5	3	1	6	8	6	8	9	9	9
$\Sigma$	5.50	5.50	5.51	5.52	5.52	5.53	5.54	5.54	5.54	5.55
($\ell_1$, m1)	(1, 0)	(1, 0)	(2, 0)	(2, 0)	(2, 0)	(2, -1)	(2, -1)	(1, 0)	(1, 0)	(1, 0)
($\ell_2$, m2)	(2, -2)	(2, -2)	(2, -2)	(3, -1)	(2, -2)	(3, -1)	(3, -1)	(2, -2)	(3, -1)	(3, -1)
($\ell_3$, m3)	(2, 1)	(2, 2)	(2, 2)	(2, 1)	(2, 1)	(2, 2)	(3, 1)	(1, 0)	(2, 1)	(2, -2)
($\ell_4$, m4)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)
$A_{\rm p}^1$	0.38	0.26	0.23	0.23	0.22	0.18	0.15	0.37	0.22	0.22
$A_{\rm p}^2$	1.49	0.28	0.34	0.19	1.49	0.18	0.18	1.46	0.17	0.20
$A_{\rm p}^3$	0.16	0.13	0.16	0.07	0.16	0.38	0.08	0.18	0.08	0.42
$A_{\rm p}^4$	0.88	0.28	0.31	0.32	0.88	0.47	0.35	0.86	0.41	0.51
K1	28	52	52	52	28	52	52	28	52	49
K2	29	53	53	53	29	53	53	29	53	50
K3	29	55	55	55	29	55	55	29	55	51
K4	22	41	41	41	22	41	41	22	41	39
i	25	45	40	40	25	25	35	25	30	25
$v_{\Omega }$	27	23	23	20	17	15	17	17	15	12
$\sigma$	5	3	1	6	5	8	8	5	9	9
$\Sigma$	5.49	5.50	5.50	5.51	5.51	5.52	5.54	5.54	5.54	5.55
($\ell_1$, m1)	(2, 0)	(1, 0)	(1, 0)	(2, 0)	(2, 0)	(2, 0)	(1, 0)	(1, 0)	(2, 0)	(2, 0)
($\ell_2$, m2)	(3, -1)	(3, -1)	(2, -1)	(3, -1)	(2, -1)	(3, -1)	(2, -1)	(3, -1)	(3, -1)	(3, -1)
($\ell_3$, m3)	(3, 1)	(3, 1)	(3, 1)	(2, 2)	(2, 2)	(2, 1)	(2, 2)	(2, 2)	(1, 0)	(2, 0)
($\ell_4$, m4)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)	(1, -1)
$A_{\rm p}^1$	0.23	0.30	0.27	0.23	0.18	0.23	0.28	0.30	0.23	0.23
$A_{\rm p}^2$	0.03	0.03	0.02	0.03	0.03	0.03	0.03	0.03	0.03	0.03
$A_{\rm p}^3$	0.16	0.16	0.17	0.82	1.21	0.15	1.21	0.82	0.14	0.11
$A_{\rm p}^4$	0.25	0.25	0.24	0.25	0.25	0.25	0.25	0.25	0.25	0.25
K1	40	40	40	40	40	40	40	40	40	40
K2	139	139	281	139	180	139	180	139	139	139
K3	19	19	15	11	9	19	9	11	42	42
K4	88	88	152	88	108	88	108	88	88	88
i	25	45	40	40	25	25	35	25	30	25
i	35	35	25	35	30	35	30	35	35	35
$v_{\Omega }$	20	20	20	20	20	20	20	20	20	20
$\sigma$	6	6	6	6	6	6	6	6	6	6
$\Sigma$	5.51	5.52	5.52	5.53	5.55	5.55	5.55	5.56	5.56	5.56

This identification is not too different from the spectroscopic one found by De Cat (2001). Our calculations clearly point towards an $\ell=1$ sectoral mode for f₄. However, the identification for the other frequencies still needs to be confirmed.

One can doubt the reliability of a mode identification by fixing K-values of SPBs. Indeed, because there are large uncertainties on the mass and radius of most of these stars, K-values can have uncertainties up to 30%, which is very large. In order to test our mode identification as done above, we performed a new one by varying the parameter from 0.7 K to 1.3 K with a step of 0.1 K and we obtained the outcome given in the middle part of Table 11.

The identification of the modes leads to exactly the same outcome as before, except that the values of $A_{\rm p}$ differ. One can conclude that the uncertainty on the K-value does not affect the identification of $(\ell,m)$. This result is not too surprising since line-profile variations of an SPB are mainly due to the horizontal velocity field variations and slightly to the vertical ones. The relevant amplitude is then the horizontal one $A_{\rm h}=A_{\rm p} ~K$, which is indeed found to be about the same for each of the modes in the two different identifications.

One can also doubt the reliability of a mode identification for SPB stars by using the non-rotating theory since their observed ratios of the rotational frequency to the pulsational frequency are in general larger than 0.1. Again to test our mode identification, we performed a new one using the formalism of Lee & Saio (1987). The K-values are then computed using the corotating angular frequency related to the observed one by $\omega_{\rm c}=\omega_{\rm {obs}}+m\Omega$. The identification is given in the lower part of Table 11.

This again leads to a very similar outcome for the wavenumbers $(\ell,m)$. Basically, the same combinations for $(\ell,m)$ occur each time. The K-values change considerably, but this is compensated by the values for $A_{\rm p}$and does not affect the mode identification appreciably. We do point out that the formalism of Lee & Saio (1987) does not apply to modes with m=0 so that axisymmetric modes mentioned in the lower part of Table 11 were computed using the non-rotating formalism.

It is clear that, particularly in the case of multiple g-modes, we need additional observational information to pinpoint definitely the wavenumbers $(\ell,m)$ of all the different modes. Our method, however, implies a serious improvement for the spectroscopic mode identification in such cases. In the particular case of HD 74195, De Cat et al. (2002) are currently using Dupret et al.'s (2002) method in order to improve the photometric mode identification. Line-profile fitting and an attempt at seismic modelling will be performed after further elimination of combinations from Table 11 according to the multicolour mode identification in progress and is beyond the scope of our current paper.

6 Conclusions

The study of the oscillations of a pulsating star allows us to probe its internal structure. A successful application of asteroseismic techniques requires the identification of many pulsation modes. Therefore, high quality data as well as powerful mode identification methods are needed. Among the techniques of mode identification from line-profile variations, only the line-profile fitting method and the moment method derive the full pulsational information. However, even with current computers, a simultaneous identification of multiple modes is not possible by direct line-profile fitting. Moreover, mode identification with the moment method was still difficult for multiperiodic stars. Indeed, because of large computation time, the previous version of the moment method did not take into account coupling terms appearing in the second and third moments of a multiperiodic star so that multiple modes were determined independently, often leading to inconsistent values of the continuous velocity parameters.

We presented a new numerical version of the moment method, which is efficient in computation time and which identifies all the modes by requiring that the rotational velocity, the inclination angle and the intrinsic line width have one unique value. Consequently, all observed terms of the first three moments can be used, in particular the constant term of the second moment which is an important constraint. By means of a new discriminant which compares theoretical to observed first three moments, the new version identifies the wavenumbers of the multiple modes simultaneously, leading to only one derived value for $v_{\Omega }$, i, and $\sigma$.

We performed a large number of tests on artificial data representing the presence of respectively one, two and three modes. It appears that the method performs very well on synthetic data sets. An application to two $\beta$ Cephei stars and one SPB star was done. We subsequently plan to use the new version of the moment method in the near future to several data sets of pulsating B stars of different kinds. Our new method is also relevant to obtain reliable mode identification in multiperiodic bright $\delta~$Scuti and $\gamma~$Doradus stars.

Acknowledgements

We thank the referee, Dr. G. Handler, for his pertinent comments which helped to improve our manuscript. This work was supported by the P.A.I. (Pôle d'Attraction Interuniversitaire) and was carried out within the Belgian Asteroseismology Group.

Appendix A: The amplitudes of the first three moments

$$A_1^j=A_{\rm p}^j ~\big\{ I~\big[C_{\ell_j}^{m_j}\big]~ + K_j I~\big[D_{\ell_j}^{m_j}\big]~ \big\}~$$,

$$C_1^j=\frac{1}{2} ~\big(A_{\rm p}^j\big)~^2 ~\big\{ I~\big[~\big(... ...big[~\big(D_{\ell_j}^{m_j}\big)~^2-~\big(F_{\ell_j}^{m_j}\big)~^2\big]~\big\}~,$$

$$D_2^j=2 \ v_\Omega \ A_{\rm p}^j ~\big\{ I~\big[E_{\ell_j}^{m_j} ... ...n\phi\big]~ + K_j I~\big[F_{\ell_j}^{m_j} \sin\theta \ \sin\phi\big]~ \big\}~,$$

$$C_{\rm b1}^{jk}=\frac{1}{2} \ A_{\rm p}^j \ A_{\rm p}^k ~\big\{ ... ...big[C_{\ell_j}^{m_j} D_{\ell_k}^{m_k}+ E_{\ell_j}^{m_j} F_{\ell_k}^{m_k}\big]~$$

$$+ K_j K_k I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k}+ F_{\ell_j}^{m_j} F_{\ell_k}^{m_k}\big]~ \big\}~,$$

$$C_{\rm s1}^{jk}=\frac{1}{2} \ A_{\rm p}^j \ A_{\rm p}^k ~\big\{ ... ...ig[C_{\ell_j}^{m_j} D_{\ell_k}^{m_k}- E_{\ell_j}^{m_j} F_{\ell_k}^{m_k}\big]~$$

$$+ K_j K_k I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k}- F_{\ell_j}^{m_j} F_{\ell_k}^{m_k}\big]~ \big\}~,$$

$$E_{12}^j=\frac{1}{2} ~\big(A_{\rm p}^j\big)~^2 ~\big\{ I~\big[~\b... ...big[~\big(D_{\ell_j}^{m_j}\big)~^2+~\big(F_{\ell_j}^{m_j}\big)~^2\big]~\big\}~,$$

$$E_{\rm {rot}}^j= v_\Omega^2 I~\big[\sin^2\theta \ \sin^2\phi\big]~,$$

$$F_1^j= \frac{1}{4} ~\big(A_{\rm p}^j\big)~^3 ~\big\{ I~\big[~\big... ...{m_j}\big)~^2\big]~ + K_j^3 I~\big[~\big(D_{\ell_j}^{m_j}\big)~^3\big]~ \big\}~$$

$$\quad -\frac{3}{4} ~\big(A_{\rm p}^j\big)~^3 ~\big\{ I~\big[C_{\el... ...2\big]~+ 2I~\big[C_{\ell_j}^{m_j} E_{\ell_j}^{m_j} F_{\ell_j}^{m_j}\big]~\big)~$$

$$\quad +K_j^2 ~\big( I~\big[C_{\ell_j}^{m_j} (F_{\ell_j}^{m_j}\big... ...~\big)~ +K_j^3 I~\big[D_{\ell_j}^{m_j} (F_{\ell_j}^{m_j}\big)~^2\big]~\big\}~,$$

$$G_2^j=3 v_\Omega (A_{\rm p}^j\big)~^2 ~\big\{ I~\big[C_{\ell_j}^{... ...heta \ \sin\phi+ D_{\ell_j}^{m_j} E_{\ell_j}^{m_j} \sin\theta \ \sin\phi\big]~$$

$$\quad + K_j^2 I~\big[D_{\ell_j}^{m_j} F_{\ell_j}^{m_j}\sin\theta \ \sin\phi\big]~\big\}~,$$

$$RST_1^j=3 v_\Omega^2 A_{\rm p}^j ~\big\{ I~\big[C_{\ell_j}^{m_j}... ...big\{ I~\big[C_{\ell_j}^{m_j}\big]~ + K_j I~\big[D_{\ell_j}^{m_j}\big]~ \big\}~$$

$$\quad + \frac{3}{4} (A_{\rm p}^j\big)~^3 ~\big\{ I~\big[(C_{\ell_j... ...l_j}^{m_j}\big)~^2\big]~ + K_j^3 I~\big[(D_{\ell_j}^{m_j}\big)~^3\big]~ \big\}~$$

$$\quad+\frac{3}{4} (A_{\rm p}^j\big)~^3 ~\big\{ I~\big[C_{\ell_j}^... ...\big]~+ 2I~\big[C_{\ell_j}^{m_j} E_{\ell_j}^{m_j} F_{\ell_j}^{m_j}\big]~\big)~$$

$$\quad +K_j^2 ~\big( I~\big[C_{\ell_j}^{m_j} ~\big(F_{\ell_j}^{m_j... ...)~ +K_j^3 I~\big[D_{\ell_j}^{m_j} ~\big(F_{\ell_j}^{m_j}\big)~^2\big]~\big\}~,$$

$$G_{\rm b2}^{jk}=- 3 v_\Omega \ A_{\rm p}^j \ A_{\rm p}^k ~\big\{ I~\big[C_{\ell_j}^{m_j} E_{\ell_k}^{m_k} \ \sin\theta \ \sin\phi\big]~$$

$$\quad + K_j I~\big[D_{\ell_j}^{m_j} E_{\ell_k}^{m_k} \ \sin\theta... ...~\big[D_{\ell_j}^{m_j} F_{\ell_k}^{m_k} \ \sin\theta \ \sin\phi\big]~ \big\}~,$$

$$G_{\rm s2}^{jk}= 3 v_\Omega A_{\rm p}^j \ A_{\rm p}^k ~\big\{ I~\big[C_{\ell_j}^{m_j} E_{\ell_k}^{m_k} \ \sin\theta \ \sin\phi\big]~$$

$$\quad + K_j I~\big[D_{\ell_j}^{m_j} E_{\ell_k}^{m_k} \ \sin\theta... ...~\big[D_{\ell_j}^{m_j} F_{\ell_k}^{m_k} \ \sin\theta \ \sin\phi\big]~ \big\}~,$$

$$F_{11}^{jkn}=- \frac{3}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} E_{\ell_n... ...K_k K_n I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~ \big\}~$$

$$\quad + \frac{1}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^n ~\big... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} C_{\ell_n... ..._k K_n I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~ \big\}~,$$

$$F_{21}^{jkn}= \frac{3}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^n... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} E_{\ell_n... ...K_k K_n I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~ \big\}~$$

$$\quad + \frac{1}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^n ~\big... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} C_{\ell_n... ..._k K_n I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~ \big\}~,$$

$$F_{31}^{jkn}=- \frac{3}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} E_{\ell_n... ...K_k K_n I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~ \big\}~$$

$$\quad + \frac{1}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^n ~\big... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} C_{\ell_n... ..._k K_n I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~ \big\}~,$$

$$F_{41}^{jkn}= \frac{3}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^n... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} E_{\ell_n... ...K_k K_n I~\big[F_{\ell_j}^{m_j} D_{\ell_k}^{m_k} F_{\ell_n}^{m_n}\big]~ \big\}~$$

$$\quad + \frac{1}{4} A_{\rm p}^j \ A_{\rm p}^k \ A_{\rm p}^n ~\big... ...n}\big]~ + K_n I~\big[C_{\ell_j}^{m_j} C_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~$$

$$\quad +K_j K_k I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} C_{\ell_n... ..._k K_n I~\big[D_{\ell_j}^{m_j} D_{\ell_k}^{m_k} D_{\ell_n}^{m_n}\big]~ \big\}~,$$

Appendix B: Three moments are sufficient for mode identification

In all versions of the moment method for slowly rotating stars, one limits the discriminating function for mode identification to the first three moments (Balona 1986a, 1987; Aerts et al. 1992; Aerts 1996). We provide here a justification for this.

For one mode, we rewrite the first three moments as follows:

$$\begin{eqnarray*}\lefteqn{ <v>(t)=A \cos(\omega t + \psi)}\\ \lefteqn{ <v^2>(t)... ...\psi) + G \sin(2 \omega t + 2 \psi)+ RST \cos(\omega t + \psi),} \end{eqnarray*}$$

with

$$\begin{eqnarray*}\left \{\! \begin{array}{lll} A= A_{\rm p} \left(c_1 + c_2 K\r... ...{6} + c_{7} K + c_{8} K^2 + c_{9} K^3\right) \end{array}\right. \end{eqnarray*}$$

where $c_1, c_2, \dots, c_9$ depend on $(\ell,m,i)$.
Aerts et al. (1992) have shown that the second moment discriminates easily between axisymmetric modes and non-axisymmetric modes.

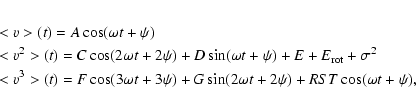
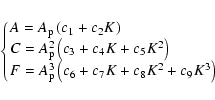
We search for different $(\ell,m)$ and $(\ell',m')$ so that <v>(t)=<v>'(t), <v²>(t)=<v²>'(t) and <v³>(t)=<v³>'(t) for all t, i.e. so that A=A', C=C', F=F' for appropriate values of the parameters. We use the fact that the K-value is determined for a given star and for a given frequency (K=K'). For chosen $(\ell,m,i)$ and $(\ell',m',i')$, we then have the following system of three equations for $A_{\rm p}, A'_{\rm p}$ and K to solve:

$$\begin{eqnarray*}\left\{ \!\begin{array}{lll} (1) A_{\rm p} \left(c_1 + c_2 K\ri... ...+ c'_{7} K + c'_{8} K^2 + c'_{9} K^3\right). \end{array}\right. \end{eqnarray*}$$

One excludes $(\ell,m,i)$ for which the first moment has no time variation, which corresponds to c₁=0 and c₂=0. One also considers $m=0,\dots,\ell$since the absolute value of the amplitudes of the moments are the same for positive and negative m.

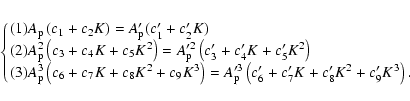
From (1) and (2) ( $A_{\rm p},A'_{\rm p} \ne 0$), one obtains an equation in K which can be solved analytically for chosen $(\ell,m,i)$ and $(\ell',m',i')$:

$$\begin{eqnarray*}&& \left(c^{2'}_1 c_3 - c_1^2 c'_3\right) + \left(c^{2'}_1 c_4 ... ...5\right) K^3 + \left(c^{2'}_2 c_5 - c^{2}_2 c'_5\right) K^4 = 0. \end{eqnarray*}$$

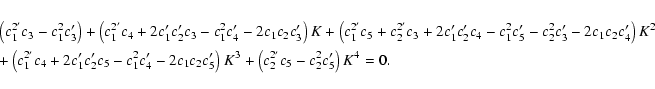
The coefficients of this equation are not simultaneously equal to zero. Consequently, the equation has four solutions or less.

From (1) and (3) as well as from (2) and (3), one obtains two equations in K, which must also be satisfied by the solutions.

We tested numerically the feasibility of more than one solution $(\ell,m,i)$ by varying $\ell$ from 0 to 4 with $m=0,\dots,\ell$. We varied i from 0$^{\circ}$ to 90$^{\circ}$ with a step of 1$^{\circ}$. For each combination $(\ell,m,i)$ and $(\ell',m',i')$, we searched for solutions which satisfy the equations in K. Note that we did not confront an axisymmetric mode with a non-axisymmetric mode since they are discriminated by the behaviour of the second moment. We did not confront the same couples of wavenumbers with different i either.

The outcome is that the system of three Eqs. (1)-(3) has no solution for each tested case. So the first three moments discriminate the different modes whatever the values of the velocity parameters are.

In practice, because of too few and/or too noisy data, and because of the uncertainty of K, it obviously happens that several couples $(\ell,m)$ fit the moment variations with almost the same quality. However, the message we want to bring here is that it in principle suffices to consider the three moments to discriminate between the wavenumbers.

References

 
• Aerts, C., De Pauw, M., & Waelkens, C. 1992, A&A, 266, 294 In the text NASA ADS  
• Aerts, C. 1996, A&A, 314, 115 In the text NASA ADS  
• Aerts, C., De Cat, P., Cuypers, J., et al. 1998, A&A, 329, 137 In the text NASA ADS  
• Aerts, C., Lehmann, H., Briquet, M., et al. A&A, submitted In the text  
• Balona, L. A. 1986a, MNRAS, 219, 111 In the text NASA ADS  
• Balona, L. A. 1986b, MNRAS, 220, 647 NASA ADS  
• Balona, L. A. 1987, MNRAS, 224, 41 In the text NASA ADS  
• Chapellier, E., Lecontel, J. M., Lecontel, D., et al. 1995, A&A, 304, 406 In the text NASA ADS  
• Cuypers, J., Aerts, C., Buzasi, D., et al. 2002, A&A, 392, 599 In the text NASA ADS  
• De Cat, P. 2001, An observational study of bright southern slowly pulsating B stars, Ph.D. Thesis (Katholieke Universiteit Leuven, Belgium) In the text  
• De Ridder, J., Dupret, M.-A., Neuforge, C., & Aerts, C. 2002a, A&A, 385, 572 In the text NASA ADS  
• De Ridder, J., Molenberghs, G., & Aerts, C. 2002b, in Asteroseismology across the HR diagram (Kluwer Academic Publishers), in press In the text  
• Dupret, M.-A., De Ridder, J., Neuforge, C., et al. 2002, A&A, 385, 563 In the text NASA ADS  
• Lee, U., & Saio, H. 1987, MNRAS, 224, 513 In the text NASA ADS  
• Lee, U., & Saio, H. 1990, ApJ, 349, 570 NASA ADS  
• Lehmann, H., Harmanec, P., Aerts, C., et al. 2001, A&A, 367, 236 In the text NASA ADS  
• Mathias, P., Aerts, C., de Pauw, M., et al. 1994, A&A, 283, 813 In the text NASA ADS  
• Schrijvers, C., Telting, J. H., Aerts, C., et al. 1997, A&AS, 121, 343 In the text NASA ADS  
• Townsend, R. H. D. 1997, MNRAS, 284, 839 In the text NASA ADS

 

Online Material

 

Table 1: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for two modes. The input parameters are shown, followed by the five best solutions of the mode identification. $A_{\rm p}$ is the amplitude of the radial part of the pulsation velocity, expressed in km s^-1; i is the inclination angle; $v_{\Omega }$is the projected rotational velocity, expressed in km s^-1 and $\sigma$ is the intrinsic line-profile width, also expressed in km s^-1.

($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, -1)	(1, 0)	2.25	0.53	65.54	12.03	6	25.86	5.5
(1, -1)	(1, 0)	2.86	0.58	56.64	10.39	5	22	4	1.68
(1, -1)	(2, 0)	2.86	0.32	56.64	10.39	5	22	4	1.77
(1, -1)	(3, 0)	2.86	0.58	56.64	10.39	5	22	4	2.85
(1, 1)	(1, 0)	2.86	0.58	56.64	10.39	5	22	4	4.99
(1, 1)	(2, 0)	2.86	0.32	56.64	10.39	5	22	4	5.07
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 0)	(1, 1)	10.38	21.92	0.082	0.086	16	23.52	5.5
(2, 0)	(1, 1)	9.99	23.27	0.094	0.099	15	21	7	1.53
(1, 0)	(3, 3)	9.06	93.26	0.094	0.099	35	10	7	1.68
(1, 0)	(2, 1)	7.92	12.82	0.094	0.099	20	25	3	1.87
(2, 0)	(2, 1)	10.82	12.82	0.094	0.099	20	24	4	1.95
(2, 0)	(3, 1)	9.99	24.59	0.094	0.099	15	13	10	1.95
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 2)	(1, -1)	1.69	0.77	6.48	17.40	52	19.33	5.5
(3, 2)	(1, -1)	1.45	0.52	8.20	22.02	60	19	5	2.56
(1, -1)	(2, 2)	4.90	2.19	8.20	22.02	20	14	1	2.87
(3, 2)	(2, 2)	2.64	0.61	4.41	11.86	60	19	5	2.99
(1, -1)	(1, -1)	3.37	0.90	8.20	22.02	30	17	6	3.17
(2, 2)	(1, -1)	10.00	1.90	4.41	11.86	25	16	3	3.29
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -3)	(2, 0)	32.97	9.60	0.085	0.095	87	10.14	5.5
(3, -3)	(2, 0)	38.49	10.44	0.051	0.057	80	9	5	2.39
(2, -2)	(2, 0)	17.16	11.88	0.051	0.057	75	18	2	2.40
(3, -3)	(1, 1)	38.49	5.42	0.051	0.057	80	9	5	2.53
(3, -3)	(2, 1)	49.42	10.12	0.051	0.057	65	8	3	2.57
(3, -2)	(1, 1)	40.01	6.17	0.051	0.057	60	11	5	2.64
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 2)	(1, -1)	4.02	0.91	5.61	19.74	37	19.14	5.5
(1, -1)	(1, -1)	2.88	0.66	7.05	24.79	45	23	2	2.19
(2, 2)	(1, -1)	4.30	1.18	3.79	13.35	45	23	1	2.20
(1, -1)	(2, 2)	6.09	1.67	4.34	15.25	30	21	3	2.23
(3, 1)	(1, -1)	2.10	0.46	7.05	24.79	90	22	1	3.04
(2, 2)	(3, 1)	2.16	0.85	3.79	13.35	85	22	2	3.19

 

Table 2: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for two modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, -1)	(1, -1)	30.45	21.69	0.085	0.099	17	10.84	5.5
(3, -1)	(2, -1)	40.09	11.17	0.054	0.062	30	16	2	2.30
(3, -1)	(1, -1)	42.16	15.91	0.054	0.062	25	14	3	2.52
(2, -1)	(2, -1)	29.18	15.16	0.054	0.062	20	14	6	2.53
(3, -2)	(2, -2)	46.16	12.86	0.054	0.062	60	14	4	2.54
(2, -1)	(1, -1)	29.18	19.72	0.054	0.062	20	15	6	2.56
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 0)	(1, 1)	0.45	6.98	11.45	4.91	16	23.52	5.5
(2, 0)	(1, 1)	0.30	1.84	16.99	5.21	15	19	8	1.88
(1, 0)	(1, 1)	0.58	1.84	16.99	5.21	15	19	8	1.91
(3, 0)	(1, 1)	0.69	1.84	9.14	12.82	10	16	9	2.44
(2, -1)	(1, 1)	0.70	1.84	16.99	3.97	20	18	8	3.72
(1, 0)	(3, 2)	2.93	1.84	9.14	2.67	70	25	1	3.74
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -2)	(2, 2)	35.19	13.21	0.086	0.091	52	15.82	5.5
(3, -2)	(2, 2)	36.24	12.33	0.071	0.075	55	16	4	2.39
(3, -3)	(3, 2)	37.90	30.83	0.071	0.075	75	13	2	2.57
(2, -2)	(2, 2)	30.80	16.56	0.071	0.075	45	19	2	2.79
(3, -3)	(2, 2)	37.90	8.85	0.071	0.075	75	13	5	2.87
(3, -3)	(3, 1)	34.14	23.50	0.071	0.075	90	14	4	3.43
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 3)	(2, 1)	2.04	1.88	5.14	8.81	81	24.33	5.5
(3, 3)	(2, 1)	1.35	1.10	7.84	13.45	80	26	4	2.25
(3, 3)	(3, 0)	2.22	0.98	5.43	9.31	70	23	7	2.82
(3, 3)	(2, 0)	2.46	0.92	4.22	7.24	80	25	6	2.85
(3, 3)	(2, -1)	1.35	1.10	7.84	13.45	80	26	4	3.53
(3, 3)	(3, 1)	4.32	0.72	6.64	11.38	45	17	8	3.68
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 2)	(1, -1)	36.20	7.24	0.078	0.097	52	19.33	5.5
(3, 2)	(1, -1)	36.61	6.96	0.076	0.095	55	20	5	1.79
(2, 2)	(1, -1)	37.95	8.88	0.076	0.095	40	21	5	2.07
(3, 2)	(2, -1)	36.61	8.36	0.076	0.095	55	20	5	2.16
(2, 2)	(2, -1)	37.95	7.99	0.076	0.095	40	21	5	2.45
(3, 2)	(1, 0)	39.91	5.69	0.076	0.095	45	16	7	2.93

 

Table 3: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for two modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 1)	(1, 0)	16.10	4.80	0.080	0.095	37	11.91	5.5
(2, 1)	(1, 0)	22.63	4.48	0.054	0.064	25	10	6	1.95
(1, 1)	(1, 0)	34.83	4.33	0.054	0.064	20	10	6	2.01
(2, 1)	(2, 0)	27.09	6.17	0.054	0.064	20	8	6	2.07
(3, 1)	(1, 0)	44.34	4.33	0.054	0.064	20	6	2	2.08
(3, 1)	(2, 0)	44.34	6.17	0.054	0.064	20	6	1	2.13
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -1)	(2, -2)	0.84	0.21	16.40	27.36	86	24.62	5.5
(3, -1)	(2, -2)	0.88	0.23	15.54	25.93	90	27	3	1.83
(1, 1)	(2, -2)	1.04	0.37	19.43	32.42	45	19	10	1.94
(1, 1)	(3, -1)	0.89	0.19	25.26	42.14	40	16	11	2.28
(1, 1)	(2, -1)	1.13	0.34	13.60	22.69	65	28	2	2.64
(1, 1)	(3, -2)	0.59	0.31	25.26	42.14	75	14	11	3.16
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, 1)	(1, 0)	25.54	4.34	0.080	0.095	27	11.78	5.5
(1, 1)	(1, 0)	74.02	4.41	0.053	0.063	10	4	4	2.07
(1, 1)	(2, 0)	29.54	7.27	0.053	0.063	25	10	6	2.12
(2, 1)	(2, 0)	23.82	7.27	0.053	0.063	25	9	6	2.12
(2, 1)	(1, 0)	18.44	5.56	0.053	0.063	40	14	4	2.16
(3, 1)	(1, 0)	41.23	4.71	0.053	0.063	25	7	3	2.31
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -2)	(2, -1)	0.54	0.35	21.86	16.32	47	15.094	5.5
(3, -2)	(2, -1)	0.94	0.62	12.30	9.18	50	15	6	1.88
(3, -3)	(2, -1)	0.86	0.35	22.84	17.06	55	11	6	2.10
(3, -3)	(2, -2)	0.47	0.33	22.84	17.06	90	13	7	2.22
(3, -1)	(2, -1)	0.44	0.38	22.84	17.06	30	19	2	2.59
(3, -2)	(2, -2)	0.55	0.41	22.84	17.06	65	18	3	2.60
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -1)	(2, 1)	34.05	7.83	0.084	0.093	42	12.49	5.5
(3, -1)	(1, 1)	33.13	9.81	0.058	0.065	35	12	6	2.27
(3, -1)	(2, 1)	33.13	8.60	0.058	0.065	35	12	6	2.29
(3, -2)	(1, 1)	58.29	5.81	0.058	0.065	75	11	2	2.55
(2, -1)	(2, 1)	17.56	9.31	0.058	0.065	60	20	1	2.65
(2, -1)	(1, 1)	15.47	8.75	0.058	0.065	40	17	5	2.67

 

Table 4: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for two modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -3)	(2, 1)	0.57	0.64	40.24	8.95	52	18.29	5.5
(3, -3)	(2, 1)	0.51	1.89	26.24	5.83	75	19	5	2.77
(3, -2)	(2, 1)	0.26	0.53	48.73	10.84	50	22	2	2.99
(3, -3)	(2, 0)	0.26	0.71	48.73	10.84	80	18	6	3.50
(3, -3)	(3, 0)	0.55	1.75	26.24	5.83	70	18	5	3.56
(3, -3)	(3, 1)	1.31	1.57	26.24	5.83	45	14	1	3.60
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 0)	(2, 2)	12.62	44.62	0.082	0.082	26	29.84	5.5
(2, 0)	(2, 2)	10.02	68.16	0.11	0.11	20	25	9	2.01
(2, 0)	(3, 2)	16.22	25.03	0.11	0.11	35	30	5	2.02
(1, 0)	(2, 2)	7.53	68.16	0.11	0.11	20	25	9	2.22
(1, 0)	(3, 2)	7.36	108.36	0.11	0.11	15	13	2	2.31
(3, 0)	(2, 2)	20.27	120.87	0.11	0.11	15	17	10	3.18
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 0)	(3, 2)	1.52	1.93	11.45	7.49	32	10.35	5.5
(3, 1)	(3, 2)	3.42	2.44	7.03	4.60	70	16	1	3.78
(3, 0)	(3, 2)	3.29	2.09	7.03	4.60	45	14	2	4.04
(3, 0)	(2, 2)	1.74	5.31	7.03	4.60	30	19	1	4.31
(2, 0)	(3, 2)	3.81	1.95	7.03	4.60	50	14	6	4.50
(2, 0)	(2, 2)	3.81	2.25	7.03	4.60	50	20	1	4.78
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 1)	(2, -1)	44.57	43.88	0.080	0.097	86	24.54	5.5
(3, 1)	(2, -1)	42.84	33.76	0.095	0.11	85	25	6	2.59
(3, 1)	(1, 0)	42.84	35.41	0.095	0.11	85	22	9	3.29
(3, 1)	(2, 1)	42.84	33.76	0.095	0.11	85	27	3	3.30
(2, 2)	(3, -1)	25.31	19.44	0.095	0.11	50	13	13	3.43
(2, 2)	(2, -1)	14.94	33.76	0.095	0.11	85	16	12	3.57
($\ell_1$, m1)	($\ell_2$, m2)	$A_{\rm p}^1$	$A_{\rm p}^2$	K1	K2	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 1)	(1, 0)	1.11	0.68	7.81	12.03	16.62	32	5.5
(2, 1)	(2, 0)	1.43	0.31	8.78	13.52	20	11	8	2.47
(2, 1)	(1, 0)	2.15	1.02	4.73	7.28	25	12	8	2.48
(3, 1)	(1, 0)	2.22	1.02	4.73	7.28	25	5	9	2.49
(3, 1)	(2, 0)	1.22	0.35	8.78	13.52	25	4	9	2.49
(3, 3)	(1, 0)	5.03	1.44	4.73	7.28	50	3	7	2.64

 

Table 5: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for three modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 0)	(1, -1)	(3, 1)	1.45	0.67	0.57	11.45	14.11	13.75	73	10.72	5.5
(3, 0)	(1, -1)	(3, 1)	1.17	0.53	0.38	14.88	18.34	17.87	75	10	6	2.07
(3, 0)	(2, 2)	(3, 1)	1.17	0.30	0.38	14.88	18.34	17.87	75	12	5	2.11
(2, 1)	(1, -1)	(3, 1)	4.03	0.65	0.33	11.45	14.11	13.75	85	7	2	2.28
(3, 0)	(2, 2)	(1, -1)	2.16	0.55	0.46	8.01	9.87	9.62	75	11	6	2.29
(3, 0)	(1, -1)	(1, -1)	2.16	0.93	0.46	8.01	9.87	9.62	75	11	6	2.30
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, -1)	(1, -1)	(2, 1)	25.13	14.05	10.05	0.084	0.086	0.092	64	19.87	5.5
(2, -1)	(1, -1)	(2, 1)	28.31	15.86	11.51	0.084	0.085	0.092	60	16	7	2.22
(1, -1)	(1, -1)	(1, 1)	17.00	15.15	6.91	0.084	0.085	0.092	65	19	6	2.44
(1, -1)	(1, -1)	(2, 1)	18.81	16.77	10.61	0.084	0.085	0.092	55	17	7	2.46
(2, -1)	(1, -1)	(1, 1)	28.31	15.86	7.23	0.084	0.085	0.092	60	18	6	2.47
(1, -1)	(1, -1)	(2, 1)	17.00	15.15	13.01	0.084	0.085	0.092	65	20	5	2.53
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 2)	(2, -2)	(1, 0)	1.55	0.50	0.31	7.6	20.46	16.31	44	11.86	5.5
(3, 2)	(2, -2)	(2, -1)	1.34	0.51	0.15	9.12	24.55	19.57	40	14	5	2.06
(3, 2)	(2, -2)	(1, 0)	1.46	0.56	0.27	8.36	22.51	17.94	40	14	5	2.07
(3, 2)	(2, -2)	(2, 0)	2.26	0.87	0.41	5.32	14.32	11.41	40	14	5	2.21
(3, 2)	(3, -1)	(2, 0)	1.82	0.24	0.13	9.88	26.60	21.20	30	11	5	2.26
(3, 2)	(3, -1)	(1, 0)	1.82	0.24	0.20	9.88	26.60	21.20	30	11	5	2.30
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, 1)	(3, -2)	(2, 0)	3.01	0.21	0.21	7.35	49.73	16.31	37	22.43	5.5
(1, 1)	(3, -2)	(1, 0)	2.85	0.19	0.26	7.35	49.73	16.31	40	25	2	1.87
(1, 1)	(3, -2)	(2, 0)	3.12	0.21	0.28	6.61	44.76	14.68	40	25	1	1.92
(1, 1)	(3, -2)	(2, -1)	3.45	0.24	0.20	5.88	39.78	13.05	40	25	2	2.28
(1, 1)	(3, -3)	(2, -1)	1.77	0.21	0.13	9.56	64.65	21.20	55	22	5	2.48
(1, 1)	(3, -3)	(1, 0)	2.05	0.33	0.22	9.56	64.65	21.20	45	19	6	2.61
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, -1)	(1, 0)	(2, 2)	0.85	1.54	0.29	13.93	12.03	10.90	68	13.00	5.5
(2, -2)	(1, 0)	(1, -1)	0.56	2.06	0.42	15.33	13.23	11.99	75	9	7	2.20
(2, -2)	(1, 0)	(2, 2)	0.62	2.25	0.27	13.93	12.03	10.90	75	9	7	2.20
(2, -1)	(1, 0)	(1, -1)	0.82	1.56	0.44	15.33	13.23	11.99	70	12	6	2.22
(2, -1)	(1, 0)	(2, 2)	0.90	1.70	0.29	13.93	12.03	10.90	70	15	4	2.23
(2, -1)	(2, 0)	(1, -1)	0.58	1.14	0.63	13.93	12.03	10.90	45	9	7	2.28

 

Table 6: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for three modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, 0)	(1, -1)	(1, 1)	0.91	0.77	1.39	11.45	28.75	8.19	27	23.57	5.5
(1, 0)	(1, -1)	(1, 1)	1.13	0.87	1.48	9.16	23.00	6.55	30	26	3	2.15
(2, 0)	(1, -1)	(1, 1)	0.54	0.83	1.44	11.45	28.75	8.19	25	22	7	2.24
(1, 0)	(2, 2)	(1, 1)	1.17	2.40	2.42	8.01	20.12	5.73	20	21	2	2.68
(2, 0)	(2, 2)	(1, 1)	0.67	2.40	2.42	8.01	20.12	5.73	20	21	2	2.77
(2, 0)	(1, -1)	(2, 2)	0.43	1.34	5.55	11.45	28.75	8.19	15	14	8	2.93
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -2)	(1, 1)	(3, 2)	0.60	1.72	0.70	26.05	8.74	8.29	34	14.14	5.5
(3, -2)	(1, 1)	(3, 2)	0.72	2.09	0.88	20.84	6.99	6.63	35	16	5	2.34
(3, -2)	(1, -1)	(3, 2)	0.72	2.09	0.88	20.84	6.99	6.63	35	16	5	3.13
(3, -3)	(1, 1)	(3, 2)	0.72	1.38	0.63	20.84	6.99	6.63	60	18	3	3.43
(3, -2)	(1, 1)	(2, 2)	1.38	3.17	2.74	18.24	6.12	5.80	25	13	1	3.69
(3, -3)	(1, -1)	(3, 2)	1.07	1.39	0.54	26.05	8.74	8.29	45	14	2	3.71
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 0)	(1, 0)	(2, 2)	0.49	0.55	6.00	11.45	12.03	3.91	22	24.72	5.5
(2, 0)	(1, 0)	(2, 2)	0.49	0.61	15.52	10.30	10.82	3.52	15	17	8	2.06
(2, 0)	(1, 0)	(3, 2)	0.63	0.76	11.75	8.01	8.42	2.74	15	7	10	2.12
(2, 0)	(2, 0)	(2, 2)	0.49	0.32	15.52	10.30	10.82	3.52	15	17	8	2.15
(1, 0)	(1, 0)	(2, 2)	0.93	0.61	15.52	10.30	10.82	3.52	15	17	8	2.24
(1, 0)	(2, 0)	(1, -1)	0.68	0.24	3.41	14.88	15.64	5.08	20	28	2	2.24
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, 0)	(3, 3)	(1, 1)	1.44	1.94	0.49	11.45	6.33	12.40	56	15.29	5.5
(1, 0)	(3, 3)	(1, 1)	0.93	1.96	0.41	14.88	8.23	16.12	50	13	6	2.15
(2, -1)	(3, 3)	(1, 1)	2.00	1.32	0.45	10.30	5.70	11.16	80	16	4	2.54
(2, -1)	(3, 3)	(2, 0)	1.06	1.52	0.48	10.30	5.70	11.16	70	16	5	2.78
(1, 0)	(3, 3)	(3, 0)	2.49	2.15	0.54	8.01	4.43	8.68	65	16	5	2.81
(2, -1)	(3, 3)	(3, -1)	2.54	1.68	0.67	8.01	4.43	8.68	80	16	4	2.81
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 3)	(2, 0)	(1, 0)	1.47	0.65	0.86	7.67	12.03	16.31	75	10.71	5.5
(3, 3)	(2, 0)	(1, 0)	2.05	0.88	1.11	5.37	8.42	11.41	75	11	6	2.26
(3, 3)	(3, 0)	(1, 0)	2.49	0.97	0.68	5.37	8.42	11.41	65	10	6	2.28
(3, 3)	(2, 0)	(2, -2)	2.23	1.08	0.26	5.37	8.42	11.41	70	11	6	2.33
(3, 3)	(3, 0)	(2, -1)	2.49	0.97	0.30	5.37	8.42	11.41	65	10	6	2.34
(3, 3)	(2, 0)	(2, -1)	1.12	0.48	0.25	9.97	15.64	21.20	75	11	6	2.36

 

Table 7: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for three modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, 1)	(2, 1)	(2, -2)	1.88	0.61	0.09	8.38	8.74	45.84	57	21.28	5.5
(1, 1)	(2, 1)	(2, -2)	1.35	0.68	0.05	10.89	11.36	59.60	70	23	3	2.04
(1, 1)	(2, 1)	(3, -1)	1.80	0.44	0.08	10.89	11.36	59.60	45	17	8	2.21
(1, 1)	(2, 1)	(2, -1)	1.93	0.47	0.05	10.05	10.48	55.01	45	19	7	2.27
(3, -1)	(2, 0)	(2, -2)	2.41	0.99	0.09	5.86	6.11	32.09	85	22	3	2.60
(1, 1)	(2, 1)	(2, 0)	3.69	0.69	0.03	10.89	11.36	59.60	20	10	10	2.60
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 2)	(3, 2)	(1, 0)	110.38	100.95	4.34	0.078	0.080	0.095	26	10.44	5.5
(3, 2)	(3, 2)	(2, 0)	82.39	75.46	14.96	0.048	0.049	0.058	40	12	7	3.62
(3, 2)	(3, 2)	(1, 0)	82.39	75.46	5.38	0.048	0.049	0.058	40	12	7	3.67
(3, 2)	(3, 2)	(1, -1)	86.03	78.79	6.21	0.048	0.049	0.058	40	11	8	4.39
(3, 2)	(3, 2)	(2, -1)	82.39	75.46	9.45	0.048	0.049	0.058	40	11	8	4.87
(3, 2)	(3, 2)	(1, 1)	86.03	78.79	6.21	0.048	0.049	0.058	70	17	4	4.88
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 0)	(3, 1)	(1, 1)	0.42	4.90	7.28	11.45	2.74	3.15	8	23.57	5.5
(2, 0)	(2, 1)	(1, 1)	0.58	13.17	14.55	8.01	1.92	2.21	5	22	5	2.26
(1, 0)	(2, 1)	(1, 1)	1.03	13.17	14.55	8.01	1.92	2.21	5	22	5	2.32
(3, 0)	(2, 1)	(1, 1)	0.93	11.76	13.20	9.16	2.19	2.52	5	22	3	3.11
(2, 0)	(2, -1)	(1, -1)	0.58	13.17	14.55	8.01	1.92	2.21	5	22	5	3.29
(2, 0)	(3, 1)	(1, 1)	0.43	3.97	5.83	11.45	5.83	2.64	10	27	1	3.32
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, -3)	(3, -1)	(2, 1)	1.14	0.43	0.24	34.30	16.43	11.95	38	13.00	5.5
(3, -3)	(3, -1)	(2, 1)	1.41	0.64	0.31	24.01	11.50	8.37	40	15	7	2.76
(3, -3)	(2, -2)	(2, 1)	0.49	0.56	0.40	24.01	11.50	8.37	65	22	7	2.77
(3, -3)	(2, -2)	(3, 0)	0.57	0.62	0.54	24.01	11.50	8.37	60	20	8	2.81
(3, -3)	(2, -2)	(2, 0)	0.44	0.52	0.59	24.01	11.50	8.37	70	21	8	2.82
(3, -2)	(2, -1)	(2, 1)	0.70	0.53	0.36	24.01	11.50	8.37	30	19	8	2.94
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, -1)	(3, 1)	(3, -2)	0.38	0.88	0.04	21.71	7.33	135.78	33	22.43	5.5
(2, -1)	(3, 1)	(3, -2)	0.53	1.27	0.05	15.20	5.13	95.05	35	23	5	1.78
(2, -1)	(3, 1)	(3, -3)	0.50	1.38	0.14	15.20	5.13	95.05	40	21	6	2.88
(2, -2)	(3, 1)	(3, -2)	0.54	0.88	0.02	28.22	9.53	176.52	45	24	1	3.00
(2, -2)	(3, 1)	(3, -3)	1.21	1.38	0.14	15.20	2.30	95.05	40	20	6	3.16
(1, 0)	(3, 1)	(3, -2)	0.72	1.25	0.07	15.20	5.13	95.05	30	20	8	3.38

 

Table 8: Examples of mode identification through the discriminant $\Sigma$with the new version of the moment method for three modes. The input parameters are shown, followed by the five best solutions of the mode identification. The meanings of the symbols are the same as in Table 1.

($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 2)	(1, 1)	(2, 1)	26.12	14.77	8.92	0.077	0.081	0.091	58	28.15	5.5
(2, 2)	(1, 1)	(1, 1)	25.32	14.33	6.66	0.102	0.107	0.121	70	28	6	1.86
(2, 2)	(1, 1)	(2, 1)	23.96	13.94	19.93	0.102	0.107	0.121	75	29	4	1.99
(2, 2)	(2, 1)	(1, 1)	27.23	27.97	6.91	0.102	0.107	0.121	65	26	7	2.57
(2, 2)	(2, 1)	(2, 1)	38.16	21.77	10.13	0.102	0.107	0.121	50	23	9	3.05
(3, 2)	(1, 1)	(1, 1)	67.14	14.86	6.91	0.102	0.107	0.121	70	22	1	3.20
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, -1)	(2, 2)	(3, 2)	1.95	8.23	2.29	20.64	5.18	6.30	18	11.86	5.5
(1, -1)	(2, 2)	(3, 2)	1.50	5.82	1.55	24.77	6.22	7.56	20	14	7	2.34
(1, -1)	(2, 2)	(2, 2)	2.03	6.24	2.82	14.45	3.63	4.41	25	20	6	3.58
(1, -1)	(3, 2)	(3, 2)	1.72	4.44	2.00	14.45	3.63	4.41	30	23	4	3.68
(1, -1)	(1, 1)	(3, 2)	2.21	4.53	2.30	16.51	4.14	5.04	20	14	9	3.74
(1, -1)	(1, -1)	(3, 2)	0.83	1.81	0.57	26.84	6.74	8.19	35	24	2	3.75
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(1, 0)	(1, 1)	(3, 1)	13.79	18.09	20.30	0.08	0.081	0.092	43	18.72	5.5
(1, 0)	(1, 1)	(3, 1)	14.30	20.86	27.55	0.078	0.077	0.087	40	17	6	2.08
(1, 0)	(1, 1)	(2, 1)	19.09	16.34	11.00	0.078	0.077	0.087	55	21	4	2.51
(1, 0)	(1, 1)	(1, 1)	15.49	18.95	9.19	0.078	0.077	0.087	45	19	6	2.89
(1, 0)	(2, 1)	(2, 1)	15.49	21.32	10.34	0.078	0.077	0.087	45	17	7	3.01
(1, 0)	(2, 1)	(1, 1)	12.66	24.70	13.03	0.078	0.077	0.087	30	11	9	3.15
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(2, 1)	(2, 2)	(3, 1)	2.21	13.34	0.64	5.22	3.05	6.58	17	21.28	5.5
(2, 1)	(2, 2)	(3, 1)	1.48	8.42	0.45	6.79	3.96	8.56	20	25	1	2.42
(3, 1)	(3, 2)	(3, 3)	2.40	3.08	2.83	3.65	2.13	4.61	40	18	9	2.92
(2, 1)	(1, -1)	(3, 1)	1.91	5.87	0.57	6.79	3.96	8.56	15	22	7	3.10
(3, 1)	(3, 2)	(3, -3)	1.48	4.47	0.45	6.79	3.96	8.56	20	27	1	3.19
(2, 1)	(2, 2)	(3, -1)	1.59	9.06	0.49	6.27	3.66	7.90	20	25	1	3.36
($\ell_1$, m1)	($\ell_2$, m2)	($\ell_3$, m3)	$A_{\rm p}^1$	$A_{\rm p}^2$	$A_{\rm p}^3$	K1	K2	K3	i	$v_{\Omega }$	$\sigma$	$\Sigma$
(3, 3)	(2, 2)	(1, 1)	164.32	43.79	8.68	0.075	0.079	0.092	42	18.72	5.5
(3, 3)	(2, 2)	(1, 1)	123.82	34.74	7.49	0.071	0.075	0.087	55	20	8	4.02
(3, 3)	(3, 2)	(1, 1)	123.82	63.13	10.40	0.071	0.075	0.087	55	19	3	4.30
(3, 3)	(3, 2)	(2, 1)	123.82	63.13	10.40	0.071	0.075	0.087	55	19	3	4.30
(3, 3)	(2, 2)	(2, 1)	151.52	39.75	9.92	0.071	0.075	0.087	50	17	1	4.50
(3, 3)	(2, 2)	(1, 0)	151.52	39.75	6.74	0.071	0.075	0.087	50	18	1	4.89