A&A 398, 677-685 (2003)
DOI: 10.1051/0004-6361:20021679

A photometric mode identification method, including an improved non-adiabatic treatment of the atmosphere[*]

M.-A. Dupret 1 - J. De Ridder 2 - P. De Cat 2,[*] - C. Aerts 2 - R. Scuflaire 1 - A. Noels 1 - A. Thoul 1,[*]


1 - Institut d'Astrophysique et de Géophysique de l'Université de Liège, allée du 6 Août 17, 4000 Liège, Belgium
2 - Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200, 3001 Leuven, Belgium

Received 17 September 2002 / Accepted 7 November 2002

Abstract
We present an improved version of the method of photometric mode identification of Heynderickx et al. (1994). Our new version is based on the inclusion of precise non-adiabatic eigenfunctions determined in the outer stellar atmosphere according to the formalism recently proposed by Dupret et al. (2002a). Our improved photometric mode identification technique is therefore no longer dependent on ad hoc parameters for the non-adiabatic effects. It contains the complete physical conditions of the outer atmosphere of the star, provided that rotation does not play a key role. We apply our method to the two slowly pulsating B stars HD 74560 and HD 138764 and to the ${\beta }$ Cephei star EN (16) Lac. Besides identifying the degree $\ell $ of the pulsating stars, our method is also a tool for improving the knowledge of stellar interiors and atmospheres, by imposing constraints on parameters such as the metallicity and the mixing-length parameter $\alpha$(a procedure we label non-adiabatic asteroseismology).

Key words: stars: oscillations - stars: atmospheres - stars: variables: general


1 Introduction

A crucial problem in asteroseismology is mode identification. Firstly because, from a theoretical point of view, despite the linear non-adiabatic predictions, the mode selection mechanisms are not well understood for many kinds of pulsating stars ($\delta$ Scuti, ${\beta }$ Cephei, slowly pulsating B stars, $\gamma$ Doradus, roAp stars, ...). Secondly because, from an observational point of view, we do not resolve the disks of stars other than the Sun so that we can only observe disk-integrated quantities. Thirdly, the rotational splittings and the "avoided crossing'' effect produce such a complicated power spectrum that a mode identification based on the frequencies alone is generally impossible.

Currently, both spectroscopic and photometric mode identification techniques are being used. The latter methods are based on multi-colour photometry, and are the subject of this paper. The principle of these methods is to observe the photometric variations due to stellar oscillations in different colours and compare them to the theoretical predictions at the appropriate wavelengths (Dziembowski 1977b; Stamford & Watson 1981; Watson 1988; Garrido et al. 1990; Heynderickx et al. 1994; Garrido 2000). However, all these methods have an important drawback: their theoretical predictions are very sensitive to the non-adiabatic temperature variations at the photosphere (Cugier et al. 1994; Balona & Evers 1999).

Dupret et al. (2002a) developed a non-adiabatic code including a detailed treatment of the pulsation in the outer atmosphere. In this paper, we show how this non-adiabatic treatment opens the way to a significant improvement of the discriminant power of mode identification methods based on multi-colour photometry. Indeed, by using Dupret et al.'s calculations, we are able to eliminate the weakest point of the mode identification method, namely the ad hoc parameters to express the non-adiabaticity. We present the results obtained for two slowly pulsating B stars (SPBs) observed by De Cat & Aerts (2002) and for the ${\beta }$ Cephei star EN (16) Lac.

2 Monochromatic magnitude variations of a non-radially pulsating star

Theoretical expressions for the monochromatic magnitude variations of a non-radially pulsating star have been derived by different authors. Dziembowski (1977b) was the first to derive an expression for the bolometric magnitude variation of a non-radially pulsating star. He suggested also that a Wesselink technique could be formulated from these expressions. Balona & Stobie (1979) recast the suggestion of Dziembowski in an observationally feasible way. Stamford & Watson (1981) derived an expression for the monochromatic magnitude variations of a non-radially pulsating star. They proposed to compute the local emergent monochromatic flux variation on the base of equilibrium atmosphere models (see Eq. (2) below) and they simplified the way to compute the influence of the stellar surface distortion. Watson (1988) improved the method by taking the variation of the limb darkening into account (see Eq. (3) below), and discussed the importance of the different terms in the equation giving the monochromatic magnitude variations of a non-radially pulsating star. Garrido et al. (1990) and Garrido (2000) derived a method of mode identification using Strömgren photometry, based on the formalism of Watson (1988), and applied it to $\delta$ Scuti and $\gamma$ Doradus stars. Heynderickx et al. (1994) derived an expression for the surface distortion of a non-radially pulsating star in a Lagrangian formalism. He developed a method of mode identification based on photometric amplitude ratios and applied it to ${\beta }$ Cephei stars.

In all the previously cited papers, the non-adiabatic character of the pulsation was neglected or treated with an ad hoc parameter. Cugier et al. (1994) were the first to use non-adiabatic computations for photometric mode identification, using the non-adiabatic pulsation code of Dziembowski (1977a). The same code was also used by Balona & Evers (1999) for mode identifications of $\delta$ Scuti stars. Townsend (2002) used a non-adiabatic code for the photometric modelling of SPBs.

It is useful to detail the assumptions made, sometimes implicitly, by the previous authors and in our method, in order to derive an expression for the monochromatic magnitude variations of a non-radially pulsating star. In Sects. 3 and 4, we will put forward the improvement and specificities of our method, compared to the one of the previous authors.

a1)
We work in the linear approximation.
a2)
We neglect the coupling of modes due to the interaction between rotation and pulsation. The angular dependence of a non-radial mode is thus described by a single spherical harmonic.
a3)
We assume that the gas column of the atmosphere at a given angular position ($\theta$, $\phi$) is well described by a plane parallel atmosphere, which we call the local atmosphere.
a4)
For the geometrical distortion of the stellar surface, we work in the one-layer approximation. It is assumed that the visible part of the star, i.e. the photosphere, can be described by a single surface which is spherical at equilibrium. The radius R0 of this sphere is the radius of the star, and in our method, we assume that it corresponds to the layer where the local temperature is equal to the effective temperature of the star. During the pulsation, it is assumed that this surface follows the movement of the matter. The surface distortion can therefore be deduced from the displacement field: $\vec{\xi}(R_0, \theta, \phi, t)$.
a5)
We assume that, during the pulsation cycle, the monochromatic outwards flux $\vec{F_{\lambda}}^+$ of the local atmosphere is, for each given time, the same as the monochromatic outwards flux of an equilibrium plane parallel atmosphere model.
a6)
We assume that, during the pulsation cycle, $\vec{F_{\lambda}}^+$ remains perpendicular to the photosphere.
a7)
We assume that $\vec{F_{\lambda}}^+$ does not depend on the optical depth in the local atmosphere.
a8)
We assume that the local atmosphere depends only on two varying parameters: the local effective temperature and the local effective gravity. The chemical composition of the local atmosphere is assumed to remain constant.
a9)
We assume that during the pulsation cycle, the limb darkening law  $h_{\lambda}$ of the local atmosphere is, for each given time, the same as the limb darkening law of an equilibrium plane parallel atmosphere model with the orientation given by assumptions (a4) and (a6).
Assumption (a4) needs some precision. We have shown in Dupret et al. (2002a) that the relative Lagrangian variation of the optical depth ( $\delta\tau/\tau$) is not negligible in stellar atmospheres. However, on the basis of non-adiabatic computations, we have checked that the relative difference between the displacement of constant optical depth layers and the "real'' displacement of the matter ( $\delta\tau/(\kappa~\rho~ R_0)$) is very small. For example, $\vert\delta\tau\vert/(\kappa~\rho~R_0)\simeq 0.005$ at the photosphere of a typical ${\beta }$ Cephei model and for the fundamental radial mode, with a relative radial displacement normalized to 1 at the photosphere. Therefore assumption (a4) is appropriate for the determination of the geometrical distorsion of the stellar surface (at least for g-modes and moderate order p-modes). However, we showed in Dupret et al. (2002a) that it is not appropriate to assume that the Lagrangian variation of the temperature is equal to the variation of the temperature at constant optical depth, because $\partial\ln T/\partial\tau~\vert\delta\tau\vert$ is not negligible compared to  $\vert\delta T/T\vert$ at the photosphere.

We note that assumption (a7) concerns only the flux. We do not make this hypothesis for the temperature which depends strongly on the optical depth in stellar atmospheres (see Dupret et al. 2002a, Fig. 1).

Assumptions (a5) and (a9) have the same physical justification as explained in Dupret et al. (2002a). Because of the very small thermal relaxation time of the atmosphere, we assume that, at each time of the pulsation cycle, the local atmosphere remains in radiative equilibrium. Using this assumption, Dupret et al. (2002a) assumed that, during the pulsation cycle, the temperature distribution ($T(\tau)$ law) in the local atmosphere was, for each given time, the same as the temperature distribution of an equilibrium atmosphere model. For the same physical reasons, we make now the same assumption for the local monochromatic outwards flux $\vec{F_{\lambda}}^+$ and for the limb darkening law  $h_{\lambda}$.

From assumptions (a5), (a7) and (a8), the monochromatic outward flux in the local atmosphere is given by:

 
$\displaystyle \left(F_{\lambda}^+\right)_0 + \delta F_{\lambda}^+(\theta, \phi,... ..._{\rm eff}(\theta, \phi, t) ,~ g_0 + \delta g_{\rm e}(\theta, \phi, t)~\right],$     (1)

where $F_{\lambda}^+ = \left\vert\vec{F_{\lambda}}^+\right\vert$. In the linear approximation, we have thus by perturbing Eq. (1):
 
                     $\displaystyle \frac{\delta F_{\lambda}^+}{F_{\lambda}^+}$ = $\displaystyle \left(\frac{\partial \ln F_{\lambda}^+}{\partial \ln T_{\rm eff}}... ...l \ln F_{\lambda}^+}{\partial \ln g}\right)~ \frac{\delta g_{\rm e}}{g_{\rm e}}$  
  $\textstyle \equiv$ $\displaystyle \alpha_{T\lambda}\:\frac{\delta T_{\rm eff}}{T_{\rm eff}} \:+\:\alpha_{g\lambda}\: \frac{\delta g_{\rm e}}{g_{\rm e}}\cdot$ (2)

Equation (1) was first proposed by Stamford & Watson (1981). We proceed similarly for the variation of the monochromatic limb darkening. From assumptions (a4), (a6), (a8) and (a9), we obtain in the linear approximation:
 
$\displaystyle \frac{\delta h_{\lambda}}{h_{\lambda}} =\left(\frac{\partial \ln ... ...\frac{\partial \ln h_{\lambda}}{\partial \mu}\right)~ \delta\left(\mu\right)\:,$     (3)

where $h_{\lambda}$ is the normalized limb darkening law ( $\int_0^1 h_\lambda(\mu)\:\mu\:{\rm d}~\mu\;=\;1$), $\mu=\vec{n}\cdot\vec{e_{z'}}$, $\vec{n}$ is the normal to the photosphere and  $\vec{e_{z'}}$ is the unit vector pointing towards the observer. A similar equation was first proposed by Watson (1988).

We denote by $\epsilon$ the amplitude of relative radial displacement in the photosphere:

 \begin{displaymath} \xi_r(\theta, \phi, t) \;=\; R_0~\epsilon~P_\ell^m (\cos \theta)~ \cos(\sigma~t~+~m~\phi)\:, \end{displaymath} (4)

where $\theta$ and $\phi$ are the usual spherical coordinates with respect to the polar (rotation) axis of the star, $P_\ell^m (x)$ is the associated Legendre function of degree $\ell $ and azimuthal number m and $\sigma$ is the angular oscillation frequency.

The quantities $\delta T_{\rm eff} / T_{\rm eff}$ and $\delta g_{\rm e} / g_{\rm e}$ can be computed by the non-adiabatic code of Dupret et al. (2002a). Because the Eulerian variation of the gravitational potential at the surface is always very small ( $\vert\psi'\vert~\ll~\vert g~\xi_r\vert$), it appears that in very good approximation, $\delta g_{\rm e} / g_{\rm e}$ is in opposite phase with the radial displacement. These two quantities can be expressed in term of the associated Legendre functions:

  
                  $\displaystyle \frac{\delta T_{\rm eff}}{T_{\rm eff}} (\theta, \phi, t)$ = $\displaystyle f_{\rm T}\:\epsilon\:P_\ell^m (\cos \theta) \:\cos(\sigma~t~+~m~\phi~+~\psi_{\rm T}) ~,$ (5)
$\displaystyle \frac{\delta g_{\rm e}}{g_{\rm e}} (\theta, \phi, t)$ = $\displaystyle -~f_{\rm g}\:\epsilon\:P_\ell^m (\cos \theta)\:\cos(\sigma~t~+~m~\phi)\:,$ (6)

where $f_{\rm T}$ and $f_{\rm g}$ are the amplitudes of $\delta T_{\rm eff} / T_{\rm eff}$ and $\delta g_{\rm e} / g_{\rm e}$ corresponding to a normalized radial displacement at the photosphere. On the basis of the previous assumptions and equations, an expression can be derived for the monochromatic magnitude variation of a non-radially pulsating star:
 
                      $\displaystyle \delta m_\lambda$ = $\displaystyle -\:\frac{2.5}{\ln 10}\;\epsilon~\:P_\ell^m(\cos i)\:b_{\ell\lambda}$  
    $\displaystyle \times ~\Big(~-\:(\ell-1)(\ell+2)\:\cos(\sigma~t)$  
    $\displaystyle +\;f_{\rm T}\:\cos(\sigma~t + \psi_{\rm T}) ~\left(\alpha_{{\rm T}\lambda}~+~\beta_{{\rm T}\lambda}~\right)$  
    $\displaystyle -\;f_{\rm g}\:\cos(\sigma~t)~\left(\alpha_{{\rm g}\lambda}~+~ \beta_{{\rm g}\lambda} ~\right)~\Big)\:,$ (7)

where $\delta m_\lambda$ is the variation of the monochromatic magnitude as seen by the observer, i is the inclination angle between the stellar axis and the direction towards the observer and
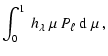                  $\displaystyle b_{\ell\lambda}$ $\textstyle \equiv$ $\displaystyle \int_0^1~h_\lambda\:\mu \:P_\ell\:{\rm d}~\mu\:,$ (8)
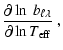$\displaystyle \beta_{T\lambda}$ $\textstyle \equiv$ $\displaystyle \frac{\partial\ln~b_{\ell\lambda}}{\partial\ln T_{\rm eff}}\:,$ (9)
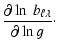$\displaystyle \beta_{g\lambda}$ $\textstyle \equiv$ $\displaystyle \frac{\partial\ln~b_{\ell\lambda}}{\partial\ln g}\cdot$ (10)

For the derivations leading to Eq. (7), we refer to Dziembowski (1977b), Stamford & Watson (1981), Watson (1988) and Heynderickx et al. (1994).

In Eq. (7), the term proportional to $(\ell-1)(\ell+2)$ corresponds to the influence of the stellar surface distortion, the term proportional to $f_{\rm T}$ corresponds to the influence of the local effective temperature variation and the term proportional to $f_{\rm g}$ corresponds to the influence of the local effective gravity variation. In our applications, we computed the coefficients  $\alpha_{{\rm T}\lambda}$ and  $\alpha_{{\rm g}\lambda}$ (derivatives of the monochromatic flux) from the models of Kurucz (1993). An analytical law for the limb darkening is needed for the computation of  $b_{\ell\lambda}$ and its derivatives. For the present paper, we used a quadratic law (Wade & Rucinski 1985). We note that an improved non-linear limb darkening law has been proposed by Claret (2000), but his computations were only done for Strömgren filters, while our applications concern Geneva and Johnson filters.

In multi-colour photometry, one observes the integral of the monochromatic magnitude variation over the response of the filter:

 \begin{displaymath}\delta m_i\:=\:\frac{\int_{\lambda_{\rm min}}^{\lambda_{\rm m... ...a_{\rm min}}^{\lambda_{\rm max}}w_i(\lambda)~{\rm d}\lambda}~, \end{displaymath} (11)

where $w_i(\lambda)$ is the response curve of the filter i. Therefore, the different terms of Eq. (7) depending on $\lambda$ have to be integrated, following Eq. (11).

   
3 Our version of the mode identification method

The linear theory does not permit us to predict the amplitudes of the eigenfunctions. Therefore, it is appropriate to use amplitude ratios and phase differences between different filters when comparing the theoretical predictions to the observations. On one hand, for $\delta$ Scuti stars, the observations and the theoretical predictions give significant phase-lags between the different filters. Mode identification methods using these phase-lags have been proposed by Garrido et al. (1990) and Balona & Evers (1999). On the other hand, for ${\beta }$ Cephei stars, SPBs and $\gamma$ Doradus stars, no phase-lags are observed (in agreement with the small phase-lags predicted by the theory). For the latter stars, mode identification methods based on amplitude ratios are thus appropriate (Heynderickx et al. 1994). We adopt here such a method. The theoretical procedure of our mode identification method is the following:

1.
We compute a stellar model with the appropriate effective temperature, luminosity and mass. In our applications, we used the new Code Liégeois d'Évolution Stellaire written by one of us (R. Scuflaire).
2.
We perform non-adiabatic computations for different degrees $\ell $ and for pulsation frequencies close to the observed ones. In our applications, we used the non-adiabatic code by Dupret et al. (2002a). These computations give the coefficients $f_{\rm T}$, $\psi _{\rm T}$ and $f_{\rm g}$ for different degrees $\ell $.
3.
For each filter j and for each $\ell $, we compute
 
                $\displaystyle A_{j,{\rm th}}$ = $\displaystyle \vert b_{\ell~j}\vert~\Big\vert\:(1-\ell)(\ell+2)$  
    $\displaystyle +\; f_{\rm T}\;{\rm e}^{{\rm i} \psi_{\rm T}} \left(\alpha_{{\rm T}~j}~+~\beta_{{\rm T}~j}~\right)$  
    $\displaystyle -\;f_{\rm g}~\left(\alpha_{{\rm g}~j}~+~\beta_{{\rm g}~j} ~\right)\Big\vert\:,$ (12)

using the atmosphere models of Kurucz (1993) to compute  $\alpha_{\rm T}$ and  $\alpha_{\rm g}$.
4.
We choose a reference filter (indicated with subindex 1). For B stars, this reference filter is the U filter giving the highest amplitudes and thus the highest S/N ratio. We compare the theoretical amplitude ratios $(A_{j,{\rm th}}/A_{1,{\rm th}})$ to the observed amplitude ratios $(A_{j,{\rm obs}}/A_{1,{\rm obs}})$. The identified degree $\ell $ is the value which minimizes the $\chi^2$:

\begin{displaymath}\sum_{j=2}^k~\left[~\frac{A_{j,{\rm th}}}{A_{1,{\rm th}}}~-~ \frac{A_{j,{\rm obs}}}{A_{1,{\rm obs}}}~\right]^2, \end{displaymath} (13)

where k is the number of filters.
We note that the non-adiabatic predictions depend on some dominant parameters of the theoretical models (e.g. the metallicity for ${\beta }$ Cephei stars and SPBs, the mixing length parameter $\alpha$ for $\delta$ Scuti and $\gamma$ Doradus stars). Therefore, these parameters can be constrained by a feed-back process after a unique mode identification is achieved. We call this feed-back process non-adiabatic asteroseismology, in which we iterate the procedure described above by adjusting the stellar parameters for the identified mode, until we find the best fit between theory and observations. We will illustrate this feed-back process below for the estimation of the metallicity of the ${\beta }$ Cephei star EN Lac.

   
4 Comparison with other methods

The difference between our method and the one proposed by other authors is in the way of estimating the influence of the effective temperature variation and the effective gravity variation in Eqs. (7) and (12).

4.1 Mechanical boundary condition

As a preliminary for the estimation of the relative effective temperature variation $\delta T_{\rm eff} / T_{\rm eff}$ and the relative effective gravity variation $\delta g_{\rm e} / g_{\rm e}$, the first step of the procedure followed by Watson (1988), Heynderickx et al. (1994), Cugier et al. (1994) and Balona & Evers (1999) was to compute $\delta P/P$ at the photosphere. As initially proposed by Buta & Smith (1979), they used the following formula:

 \begin{displaymath} \frac{\delta P}{P} \;=\; \Big(~\ell(\ell+1)~K\:-\:4\:-\:K^{-1}~\Big) ~\frac{\xi_{\rm r}}{R_0}\:, \end{displaymath} (14)

where K (sometimes denoted by $\alpha_{\rm h}$) is given by

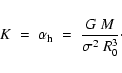\begin{displaymath}K\;=\;\alpha_{\rm h}\;=\;\frac{G~M}{\sigma^2~R_0^3}\cdot \end{displaymath} (15)

Equation (14) is deduced from the "classical'' mechanical boundary condition (Cox 1980, Eq. (17.69')), by neglecting the Eulerian variation of the gravitational potential at the photosphere (Cowling approximation). The advantage of Eq. (14) is that it gives $\delta P/P$, without having to compute numerically the adiabatic or non-adiabatic eigenfunctions throughout the entire star. Assuming that:

 \begin{displaymath} \frac{\delta P}{P} (\theta, \phi, t) \;=\; -\:C\:\epsilon\:P_\ell^m (\cos \theta)\: \cos(\sigma~t~+~m~\phi)\:, \end{displaymath} (16)

we have therefore:

 \begin{displaymath} C \;=\; 4\:+\:K^{-1} \:-\:\ell(\ell+1)~K\:. \end{displaymath} (17)

4.2 Influence of the effective temperature variation

Watson (1988), Garrido et al. (1990) and Heynderickx et al. (1994) related the Lagrangian temperature variation to the Lagrangian pressure variation at the photosphere by introducing a free ad-hoc parameter R describing the departure from adiabatic conditions. Moreover, they assumed that the Lagrangian temperature variation is equal to the local effective temperature variation at the photosphere:

 \begin{displaymath} \frac{\delta T_{\rm eff}}{T_{\rm eff}}\;=\; \frac{\delta T}{T}\cdot \end{displaymath} (18)

The coefficient $f_{\rm T}$ is then given by:
 
                           $\displaystyle f_{\rm T}$ = $\displaystyle R\;\frac{\Gamma_2-1}{\Gamma_2}\;\vert C\vert$  
  = $\displaystyle R\;\frac{\Gamma_2-1}{\Gamma_2}\; \big\vert~4\:+\:K^{-1} \:-\:\ell(\ell+1)~K~\big\vert\:.$ (19)

In the adiabatic case, R=1. Concerning the phase-lag  $\psi _{\rm T}$, Heynderickx et al. (1994) take the adiabatic value of  $180^{\circ}$ for the applications to ${\beta }$ Cephei stars and Garrido et al. (1990) let  $\psi _{\rm T}$be a free parameter between  $90^{\circ}$ and  $135^{\circ}$for the applications to $\delta$ Scuti stars.

Our approach does not make any of these assumptions. We rigorously compute both the amplitude and the phase of the local effective temperature variation by non-adiabatic computations throughout the entire star and, in particular, throughout the entire non-grey atmosphere.

Cugier et al. (1994) and Balona & Evers (1999) performed non-adiabatic computations in order to determine $f_{\rm T}$ and  $\psi _{\rm T}$ in a more rigorous way. In their method, they assume also that the Lagrangian temperature variation is equal to the local effective temperature variation at the photosphere (Eq. (18)). We do not make this assumption in our method, since we have shown in Dupret et al. (2002a) that the Lagrangian variation of the temperature at the photosphere is different from the variation of the local effective temperature, because of the significant Lagrangian variation of the optical depth.

4.3 Influence of the effective gravity variation

Stamford & Watson (1981), Watson (1988), Garrido et al. (1990) and Heynderickx et al. (1994) related the coefficient $f_{\rm g}$ corresponding to the effective gravity variation (i.e. the gravity variation corrected for the pulsational acceleration) to the Lagrangian pressure variation by the following equation:

 \begin{displaymath} f_{\rm g}\;=\;p^*~C\;=\; \left(\frac{\partial\ln g}{\partial\ln P_{\rm g}}\right)_{\tau=1}\:C\:, \end{displaymath} (20)

where p* is computed from equilibrium atmosphere models such as the models of Kurucz (1993). Some authors (Cugier et al. 1994; Balona & Evers 1999) proposed to take p* = 1.

Dupret et al. (2002a, Eq. (24)) proposed a more accurate way to determine $\delta g_{\rm e} / g_{\rm e}$. In our method, $f_{\rm g}$ is given by:

 \begin{displaymath} f_{\rm g} \:=\: \left\vert\frac{R_0~\partial\psi' / \parti... ...~R_0^3}{M_{\rm r}} ~ - \left(2 + K^{-1}\right)\right\vert~. \end{displaymath} (21)

Under the Cowling approximation and neglecting the density at the photosphere compared to the mean density of the star, Eq. (21) gives:

 \begin{displaymath} f_{\rm g}\;=\; 2 \:+\: K^{-1}\;. \end{displaymath} (22)

The correction leading to Eq. (22) was also proposed by Cugier & Daszynska (2001). The difference between Eqs. (22) and (20) with p*=1 is due to the fact that the Lagrangian variation of surface elements of the photosphere ( $2-\ell(\ell+1)K$) affects the Lagrangian variation of the pressure described in Eq. (17), but does not affect the Lagrangian variation of the effective gravity. A simple comparison shows that:
For p-modes: K is small so that the difference between Eqs. (17) and (22) is approximately 2.
For high-order g-modes: K is large, so that the difference between Eqs. (17) and (22) becomes very important!
Therefore, our improvement in the determination of the effective gravity variation has the largest impact on the photometric mode identification of g-mode pulsators such as SPBs and $\gamma$ Doradus stars.

5 Applications

In this section, we present the application of our mode identification method to two SPBs and one ${\beta }$ Cephei star. The theoretical stellar models we used have been computed by the Code Liégeois d'Évolution Stellaire (CLÉS).

5.1 Slowly pulsating B stars

The two SPBs for which we performed non-adiabatic computations and a photometric mode identification are HD 74560 and HD 138764. Data obtained with Geneva photometry were taken from De Cat & Aerts (2002). We give in Table 1 the effective temperature and the gravity of these two stars, as derived from the most recent calibration of Künzli et al. (1997). We selected then theoretical models closest to these observations and their global characteristics are given in Tables 2 and 3. Numerous additional applications to other SPBs will be presented in De Cat et al. (in preparation).


   
Table 1: Effective temperature and gravity of the stars HD 74560 and HD 138764 as deduced from Geneva calibrations of Künzli et al. (1997).

HD 74560		 $T_{\rm eff} = 16210\:\pm\:150$ K $\log g = 4.15\:\pm\:0.14 $

HD 138764		 $T_{\rm eff} = 14050\:\pm\:80$ K $\log g = 4.20\:\pm\:0.12 $


   
Table 2: Global characteristics of the theoretical model of HD 74560.

$M/M_{\odot} = 4.9 $		 $T_{\rm eff} = 16~205 $ K $\log (L/L_{\odot}) = 2.7521 $

$\log g = 4.1677 $		 $R/R_{\odot} = 3.0208 $ age (My) = 24.5

X = 0.7		 Z = 0.02 no overshooting


   
Table 3: Global characteristics of the theoretical model of HD 138764.

$M/M_{\odot} = 3.9 $		 $T_{\rm eff} = 14047 $ K $\log (L/L_{\odot}) = 2.3760 $

$\log g = 4.1964 $		 $R/R_{\odot} = 2.6073 $ age (My) = 38

X = 0.7		 Z = 0.02 no overshooting


   
Table 4: Non-adiabatic results and mode identification for the star HD 74560. Degree $\ell $, radial order, amplitude of local effective temperature variation $f_{\rm T}$ and phase-lag $\psi _{\rm T}$ for the modes with theoretical frequency closest to the observed dominant frequency f=0.64472 c d-1. The identified mode is given in bold.

$\ell $		 gn $f_{\rm T}$ $\psi_{\rm T}~(\hbox{$^\circ$ })$

1		 ${\vec g}_{17}$ 10.08 -23.0
2 g29 22.38 -8.2
3 g41 36.01 1.3


   
Table 5: Non-adiabatic results and mode identification for the star HD 138764. Degree $\ell $, radial order, $f_{\rm T}$ and  $\psi _{\rm T}$ for the modes with theoretical frequency closest to the observed dominant frequency f=0.7944 c d-1. The identified mode is given in bold.

$\ell $		 gn $f_{\rm T}$ $\psi_{\rm T}~(\hbox{$^\circ$ })$

1		 g16 5.59 -23.2
2 g28 17.23 -9.3
3 g40 31.57 1.4


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3095f1.eps} \end{figure} Figure 1: $f_{\rm T}$ (local effective temperature variation for a normalized radial displacement at the photosphere) as function of the pulsation frequency (in c d-1), for different modes of the SPB star HD 74560. The "+'' correspond to modes of degree $\ell =1$, the "$\times $'' correspond to modes of degree $\ell =2$ and the asterisks correspond to modes of degree $\ell =3$. The vertical line corresponds to the observed frequency of the dominant mode.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3095f2.eps} \end{figure} Figure 2: $\psi _{\rm T}$ (phase difference between the local effective temperature variation and the radial displacement at the photosphere in degrees) as function of the pulsation frequency in c d-1, for different modes of the SPB star HD 74560. The "+'' correspond to modes of degree $\ell =1$, the "$\times $'' correspond to modes of degree $\ell =2$ and the asterisks correspond to modes of degree $\ell =3$. The vertical line corresponds to the observed frequency of the dominant mode.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3095f3.eps} \end{figure} Figure 3: $f_{\rm T}$ as function of the pulsation frequency in c d-1, for different modes of the SPB star HD 138764. The "+'' correspond to modes of degree $\ell =1$, the "$\times $'' correspond to modes of degree $\ell =2$ and the asterisks correspond to modes of degree $\ell =3$. The vertical line corresponds to the observed frequency of the dominant mode.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS3095f4.eps} \end{figure} Figure 4: $\psi _{\rm T}$ (in degrees) as function of the pulsation frequency in c d-1, for different modes of the SPB star HD 138764. The "+'' correspond to modes of degree $\ell =1$, the "$\times $'' correspond to modes of degree $\ell =2$ and the asterisks correspond to modes of degree $\ell =3$. The vertical line corresponds to the observed frequency of the dominant mode.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3095f5.eps} \end{figure} Figure 5: Amplitude ratios obtained with Geneva photometry for the dominant mode of the SPB star HD 74560. The bullets with error bars correspond to the observations. The lines correspond to the theoretical predictions for different degrees $\ell $: solid line for $\ell =1$, dashed line for $\ell =2$ and dot-dashed line for $\ell =3$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{MS3095f6.eps} \end{figure} Figure 6: Amplitude ratios obtained with Geneva photometry for the dominant mode of the SPB star HD 138764, same caption as in Fig. 5.
Open with DEXTER

In Figs. 1 and 3, we give the values of $f_{\rm T}$(local effective temperature variation for a normalized radial displacement at the photosphere) and in Figs. 2 and 4 those of  $\psi _{\rm T}$ (phase difference between the local effective temperature variation and the radial displacement at the photosphere, in degrees) for different modes of the two SPBs, as a function of the pulsation frequency in c d-1, as computed by our non-adiabatic code. In these figures, the vertical line corresponds to the observed frequency of the dominant mode. We see that, for a given frequency, the amplitude and phase-lag depend strongly on the degree $\ell $. The physical explanation is the following. The term corresponding to the transversal compression in the equation of mass conservation is proportional to $\ell(\ell+1)$. For high-order g-modes, this term dominates, which implies a strong dependence on $\ell $ of the eigenfunctions. The phase-lags ( $\psi _{\rm T}$) are relatively close to zero, which is in agreement with the observations.

In Tables 4 and 5, we give for the two stars, the degree $\ell $, the radial order, $f_{\rm T}$ and  $\psi _{\rm T}$ for the modes with theoretical frequency closest to the observed frequency. The identified mode is given in bold.

In Figs. 5 and 6, we give the amplitude ratios obtained from Geneva photometry for the dominant modes of the two stars. The bullets with error bars correspond to the observations. The full lines correspond to the theoretical predictions for different degrees $\ell $: solid line for $\ell =1$, dashed line for $\ell =2$ and dot-dashed line for $\ell =3$. For both stars, a solution inside the error bars is found, and the identified degree is $\ell =1$. These photometric mode identifications are in very good agreement with the spectroscopic mode identifications performed by De Cat et al. (in preparation) using the moment method.

5.2 The ${\beta }$ Cephei star EN (16) Lac

We present now the application of our method to the ${\beta }$ Cephei star EN Lac. This star has been studied by many authors. We refer to Chapellier et al. (1995) and Lehmann et al. (2001) for a summary of the observational studies and to Dziembowski & Jerzykiewicz (1996) for the first seismic study of this ${\beta }$ Cephei star. In this section, we illustrate the process we term non-adiabatic asteroseismology, by deriving constraints on the metallicity of the star. The three observed frequencies used in our study were taken from Lehmann et al. (2001) and the photometric amplitudes obtained with Johnson filters were derived by Jerzykiewicz (1993).


   
Table 6: Global characteristics of the theoretical models of EN Lac.

Model 1a		    

$M/M_{\odot} = 9.4 $		 $T_{\rm eff} = 22~105 $ K $\log (L/L_{\odot}) = 3.8992 $

$\log g = 3.8429 $		 age (My) = 16.2 Z = 0.015

Model 1b		    

$M/M_{\odot} = 9.7 $		 $T_{\rm eff} = 22~545 $ K $\log (L/L_{\odot}) = 3.9405 $

$\log g = 3.8494 $		 age (My) = 15.15 Z = 0.015

Model 2a		    

$M/M_{\odot} = 9.5 $		 $T_{\rm eff} = 21~756 $ K $\log (L/L_{\odot}) = 3.8769 $

$\log g = 3.8421 $		 age (My) = 15.9 Z = 0.02

Model 2b		    

$M/M_{\odot} = 10 $		 $T_{\rm eff} = 22~491 $ K $\log (L/L_{\odot}) = 3.9442 $

$\log g = 3.8548 $		 age (My) = 13.95 Z = 0.02

Model 3a		    

$M/M_{\odot} = 9.7 $		 $T_{\rm eff} = 21~646 $ K $\log (L/L_{\odot}) = 3.8739 $

$\log g = 3.8454 $		 age (My) = 14.85 Z = 0.025

Model 3b		    

$M/M_{\odot} = 10.3 $		 $T_{\rm eff} = 22~481 $ K $\log (L/L_{\odot}) = 3.9532 $

$\log g = 3.8579 $		 age (My) = 12.9 Z = 0.025

Aerts et al. (2002) showed convincingly that the spectroscopic mode identification is fully compatible with the photometric one for this star, and points towards a radial mode for the first frequency ( f1=5.9112 c d-1), an $\ell =2$ mode for the second frequency ( f2=5.8551 c d-1) and an $\ell =1$ mode for the third frequency ( f3=5.5033 c d-1). We therefore adopt this result here. We present the results of the amplitude ratios obtained for models with different metallicities. The choice of the models has been made with the following procedure. We computed models with 3 different metallicities: Z = 0.015, Z = 0.02 and Z = 0.025. Because of the uncertainties in the calibration of the effective temperature of EN Lac (see Jerzykiewicz & Sterken 1980; Shobbrook 1985 and Dziembowski & Jerzykiewicz 1996), we computed for each metallicity two evolutionary tracks with two different masses. For each evolutionary track, we subsequently selected the model giving the best agreement between the theoretical and observed frequencies, relying on the unambiguous mode identification. In all these models, X = 0.7 and there is no overshooting. Their global characteristics are given in Table 6.

In Fig. 7, we present the values of $f_{\rm T}$as a function of the pulsation frequency in c d-1, for different modes and for the six models of EN Lac given in Table 6. The three vertical lines correspond to the three observed frequencies. We see that, the higher the metallicity, the lower the amplitude of the local effective temperature variation for a normalized radial displacement ($f_{\rm T}$). The physical origin of this phenomenon is explained in Fig. 8, where we show the amplitudes of the luminosity variation $\vert\delta L/L\vert$ as a function of the logarithm of temperature, from the center to the surface of the star, for the radial fundamental mode and for the models 1a, 2a and 3a of Table 6. The higher the metallicity, the more efficient the $\kappa$ mechanism, which implies a more important decrease of the luminosity variation in the driving region. Therefore, the amplitude of the luminosity variation and of the local effective temperature variation at the photosphere are smaller for a normalized displacement. The phase differences between the local effective temperature variation and the radial displacement at the photosphere we obtained for the different models are very close to $180^{\circ}$ (in agreement with the observations) and we do not give them here. By comparing in Fig. 7 the results obtained for the cold models (models 1a, 2a and 3a) and the hot models (models 1b, 2b and 3b), we see that changing the values of  $T_{\rm eff}$ within its observational error bars (keeping the metallicity constant) has only a very small effect on the non-adiabatic results.

  \begin{figure} \par\includegraphics[width=8.8cm]{MS3095f7.eps} \end{figure} Figure 7: $f_{\rm T}$ (local effective temperature variation for a normalized radial displacement at the photosphere) as function of the pulsation frequency in c d-1, for different modes ( $0~\le~\ell~\le~2$) and for the six different models of the star EN Lac given in Table 6. The "$\times $'' correspond to modes of the model 1a, the "+'' correspond to the model 1b, the full and empty squares correspond to the models 2a and 2b respectively, the full and empty circles correspond to the models 3a and 3b respectively. The three vertical lines correspond to the three observed frequencies: $\nu _1=5.9112$ c d-1, $\nu _2=5.8551$ c d-1 and $\nu _3=5.5033$ c d-1.
Open with DEXTER

We present in Fig. 9 the theoretical amplitude ratios (Johnson photometry) obtained for three models of EN Lac with different metallicities (Table 6, models 1a, 2a and 3a), and for the fundamental radial mode. We see that the model with Z=0.015 gives the best agreement between the theoretical and observed amplitude ratios. We have checked explicitly that all the modes in the observed range of frequencies remain unstable for this low metallicity; lower values are not compatible with mode excitation.

The confrontation between the theoretical and observed amplitude ratios can thus be used as a constraint on the metallicity of stars driven by the metal opacity bump (${\beta }$ Cephei and Slowly Pulsating B stars), once we know the identification of the mode. We have seen in Fig. 7 that the non-adiabatic predictions and thus the theoretical amplitude ratios are little affected by the uncertainties on  $T_{\rm eff}$ for a given metallicity, so that the constraints we derived on the metallicity are reliable. This way of determining the metallicity may even turn out to be more precise than the classical method based on the analysis of the spectrum. We plan to validate our method to derive the metallicity by this feed-back process by confronting our predictions to those of ${\beta }$ Cephei stars for which the metallicity is known with high accuracy.

We note that, for rapidly rotating ${\beta }$ Cephei stars, the interaction between pulsation and rotation can affect significantly the photometric amplitudes and phase-lags as shown recently by Daszynska et al. (2002). This interaction was not yet taken into account in our current non-adiabatic treatment.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{3095f8.eps} \end{figure} Figure 8: Amplitude of luminosity variation $\vert\delta L/L\vert$ as function of the logarithm of temperature for the fundamental radial mode, for models of EN Lac with different metallicities (models 1a, 2a and 3a of Table 6). The solid line corresponds to the model with Z = 0.015, the dashed line to the model with Z = 0.02 and the dotted line to the model with Z = 0.025.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{3095f9.eps} \end{figure} Figure 9: Observed and theoretical amplitude ratios (Johnson photometry) for the radial fundamental mode obtained for three models of EN Lac with different metallicities (Table 6, models 1a, 2a and 3a). The solid line corresponds to the model with Z = 0.015, the dashed line to the model with Z = 0.02 and the dotted line to the model with Z = 0.025. The error bars correspond to the observations.
Open with DEXTER

6 Conclusions

We have presented an improvement of the often-used photometric mode identification method. Our version of this method is based on precise non-adiabatic computations in which special attention is paid to the treatment of the pulsation in the stellar atmosphere (Dupret et al. 2002a). We have applied our new version of the method to identify the main mode of two SPBs (HD 74560 and HD 138764) and one ${\beta }$ Cephei star (EN Lac, see also Aerts et al. 2002). In both cases, our photometric mode identifications were in very good agreement with the spectroscopic mode identifications, which are far less sensitive to temperature variations (De Ridder et al. 2002). We have shown also that the confrontation between the non-adiabatic theoretical predictions and the observations can give interesting constraints on the models. We have used the term non-adiabatic asteroseismology for this feed-back process. More precisely, for ${\beta }$ Cephei stars and SPBs, the non-adiabatic predictions are very sensitive to the metallicity, so that this parameter can be constrained for these stars once definite mode identification is achieved. For $\delta$ Scuti and $\gamma$ Doradus stars, the non-adiabatic predictions are very sensitive to the characteristics of the thin superficial convection layer (Balona & Evers 1999; Moya et al. 2002; Dupret et al. 2002b). Therefore, it is to be expected that a feed-back process similar to the one we presented will lead to a significant improvement of our understanding of this convection layer.

Acknowledgements
Part of this work was supported by the F.R.I.A. (Fonds pour la formation à la Recherche dans l'Industrie et dans l'Agriculture). The authors are members of the Belgian Asteroseismology Group (BAG, http://www.ster.kuleuven.ac.be/~conny/bag.html).

References

 

Copyright ESO 2003