The prevalence of differential analysis is a first indication that a reliable
zero point may be found for the catalog data. The first step in calculating
those data may now be taken by sorting the extended sample in a somewhat different
way. Two classes of accepted results are established, with one class including
results from all analyses for which extrinsic zero points can be calculated
(again see Sect. 3.2). Some results in this class have small values of ![]() ,
while others contribute to the fourth through the seventh lines in Table 1.
The other class considered here includes only results from differential analyses
relative to the Sun for which the
,
while others contribute to the fourth through the seventh lines in Table 1.
The other class considered here includes only results from differential analyses
relative to the Sun for which the ![]() limits given above are always satisfied.
No distinctions among these results are made which are based on their input solar
equivalent widths (EWs) This procedure will be justified in
Sect. 3.4
limits given above are always satisfied.
No distinctions among these results are made which are based on their input solar
equivalent widths (EWs) This procedure will be justified in
Sect. 3.4![]() .
.
The second step is to edit the extended sample. Papers are deleted from that sample for reasons given in Table 2. After the deletions are performed, the remaining sample is augmented by adding data from Nissen (1981). Nissen's results are from photometry of one cluster of weak lines and a second cluster of moderately-saturated lines.
| Reason |
| DCOG result-not used for certain metal-poor stars |
| EWs from a blanketed wavelength region |
|
|
| Few or no lines on linear part of curve of growth |
| Further analysis of program stars may not take place |
| Noisy EWs |
| Only one result in catalog
|
| Only previously published stellar EWs used |
| Results superseded by improved analysis |
| Subsequent analysis indicates systematic error |
| Values of
|
|
The third step in the analysis is to apply an initial set of corrections to the data. These corrections are made only if they can be based on published numerical results. When necessary, solar values of [Fe/H] are corrected to the Liège EW system (see Delbouille et al. 1973; Rutten & van der Zalm 1984a, 1984b). Corrections are also applied if incompatible solar and stellar model atmospheres have been used (see examples (5) and (6) in Appendix A). The entire data base is also corrected to a temperature scale which is described in a companion paper (see Taylor 2003). This part of the correction procedure is described in more detail in Sects. 3.4 through 3.6 of T94.
For each data set which requires an extrinsic zero point, a special reduction procedure is adopted. One or more stars with data in the set are designated as ad hoc standard stars. Averaged values of [Fe/H] for those stars are then calculated from data sets with reliable zero points. Finally, corrections for the problem data sets are derived, with a "comparison algorithm'' being applied if necessary (see Taylor 1999a, Sect. 4.3).
The fourth step in the analysis is to calculate overall averages from the data.
For each star considered, this averaging yields a mean value of [Fe/H], an rms
error of the mean, and a number of effective degrees of freedom![]() . Each input
datum is weighted by the inverse square of an input rms error. The integrity of the
resulting mean values of [Fe/H] must be checked by performing a zero-point
analysis, and that test will be described in the next section. For the moment,
attention is focused on the input rms errors.
. Each input
datum is weighted by the inverse square of an input rms error. The integrity of the
resulting mean values of [Fe/H] must be checked by performing a zero-point
analysis, and that test will be described in the next section. For the moment,
attention is focused on the input rms errors.
Each block of input data is assigned to rms error class S, N, or W. Class N contains data which are quoted in the literature without errors from EW scatter, while class W data are quoted with such errors. For the most part, older papers are in class N, while more recent papers are in class W. Data are assigned to class S if there are reliable rms errors for them in the literature. They are also assigned to this class if special rms errors have been derived for them by using the comparison algorithm. Further discussion of class S data is given in Sect. 4.1 of T94.
For all data without reliable published rms errors, those errors are derived
from scatter in residuals from averaged values of [Fe/H]. A sample of such
scatter is given in Fig. 1, where residuals for part of the Edvardsson et al. (1993) data are depicted. The procedure for deriving class N
errors is adopted unchanged from Sect. 3.8 of T94. An improved procedure for
deriving the counterpart class W error is described in Appendix B of this
paper. The resulting values of the two errors are as follows:
| (2) |
and
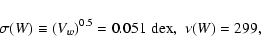 |
(3) |
with Vw being defined in Appendix B. Vw is added to a
contribution from EW scatter to obtain errors for class W data
(again see Appendix B).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2858f1.eps}
\end{figure}](/articles/aa/full/2003/05/aa2858/Timg18.gif) |
Figure 1: For the data of Edvardsson et al. (1993), residuals from averaged values of [Fe/H] (in dex) are plotted against HD number. Only data for HD numbers which equal 99 999 or less are plotted. The solid line applies for a residual of zero, while the dashed line is the mean residual. The adopted reduction of the Edvardsson et al. data is that of the authors themselves, not the subsequent reduction by Gratton et al. (Table 3). |
The rms errors in Eqs. (2) and (3) contribute to useful insights about the
input catalog data. An F test shows that
![]() at a
confidence level C > 99.9%. One might think this to be an expected
result, since it implies that more recent values of [Fe/H] are more precise
than their older counterparts. However, no comparable trend can be found for
evolved stars (see Sect. 4.6 of Taylor 1999a). In addition, if
at a
confidence level C > 99.9%. One might think this to be an expected
result, since it implies that more recent values of [Fe/H] are more precise
than their older counterparts. However, no comparable trend can be found for
evolved stars (see Sect. 4.6 of Taylor 1999a). In addition, if ![]() is
about 10 or greater,
is
about 10 or greater,
![]() is substantially larger than the error
contribution from EW scatter. Again, a similar result holds for evolved stars
(see Sect. 5.3 of Taylor 1999a). Apparently most of the scatter in the
input data is from one or more sources other than EW scatter.
is substantially larger than the error
contribution from EW scatter. Again, a similar result holds for evolved stars
(see Sect. 5.3 of Taylor 1999a). Apparently most of the scatter in the
input data is from one or more sources other than EW scatter.
The zero-point assessment referred to above is performed by searching for
papers whose data yield precise average residuals. These averages are calculated
by using an interim solution in which no corrections have yet been made for the
non-zero mean residuals which will ultimately be found. To estimate the statistical
significance of each averaged residual, a t test is used to derive a value of
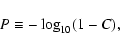 |
(4) |
with C being the confidence level for rejecting the null hypothesis that the true average is zero. The resulting values of P are given with the averaged residuals in Tables 3-5.
| No. of | No. of | Mean | ||
| Source | papers | stars |
|
|
|
Boesgaard |
6 | 62 |
|
- |
| Cayrel de Strobel |
13 | 33 |
|
- |
| Gratton (group 1) |
6 | 83 |
|
- |
| da Silva |
6 | 18 |
|
- |
| Chen et al. (2000) | 1 | 43 |
|
- |
| Favata et al. (1997) | 1 | 30 |
|
- |
| Feltzing; Neuforge-Verheecke & | ||||
| Magain |
3 | 15 |
|
- |
| Fuhrmann (1998) | 1 | 46 |
|
- |
| Santos et al. (2001) | 1 | 42 |
|
- |
| Edvardsson et al. (1993) |
1 | 137 |
|
2.94 |
| Nissen (1981) |
1 | 111 |
|
2.24 |
|
Table 3 contains the most encouraging results found. For the last two entries
in the table,
![]() (C > 0.95). However, the listed mean residuals
are small, and it seems probable that their nonzero status would not have been
recognized if unusually large numbers of contributing data had not been available.
For the remaining entries, P < 1.3. In these cases, the null hypothesis stating
that the averages are zero is maintained
(C > 0.95). However, the listed mean residuals
are small, and it seems probable that their nonzero status would not have been
recognized if unusually large numbers of contributing data had not been available.
For the remaining entries, P < 1.3. In these cases, the null hypothesis stating
that the averages are zero is maintained![]() . Note that each of
the first four entries in Table 3 is from a series of six or more papers
produced by a given author and collaborators.
. Note that each of
the first four entries in Table 3 is from a series of six or more papers
produced by a given author and collaborators.
| No. of | No. of | Mean | ||
| Source | papers | stars |
|
|
|
Balachandran (1990) |
1 | 63 |
|
> 6 |
| Boesgaard & Lavery (1986) |
1 | 11 |
|
3.28 |
| Clegg (1977) |
1 | 11 |
|
4.15 |
| Gratton (group 2) |
2 | 16 |
|
1.46 |
| Pasquini et al. (1994) |
1 | 26 |
|
> 6 |
| Thévenin et al. (1986) |
1 | 10 |
|
3.27 |
| Varenne & Monier (1999) |
1 | 19 |
|
> 6 |
|
In Table 4, results with P > 1.3 are listed if they can be attributed plausibly to a known source of possible zero-point error. The following sources are considered.
Like Table 4, Table 5 contains entries with
![]() .
However, none of the
explanations listed above will work for those entries. They show that
even when zero-point procedures with every appearance of rigor are applied, the
resulting values of [Fe/H] can sometimes have appreciable offsets.
.
However, none of the
explanations listed above will work for those entries. They show that
even when zero-point procedures with every appearance of rigor are applied, the
resulting values of [Fe/H] can sometimes have appreciable offsets.
| No. of | No. of | Mean | ||
| Source | papers | stars |
|
|
| Bikmaev et al. (1990) | 1 | 15 |
|
3.77 |
| Edvardsson et al. (1993) |
1 | 186 |
|
> 6 |
| Fulbright (2000) | 1 | 38 |
|
> 6 |
| Gonzalez |
6 | 21 |
|
3.31 |
| Hartmann & Gehren (1988) |
1 | 4 |
|
> 6 |
|
Overall, one can say that Tables 3 through 5 do not support extreme conclusions.
Tables 4 and 5 show that there is more zero-point diversity than might have been
hoped. On the other hand, Table 3 suggests that a meaningful zero point may
nevertheless be found in the data. To see whether this is the case, corrections
are first made by subtracting the listed offsets from the data to which the offsets
apply. This is done if P > 1.3. Corrections
![]() dex are
applied to 18% of the input data. For an additional 18% of the data,
dex are
applied to 18% of the input data. For an additional 18% of the data,
![]() dex.
dex.
A revised version of the catalog is now produced, and check statistics are calculated. Numerical values for those statistics are listed in Table 6. One set of tests is applied to data of classes N and W which were not obtained by using solar EWs derived from stellar spectrographs. No detectable offset is found. In the fourth row of the table, the overall zero points for data of classes N and W are compared. Again no detectable offset is found, suggesting that the older data are on the same zero point as their more recently derived counterparts. It seems fair to assume that such results are obtainable only because the data are on a common zero point.
| Mean | ||
|
|
|
|
| N(no) - W(yes) | 42 | |
| W(no) - W(yes) | 91 |
|
| Net correction |
113 |
|
| N(all) - W(all) | 135 |
|
|
Copyright ESO 2003