A&A 398, 631-638 (2003)
DOI: 10.1051/0004-6361:20021698
John M. Porter
Astrophysics Research Institute, Liverpool John Moores University,
Twelve Quays House, Egerton Wharf, Birkenhead,
CH41 1LD, UK
Received 22 October 2001 / Accepted 19 November 2002
Abstract
Two models of the circumstellar disc around supergiant B[e]
stars are discussed: an equatorial wind model produced by wind
bi-stability, and a Keplerian viscous disc model.
Both models are successful in providing a site for dust formation once
they have cooled sufficiently.
However, the optical-infra-red continuum is calculated and
it is found that both models have significant trouble in accounting for
observations.
In particular the optical-near-IR emission is accounted for, but the
dust emission is underestimated by at least an order of magnitude.
Variations in the structure of the models (the temperature variation
with radius, the density structure and the dust opacity) are investigated to
assess how (in)appropriate the standard models are for supergiant B[e]
star discs.
Changing the temperature structure, and making simple dust opacity
changes within the disc has little effect
on the resultant continuum emission.
By altering the density structure of the discs, the
continuum may be accounted for by both models:
the equatorial wind model requires a very flat density profile which
is impossible to explain with any accelerating wind, and the viscous disc
model's density structure is required to fall off less steeply with
radius than would have been expected, although this may be explained
from consideration of viscous processes in the disc.
It is recognised that both theoretical interpretations have
difficulties and unsolved problems.
Key words: stars: emission-line, Be - stars: supergiants - stars: circumstellar matter - stars: individual: R126 (HD 37974)
Observations of supergiant B[e] stars (denoted sgB[e] stars hereafter
- see Lamers et al. 1998 for a classification system)
show several features:
infra-red (IR) continuum
excesses and far-IR dust emission (e.g. see Zickgraf
1992); broad (![]() 103 km s-1) UV resonance
lines; in the optical there are strong Balmer lines (H
103 km s-1) UV resonance
lines; in the optical there are strong Balmer lines (H![]() equivalent
widths of >102 Å), and
narrow (10 s of km s-1) permitted and forbidden line emission.
These stars have
typical stellar parameters of
equivalent
widths of >102 Å), and
narrow (10 s of km s-1) permitted and forbidden line emission.
These stars have
typical stellar parameters of
![]() -70
-70 ![]() ,
,
![]() -100
-100 ![]() ,
,
![]() -30 000 K (Zickgraf et al.
1986).
-30 000 K (Zickgraf et al.
1986).
Zickgraf et al. (1985) proposed that the observations could be explained with a multicomponent wind structure: a fast line-driven wind (appropriate for a hot star) over the poles and a dense disc of outflowing gas in the equatorial plane. This geometry has received some corroboration from polarimetry (Zickgraf & Schulte-Ladbeck 1989; Oudmaijer et al. 1998).
Whilst there is a good physical explanation of the fast polar wind, (Castor et al. 1975) the formation mechanism (and indeed the structure) of the dense equatorial flow is still largely unknown. An excellent attempt at explaining the equatorial flow has been made by Lamers & Pauldrach (1991 - rotationally-induced wind bi-stability), which has been recently advanced by Pelupessy et al. (2000) who suggest that wind compression due to its rotation (Bjorkman & Cassinelli 1993) may also play a part in the generation of the disc (although wind compression was found by Owocki et al. 1996 and also by Petrenz & Puls 2000 to be strongly inhibited in rotating winds). Zickgraf et al. (1996) fit a wind-like flow with a "beta'' type velocity law to observations of the UV metallic lines of R50 and Hen S22 (interpreted as edge-on stars) and found acceptable fits with wind terminal velocities of 60-80 km s-1.
Oudmaijer et al. (1998) present a hydrodynamical model of the flow
around HD 87643 in which a line-driven wind is driven partly by
luminosity from a Keplerian reprocessing disc.
As well as producing a fast polar wind, their
model produces a region several scale-heights above the equatorial
plane which has intermediate velocities (![]() 100 km s-1), and hence
they point to this region being responsible for the permitted line
emission. However, they did not discuss the disc formation, being more
concerned with the intermediate and fast radiatively driven flows.
100 km s-1), and hence
they point to this region being responsible for the permitted line
emission. However, they did not discuss the disc formation, being more
concerned with the intermediate and fast radiatively driven flows.
Given the current uncertainties in the sgB[e] stars' disc origin, a model for an equatorial wind produced by the bi-stability mechanism, and also a model for a viscous Keplerian disc (similar to that currently gaining acceptance in the classical-Be star community) are directly compared. The aim of this study is to assess if either model can be ruled out, or (at least) if one model can be strongly favoured over the other as the more likely disc structure of sgB[e] stars. As a first step, the optical-IR spectral energy distribution is calculated and compared to observations (the line emission is returned to in the discussion). This is not a trivial task as a successful model must also provide a site for the formation of dust. In Sect. 2 the density and velocities of both the equatorial wind model and the viscous disc model are discussed, along with a heuristic argument for the temperature profile. The possibility of the flow forming dust is considered in Sect. 3. In Sect. 4 the continuum emission is calculated and its variation with relevant parameters presented. A discussion is given in Sect. 5 and conclusions in Sect. 6.
The main concern of this study is to examine if either model can
account for the continuum observations of sgB[e] stars.
Most
previous work has examined aspects of wind models (for example
Bjorkman 1998, presents results of a wind compression model)
whilst this is
the first time a viscous disc model has been applied to sgB[e] stars.
During the
course of the study, values for the stellar parameters, fast polar
wind etc. are taken from the Large Magellanic Cloud star R126:
![]() ,
,
![]() ,
,
![]() K
(Zickgraf et al. 1985),
the fast polar wind parameters vary widely in the literature: a
mass-loss rate of
K
(Zickgraf et al. 1985),
the fast polar wind parameters vary widely in the literature: a
mass-loss rate of
![]() -
-
![]() ,
and terminal velocity of
,
and terminal velocity of
![]() was calculated by Zickgraf et al. (1985), whilst Bjorkman
(1998) gives
was calculated by Zickgraf et al. (1985), whilst Bjorkman
(1998) gives
![]() and
and
![]() from Kudritzki et al.'s (1989) "cooking recipe''.
The adopted nomenclature used in this paper is that mass-loss
rates will be quoted as a mass-flux multiplied by 4
from Kudritzki et al.'s (1989) "cooking recipe''.
The adopted nomenclature used in this paper is that mass-loss
rates will be quoted as a mass-flux multiplied by 4![]() i.e. the rate
is quoted as if the mass-loss was present over the whole star. This
should be particularly noted when considering the mass flux through
the disc.
i.e. the rate
is quoted as if the mass-loss was present over the whole star. This
should be particularly noted when considering the mass flux through
the disc.
The popular model for the equatorial density enhancement of sgB[e]
circumstellar media is one based on radiatively-driven
winds. Support for this model came in 1991 when the bi-stability
model was presented, in which the stellar wind parameters (mass-loss rate and
velocity)
"jump'' over a band centered on the equator of the star as the
driving species and lines change at temperatures
in the region of 25 000 K
due to the changing conditions at the photosphere
from a gravity-darkened fast rotating star (Lamers & Pauldrach 1991;
Vink et al. 1999, and Pelupessy et al. 2000)
The model is characterised by a latitudinal varying mass flux rate
![]() and wind speed
and wind speed
![]() .
At the jump latitude
.
At the jump latitude ![]() ,
,
![]() increases and
increases and ![]() decreases producing a large increase in density
decreases producing a large increase in density
![]() .
Within this high density, low velocity region (representing the "disc''),
the radial velocity is
.
Within this high density, low velocity region (representing the "disc''),
the radial velocity is
![]() and density is
and density is
![]() .
The model requires that the star is rotating at a substantial fraction
(>
.
The model requires that the star is rotating at a substantial fraction
(>![]() )
of its critical speed (where centrifugal forces balance
gravity). The azimuthal velocity of the wind in the disc
)
of its critical speed (where centrifugal forces balance
gravity). The azimuthal velocity of the wind in the disc
![]() decreases with radius from the star due to angular momentum
conservation and so is not very important dynamically in the disc.
The disc thickness is determined by the value of
decreases with radius from the star due to angular momentum
conservation and so is not very important dynamically in the disc.
The disc thickness is determined by the value of ![]() where the bi-stability jump occurs, and so depends on the rotation
rate and how close the effective temperature is to the jump temperature.
where the bi-stability jump occurs, and so depends on the rotation
rate and how close the effective temperature is to the jump temperature.
Within the disc, the density and radial and azimuthal velocities
follow the form
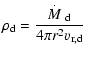 |
(1) | ||
| (2) | |||
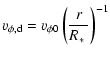 |
(3) |
The model of viscous outflowing discs has been discussed by Lee et al. (1991) and Okazaki (2001) and applied to classical Be star observations by Porter (1999). In this model, the angular momentum distribution within the disc is determined by viscosity, in a similar way to the more familiar accretion disc. However, in this case the angular momentum source for viscous discs is the central star (which acts as an angular-momentum sink for accretion discs). In common with the bi-stability mechanism, this model also requires that the star is a fast rotator - indeed it insists that the equatorial region is rotating at Keplerian speeds. The weak link in the model for classical Be stars (which will also feature in this application to sgB[e] stars) is that the mechanism to inject angular momentum in to the disc at its inner regions is still largely unknown - often quoted candidates are pulsation and magnetic fields.
The solution of the equations of mass continuity and angular momentum
conservation in the radial and azimuthal co-ordinates produce a disc
which has surface-density, radial and azimuthal velocity are
well represented in the inner ![]() 102
102 ![]() by power laws in
radius (Okazaki 2001).
by power laws in
radius (Okazaki 2001).
In particular the discs are close to Keplerian
![]() ,
the radial velocity increases linearly with radius
,
the radial velocity increases linearly with radius
![]() (and is subsonic until large radii), and the
surface-density
(and is subsonic until large radii), and the
surface-density ![]() (the density integrated through the disc)
decreases as
(the density integrated through the disc)
decreases as
![]() .
The disc
flares - the scale height H of the disc increases with radius as
.
The disc
flares - the scale height H of the disc increases with radius as
![]() where G is the gravitational
constant,
where G is the gravitational
constant, ![]() is the stellar mass and
is the stellar mass and ![]() is the sound
speed.
The viscous disc
density and velocities are
is the sound
speed.
The viscous disc
density and velocities are
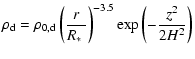 |
(4) | ||
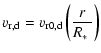 |
(5) | ||
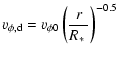 |
(6) |
The form of temperature profile for a disc is difficult to
determine without a full calculation. However a simple argument can be
applied to both equatorial winds and viscous discs which can provide an
estimate of the radial variation of temperature.
It is assumed that the disc will have a constant temperature with
radius until a cooling radius rc, and beyond this the disc will cool.
In the limit that no radiation of any wavelength
impinges on the disc, it will cool adiabatically such that
![]() .
However, it is most likely that the disc will act as a reprocessing
disc: it will absorb radiation from the star, and re-emit at its local
equilibrium temperature
.
However, it is most likely that the disc will act as a reprocessing
disc: it will absorb radiation from the star, and re-emit at its local
equilibrium temperature ![]() .
Hence the total energy emitted by the
disc (
.
Hence the total energy emitted by the
disc (
![]() )
is proportional to the flux recieved, which in
turn is proportional to r-3 (r-2 from the dilution of the
radiation field, and an extra factor of r-1 from the cosine term
produced
by the geometric reduction of the projected disc area).
Hence these reprocessing disc have
)
is proportional to the flux recieved, which in
turn is proportional to r-3 (r-2 from the dilution of the
radiation field, and an extra factor of r-1 from the cosine term
produced
by the geometric reduction of the projected disc area).
Hence these reprocessing disc have
![]() or
or
![]() .
This argument is valid for both equatorial winds, and viscous discs.
.
This argument is valid for both equatorial winds, and viscous discs.
The cooling will change the metallic species responsible for the absorption and scattering of the equatorial wind and hence may lead to a more complicated discussion of the wind driving. This has already been implicitly taken into account by using the slowly accelerating beta-velocity law fitted to the UV lines from Zickgraf et al. (1996).
Cooling will effect the viscous disc:
once the temperature in the viscous disc varies, then the density and
velocity profiles are also affected. This is due to the torques
changing as the viscosity
![]() alters (
alters (![]() is the
Shakura & Sunyaev 1973 viscosity parameter). This is a
result of the sound speed
is the
Shakura & Sunyaev 1973 viscosity parameter). This is a
result of the sound speed ![]() and also the disc scale
height
and also the disc scale
height
![]() changing. To ensure mass and
angular momentum conservation, the density, radial velocity and scale
height change to
changing. To ensure mass and
angular momentum conservation, the density, radial velocity and scale
height change to
| (7) | |||
| (8) | |||
| (9) |
Any model which attempts to explain the properties of sgB[e] star circumstellar matter must also provide a site for dust formation. To produce dust, two criteria need to be fulfilled: the temperature of the gas must be lower than the sublimation temperature of the dust (around 1500 K depending on the chemical composition of the dust), and secondly, the number density of the species involved in the formation of the dust needs to be above a critical value.
It is expected that sgB[e] stars' dust will be silicate based, as
carbon is depleted due to the CNO processing cycle in
massive stars, and indeed sgB[e] stars do show features due to
silicates in their spectra (e.g. Voors 1999).
Examination of the 8-13 ![]() m spectra of R126 presented in Roche
et al. (1993) shows that there are no strong emission features, which
suggests silicate dust is not present.
However, suppression of the silicate feature
may be achieved by having large grains (
m spectra of R126 presented in Roche
et al. (1993) shows that there are no strong emission features, which
suggests silicate dust is not present.
However, suppression of the silicate feature
may be achieved by having large grains (
![]() m),
or by not
having a stratified disc structure (leading to any optically thin
"atmosphere'' region) i.e. the emitting region is completely
optically thick (see Dullemond et al. 2001 and Meeus et al. 2002).
m),
or by not
having a stratified disc structure (leading to any optically thin
"atmosphere'' region) i.e. the emitting region is completely
optically thick (see Dullemond et al. 2001 and Meeus et al. 2002).
Gail & Sedlmyar (1988) showed that a critical number density can be
derived by comparing the timescale
for the chemical reactions responsible for dust formation
![]() to the timescale for a parcel of gas to change in
density and temperature
to the timescale for a parcel of gas to change in
density and temperature
![]() (i.e. an expansion
timescale). Grain growth will occur if
(i.e. an expansion
timescale). Grain growth will occur if
![]() .
Gail & Sedlmyar find that this occurs for any size of grain if the
number density of the growth species is larger than
a minimum density
.
Gail & Sedlmyar find that this occurs for any size of grain if the
number density of the growth species is larger than
a minimum density
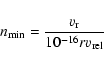 |
(10) |
The value of ![]() is taken to be
is taken to be
![]() corresponding to 1/3 of Solar silicon abundance
appropriate for the LMC metallicity.
As an example calculation of
corresponding to 1/3 of Solar silicon abundance
appropriate for the LMC metallicity.
As an example calculation of
![]() ,
the sound speed (approximating to
,
the sound speed (approximating to
![]() )
has been calculated assuming that for both the
equatorial wind and the viscous disc models, cooling takes place beyond
)
has been calculated assuming that for both the
equatorial wind and the viscous disc models, cooling takes place beyond
![]() ,
and that the
temperature profile is
,
and that the
temperature profile is
![]() thereafter.
Finally the temperatures at
thereafter.
Finally the temperatures at
![]() are taken to be 0.8
are taken to be 0.8
![]() and 0.5
and 0.5
![]() for the equatorial wind and disc models
respectively. The results of this calculation are shown in Fig. 1.
for the equatorial wind and disc models
respectively. The results of this calculation are shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2016f1.eps}\end{figure}](/articles/aa/full/2003/05/aa2016/Timg87.gif) |
Figure 1:
Comparison of number density of carbon (solid line) with
|
| Open with DEXTER | |
The equatorial wind is assumed to have the same parameters as
described in Sect. 2.1.1:
(![]() and wi = 0.1) and a mass-loss rate of
and wi = 0.1) and a mass-loss rate of
![]()
![]() yr-1 (this rate has been chosen as it produces a dense
enough disc to acccount for the near-IR emission of the model star
R126 (see Sect. 5).
Figure 1 shows the number density of this wind model as well as the
critical number density required to form dust.
It can be seen that dust can only form for
yr-1 (this rate has been chosen as it produces a dense
enough disc to acccount for the near-IR emission of the model star
R126 (see Sect. 5).
Figure 1 shows the number density of this wind model as well as the
critical number density required to form dust.
It can be seen that dust can only form for
![]() .
The arrow in Fig. 1 shows the radius where the temperature
falls to 1500 K - this occurs at a radius of 41
.
The arrow in Fig. 1 shows the radius where the temperature
falls to 1500 K - this occurs at a radius of 41 ![]() .
Therefore there
exists a region from
.
Therefore there
exists a region from ![]() 40-50
40-50 ![]() where the gas is dense enough
and cool enough for dust formation.
where the gas is dense enough
and cool enough for dust formation.
Figure 1 also shows the number density within a viscous disc
with
![]() g cm-3 (again chosen to reproduce the
near-IR emission, see Sect. 5) and
g cm-3 (again chosen to reproduce the
near-IR emission, see Sect. 5) and
![]() km s-1 (where
km s-1 (where
![]() is the viscosity parameter,
T4 is the disc temperature in 104 K and
is the viscosity parameter,
T4 is the disc temperature in 104 K and ![]() and
and ![]() are in
Solar units - see Eq. (6) of Porter 1998). Again the cooling radius is
set to
are in
Solar units - see Eq. (6) of Porter 1998). Again the cooling radius is
set to
![]() .
For
.
For
![]() the number density in the disc is
high enough to enable dust to form. The radius where the temperature
falls to 1500 K is 23
the number density in the disc is
high enough to enable dust to form. The radius where the temperature
falls to 1500 K is 23 ![]() ,
well within the region where dust may form.
,
well within the region where dust may form.
Both the viscous disc model and the wind model have a region where
their number density is larger than the critical value for dust
formation, implying that both models can form dust, with the proviso
that the temperature must also be below the sublimation temperature
![]() .
The major difference between the models is for
.
The major difference between the models is for
![]() ,
which is
significantly lower for the viscous disc model as its radial
velocity is far lower than for the equatorial wind model.
Both models are successful in providing a site for dust
formation, and so both are still good candidates for the actual discs
of sgB[e] stars.
,
which is
significantly lower for the viscous disc model as its radial
velocity is far lower than for the equatorial wind model.
Both models are successful in providing a site for dust
formation, and so both are still good candidates for the actual discs
of sgB[e] stars.
The
continuum emission is now calculated from the density fields in the
models and compared to observations of R126.
The model includes a fast polar wind (with a fixed mass-loss rate of
![]() ), the disc models described in the last section, and
dust (where it exists) in the disc.
Although the fast polar wind is included, its contribution to the
final flux is negligible, and is only included for completeness.
In order to calculate the excess emission in the optical - IR, the
prescription of Waters (1986) is used.
The star is assumed to be pole-on.
), the disc models described in the last section, and
dust (where it exists) in the disc.
Although the fast polar wind is included, its contribution to the
final flux is negligible, and is only included for completeness.
In order to calculate the excess emission in the optical - IR, the
prescription of Waters (1986) is used.
The star is assumed to be pole-on.
The viscous disc model requires that the density
![]() ,
the dust
formation temperature
,
the dust
formation temperature
![]() and the cooling radius
and the cooling radius ![]() are specified to calculate the emission. The equatorial wind model
requires a mass-loss rate
are specified to calculate the emission. The equatorial wind model
requires a mass-loss rate
![]() ,
a terminal velocity
,
a terminal velocity
![]() ,
the
value of
,
the
value of ![]() for the velocity law and a flow opening angle, as
well as the dust temperature and cooling radius:
for the velocity law and a flow opening angle, as
well as the dust temperature and cooling radius: ![]() is fixed
at
is fixed
at ![]() ,
the terminal velocity
,
the terminal velocity
![]() km s-1, and the
opening angle to
km s-1, and the
opening angle to ![]() hereafter.
hereafter.
The number density
is calculated where the temperature falls below
![]() and
compared to the minimum number density for dust formation from Eq. (10).
If dust is found to form, the optical depth through the disc at that
radii is
and
compared to the minimum number density for dust formation from Eq. (10).
If dust is found to form, the optical depth through the disc at that
radii is
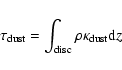 |
(11) |
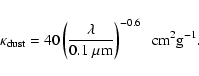 |
(12) |
The emitted flux is then integrated over the disc area,
which, for face-on discs, produces
![\begin{displaymath}F_\nu = \frac{1}{D^2} \int^{R_{\rm disc}}_{R_\ast} \pi B_\nu[T(r)] (1 - {\rm
e}^{-\tau_{\rm dust}} ) 2\pi r {\rm d}r
\end{displaymath}](/articles/aa/full/2003/05/aa2016/img110.gif) |
(13) |
The UBVRIJHKLMN photometry for R126 is taken from Zickgraf et al.'s
(1985) compilation, and
is supplemented by 12 ![]() m and 25
m and 25 ![]() m IRAS points from Schwering
(1989).
The reddening to the object was taken to be
E(B-V)=0.25 from
Zickgraf et al. (1985). The calculated emission from the model has
been reddened with the expression given in Howarth (1983) and
the model flux in the V band has been normalised
to the R126 observations for all models.
The underlying photospheric continuum is a Kurucz 22 000 K,
m IRAS points from Schwering
(1989).
The reddening to the object was taken to be
E(B-V)=0.25 from
Zickgraf et al. (1985). The calculated emission from the model has
been reddened with the expression given in Howarth (1983) and
the model flux in the V band has been normalised
to the R126 observations for all models.
The underlying photospheric continuum is a Kurucz 22 000 K,
![]() ATLAS9 model.
ATLAS9 model.
The proceedure used to fit the photometry involves a search over the
mass-loss rate
![]() ,
dust formation temperature and cooling
radius for the
equatorial wind model. The viscous disc model has the density
normalization
,
dust formation temperature and cooling
radius for the
equatorial wind model. The viscous disc model has the density
normalization ![]() ,
dust formation temperature and cooling radius
varied to find the best fit.
The results are summarised in Table 1: the various parameters for the
models are given, along with their
,
dust formation temperature and cooling radius
varied to find the best fit.
The results are summarised in Table 1: the various parameters for the
models are given, along with their ![]() evaluation of fit.
Best-fit values to the optical-near-IR data produces values of
evaluation of fit.
Best-fit values to the optical-near-IR data produces values of
![]()
![]() yr-1 and
yr-1 and
![]() g cm-3 for both models respectively. The
equivalent mass loss rate for the viscous disc model is
g cm-3 for both models respectively. The
equivalent mass loss rate for the viscous disc model is
![]()
![]() yr-1: although it appears counterintuitive that this is less
than the polar (fast wind) mass loss rate, it is reconciled in that
the mechanism for mass ejection into the viscous disc is not the same
as over the poles (indeed the cause for mass injection in to the disc
it is still unknown). Hence the equatorial mass loss rate need not
bear any relation to the polar mass loss rate.
yr-1: although it appears counterintuitive that this is less
than the polar (fast wind) mass loss rate, it is reconciled in that
the mechanism for mass ejection into the viscous disc is not the same
as over the poles (indeed the cause for mass injection in to the disc
it is still unknown). Hence the equatorial mass loss rate need not
bear any relation to the polar mass loss rate.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2016f2.eps}\end{figure}](/articles/aa/full/2003/05/aa2016/Timg119.gif) |
Figure 2:
Dust optical depths within the discs at a wavelength of
5 |
| Open with DEXTER | |
There is a significant problem with the dust emission for both models
in that the optical depths where dust forms is not large enough to
generate the observed emission. To illustrate this, Fig. 2 shows the
dust optical depth
![]() (and density and disc
scale-height) for both models as a function of radius.
It can be clearly seen that the
optical depth is significantly less than unity at the dust formation
radius, and
decreases with radius. Therefore it might be expected that the
continuum emission will not be able to reproduce the obserevational
data.
Figure 3 displays the full spectrum for both models. As can be seen the
optical to near-IR flux is reproduced, although longward of
(and density and disc
scale-height) for both models as a function of radius.
It can be clearly seen that the
optical depth is significantly less than unity at the dust formation
radius, and
decreases with radius. Therefore it might be expected that the
continuum emission will not be able to reproduce the obserevational
data.
Figure 3 displays the full spectrum for both models. As can be seen the
optical to near-IR flux is reproduced, although longward of ![]()
![]() m the dust emission is too low by about an order of magnitude.
m the dust emission is too low by about an order of magnitude.
How may this be remedied? Or are the two proposed models to be
rejected?
To produce the observed emission, the optical depth
![]() needs to be increased by one to two orders of magnitude. For these
models this requires a significant increase in density. A global
increase in the density (corresponding to increases in
needs to be increased by one to two orders of magnitude. For these
models this requires a significant increase in density. A global
increase in the density (corresponding to increases in
![]() and
and
![]() )
would produce too much emission in the optical-near-IR
range, and so may be ruled out.
Increasing the opening angle for the equatorial wind model (or
decreasing the terminal velocity) will also
produce the same effect of increasing the emission at all wavelengths,
and not simply the dust emission.
To investigate how dependent the models are to the input assumptions,
several changes are made in turn to the standard models:
the temperature power law indices are made free parameters, the dust
opacity is set to that appropriate to Solar metallicity, and finally,
the density power law indices are made free parameters.
)
would produce too much emission in the optical-near-IR
range, and so may be ruled out.
Increasing the opening angle for the equatorial wind model (or
decreasing the terminal velocity) will also
produce the same effect of increasing the emission at all wavelengths,
and not simply the dust emission.
To investigate how dependent the models are to the input assumptions,
several changes are made in turn to the standard models:
the temperature power law indices are made free parameters, the dust
opacity is set to that appropriate to Solar metallicity, and finally,
the density power law indices are made free parameters.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2016f3.eps}\end{figure}](/articles/aa/full/2003/05/aa2016/Timg122.gif) |
Figure 3: Continuum emission from the star (R126) and the two best-fit models. The total model flux (solid line) consists of Kurucz model atmosphere (long dashed line), free-free and free-bound emission (dotted line) and dust emission (short-dashed line) for the "standard'' models. The model has been normalised to the R126 data of Zickgraf et al. (1985) in the V band. The left panel is for the equatorial wind model, and the right panel is for the viscous disc model. Model parameters are given in Table 1. |
| Open with DEXTER | |
| Model | m |
|
|
|
density | |
| 1. Wind | 0.75 | 2.3 | 1400 | 40 |
|
407 |
| 2. Viscous disc | 0.75 | 2.0 | 1600 | 40 |
|
403 |
| 3. Wind | 0.60 | 1.1 | 1400 | 40 |
|
359 |
| 4. Viscous disc | 0.50 | 2.1 | 1500 | 40 |
|
397 |
| 5. Wind | 0.75 | 2.0 | 1300 | 120 |
|
316 |
| 6. Viscous disc | 0.75 | 2.9 | 1400 | 120 |
|
313 |
| 7. Wind | 0.75 | 3.5 | 700 | 40 |
|
64 |
| 8. Viscous disc | 0.75 | 6.5 | 800 | 40 |
|
61 |
It is possible that the temperature profile that has been used is not
correct, although the disc must cool in order for it to form
dust.
To assess whether the observations may be fitted using a different
temperature profile, beyond the cooling radius, the power law
![]() has been varied using different values of m, from
0.4 to 1.5 and the best fit models calculated.
The best-fit parameters are shown in Table 1.
The temperature-power law index of the best models is m = 0.6 for the
equatorial wind and m = 0.5 for the viscous disc.
has been varied using different values of m, from
0.4 to 1.5 and the best fit models calculated.
The best-fit parameters are shown in Table 1.
The temperature-power law index of the best models is m = 0.6 for the
equatorial wind and m = 0.5 for the viscous disc.
In the case of the equatorial wind the best-fit dust temperature is identical to the standard wind model (1400 K), and the cooling radius is slightly smaller. However, the fit is again characterised by a significant underestimate of the dust emission indicating that variation of the temperature power law produces a negligible effect on the resultant spectrum. The viscous disc produces a slightly cooler dust formation temperature (1500 K) than in the standard case (1600 K). However, as in the wind case, the fit is barely improved with significant underestimate of the dust emission.
Both of these models are presented in Fig. 4. It appears that the failure of the standard models to reproduce the observations is not dominated by the temperature profile in either model.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2016f4.eps}\end{figure}](/articles/aa/full/2003/05/aa2016/Timg131.gif) |
Figure 4:
As Fig. 3 except that the temperature power law index is a free
parameter.
The left panel is for the equatorial wind
model with
|
| Open with DEXTER | |
Whilst so far the opacity from Wood et al. (2002) has been used, corrected to take account of the lower metallicity of the LMC, here the normalization for Solar metallicity is used (i.e. the LMC star R126 is assumed to have Solar metallicity). This illustrates the effect of increasing the opacity, whilst keeping the form of the density field the same as in the standard cases.
The dust opacity used here is
![]()
![]() m
m
![]() ,
and the best-fitting models are shown in Fig. 5 (with
parameters in Table 1: models 5 and 6).
Formally, from the
,
and the best-fitting models are shown in Fig. 5 (with
parameters in Table 1: models 5 and 6).
Formally, from the ![]() values in Table 1, it can be seen that
increasing the dust opacity decreases the residuals. However, the best
fitting models (Fig. 5) are still woefully inadequate in accounting for
the dust emission.
values in Table 1, it can be seen that
increasing the dust opacity decreases the residuals. However, the best
fitting models (Fig. 5) are still woefully inadequate in accounting for
the dust emission.
Further increase in the dust opacity should provide a high enough optical depth to account for observations. However, this would require an exceptionally large metallicity for this star which is physically very difficult to justify at this stage of evolution of the star, and therefore this possibility is disregarded in favour of the dynamical arguments given later.
The standard density profiles for the wind model (Eq. (1)) is now changed
to a pure power law form:
![]() (where
(where ![]() is a normalization density at
is a normalization density at
![]() ).
The sole difference between the two models now is (i) that the equatorial
wind model
has a disc with a constant opening angle (20
).
The sole difference between the two models now is (i) that the equatorial
wind model
has a disc with a constant opening angle (20![]() ), whereas the
viscous disc flares, and (ii) that the density falls exponentially
with height away from the equatorial plane for the viscous disc.
Only the temperature power
law index is fixed (with m=0.75), and the best-fit model search is
conducted over dust
temperature
), whereas the
viscous disc flares, and (ii) that the density falls exponentially
with height away from the equatorial plane for the viscous disc.
Only the temperature power
law index is fixed (with m=0.75), and the best-fit model search is
conducted over dust
temperature
![]() ,
density power law index n, density
normalization
,
density power law index n, density
normalization ![]() ,
and cooling radius
,
and cooling radius ![]() .
.
The best-fitting equatorial wind model is shown in Fig. 6, and provides
an excellent description of the continuum flux of R126. The parameters
of this fit are n = 1.7 and
![]() g cm-3, cooling radius of
g cm-3, cooling radius of
![]() and dust
temperature of
and dust
temperature of
![]() K.
A literal interpretation of this best fit solution would predict that
the radial velocity actually decreases with radius (from comparison with Eq. (1)),
which indicates that the simple wind model is an erroneous description of
the actual disc around R126.
K.
A literal interpretation of this best fit solution would predict that
the radial velocity actually decreases with radius (from comparison with Eq. (1)),
which indicates that the simple wind model is an erroneous description of
the actual disc around R126.
The best fiting viscous disc model is also shown in Fig. 6 and also
provides a good fit to the data.
The density of this model is
![]() g cm-3
(note this is significantly higher than the best fitting equatorial
wind model), and the
density power law index is n = 2.7, the cooling radius is
g cm-3
(note this is significantly higher than the best fitting equatorial
wind model), and the
density power law index is n = 2.7, the cooling radius is
![]() and the dust
formation temperature is
and the dust
formation temperature is
![]() K.
K.
For both the equatorial wind, and the viscous disc
the
![]() values have been inspected for
different models around this minimum, in order to
estimated the variation in the parameters.
A value of
values have been inspected for
different models around this minimum, in order to
estimated the variation in the parameters.
A value of ![]() is obtained which is twice the best fitting
model if parameter
uncertainties are
is obtained which is twice the best fitting
model if parameter
uncertainties are
![]() ,
,
![]()
![]() K, and
K, and
![]() .
Clearly the least constrained parameter is the cooling radius.
.
Clearly the least constrained parameter is the cooling radius.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2016f5.eps}\end{figure}](/articles/aa/full/2003/05/aa2016/Timg147.gif) |
Figure 5:
As Fig. 3 except that the dust opacity normalization is appropriate
for Solar metallicity:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2016f6.eps}\end{figure}](/articles/aa/full/2003/05/aa2016/Timg148.gif) |
Figure 6:
As Fig. 3 except that the density power law is a free
parameter.
The left panel is for the equatorial wind
model with
|
| Open with DEXTER | |
It appears from the results that both the "standard'' equatorial wind
model and
the viscous disc model have trouble in generating the continuum
emission for sgB[e] stars. To do so, the density field has had to be
changed somewhat from initial theoretical expectations.
The deviations from the standard density structures of the models may
indeed highlight some aspects of the two models which have not been
considered here. The equatorial wind may be clumped at large radii,
hence producing parts of the disc which have a large dust optical
depth. However, the total emission may not necessarily increase due to
the subsequent reduction in effective emitting area (i.e. if the gas
is clumped into dense regions, the "filling factor'' of that dense gas
degreases).
The low power law index for the best fitting viscous disc model
(n = 2.7 compared to n = 3.5 for the standard model) might
indicate an extra dependence of the viscosity (and perhaps the
![]() parameterization) on the surface density, or the disc
temperature which has not been investigated here.
parameterization) on the surface density, or the disc
temperature which has not been investigated here.
Assuming that either of these models can account for all the continuum emission, can the two models both produce the observed heavy element line emission from sgB[e] stars? The equatorial wind model was introduced to do exactly that (e.g. see Zickgraf et al. 1996), and the line emission comes from the equatorial wind flow itself. Therefore, this model would seem to provide a complete description of the disc around a sgB[e] star. However, there is a difficult issue for the equatorial wind model: the electron scattering optical depth becomes larger than unity at relatively small radii. Whilst high continuum optical depths are commonplace for (approximately) spherically symmetric Wolf-Rayet winds, in this asymmetric case it may lead to problems in driving the wind. Photons cannot physically penetrate into the disc which leads to little or no radiative driving for the gas, and hence the density profile may not actually allow the gas to be driven! This might cast doubt on whether the equatorial wind model is correct in principle. However, this may also highlight that the wind may not have a velocity law typified by the "beta'' parameterization.
The production of the heavy element line emission from the viscous
disc model is slightly more complicated. The dominant velocity
component in the disc is a rotational one, and therefore optically
thin emission lines should exhibit double-peaked profiles (similar to
those observed in classical Be stars). However, the model in Oudmaijer
et al. (1998), provides a separate site for line emission with a
dominant radial component of velocity: a disc wind. Here, the emission
from the reprocessing disc helps to drive a flow from
the upper and lower surfaces of the disc to relatively modest terminal
velocities ![]() 100 km s-1. The resultant line emission may have a
double-peaked disc component, but will have a large radial component
imposed on it
too. Currently, no attempt has been made to synthesize line profiles
from the work presented by Oudmaijer et al. An issue to resolve here is
whether there is enough flow generated in the disc-wind to account for
the lines observed in sgB[e] stars.
100 km s-1. The resultant line emission may have a
double-peaked disc component, but will have a large radial component
imposed on it
too. Currently, no attempt has been made to synthesize line profiles
from the work presented by Oudmaijer et al. An issue to resolve here is
whether there is enough flow generated in the disc-wind to account for
the lines observed in sgB[e] stars.
A weakness for the viscous disc model is that the source of angular momentum required to supply the disc is still unidentified (although candidates exist: pulsation and/or magnetic fields). Until a coherent theory of angular momentum transfer from the star to the disc is produced, then the viscous disc model will only remain a promising candidate. Note that if the viscous disc model is the correct structure, then it is possible that the way in which classical Be stars supply angular momentum to their discs is the same for sgB[e] stars. In this case then the sgB[e] stars will be invaluable as they have a different envelope structure than classical Be stars, but it might be likely that both supply angular momentum in the same fashion.
From the results above, it is difficult to make a strong case which will prefer one model over the other, or even that either model is appropriate. Clearly, the discs of sgB[e] stars are not the simple radiation driven flows, nor the simple viscous discs that have been previously suggested.
Both of the models that have been presented in this study are apparently incapable of reproducing the observational results - in their simplest form. Whilst both meet the requirements for the formation of dust they are unable to yield the necessary broad-band fluxes.
The first model is the enhanced equatorial flow from Lamers & Pauldrach's bi-stability theory (1991); the other is the viscous disc model. The densities are alike, but the velocity fields are disparate. Both competing paradigms expect that the central supergiant star is rotating at a significant fraction of its break-up speed.
By relaxing several assumptions (regarding the temperature profile, the dust opacity, and the density profile), the applicability of the models have been tested. It is found that the models are unable to reproduce the observations unless the disc density field is significantly altered, although then a good representation of the observations can be obtained.
There are possibilities for both models to produce the observed permitted and forbidden line emission: the equatorial wind model produces the emission itself, and the viscous disc model produces a disc-wind from it's surfaces which may produce the lines (although this remains untested).
In both the equatorial wind model and the viscous disc model, there is still work to be undertaken to understand the form of the density profile necessary to account for observations. Clearly both models in their simplest form are inadequate as a description of the discs of sgB[e] stars.
Acknowledgements
JMP would like to thank Simon Clark, Atsuo Okazaki, Toby Moore and Lee Howells for help in preparing and commenting on previous drafts of this paper, and Jon Bjorkman for his useful input regarding dust emission. JMP also thanks the anonymous referees for making useful comments on the submitted versions.