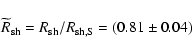A&A 398, 195-202 (2003)
DOI: 10.1051/0004-6361:20021650
BeppoSAX observation of the composite remnant G327.1-1.1
F. Bocchino1 -
R. Bandiera2
1 - Osservatorio Astronomico di Palermo, Piazza del Parlamento 1,
90134 Palermo, Italy
2 -
Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5,
50125 Firenze, Italy
Received 30 July 2002 / Accepted 11 November 2002
Abstract
We report an X-ray study of the composite supernova remnant
G327.1-1.1, with particular emphasis on its thermal emission. By virtue of a
combined spatial and spectral analysis, we have been able to model the
X-ray emission of the remnant as a sum of two components: a non-thermal
component, due to the pulsar nebula and the pulsar itself, and a
thermal component, of which we have analysed spectrum and morphology,
after proper subtraction of the plerion. We discuss three possible
interpretations of the thermal emission of G327.1-1.1: pure Sedov expansion,
expansion through a
inhomogeneous medium with evaporation from ISM clouds, and radiative
expansion. On the light of our new data and
interpretation, we have re-derived all the physical parameters of this SNR. In
the framework of Sedov or radiative expansion we derive a longer age
than previously estimated (
 yr), thus not requiring a high
velocity for the pulsar.
yr), thus not requiring a high
velocity for the pulsar.
Key words: acceleration of particles - radiation mechanisms: non-thermal -
ISM: clouds - ISM: individual objects: G327.1-1.1 - ISM: supernova remnants
The class of supernova remnants (SNRs) contains a wide variety of objects, that
cannot be accounted for by the traditional subdivision in just two categories,
namely shell-like remnants (powered by a blast wave expanding in the ambient
medium) and filled-center (or Crab-like, or plerionic) remnants (powered by a
spinning-down pulsar).
The class of composite SNRs has in fact been introduced (Helfand & Becker 1987) in
order
to arrange a number of objects that neither could be classified as pure
shell-like nor as pure filled-center remnants.
This classification was originally only morphological, by requiring just the
coexistence of a shell and of a center-filled component: the underlying belief
was that
the inner component always has a plerionic nature.
Such scenario, originally devised for objects in which both components are
detected in radio,
seemed to apply also to those appearing as pure shells in radio, but with
a centrally peaked emission in X rays.
A natural explanation was that in these SNRs the central X-ray component is due
to synchrotron emission of plerionic nature, which happens to be too weak in
radio.
From the analysis of the X-ray spectra however it became clear that for
a large fraction of composite SNRs (the so-called "mixed-morphology''
remnants) the emission from the central component is thermal. Along
this line White & Long (1991, hereafter WL) presented a model showing that
a centrally peaked (thermal) X-ray emission characterizes SNRs in which
the blast wave is expanding in a cloudy interstellar medium and induces
a delayed evaporation of the clouds. This model has been applied to
several SNRs, although its validity is still under debate. For
instance Rho et al. (1994) found that the radial profiles of SNR W44 are
nicely fitted by a WL model; but Harrus et al. (1997) then showed that this
model fails in dating the SNR, and suggested an alternative scenario
based on the idea that the shock has reached the radiative phase. A
more detailed radiative model for W44 has been recently presented
(Cox et al. 1999; Shelton et al. 1999), which includes thermal conduction and a
density gradient in the ambient medium. An alternative suggestion
(Petruk 2001) is that even a shell-type SNR which expands in a
strong density gradient may mimic a center-filled morphology, if seen
with a peculiar orientation. Further investigation is still required
to clarify which scenario is the most appropriate to describe the majority
of thermal X-ray SNRs with a center-filled morphology.
On the observational side, the diagnostics and even the recognition of
mixed-morphology SNRs are not easy tasks.
The determination of the nature (thermal or non-thermal) of the central X-ray
component on the basis of its X-ray spectrum is in principle straightforward.
However a thermal and a non-thermal component may coexist in the same remnant,
in which case both a high spatial resolution and a broad-spectrum sensitivity
are required in order to study them separately.
The coexistence, in composite SNRs, of more components typically implies
a dynamical interaction between them, a study of which may provide
important clues on the physical conditions.
For instance,
an X-ray spectral determination of the pressure in the shell component,
together with the requirement of a pressure balance between the thermal remnant
and the plerion, allows an estimate of the plerionic magnetic field.
Although there are various composite SNRs that in X rays show both a shell-like
and a plerionic component, up to now only in one case (W44) a plerionic
component is clearly seen coexisting with a centrally peaked thermal X-ray
component.
In this paper we suggest that also SNR G327.1-1.1 may present
such coexistence, and be in
various respects similar to W44.
G327.1-1.1 is a composite SNR with a rather complex structure. Details of
its morphology have been revealed only recently at radio wavelengths,
by the 843 MHz MOST SNR survey (Whiteoak & Green 1996). In particular its
plerionic component is substantially offset with respect to the
centroid of an otherwise rather symmetric remnant.
A recent Chandra observation has in fact confirmed the presence of a
compact source (P.O. Slane, private communication) on the tip of a
finger-like feature extending from the radio plerion to the north-west
direction, which also coincides with a hard X-ray source
(Sun et al. 1999, hereafter SWC). On the other hand, the thermal
component of G327.1-1.1 has not been mapped in detail, and its origin is still
uncertain. SWC interpreted it as a
thermal shell, and applied the Sedov solution to derive the shell
parameters. However, the presence of the strong non-thermal nebula
prevented them from showing the putative limb-brightened X-ray morphology
of the thermal emission. In this work, we attempt to derive the
spatial morphology of the thermal component.
The plan of the paper is the following: in Sect. 2 the observation is
described; Sect. 3 presents results from a joined spectral and spatial analysis
of the data; Sect. 4 is devoted to a discussion on the nature of G327.1-1.1; Sect. 5
concludes.
The BeppoSAX imaging instruments are the Medium-Energy Concentrator Spectrometer
(MECS; 1.8-10 keV; Boella et al. 1997) and the Low-Energy Concentrator
Spectrometer (LECS; 0.1-10 keV; Parmar et al. 1997).
The MECS consists of two grazing incidence telescopes with imaging gas
scintillation proportional counters in their focal planes.
The LECS uses an identical concentrator system as the MECS, but utilizes an
ultra-thin entrance window and a driftless configuration to extend the
low-energy response to 0.1 keV.
The fields of view (FOV) of the LECS and MECS are circular with diameters of 37 and 56
and 56 ,
respectively.
In the overlapping energy range, the space resolution of both instruments is
similar and corresponds to 90% encircled energy within a radius of
,
respectively.
In the overlapping energy range, the space resolution of both instruments is
similar and corresponds to 90% encircled energy within a radius of 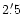 at 1.5 keV.
In addition, the BeppoSAX payload includes two high energy instruments - the High
Pressure Gas Scintillation Proportional Counter (HPGSPC; 5-120 keV; Manzo et al. 1997) and the Phoswich Detection System (PDS; 15-300 keV; Frontera et al. 1997).
at 1.5 keV.
In addition, the BeppoSAX payload includes two high energy instruments - the High
Pressure Gas Scintillation Proportional Counter (HPGSPC; 5-120 keV; Manzo et al. 1997) and the Phoswich Detection System (PDS; 15-300 keV; Frontera et al. 1997).
The region of sky containing G327.1-1.1 was observed between 1999 March 14 and March 16.
The pointing direction was RA =
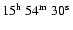 ,
Dec =
,
Dec =
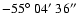 (J2000).
In order to avoid solar scattered emission and other contaminating effects,
data were limited to intervals when the elevation angle above the
Earth's limb was >
(J2000).
In order to avoid solar scattered emission and other contaminating effects,
data were limited to intervals when the elevation angle above the
Earth's limb was >
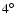 and when the instrument configurations were
nominal.
The screened exposures in the LECS and MECS are 31.0 ks and 82.5 ks,
respectively.
The LECS and MECS images are shown in Fig. 1.
G327.1-1.1 is located, in both images, near the field center, as a resolved peak
centered near RA =
and when the instrument configurations were
nominal.
The screened exposures in the LECS and MECS are 31.0 ks and 82.5 ks,
respectively.
The LECS and MECS images are shown in Fig. 1.
G327.1-1.1 is located, in both images, near the field center, as a resolved peak
centered near RA =
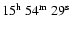 ,
Dec =
,
Dec =
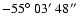 (J2000).
(J2000).
An unresolved peak not related to G327.1-1.1, located at position RA
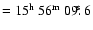 ,
Dec
,
Dec
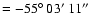 ,
with a hard power-law spectrum, is also
present in MECS2 data.
However it neither appears in LECS nor in MECS3 data, nor it is present in
existing catalogs (e.g. RASS).
Since the spectral response of MECS2 and MECS3 are similar, if this source were
real the only way to miss it in MECS3 data would be to have it right behind a
rib of the strongback: however only soft sources can be hidden completely in
this way; while ribs are transparent above 5 keV.
Of course it cannot be an effect of source variability, because the
integrations of the two MECS are virtually contemporaneous.
Moreover in a nearby archival BeppoSAX observation (Target: HD 141926, Obs. Code:
20309004), this source again appears in MECS2, while it does not in MECS3.
The conclusion we have reached is that the peak seen in MECS2 is a ghost
image.
It cannot be due to problems in the electronics, because it is also visible in
the archival MECS2 image, while tests on dark and bright earth exposure close
in time to our observation do not reveal anything abnormal.
The peak is presumably produced by a bright source located just outside the field of view (but that
has not been identified), and
therefore we have simply not considered it in the further analysis.
Anyway it does not seem to affect the data in the direction of G327.1-1.1.
We thank F. Fiore and G. Cusumano, of the BeppoSAX team, for their valuable advice
during the analysis of the nature of this source.
,
with a hard power-law spectrum, is also
present in MECS2 data.
However it neither appears in LECS nor in MECS3 data, nor it is present in
existing catalogs (e.g. RASS).
Since the spectral response of MECS2 and MECS3 are similar, if this source were
real the only way to miss it in MECS3 data would be to have it right behind a
rib of the strongback: however only soft sources can be hidden completely in
this way; while ribs are transparent above 5 keV.
Of course it cannot be an effect of source variability, because the
integrations of the two MECS are virtually contemporaneous.
Moreover in a nearby archival BeppoSAX observation (Target: HD 141926, Obs. Code:
20309004), this source again appears in MECS2, while it does not in MECS3.
The conclusion we have reached is that the peak seen in MECS2 is a ghost
image.
It cannot be due to problems in the electronics, because it is also visible in
the archival MECS2 image, while tests on dark and bright earth exposure close
in time to our observation do not reveal anything abnormal.
The peak is presumably produced by a bright source located just outside the field of view (but that
has not been identified), and
therefore we have simply not considered it in the further analysis.
Anyway it does not seem to affect the data in the direction of G327.1-1.1.
We thank F. Fiore and G. Cusumano, of the BeppoSAX team, for their valuable advice
during the analysis of the nature of this source.
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3891f1a.eps}\vspace{3mm}
\includegraphics[width=8.8cm]{h3891f1b.eps}\end{figure}](/articles/aa/full/2003/04/aah3891/Timg25.gif) |
Figure 1:
0.1 -2 keV LECS image (top) and 2 -10 keV MECS image
(bottom) of the region of G327.1-1.1. Pixel size is 64
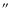 and
32
and
32
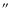 respectively, and a smoothing of 2 pixels has been
applied. The images are exposure, vignetting and background
corrected. LECS contours are at 0.7, 1.3 and
respectively, and a smoothing of 2 pixels has been
applied. The images are exposure, vignetting and background
corrected. LECS contours are at 0.7, 1.3 and
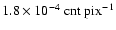 ,
while MECS contours are at 1/16, 1/8, 1/4
and 1/2 of the peak value ( ,
while MECS contours are at 1/16, 1/8, 1/4
and 1/2 of the peak value (
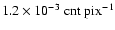 ). ). |
| Open with DEXTER |
The thermal and non-thermal components of G327.1-1.1 are only partially resolved by
BeppoSAX, and therefore an accurate analysis is required to separate them.
This analysis should take advantage of the differences in the spectra of
the (soft) thermal and (hard) non-thermal components, as well as of the
differences in their position and size.
We have performed spectral fits using different spatial and spectral
selections of the available photons, and combined the results.
In all cases we exclude photons with energies which are outside the ranges
0.1-8 keV for LECS and 1.6-10.5 keV for MECS.
Fittings have used, separately or in combination, the following two emission
components: a non-thermal
component, modelled as a power law with photon index 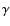 ,
and a thermal one, modelled as
due to ionized plasma hit by the shock wave ( MEKAL
model in XSPEC V11.0).
Reference abundances are from Anders & Grevesse (1989), while
the interstellar absorption has been modelled using the Morrison & McCammon (1983)
cross-sections.
The background was taken in a sector located to NE of G327.1-1.1, with radial
distances ranging from 10
,
and a thermal one, modelled as
due to ionized plasma hit by the shock wave ( MEKAL
model in XSPEC V11.0).
Reference abundances are from Anders & Grevesse (1989), while
the interstellar absorption has been modelled using the Morrison & McCammon (1983)
cross-sections.
The background was taken in a sector located to NE of G327.1-1.1, with radial
distances ranging from 10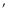 to 20
to 20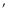 (an area reasonably free from point-like sources), and then corrected for vignetting and extraction areas.
(an area reasonably free from point-like sources), and then corrected for vignetting and extraction areas.
We have first extracted a spectrum from a circular region with
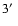 radius, centered on the X-ray peak position
(hereafter referred to as the
"plerion" region), with the aim of minimizing the contribution of the thermal
component.
For the spectral fitting we have generated an
"ad-hoc" response file which takes into account the source extension, that has
been estimated in the following way.
In the 2-10 keV MECS band the apparent size of
the source, as derived with a Gaussian fit, is
radius, centered on the X-ray peak position
(hereafter referred to as the
"plerion" region), with the aim of minimizing the contribution of the thermal
component.
For the spectral fitting we have generated an
"ad-hoc" response file which takes into account the source extension, that has
been estimated in the following way.
In the 2-10 keV MECS band the apparent size of
the source, as derived with a Gaussian fit, is
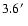 (FWHM),
while that of the MECS Point spread Function (PSF, obtained by a
similar fit to the archive observation of Cyg X-1) in the same energy range
is
(FWHM),
while that of the MECS Point spread Function (PSF, obtained by a
similar fit to the archive observation of Cyg X-1) in the same energy range
is
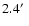 :
therefore the intrinsic size of the source can be estimated
as
:
therefore the intrinsic size of the source can be estimated
as
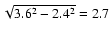
 (FWHM), with an uncertainty
(FWHM), with an uncertainty
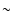 0.3
0.3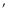 .
.
We have performed different fits (labelled as Fit A, B and C) to the spectrum
of the plerion region, whose results are reported in Table 1.
A pure power-law model using the LECS+MECS data (Fit A) provides a good
overall fit of the spectra in terms of 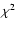 test, but
tends to underestimate the flux below 1 keV. The addition of a
thermal component is needed in order to have the spectra well fitted over the
whole LECS+MECS bandwidth (Fit B). It is worth noting that both the value of the
absorption and that of the power-law index are significantly different from the
values obtained with the pure power-law model. The results of Fit B are
confirmed by a pure power-law fit which uses only the 2-10 keV data of both
instruments (Fit C), where the contribution of the thermal component is minor.
Therefore we have decided to take the parameters of Fit B as our best guess
for the plerion.
test, but
tends to underestimate the flux below 1 keV. The addition of a
thermal component is needed in order to have the spectra well fitted over the
whole LECS+MECS bandwidth (Fit B). It is worth noting that both the value of the
absorption and that of the power-law index are significantly different from the
values obtained with the pure power-law model. The results of Fit B are
confirmed by a pure power-law fit which uses only the 2-10 keV data of both
instruments (Fit C), where the contribution of the thermal component is minor.
Therefore we have decided to take the parameters of Fit B as our best guess
for the plerion.
We have then performed a set of fits using a larger extraction region
(Fit D and E), that is
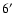 for MECS and
for MECS and
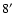 for LECS. The
aim of this selection is to include as much as possible the
contribution of the thermal component. The response has been generated
consistently, assuming a putative size for the shell, estimated using
the corrected LECS image in the 0.1-1 keV band (Fig. 4-top)
and applying the same procedure as that described for the plerionic
component: The measured, PSF and deconvolved size are respectively
for LECS. The
aim of this selection is to include as much as possible the
contribution of the thermal component. The response has been generated
consistently, assuming a putative size for the shell, estimated using
the corrected LECS image in the 0.1-1 keV band (Fig. 4-top)
and applying the same procedure as that described for the plerionic
component: The measured, PSF and deconvolved size are respectively
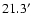 ,
,
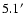 and
and
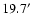 FWHM. The results of
these fits are also reported in Table 1. Again the
two-component fit (Fit E) is statistically to be preferred to the pure
power-law one (Fit D): the
FWHM. The results of
these fits are also reported in Table 1. Again the
two-component fit (Fit E) is statistically to be preferred to the pure
power-law one (Fit D): the 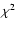 decrease between the two is
significant at the 99.9% confidence level. The two-component fit of this spectrum
is shown in Fig. 2, while the contour levels for the
determination of the temperature and interstellar absorption are
reported in Fig. 3. The contribution of the thermal
component to the observed spectrum is low. We have estimated that the
thermal contribution to the total absorbed 0.5-10 keV flux is
decrease between the two is
significant at the 99.9% confidence level. The two-component fit of this spectrum
is shown in Fig. 2, while the contour levels for the
determination of the temperature and interstellar absorption are
reported in Fig. 3. The contribution of the thermal
component to the observed spectrum is low. We have estimated that the
thermal contribution to the total absorbed 0.5-10 keV flux is  10%,
and decreases to 0.4% in the 2-10 keV band.
10%,
and decreases to 0.4% in the 2-10 keV band.
When compared with previous X-ray spectral analyses, we find a lower value for
the temperature and a higher value of 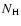 :
Seward et al. (1996) in fact derived
:
Seward et al. (1996) in fact derived
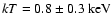 and
and
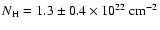 ,
while SWC gave
,
while SWC gave
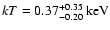 and
and
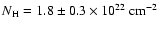 .
When the quoted uncertainties are taken into account, our results are still
marginally consistent with those of Seward et al. (1996) and SWC.
The discrepancy should be ascribed to differences in the
instrumental response of LECS (used here) and ROSAT PSPC (used both by SWC and
by Seward et al. (1996) for the soft band).
.
When the quoted uncertainties are taken into account, our results are still
marginally consistent with those of Seward et al. (1996) and SWC.
The discrepancy should be ascribed to differences in the
instrumental response of LECS (used here) and ROSAT PSPC (used both by SWC and
by Seward et al. (1996) for the soft band).
![\begin{figure}
\par\includegraphics[angle=-90,width=4.3cm,clip]{h3891f2a.ps}\hspace*{1mm}
\includegraphics[angle=-90,width=4.3cm,clip]{h3891f2b.ps} \end{figure}](/articles/aa/full/2003/04/aah3891/Timg43.gif) |
Figure 2:
Folded ( left) unfolded ( right) spectrum of the
of G327.1-1.1, with best-fit power-law + thermal models. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.2cm,clip]{h3891f3.ps} \end{figure}](/articles/aa/full/2003/04/aah3891/Timg44.gif) |
Figure 3:
Confidence (1-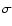 ,
2- ,
2-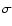 and 3-
and 3-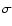 level)
contours in the
level)
contours in the
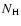 - -
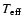 parameter plane
derived for the total fit (Fit E in Table 1)
to the LECS+MECS spectrum of G327.1-1.1.
parameter plane
derived for the total fit (Fit E in Table 1)
to the LECS+MECS spectrum of G327.1-1.1. |
| Open with DEXTER |
In order to further disentangle the image of the thermal component from
the total image, in a low-energy image we have subtracted the plerionic
component, by using the following approach. First, we have extracted
the MECS image in the 2-10 keV energy band, in which the
contribution of the thermal component is far below the one of the
plerion. Then we have convolved that image in order to simulate the
effect of the LECS PSF at 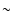 1 keV (we have found appropriate a
convolution with a Gaussian of 5
1 keV (we have found appropriate a
convolution with a Gaussian of 5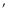 FWHM). Using the plerion
best-fit model (Fit B) reported in Table 1, we have scaled
its image in order to reproduce the LECS image of the plerion only at
0.1-1 keV. Finally, we have subtracted it from the original LECS
image of G327.1-1.1 in the 0.1-1 keV band. The result is shown in
Fig. 4.
FWHM). Using the plerion
best-fit model (Fit B) reported in Table 1, we have scaled
its image in order to reproduce the LECS image of the plerion only at
0.1-1 keV. Finally, we have subtracted it from the original LECS
image of G327.1-1.1 in the 0.1-1 keV band. The result is shown in
Fig. 4.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3891f4.eps} \end{figure}](/articles/aa/full/2003/04/aah3891/Timg45.gif) |
Figure 4:
0.1 -1 keV image of the thermal component obtained by
subtracting a scaled and smoothed MECS image from the total LECS
image in the same band. The 843 MHz total intensity radio contours
of Whiteoak & Green (1996) are overlaid (solid), as well as surface
brightness contours at 20%, 40%, 60% and 80% of the peak value.
The thermal emission extends beyond the plerion in the NE and SE
direction. |
| Open with DEXTER |
The image is composed of a large diffuse component located in the
eastern part of the radio shell and a small X-ray blob located near
the western rim. The center of the large diffuse component is located
at RA
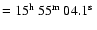 ,
Dec
,
Dec
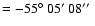 ,
and it is displaced by
,
and it is displaced by 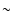
 from
the radio SNR center and by
from
the radio SNR center and by 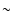
 from the plerion center.
The observed size of this component is
from the plerion center.
The observed size of this component is 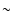
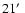 FWHM. An
interesting point is that the image of the thermal component does not
show a complete shell structure. It could be interpreted as partial
shell SNR, with a possible extension of the X-ray emission in the inner
region. The absence of a limb can be inferred also from a PSPC image
of the whole X-ray SNR, as obtained by Seward et al. (1996).
FWHM. An
interesting point is that the image of the thermal component does not
show a complete shell structure. It could be interpreted as partial
shell SNR, with a possible extension of the X-ray emission in the inner
region. The absence of a limb can be inferred also from a PSPC image
of the whole X-ray SNR, as obtained by Seward et al. (1996).
We have searched for pulsation in the events collected in the region of
the plerion defined above. We have found no pulsation at the 99%
confidence limit, with an upper limit at the same level of confidence
of 19.4% in the 0.1-256 Hz frequency range.
SWC have discussed a scenario in which the shell component of G327.1-1.1 is expanding adiabatically in a homogeneous medium, and have thoroughly used
for it the well known Sedov (1959) analytic solution.
In this way SWC obtained a self-consistent scenario according to
which the remnant is
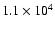 yr old and expands adiabatically in an ambient
medium with a density of
yr old and expands adiabatically in an ambient
medium with a density of
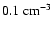 .
.
The two substantially new facts with respect to the starting point of their
analysis are that the X-ray structure cannot now be interpreted as a complete
shell, and that the effective temperature turned out
to be lower than previously determined.
Moreover, with respect to SWC we use a slightly higher estimate of
the average diameter of the SNR, namely 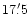 , as derived from the size of
the radio shell (Whiteoak & Green 1996).
, as derived from the size of
the radio shell (Whiteoak & Green 1996).
Let us first re-evaluate some parameters of G327.1-1.1 assuming a Sedov (1959)
scenario.
In this way we derive how the difference from SWC in the starting point is going to
affect the result.
The basic relations for the effective temperature (
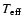 ), the age of the SNR
(
), the age of the SNR
(
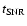 ), the emission measure parameter (
), the emission measure parameter (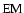 )
defined as
)
defined as
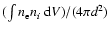 ,
the radius of the shock (
,
the radius of the shock (
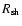 )
and the total swept mass (
)
and the total swept mass (
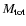 )
are respectively:
)
are respectively:
where
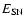 is the supernova energy,
is the supernova energy,
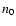 is the atomic number density in the
ambient medium (with standard abundances;
is the atomic number density in the
ambient medium (with standard abundances;
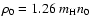 ), d indicates the SNR distance,
), d indicates the SNR distance,
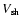 and
and
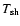 are respectively the shock velocity and the post-shock
temperature: the shock has been modelled assuming it to be a strong
non-radiative shock with temperature equilibration between ions and electrons.
are respectively the shock velocity and the post-shock
temperature: the shock has been modelled assuming it to be a strong
non-radiative shock with temperature equilibration between ions and electrons.
Using the information on G327.1-1.1 angular size, the above relations translate into
the following ones:
| |
|
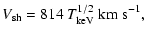 |
(6) |
| |
|
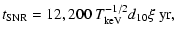 |
(7) |
| |
|
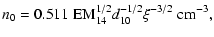 |
(8) |
| |
|
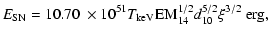 |
(9) |
| |
|
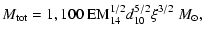 |
(10) |
| |
|
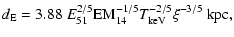 |
(11) |
which directly link physical and observable quantities.
In these equations
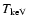 is the effective temperature, in keV;
is the effective temperature, in keV;
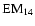 is the emission measure parameter, in units of
is the emission measure parameter, in units of
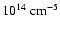 ;
d10 is the G327.1-1.1 distance, in units of 10 kpc; and E51 is the
supernova energy, when assumed, in units of
;
d10 is the G327.1-1.1 distance, in units of 10 kpc; and E51 is the
supernova energy, when assumed, in units of
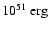 .
The quantity
.
The quantity 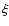 indicates the SNR angular size, in units of the G327.1-1.1 one.
The physical quantities as derived from our spectral fit in Sedov approximation
are listed in the first column of Table 2.
It is apparent that, while
the swept mass is much larger than any reasonable
stellar mass, the SNR shock is slow, so that the resulting supernova
energy is rather normal for any reasonable distance value.
indicates the SNR angular size, in units of the G327.1-1.1 one.
The physical quantities as derived from our spectral fit in Sedov approximation
are listed in the first column of Table 2.
It is apparent that, while
the swept mass is much larger than any reasonable
stellar mass, the SNR shock is slow, so that the resulting supernova
energy is rather normal for any reasonable distance value.
In other terms, assuming the standard value
of
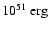 for the supernova energy, we derive a distance between 4.8 and 16.2 kpc, which is in agreement with published distance
estimates, ranging from 6.5 kpc (Seward et al. 1996) to 9 kpc (SWC),
as well with the distance estimated from the
for the supernova energy, we derive a distance between 4.8 and 16.2 kpc, which is in agreement with published distance
estimates, ranging from 6.5 kpc (Seward et al. 1996) to 9 kpc (SWC),
as well with the distance estimated from the 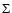 -D empirical relation
(Case & Bhattacharya 1998).
The average 1 GHz surface brightness of the G327.1-1.1 shell component is
-D empirical relation
(Case & Bhattacharya 1998).
The average 1 GHz surface brightness of the G327.1-1.1 shell component is
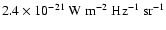 (5.6 Jy at 843 GHz, with a
spectral index
(5.6 Jy at 843 GHz, with a
spectral index 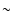 -0.4; SWC): this translates into a shell diameter of
-0.4; SWC): this translates into a shell diameter of
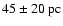 ,
and then into a distance estimate of
,
and then into a distance estimate of 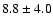 kpc.
kpc.
To summarize the results of our Sedov fit compared to those of SWC (using the
same assumed distance of 9 kpc), we find a SNR 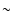 2.4 times older and with
2.4 times older and with
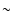 4.7 times more energy, expanding in a medium
4.7 times more energy, expanding in a medium 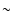 3.9 times denser.
The swept mass is 12.5 times larger than that derived by SWC.
3.9 times denser.
The swept mass is 12.5 times larger than that derived by SWC.
The last row in Table 2 gives the efficiency in radiative
cooling, defined as the ratio between the SNR age and the present cooling time
right behind the shock, which can be expressed in terms of the observed
quantities as:
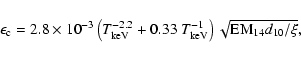 |
(12) |
where for the cooling coefficient we have used the formula
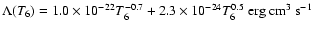 ,
with T6 in units of
,
with T6 in units of
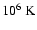 (McCray 1987).
A value for
(McCray 1987).
A value for
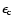 much smaller than unity is required in order to test the
adiabaticity condition, as required by the Sedov model.
However Fig. 5 shows that,
since
much smaller than unity is required in order to test the
adiabaticity condition, as required by the Sedov model.
However Fig. 5 shows that,
since
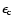 is strongly decreasing with T, fits
giving low values for
is strongly decreasing with T, fits
giving low values for
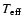 also imply relevant radiative losses.
also imply relevant radiative losses.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3891f5.ps}\end{figure}](/articles/aa/full/2003/04/aah3891/Timg96.gif) |
Figure 5:
Efficiency of radiative cooling (
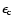 ,
scaled with
d101/2), evaluated using Sedov solutions.
The solid straight lines show levels of the radiative
efficiency in the ,
scaled with
d101/2), evaluated using Sedov solutions.
The solid straight lines show levels of the radiative
efficiency in the
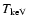 - -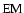 plane.
The best fit solution (
plane.
The best fit solution (
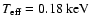 ; ;
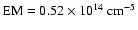 )
is
indicated by a cross.
The confidence contours are at 1- )
is
indicated by a cross.
The confidence contours are at 1-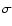 ,
2- ,
2-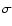 and 3-
and 3-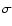 level
(computed from Fit E in Table 1).
level
(computed from Fit E in Table 1). |
| Open with DEXTER |
The possible extension of the thermal X-ray component to the inner
shell regions, together with the non-negligible radiative cooling,
leads us to consider scenarios alternative to the Sedov one for the
evolution of G327.1-1.1.
Let us first examine the WL model, describing (by a class of self-similar
solutions) a wide range of conditions under which a SNR may expand in a cloudy
interstellar medium.
In this scenario, a delayed evaporation of the clouds causes
the central density to increase with respect to the pure Sedov case.
This class of solutions depends on two parameters: the mass fraction in clouds
(C) and the cloud evaporation time scaled with the SNR age (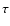 ).
The solutions converge to the Sedov case when the mass deposition is small,
either because little mass is contained in the clouds (
).
The solutions converge to the Sedov case when the mass deposition is small,
either because little mass is contained in the clouds (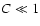 )
or because
the clouds
have anyway released little mass during the SNR lifetime (
)
or because
the clouds
have anyway released little mass during the SNR lifetime (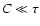 ).
Here we assume that the mass in clouds is large (
).
Here we assume that the mass in clouds is large (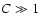 ), but the evaporation
time is long (
), but the evaporation
time is long (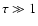 ): in this case the solutions form a one-parameter
class, depending on just
): in this case the solutions form a one-parameter
class, depending on just 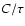 (these solutions are approximately valid also
for
(these solutions are approximately valid also
for
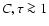 ).
).
We have qualitatively compared the radial profile of the thermal
component (using the center coordinates reported in Sect. 3.2) with the
WL predicted profiles for various value of the 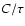 parameter. We
found a reasonable matching, considering the uncertainties involved,
for
parameter. We
found a reasonable matching, considering the uncertainties involved,
for 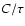 in the range between 2.5 and 4.0. These uncertainties
originate not only from the faintness of the source, but also from
deviations from the assumed spherical symmetry as well as from a non
perfect subtraction of the plerionic component: all of these effects,
with the present data, are even difficult to quantify. Therefore,
under the assumption that WL models are appropriate to model the
G327.1-1.1 thermal component, we can estimate
in the range between 2.5 and 4.0. These uncertainties
originate not only from the faintness of the source, but also from
deviations from the assumed spherical symmetry as well as from a non
perfect subtraction of the plerionic component: all of these effects,
with the present data, are even difficult to quantify. Therefore,
under the assumption that WL models are appropriate to model the
G327.1-1.1 thermal component, we can estimate
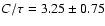 .
By using
the results tabulated by WL we derive which correction factors must be
applied to the Sedov estimates.
.
By using
the results tabulated by WL we derive which correction factors must be
applied to the Sedov estimates.
For instance
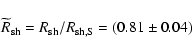 |
(13) |
shows how much the shock radius shrinks with respect to the Sedov case (for
fixed
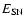 ,
,
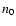 and
and
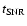 ): with reference to the quantity K, defined in
Eq. (7) of WL, the relation
): with reference to the quantity K, defined in
Eq. (7) of WL, the relation
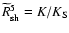 holds.
Moreover the equations
holds.
Moreover the equations
refer to comparisons with the Sedov solution keeping
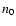 and
and
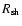 constant. The above scaling factors are evaluated by interpolating data from
Table 6 of WL. In the above expressions we have used the index
constant. The above scaling factors are evaluated by interpolating data from
Table 6 of WL. In the above expressions we have used the index
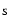 to
indicate the values in the Sedov solution.
to
indicate the values in the Sedov solution.
Therefore the corrections required to derive, for the WL model, the relations
equivalent to Eqs. (6)-(11) for the associated Sedov case are:
| |
|
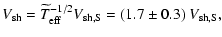 |
(17) |
| |
|
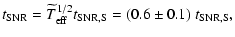 |
(18) |
| |
|
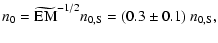 |
(19) |
| |
|
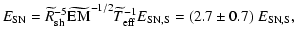 |
(20) |
| |
|
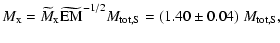 |
(21) |
| |
|
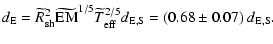 |
(22) |
It should be noted that here by "associated'' WL and Sedov solutions we
indicate those showing the same observed properties (i.e. size,
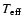 and
and
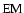 ).
).
The values of the parameters derived with the WL model are also given in
the second column of Table 2.
Compared to the pure Sedov case, now the ambient
(intercloud) density results to be lower, while the shock velocity is higher
(which also makes the SNR younger). The distance estimate based on the
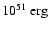 energy requirement now gives
energy requirement now gives 
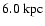 ,
still
compatible with the lowest distance estimates for this source
(Seward et al. 1996). The cooling efficiency
,
still
compatible with the lowest distance estimates for this source
(Seward et al. 1996). The cooling efficiency
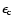 (in the
intercloud medium) can be evaluated from Eq. (12), by substituting
(in the
intercloud medium) can be evaluated from Eq. (12), by substituting
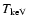 with
with
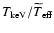 and
and
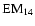 with
with
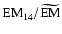 :
it results much smaller (
:
it results much smaller (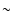
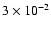 )
than in the Sedov case.
)
than in the Sedov case.
On the basis of our analysis, a WL model fits the average radial profile of the
Thermal
remnant better than the Sedov model.
Moreover the WL model gives reasonable values of the SNR parameters, even
though: 1. it leads to a rather small SNR age, with problems for the offset of
the associated neutron star (see below); 2. for a standard SNR energy, it leads
to a distance somehow smaller than what estimated by other methods.
A further scenario which may account for thermal X-ray from inner regions
is that of a SNR in radiative phase (with in addition possible
effects, like thermal conduction and flux saturation). A common property of
non-radiative spherical shocks expanding in a homogeneous medium is the
presence in the inner region of a hot and thin medium, which therefore behaves
as a very low efficiency emitter, and forms the typical hollow sphere
emission pattern of shell-type SNRs. In a cloud evaporation model (as WL, see
above), this region is filled with material originally stored in small clouds.
But since inside the shell the pressure equilibrium is roughly maintained, it
would be sufficient to cool down this gas (even without adding further material)
in order to make it denser.
Unfortunately no self-similar solution is known for radiative shell-type SNRs,
and therefore a quantitative description of this class of objects requires to
develop numerical models, which are beyond the scope of this work. Models of
this kind have been already developed, for instance for W44, by various
authors (Harrus et al. 1997; Cox et al. 1999; Shelton et al. 1999). Here let us simply compare the basic
parameters of G327.1-1.1 and W44 to infer their relative evolutive conditions,
under the assumption that both have reached the radiative phase.
Table 3 lists, for both remnants, some basic parameters, either
observed or derived: in the latter case a Sedov model has been used for the
derivation. Thus if these SNRs are no longer in Sedov phase, the listed values
are
inaccurate (even though, simply for dimensional arguments, not too far from the
correct values).
For instance the absolute ages, as reported in Table 3, may be
understimated since in radiative phase the SNRs must have decelerated with
respect to the Sedov phase. We know this is the case for W44, where the Sedov
estimate is about half of what derived from more detailed NEI models, as
well as half of the pulsar spin-down age (Harrus et al. 1997).
If also G327.1-1.1 is in radiative phase, its true age may be substantially larger
than 29 000 yr (as from Table 3). At any rate, if we exclude the WL scenario, this SNR must be much
older than originally estimated by SWC (11 000 yr). An implication would be that the
lower limit on the velocity of the compact object (>600 km s-1, as from SWC,
in order to account for the displacement of the compact source from the SNR
center)
can be lowered by a factor 3 or even more: therefore in this case there is
no need for an anomalous pulsar velocity.
Although some values listed in Table 3 may be inaccurate in an
absolute sense, we are confident that they may still be used for a comparative
analysis
of the two SNRs. For instance G327.1-1.1 looks older than W44; it also expands
with a lower velocity, and in a slightly thinner medium. Moreover, as shown in
the last line of the table, the cooling efficiency in G327.1-1.1 is much
higher than in
W44, and this fact strengthens the idea that, if a radiative scenario results
to be appropriate
to the case of W44, it should be even more reasonable for G327.1-1.1.
Although expanding in a higher ambient density,
G327.1-1.1 radio shell is about 3 times fainter than W44: also this difference
could be a consequence of its age.
The fact that high resolution maps of the radio continuum from W44 present a
strongly filamented pattern has been taken (Cox et al. 1999) as evidence for
the remnant being in radiative phase.
If this is the case, higher resolution radio maps of G327.1-1.1, able to test the
presence of filamentation, could be valuable to shed light on the evolutive
phase of this remnant.
Like W44, G327.1-1.1 shows both a shell and a plerionic component in
radio, while a thermal filled-centre and a non-thermal component in X rays: the
main difference is that in G327.1-1.1 the plerionic component is more prominent than
in W44.
Another similarity between W44 and G327.1-1.1 is the
displacement of the plerionic component from the shell centroid, as well as
its bow shock shape.
An analysis of the integrated spectrum of the plerionic component can be
carried on in a very similar way as already done by SWC. Our estimate of the
0.5-10 keV luminosity of the plerion (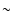
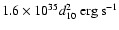 )
is
about 0.5 times that estimated by SWC; moreover the age we find is at least a
factor 2.4 larger, and all this affects the derivation of pulsar and nebular
parameters.
)
is
about 0.5 times that estimated by SWC; moreover the age we find is at least a
factor 2.4 larger, and all this affects the derivation of pulsar and nebular
parameters.
By applying an empirical relation (Seward & Wang 1988),
SWC used the X-ray nebular luminosity (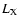 )
to infer the pulsar spin down
power (
)
to infer the pulsar spin down
power (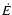 ), which for a magnetic dipole braking is proportional to
), which for a magnetic dipole braking is proportional to
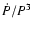 .
The age estimate (
.
The age estimate (
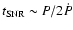 )
is the other relation which allows
one separating the pulsar timing parameters P and
)
is the other relation which allows
one separating the pulsar timing parameters P and 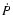 ,
and to estimate
also the pulsar surface field: SWC report
,
and to estimate
also the pulsar surface field: SWC report
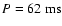 and
and
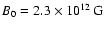 .
Since by this procedure
.
Since by this procedure
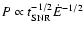 ,
while
,
while
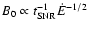 ,
our revised values lead
to a somehow shorter period (<
,
our revised values lead
to a somehow shorter period (<
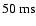 )
and to a lower surface field
(<
)
and to a lower surface field
(<
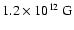 ).
The presence of a faster, and lower-B pulsar compared to that in W44 is in fact
required by the presence of a reasonably bright, although aged, plerion.
).
The presence of a faster, and lower-B pulsar compared to that in W44 is in fact
required by the presence of a reasonably bright, although aged, plerion.
SWC also used a spectral break in the nebular spectrum (at about
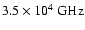 )
to infer a nebular field
)
to infer a nebular field
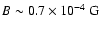 .
Since the
field derived in this way is
.
Since the
field derived in this way is
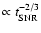 ,
we infer instead a nebular field
,
we infer instead a nebular field 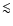
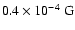 .
For a radius of
.
For a radius of 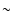
 for the (radio) plerion, the total magnetic energy is
for the (radio) plerion, the total magnetic energy is
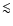
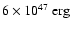 .
The plerion is then slightly underpressured (
.
The plerion is then slightly underpressured (
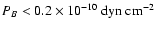 ),
compared to the thermal remnant, if in Sedov or WL regime; while a better
pressure balance may be attained if the shell is in radiative expansion.
Anyway the uncertainties involved in these estimates are too large to take
this as a strong argument in favour of a radiative shell.
),
compared to the thermal remnant, if in Sedov or WL regime; while a better
pressure balance may be attained if the shell is in radiative expansion.
Anyway the uncertainties involved in these estimates are too large to take
this as a strong argument in favour of a radiative shell.
We have used a BeppoSAX X-ray observation of G327.1-1.1 to study the origin of
its X-ray emission, with particular emphasis on its thermal component,
which has not been studied in detail in the literature, because of
its superposition with the bright non-thermal plerion. We fitted the
plerion and the total SNR spectrum with a combination of thermal
and non-thermal models, finding an X-ray temperature
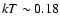 keV for the hot plasma and a power-law photon index
keV for the hot plasma and a power-law photon index 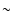 2.2 for
the plerion. Using the flux derived for the non-thermal plerion, we
have subtracted the non-thermal component from the total 0.1-1 keV SNR
image, thus obtaining for the first time an image of the thermal hot
plasma.
2.2 for
the plerion. Using the flux derived for the non-thermal plerion, we
have subtracted the non-thermal component from the total 0.1-1 keV SNR
image, thus obtaining for the first time an image of the thermal hot
plasma.
The emission from the plasma is not
confined to a bright shell, and shows possible emission for inner regions.
We have then examined for this SNR also scenarios different from the Sedov one.
The model of
SNR expansion in a medium with evaporative clouds developed by
White & Long (1991) may account for the observations,
although it may imply an age
and distance for this object which are somehow smaller than expected.
We have
shown that a radiative expansion with strong central cooling may also
describe the data. We have derived and compared the remnant
characteristic parameters for the various scenarios, either Sedov, or
White & Long (1991), or
radiative model, showing that the last model implies a very long age
(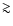
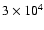 yr): in this case the observed offset of the associated
pulsar may be accounted for without requiring a too high spatial
velocity for it.
yr): in this case the observed offset of the associated
pulsar may be accounted for without requiring a too high spatial
velocity for it.
A comparison with W44, a remnant for which there is also evidence of
radiative expansion, indicates that G327.1-1.1 may be substantially more
evolved than W44. Future high sensitivity X-ray and radio observations
are strongly encouraged, because they may dissipate any doubt about
the evolutionary stage of this object and in particular of its shell.
Finally, we have also revised the estimate of the pulsar and nebular
magnetic field.
Acknowledgements
F. Bocchino acknowledges partial support from MIUR and ASI.
This work has been partly supported by MIUR under Grant Cofin2001-02-10.
-
Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197
In the text
NASA ADS
-
Boella, G., Butler, R. C., Perola, G. C., et al. 1997, A&AS, 122, 299
In the text
NASA ADS
-
Case, G. L., & Bhattacharya, D. 1998, ApJ, 504, 761
In the text
NASA ADS
-
Cox, D. P., Shelton, R. L., Maciejewski, W., et al. 1999, ApJ, 524, 179
In the text
NASA ADS
-
Frontera, F., Costa, E., dal Fiume, D., et al. 1997, A&AS, 122, 357
In the text
NASA ADS
-
Harrus, I. M., Hughes, J. P., Singh, K. P., Koyama, K., & Asaoka, I. 1997, ApJ, 488, 781
In the text
NASA ADS
-
Helfand, D. J., & Becker, R. H. 1987, ApJ, 314, 203
In the text
NASA ADS
-
Manzo, G., Giarrusso, S., Santangelo, A., et al. 1997, A&AS, 122, 341
In the text
NASA ADS
-
McCray, R. A. 1987, in Spectroscopy of Astrophysical Plasmas, ed. A. Dalgarno, & D. Layzer (Cambridge University Press), 255
In the text
-
Morrison, R., & McCammon, D. 1983, ApJ, 270, 119
In the text
NASA ADS
-
Parmar, A. N., Martin, D. D. E., Bavdaz, M., et al. 1997, A&AS, 122, 309
In the text
NASA ADS
-
Petruk, O. 2001, A&A, 371, 267
In the text
NASA ADS
-
Rho, J., Petre, R., Schlegel, E. M., & Hester, J. J. 1994, ApJ, 430, 757
In the text
NASA ADS
-
Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press)
In the text
-
Seward, F. D., Kearns, K. E., & Rhode, K. L. 1996, ApJ, 471, 887
In the text
NASA ADS
-
Seward, F. D., & Wang, Z. 1988, ApJ, 332, 199
In the text
NASA ADS
-
Shelton, R. L., Cox, D. P., Maciejewski, W., et al. 1999, ApJ, 524, 192
In the text
NASA ADS
-
Sun, M., Wang, Z., & Chen, Y. 1999, ApJ, 511, 274
In the text
NASA ADS
-
White, R. L., & Long, K. S. 1991, ApJ, 373, 543
In the text
NASA ADS
-
Whiteoak, J. B. Z., & Green, A. J. 1996, A&AS, 118, 329
In the text
NASA ADS
Copyright ESO 2003
![\begin{figure}
\par\includegraphics[width=8.8cm]{h3891f1a.eps}\vspace{3mm}
\includegraphics[width=8.8cm]{h3891f1b.eps}\end{figure}](/articles/aa/full/2003/04/aah3891/Timg25.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=4.3cm,clip]{h3891f2a.ps}\hspace*{1mm}
\includegraphics[angle=-90,width=4.3cm,clip]{h3891f2b.ps} \end{figure}](/articles/aa/full/2003/04/aah3891/Timg43.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.2cm,clip]{h3891f3.ps} \end{figure}](/articles/aa/full/2003/04/aah3891/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3891f4.eps} \end{figure}](/articles/aa/full/2003/04/aah3891/Timg45.gif)
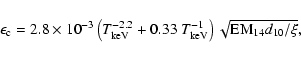
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3891f5.ps}\end{figure}](/articles/aa/full/2003/04/aah3891/Timg96.gif)