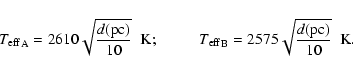Up: The 0.4- eclipsing binary Cancri
4 Absolute dimensions and effective temperatures
The absolute dimensions of the CU Cnc components can be readily determined
by combining the photometric parameters in Table 3 with the
spectroscopic solution from D99. When doing so, we obtain the physical
properties listed in Table 4.
The absolute value of the effective temperature for eclipsing
binaries cannot be determined from the light curves alone and independent
methods must be used. Temperature determination is usually quite
problematic when one has to deal with very cool stars such as CU Cnc. Two
independent approaches present themselves to estimate the effective
temperature of CU Cnc: one based on photometric calibrations and one based
on the known absolute dimensions and distance.
Synthetic colors, which are the base of photometric calibrations, are
computed by modelling the stellar atmospheres. Albeit some discrepancies
remain, M-star model atmospheres have made significant progress over the
past decade (Allard et al. 1997). Line opacities from a large
number of molecular species are now included in the calculations and
substantial improvements have been made in the input physics, particularly
the equation of state. For cool stars, the infrared colors are especially
suited to estimate the effective temperature because most of the stellar
flux is emitted in that wavelength range. Thus, we collected from the
literature the available magnitudes and colors for CU Cnc, which are
listed in Table 5. Simple linear transformations were applied
to refer the observed magnitudes and colors to the photometric systems
most widely used.
The magnitudes and color indices in Table 5 correspond to the
combined light of the two components of CU Cnc. Since the effective
temperatures of the two components are very similar, it is justified to
use the joint color indices as those representing the "mean'' component
of CU Cnc. To estimate the mean effective temperature we employed a number
of modern photometric calibrations. We assumed no interstellar reddening
in our calculations as expected for a system that lies less than 20 pc
away. The resulting temperatures, together with the references, atmosphere
model names, and comments, are presented in Table 6. Most of
the calibrations are based upon synthetic colors and model atmosphere
calculations, except for Leggett (1992), who provides an empirical
calibration. There is remarkably good agreement between all the
temperature estimates. A plain average of the independent values (i.e.,
excluding one of the redundant temperatures from the BaSeL model) yields
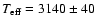 K. The formal error, however, does not reflect any
possible systematics that could be present in the calibration. We have
thus adopted a more realistic error value of
K. The formal error, however, does not reflect any
possible systematics that could be present in the calibration. We have
thus adopted a more realistic error value of
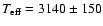 K
based on the results of Leggett et al. (1996).
K
based on the results of Leggett et al. (1996).
As mentioned above, there is an alternative approach to compute the
temperature of the components based on the method described in Ribas et al. (1998). This is a simple method that relates the observed
radius and luminosity with the temperature. In the case of CU Cnc, the
absolute radii of the components are given in Table 4. The
empirical luminosities were computed from the apparent magnitudes, the
parallax in the Hipparcos catalogue (ESA 1997) and a bolometric
correction. The latter is especially delicate because bolometric
correction calibrations are known to be the source of systematic errors.
To minimise these, we used the bolometric correction in the K band,
which was computed from the models of Allard et al. (2000) and
resulted in
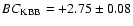 mag. This leads to an
apparent bolometric luminosity of
mag. This leads to an
apparent bolometric luminosity of
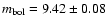 .
From the
luminosity ratio, the individual bolometric magnitudes can be computed and
we find
.
From the
luminosity ratio, the individual bolometric magnitudes can be computed and
we find
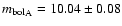 and
and
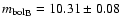 .
The absolute bolometric magnitudes follow from
introducing the Hipparcos distance:
.
The absolute bolometric magnitudes follow from
introducing the Hipparcos distance:
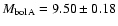 and
and
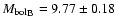 .
The effective temperature of each
component can be computed in a straightforward manner and we obtain
.
The effective temperature of each
component can be computed in a straightforward manner and we obtain
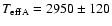 K and
K and
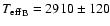 K.
K.
The agreement with the photometric determinations described above is not
perfect but nevertheless fairly good given the uncertainties. The values
agree within one sigma of their respective error bars. However, a caveat
is due at this point. As it turns out, there are reasonable concerns about
the accuracy of the Hipparcos parallax, even taking into account its
relatively large error (see Table 4). CU Cnc is a faint
object near the threshold for detection by Hipparcos. Thus, the individual
transit data are of poor quality. A reanalysis of the transit data
(considering also the visual component) has not provided any better
results (Arenou 1999, priv. comm.). As a reference, we have computed the
temperature of CU Cnc as a function of the distance![[*]](/icons/foot_motif.gif) :
:
Given the concerns with the Hipparcos distance raised above, we prefer to
adopt the temperatures derived from photometric calibrations. The final
adopted individual temperatures for CU Cnc (computed from the average
temperature and the temperature ratio derived from the light curves) are
listed in Table 4 along with their associated errors. Also
included in Table 4 are the absolute magnitudes of the
components in the V band, which have been computed from the parallax
listed in the Hipparcos catalogue. Note that an empirical determination of
the bolometric correction for each component follows from the comparison
of the V-band absolute magnitude with the bolometric magnitudes
(resulting from the radii, effective temperatures and
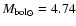 ).
).


Up: The 0.4- eclipsing binary Cancri
Copyright ESO 2003