A&A 398, 229-237 (2003)
DOI: 10.1051/0004-6361:20021601

The IR-colour-mass-loss relation of carbon-rich, dust-driven superwinds and a synthetic ($\vec J$-$\vec K$, $M_{\bf Bol}$) diagram

K.-P. Schröder ^1,2 - A. Wachter ^1,2 - J. M. Winters ^3,4

1 - Astronomy Centre, CPES, University of Sussex, Falmer, Brighton BN1 9QJ, UK
2 - Zentrum f. Astron. u. Astrophys., Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
3 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
4 - LERMA, FRE-K2460, Observatoire de Paris, 61 avenue de l'Observatoire, 75014 Paris, France

Received 19 June 2002 / Accepted 4 November 2002

Abstract
We derive relations between mass-loss rates and IR-colours (J-K, H-K, K-L, L-M and K-[12]) for the carbon-rich, dust-driven stellar winds of extreme tip-AGB objects by applying a maximum-likelihood procedure to a representative set of 50 self-consistent, pulsating wind models. The J-K index shows the largest mass-loss related IR excess, which is consistent with observations. All synthetic IR-colours depend, in addition, on the luminosity of the individual model star. Consequently, the superwind mass-loss rates may be determined from observation by $\log{\dot{M}} = -8.20 + 0.156$ (J-K) $- 0.463~{M_{\rm Bol}}$, for J-K $\ga 4$. As a case study for the interpretation of IR photometric data, we quantify the collective and individual tip-AGB mass-loss of the solar neighbourhood stellar population by means of a matching synthetic stellar sample, its IR properties and its present-day mass-loss distribution. The synthetic stars are generated on a grid of evolution tracks with a consistent mass-loss description (see Schröder et al. 1999; Wachter et al. 2002) and an IMF and SFR found in the local stellar population (Schröder & Sedlmayr 2001). The display of the tip-AGB stars in a (J-K, $M_{\rm Bol}$) diagram could be compared directly with observations once appropriate data become available. On a basis of 1.4 million stars brighter than M_V = 4.0, our synthetic present-day sample includes 5067 giant stars with B-V > 1.4, and the collective mass-loss rate is 5.0 $\times$ $10^{-4}~M_{\odot}$ yr^-1. There are 20 carbon-rich supergiants with an IR excess of J-K > 4.0 and a mass-loss rate well in excess of $10^{-6}~M_{\odot}$ yr^-1, including 10 dust-enshrouded, extreme tip-AGB stars with J-K > 6.0, seen in their short-lived ($\approx$30 000 yrs) superwind phase with $\dot{M} > 10^{-5}~M_{\odot}$ yr^-1. They produce about 50% of the collective mass-loss of the whole sample.

Key words: stars: carbon - stars: circumstellar matter - stars: evolution - stars: late-type - stars: mass-loss - infrared: stars

1 Introduction

Moderate-mass stars (i.e., according to Schröder et al. 1999, from $M_i \ga 1.3~M_{\odot}$, and up to $8~M_{\odot}$), when arriving on the tip-AGB, develop dust-driven, cool winds with mass-loss rates in excess of $10^{-5}~M_{\odot}$ yr^-1 (often referred to as "superwinds'', see Renzini 1981). Once a galaxy is several billion years old (the evolution time-scale of most moderate mass stars), these very cool and luminous giants make a significant contribution to the galactic mass-injection rate. They become strongly enshrouded in their dust-forming circumstellar envelopes, and IR observations are required to detect them with sufficient sensitivity. The importance of the tip-AGB for the galactic mass-recycling process and the chemical evolution has long been fully recognized and is reflected in the large observational and theoretical progress made in the past 2 decades (see the substantial review by Habing 1996).

Still, it is not possible to account for the dust-enshrouded tip-AGB stars of the solar neighbourhood in an absolute way by observations alone, see e.g. van Loon (2000). Rather, any mass-loss assessment of individual sources usually involves a parameterized radiative transfer code and depends on the model assumptions made (e.g. van Loon et al. 1999). Unfortunately, galactic distances and luminosities are often mere estimates since there are no objects of this kind near enough to yield precise Hipparcos parallax measurements. Rather, the superwind-phase is so short-lived that a very large volume is required to find a reasonable number of these extreme tip-AGB stars. This has motivated the recent deep photometric IR survey DENIS, by which large numbers of tip-AGB stars have been observed at the known distances of the Magellanic clouds (see Cioni et al. 2001). They form very large samples which are complete within their space volume and luminosity threshold, but their sub-solar metallicity must be accounted for. Consequently, direct and quantitative relations between the mass-loss rate and the observed IR colours, ideally for a range of solar and sub-solar metallicities, are most desirable.

For a small sample of about 40 well observed sources in the solar neighborhood, tight (semi-)empirical relations between the individual mass loss rate and near infrared color indices (e.g., J-K) have indeed been found by Le Bertre (1997) for carbon stars, and by Le Bertre & Winters (1998) for oxygen-rich Mira variables. These relations have been derived by a phase-dependent spectral modeling and, in principle, allow to determine the mass loss rate from a suitable near infrared color index alone, independent of the distance to the source. Of course, these relations depend on the assumptions made in the spectral modeling (e.g., the dust-to-gas ratio is assumed to be constant), and they should be confirmed on a larger sample of well observed sources (i.e. a near infrared monitoring over several pulsation periods is required for this approach.)

On the other hand, a quantitative description of individual tip-AGB stars and their mass-loss is also possible by a theoretical and computational approach, independent of any observation: Schröder et al. (1999) combined a theoretical mass-loss description (Arndt et al. 1997) with actual stellar models obtained from a fast and well tested evolution code. The theoretical mass-loss rates are based on a larger number of sophisticated numerical models of a pulsating, dust-driven cool wind. These wind models, which describe the time-dependent dust-formation, radiation transport and radiative acceleration in a self-consistent way, have been developed over the past 10 years by the Sedlmayr group. Their complex treatment of dust-driven winds has been described by a number of papers, e.g.: Fleischer et al. (1992), Sedlmayr (1994), Sedlmayr & Winters (1997), Winters et al. (2000b).

The resulting mass-loss rate - colour relations are in agreement with the (semi-)empirical relations within about a factor of 2 for the mass-loss (Winters et al. 2000b). However, the theoretical relations, obtained from an unselected set of about 150 models, show a much larger scatter than the (semi-)empirical ones (obtained from about 20 sources), which is mainly induced by the large parameter range covered by the model grid. The most typical outflow velocities for extreme tip-AGB objects (Habing 1996) of 10 to 15 km s^-1 can be matched well by the wind models, see a case study of Winters et al. (2000a) on IRC+10216. The models used here have $v_{\rm end}$ values which mostly fall in the range of 8 to 22 km s^-1 (see Table 1). In addition, we used some models with a large C:O abundance ratio of $\epsilon_{\rm C}$/ $\epsilon_{\rm O} = 1.8$, which produce higher outflow velocities but, in any case, normal mass-loss rates (see the discussion in Winters et al. 2000b).

From the work of Schröder et al. (1999), the following picture emerges for the evolution of C-rich mass-loss on the tip-AGB: Only stars with an initial mass M_i of more than 1.3 $M_{\odot}$ can become bright enough on the tip AGB to exceed the Eddington-type, critical luminosity $L_{\rm c}$ for a stable, C-rich, dust-driven wind. To account for the moderate mass-loss of AGB (and RGB) stars with luminosities lower than $L_{\rm c}$(and warmer photospheres), we use an empirically calibrated mass-loss relation, mainly based on the Reimers equation (for details, see Schröder et al. 1999). This RGB and earlier AGB mass-loss, as well as the empirically adjusted overshoot and mixing parameters (Schröder et al. 1997) determine the mass of the H-rich stellar envelope of the tip-AGB star. Once that star evolves beyond $L_{\rm c}$, then with (mostly) effective temperature $T_{\rm eff} \la 3200$ K, an increasingly strong, dust-driven superwind depletes the envelope mass of the giant as both $T_{\rm eff}$ and gravity g decrease further, until the stellar core comes near to exposure.

The superwind mass loss evolves in a consistent interaction with the main stellar properties (i.e., $T_{\rm eff}$, L_* and M_*). But the basic superwind time scale depends only on the ratio of the remaining mass of the H-rich stellar envelope (between 0.5 and more than 1 $M_{\odot}$) over the mean superwind mass-loss rate (between 10^-5 and  $10^{-4}~M_{\odot}$ yr^-1). Over the range of stellar masses studied here, we obtain a superwind time scale of about 30 000 years. This is in good agreement with the mass-loss requirements for the formation of planetary nebulae (PN).

For the post-AGB, mixing becomes as important to the evolution time-scale as is mass-loss, since the nuclear burning time-scales are no longer much larger than the mixing time-scales. Unlike Blöcker's detailed tip-AGB evolution computations (1995), the code used here does not provide an adequate description of this particular problem. Also, the mass-loss of this phase is no longer dust-driven and its description would be a guess. Therefore, we cannot provide any duration of the transition to the onset of radiative ionization.

As the next step, we undertook a quantitative study of the collective tip-AGB mass-loss of a whole stellar sample, with the same IMF and SFR as of the solar neighbourhood (Schröder & Sedlmayr 2001). Very recently, this work has been updated by Wachter et al. (2002), where we derive and apply an improved mass-loss relation, based only on the principal stellar parameters (M_*, $T_{\rm eff}$, and L_*). The same maximum-likelihood procedure as used by Arndt et al. (1997) was now applied to a larger number (50) of wind models to fit the resulting set of time-averaged mass-loss rates as a function of the input parameters. But in contrast to Arndt et al. (1997), evident dependence on some model parameters was not eliminated by averaging. Rather, the set of models used is now restricted to those parameters which yield best match to IR colours and variability of real objects. In addition, the period term in the mass-loss relation is taken into account but substituted by an empirical period-luminosity relation.

The scope of this paper is now to make a first step to link these tip-AGB wind and evolution models with observation, since there is a wealth of IR photometric data available today (e.g., Omont et al. 1999; Loup et al. 1999). While our approach is still restricted to solar metallicity, work is in progress to directly address the LMC and SMC data. Furthermore, our method is complementary to the above-mentioned (semi-) empirical relations. Also, while these are limited to J-K < 6.5, we can describe even the most extreme cases of dust-enshrouded tip-AGB objects, which remain invisible in the J band.

2 IR-colour- $\dot{{\vec M}}$ relations from pulsating dust-driven, carbon-rich superwind models

Figure 1: Individual, time-averaged wind model J-K IR-colours in a 3D plot, over both mass-loss rate $\dot{M}$ (MLR) and stellar luminosity (L). The best-fit representation is visualized by a broken plane. The viewing angle reveals the strong dependence of J-K on $\dot{{\it M}}$ and gives an account of any model-to-model variation, while the dependence on luminosity is reflected by the plane's tilt, downwards with increasing L.

Open with DEXTER

We base the description of the relation between IR-colours and time-averaged mass-loss (and luminosity, see below) on the same selection of models which was already used by Wachter et al. (2002). This approach provides consistency with their mass-loss description, used here for the grid of evolution tracks, on which we base our synthetic stellar sample (see next section).

This set of wind models is a physically meaningful choice of the dynamical model parameters (mostly the velocity amplitude of the pulsating lower boundary condition, $\Delta v$), in order to best represent the IR variability (i.e., the amplitudes) of a few observed key objects. In addition, it is important for the IR-colour/mass-loss relation of dust-driven mass-loss that all wind models consistently operate above their critical luminosity $L_{\rm c}$, i.e. with a ratio of radiative over gravitational acceleration $\alpha > 1$ - which was the other selection criterion used by Wachter et al. (2002). For this work, we removed a small number of remaining borderline cases with $L_* \la L_{\rm c}$, since the IR properties of a dust-driven wind change significantly around $L_{\rm c}$. Table 1 gives a listing of the final set of wind models, their IR properties, and their relevant input parameters.

The same maximum-likelihood procedure as the one employed by Arndt et al. (1997) and by Wachter et al. (2002) was used. It gives the optimal fit to any set of quantities by means of a multi-parameter representation. However, now the time-averaged IR-colours (J-K, H-K, K-L, L-M and K-[12]) take, one by one, the rôle of the quantity to be represented. Consequently, mass-loss is now one of the parameters here.

In order to obtain a reliable, multi-parameter representation with the limited number of models available (50, listed in Table 1), we had to restrict the number of relevant parameters as much as possible. The primary parameter is, of course, the mass-loss $\dot{M}$. In addition, inspection of pairs of models, which had all but one parameter matching each other, revealed a consistent dependence on the luminosity which clearly dominates any statistical variation of the time-averaged quantities. The same method did not show any additional, conclusive dependence on period, effective temperature, nor on the C/O ratio. If there is any, it would be too subtle to be resolved by the present set of wind models. That does not mean, however, that there is no relation between the IR properties and those parameters. Rather, any such effects are already accounted for indirectly by the primary term, since the mass-loss rate itself depends on, for example, the effective temperature (see, e.g., Winters et al. 2000b; Wachter et al. 2002).

 

 

Table 1: Listing of the selected wind models used, including IR and mass-loss properties.

No.	$M_\star$/$M_{\odot}$	$T_{\rm eff}$/K	L/$L_\odot$	$\epsilon_{\rm C}$/ $\epsilon_{\rm O}$	P/d	$\langle \dot M \rangle$	$v_{\rm end}$	J-K	H-K	K-L	L-M	K-[12]	W-No.
1	0.63	3000	8000	1.30	820	3.0e-5	14.3	8.92	3.80	4.22	1.16	7.58	w155
2	0.70	3000	12000	1.30	1100	6.2e-5	16.6	10.55	4.49	5.04	1.43	9.15	w156
3	0.70	3500	12000	1.30	650	1.0e-5	19.5	3.89	1.72	2.08	0.52	3.87	w174
4	0.80	2200	15000	1.30	300	1.1e-4	16.6	13.66	5.89	6.57	2.00	12.11	w38
5	0.80	2400	7500	1.50	104	1.4e-5	21.4	7.42	3.23	3.61	1.04	6.62	w125
6	0.80	2550	7500	1.50	104	6.0e-6	20.9	4.51	2.00	2.36	0.62	4.31	w130
7	0.80	2600	5000	1.30	300	7.4e-6	8.6	5.89	2.57	2.96	0.83	5.52	w49
8	0.80	2600	5000	1.30	350	6.4e-6	8.4	7.06	3.05	3.47	0.99	6.40	w110
9	0.80	2600	5000	1.30	400	1.3e-5	9.1	7.51	3.23	3.64	1.03	6.73	w44
10	0.80	2600	5000	1.30	500	1.3e-5	9.3	7.94	3.41	3.85	1.12	7.14	w111
11	0.80	2600	5000	1.30	600	1.6e-5	9.6	8.93	3.84	4.29	1.25	7.89	w112
12	0.80	2600	6000	1.30	400	1.6e-5	10.0	8.00	3.45	3.90	1.14	7.25	w51
13	0.80	2600	7000	1.30	450	1.9e-5	10.8	7.96	3.43	3.89	1.13	7.24	w60
14	0.80	2600	7500	1.30	300	1.0e-5	11.8	5.77	2.53	2.93	0.82	5.44	w113
15	0.80	2600	7500	1.30	450	2.5e-5	11.3	8.17	3.53	4.02	1.17	7.55	w48
16	0.80	2600	7500	1.30	600	5.1e-5	11.8	11.78	5.06	5.66	1.68	10.41	w114
17	0.80	2600	7500	1.30	800	3.6e-5	13.1	10.02	4.30	4.79	1.39	8.79	w141
18	0.80	2600	10000	1.30	640	5.0e-5	12.8	10.27	4.43	4.95	1.43	9.05	w63
19	0.80	2600	12000	1.30	800	7.0e-5	16.2	10.58	4.57	5.13	1.50	9.48	w61
20	0.80	2600	15000	1.30	1000	9.9e-5	16.6	11.81	5.12	5.72	1.71	10.57	w62
21	0.80	2700	5000	1.30	300	3.9e-6	8.4	4.37	1.91	2.27	0.59	4.26	w167
22	0.80	2700	5000	1.30	350	5.6e-6	9.4	5.56	2.41	2.79	0.75	5.12	w168
23	0.80	3000	7500	1.50	400	9.0e-6	21.6	5.84	2.52	2.89	0.77	5.33	w124
24	0.80	3000	7500	1.80	450	8.3e-6	31.6	6.00	2.59	2.93	0.78	5.35	w32
25	0.80	3000	7500	1.80	650	1.0e-5	34.2	6.32	2.73	3.11	0.85	5.78	w31
26	0.80	3000	15000	1.50	300	1.7e-5	25.0	5.28	2.29	2.71	0.72	5.21	w30
27	0.80	3000	15000	1.50	650	3.0e-5	26.1	7.72	3.30	3.76	1.04	6.98	w28
28	0.80	3000	15000	1.50	800	4.1e-5	25.4	9.04	3.85	4.34	1.22	7.97	w29
29	0.84	3000	20000	1.30	1200	7.9e-5	19.6	9.80	4.18	4.69	1.32	8.53	w157
30	0.84	3500	20000	1.30	880	2.0e-5	20.6	4.69	2.06	2.46	0.66	4.60	w177
31	0.84	3700	20000	1.30	710	1.1e-5	16.1	3.05	1.39	1.79	0.46	3.45	w178
32	0.94	3000	25000	1.30	1300	8.8e-5	20.7	9.50	4.05	4.55	1.28	8.28	w158
33	0.94	3500	25000	1.30	1000	2.3e-5	22.0	4.78	2.09	2.48	0.67	4.68	w180
34	0.94	3700	25000	1.30	810	1.2e-5	18.1	2.87	1.31	1.68	0.42	3.23	w181
35	0.94	3900	25000	1.30	1300	2.5e-5	21.9	3.99	1.75	2.15	0.58	4.14	w183
36	1.00	2400	12000	1.30	300	2.6e-5	13.6	6.96	3.04	3.44	0.99	6.43	w122
37	1.00	2400	12000	1.30	500	5.9e-5	13.4	10.89	4.71	5.23	1.55	9.66	w144
38	1.00	2400	12000	1.30	600	7.7e-5	14.7	11.59	5.02	5.57	1.67	10.33	w120
39	1.00	2400	12000	1.30	800	7.9e-5	14.4	11.80	5.11	5.66	1.71	10.49	w145
40	1.00	2600	10000	1.30	640	4.3e-5	12.6	9.59	4.12	4.64	1.36	8.62	w64
41	1.00	2600	10000	1.80	650	2.6e-5	31.8	9.35	4.02	4.48	1.31	8.25	w13
42	1.00	2800	7000	1.30	400	5.4e-6	9.7	4.24	1.87	2.22	0.58	4.14	w78
43	1.00	2800	8000	1.30	400	5.1e-6	12.0	4.22	1.86	2.22	0.58	4.09	w97
44	1.00	2800	10000	1.30	640	1.8e-5	12.9	6.54	2.80	3.22	0.88	5.97	w69
45	1.00	2900	10000	1.25	578	9.6e-6	10.5	4.42	1.94	2.30	0.60	4.34	w72
46	1.00	2900	10000	1.30	578	1.3e-5	13.1	5.43	2.35	2.75	0.75	5.21	w71
47	1.20	2600	7000	1.30	400	6.1e-6	7.9	5.74	2.50	2.88	0.79	5.24	w53
48	1.20	2800	10000	1.40	400	9.8e-6	16.9	4.94	2.16	2.50	0.66	4.65	w126
49	1.20	2800	10000	1.50	400	1.6e-5	20.6	6.93	2.99	3.39	0.95	6.38	w108
50	1.20	2800	10000	1.80	400	1.3e-5	30.9	6.46	2.79	3.16	0.88	5.93	w109

	Figure 2: AGB evolution of a star with $M_i = 1.85 M_{\odot }$ in the ( $M_{\rm Bol}$, J-K) diagram. Age intervals of 5000 yrs are marked (o) from the tip of the AGB onwards in order to show the accelerated evolution through the most extreme mass-loss (i.e., J-K > 6), and to better distinguish between regular evolution and rapid changes during thermal pulses.
Open with DEXTER

With stellar properties given in solar units, and $\dot{M}$ in $M_{\odot}$ yr^-1, the time-averaged IR colours of the pulsating wind models can be expressed in terms of the time-averaged mass-loss rate by the following relations:

$$\begin{eqnarray*}&& J-K = 7.05 + C_{J\!-\!K}\; (\log{\dot{M}} + 4.66) 7.4 \; (\... ...L\!-\!M}\; (\log{\dot{M}} + 4.66) - 1.04 \; (\log{L_*} - 4.0). \end{eqnarray*}$$

For $0.5 \times 10^{-5} < \dot{M} < 2.2 \times 10^{-5}$, we find $C_{J\!-\!K}$ = 6.39, $C_{H\!-\!K}$ = 2.67, $C_{K\!-\!L}$ = 2.81, and $C_{L\!-\!M}$ = 0.92. For larger mass-loss rates, these slopes increase to 9.25 (J-K), 3.96 (H-K), 4.24 (K-L), and 1.35 (L-M), respectively.

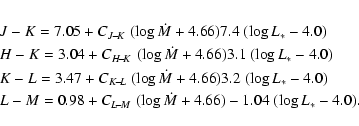
Another sensitive and popular indicator of mass-loss is the K-[12] index, for all cases in which the IRAS $12~\mu$m band flux is available. For K-[12] we find:

$$\begin{eqnarray*}K-[12] = 6.48 + C_{K\!-\!12} \; (\log{\dot{M}} + 4.66) - ~5.85 \; (\log{L_*} - 4.0) \end{eqnarray*}$$

with $C_{K\!-\!12}$ = 5.27 for $0.5 \times 10^{-5} < \dot{M} < 2.2 \times 10^{-5}$, changing to 7.67 for larger mass-loss rates.

Since these relations are restricted to strong mass-loss ( $\dot{M} \ga 0.5 \times 10^{-5}$), they are valid for IR colours (depending on the stellar luminosity) J-K and K-[12] $\ga$ 4, H-K and K-L $\ga$ 2, and L-M $\ga$ 0.5, only. This restricted application corresponds to extreme tip-AGB, C-rich objects with $L_* > L_{\rm c}$ and $T_{\rm eff} \la 3500$ K.

Representative for all five of the above relations, Fig. 1 shows a 3D-display of the individual, time-averaged J-Kmodel colours together with the best-fitting, broken plane according to the representation obtained above. The viewing angle reveals the strong dependence of J-K on $\dot{M}$, and the intrinsically variable conditions in the wind models are reflected in a stochastic spreading of the individual values. However, the above formulae give a very good representation: The typical mean deviation is about 6%, and all correlation coefficients are about 0.96 or better.

The critical luminosity $L_{\rm c}$ of the dust-driven winds is, in fact, defined in terms of L_*/M_* (see Schröder et al. 1999). In a very simplified picture, $L_{\rm c}$ represents the balance between radiation pressure and gravity for the average dust grain. Therefore, we also tried best-fit representations of the IR colours with an L_*/M_* (rather than L_*) term. Over the rather narrow mass range of the wind models (from 0.63 to 1.2 $M_{\odot}$, see Table 1), the respective correlation is just a little inferior (by about 1%). An explanation may be that the mass-loss rate does not depend on the radiative acceleration $\alpha = g^{\rm rad}/g^{\rm grav}~~(\propto\!\!\!L_*/M_*$) itself, but on the density in the sonic region, where $\alpha$ reaches a value of about 1.

As far as individual tip-AGB objects are concerned, the L_* term (rather than L_*/M_*) brings along the big advantage that superwind mass-loss rates can be determined from photometric observation alone - provided, of course, the luminosity is known reasonably well. For example: $\log{\dot{M}} = -8.20 + 0.156 \;(J\!\! -\!\! K) - 0.463 \; M_{\rm Bol}$ over $4 \la$ J-K $\la 7$.

Since large data sets of stars observed by IR photometry have become available, recently, we also want to address the exact, collective tip-AGB mass-loss of a stellar population. In principle, it can be derived from a complete sample of giants by finding a best matching synthetic sample with respect to the (J-K, $M_{\rm Bol}$) diagram. To illustrate this approach for future applications, we devote the next section to a synthetic sample which would match a solar neighbourhood stellar population.

3 A synthetic ($\vec J$-$\vec K$, ${\vec M}_{\rm Bol}$) diagram for the solar neighbourhood tip-AGB

From all IR colour indices considered here, J-K depends most sensitively on the mass-loss rate as its relation has the largest C value. Consequently, we have chosen to plot our representative synthetic sample of tip-AGB stars in a (J-K, $M_{\rm Bol}$) diagram. In this visualization of our synthetic stars, the dust-enshrouded objects stand out best, and a direct comparison with observation can easily be made.

The evolution tracks and the mass-loss description, which form the basis for the generation of the synthetic tip-AGB giant stars, are the same as those of our previous publication (Wachter et al. 2002). Table 4 therein gives the basic properties of every second of the evolution models with a complete superwind phase. The latter is based on our description of a carbon-rich mass-loss according to detailed, pulsating wind models, which is fed into the outer boundary condition of the evolution code, developed by Eggleton and collaborators (see Pols et al. 1998 and references therein). Representative for other models, Fig. 2 shows the AGB and tip-AGB track of our model with an initial mass of 1.85 $M_{\odot}$. The track is plotted over $M_{\rm Bol}$ and J-K, using the IR-colour-$\dot{M}$ relation for the superwind phase, as derived in the previous section.

Our grid of evolution models covers all masses from M_i = 0.9 to $16~M_{\odot}$ (see Schröder & Sedlmayr 2001), but not all these stars turn C-rich on their tip-AGB. This concerns stars at the lower end of the (initial) mass range ( $M_i \la 1.5~M_{\odot}$ according to Groenewegen et al. 1995), as well as those with hot bottom burning ( $M_i \ga 3~M_{\odot}$). The dust-formation during the superwind then depends on oxygen-rich chemistry, for which we do not have a synthetic mass-loss description yet. Consequently, our models of stars, which presumably remain O-rich to the very tip-AGB, must miss out on their superwind phase. Hence, some related objects probably remain unaccounted for by the synthetic stellar sample presented here (see our discussion in Sect. 4). All mass-loss prior to the superwind phase is represented mainly by a recalibrated Reimers law, see Schröder et al. (1999) for details.

	Figure 3: Mass-loss rate distribution of the synthetic giant sample - hatched: RGB giants; see text for more details.
Open with DEXTER

The procedure to randomly distribute synthetic stars in time and mass on a fine-meshed grid of evolution models is the same as the one used and described by Schröder & Sedlmayr (2001). In the same paper, we derived the IMF of the solar neighbourhood by finding a matching synthetic stellar sample to a complete, observed sample, based on the Hipparcos catalogue entries for d < 50 pc distance. The synthetic sample presented here has been generated with the same IMF, ${\rm d}N/{\rm d}\log{M_i} \propto M_i^{-1.7}$ for $M_i < 1.8~M_{\odot}$, and $\propto M_i^{-1.9}$, else. In order to obtain sufficient numbers of tip-AGB giants, we used a 1000 times larger sample: $1.4 \times 10^6$ present-day stars more luminous than $M_{\rm V} = 4.0$ were generated by an apparent SFR of $1.14 \times 10^{-3} \; {\rm e}^{-(t_{*9}/6.3)}$ stars with $0.9 < M_i/M_{\odot} < 12$ per year, with t_*9 as the star's age in Gyrs ( 0 < t_*9 < 12). On this basis, there is a total of 5067 red giants (B-V > 1.4) with a mass-loss ranging between $\approx$10^-9 and $10^{-4}~M_{\odot}$ yr^-1 (see Fig. 3).

In order to apply the appropriate description of IR properties to each synthetic star, we distinguish between four cases:

(1) Stars with very little mass-loss, where the J-K index is defined by the "naked'' photosphere of the giant: For this case, which applies to most objects which are still ascending on the AGB (or RGB), we adopted the J-K colours of model photospheres from Bessel et al. (1989), represented by the expression J-K  $= 0.928 - 0.00428 \; (T_{\rm eff}/K - 4000)$.

(2) Stars with mass-loss which are still O-rich, as they (i) have yet to advance further on the tip-AGB, or as (ii) some are very luminous, massive stars where hot-bottom burning destroys the newly produced carbon. The IR properties of these O-rich stars are best described by the (semi-)empirical relation derived from O-rich winds by Le Bertre & Winters (1998): J-K  $= 0.65 - 2.5/(\log{\dot{M}} + 4.25)$.

(3) Tip-AGB stars which have just turned C-rich, with a moderate, dust-driven mass-loss: Since the observed lower luminosity limit for C-rich stars lies just a little below the critical luminosity for the dust-driven, C-rich winds (see Schröder et al. 1999, and references therein), we adopted $\log{L_*} > \log{L_{\rm c}} -0.1$for this group. For the J-K index of these stars we use a semi-empirical relation which is a best match of the C-rich mass-loss rates given by Le Bertre (1997), specifically in the range of $2.5 \la$ J-K $\la 4$: J-K  $= -0.10 - 6.0/(\log{\dot{M}} + 4.00)$. By a random spread of $\pm 0.5^{\rm mag}$ we account for the observed variability.

	Figure 4: Enlarged view of the same mass-loss rate distribution as in Fig. 3: the dust-enshrouded tip-AGB stars with noticeable IR excess.
Open with DEXTER

(4) The objects which exceed the critical luminosity $L_{\rm c}$ of our models to drive a stable superwind: Based on the results of Schröder et al. (1999, Fig. 1), we approximated $L_{\rm c}(M_*, T_{\rm eff})$ by the relation $\log{L_{\rm c}/M_*} = 3.80 + 4. \; (\log{T_{\rm eff}}-3.45)$. For synthetic stars of this group, J-K is given by the relation derived in the previous section, with J-K > 4.

	Figure 5: The resulting synthetic ( $M_{\rm Bol}$, J-K) diagram for the synthetic sample. Supposedly O-rich stars are marked by a cross, RGB stars by a circle, and C-rich stars by a square. See Table 2 for the properties of the dust-enshrouded, carbon-rich tip-AGB stars with J-K > 4.0.
Open with DEXTER

 

 

Table 2: Properties of the 20 dust-enshrouded, carbon-rich tip-AGB objects in our synthetic sample with J-K > 4.0 seen in Figs. 4 and 5, organized by increasing J-K colour: J-K, mass-loss rate, initial mass, present mass, age, effective temperature and luminosity.

J-K	$\dot{M} [M_{\odot}~{\rm yr}^{-1}]$	$M_i/M_{\odot}$	$M_*/M_{\odot}$	Age /yrs	$T_{\rm eff}$ /K	$\log{L_*/L_{\odot}}$
4.07	$2.5 \times 10^{-6}$	1.83	1.40	$1.73 \times 10^9$	2563	3.870
4.11	$3.9 \times 10^{-6}$	2.47	2.00	$8.24 \times 10^8$	2636	4.058
4.56	$7.4 \times 10^{-6}$	1.95	1.51	$1.53 \times 10^9$	2544	3.923
4.78	$4.6 \times 10^{-6}$	1.54	0.65	$2.66 \times 10^9$	2928	3.713
5.01	$1.7 \times 10^{-5}$	2.76	2.17	$5.98 \times 10^8$	2565	4.172
5.32	$4.4 \times 10^{-6}$	1.21	0.84	$6.50 \times 10^9$	2552	3.621
5.33	$6.7 \times 10^{-6}$	1.56	1.14	$2.66 \times 10^9$	2525	3.777
5.63	$8.1 \times 10^{-6}$	1.74	0.66	$2.01 \times 10^9$	3022	3.812
5.77	$6.1 \times 10^{-6}$	1.31	0.92	$4.87 \times 10^9$	2524	3.683
5.97	$1.0 \times 10^{-5}$	1.67	1.21	$2.35 \times 10^9$	2476	3.843
6.82	$1.1 \times 10^{-5}$	1.67	0.73	$2.35 \times 10^9$	2731	3.754
6.67	$2.1 \times 10^{-5}$	2.55	1.64	$8.25 \times 10^8$	2497	4.031
7.02	$1.2 \times 10^{-5}$	1.41	0.94	$3.75 \times 10^9$	2438	3.754
7.26	$1.1 \times 10^{-5}$	1.48	0.76	$2.97 \times 10^9$	2542	3.709
7.29	$1.1 \times 10^{-5}$	1.48	0.75	$2.97 \times 10^9$	2542	3.715
7.97	$1.9 \times 10^{-5}$	1.48	0.92	$2.97 \times 10^9$	2403	3.810
8.01	$1.8 \times 10^{-5}$	1.68	0.81	$2.17 \times 10^9$	2483	3.791
8.70	$3.9 \times 10^{-5}$	2.46	1.38	$8.25 \times 10^8$	2377	4.080
9.30	$3.6 \times 10^{-5}$	2.16	1.11	$1.27 \times 10^9$	2377	3.949
11.31	$8.3 \times 10^{-5}$	2.66	1.31	$7.00 \times 10^8$	2333	4.137

Among the so characterized synthetic giants, there is a total of 20 tip-AGB stars in group (4) with a mass-loss rate $\dot{M}$ well in excess of $10^{-6}~M_{\odot}~{\rm yr}^{-1}$ (see Fig. 4 and a detailed listing in Table 2). This includes 10 dust-enshrouded objects with J-K > 6.0 which would be difficult to observe, all in their superwind phase (i.e. their final 30 000 yrs on the tip-AGB, with $\dot{M} > 10^{-5}~M_{\odot}~{\rm yr}^{-1}$). These objects are easily identified in Fig. 5, the (J-K, $M_{\rm Bol}$) diagram which results from the properties of our synthetic sample.

The collective mass-loss rate of the whole stellar sample presented here is $5.0 \times 10^{-4}~M_{\odot}$ yr^-1. To this, the only 20 stars with J-K > 4.0 contribute $3.3 \times 10^{-4}~M_{\odot}$ yr^-1. The 10 superwind objects alone contribute $2.6 \times 10^{-4}~M_{\odot}$ yr^-1, which is about half of the collective stellar mass-loss rate!

4 Discussion

The motivation of this work is to provide an independent theoretical approach to derive the mass injection rates from stellar samples in terms of synthetic-colour / mass-loss rate relations, including the most extreme cases of dust-enshrouded objects (J-K > 6). For this purpose, we studied the time-averaged properties of selfconsistent, dust-driven and pulsating wind models. In the resulting IR colour relation with mass-loss, we find an additional, significant dependence on the luminosity. Hence, mass-loss rates can be derived for individual objects from observation alone, if the distance is known.

More accurate is the assessment of the collective mass-loss of a whole sample of stars, provided the IMF is known, by a direct comparison with a matching synthetic sample in the (J-K, $M_{\rm Bol}$) diagram. For our synthetic stellar sample of tip-AGB stars representing the solar neighbourhood stellar population, we find a small but crucial number of stars with extreme mass-loss. In observed samples, these are likely to remain undetected.

Unfortunately, a suitable observed sample does not yet exist, mostly because the distances to appropriate objects are still just too badly known. The best complete tip-AGB star samples available to date are those of the Magellanic clouds (Loup et al. 1999). However, for a comparison in the (J-K, $M_{\rm Bol}$) diagram between our synthetic sample and the observed LMC or SMC tip-AGB stars we must keep in mind that the initial metallicities are not the same. Van Loon (2000) finds evidence that the mass-loss rate depends only weakly on initial metallicity, but the dust-to-gas ratio depends approximately linearly on it. Work on appropriate models for smaller metallicities is in progress but must remain the scope of a future publication.

In a qualitative comparison, the synthetic (J-K, $M_{\rm Bol}$) diagram presented here resembles its observed LMC counterpart (Loup et al. 1999) quite well, with one exception: While the synthetic IR colours, in some extreme cases, reach out to J-K $\approx$ 12, only values up to about 5 have been observed in the Magellanic clouds. This should not come as a surprise, though, since (1) the lower metallicities in the LMC cause a lower dust-to-gas ratio with, accordingly, lower IR optical depth, and (2) the most dust-enshrouded objects (J-K $\ga$ 6) are so much obscured by their circumstellar extinction that they would simply not be observable at the distance of the LMC, given the DENIS threshold (J < 16, K < 14). For example, the prototypical dust enshrouded carbon star IRC +10216 with a J-K of just 6 would, at the distance of the LMC, have $J \approx 20$ and $K \approx 14$.

A related question is the choice of reasonable IR opacities by the code (see Winters et al. 2000 for details). The good coincidence between IR colours and amplitudes of synthetic light curves of matching wind models on the one hand, and real objects on the other (Wachter et al. 2002), suggests to us that the adopted IR opacities (Preibisch et al. 1993) are appropriate.

While a large number of AGB-stars with O-rich winds are included in our synthetic sample, with $\dot{M}$ up to about $o(10^{-6})~M_{\odot}$ yr^-1 (see group (2) mentioned in the previous section), we have not been able to account for any tip-AGB objects with O-rich superwinds. These provide an additional mass-loss which remains to be quantified. Theoretical work on suitable wind models with an O-rich dust-formation chemistry is progressing (Jeong et al. 1999), but the number of first generation numerical simulations is still insufficient to derive representations of the respective mass-loss and IR properties.

The actual number of unaccounted O-rich stars with strong mass-loss depends on how large the range of initial masses is, over which stars do in fact turn C-rich on the tip-AGB: An upper mass limit is set by the effect of hot-bottom-burning which causes massive stars to remain O-rich. According to Blöcker (1999), this is expected to occur with initial masses of $M_i \ga 4$ to 5 $M_{\odot}$. Due to the steepness of the IMF, that upper limit would imply only a small fraction of objects with an O-rich superwind.

By contrast, the ratio of O-rich to C-rich PNs (about 40%:60%, Zuckerman & Aller 1986; Parthasarathy 1999) would suggest a larger fraction of stars ending with O-rich superwinds, but only if indeed every PN was the result of such a superwind. Also, a fraction of the observed PNs could actually be the result of a wider binary system, triggered by a common envelope phase before the giant primary turned C-rich. The LMC tip-AGB sample of Loup et al. (1999), finally, suggests a fraction of just over 20% of O-rich objects among the dust-enshrouded tip-AGB stars (which would be about 4 stars with respect to the 20 C-rich giants of group 4). But we must keep in mind that the fraction of C-rich tip-AGB objects may well be higher with lower metallicity, as in the LMC.

In our model grid, we adopted an upper mass-limit of $M_i \approx 3~M_{\odot}$ for the stars which leave the tip-AGB with a C-rich superwind. Hence, there remains a mass range of $0.5 \la \log{M_i} \la 0.9$ for the unaccounted O-rich superwind objects (more massive stars lead to a SN). By comparison, the mass range of the 20 synthetic, supposedly C-rich stars of group (4) is $0.1 \la \log{M_i} \la 0.5$. With an IMF $\propto M_i^{-1.7}$, the number of O-rich objects in their superwind phase should then be 5 $\times$ smaller (even less, if the IMF is steeper in this mass range). If the O-rich dust-driven wind phases were of a similar duration as those of our 20 C-rich stars, this would correspond to just about 4 unaccounted tip-AGB, O-rich objects with $\dot{M} > 4 \times 10^{-6}~M_{\odot}$ yr^-1.

In addition, there appears to be observational evidence (Groenewegen et al. 1995) that stars with $M_i \la 1.5~M_{\odot}$ may not become C-rich, either. But this lower mass threshold is quite close to the one we find ($\approx$ $1.3~M_{\odot}$) for a C-rich star to develop a regular superwind (i.e., for exceeding $L_{\rm c}$ for a time longer than $\approx$10⁴ yr). The remaining difference may provide a margin of stars with significant ( $o(10^{-6})~M_{\odot}$ yr^-1) mass-loss which remain O-rich to their end but here were accounted for as C-rich.

Certainly, a lot more work needs to be done to address the afore-mentioned unsolved problems. So far, the dust-enshrouded objects in our synthetic sample represent the main present-day contributors to the collective mass-loss for, at least, the mass-range between about 1.5 and 3 $M_{\odot}$, which is a substantial fraction of the stellar population that develops cool winds.

In any case, the creation of synthetic stellar samples offers a direct way to compare theoretical expectations with observational evidence. In combination with large, volume-limited samples of real stars with observed IR colours and C:O ratio, this approach will help to resolve the open questions and, finally, it will give a quantitative interpretation of the observations in terms of mass-loss rates.

Acknowledgements

This work has been supported by a Marie Curie Fellowship of the European Community programme HUMAN POTENTIAL under the contract number HPMT-CT-2000-00096 given to AW, to work at the Physics & Astronomy department of Sussex University. KPS and JMW wish to acknowledge conference travel support from the Royal Society, and from a visitor grant held by A. Liddle (University of Sussex Astromy Centre), respectively. JMW acknowledges financial support by the CNRS. We also wish to thank T.U. Arndt, who kindly provided his maximum-likelihood code, and the anonymous referee for his helpful remarks.

References

 
• Arndt, T. U., Fleischer, A. J., & Sedlmayr, E. 1997, A&A, 327, 614 In the text NASA ADS  
• Bessell, M. S., Brett, J. M., Scholz, M., & Wood, P. R. 1989, A&AS, 77, 1 In the text NASA ADS  
• Blöcker, T. 1995, A&A, 297, 727 NASA ADS  
• Blöcker, T. 1999, in Asymptotic Giant Branch Stars, ed. T. Le Bertre, A. Lèbre, & C. Waelkens, Proc. IAU Symp. ASP, 191, 21 In the text  
• Cioni, M.-R.L., Marquette, J.-B., Loup, C., et al. 2001, A&A, 377, 945 In the text NASA ADS  
• Fleischer, A. J., Gauger, A., & Sedlmayr, E. 1992, A&A, 266, 321 In the text NASA ADS  
• Groenewegen, M. A. T., van den Hoek, L. B., & de Jong, T. 1995, A&A, 293, 381 In the text NASA ADS  
• Habing, H. J. 1996, A&ARv, 7, 97 In the text NASA ADS  
• Jeong, K. S., Winters, J. M., & Sedlmayr, E. 1999, in Asymptotic Giant Branch Stars, ed. T. Le Bertre, A. Lèbre, & C. Waelkens, Proc. IAU Symp. ASP, 191, 233 In the text  
• Le Bertre, T. 1997, A&A, 324, 1059 In the text NASA ADS  
• Le Bertre, T., & Winters, J. M. 1998, A&A, 334, 173 In the text NASA ADS  
• Loup, C., Josselin, E., Cioni, M.-R., et al. 1999, in Asymptotic Giant Branch Stars, ed. T. Le Bertre, A. Lèbre, & C. Waelkens, Proc. IAU Symp. ASP, 191, 561 In the text  
• Omont, A., Ganesh, S., Alard, C., et al. 1999, A&A, 348, 755 In the text NASA ADS  
• Parthasarathy, M. 1999, in Asymptotic Giant Branch Stars, ed. T. Le Bertre, A. Lèbre, & C. Waelkens, Proc. IAU Symp. ASP, 191, 475 In the text  
• Pols, O. R., Schröder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 In the text NASA ADS  
• Preibisch, Th., Ossenkopf, V., Yorke, H. W., & Henning, Th. 1993, A&A, 279, 577 In the text NASA ADS  
• Renzini, A. 1981, in Physical Processes in Red Giants, ed. Jr. I. Iben, & A. Renzini (Reidel, Dordrecht), 431 In the text  
• Schröder, K.-P., Pols, O. R., & Eggleton, P. P. 1997, MNRAS, 285, 696 In the text NASA ADS  
• Schröder, K.-P., Winters, J. M., & Sedlmayr, E. 1999, A&A, 349, 898 In the text NASA ADS  
• Schröder, K.-P., & Sedlmayr, E. 2001, A&A, 366, 913 In the text NASA ADS  
• Sedlmayr, E. 1994, in Molecules in the Stellar Environment, ed. U. G. Jørgensen, Proc. IAU Colloq. (Springer, Berlin), 146, 163 In the text  
• Sedlmayr, E., & Winters, J. M. 1997, in Stellar Atmospheres: Theory and Observations, Proc. EADN Astrophysics School IX, ed. J. P. De Greve, R. Blomme, & H. Hensberge, Lecture Notes in Physics (Springer, Berlin), 497, 89 In the text  
• van Loon, J. Th., Groenewegen, M. A. T., de Koter, A., et al. 1999, A&A, 351, 559 In the text NASA ADS  
• van Loon, J. Th. 2000, A&A, 354, 125 In the text NASA ADS  
• Wachter, A., Schröder, K.-P., Winters, J. M., Arndt, T. U., & Sedlmayr, E. 2002, A&A, 384, 452 In the text NASA ADS  
• Winters, J. M., Keady, J. J., Gauger, A., & Sada, P. V. 2000a, A&A, 359, 651 In the text NASA ADS  
• Winters, J. M., Le Bertre, T., Jeong, K. S., Helling, Ch., & Sedlmayr, E. 2000b, A&A, 361, 641 In the text NASA ADS