A&A 398, 159-168 (2003)
DOI: 10.1051/0004-6361:20021626

H II regions in symbiotic binaries and their radio emission

A. J. Gawryszczak - J. Miko\lajewska - M. Rózyczka

Nicolaus Copernicus Astronomical Center, Bartycka 18, Warsaw 00-716, Poland

Received 28 August 2002 / Accepted 25 October 2002

Abstract
The slow and dense wind from a symbiotic red giant (RG) can be significantly deflected toward the orbital plane by the gravitational pull of the companion star. In such an environment, the ionizing radiation from the companion creates a highly asymmetric H II region. We present three-dimensional models of H II regions in symbiotic S-type systems, for which we calculate radio maps and radio spectra. We show that the standard assumption of spherically symmetric RG wind results in wrong shapes, sizes and spectra of ionized regions, which in turn affects the observational estimates of orbital separation and mass loss rate. A sample of radio maps and radio spectra of our models is presented and the results are discussed in relation to observational data.

Key words: stars: winds, outflows - stars: binaries: symbiotic - hydrodynamics


   
1 Introduction

Symbiotic stars are binary systems consisting of a red giant (RG) as the primary, and a post-AGB star or MS-dwarf as the secondary. The RG primary is the source of a high density wind accreted by the secondary. In closer binaries ( $a < 10~{\rm AU}$) the wind is significantly deflected toward the orbital plane by the gravitational pull of the secondary (see Gawryszczak et al. 2002, and references therein). This process results in an enhanced density region at the orbital plane, with a disk-like density maximum surrounding the secondary.

Radio emission from symbiotic stars is dominated by ff radiation from the ionized gas. The ff spectrum of an H II region consists of three parts: optically thick at low frequencies (with spectral index $\alpha\ge0.6$), optically thin at high frequencies (with $\alpha\approx-0.1$), and optically semi-thick at intermediate frequencies around a turnover frequency $\nu_{\rm t}$, with $\alpha$ smoothly decreasing from its optically thick value to -0.1. Taylor & Seaquist (1984) show that orbital separation a, ionizing luminosity $L_{\rm ph}$, and the ratio of mass-loss rate to wind velocity $\frac{\dot{M}}{v}$ may be derived from such observables as turnover frequency, monochromatic flux at that frequency $S_{\rm t}$, and the value of the optically thick spectral index.

However, their calculations are based on the spherical wind model originally developed by Seaquist et al. (1984) (hereafter STB), which, as we mentioned above, is incorrect in closer systems. Good examples of such systems are symbiotic S-type systems, containing a normal M giant and having orbital periods of order a few years (e.g. Belczynski et al. 2000, and references therein).

Recently, Miko\lajewska & Ivison (2001) have obtained for the first time the spectral energy distribution (SED) at wavelengths between $6~{\rm cm}$ and $0.85~{\rm mm}$ for one of the prototypical S-type systems, CI Cyg, during quiescence. Their data allowed to determine $\nu_{\rm t}$ and the optically thin ff emission measure, from which a lower limit to $L_{\rm ph}$ and an estimate of a were calculated within the STB framework. Unfortunately, the comparison of these estimates with the known orbital and stellar parameters of CI Cyg poses a serious problem for the STB model. In particular, a is overestimated by a factor of $\sim $35, whereas $L_{\rm ph}$ (whose value is known from optical/UV H I emission lines and He II bf+ff continuum) is underestimated by a factor of $\sim $20.

The above inconsistency strongly indicates that the STB model needs revision. The most obvious improvements are related to the asphericity of the wind, as suggested both by numerical work (see Gawryszczak et al. 2002, and references therein) and observations. From the observational point of view there is little doubt about the origin of the ionized medium. The mm radio emission shows some correlation with the mid-IR flux, and the radio luminosity increases with the ${\rm K}-[12]$ colour. This indicates that warm dust is involved in the mass flow along with the ionized gas, and suggests that the red giant is the source of this material (Miko\lajewska et al. 2002a). Such a picture is also supported by the spectral analysis of symbiotic nebulae which showed CNO abundances similar to those observed in normal red giants (Nussbaumer et al. 1988) Optical and radio imaging of symbiotic stars reveal aspherical nebulae, often with bipolar lobes and jet-like components (Corradi et al. 1999). It is hard to explain how such structures might develop if the RG wind were spherical. Additional, indirect evidence for the asphericity of the RG wind comes from emission line profiles. It is based on the stationary, blueshifted ${\rm H}_\alpha$ absorption originating close to the orbital plane and indicating that the ionized region is probably bounded on all sides by a significant amount of dense neutral material (see the discussion in Gawryszczak et al. 2002).

In the present paper we account for the asphericity of the RG as resulting from the interaction with the secondary. With the help of 3-D hydrodynamical models we demonstrate that H II regions ionized by the secondary in S-type systems must indeed have shapes, sizes and spectra significantly different from those obtained by STB. A representative sample of radio spectra and radio maps of our models is also generated.

In Sect. 2 we discuss the numerical techniques used in this work and details of the physical setup of our models. The models are presented in Sect. 3. In Sect. 4 the results of our simulations are compared to observed symbiotic systems and a brief summary of our work is provided.

   
2 Methods and assumptions

The aim of the present paper is to study the properties of H II regions in symbiotic S-type stars. In such systems the H II region develops in a dense RG wind whose density distribution is modified by the gravitational pull of the secondary. As a highly aspherical distribution may result even in cases when the wind is originally spherically symmetric, a multidimensional approach to the problem is necessary.

We begin with 3-D hydrodynamical simulations of RG winds interacting with the companion to the mass-losing star. The simulations are performed with the help of the Smoothed Particle Hydrodynamics (SPH) technique. An inertial coordinate system is used, with the origin at the mass center of the binary.

Our implementation of the SPH is based on variable smoothing length with spline kernel introduced by Monaghan & Lattanzio (1985). The number of neighbouring particles is set to 40. For practical reasons (CPU time), the total number of particles in the computational domain is limited to 105. Whenever this limit is exceeded, those most distant from the system are removed from the domain. The distance beyond which removals occur ( $r_{\rm rem}$) stabilizes within several orbital periods of the binary, and an almost stationary rotating density distribution is obtained. The validity of such an approach was demonstrated by Gawryszczak et al. (2002). With the above limit imposed on the number of particles, $r_{\rm rem}$ does not exceed $60~{\rm AU}$ (see Table 1).

Within $0.1~{\rm AU}$ from the secondary we remove all particles with velocities directed toward the secondary. This procedure is applied to avoid prohibitively short time-steps.

There are good reasons to believe that RG winds are intrinsically aspherical (see e.g. Frankowski & Tylenda 2001; Dorfi & Höfner 1996; Reimers et al. 2000, and references therein). The asphericity may result from internal processes taking place in the star and/or presence of the secondary. However, since the theory is not yet advanced enough for precise quantitative predictions, these effects are not included in our models. In particular, we assume that although the RG rotates synchronously it does not fill its Roche lobe, so that the mass flow through the inner Lagrangian point can be neglected. In effect, the wind is represented by a stream of particles launched at a constant rate from points distributed randomly and uniformly on the RG surface. The initial temperature of the wind is $3000~{\rm K}$, and the initial velocity of wind particles is set to $1~{\rm km~s^{-1}}$ (note that, as the wind propagates across the grid its velocity increases; a measure of the terminal wind velocity is introduced and explained in the following paragraphs). Both temperature and velocity of the wind are constant on the surface of the star.

Further, we assume that the wind is composed of dust and ideal monoatomic gas which are dynamically coupled (i.e. they move at the same velocity). The details of wind acceleration process are not followed. Instead, we assume that the gravity of the red giant is balanced by radiation pressure on the dust, so that it does not appear explicitly in our equations. Thus, if the RG were single, the only force acting on the wind would be due to gas-pressure gradients, whereas in a binary the wind is additionally subject to the gravity of the companion. Such an approximation may seem rather crude; however Gawryszczak et al. (2002) demonstrated that it leads to terminal velocities comparable to those obtained by Winters et al. (2000) for winds in which radiation pressure nearly balances the gravity of the wind source.

Finally, we neglect radiation pressure from the secondary (note that in the case of a white dwarf,for any reasonable grain size the force due to radiation pressure on dust grains is much smaller than gravity). Self-gravity of the wind and any explicit radiative heating or cooling are also neglected. The effects of cooling are accounted for by a nearly isothermal equation of state employed for the wind ( $p = \kappa \rho^\gamma$, with $\gamma = 1.01$). A likely source of strong nonaxisymmetric effects is magnetic field, as the MHD collimation may be much more efficient than the gravitational focusing discussed here (see García-Segura et al. 1999; García-Segura & López 2000; García-Segura et al. 2001, and references therein). However, there is no information available about magnetic fields in symbiotic systems and we feel that it is too early to incorporate them into models: the number of free parameters would simply grow too large.

   
3 Results

All binaries considered here consist of a $1.0~M_{\hbox{$\odot$ }}$ red giant and a $0.6~M_{\hbox{$\odot$ }}$ white dwarf. The orbital separation a varies between 1 and  $4~{\rm AU}$, which is representative of S-type symbiotic systems. Following Miko\lajewska et al. (2002a) a mass loss rate of $\dot{M}= 10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$ is adopted for the RG wind, while the ionizing luminosity of the secondary $L_{\rm ph}$ varies between $4\times10^{44}$ and $8\times10^{45}~{\rm phot~s^{-1}}$. The latter range is compatible with estimates based on mm/submm observations (Ivison & Seaquist 1995; Miko\lajewska & Ivison 2001), but is a factor of $\sim $10 smaller than estimates based on studies of optical/UV H I and He II emission lines and bf+ff continuum (Miko\lajewska & Ivison 2001; Miko\lajewska et al. 2002a).

The choice of the lower estimate is dictated by the size of our hydrodynamical wind models ( $60\div100~{\rm AU}$ in diameter), which at $L_{\rm ph}\ga10^{46}$ would be practically entirely ionized. The parameters of symbiotic binary models obtained in this work are listed in Table 1 ( $v_{\rm av}$ in Col. 3 is a measure of the wind velocity; see Sect. 3.2 for an explanation). The radius of the red giant is in all cases equal to $0.5~{\rm AU}$. A simple method of scaling our results to combinations of $\dot{M}$ and $L_{\rm ph}$ not covered by actual calculations is given in Sect. 3.3.

   
3.1 RG wind models

For each binary in Table 1 we integrate the equations of hydrodynamics until the density distribution of the RG wind relaxes to a stationary state. Density distributions of the relaxed models are shown in (Fig. 1). The general effect of the secondary is to deflect the RG wind toward the orbital plane, and as a result the relaxed density distributions are flattened. This flattening weakens with increasing orbital separation because of the increasing ratio of the wind velocity at the secondary's orbit to the orbital velocity of the secondary. However, all models develop a high density region in the form of a disk around the secondary.


  \begin{figure} \par\includegraphics[width=13cm,clip]{aa3046f1.eps}\par\end{figure} Figure 1: Density distributions of models A, B and C. The logarithmic density scale spans 5 orders of magnitude. In each frame a region of $40\times40~{\rm AU}$ is shown. The system rotates counterclockwise.
Open with DEXTER


  
Table 1: List of models.
\begin{table} \begin{displaymath} \begin{array}{lllllll} \hline\hline \noalig... ...5}\\ \noalign{\smallskip } \hline \end{array} \end{displaymath} \end{table}

All models also display a three-dimensional spiral structure resulting from the shock wave excited by the motion of the secondary across the RG wind. The spirals are a very general feature of slow winds in binary systems, and they were also observed in simulations reported by Mastrodemos & Morris (1998, 1999) or Gawryszczak et al. (2002). As one might expect, in closer binaries the spiral is more tightly wound than in the wider ones.

In the closest binary funnel-like density minima oriented perpendicularly to the orbit are also observed. Two effects contribute to the formation of these funnels. First, in a close binary the wind is emitted from a source moving with a high orbital velocity, and as such it carries appreciable angular momentum. Away from the orbital plane the centrifugal force associated with that momentum causes the wind gas to clear the vicinity of the polar axis. Secondly, and unlike that of the primary, the gravity of the secondary is not balanced by radiation pressure, and the wind flowing perpendicularly to the orbit is retarded.

Below we argue that all these features (flattening, spirals and funnels) are important factors influencing the observational properties of the H II regions created in the RG wind by the ionizing radiation from the secondary.

   
3.2 Shapes and sizes of H II regions

Once the RG wind has been relaxed, its density distribution is smoothed by averaging over several tens of consecutive time steps. The aim of this procedure is to reduce the numerical noise resulting from the "grainy" nature of the SPH models. The smoothed density is mapped onto a spherical grid centered on the secondary, with grid points spaced uniformly in angular coordinates and concentrated at the secondary in the radial coordinate. Then, the source of ionizing photons is turned on at the location of the secondary, and the boundary of the H II region is found in a local Strömgren sphere approximation (i.e. Strömgren radii are calculated for all directions defined by grid points in angular coordinates). An example result of this procedure is shown in Fig. 2. Separate treatment of ionization and dynamics is justified by the fact that the recombination time is one order of magnitude shorter than the orbital period at the edge of our computational domain, and more than 3 orders of magnitude near the secondary.

In the approach developed by STB, the shape and size of the H II region are uniquely determined by the value of the parameter X, which is a combination of the mass loss rate, wind velocity, orbital separation, and ionizing luminosity:

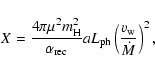\begin{displaymath}X=\frac{4\pi \mu^2 m_{\rm H}^2}{\alpha_{\rm rec}} a L_{\rm ph} \left(\frac{v_{\rm w}}{\dot{M}}\right)^2, \end{displaymath} (1)

where $\alpha_{\rm rec}$ and $v_{\rm w}$ are recombination coefficient and wind velocity (which is constant in space and time), while $\mu$ and $m_{\rm H}$ have their standard meaning.

While STB assume a wind of constant velocity, in our models the flow accelerates with the distance from the RG, and the acceleration proceeds at a variable (location-dependent) rate. This is due partly to thermal pressure gradients, and partly to the centrifugal force associated with the angular momentum transferred to the wind from the secondary; see Gawryszczak et al. (2002). In order to calculate X from our models, we use a density-weighted velocity $v_{\rm av}$, averaged over the whole solid angle (the averaging is performed near the edge of the computational domain). For each binary a range of H II regions with different X-values may then be easily generated by allowing for variations in $L_{\rm ph}$ (alternatively, $\dot{M}$ may be scaled by multiplying the density of the RG wind in each grid cell by the same factor).

To obtain the STB counterpart of our model, for the same $\dot{M}$ a density distribution of the spherical wind from the primary is calculated, assuming $v_{\rm w}=v_{\rm av}$. An appropriate part of that distribution is fed into the spherical grid centered on the secondary, and the same Strömgren-routine is employed to find the boundary of H II region. We checked that the boundary found this way agrees to within a few percent with the boundary derived from Eq. (1) of STB.

  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{3046f2.eps}} \end{figure} Figure 2: 3D view of the H II region boundary in model B with $L_{\rm ph}=2.4\times 10^{45}$. A region of $10\times10\times10~{\rm AU}$ is shown.
Open with DEXTER

The two sets of H II regions are compared in Fig. 3. The upper part of each frame shows our model, and the lower one - the corresponding model obtained within the framework of STB (note that all displayed models are symmetric with respect to the orbital plane).

A clear general trend may be observed: for wide binaries and intense ionizing fluxes (see lower right corner of Fig. 3) the shapes and sizes of our H II regions converge to those of STB. On the other hand, for close binaries and/or low ionizing luminosities, our H II regions become entirely different from those of STB: they are not axially symmetric, and their shapes may be fairly complicated (see Fig. 2 and the left column of Fig. 3). Another discrepancy concerns a large part of the space to the right of the secondary in Fig. 3, which in our models is screened from UV photons by the dense disk around the secondary. This neutral region, best visible in the upper right frames of Fig. 3, does not have its counterpart in STB models, and it only disappears when $L_{\rm ph}$ is large enough to ionize the disk.

Note also that our H II regions are generally smaller than those of STB. This is due to the fact that the density of our RG wind is enhanced in the orbital plane compared to the spherically symmetric wind with the same mass loss rate and velocity. However, in the closest binary with the lowest $L_{\rm ph}$ our H II region becomes much larger than its STB counterpart. This is because the low-density funnels, which are very well developed in this case, are easily ionized, causing the H II region to evolve into a pair of semi-infinite jet-like lobes (upper left frame of Fig. 3).

  \begin{figure} \includegraphics[width=13cm,clip]{aa3046f3.eps} \end{figure} Figure 3: A sample of H II region shapes. H II region boundary is plotted in a plane which is perpendicular to the orbit and contains the centers of both stars. In every frame our model (top) is compared to its STB counterpart (bottom) obtained for the same value of X. The columns illustrate the effect of increasing luminosity, (or, equivalently, of increasing X). In each frame a region of $80\times80~{\rm AU}$ is shown; ionized regions are white.
Open with DEXTER

   
3.3 Spectra

The spherical grid centered on the secondary and containing the smoothed density distribution is also used to derive the ff spectra of our models. Monochromatic volume emissivity of the ionized gas is calculated with the help of formulae taken from Lang (1980). Subsequently, a viewing direction is chosen and the emissivity is integrated along the line of sight until the optical depth of 5 is reached (or across the whole H II region in optically thin cases). Observed monochromatic intensities are calculated for an assumed distance of $1~{\rm kpc}$ between the observer and the radiation source.

The resulting spectra of all models presented in Fig. 3 are displayed in Fig. 4 (note that in both figures the models are arranged in the same way, but the whole Fig. 4 is rotated counterclockwise by 90 $\hbox{$^\circ$ }$). For comparison, the corresponding STB spectra are also shown. All spectra may easily be scaled to other values of $\dot{M}$ and $L_{\rm ph}$; the corresponding procedure is illustrated in Fig. 5.

As one might expect, in wider systems with high $L_{\rm ph}$ our spectra almost entirely converge to those of STB, while they are significantly different in close systems with low $L_{\rm ph}$. In such systems our spectral index may be smaller or larger than that of STB; the same is true for turnover frequency and intensity. To make things even more complicated, some spectra exhibit more than one turnover. This is because in some models the distribution of density along the line of sight cannot be approximated by a single power law.

In general, the differences between the spectra of the same system viewed "pole-on'' and along the line joining the stars (with the primary in front of the secondary) are larger in our models than in those of STB (slopes and turnover frequencies are however almost insensitive to such a change of viewing direction). On the other hand, our models predict weaker spectral variations with the orbital phase. This behaviour is explained by the fact that in our models the distinguished direction is perpendicular to the orbital plane, whereas the H II regions of STB are axially symmetric with respect to the line joining the stars.

   
3.4 Radio maps

Based on density distributions inside the ionized regions and the above described integration technique we derive maps of monochromatic ff emission from our models at $5~{\rm GHz}$. Depending on viewing angle and parameters of the binary, the maps display a rich variety of morphologies, of which a sample is shown in Fig. 6. In some frames the outer boundary of the RG wind model is visible as a regular circular contour. In such cases part of the emission is obviously not accounted for; however it never amounts to more that a few per cent of the total emission at $5~{\rm GHz}$. Like in the case of spectra, the intensities indicated in the maps correspond to a distance of $1~{\rm kpc}$ between the observer and the symbiotic binary. The following observations can be made:


  \begin{figure} \par\mbox{ \includegraphics[angle=90,width=3.4cm,clip]{aa3046f4L... ...m} \includegraphics[angle=90,width=4.15cm,clip]{aa3046f4Rc.eps} } \end{figure} Figure 4: Radio spectra of models shown in Fig. 3. In all cases $\dot{M}=10^{-7}$. Solid and dashed lines: our models viewed pole-on and along the line joining the stars (with the primary in front of the secondary), respectively. Dotted and dot-dashed lines: corresponding STB models viewed pole-on and along the line joining the stars, respectively.
Open with DEXTER


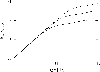  \begin{figure} \resizebox{8.8cm}{!}{\includegraphics{aa3046f5.eps}} \end{figure} Figure 5: Scaling of the spectra. Compared are variants of model B with $\dot{M}=10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr^{-1}},\ L_{\rm ph}=2.4\times10^{45}$ (solid line), $\dot{M}=3\times10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr^{-1}},\ L_{\rm ph}=2.16\times10^{46}$ (dashed line) and $\dot{M}=3\times10^{-8}~M_{\hbox{$\odot$ }}~{\rm yr^{-1}},\ L_{\rm ph}=2.16\times10^{44}$ (dot-dashed line). All three H II regions have the same shape and size. Their spectra are practically identical, except that they are shifted by approximately one order of magnitude in $S_\nu $ and a factor of $\sim $3 in $\nu $ for every factor of $\sim $3 in $\dot{M}$ accompanied by one order of magnitude increase in $L_{\rm ph}$.
Open with DEXTER

The bipolar structure shown by our maps could be easily resolved by MERLIN after its upgrade is complete (e-MERLIN). Even now, MERLIN has sufficient resolution ( $40~{\rm mas}$ at $5~{\rm GHz}$ where it is most sensitive) but its sensitivity is too low. However, e-MERLIN, with its new 15 and $22~{\rm GHz}$ receivers will be able to perform imaging at a resolution of $\sim $8 AU at $1~{\rm kpc}$ for sources as weak as a few of $\mu{\rm Jy}$.

   
4 Discussion

We have demonstrated that the STB model is not applicable to systems with $a\la 4$ and $X\la 2$. In such systems the H II region is not axially symmetric, and in most cases it is much smaller than its STB counterpart. This is because the basic STB assumption of a spherically symmetric RG wind is violated. Even if the wind is emitted uniformly from the whole surface of the red giant, it immediately loses its original symmetry due to gravitational attraction of the secondary. As a result, a large-scale density enhancement develops in the orbital plane, with many smaller scale substructures (funnels, spirals and a compact circumsecondary disk). Factors not accounted for in our simulations (RG wind originally enhanced in the orbital plane and/or outflow through the inner Lagrangian point) can only amplify this effect. Based on Fig. 3 the following qualitative predictions can be made: In fact, the first prediction has already been observationally verified. For many S-type systems there are strong indications for low values of X ($\la 1/3$; Mürset et al. 1991) and/or H II which are ionization-bounded at least in the orbital plane (Ivison et al. 1994). In accordance with Fig. 3, such nebulae have also been observed for larger X's. Recently, Quiroga et al. (2002) have shown that in the case of AR Pav, the central absorption in ${\rm H}_\alpha$ is formed in a neutral portion of the RG wind which is strongly concentrated towards the orbital plane, (with the total hydrogen column density $N({\rm H})\ga {\rm a\ few} \times 10^{21}~{\rm cm}^{-2}$).
  \begin{figure} \par { \includegraphics[width=4cm,clip]{3046f6a1.eps}\hspace*{1.... ...}\hspace*{1.4cm} \includegraphics[width=4cm,clip]{3046f6c5.eps} } \end{figure} Figure 6: Selected radiomaps at $5~{\rm GHz}$. Radio intensity is shown on a logarithmic scale, with solid contours plotted every order of magnitude (except for frames 5a-c, where a linear scale is used). Every frame covers an area of $80\times80~{\rm AU}$. Left column: side view (line of sight perpendicular to the line joining the stars in the orbital plane). Right column: pole-on view (line of sight perpendicular to the orbit). Middle column: intermediate case with line of sight inclined $45\hbox {$^\circ $ }$ to the orbital plane. The jagged appearance of some maps is an artifact due partly to limited resolution of the grid on which the boundary of the H II region is defined. Model parameters: 1a-c: $a=1,~\dot{M}=10^{-7},~L_{\rm ph}=7.3\times10^{44},~X=0.2$; 2a-c: $a=1,~\dot{M}=10^{-7},~L_{\rm ph}=2.2\times10^{45},~X=0.6$; 3a-c: $a=2,~\dot{M}=10^{-7},~L_{\rm ph}=8.0\times10^{45},~X=2.0$; 4a-c: $a=4,~\dot{M}=10^{-7},~L_{\rm ph}=4.0\times10^{45},~X=2.0$; 5a-c: $a=4,~\dot{M}=10^{-8},~L_{\rm ph}=4.0\times10^{43},~X=2.0$. Average radio luminosity integrated over frames is $0.01,% \ 0.10,% \ 0.20,% \ 0.35% \ {\rm and}\ 0.05~{\rm mJy}$ for rows 1-5, respectively.
Open with DEXTER

In systems with $a\la2$ and $X\la 1$ our radio spectra significantly diverge from those of STB. First, the location and extent of the transition region between optically thin and optically thick parts of the spectrum are different. Second, the shape of the transition region is more complicated in our models. Third, our models radiate much less energy in the optically thick part of the spectrum than their STB counterparts (the difference can amount to two orders of magnitude).

The latter result can be understood as a simple consequence of the smaller spatial extent of our H II regions (the optically thick flux is roughly proportional to the projected surface area of the ionized part of the wind). In principle, the remaining predictions could be verified by spectroscopic observations. Unfortunately, observational data, especially at higher frequencies, are still too poor to discriminate between various theoretical models. The broadest survey available, reported by Miko\lajewska et al. (2002a,b) is based on mm/submm observations of a sample of 20 S-type systems in quiescence. Radio emission from these systems is found to be optically thick at least up to $\sim $1.3 mm $(243~{\rm GHz} = \nu_t$ = turnover frequency). This is compatible both with the STB model, which for typical quiescent S-type systems predicts $\nu_{\rm t}\ga 300~{\rm GHz}$ (Seaquist et al. 1993), and with our simulations (see Fig. 4).

At present the only system which allows for a quantitative analysis of the spectrum is CI Cyg, where $\nu_{\rm t}\approx 30~{\rm GHz}$. For the STB model the outcome of such an analysis is rather unfavourable. In their framework the orbital separation may be estimated from

 \begin{displaymath}a=300\bigg(\frac{T_{\rm e}}{10^4~{\rm K}}\bigg)^{-\frac{1}{2}... ...gg)^{\frac{1}{2}} \bigg(\frac{d}{{\rm kpc}}\bigg){~{\rm AU}}, \end{displaymath} (2)

where $T_{\rm e}$ is the electron temperature of the ionized wind, and $S_{\rm t}$ is the flux received at the turnover frequency. This estimate should be accurate within a factor of 2 for a range of X covering two orders of magnitude. However, in the case of CI Cyg it overestimates a by a factor of 35 ( $70~{\rm AU}$ compared to $\sim $2 AU obtained from the spectroscopic orbit solution. On the other hand, if one inserts a=2in (2) and calculates the turnover flux, then the derived $S_{\rm t}$ is 103 times lower than the actually observed one.

The STB framework also provides an estimate for $L_{\rm ph}$

 
$\displaystyle L_{\rm ph}=10^{56}\alpha_{\rm rec} \bigg(\frac{T_{\rm e}}{10^4~{\... ...}{{\rm mJy}}\bigg) \bigg(\frac{d}{{\rm kpc}}\bigg)^2{~{\rm phot}~{\rm s}^{-1}},$     (3)

where $S_{\rm\nu}$ is the flux received in the optically thin part of the spectrum at frequency $\nu $ (Ivison & Seaquist 1995). However, for CI Cyg formula (3) yields a value 20 times lower than that obtained from optical/UV H I and He II emission lines and bf+ff continuum.

Other inconsistencies between the observed spectrum of CI Cyg and the STB model are discussed by Miko\lajewska & Ivison (2001), who suggest that the STB approach might not apply to this system because it is likely that the red giant fills or nearly fills its Roche lobe, and the mass loss is concentrated in a stream flowing through the inner Lagrangian point. If this is really the case, then our models, which predict concentration of the outflow in the equatorial plane and formation of the circumsecondary disk, should provide a better approximation of the observed spectrum than that obtained within the STB framework.

Unfortunately, in this particular system they do not perform much better. A glance at Fig. 4 indicates that in order to obtain $\nu_{\rm t}$ as low as $\sim $30 GHz we would have to assume an unacceptably low $L_{\rm ph}$ and/or $\dot{M}$ much lower than $10^{-7}~M_{\hbox{$\odot$ }}~{\rm yr}^{-1}$. A likely solution to this problem is suggested by the spectrum for $a=1~{\rm AU},\ X=0.2$ in Fig. 4, which is the only one showing an excess in the optically thick part. With increasing $\dot{M}$ and $L_{\rm ph}$ the excess would shift to higher frequencies, mimicking the turnover observed in CI Cyg. The fact that the spectrum obtained for $a=1~{\rm AU}$ offers a better fitting possibility for the system with $a=2~{\rm AU}$ seems to indicate that our model of the latter underestimates the density of the circumsecondary disk and/or overestimates the density of the funnels. Such a conclusion is compatible with arguments concerning the outflow through the inner Lagrangian point. The deciding tests of our results will become possible when high-resolution radio maps of S-type systems are obtained. Our results suggest that S-type systems will be interesting targets for e-MERLIN and ALMA.

While the models presented here are closer to reality than those obtained within the STB approach, there is still a considerable room for improvements. We have only marginally resolved the disk around the secondary, whose shape and extent may strongly influence shape and extent of the H II region. To improve on that, future work should include effects of radiation transfer and viscosity, increase the mass-resolution of the SPH code and, accordingly, decrease its time-step. Note, however, that with radiation transfer and viscosity included, the simple scaling relation presented in Fig. 5 would not work. This means that RG wind models extending to hundreds of ${\rm AU}$ would have to be obtained in order to generate H II regions emitting as much energy in the optically thin regime as the observed ones. Such simulations would push the CPU requirements beyond currently acceptable limits. When they are hopefully done in the future and a reliable thermal structure of the flow is obtained, the thermal ionization should be taken into account, which at least in some cases may significantly contribute to the radio spectra.

Acknowledgements
This research was supported by the Committee for Scientific Research through grants 2P03D 014 19 and 5P03D 019 20.

References

 

Copyright ESO 2003