A&A 397, 825-829 (2003)
DOI: 10.1051/0004-6361:20021599
Images for an isothermal ellipsoidal gravitational
lens from a single real algebraic equation
H. Asada1,2 -
T. Hamana3 -
M. Kasai1
1 - Faculty of Science and Technology,
Hirosaki University, Hirosaki 036-8561, Japan
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str. 1,
85741 Garching, Germany
3 -
National Astronomical Observatory,
Mitaka 181-8588, Japan
Received 30 September 2002 / Accepted 4 November 2002
Abstract
We present explicit expressions for the lens equation
for a cored isothermal ellipsoidal gravitational lens as
a single real sixth-order algebraic equation in two approaches;
2-dimensional Cartesian coordinates and 3-dimensional polar ones.
We find a condition for physical solutions which correspond to
at most five images. For a singular isothermal ellipsoid,
the sixth-order equation is reduced to fourth-order one for which
analytic solutions are well-known. Furthermore, we derive
analytic criteria for determining the number of images
for the singular lens, which give us simple expressions for
the caustics and critical curves.
The present formulation offers a useful way for studying
galaxy lenses frequently modeled as isothermal ellipsoids.
Key words: gravitational lensing -
galaxies: general -
cosmology: theory
Gravitational lensing due to a galaxy is important for
probing mass distributions and determining cosmological
parameters. Galaxy lenses are often modeled as cored
isothermal ellipsoids. Although the ellipsoidal model is
quite simple, it enables us to understand a number of
physical properties of the galactic lens. Furthermore, it
fits well with mass profiles implied by observations
(For instance, Binney & Tremaine 1987).
Until now, the lens equation for the cored isothermal ellipsoid
has been solved numerically as a nonlinearly coupled system.
For a binary gravitational lens, it has recently been shown
that the lens equation is reduced to a single real fifth-order
algebraic equation (Asada 2002).
Also for a singular isothermal ellipsoidal lens, furthermore,
the apparently coupled lens equations can be reduced to
a single equation (Schneider et al. 1992),
though explicit expressions were not given there.
Along this course, we reexamine the coupled lens equations
for the cored isothermal ellipsoid.
The main purpose of the present paper is to show that
they are reduced to a single equation with a condition for
physical solutions and to give analytic criteria for determining
the number of images for isothermal ellipsoidal lenses.
First, let us consider the singular isothermal ellipsoidal lens
with ellipticity
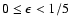 .
A condition that
the surface mass density projected onto the lens plane
must be non-negative everywhere puts a constraint
on the ellipticity as
.
A condition that
the surface mass density projected onto the lens plane
must be non-negative everywhere puts a constraint
on the ellipticity as
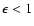 .
A tighter constraint
.
A tighter constraint
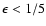 comes from that the density
contours must be convex, which is reasonable
for an isolated relaxed system.
The lens equation is expressed as
comes from that the density
contours must be convex, which is reasonable
for an isolated relaxed system.
The lens equation is expressed as
where
 and
and
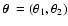 denote
the positions of the source and images, respectively.
denote
the positions of the source and images, respectively.
For simplicity, we introduce variables as
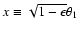 ,
,
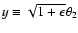 ,
,
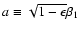 and
and
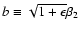 ,
so that the lens equation
can be rewritten as
,
so that the lens equation
can be rewritten as
| a |
= |
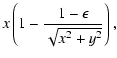 |
(3) |
| b |
= |
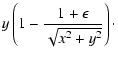 |
(4) |
There are two symmetry axes in the ellipsoid,
a=0 and b=0.
We consider a source on the axis a=0.
In this case, we can find analytic solutions for
the lens equation as follows.
We can make a replacement as
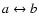 ,
,
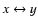 and
and
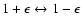 to obtain solutions for b=0.
to obtain solutions for b=0.
For a=0, Eq. (
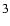 )
becomes
)
becomes
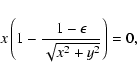 |
(5) |
which means
or
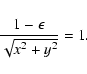 |
(7) |
In the case of x=0, Eq. (
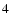 )
becomes
)
becomes
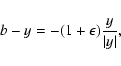 |
(8) |
which is solved as
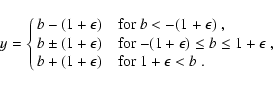 |
(9) |
Here, we should pay attention to the cases of
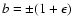 ,
since they produce a solution at the singularity
(x, y)=(0, 0) of the potential.
,
since they produce a solution at the singularity
(x, y)=(0, 0) of the potential.
Next, we consider the case of Eq. (
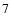 ).
Let us investigate the two cases,
).
Let us investigate the two cases,
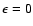 and
and
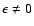 separately.
For
separately.
For
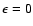 ,
Eq. (
,
Eq. (
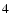 )
means
b=0, so that images become a ring as
)
means
b=0, so that images become a ring as
Below, we assume
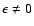 .
Eliminating
.
Eliminating
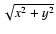 from Eqs. (
from Eqs. (
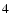 )
and (
)
and (
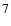 ), we obtain
), we obtain
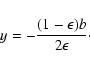 |
(11) |
Substituting this into y in Eq. (
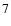 ),
we obtain
),
we obtain
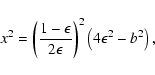 |
(12) |
which has real solutions if and only if
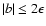 ,
,
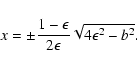 |
(13) |
Consequently, Eqs. (
 )
and (
)
and (
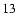 )
show that four, two or one images occur for
)
show that four, two or one images occur for
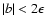 ,
,
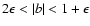 or
or
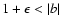 ,
respectively.
,
respectively.
In the similar manner, we obtain the solutions for b=0.
A point is that
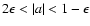 can hold
only for
can hold
only for
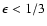 .
.
Here, we consider off-axis sources (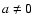 and
and 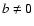 ).
In this case, Eqs. (
).
In this case, Eqs. (
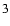 )
and
(
)
and
(
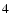 )
show
)
show 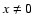 and
and 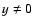 .
Eliminating
.
Eliminating
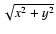 from Eqs. (
from Eqs. (
 )
and (
)
and (
 ), we obtain
), we obtain
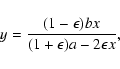 |
(14) |
which determines y uniquely for any given x.
For finite b, Eq. (
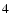 )
means that
y is also finite, so that
)
means that
y is also finite, so that
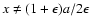 from Eq. (
from Eq. (
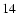 ).
Substituting Eq. (
).
Substituting Eq. (
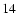 )
into Eq. (
)
into Eq. (
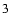 ),
we obtain the fourth-order polynomial for x as
),
we obtain the fourth-order polynomial for x as
| D(x) |
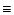 |
![$\displaystyle \left[(a-x)^2-(1-\epsilon)^2\right]
[(1+\epsilon)a-2\epsilon x]^2
+(1-\epsilon)^2b^2(a-x)^2$](/articles/aa/full/2003/03/aah4057/img63.gif) |
|
| |
= |
0 , |
(15) |
where we used 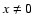 .
.
The number of real roots for a fourth-order equation is
discussed by the discriminant D4 (e.g. van der Waerden 1966),
which becomes for Eq. (
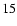 )
)
![$\displaystyle D_4=-64a^2b^2\epsilon^2(1-\epsilon)^{12}
\left[\left(a^2+b^2-4\epsilon^2\right)^3
+108a^2b^2\epsilon^2\right] .$](/articles/aa/full/2003/03/aah4057/img65.gif) |
|
|
(16) |
Namely, if
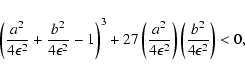 |
(17) |
the number of real roots is either four or zero, which is
determined as four by explicit solutions for on-axis sources.
Otherwise, it is two.
However, the number does not necessarily indicate
that of images as shown below.
Since 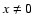 for off-axis sources, Eq. (
for off-axis sources, Eq. (
 )
is rewritten as
)
is rewritten as
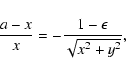 |
(18) |
whose right-hand side is necessarily negative
since
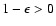 .
As a result, we find that any solution of the lens equation
must satisfy
.
As a result, we find that any solution of the lens equation
must satisfy
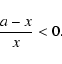 |
(19) |
This implies that x<0 or a<x for positive a,
while x<a or 0<x for negative a.
It should be noted that Eq. (
 )
always holds in the limit of
)
always holds in the limit of 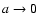 .
.
Let us investigate the number of roots in
(a-x)/x > 0,
namely an interval between 0 and a.
We find out
| D(a) |
= |
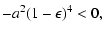 |
(20) |
| D(0) |
= |
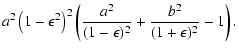 |
(21) |
If a and b satisfy
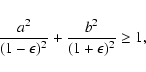 |
(22) |
D(0) is not negative, so that D(x)=0 has at least
one root between 0 and a.
For
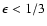 ,
Eq. (
,
Eq. (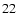 )
implies
)
implies
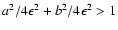 ,
so that
the left-hand side of Eq. (
,
so that
the left-hand side of Eq. (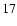 )
becomes positive.
Hence, D4 is negative, so that D(x)=0 has two roots.
As a result, it has only one root in the interval, which means
only one image appears.
Unless Eq. (
)
becomes positive.
Hence, D4 is negative, so that D(x)=0 has two roots.
As a result, it has only one root in the interval, which means
only one image appears.
Unless Eq. (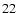 )
holds, D(0) is negative, so that
the number of roots for D(x)=0 for
(a-x)/x < 0,
namely that of images are four or two, respectively
for D4>0 or <0.
)
holds, D(0) is negative, so that
the number of roots for D(x)=0 for
(a-x)/x < 0,
namely that of images are four or two, respectively
for D4>0 or <0.
The inner and outer caustics (Fig. 1) are given by
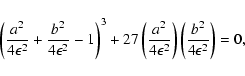 |
(23) |
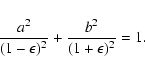 |
(24) |
The inner caustic given by Eq. (
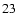 )
is an asteroid
which is parametrized as
)
is an asteroid
which is parametrized as
| a |
= |
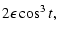 |
(25) |
| b |
= |
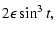 |
(26) |
where
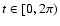 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{caustics.eps}
\end{figure}](/articles/aa/full/2003/03/aah4057/Timg86.gif) |
Figure 1:
Caustics for a singular isothermal ellipsoidal lens
in the physical coordinates
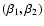 .
For .
For
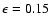 ,
the solid curve denotes the inner caustic,
and the dashed one for the outer caustic. Sources locate at
(0, 0.1), (0, 0.5) and (0, 1.3), denoted by
the circle, filled disk and square, respectively. ,
the solid curve denotes the inner caustic,
and the dashed one for the outer caustic. Sources locate at
(0, 0.1), (0, 0.5) and (0, 1.3), denoted by
the circle, filled disk and square, respectively. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{critical.eps}
\end{figure}](/articles/aa/full/2003/03/aah4057/Timg87.gif) |
Figure 2:
Critical curves for a singular isothermal ellipsoidal
lens in the physical coordinates
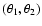 .
For .
For
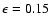 ,
the solid curve denotes the outer critical curve
which corresponds to the inner caustic. The origin corresponds to
the outer caustic. The images correspond to the sources in Fig. 1. ,
the solid curve denotes the outer critical curve
which corresponds to the inner caustic. The origin corresponds to
the outer caustic. The images correspond to the sources in Fig. 1. |
| Open with DEXTER |
The critical curves on the lens plane correspond to the caustics
on the source plane (Schneider et al. 1992).
We introduce the polar coordinates as
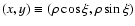 .
By substituting Eqs. (
.
By substituting Eqs. (
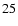 )
and (
)
and (
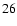 )
with
)
with 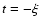 into the lens Eqs. (
into the lens Eqs. (
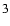 )
and
(
)
and
(
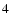 ), we obtain the parametric representation of
the critical curve as
), we obtain the parametric representation of
the critical curve as
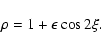 |
(27) |
In the similar manner to the outer caustic given by
Eq. (
 ), we find
), we find
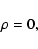 |
(28) |
which is the origin in (x, y) (Fig. 2).
Let us consider a cored isothermal ellipsoidal lens
with the angular core radius c.
The lens equation is expressed as
| a |
= |
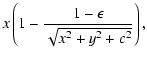 |
(29) |
| b |
= |
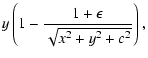 |
(30) |
which are apparently similar to the set of
Eqs. (
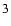 )
and (
)
and (
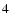 ).
However, there are differences in their algebraic properties
as shown below.
).
However, there are differences in their algebraic properties
as shown below.
We consider a source on the axis a=0.
In this case, we can find analytic solutions for
the lens equation as follows.
To consider the case of b=0, it is enough to make a
replacement as
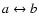 ,
,
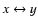 and
and
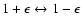 .
.
For a=0, Eq. (
 )
becomes
)
becomes
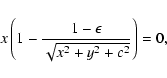 |
(31) |
which means
or
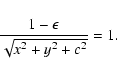 |
(33) |
In the case of x=0, Eq. (
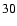 )
becomes the fourth-order polynomial for y as
)
becomes the fourth-order polynomial for y as
| E(y) |
 |
![$\displaystyle y^4-2by^3+[b^2+c^2-(1+\epsilon)^2]y^2
-2bc^2y+b^2c^2$](/articles/aa/full/2003/03/aah4057/img105.gif) |
|
| |
= |
0 . |
(34) |
Explicit solutions for a fourth-order equation take
a lengthy form (e.g. van der Waerden 1966).
Now, Eq. (
 )
implies
)
implies
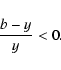 |
(35) |
Using
| E(0) |
= |
b2c2>0 , |
(36) |
| E(b) |
= |
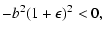 |
(37) |
we find that E(y) has at least one zero point
between 0 and b. In other words, E(y)=0 has
at most three roots for (b-y)/y<0.
Next, we consider the case of Eq. (
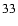 ).
For
).
For
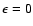 ,
Eq. (
,
Eq. (
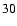 )
means b=0,
so that a ring image appears at
)
means b=0,
so that a ring image appears at
We assume
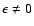 in the following.
Eliminating
in the following.
Eliminating
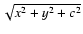 from Eqs. (
from Eqs. (
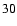 )
and (
)
and (
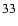 ), we obtain
), we obtain
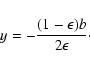 |
(39) |
Substituting this into y in Eq. (
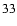 ),
we obtain
),
we obtain
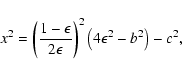 |
(40) |
which has the real solutions
![\begin{displaymath}x=\pm\frac{1-\epsilon}{2\epsilon} \sqrt{4\epsilon^2
\Bigl[1-\left(\frac{c}{1-\epsilon}\right)^2\Bigr]-b^2} ,
\end{displaymath}](/articles/aa/full/2003/03/aah4057/img116.gif) |
(41) |
if and only if
![\begin{displaymath}b^2\leq 4\epsilon^2
\Bigl[1-\left(\frac{c}{1-\epsilon}\right)^2\Bigr] \cdot
\end{displaymath}](/articles/aa/full/2003/03/aah4057/img117.gif) |
(42) |
Here, we consider off-axis sources (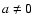 and
and 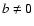 ).
In this case, Eqs. (
).
In this case, Eqs. (
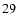 )
and
(
)
and
(
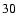 )
imply
)
imply 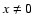 and
and 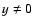 .
Eliminating
.
Eliminating
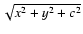 from Eqs. (
from Eqs. (
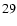 )
and (
)
and (
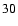 ), we obtain
), we obtain
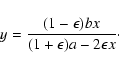 |
(43) |
Equation (
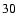 )
shows that y is finite
for finite b, so that
)
shows that y is finite
for finite b, so that
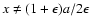 from
Eq. (
from
Eq. (
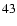 ).
Substituting Eq. (
).
Substituting Eq. (
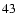 )
into Eq. (
)
into Eq. (
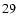 ),
we obtain the sixth-order polynomial for x as
),
we obtain the sixth-order polynomial for x as
This equation has at most six real solutions whose
analytic expressions can not be given by algebraic manners
(e.g. van der Waerden 1966).
As shown below, however, six real roots never mean
six images.
In the same manner as for the singular isothermal ellipsoid,
we obtain a condition for x as
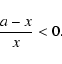 |
(45) |
Let us prove that there exists a root between 0 and a.
We can find out
| F(0) |
= |
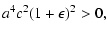 |
(46) |
| F(a) |
= |
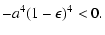 |
(47) |
Since F(x) is a continuous function, F(x)=0 has
at least one root in the interval.
For
(a-x)/x < 0, consequently, F(x)=0 has at most
five solutions. Since the polynomial is sixth-order,
the discriminant is not sufficient to determine the exact
number of roots. Hence, the determination is beyond
the scope of our paper.
Up to this point, we have used 2-dimensional Cartesian
coordinates: We must solve Eq. (
 )
and
choose appropriate roots which satisfy the inequality
by Eq. (
)
and
choose appropriate roots which satisfy the inequality
by Eq. (
 ).
Here, we adopt 3-dimensional polar coordinates
to simplify the inequality, as shown below.
By taking c as a fictitious third dimension, we define
).
Here, we adopt 3-dimensional polar coordinates
to simplify the inequality, as shown below.
By taking c as a fictitious third dimension, we define
where we can assume
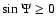 .
Then, Eqs. (
.
Then, Eqs. (
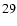 )
and (
)
and (
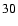 )
are rewritten as
)
are rewritten as
| a |
= |
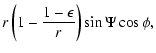 |
(52) |
| b |
= |
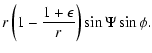 |
(53) |
We concentrate on off-axis sources (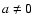 and
and 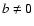 ).
).
Eliminating 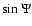 from Eqs. (
from Eqs. (
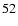 )
and (
)
and (
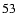 ), we obtain
), we obtain
![\begin{displaymath}\tan\phi=\frac{b[r-(1-\epsilon)]}{a[r-(1+\epsilon)]} ,
\end{displaymath}](/articles/aa/full/2003/03/aah4057/img145.gif) |
(54) |
which determines  uniquely for any given r.
Equations (
uniquely for any given r.
Equations (
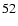 )
and (
)
and (
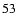 )
show that
)
show that
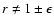 for nonvanishing a and b,
since
for nonvanishing a and b,
since 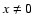 and
and 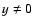 mean
mean
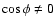 and
and
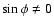 .
Hence, Eqs. (
.
Hence, Eqs. (
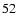 )
and (
)
and (
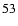 )
can be rewritten as
)
can be rewritten as
| x |
= |
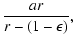 |
(55) |
| y |
= |
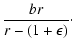 |
(56) |
Substituting these into
r2=x2+y2+c2, we obtain
the sixth-order equation for r as
which has at most six real solutions.
Let us show that there are at most five roots
compatible with 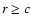 .
Using
.
Using
![$G(c)=-a^2c^2[c-(1+\epsilon)]^2-b^2c^2[c-(1-\epsilon)]^2 < 0$](/articles/aa/full/2003/03/aah4057/img159.gif) and
and
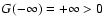 for a continuous function G(r),
we find that G(r)=0 has at least one root for r<c.
Consequently, it has at most five roots for
for a continuous function G(r),
we find that G(r)=0 has at least one root for r<c.
Consequently, it has at most five roots for 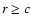 .
.
We should note that r and  are not enough to
determine the location of images. A strategy for determining
the location is as follows:
First, we solve Eq. (
are not enough to
determine the location of images. A strategy for determining
the location is as follows:
First, we solve Eq. (
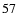 )
for
)
for 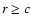 .
Next, we substitute r into Eqs. (
.
Next, we substitute r into Eqs. (
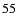 )
and (
)
and (
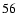 )
to obtain the image position as
(x, y).
)
to obtain the image position as
(x, y).
We have carefully reexamined the lens equation for a cored
isothermal ellipsoid both in 2-dimensional Cartesian and
3-dimensional polar coordinates.
We have shown that the nonlinearly coupled equations are
reduced to a single real sixth-order polynomial
Eq. (
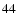 )
or (
)
or (
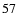 ), which coincides
with the fourth-order equation for a singular isothermal ellipsoid
as the core radius approaches zero.
For the singular case, explicit expressions of image positions
for sources on the symmetry axis are given by Eqs. (
), which coincides
with the fourth-order equation for a singular isothermal ellipsoid
as the core radius approaches zero.
For the singular case, explicit expressions of image positions
for sources on the symmetry axis are given by Eqs. (
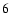 ),
(
),
(
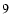 ), (
), (
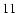 )
and (
)
and (
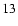 ).
Furthermore, we have presented analytic criteria for determining
the number of images, which correspond to the caustics
given by Eqs. (
).
Furthermore, we have presented analytic criteria for determining
the number of images, which correspond to the caustics
given by Eqs. (
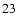 )
and (
)
and (
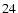 ).
Consequently, analytic expressions for the critical curves are
given by Eqs. (
).
Consequently, analytic expressions for the critical curves are
given by Eqs. (
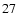 )
and (
)
and (
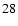 ).
We have shown for the cored case that a condition
Eq. (
).
We have shown for the cored case that a condition
Eq. (
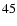 )
or (
)
or (
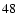 )
gives us physical solutions of the sixth-order polynomial,
which are at most five images.
)
gives us physical solutions of the sixth-order polynomial,
which are at most five images.
The present formulation based on the one-dimensional Eq. (
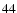 )
or (
)
or (
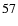 )
enables us to study
a cored isothermal ellipsoidal lens with considerable efficiency
and accuracy, in comparison with previous two-dimensional
treatments for which there are no well-established numerical methods
(Press et al. 1988).
Particularly for a source close to the caustics, the image
position is unstable so that careful computations are needed.
The amount of computations can be reduced by our approach.
As a result, it must be powerful in rapid and accurate parameter
fittings to observational data.
)
enables us to study
a cored isothermal ellipsoidal lens with considerable efficiency
and accuracy, in comparison with previous two-dimensional
treatments for which there are no well-established numerical methods
(Press et al. 1988).
Particularly for a source close to the caustics, the image
position is unstable so that careful computations are needed.
The amount of computations can be reduced by our approach.
As a result, it must be powerful in rapid and accurate parameter
fittings to observational data.
Acknowledgements
We would like to thank M. Bartelmann for carefully reading
the manuscript and for a number of encouraging comments.
H.A. would like to thank M. Bartelmann, L. Rezzolla and J. Miller
for hospitality at the Max-Planck-Institut für Astrophysik
and the Scuola Internazionale Superiore di Studi Avanzati,
respectively, where a part of this work was done.
This work was supported in part by a Japanese Grant-in-Aid
for Scientific Research from the Ministry of Education,
No. 13740137 (H.A.) and the Sumitomo Foundation (H.A.).
- Asada, H. 2002, A&A, 390, L11
In the text
NASA ADS
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics
(Princeton University Press)
In the text
- Press, W. H., Flannery, B. P., Teukolsy, S. A., &
Vetterling, W. T. 1988, Numerical Recipes in C
(Cambridge University Press)
In the text
- Schneider, P., Ehlers, J., & Falco, E. E. 1992,
Gravitational Lenses (Springer-Verlag)
In the text
- van der Waerden, B. L. 1966, Algebra I (Springer)
In the text
Copyright ESO 2003
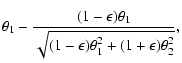
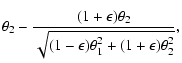
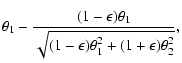
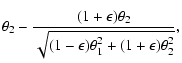
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
so that the lens equation
can be rewritten as
,
so that the lens equation
can be rewritten as
![]() )
becomes
)
becomes
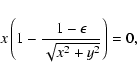
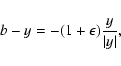
![]() ).
Let us investigate the two cases,
).
Let us investigate the two cases,
![]() and
and
![]() separately.
For
separately.
For
![]() ,
Eq. (
,
Eq. (
![]() )
means
b=0, so that images become a ring as
)
means
b=0, so that images become a ring as
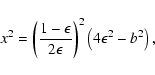
![]() can hold
only for
can hold
only for
![]() .
.
![]() )
)
![]() for off-axis sources, Eq. (
for off-axis sources, Eq. (
![]() )
is rewritten as
)
is rewritten as
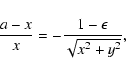
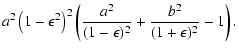
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{caustics.eps}
\end{figure}](/articles/aa/full/2003/03/aah4057/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{critical.eps}
\end{figure}](/articles/aa/full/2003/03/aah4057/Timg87.gif)
![]() .
By substituting Eqs. (
.
By substituting Eqs. (
![]() )
and (
)
and (
![]() )
with
)
with ![]() into the lens Eqs. (
into the lens Eqs. (
![]() )
and
(
)
and
(
![]() ), we obtain the parametric representation of
the critical curve as
), we obtain the parametric representation of
the critical curve as
![]() )
becomes
)
becomes
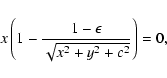
![]() )
becomes the fourth-order polynomial for y as
)
becomes the fourth-order polynomial for y as
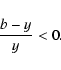
![]() ).
For
).
For
![]() ,
Eq. (
,
Eq. (
![]() )
means b=0,
so that a ring image appears at
)
means b=0,
so that a ring image appears at
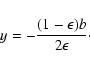
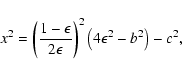
![\begin{displaymath}x=\pm\frac{1-\epsilon}{2\epsilon} \sqrt{4\epsilon^2
\Bigl[1-\left(\frac{c}{1-\epsilon}\right)^2\Bigr]-b^2} ,
\end{displaymath}](/articles/aa/full/2003/03/aah4057/img116.gif)
![\begin{displaymath}b^2\leq 4\epsilon^2
\Bigl[1-\left(\frac{c}{1-\epsilon}\right)^2\Bigr] \cdot
\end{displaymath}](/articles/aa/full/2003/03/aah4057/img117.gif)
![]() from Eqs. (
from Eqs. (
![]() )
and (
)
and (
![]() ), we obtain
), we obtain
![]() are not enough to
determine the location of images. A strategy for determining
the location is as follows:
First, we solve Eq. (
are not enough to
determine the location of images. A strategy for determining
the location is as follows:
First, we solve Eq. (
![]() )
for
)
for ![]() .
Next, we substitute r into Eqs. (
.
Next, we substitute r into Eqs. (
![]() )
and (
)
and (
![]() )
to obtain the image position as
(x, y).
)
to obtain the image position as
(x, y).
![]() )
or (
)
or (
![]() )
enables us to study
a cored isothermal ellipsoidal lens with considerable efficiency
and accuracy, in comparison with previous two-dimensional
treatments for which there are no well-established numerical methods
(Press et al. 1988).
Particularly for a source close to the caustics, the image
position is unstable so that careful computations are needed.
The amount of computations can be reduced by our approach.
As a result, it must be powerful in rapid and accurate parameter
fittings to observational data.
)
enables us to study
a cored isothermal ellipsoidal lens with considerable efficiency
and accuracy, in comparison with previous two-dimensional
treatments for which there are no well-established numerical methods
(Press et al. 1988).
Particularly for a source close to the caustics, the image
position is unstable so that careful computations are needed.
The amount of computations can be reduced by our approach.
As a result, it must be powerful in rapid and accurate parameter
fittings to observational data.