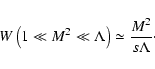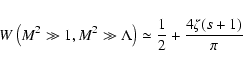A&A 397, 777-788 (2003)
DOI: 10.1051/0004-6361:20021548
Cosmic ray transport in anisotropic magnetohydrodynamic turbulence
II. Shear Alfvèn waves
A. Teufel 1 - I. Lerche 2 -
R. Schlickeiser 1
1 - Institut für Theoretische Physik, Lehrstuhl IV:
Weltraum- und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum, Germany
2 -
Department of Geological Sciences, University of South
Carolina, Columbia, SC 29208, USA
Received 31 May 2002 / Accepted 23 October 2002
Abstract
Observations of interstellar turbulence imply that
the power spectrum of the wave turbulence must
be highly anisotropic. This anisotropy has to be included
when transport of high energy cosmic rays in
the Galaxy is discussed. Here we evaluate the relevant cosmic ray
transport parameters in the presence of anisotropic shear Alfvèn wave turbulence,
which have no contribution from the transit-time damping interaction and are
entirely due to gyroresonant interactions.
By averaging the respective Fokker-Planck coefficient over the particle
pitch-angle we calculate the momentum and spatial diffusion coefficients for
different anisotropy parameters.
For strongly perpendicular turbulence (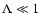 )
we obtain that the momentum
diffusion coefficient is proportional to
)
we obtain that the momentum
diffusion coefficient is proportional to
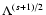 ,
whereas for
strongly parallel turbulence (
,
whereas for
strongly parallel turbulence (
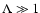 )
the momentum diffusion
coefficient is a constant.
We also calculate the anisotropy dependence of the spatial diffusion coefficient and
the mean free path for pure Alfvèn turbulence.
For all coefficients we discuss the rigidity dependence for
different cosmic ray particles and compare with earlier calculations of transport parameters
for slab-type Alfvèn turbulence.
)
the momentum diffusion
coefficient is a constant.
We also calculate the anisotropy dependence of the spatial diffusion coefficient and
the mean free path for pure Alfvèn turbulence.
For all coefficients we discuss the rigidity dependence for
different cosmic ray particles and compare with earlier calculations of transport parameters
for slab-type Alfvèn turbulence.
Key words: magnetohydrodynamics (MHD) - plasmas - turbulence - cosmic rays - ISM: magnetic fields
Observations of interstellar scintillations (Rickett 1990; Spangler
1991), general theoretical considerations (Goldreich & Sridhar
1995), and comparison of interstellar radiative cooling in HII-regions
and in the diffuse interstellar medium with linear Landau damping estimates for
fast-mode decay (Lerche & Schlickeiser 2001a), all strongly imply that
the power spectrum of wave turbulence in the interstellar medium must
be highly anisotropic. It is not clear from the observations whether the
turbulence spectrum is oriented mainly parallel or mainly perpendicular to the
ambient magnetic field, either will satisfy the needs of balancing wave damping
energy input against radiative cooling.
This anisotropy must be included when transport of high energy cosmic rays in
the Galaxy is discussed (Chandran 2001; Yan & Lazarian 2002).
In the first paper of this series (Lerche & Schlickeiser
2001b - hereafter referred to LS) we have started to evaluate the relevant cosmic ray
transport parameters in the presence of anisotropic fast
magnetosonic plasma wave turbulence. All technical details of the
calculation of Fokker-Planck coefficients and their relation
to the transport parameters of the cosmic ray diffusion-convection equation
(as the parallel mean free path, the rate of adiabatic deceleration and
the momentum diffusion coefficient) were presented there (see LS Sects. 2 and 3).
However, in order to calculate these transport parameters
in the interstellar medium
we have to investigate (analogously to the analysis in LS for fast magnetosonic
waves) also the influence of the anisotropy parameter on
the Fokker-Planck coefficients for shear Alfvèn waves, because
interstellar plasma turbulence most probably is a mixture of fast magnetosonic waves and
shear Alfvèn waves. This analysis is the subject of the present paper. In order to
avoid unnecessary repititions we will use the same notation and will
frequently refer to equations in paper LS.
As LS we base our analysis on the quasilinear approximation.
Because of the complicated nonlinear equations of motion of charged
particles in partially random electromagnetic fields there are only
two methods to study theoretically particle acceleration: (i) numerical
simulations of highly idealized configurations, and
(ii) quasilinear theory. Both have their advantages and shortcomings, and they
complement each other. The quasilinear approach to the interaction of charged
particles with parially random electromagnetic fields (
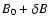 ,
,
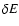 )
is
a first-order perturbation calculation in the ratio
)
is
a first-order perturbation calculation in the ratio
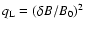 and requires
smallness of this ratio with respect to unity.
and requires
smallness of this ratio with respect to unity.
Obviously, besides limited computer power numerical simulations require the
precise knowledge of many important input plasma parameters as well as the
specification of initial and boundary conditions which
at least for the more distant cosmic objects are not known.
By chosing the wrong input plasma quantities one may end up in an
irrelevant range of solution space. Of course, when all these input
quantities are known and given, the simulations result in a very accurate and
detailed description of the acceleration processes on all spatial, momentum and
time scales of interest.
On the other hand, the discussion of the accuracy of quasilinear theory
is legendary in the literature of theoretical plasma physics especially in
its application to plasma fusion devices.
The quasilinear approach to the interaction of charged
particles with parially random electromagnetic fields (
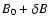 ,
,
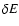 )
is
a first-order perturbation calculation in the ratio
)
is
a first-order perturbation calculation in the ratio
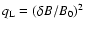 and requires
smallness of this ratio with respect to unity. More quantitaively,
in the context of astrophysical
cosmic ray propagation studies Michalek & Ostrowski (1996) have compared the quasilinear
values of cosmic ray transport parameters with the results of Monte Carlo
simulations of the cosmic ray transport. They calculated numerically the trajectories in phase
space of relativistic cosmic ray particles in an uniform magnetic field of strength B0with superposed plane parallel propagating Alfvèn waves of total magnetic field strength
and requires
smallness of this ratio with respect to unity. More quantitaively,
in the context of astrophysical
cosmic ray propagation studies Michalek & Ostrowski (1996) have compared the quasilinear
values of cosmic ray transport parameters with the results of Monte Carlo
simulations of the cosmic ray transport. They calculated numerically the trajectories in phase
space of relativistic cosmic ray particles in an uniform magnetic field of strength B0with superposed plane parallel propagating Alfvèn waves of total magnetic field strength
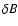 .
By averaging over these trajectories the values of the transport parameters were
derived. The calculations were performed for various wave amplitudes
.
By averaging over these trajectories the values of the transport parameters were
derived. The calculations were performed for various wave amplitudes
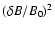 ranging
from 0.225 to 4.0 for a Kolmogorov turbulence spectrum. Over the whole range of wave
amplitudes the agreement between simulated and quasilinear values of the cosmic ray transport
parameters is remarkably good, and within factors of order 2 even at large amplitudes. These
calculations demonstrate that, for small-amplitude (
ranging
from 0.225 to 4.0 for a Kolmogorov turbulence spectrum. Over the whole range of wave
amplitudes the agreement between simulated and quasilinear values of the cosmic ray transport
parameters is remarkably good, and within factors of order 2 even at large amplitudes. These
calculations demonstrate that, for small-amplitude (
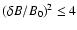 )
plasma wave fields,
quasilinear theory provides a reasonable description of cosmic ray transport.
)
plasma wave fields,
quasilinear theory provides a reasonable description of cosmic ray transport.
From careful measurements of the interstellar turbulence Spangler (1991) as well as Minter &
Spangler (1997) estimate the mean of the interstellar magnetic field fluctuations due to
turbulence of
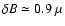 G. Combined with studies of the rotation and dispersion
measure of 185 pulsars (Lyne & Smith 1989) that indicate an average field strength of about 2-
G. Combined with studies of the rotation and dispersion
measure of 185 pulsars (Lyne & Smith 1989) that indicate an average field strength of about 2-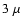 G, it seems that for the interstellar medium the requirement of small turbulence
amplitudes (
G, it seems that for the interstellar medium the requirement of small turbulence
amplitudes (
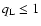 )
for the applicability of the quasilinear approximation
is well fulfilled.
)
for the applicability of the quasilinear approximation
is well fulfilled.
A second assumption for the applicability of the quasilinear approximation concerns
the coherence scale of the fluctuating electromagnetic fields 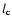 which in our
case is related to the plasma wave autocorrelation time
which in our
case is related to the plasma wave autocorrelation time 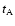 ,
i.e. the time for
relative phases of the waves to randomize due to the difference in wave phase
velocities, through
,
i.e. the time for
relative phases of the waves to randomize due to the difference in wave phase
velocities, through
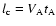 .
The wave autocorrelation time has to be smaller
than the particle trapping time. The physical arguments for this condition
have been discussed by e.g. Karimabadi et al. (1992). Because the quasilinear
Fokker-Planck description of cosmic ray transport is based
on the Markovian assumption, it is necessary to introduce a decay in the wave's
autocorrelation function entering the Fokker-Plack coefficients in order to avoid
their quasi-periodicity which would be in conflict with the Markovian assumption.
Karimabadi et al. (1992) have discussed both linear and nonlinear processed providing
the decays of correlation functions.
.
The wave autocorrelation time has to be smaller
than the particle trapping time. The physical arguments for this condition
have been discussed by e.g. Karimabadi et al. (1992). Because the quasilinear
Fokker-Planck description of cosmic ray transport is based
on the Markovian assumption, it is necessary to introduce a decay in the wave's
autocorrelation function entering the Fokker-Plack coefficients in order to avoid
their quasi-periodicity which would be in conflict with the Markovian assumption.
Karimabadi et al. (1992) have discussed both linear and nonlinear processed providing
the decays of correlation functions.
Probably the most relevant decay process
for interstellar cosmic ray propagation is the presence of interstellar
wave damping in the partially ionised diffuse intercloud medium at a rate
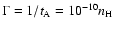 s-1 (Kulsrud & Pearce 1969; Ferriere et al. 1988).
As has been shown by Schlickeiser & Achatz (1993) plasma wave damping leads to
Breit-Wigner-type resonance broadening, and due to the overlapping of the
broadened resonances in phase space the correlation functions decay to zero at times
s-1 (Kulsrud & Pearce 1969; Ferriere et al. 1988).
As has been shown by Schlickeiser & Achatz (1993) plasma wave damping leads to
Breit-Wigner-type resonance broadening, and due to the overlapping of the
broadened resonances in phase space the correlation functions decay to zero at times
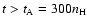 yrs avoiding
their quasi-periodic behaviour. Therefore a
necessary condition for the validity of interstellar quasilinear cosmic ray transport
parameters is
yrs avoiding
their quasi-periodic behaviour. Therefore a
necessary condition for the validity of interstellar quasilinear cosmic ray transport
parameters is
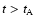 which is equivalent to the condition that the derived
scattering mean free path
which is equivalent to the condition that the derived
scattering mean free path
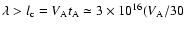 km s-1)
km s-1)
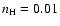 pc is larger than the coherence scale. Phenomenologically inferred estimates of the interstellar cosmic ray
scattering length from the cosmic ray lifetime measurements indicate values of
pc is larger than the coherence scale. Phenomenologically inferred estimates of the interstellar cosmic ray
scattering length from the cosmic ray lifetime measurements indicate values of
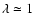 pc so that this additional condition also is fulfilled.
pc so that this additional condition also is fulfilled.
Adopting the same anisotropic magnetic turbulence tensor (Eqs. LS(10)-LS(12))
the three relevant quasilinear
Fokker-Planck coefficients for shear Alfvèn waves with vanishing
magnetic helicity are (Schlickeiser 2002,
Ch. 13.1)
with
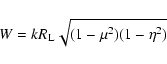 |
(2) |
where I0j reflects the two intensity components of turbulence forward and
backward to the ambient magnetic field, and we have taken both to have the same
spectral shape to be in accord with observations. Then
I0+ +I0-=I0,
where I0 is given by Eq. LS(4).
In Eq. (2) we introduced the cosmic ray particle
gyroradius
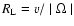 .
.
One immediately notes that if n = 0 in Eq. (1) all three
Fokker-Planck coefficients are zero,
so there is no transit-time damping contribution for Alfvèn waves. The
contributions for
therefore 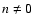 are customarily referred to as gyroresonant contributions.
are customarily referred to as gyroresonant contributions.
Because we are concerned with the transport of very energetic
particles
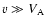 we do not lose much generality if we extend the
turbulence power spectrum
to infinetely large wavenumbers, i.e.
we do not lose much generality if we extend the
turbulence power spectrum
to infinetely large wavenumbers, i.e.
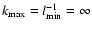 .
After some straightforward algebra, one can write the gyroresonance
contributions as
.
After some straightforward algebra, one can write the gyroresonance
contributions as
where
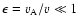 .
Together with
.
Together with
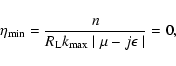 |
(4) |
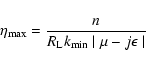 |
(5) |
and
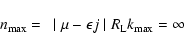 |
(6) |
we obtain
Without further information on the relative strengths of I0- to
I0+ it is not possible to take the gyroresonance contributions
much further. In the following we treat the symmetric case
where
I0-=I0+, to illuminate the changes in the Fokker-Planck
coefficients brought about by the anisotropic nature of the plasma
wave turbulence.
From Eq. (7) we obtain for the symmetric wave case
I0-=I0+
Note that
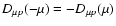 is antisymmetric in
is antisymmetric in 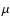 ,
so that the rate of adiabatic acceleration D in Eq. (LS(8))
,
so that the rate of adiabatic acceleration D in Eq. (LS(8))
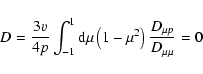 |
(9) |
is identically zero in the symmetric wave intensity case
I0+=I0-=I0/2.
Again from Eq. (7) we obtain
and
Now we must approximate the term
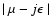 .
For doing this we consider two cases.
.
For doing this we consider two cases.
This case is treated in detail in Appendices A and B, where we derive
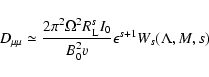 |
(12) |
with
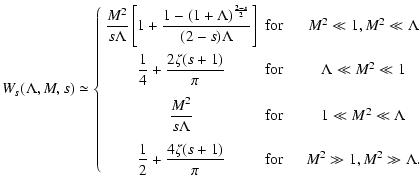 |
|
|
(13) |
With
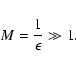 |
(14) |
Equation (13) reduces to
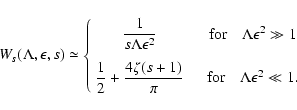 |
(15) |
For large pitch angles
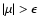 we obtain (again from Appendices A and B)
we obtain (again from Appendices A and B)
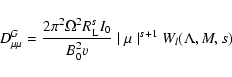 |
(16) |
with
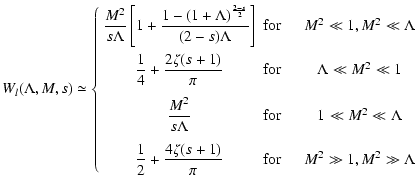 |
|
|
(17) |
but now with
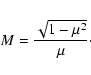 |
(18) |
Using Eq. (10) and the definition of the momentum diffusion coefficient A (Eq. LS(9)) we obtain for cosmic rays with gyroradii
much less than
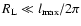
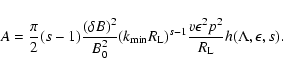 |
(19) |
In deriving this equation we have used
| |
|
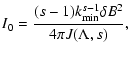 |
|
| |
|
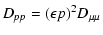 |
(20) |
and
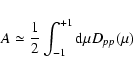 |
(21) |
to lowest order in 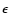 .
For the anisotropy function
.
For the anisotropy function
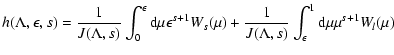 |
|
|
(22) |
and with Eq. (15) we obtain
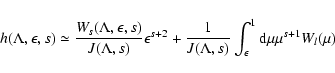 |
(23) |
with the integral
from LS.
For this case it is easy to write down Wl (see Eq. (17))
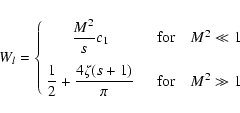 |
(25) |
with
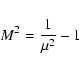 |
(26) |
and
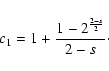 |
(27) |
For h we use
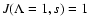 from Eq. (24) and split the second integral of Eq. (23)
from Eq. (24) and split the second integral of Eq. (23)
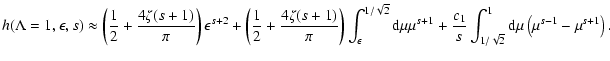 |
|
|
(28) |
These integrals are elementary and we obtain to lowest order in 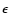
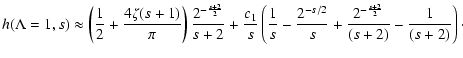 |
|
|
(29) |
In this case we obtain from Eq. (17)
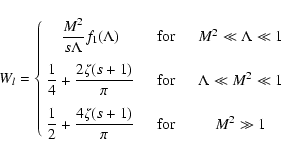 |
(30) |
with the function
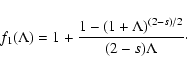 |
(31) |
For h we now find
These integrals are elementary too, so that
to lowest order in 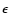 .
If we use
.
If we use
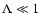 we find
we find
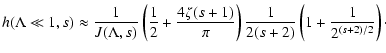 |
|
|
(34) |
Now we must calculate
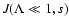 .
To do this we can use
.
To do this we can use
to obtain
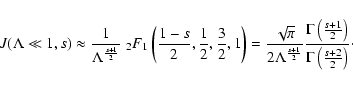 |
(36) |
According to Eq. (34) we thus derive
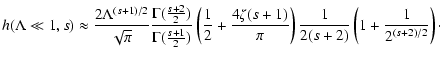 |
|
|
(37) |
In this case we obtain
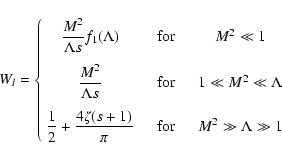 |
(38) |
and for h we now find
where we have used
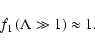 |
(40) |
Like in the cases before the integrals are elementary yielding
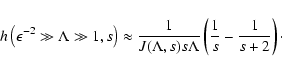 |
(41) |
Now we must calculate
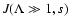 .
With Eq. (24) it is easy to show that
.
With Eq. (24) it is easy to show that
So the final result for this case is
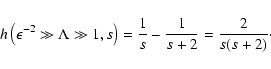 |
(43) |
In this case we always have
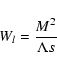 |
(44) |
and
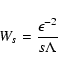 |
(45) |
and with Eq. (42) we obtain for the function h
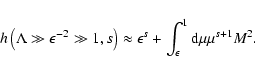 |
(46) |
To lowest order in 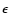 we find the same result as in the third case
we find the same result as in the third case
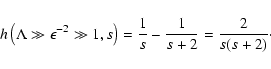 |
(47) |
So we always have in the case of parallel turbulence
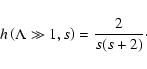 |
(48) |
In Table 1 we have listed the results for the three different cases of anisotropy and for s=5/3. Also we have calculated the
three cases numerically. The agreement ist very good in the cases two and three and acceptable in the first case.
Figure 1 shows the numerical result for the case s=5/3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3732F1.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg135.gif) |
Figure 1:
Numerical result for the anisotropy function
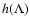 for the case s=5/3.
for the case s=5/3. |
| Open with DEXTER |
So the final result of this chapter is, that we can write down the momentum diffusion coefficient A as
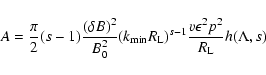 |
(49) |
with the energy independent anisotropy function
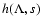 .
Introducing the rigidity r and the parameter r0
.
Introducing the rigidity r and the parameter r0
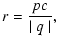 |
|
|
|
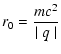 |
|
|
(50) |
we can write Eq. (49) as
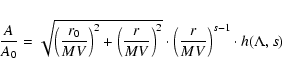 |
(51) |
with
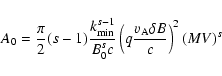 |
(52) |
where we have used
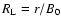 and
and
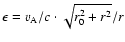 .
It is easy to see, that we obtain the same A0 for electrons, positrons and protons. Figure 2 shows A / A0 as a function
of the rigidity for electrons, positrons and protons for small, medium and large values of the anisotropy parameter
.
It is easy to see, that we obtain the same A0 for electrons, positrons and protons. Figure 2 shows A / A0 as a function
of the rigidity for electrons, positrons and protons for small, medium and large values of the anisotropy parameter
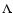 and s=5/3. Figure 1 shows the rigidity independent function
and s=5/3. Figure 1 shows the rigidity independent function
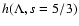 .
At nonrelativistic rigidities we find
.
At nonrelativistic rigidities we find
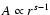 whereas at relativistic rigidities
whereas at relativistic rigidities
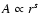 .
Also note that for relativistic rigidities electrons, positrons and protons approach the same A / A0.
For all the calculations we restricted our analysis to 1 < s < 2,
.
Also note that for relativistic rigidities electrons, positrons and protons approach the same A / A0.
For all the calculations we restricted our analysis to 1 < s < 2,
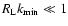 and
and
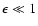 .
Note also that for electrons and positrons of rigidities
r < 102 MV deviations
of the Alfvèn branch dispersion relation from the linear form
.
Note also that for electrons and positrons of rigidities
r < 102 MV deviations
of the Alfvèn branch dispersion relation from the linear form
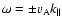 have
been neglected in our calculations.
have
been neglected in our calculations.
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{H3732F2.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg149.gif) |
Figure 2:
The momentum diffusion coefficient A/A0 for electrons, positrons and protons for
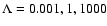 . . |
| Open with DEXTER |
From LS and with
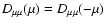 we have
we have
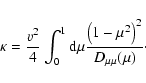 |
(53) |
Together with Eq. (12) and Eq. (16) we obtain
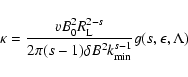 |
(54) |
with
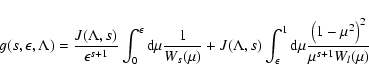 |
(55) |
and
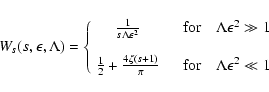 |
(56) |
and with Eq. (17) for Wl. This can be written as
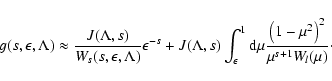 |
(57) |
Here the function g can be written as
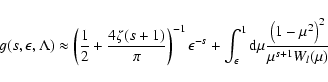 |
(58) |
what is equal to
To lowest order in 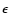 we finally find
we finally find
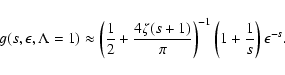 |
(60) |
For this case we can do the same calculations and approximations as in the case before and we obtain
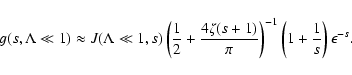 |
(61) |
But in the third case we obtain with our approximations
In this last case we obtain for the function g
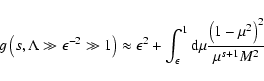 |
(63) |
where we used Eq. (42) again. To lowest order in 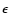 we finally obtain
we finally obtain
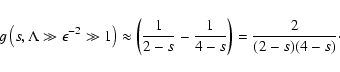 |
(64) |
If we restrict our analysis to the case of
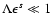 we always have
we always have
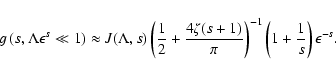 |
(65) |
We have also calculated the ratio g / J for the this case and for s=5/3 numerically. For s=5/3 the analytic result is
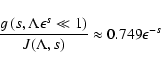 |
(66) |
whereas the numerical calculations yields
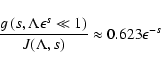 |
(67) |
in reasonable agreement. For s=5/3 we calculated the function g for different anisotropy parameters in Table 2.
If we restrict our analysis to
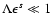 we obtain for the spatial diffusion coefficient
we obtain for the spatial diffusion coefficient
![\begin{displaymath}%
{\kappa \over \kappa_0} = { \left( {r \over MV} \right)^3 \...
...{r \over MV} \right)^2
\right]^{(s+1)/2} } \cdot J(\Lambda, s)
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img177.gif) |
(68) |
with
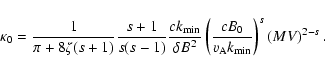 |
(69) |
It is easy to see, that we obtain the same 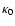 for electrons, positrons and protons.
Figure 3 shows the function
for electrons, positrons and protons.
Figure 3 shows the function
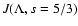 and Fig. 4 shows
and Fig. 4 shows
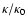 as a function
of the rigidity for electrons, positrons and protons for small, medium and large values of the anisotropy parameter
as a function
of the rigidity for electrons, positrons and protons for small, medium and large values of the anisotropy parameter
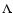 and s=5/3.
For nonrelativistic rigidities we obtain
and s=5/3.
For nonrelativistic rigidities we obtain
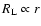 ,
,
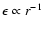 and
and
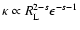 .
Therefore we find that for
nonrelativistic rigidities the spatial diffusion coefficients are proportional to r3 whereas for relativistic
rigidities
.
Therefore we find that for
nonrelativistic rigidities the spatial diffusion coefficients are proportional to r3 whereas for relativistic
rigidities
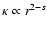 .
At relativistic rigidities the diffusion coefficients of
electrons, positrons and protons are the same.
.
At relativistic rigidities the diffusion coefficients of
electrons, positrons and protons are the same.
We now are able to calculate the mean free path which is connected with the spatial diffusion coefficient through
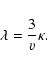 |
(70) |
This can be written as
![\begin{displaymath}%
{\lambda \over \lambda_0} = { \left( {r \over MV} \right) ^...
...eft( {r \over MV} \right)^2
\right]^{s/2}} \cdot J(\Lambda, s)
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img187.gif) |
(71) |
with
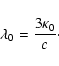 |
(72) |
Figure 5 shows
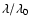 as a function
of the rigidity for electrons, positrons and protons for small, medium and large values of the anisotropy parameter
as a function
of the rigidity for electrons, positrons and protons for small, medium and large values of the anisotropy parameter
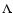 and s=5/3.
and s=5/3.
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{H3732F4.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg189.gif) |
Figure 4:
The spatial diffusion coefficient
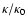 for electrons, positrons and protons for
for electrons, positrons and protons for
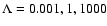 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{H3732F5.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg190.gif) |
Figure 5:
The mean free path
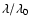 for electrons, positrons and protons for
for electrons, positrons and protons for
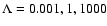 . . |
| Open with DEXTER |
We are also able to give asymptotic formulas for the rigidity.
We can use this formulas for the mean free path if
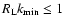 and
and
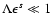 .
.
In order to discuss the influence of the turbulence anisotropy
it is instructive to compare our results with the spatial and
momentum diffusion coefficients calculated for pure slab-type turbulence
(Schlickeiser 1989, 2002; Dung & Schlickeiser 1990a,b).
In the limit of vanishing magnetic and cross helicity, and
turbulence spectral indices s<2, one finds
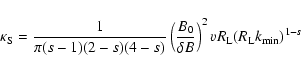 |
(74) |
and
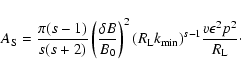 |
(75) |
Using Eq. (50) we obtain for the ratio of the momentum diffusion coefficient for anisotropic
Alfvènic turbulence to slab Alfvènic turbulence
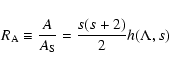 |
(76) |
which is independent of cosmic ray rigidity and only determined by the anisotropy function
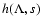 and the turbulence spectral index s. According to the behaviour of
the anisotropy function summarized in Table 1 we find values for the ratio (76)
close to unity for isotropic turbulence
(
and the turbulence spectral index s. According to the behaviour of
the anisotropy function summarized in Table 1 we find values for the ratio (76)
close to unity for isotropic turbulence
(
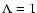 )
and strongly parallel turbulence (
)
and strongly parallel turbulence (
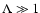 ), whereas for
strongly perpendicular turbulence (
), whereas for
strongly perpendicular turbulence (
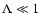 )
momentum diffusion
is much reduced as compared to the slab case because the ratio (76) varies
proportional to
)
momentum diffusion
is much reduced as compared to the slab case because the ratio (76) varies
proportional to
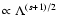 .
For isotropic and strongly parallel turbulence
the momentum diffusion coefficient agree well with the slab momentum diffusion coefficient,
both in rigidity dependence and in absolute value.
.
For isotropic and strongly parallel turbulence
the momentum diffusion coefficient agree well with the slab momentum diffusion coefficient,
both in rigidity dependence and in absolute value.
Using Eq. (60) we obtain for the ratio of the spatial diffusion coefficient for anisotropic
turbulence to slab turbulence
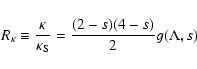 |
(77) |
with the anisotropy function
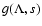 from Table 2.
We first note that for relativistic cosmic ray particles this ratio is independent of
cosmic ray rigidity but much larger unity due to the large factor
from Table 2.
We first note that for relativistic cosmic ray particles this ratio is independent of
cosmic ray rigidity but much larger unity due to the large factor
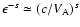 .
Obviously, for non-slab turbulence relativistic cosmic ray diffusion
is much more rapid than for slab turbulence, i.e. the diffusion time scale to
.
Obviously, for non-slab turbulence relativistic cosmic ray diffusion
is much more rapid than for slab turbulence, i.e. the diffusion time scale to
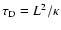 ,
where L denotes a length scale, is much shorter in anisotropically
distributed Alfvènic turbulence than in slab Alfvènic turbulence of equal total magnitude
,
where L denotes a length scale, is much shorter in anisotropically
distributed Alfvènic turbulence than in slab Alfvènic turbulence of equal total magnitude
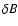 .
.
Secondly, we note that for non-relativistic cosmic ray particles the spatial diffusion
coefficient ratio (77) becomes smaller due to its
rigidity dependence,
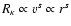 .
This modified rigidity dependence
can have significant implications for quantitative studies of semirelativistic
cosmic rays as the Boron-Carbon ratio (e.g. Strong & Moskalenko 1998;
Maurin et al. 2001) that sofar are based on slab transport parameters only.
.
This modified rigidity dependence
can have significant implications for quantitative studies of semirelativistic
cosmic rays as the Boron-Carbon ratio (e.g. Strong & Moskalenko 1998;
Maurin et al. 2001) that sofar are based on slab transport parameters only.
With this second paper we have continued to evaluate the relevant cosmic ray
transport parameters in the presence of anisotropic plasma wave turbulence.
Using the estimates of the anisotropy parameter in the strongly
parallel and perpendicular regimes, based on linear Landau damping balancing
radiative loss in the diffuse interstellar medium,
we have calculated the Fokker-Planck coefficients,
the momentum (A) and spatial diffusion coefficient (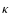 )
and the mean free path
of cosmic ray particles for pure Alfvèn waves.
We show that for Alfvèn waves there is no transit-time damping
interaction so that the contributions to spatial and momentum diffusion
solely result from gyroresonant interactions.
)
and the mean free path
of cosmic ray particles for pure Alfvèn waves.
We show that for Alfvèn waves there is no transit-time damping
interaction so that the contributions to spatial and momentum diffusion
solely result from gyroresonant interactions.
We determined the detailed anisotropy dependence of the spatial and momentum diffusion
coefficients in the limits of strongly parallel, strongly perpendicular and isotropic
Alfvènic turbulence. We also compared our results with earlier calculations of these two
transport parameters in slab Alfvènic turbulence. Here we found that
for isotropic and strongly parallel turbulence
the momentum diffusion coefficient agree well with the slab momentum diffusion coefficient,
both in rigidity dependence and in absolute value. However, in case of spatial diffusion
we established that in non-slab Alfvènic turbulence relativistic cosmic ray diffusion
is much more rapid than in slab Alfvènic turbulence of equal total magnitude
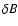 .
At non-relativistic cosmic ray rigidities anisotropic Alfvènic turbulence
yields a different rigidity dependence than slab Alfvènic turbulence.
.
At non-relativistic cosmic ray rigidities anisotropic Alfvènic turbulence
yields a different rigidity dependence than slab Alfvènic turbulence.
Combined with results for fast magnetosonic waves (LS) we will be able to determine
the cosmic ray transport parameters also for a mixed turbulence, because
interstellar plasma turbulence is a mixture of fast magnetosonic waves and shear
Alfvèn waves. This analysis will be the subject of the third paper of this
series.
Acknowledgements
We gratefully acknowledge support by the
Deutsche Forschungsgemeinschaft through Sonderforschungsbereich 191.
AT acknowledges the financial support by the Verbundforschung, grant DESY CH1PCA6.
We start from Eq. (10)
and use the substitution
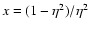 .
With this transformation we obtain
.
With this transformation we obtain
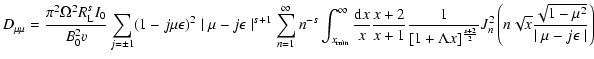 |
|
|
(79) |
with
![\begin{displaymath}%
x _{{\rm min}} = {1 \over {\rm min} ^{2} [1, \eta_{{\rm max}}]} - 1.
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img209.gif) |
(80) |
For small pitch angles
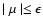 we can use
the approximation
we can use
the approximation
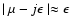 and
and
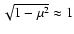 .
So we obtain
.
So we obtain
![$\displaystyle %
D_{\mu\mu} = {\pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I_{0} \over B...
...} {J _{n} ^{2} \left( n \sqrt{x} M \right) \over [1 + \Lambda x]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img213.gif) |
|
|
(81) |
with
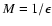 .
In lowest order of
.
In lowest order of 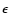 we can use
we can use
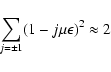 |
(82) |
to obtain approximately
![\begin{displaymath}%
D_{\mu\mu} \simeq {2 \pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I_...
...eft( n \sqrt{x} M \right) \over [1 + \Lambda x]^{s+2 \over 2}}
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img216.gif) |
(83) |
and
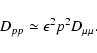 |
(84) |
For pitch angles
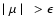 we can use
the approximation
we can use
the approximation
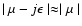 and
we obtain
and
we obtain
![$\displaystyle %
D_{\mu\mu} \simeq {\pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I_{0} \o...
...} {J _{n} ^{2} \left( n \sqrt{x} M \right) \over [1 + \Lambda x]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img220.gif) |
|
|
(85) |
with
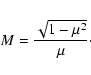 |
(86) |
To lowest order of 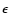 we can use Eq. (A.82) again. So we obtain
we can use Eq. (A.82) again. So we obtain
![$\displaystyle %
D_{\mu\mu} ^{G} \simeq
{2 \pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I...
...ver [1 + \Lambda x]^{s+2 \over 2}},\;
\;
D_{pp}\simeq \epsilon ^2p^2D_{\mu\mu}.$](/articles/aa/full/2003/03/aah3732/img221.gif) |
|
|
(87) |
For both cases we must calculate the expression
![\begin{displaymath}%
W( \Lambda, M, s, x_{{\rm min}}) =
\sum _{n=1} ^{\infty} n ...
...left(n \sqrt{x} M\right) \over [1 + \Lambda x] ^{s+2 \over 2}}
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img222.gif) |
(88) |
that is evaluated in Appendix B.
We restrict the analysis to cosmic ray particles with
gyroradii
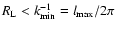 .
In this case
.
In this case
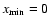 and we obtain
and we obtain
![$\displaystyle %
W(\Lambda, M, s, x_{{\rm min}} = 0) = W(\Lambda, M, s) = \sum _...
... _{n} ^{2} \left(n M x ^{1/2}\right) \over [1 + \Lambda x] ^{s+2 \over 2}}\cdot$](/articles/aa/full/2003/03/aah3732/img226.gif) |
|
|
(89) |
We can split this integral into two parts
and we must appoximate the two sums.
To approximate the first sum we use the Kapteyn series (Watson 1966, p. 557) for real 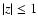
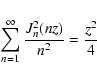 |
(91) |
so that
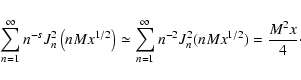 |
(92) |
The second sum can be approximated with
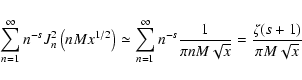 |
(93) |
where we neglect the oscillating part in the approximation of the Bessel
function for large arguments (Abramowitz & Stegun 1972). With
Eqs. (B.92) and (B.93) we obtain
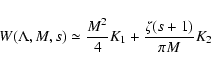 |
(94) |
with the integrals
![\begin{displaymath}%
K_{1}(M)=
\int _{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1}
[1 + \Lambda x]^{-{s+2\over 2}}
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img236.gif) |
(95) |
and
![\begin{displaymath}%
K_{2}(M)= \int _{M^{-2}} ^{\infty} {\rm d}x
{x+2 \over x+1}
x^{-3/2}[1 + \Lambda x]^{-{s+2\over 2}}.
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img237.gif) |
(96) |
We consider the two integrals in the limits of small and large M 2 and
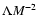 in turn.
in turn.
Here
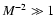 so that
so that
Likewise
![$\displaystyle K_2\simeq \int_{M^{-2}}^\infty
{\rm d}x x^{-3/2} [1 + \Lambda x]^...
...left({s+2 \over 2},{s+3 \over 2};{s+5 \over 2};{-M^2 \over \Lambda}\right)\cdot$](/articles/aa/full/2003/03/aah3732/img246.gif) |
|
|
(98) |
For Eq. (B.94) we then obtain approximately
in the limit
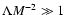 we find
we find
![$\displaystyle W\left(M^{2} \ll 1, M^2 \ll \Lambda, s\right)\simeq
{M^2\over s\L...
... }
\left[ 1+{1\over (2-s)\Lambda }\left[1-(1+\Lambda )^{(2-s)/2}\right] \right]$](/articles/aa/full/2003/03/aah3732/img252.gif) |
|
|
(100) |
where we have used the following approximations and relations for the hypergeometric functions (Magnus et al. 1966):
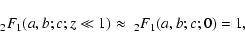 |
(101) |
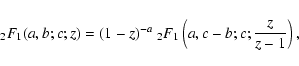 |
(102) |
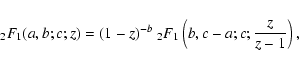 |
(103) |
and if c > a+b
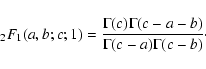 |
(104) |
Here we obtain for Eq. (B.99) approximately
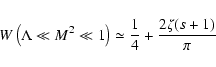 |
(105) |
where we have used the same relations and approximations (Eqs. (B.101)-(B.104))
as in the last case.
In this case
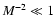 is a small quantity, and K1 is approximately
is a small quantity, and K1 is approximately
![\begin{displaymath}%
K_1 \simeq
2\int _{0} ^{M^{-2}} {\rm d}x [1 + \Lambda x]^{...
...mbda }\left[1 - \left(1 + \Lambda M^{-2}\right)^{-s/2}\right].
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img259.gif) |
(106) |
Likewise, K2 can be approximated as
For Eq. (B.94) we then obtain approximately
With the transformation formula (Abramowitz & Stegun 1972)
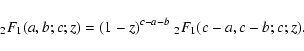 |
(109) |
Equation (B.108) reduces to
in the limit
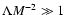 and
and
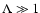 and with Eq. (B.101)-(B.104)
we obtain
and with Eq. (B.101)-(B.104)
we obtain
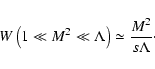 |
(111) |
In the last case we obtain for Eq. (B.108) approximately
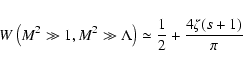 |
(112) |
where we have used the same relations and approximations as in the first three cases.
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions, National Bureau of Standards, Washington
In the text
- Chandran, B. 2001, Phys. Rev. Lett., 85, 4656
In the text
- Dung, R., & Schlickeiser, R. 1990a, A&A, 237, 504
In the text
NASA ADS
- Dung, R., & Schlickeiser, R. 1990b, A&A, 240, 537
NASA ADS
- Ferriere, K. M., Zweibel, E. G., & Shull, J. M. 1988, ApJ, 332, 984
In the text
NASA ADS
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763
In the text
NASA ADS
- Karimabadi, H., Krauss-Varban, D., & Terasawa, T. 1992, J. Geophys. Res., 97, 13853
In the text
- Kulsrud, R., & Perace, W. P. 1969, ApJ, 156, 445
In the text
NASA ADS
- Lerche, I., & Schlickeiser, R. 2001a, A&A, 366, 1008
In the text
NASA ADS
- Lerche, I., & Schlickeiser, R. 2001b, A&A, 378, 279 (LS)
In the text
NASA ADS
- Lyne, A. G., & Smith, F. G. 1989, MNRAS, 237, 533
In the text
NASA ADS
- Magnus, W., Oberhettinger, F., & Soni, R. P. 1966, Formulas and Theorems for the Special Functions of Mathematical Physics (Springer-Verlag Berlin, Heidelberg, New York)
In the text
- Maurin, D., Donato, F., Taillet, R., & Salati, P. 2001, ApJ, 555, 585
In the text
NASA ADS
- Minter, A. H., & Spangler, S. R. 1997, ApJ, 485, 182
In the text
NASA ADS
- Michalek, G., & Ostrowski, M. 1996, Nonlinear Processes in Geophysics, 3, 66
In the text
- Rickett, B. J. 1990, ARA&A, 28, 561
In the text
NASA ADS
- Schlickeiser, R. 1989, ApJ, 336, 264
In the text
NASA ADS
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Springer-Verlag, Berlin)
In the text
- Schlickeiser, R., & Achatz, U. 1993, J. Plasma Phys., 49, 63
In the text
- Spangler, S. R. 1991, ApJ, 376, 540
In the text
NASA ADS
- Strong, A. W., & Moskalenko, I. V. 1998, ApJ, 509, 212
In the text
NASA ADS
- Yan, H., & Lazarian, A. 2002, Phys. Rev. Lett., in press
In the text
- Watson, G. N. 1966, A treatise on the Theory of Bessel Functions (Cambridge University Press)
In the text
Copyright ESO 2003
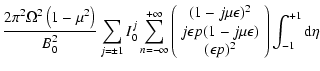
![$\displaystyle \times{1 + \eta ^2 \over \left[\eta ^2 + \Lambda\left(1-\eta^2\right)\right]^{s+2 \over 2} }$](/articles/aa/full/2003/03/aah3732/img43.gif)
![$\displaystyle \times \int _{k_{{\rm min}}} ^{k_{{\rm max}}} {\rm d}k k^{-s} \de...
...- jV_{{\rm A}}) \eta k + n \Omega\right] \left( {n J_{n}(W) \over W} \right) ^2$](/articles/aa/full/2003/03/aah3732/img44.gif)
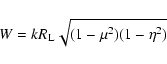
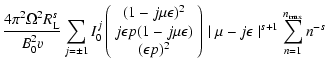
![$\displaystyle \times\int _{\eta_{{\rm min}}} ^{{\rm min}[1, \eta{_{\rm max}}]}
...
...+1} \over \left[\eta ^2 + \Lambda \left(1- \eta ^2\right)\right]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img51.gif)
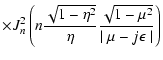
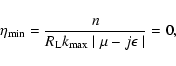
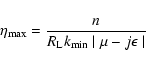
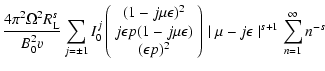
![$\displaystyle \times\int _{0} ^{{\rm min}[1, \eta{_{\rm max}}]} d \eta
{\left(1...
...+1} \over \left[\eta ^2 + \Lambda \left(1- \eta ^2\right)\right]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img58.gif)
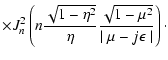
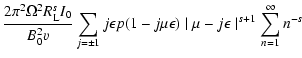
![$\displaystyle \times\int _{0} ^{{\rm min}[1, \eta{_{\rm max}}]} {\rm d} \eta
{\...
...+1} \over \left[\eta ^2 + \Lambda \left(1- \eta ^2\right)\right]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img62.gif)
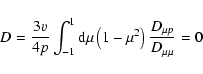
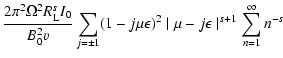
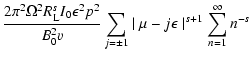
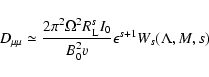
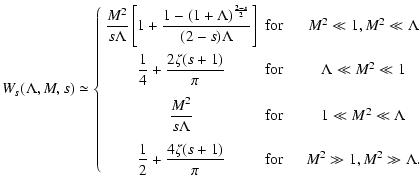
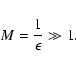
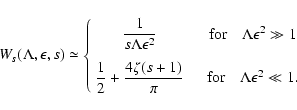
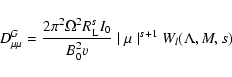
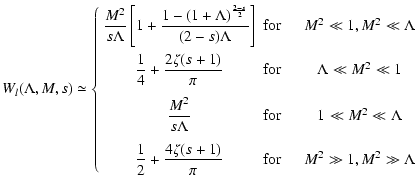
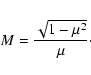
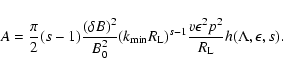
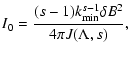
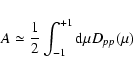
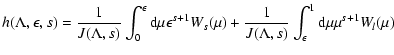
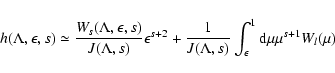
![$\displaystyle \int _{0} ^{1} {\rm d} \eta \left[ \eta ^{2} + \Lambda \left( 1 - \eta ^{2} \right) \right] ^{-(2+s)/2}$](/articles/aa/full/2003/03/aah3732/img86.gif)
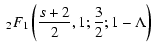
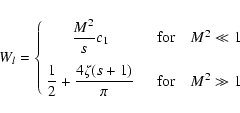
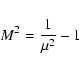
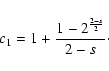
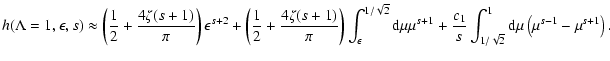
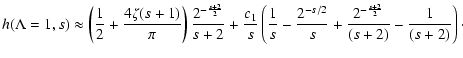
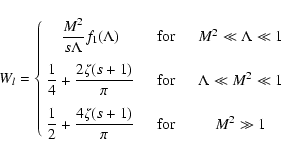
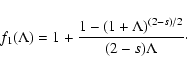
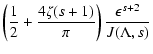
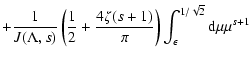
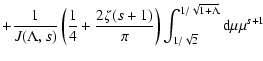
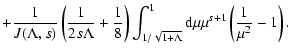
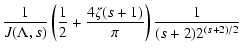
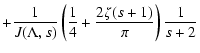
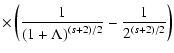
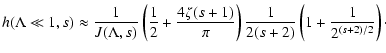
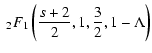
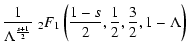
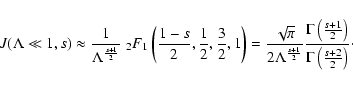
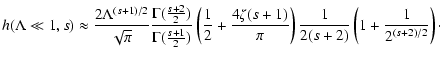
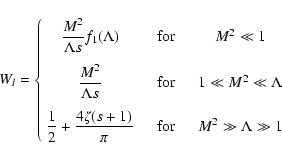
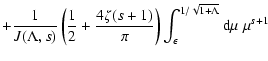
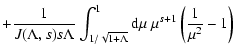
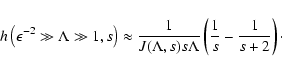
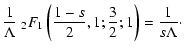
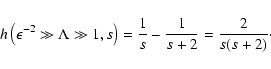
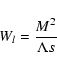
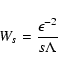
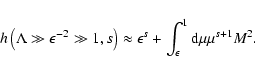
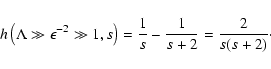
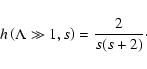
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3732F1.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg135.gif)
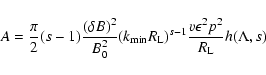
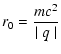
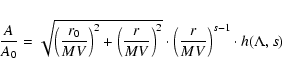
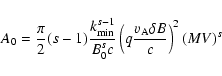
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{H3732F2.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg149.gif)
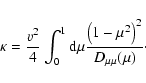
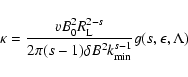
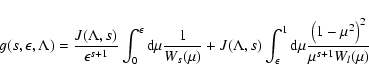
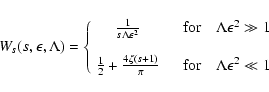
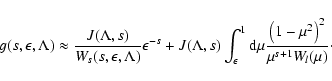
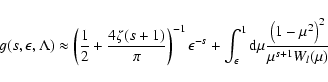
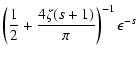
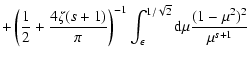
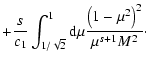
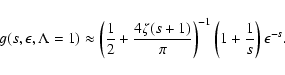
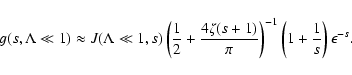
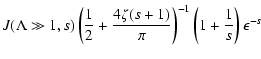
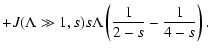
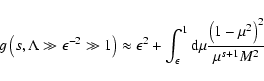
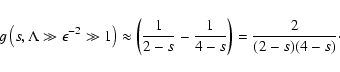
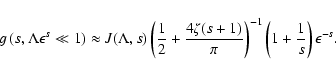
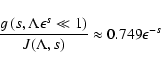
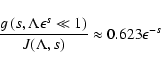
![\begin{displaymath}%
{\kappa \over \kappa_0} = { \left( {r \over MV} \right)^3 \...
...{r \over MV} \right)^2
\right]^{(s+1)/2} } \cdot J(\Lambda, s)
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img177.gif)
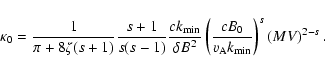
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H3732F3.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg185.gif)
![\begin{displaymath}%
{\lambda \over \lambda_0} = { \left( {r \over MV} \right) ^...
...eft( {r \over MV} \right)^2
\right]^{s/2}} \cdot J(\Lambda, s)
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img187.gif)
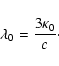
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{H3732F4.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg189.gif)
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{H3732F5.eps}\end{figure}](/articles/aa/full/2003/03/aah3732/Timg190.gif)
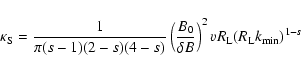
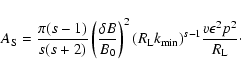
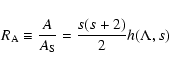
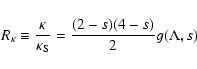
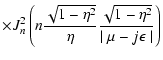
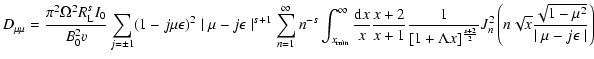
![\begin{displaymath}%
x _{{\rm min}} = {1 \over {\rm min} ^{2} [1, \eta_{{\rm max}}]} - 1.
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img209.gif)
![$\displaystyle %
D_{\mu\mu} = {\pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I_{0} \over B...
...} {J _{n} ^{2} \left( n \sqrt{x} M \right) \over [1 + \Lambda x]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img213.gif)
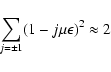
![\begin{displaymath}%
D_{\mu\mu} \simeq {2 \pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I_...
...eft( n \sqrt{x} M \right) \over [1 + \Lambda x]^{s+2 \over 2}}
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img216.gif)
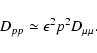
![$\displaystyle %
D_{\mu\mu} \simeq {\pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I_{0} \o...
...} {J _{n} ^{2} \left( n \sqrt{x} M \right) \over [1 + \Lambda x]^{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img220.gif)
![$\displaystyle %
D_{\mu\mu} ^{G} \simeq
{2 \pi ^{2} \Omega ^2 R_{{\rm L}} ^{s} I...
...ver [1 + \Lambda x]^{s+2 \over 2}},\;
\;
D_{pp}\simeq \epsilon ^2p^2D_{\mu\mu}.$](/articles/aa/full/2003/03/aah3732/img221.gif)
![\begin{displaymath}%
W( \Lambda, M, s, x_{{\rm min}}) =
\sum _{n=1} ^{\infty} n ...
...left(n \sqrt{x} M\right) \over [1 + \Lambda x] ^{s+2 \over 2}}
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img222.gif)
![$\displaystyle %
W(\Lambda, M, s, x_{{\rm min}} = 0) = W(\Lambda, M, s) = \sum _...
... _{n} ^{2} \left(n M x ^{1/2}\right) \over [1 + \Lambda x] ^{s+2 \over 2}}\cdot$](/articles/aa/full/2003/03/aah3732/img226.gif)
![$\displaystyle \int _{0} ^{M^{-2}} {{\rm d}x \over x} {x+2 \over x+1} [1+ \Lambda x] ^{-(s+2)/2}$](/articles/aa/full/2003/03/aah3732/img228.gif)
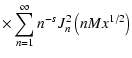
![$\displaystyle +\int _{M^{-2}} ^{\infty} {{\rm d}x \over x} {x+2 \over x+1}
[1+ ...
... x] ^{-(s+2)/2} \sum _{n=1} ^{\infty} n^{-s}
J_{n} ^{2} \left(nM x^{1/2}\right)$](/articles/aa/full/2003/03/aah3732/img230.gif)
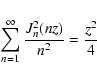
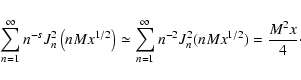
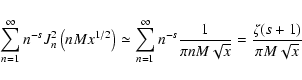
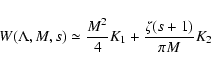
![\begin{displaymath}%
K_{1}(M)=
\int _{0} ^{M^{-2}} {\rm d}x {x+2 \over x+1}
[1 + \Lambda x]^{-{s+2\over 2}}
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img236.gif)
![\begin{displaymath}%
K_{2}(M)= \int _{M^{-2}} ^{\infty} {\rm d}x
{x+2 \over x+1}
x^{-3/2}[1 + \Lambda x]^{-{s+2\over 2}}.
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img237.gif)
![$\displaystyle 2\int _{0} ^{M^{-2}} {\rm d}x [1 + \Lambda x]^{-{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img241.gif)
![$\displaystyle \; \int _{0} ^1 {\rm d}x {x\over [1 + \Lambda x]^{s+2 \over 2}}
-\; \int _1 ^{M^{-2}} {\rm d}x [1 + \Lambda x]^{-{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img242.gif)
![$\displaystyle 2\int _{0} ^{M^{-2}} {\rm d}x [1 + \Lambda x]^{-{s+2 \over 2}}
-\int _1 ^{M^{-2}} {\rm d}x [1 + \Lambda x]^{-{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img243.gif)
![$\displaystyle {2\over s}{\partial \over \partial \Lambda }\int_0^1{\rm d}x
[1 + \Lambda x]^{-{s\over 2}}$](/articles/aa/full/2003/03/aah3732/img244.gif)
![$\displaystyle K_2\simeq \int_{M^{-2}}^\infty
{\rm d}x x^{-3/2} [1 + \Lambda x]^...
...left({s+2 \over 2},{s+3 \over 2};{s+5 \over 2};{-M^2 \over \Lambda}\right)\cdot$](/articles/aa/full/2003/03/aah3732/img246.gif)
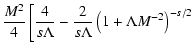
![$\displaystyle \left. + {4\over s(2-s)\Lambda ^2}\left[1-(1+\Lambda )^{(2-s)/2}\right] \right]$](/articles/aa/full/2003/03/aah3732/img249.gif)
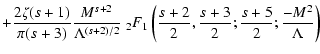
![$\displaystyle W\left(M^{2} \ll 1, M^2 \ll \Lambda, s\right)\simeq
{M^2\over s\L...
... }
\left[ 1+{1\over (2-s)\Lambda }\left[1-(1+\Lambda )^{(2-s)/2}\right] \right]$](/articles/aa/full/2003/03/aah3732/img252.gif)
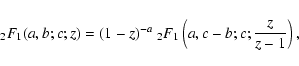
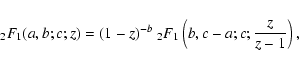
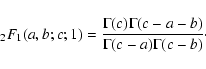
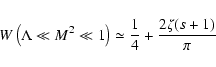
![\begin{displaymath}%
K_1 \simeq
2\int _{0} ^{M^{-2}} {\rm d}x [1 + \Lambda x]^{...
...mbda }\left[1 - \left(1 + \Lambda M^{-2}\right)^{-s/2}\right].
\end{displaymath}](/articles/aa/full/2003/03/aah3732/img259.gif)
![$\displaystyle 2\int_{M^{-2}}^\infty {\rm d}x x^{-3/2}\; [1 + \Lambda x]^{-{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img260.gif)
![$\displaystyle - \; \int_1^\infty {\rm d}x x^{-3/2}\; [1 + \Lambda x]^{-{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img261.gif)
![$\displaystyle +\int_0^{M^{-2}}{\rm d}x x^{-1/2}\; [1 + \Lambda x]^{-{s+2 \over 2}}
-\; \int_0^1{\rm d}x x^{-1/2}\; [1 + \Lambda x]^{-{s+2 \over 2}}$](/articles/aa/full/2003/03/aah3732/img262.gif)
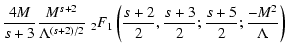
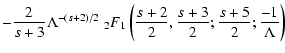
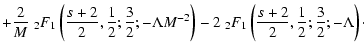
![$\displaystyle {M^2 \over s\Lambda }
\left[1-\left(1+\Lambda M^{-2}\right)^{-s/2}\right]$](/articles/aa/full/2003/03/aah3732/img267.gif)
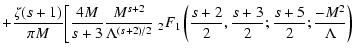
![$\displaystyle +{2\over M}
\; _2F_1\left( {s + 2 \over 2},{1\over 2};{3\over 2};...
...2\; _2F_1\left( {s + 2 \over 2},{1\over 2};{3\over 2};-\Lambda \right) \biggl].$](/articles/aa/full/2003/03/aah3732/img269.gif)
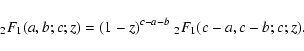
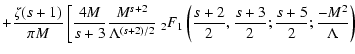
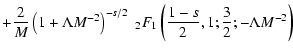
![$\displaystyle - \left. 2(1+\Lambda )^{-s/2}\; _2F_1\left({1-s\over 2},1;{3\over 2};-\Lambda \right) \right]$](/articles/aa/full/2003/03/aah3732/img273.gif)