A&A 397, 1019-1034 (2003)
DOI: 10.1051/0004-6361:20021537
E. R. Houdebine
Department of Physics (Theoretical Physics), Oxford University, 1 Keble Road, Oxford OX1 3NP, UK
Received 12 November 2001 / Accepted 1 August 2002
Abstract
We investigate the spectral signatures of stellar flares in the wavelength
range 3600 Å to 4500 Å and in broad band photometry. We study the
phenomenology of the spectral signatures and we found that flares are best
described by two main phases; an impulsive phase and a gradual
phase, for which the physical properties are different. Important spectral
differences between flares lead us to distinguish four main classes:
(i) solar-like chromospheric or two-ribbon flares, (ii) white-light flares,
(iii) combined white-light flares with distinct impulsive and gradual
phases, and (iv) non solar-like flares (usually occuring on RS CVn type stars). We show how this classification corresponds to substantial differences in the
physical properties of the flare components.
We compiled all available spectroscopic data for stellar flares. We found
several new empirical correlations between the time lags in the spectral lines
(rise and decay times). We found for instance that during the gradual phase,
the rise time in the H![]() line is well correlated to the rise time
in the Ca II K line, and that the Ca II K line is 1.63 times
slower to rise than the H
line is well correlated to the rise time
in the Ca II K line, and that the Ca II K line is 1.63 times
slower to rise than the H![]() line. Similar correlations were found
between the rise and decay times in these lines. These correlations are
evidence that there is a dominant mechanism commanding the temporal flux
evolutions during the gradual phase of flares. This mechanism applies on
time scales ranging from one minute to more than a hundred minutes.
line. Similar correlations were found
between the rise and decay times in these lines. These correlations are
evidence that there is a dominant mechanism commanding the temporal flux
evolutions during the gradual phase of flares. This mechanism applies on
time scales ranging from one minute to more than a hundred minutes.
We found correlations between the time lags and the maximum fluxes in the Johnson U-band and the spectral lines. These correlations show that the larger the flare the longer it takes to evolve.
We show that the maximum flux in the Johnson U-band correlates well, but not
linearly with the maximum flux in the H![]() line during the impulsive
phase, and over five orders of magnitude. We argue how this correlation can
provide constraints on the currently available models. The spectral line
maximum fluxes during the gradual phase also correlate with the Johnson
U-band flux, which demonstrates that somehow the impulsive and gradual phases
are physically linked. The correlation between the H
line during the impulsive
phase, and over five orders of magnitude. We argue how this correlation can
provide constraints on the currently available models. The spectral line
maximum fluxes during the gradual phase also correlate with the Johnson
U-band flux, which demonstrates that somehow the impulsive and gradual phases
are physically linked. The correlation between the H![]() and
Ca II K line fluxes during the gradual phase and the lack of
dependence of the flux ratio of those lines on flare magnitude
reveal that larger flares are not "hotter'' than smaller flares during the
gradual phase.
and
Ca II K line fluxes during the gradual phase and the lack of
dependence of the flux ratio of those lines on flare magnitude
reveal that larger flares are not "hotter'' than smaller flares during the
gradual phase.
We examine the behaviour of the spectral line widths: While the Ca II K line width shows essentially no detectable variation, the Balmer line widths show a complex dependency on the white light intensity. We distinguish three energy domains where the Balmer line widths exhibit a different behaviour: (i) for small flares, the widths remain rather constant as a function of white light intensity, which suggests that in this energy range the U-band is not a good diagnostic of the total energy release and that dense "kernels'' do not dominate the Balmer emission, (ii) for medium size flares, the widths rapidly increase with the U-band flux up to about 15 Å, which indicates that emission in the Balmer lines is then dominated by kernel emission, and (iii) for large flares the widths decrease with increasing U-band flux, which suggests that the Balmer line emission is then increasingly dominated by a radiative pumping process between the white light and the Balmer lines.
Finally, we remark that the Balmer line fluxes are well correlated to the white light flux during the impulsive phase of flares, and not only at flare maximum. We obtain a power law correlation between the Balmer line and U-band fluxes that is evidence for either a common source ("kernels'') or strongly related flare components.
Key words: stars: flare - stars: activity - stars: late-type
Observations of stellar flares show evidence of great variety in their morphology. Some flares display a strong impulsive phase when white light is emitted (Rodonó et al. 1989; Houdebine 1992a), sometimes followed by a slower gradual phase when emission lines are prominent (Hawley & Pettersen 1991; Rodonó et al. 1989). Other flares are more like the solar two-ribbon flares with no white light emission (Houdebine 1992a; Butler et al. 1986). More generally, stellar flares display a wide variety of spectral signatures and evolution time scales. Most often, intense white light emission is reported, impulsive in character, with a rise time from tens of seconds to a couple of minutes. On late type dwarfs, these white light flares share many common properties with their solar equivalent, and for that reason can be referred to as "solar type white-light flares''. However, not all flares may be of solar type. On RS CVn systems, some more complex white light flares occur, lasting for a day or more and which are generally more powerfull (e.g. Foing et al. 1994).
In fact, the typical solar flare has no detectable signature in white light, but few such events have been detected on stars. Such flares were detected in spectroscopy (e.g. Houdebine 1992a; Butler et al. 1986), X-rays (e.g. Butler et al. 1988; Doyle et al. 1988b) or other spectral domains. Ironically, this latter class of flares is the least known for stars, conversely to the Sun, because of an observational bias, i.e., very little time has been dedicated to spectroscopic or X-ray observations in comparison to photometric observations. However, we must emphasize that there is also a strong contrast effect (Houdebine 1992a), in other words, many flares have been detected as white-light flares on dMe stars because of the relative weakness of the photospheric background, when they would have been classified as normal flares on the Sun because of its much higher photospheric background.
Spectral emission lines are the most appropriate diagnostics to constrain the physical properties and motions of the flare plasmas. Unfortunately, only a few sets of observations with adequate time and spectral resolution are so far available (e.g. Rodonó et al. 1989; Hawley & Pettersen 1991; Houdebine 1992a; Gunn et al. 1994; Garcia-Alvarez et al. 2001). Furthermore, there are also few attempts to derive the physical parameters of the flare plasmas (e.g. Katsova 1990; Bruevich et al. 1990; Katsova et al. 1991; Houdebine et al. 1991; Houdebine et al. 1993a, 1993b; Gunn et al. 1994; Jevremovic et al. 1998; Garcia-Alvarez et al. 2001) or the magnetic field topology and localisation of the flare components (Houdebine et al. 1993b). Good quality spectroscopy and a correct description of the different flare components (kernels, prominences and so on) are required to constrain numerical simulations. Besides, each flare is a unique event that may depart a lot from the average flare properties, and one must combine average properties to flare details in order to constain the relevant models.
Here we aim to extract the general characteristics of flares from a compilation of medium resolution spectroscopic observations in the 3600 Å-4400 Å wavelength range. Below, we compile all available spectroscopic data of stellar flares in order to obtain empirical correlations. We emphasize that an appropriate time resolution is also required, to allow at least for the distinction in the main flare phases.
Flares exhibit quite different spectroscopic behaviour from one flare to another; some evolve on time scales of tens of seconds whereas others may last for a day or more (Katsova et al. 1999; Foing et al. 1994). First, one should distinguish between solar-type flares that evolve typically on time scales shorter than a few tens of minutes and "RS CVn'' type flares that last typically more than a couple of hours (Baliunas et al. 1984; Linsky et al. 1989; Foing et al. 1994). Although there is most likely a continuity between the two classes of flares, it is important to differentiate them because they are very different in their spectroscopic signatures and physical properties. As was proposed by Simon et al. (1980), RS CVn flares may involve magnetic fields from the two stars in the system, leading to flares with a somewhat different nature. In this study, we will deal with solar-type flares only.
Solar-type flares on stars exhibit a variety of behaviour, but there
are emerging patterns that seem to
apply to most events. For instance, some authors (e.g. Houdebine 1992a) found
that the solar description of the flare as a succession of an impulsive
phase and a gradual phase usually holds. To illustrate this, we show three
flares in Fig. 1, as observed in the H![]() line, the Ca II K line
and the continuum at about 4200 Å. At this wavelength, there are no
spectral lines and the Balmer line wing contribution is minimal.
line, the Ca II K line
and the continuum at about 4200 Å. At this wavelength, there are no
spectral lines and the Balmer line wing contribution is minimal.
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{fig1_flare_2.eps}\end{figure}](/articles/aa/full/2003/03/aah3294/Timg8.gif) |
Figure 1:
Flux time profiles in the H |
| Open with DEXTER | |
As reported by previous authors (e.g. Rodonó et al. 1989), the white light and Ca II K line best describe respectively the impulsive phase and the gradual phase. On the contrary, the Balmer lines may appear in various proportions during the two phases, particularly the gradual phase when they may be weak.
In Fig. 1 top panel, the 8:50 h UT flare on Prox Cen is dominated by a rapid rise (less than 60 s) and decay (1 to 2 min) in the continuum and the Balmer lines. A slower gradual phase is visible in the Ca II K line but not in the Balmer lines. This flare (PC1 thereafter) could be qualified as being mostly "impulsive'' in character. The second flare, at 8:21 h UT on the same day (PC2 thereafter), displays no detectable white light emission and the rise and fall in the line fluxes are slow, typical of a solar or stellar flare gradual phase. Such a flare is "gradual'' in character and is in fact the closest equivalent to the classical solar flare. Note that for those two flares on Proxima Centauri, the maximum line fluxes are almost identical (see Table 4). This shows that the energy release mechanisms behave in a rather different maner for these two flares, in one case the energy release is quite impulsive whereas in the other it is quite gradual. These flares are good examples of how varied the spectroscopic signatures can be. We may add that during the PC1 flare, the Balmer lines showed significant broadening, with a full width half maximum up to 5.2 Å decreasing rapidly, whereas for the PC2 flare they remained narrower and evolved more slowly throughout the flare (Houdebine 1990). As we shall see below, this is a general feature of flares, the impulsive phase of a flare is always accompanied by an important broadening of the Balmer and He I lines whereas the gradual phase is not.
The third flare is a combination of both an impulsive and a gradual phase with comparable magnitudes, where the two phases are well delineated by their respective spectral tracers; the white light and the Balmer lines for the impulsive phase, and the Ca II and Balmer lines for the gradual phase. This is so far probably one of the best examples of a "combined flare'', where the impulsive and gradual phases combine together with similar magnitudes.
We found that these three classes of flares, impulsive, gradual and combined are sufficient to classify all flares with spectroscopy. We list in Table 1 all flares observed spectroscopically (with adequate time resolution) with its classification according to the above description. We found that "non-white light gradual flares'' represent a minority of the events, with 25%. This is in contrast with the solar case where white light flares are relatively rare. This apparent difference may however be due, at least in part, to a contrast effect: we illustrate this point by refering to Fig. 29 in Houdebine (1992a). Light curves for three flares were reported on an absolute scale and compared to the flux emitted in the U-band by an area of 1019 cm2 on the sun (this is about the area of a white light kernel for a solar flare). Clearly, the weakest 0.3 mag flare on Proxima Centauri would have remained undetected if occuring on the Sun. It is therefore possible that, like the flares detected on stars (Table 1), most solar flares are actually white-light flares with a weak white light emission, and only a minority are "normal'' non-white light flares. One should also consider the fact that the U-band includes the Balmer recombination continuum and the higher Balmer lines in the series. Hence further studies in spectrophotometry are necessary to determine what proportion of the flares actually emit white light.
Nevertheless, it seems that flares with no white light emission do indeed exist. Such purely non-white light flares seems to have been observed on Proxima Cen (Fig. 1, PC1 flare) and UV Ceti (Butler et al. 2002). They had no detectable white light emission in spectrophotometry even though for the PC1 flare its spectral line emission was fairly strong (8 times the quiescent emission).
We notice that large flares are always combined flares whereas the impulsive
flares are always comparatively weak (Tables 1 and 4). The gradual phase in the
Balmer
lines during flares with an impulsive phase remains undetectable for a U-band
maximum flux below ![]()
![]() erg/s. The mechanism responsible for the
Balmer line emission during the gradual phase remains unclear, but this
mechanism clearly does not operate as efficiently for weak impulsive flares.
Another possible explanation is that the two phases become increasingly
blended in time when
the flare energy diminishes. This would be in agreement with the fact that the
rise and decay times in the spectral lines diminish with the flare energy (see
Sect. 4). Along the same lines, we notice that small flares are short
while large flares may last for tens of minutes (Tables 1 and 4). This is
not an observational selection effect. This
dependence of the flare duration on flare power will be developed in Sect. 4.
erg/s. The mechanism responsible for the
Balmer line emission during the gradual phase remains unclear, but this
mechanism clearly does not operate as efficiently for weak impulsive flares.
Another possible explanation is that the two phases become increasingly
blended in time when
the flare energy diminishes. This would be in agreement with the fact that the
rise and decay times in the spectral lines diminish with the flare energy (see
Sect. 4). Along the same lines, we notice that small flares are short
while large flares may last for tens of minutes (Tables 1 and 4). This is
not an observational selection effect. This
dependence of the flare duration on flare power will be developed in Sect. 4.
| Star | UT | Date | Impulsive Phase | Gradual Phase | Character | Authors | ||||||
| H I | H I | Ca II | ||||||||||
| Rise | Decay | FWHM | Rise | Decay | FWHM | Rise | Decay | |||||
| (mn) | (mn) | (Å) | (mn) | (mn) | (Å) | (mn) | (mn) | |||||
| UV Ceti | 11:19 | 08/09/79 | - | - | - | 12.5 | - | - | 20 | - | Combined? | Eason et al. (1992) |
| Prox Cen | 8:21 | 25/03/84 | - | - | - | 4.8 | 9.6 | 3.8 | 8.6 | 12.5 | Gradual | Houdebine (1990) |
| Prox Cen | 8:50 | 25/03/84 | <1.2 | 2.8 | 5.5 | - | - | - | 2.2 | 7.2 | Impulsive | Houdebine (1990) |
| AD Leo | 2:40 | 28/03/84 | 0.65 | 10.5 | - | - | - | - | - | Impulsive | Houdebine (1990) | |
| AD Leo | 3:22 | 28/03/84 | 0.5 | 9.9 | 9.7 | 18.7 | 4.9 | 13.9 | 29.1 | Combined | Rodonó et al. (1989) | |
| UV Ceti | 1:53 | 06/12/84 | - | - | - | 1.8 | 3.3 | - | 3.0 | 6.0 | Gradual | Butler et al. (1986, 2002) |
| UV Ceti | 2:03 | 06/12/84 | - | - | - | 2.4 | 6.0 | - | - | - | Gradual | Butler et al. (1986, 2002) |
| UV Ceti | 2:29 | 06/12/84 | - | - | - | 2.1 | 3.7 | - | 5.2 | 8.5 | Gradual | Butler et al. (1986, 2002) |
| UV Ceti | 2:43 | 06/12/84 | - | - | - | 4.6 | 6.0 | - | 8.0 | 19.6 | Impulsive | Butler et al. (1986, 2002) |
| UV Ceti | 3:16 | 06/12/84 | - | - | - | 1.8 | 3.3 | - | 1.8 | 4.5 | Gradual | Butler et al. (1986, 2002) |
| UV Ceti | 3:29 | 06/12/84 | 1.9 | 7.7 | - | - | - | - | 8.3 | 16.6 | Impulsive | Butler et al. (1986, 2002) |
| YZ CMi | 19:55 | 04/03/85 | 2.3 | 5.5 | 10.5 | - | - | - | - | - | Impulsive | Doyle et al. (1988) |
| AD Leo | 4:40 | 12/04/85 | 10 | - | 4.9 | 19.6 | 34.6 | 4.5 | 29.4 | 75.8 | Combined | Hawley & Pettersen (1991) |
| AT Mic | 1:12 | 20/08/85 | 2.5 | - | 11.9 | 7.7 | 25.7 | 7.3 | 11.5 | 31.6 | Combined | Garcia-Alvarez et al. (2001) |
| T48 | 13:00 | 04/12/85 | - | - | - | 48 | 114 | 5 | 81 | 127 | Combined? | Carter et al. (1988) |
| II Peg | 2:10 | 17/08/89 | 8.8 | - | 8.5 | 33.4 | 70.3 | 6.8 | 51 | 97 | Combined | Doyle et al. (1992) |
| Gl 866 | 3:27 | 11/06/91 | 1.7 | - | - | - | - | - | - | - | Impulsive | Jevremovic et al. (1998) |
| Gl 866 | 3:56 | 11/06/91 | 1.3 | 2.2 | - | - | - | - | - | - | Impulsive | Jevremovic et al. (1998) |
| Gl 866 | 4:24 | 11/06/91 | 1.5 | 6.2 | - | - | - | - | - | - | Impulsive | Jevremovic et al. (1998) |
| AD Leo | 0:45 | 14/03/98 | 0.29 | 0.68 | 4.4 | 4.5 | 7.1 | 3.2 | 0.38 | 0.59 | Combined | Jevremovic (1999) |
So far, the stellar flare phenomenology closely resembles that of solar flares.
For instance, evolution time scales are very similar; the impulsive and
gradual phases respectively last for a few minutes and few tens of minutes.
Also, the relative amplitudes of these phases can be similar to that of their
solar equivalents: In the solar case, the total emission in H![]() from
the kernels is about the same as for the ribbons (extended areas)
(Tandberg-Hanssen & Emslie 1988), which compares to the combined flares.
from
the kernels is about the same as for the ribbons (extended areas)
(Tandberg-Hanssen & Emslie 1988), which compares to the combined flares.
To conclude, we found that the spectral line and U-band time profiles obey well defined patterns except for "complex'' flares when more than one U-band event occur. From the observations gathered so far we extracted the following properties, some of which will be developed in the next section:
We compiled the rise and decay times in the Ca II K and H![]() lines for all flares where this was possible (Table 1). The rise time is the
time lag between flare onset and the time of maximum flux, and the decay time
is the time lag between maximum flux and the time when the line has decayed
to half of this value. We plot in Fig. 2
some of these delays. We found good correlations between all of the rise and
decay times except with the rise and decay times of H
lines for all flares where this was possible (Table 1). The rise time is the
time lag between flare onset and the time of maximum flux, and the decay time
is the time lag between maximum flux and the time when the line has decayed
to half of this value. We plot in Fig. 2
some of these delays. We found good correlations between all of the rise and
decay times except with the rise and decay times of H![]() for the
impulsive phase. This is due to the fact that the impulsive phase is not well
resolved, i.e. rise and decay times are typically of the order of one minute
or less and the time resolution is also about one minute in the best cases
(except for the AD Leo flare observed by Jevremovic 1999).
for the
impulsive phase. This is due to the fact that the impulsive phase is not well
resolved, i.e. rise and decay times are typically of the order of one minute
or less and the time resolution is also about one minute in the best cases
(except for the AD Leo flare observed by Jevremovic 1999).
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{fig2a_flare_2.eps}\hspace*...
...\hspace*{15mm}
\includegraphics[width=6.8cm,clip]{fig2d_flare_2.eps}\end{figure}](/articles/aa/full/2003/03/aah3294/Timg13.gif) |
Figure 2:
Rise and decay times in the Ca II K and H |
| Open with DEXTER | |
The correlation between the Ca II K and H![]() rise times is
excellent (Fig. 2a). Measurements do not depart from the correlation by more
than 2.5 min. This figure also emphasises how varied the flares can be, with rise
times from less than 2 min to more than 80 min. Furthermore, it seems
that there are no preferred time scales, and the distribution seems to reflect
the flare energy distribution - i.e. - small flares are more frequent and
evolve on smaller time scales (see Sect. 4). We give in Table 2 the parameters
for the best linear fit to the data. From this correlation, we find that the
Ca II K line is systematically 1.63 times slower to rise than the
H
rise times is
excellent (Fig. 2a). Measurements do not depart from the correlation by more
than 2.5 min. This figure also emphasises how varied the flares can be, with rise
times from less than 2 min to more than 80 min. Furthermore, it seems
that there are no preferred time scales, and the distribution seems to reflect
the flare energy distribution - i.e. - small flares are more frequent and
evolve on smaller time scales (see Sect. 4). We give in Table 2 the parameters
for the best linear fit to the data. From this correlation, we find that the
Ca II K line is systematically 1.63 times slower to rise than the
H![]() line.
line.
The correlation between the rise and decay times in the H![]() Balmer line is also
good (Fig. 2b). This line is typically 2.3 times slower to decay
than to rise. The Ca II K line decay seems to depart from this linear
behaviour (Figs. 2c and 2d). This line is very slow to decay, and we found that
the correlations were best fitted by a second degree polynomial function. We
find that for small flares the decay time is of the order of twice the rise
time whereas for larger flares this factor is of the order of 1.8. We found
a similar result for the decay time in H
Balmer line is also
good (Fig. 2b). This line is typically 2.3 times slower to decay
than to rise. The Ca II K line decay seems to depart from this linear
behaviour (Figs. 2c and 2d). This line is very slow to decay, and we found that
the correlations were best fitted by a second degree polynomial function. We
find that for small flares the decay time is of the order of twice the rise
time whereas for larger flares this factor is of the order of 1.8. We found
a similar result for the decay time in H![]() as a function of the
decay time in Ca II K (Fig. 2d). For large flares the H
as a function of the
decay time in Ca II K (Fig. 2d). For large flares the H![]() and
Ca II decay times are more
similar whereas for smaller flares the decay time in Ca II K is a factor
of two larger than that in H
and
Ca II decay times are more
similar whereas for smaller flares the decay time in Ca II K is a factor
of two larger than that in H![]() .
.
The rise and decay times obey good relationships which signifies that
there is a well defined underlying mechanism responsible for the flux time
profiles in these lines during the gradual phase. Such a mechanism necessarily
involves the natural cooling of the flare plasmas if we assume
that most of the energy release occurs during the impulsive phase and that
little heating takes place during the gradual phase. We must then center our
interpretation on how the cooling of the flare plasma can produce the observed
features. Actually, models for the cooling of the plasma (Gurzadyan 1984) and
calculations of the cooling curves from the observed time profiles (Houdebine
et al. 1991) show that it is very easy to reproduce the observed line time
profiles by the natural cooling of a flare plasma. In this
context, the rise and decay times depend on the density of the plasma, and
the longer these delays the smaller is the density (Gurzadyan 1984). According
to Gurzadyan calculations (Gurzadyan 1984, Fig. 10), the plasma density n
is related to the rise time
![]() in the Ca II K
line according to the following relationship;
in the Ca II K
line according to the following relationship;
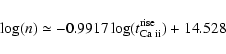 |
(1) |
Figure 2a shows that the delays may vary over more than one order of magnitude. As mentioned above, this implies that the coronal plasmas have densities varying over almost two orders of magnitude. The other correlations found between the rise and decay times and the radiated energies (Figs. 4a to 4c, see Sect. 4) are therefore evidence that large flares have lower densities than small flares. This result will be further discussed in Sect. 4. Another result that supports the cooling model is the fact that the rise and decay times in the Ca II line are usually longer than the rise and decay times in the Balmer lines (Figs. 2a and 2d). This result is expected since the gradient in the cooling curve diminishes with time and temperature (Gurzadyan 1984; Houdebine et al. 1991). In other words radiative cooling efficiency diminishes with temperature, and therefore with time. This behaviour shows that high temperature lines evolve faster than low temperature lines, and agrees with numerical models (Gurzadyan 1984).
Besides the radiative cooling, another competing mechanism that could play a role in the line time profiles during the gradual phase is X-ray backwarming. Hawley & Fisher (1992) calculated the spectra resulting from X-ray backwarming, for a series of 5 models. Their models can reproduce Balmer line fluxes. However, they fail to reproduce the Ca II to Balmer line ratios and the continuum. So far, with the present calculations it is not clear whether X-ray backwarming can explain the observed time-profiles in both the Balmer and Ca II lines, and in particular the differences in the time delays we report here. Further calculations are required to find out if X-ray backwarming can play a role in the correlations observed in Figs. 2a to 2d.
| Correlation: x, y | a | b | c | Cor. Coef. | Function y = f(x) |
| or |
|||||
| H |
1.63 | -0.425 | - | 0.997 | y = a.x + b |
| Ca II K rise, grad. | |||||
| H |
0.429 | 0.899 | - | 0.990 | y = a.x + b |
| H |
|||||
| Ca II K decay, grad./ | 3.66E-3 | 0.138 | 3.02 | 7.46 | y = a.x2 + b.x + c |
| Ca II K rise, grad. | |||||
| Ca II K decay, grad./ | 5.88E-3 | 8.9E-2 | 5.40 | 49.0 | y = a.x2 + b.x + c |
| H |
|||||
| U-band max. flux / | 0.114 | -5.90 | 103 | 8.3E-2 |
|
| H |
|||||
| U-band max. flux / | 0.130 | -6.87 | 116 | 2.2E-1 |
|
| Ca II K max. flux | |||||
| U-band max. flux / | 0.986 | -1.55 | - | 0.971 |
|
| H |
|||||
| H |
0.941 | 1.24 | - | 0.990 |
|
| Ca II K max. flux | |||||
| H |
0.932 | 1.85 | - | 0.963 |
|
| H |
|||||
| U-band max. flux / | 2.169 | -119 | 1630 | 26.5 |
|
| Ca II K rise, grad. | |||||
| Ca II K decay, grad./ | 4.38E-2 | 25.5 | - | 0.890 |
|
| Ca II K max. flux | |||||
| Ca II K rise, grad. / | 7.85E-2 | 26.3 | - | 0.826 |
|
| H |
|||||
| U-band flux / | 0.615 | 11.6 | - | 0.921 |
|
| H |
Absolute fluxes for the continuum or spectral lines were commonly derived using model photospheric calculations such as those of Mould (1976) combined with main-sequence spectral type-luminosity empirical correlations (e.g. Veeder 1974). However, both are actually rather inaccurate. The former because until recently (e.g. Allard & Hauschildt 1995) they lacked adequate opacity tables and the latter because the main-sequence at spectral type M spreads over three magnitudes and active dwarfs are often over-luminous by 1.5 mag or so (e.g. Mirzoyan 1993). This could yield fluxes under-estimated by a factor of 4 to 5 depending on the star's absolute magnitude.
Here we calculate absolute fluxes from the measured parallax.
We compile the data adopted in this study in Table 3. The data was taken
from the Hipparcos and Tycho catalogues (Turon et al. 1997), the new Gliese
Catalogue (1991) or Strassmeier et al. (1993). R-I data is from Leggett
(1992) or Gliese (1969, 1991) and homogenised to the Kron system using
Legget (1992) transformations. The effective temperatures were calculated
according to the empirical effective temperature relationship of Jones et al. (1994).
The U-band absolute fluxes were computed assuming a flux of
![]() erg/cm2/Å at Earth for a 0 mag star (Johnson
1966), and assuming an effective U-band width of 680 Å (Allen 1973).
erg/cm2/Å at Earth for a 0 mag star (Johnson
1966), and assuming an effective U-band width of 680 Å (Allen 1973).
| Star | Gl No | V | U-B | B-V | R-I | MV |
|
FU | Factor | |
| (mag) | (mag) | (mag) | (mag) | (m
|
(mag) | (K) | (erg s-1) | |||
| UV Ceti | 65A | 12.57 | 1.10 | 1.85 | 1.64 | 381 4 | 15.47 0.02 | 2735 | 1.5 E27 | 8.24 E38 |
| 65B | 12.70 | - | - | - | " | 15.60 0.02 | - | 1.3 E27 | " | |
| YZ CMi | 285 | 11.4 | 1.00 | 1.60 | 1.34 | 163 4 | 12.46 0.05 | 3023 | 3.3 E28 | 4.50 E39 |
| AD Leo | 388 | 9.40 | 1.08 | 1.54 | 1.12 | 204 3 | 10.95 0.03 | 3234 | 1.3 E29 | 2.88 E39 |
| FL Vir | 473A | 13.04 | 1.20 | 1.83 | 1.58 | 232 4 | 14.87 0.04 | 2793 | 2.4 E27 | 2.22 E39 |
| 473B | 13.30 | - | - | - | " | 15.10 0.04 | - | 1.9 E27 | " | |
| Prox Cen | 551 | 11.1 | 1.43 | 1.83 | 1.60 | 762 5 | 15.51 0.01 | 2774 | 1.1 E27 | 2.06 E38 |
| BY Dra | 719 | 8.48 | 1.04 | 0.97 | - | 58 6 | 7.29 0.21 | - | 6.7 E30 | 3.56 E40 |
| AT Mic | 799A | 10.2 | 0.88 | 1.57 | 1.33 | 117 6 | 10.54 0.11 | 3033 | 2.3 E29 | 8.74 E39 |
| AU Mic | 803 | 8.96 | 0.95 | 1.47 | 0.85 | 103 6 | 9.02 0.12 | 3493 | 9.4 E29 | 1.13 E40 |
| EV Lac | 873 | 10.26 | - | 1.61 | 1.20 | 197 4 | 11.73 0.04 | 3157 | - | 3.08 E39 |
| Gl 866 | 866 | 12.33 | 1.54 | 1.96 | 2.04 | 305 9 | 14.75 0.06 | 2350 | 1.8 E27 | 1.29 E39 |
| EQ Peg | 896A | 10.38 | 1.08 | 1.54 | 1.13 | 153 9 | 11.30 0.12 | 3224 | 9.6 E28 | 5.11 E39 |
| 896B | 12.40 | 1.12 | 1.65 | 1.62 | " | 13.32 0.12 | 2750 | 8.9 E27 | " | |
| T 48 | - | 16.31 | - | 1.07 | 1.12 | 470pc | 7.95 | 3240 | - | 2.64 E43 |
| II Peg | - | 7.5 | 0.66 | 1.01 | 0.29 | - | 5.4 | K2.5V-IV | 6.5 E31 | 1.03 E41 |
We measured the maximum fluxes in the U-band, the H![]() and the
Ca II K lines during the impulsive and the gradual phases for all
flares for which the relevant time profiles were available. We list the
results in Table 4. We plotted the H
and the
Ca II K lines during the impulsive and the gradual phases for all
flares for which the relevant time profiles were available. We list the
results in Table 4. We plotted the H![]() flux
during the impulsive phase against the U-band flux in Fig. 3a. We find a
good correlation that does not seem to be linear in a log-log scale. We
fitted the correlation with a second order polynomial function (Table 2).
For large flares the slope of the observed correlation is close to 1, i.e.,
the H
flux
during the impulsive phase against the U-band flux in Fig. 3a. We find a
good correlation that does not seem to be linear in a log-log scale. We
fitted the correlation with a second order polynomial function (Table 2).
For large flares the slope of the observed correlation is close to 1, i.e.,
the H![]() flux grows as fast as the U-band flux, but for small flares,
the slope is of the order of 0.34 which means that the U-band flux is growing
three times faster than the H
flux grows as fast as the U-band flux, but for small flares,
the slope is of the order of 0.34 which means that the U-band flux is growing
three times faster than the H![]() flux.
flux.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{fig3a_flare_2.eps}\hspace*...
...includegraphics[width=7.3cm,clip]{fig3e_flare_2.eps}\hspace*{9.7cm}
\end{figure}](/articles/aa/full/2003/03/aah3294/Timg28.gif) |
Figure 3:
We plot from a) to e) the U-band and line fluxes measured at
maximum emission. We obtain a good correlation between the U-band and
the H |
| Open with DEXTER | |
Houdebine (1992a, H92a thereafter) found a similar correlation between the
H![]() line flux and the continuum flux at 4200 Å during the impulsive
phase for four flares. The difference between the present correlation and the
one in H92a is mainly that the present correlation covers 5.5 orders of
magnitude whereas we had 3.5 orders of magnitude in H92a. Also, the
present correlation only includes the fluxes measured at flare maximum.
This correlation includes higher energy flares than in H92a and it can be
approximated by a linear relationship in the
line flux and the continuum flux at 4200 Å during the impulsive
phase for four flares. The difference between the present correlation and the
one in H92a is mainly that the present correlation covers 5.5 orders of
magnitude whereas we had 3.5 orders of magnitude in H92a. Also, the
present correlation only includes the fluxes measured at flare maximum.
This correlation includes higher energy flares than in H92a and it can be
approximated by a linear relationship in the
![]() -1032 ergs
energy range, which explains why H92a found a linear correlation.
-1032 ergs
energy range, which explains why H92a found a linear correlation.
The significant difference mentioned above between the gradient for low and
high energy flares leads to important constraints on the properties of the
impulsive phase. H92a showed that most of the spectral signatures during this
phase could be reproduced by two series of models: the models for the dense
flare kernels, and the models for the radiative pumping of the Balmer
emission by white light. But these models give a slope that is in agreement
with the correlation found in H92a between the H![]() flux and the
continuum flux, for which the slope is 0.61.
flux and the
continuum flux, for which the slope is 0.61.
However, the models presented in H92a for the radiative pumping study are
based on a relatively low pressure model chromosphere. Houdebine (1990,
H90 thereafter) studied the radiative pumping phenomenon
in the Balmer lines for two quiescent model atmospheres that are quite
different in order to evaluate the amplitude of this effect in very
different atmospheric conditions. H90 found that the chromospheric response
to the white light irradiation was significantly different for the two models.
For the low
pressure model atmosphere (series of models M.A.1 in H90) the gradient of
the growth of H![]() viz. U-band flux is of the order of 0.6 whereas
for the high pressure model atmosphere, this gradient is
viz. U-band flux is of the order of 0.6 whereas
for the high pressure model atmosphere, this gradient is ![]() 1.7.
Houdebine & Doyle (1994a) also investigated these model chromospheres and
showed that low pressure models (such as M.A.1 in H90) are inadequate. It
is therefore more likely that real effect of radiative pumping on the
atmosphere will be a large gradient of 1 or more. This means that
radiative pumping is able to reproduce the larger gradient observed for
large flares (Fig. 3a).
1.7.
Houdebine & Doyle (1994a) also investigated these model chromospheres and
showed that low pressure models (such as M.A.1 in H90) are inadequate. It
is therefore more likely that real effect of radiative pumping on the
atmosphere will be a large gradient of 1 or more. This means that
radiative pumping is able to reproduce the larger gradient observed for
large flares (Fig. 3a).
To further illustrate the effect of radiative pumping on the Balmer lines,
we plot the H![]() line profiles in Fig. 4 for the M.A.2 models in H90. 23
models were computed with increasing Balmer continuum irradiation. Model 1
corresponds to the quiescent atmosphere with no irradiation. The Balmer
continuum irradiation increases from model 1 to model 23. The resulting effect
is essentially to increase the line flux, because the Balmer continuum
radiation ionises hydrogen atoms, depletes the level 2 population, and as a
consequence depletes the Balmer line optical depths and allows the atmosphere
to radiate more in the Balmer lines. Some Balmer line profiles also become
narrower, and in particular H
line profiles in Fig. 4 for the M.A.2 models in H90. 23
models were computed with increasing Balmer continuum irradiation. Model 1
corresponds to the quiescent atmosphere with no irradiation. The Balmer
continuum irradiation increases from model 1 to model 23. The resulting effect
is essentially to increase the line flux, because the Balmer continuum
radiation ionises hydrogen atoms, depletes the level 2 population, and as a
consequence depletes the Balmer line optical depths and allows the atmosphere
to radiate more in the Balmer lines. Some Balmer line profiles also become
narrower, and in particular H![]() (see H90). The self-reversal in
H
(see H90). The self-reversal in
H![]() diminishes and eventually disapears (see H90). For further
comparison with the present observations, we plot in Fig. 5 the flux in the
Balmer series as a function of the flux in the Balmer continuum at threshold
for the M.A.2 models in H90. The effect of the Balmer continuum on the Balmer
lines is rather homogeneous along the series, and the variations are
almost linear in a log-log scale. These curves can be compared to the
correlation in Fig. 3a, providing one multiplies the theoretical fluxes by a
given area.
diminishes and eventually disapears (see H90). For further
comparison with the present observations, we plot in Fig. 5 the flux in the
Balmer series as a function of the flux in the Balmer continuum at threshold
for the M.A.2 models in H90. The effect of the Balmer continuum on the Balmer
lines is rather homogeneous along the series, and the variations are
almost linear in a log-log scale. These curves can be compared to the
correlation in Fig. 3a, providing one multiplies the theoretical fluxes by a
given area.
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{fig4.eps}\end{figure}](/articles/aa/full/2003/03/aah3294/Timg30.gif) |
Figure 4:
This figure shows the variations in the H |
| Open with DEXTER | |
In any case, the kernel models (H92a) seem unable to produce a Balmer line emission that increases as found in our correlation, i.e., a gradient that increases from small flares to large flares. Instead, in these models, increasing white light radiation implies increasing pressure and opacity in the atmosphere. This increased opacity tends to diminish the Balmer line intensity relative to the continuum intensity, as the emission tends towards that of a black-body. In other words the Balmer line equivalent widths should decrease with white light intensity for high values, and not increase as is observed. Therefore, emission from the kernels, even though it reproduces well the observed correlation for medium size flares (H92a), cannot explain the entire correlation.
Hence, the only way to explain both a varying gradient and a gradient of 1 for large flares (Fig. 3a) is to speculate that radiative pumping/backwarming represents a significant proportion of the total Balmer emission during large flares and that this proportion increases with the flare energy. Therefore, observations indicate that, for some as yet unknown reason, radiative pumping in the surrounding atmosphere and probably also backwarming by white light becomes more efficient as the flare energy increases. We speculate that this may have something to do with the height of the white light source in the atmosphere: if the source is at low atmospheric levels, it will radiate radially into the surrounding quiescent chromosphere and will affect only a small area around the flare (because the large chromospheric opacity prevents the radiation from propagating very far), while if it is located higher in the corona the area in view will be considerably larger. Observations indicate that this source of white light increases in height, or extends further in height, as the flare energy increases.
This interpretation finds additional support in the line FWHM observations: if
the flare kernels were the dominant source of radiation during the impulsive
phase, the Balmer line widths should be large for large flares as one expects
a larger heating to take place. Instead, the line widths seem to increase
till a maximum attained for a U-band energy of a few times 1026 erg/Å
and decrease for larger flares (see Fig. 7 and H92a). Indeed, for very large
flares, surprisingly, line broadening was never observed to be very large:
in Hawley & Pettersen (1991) the maximum line widths are of the order of 5 Å.
Similarly during the large flares on II Peg (Doyle et al. 1992) and T48
(Carter et al. 1988) a FWHM of only ![]() 5.5 Å was observed.
Moreover, H92a observed two components in the Balmer line profiles during
the flare on AD Leonis (Table 1). These two components seem to be respectively
the signature of the flare kernels and the flare radiative pumping/backwarming
of the surrounding chromosphere. Therefore, the variation of the line
broadening (see Sect. 5) as a function of U-band energy supports the
interpretation that the two Balmer line emission mechanisms, kernels and
radiative pumping, compete to produce the varying gradient in Fig. 3a.
5.5 Å was observed.
Moreover, H92a observed two components in the Balmer line profiles during
the flare on AD Leonis (Table 1). These two components seem to be respectively
the signature of the flare kernels and the flare radiative pumping/backwarming
of the surrounding chromosphere. Therefore, the variation of the line
broadening (see Sect. 5) as a function of U-band energy supports the
interpretation that the two Balmer line emission mechanisms, kernels and
radiative pumping, compete to produce the varying gradient in Fig. 3a.
Another part of the correlation that is difficult to explain is that for U-band
energies below 1028 erg/s. In this energy range, the gradient is only
0.34. We believe this occurs because the U-band is no longer a good tracer
of the total flare radiated energy: the evidence in Sect. 2 that there exists small
flares with no detectable white light signature (Fig. 1 and Table 1), proves
that white light is not a good diagnostic of the total radiated energy budget.
In fact, so little is known about the energy radiated accross the spectrum that
we don't yet know what spectral diagnostic could be used as a measure of the
radiated energy budget. There are some correlations between the fluxes
emitted at different wavelengths (e.g. Butler 1993; Benz & Gudel 1994) but
none that involve the total radiated energy budget. We believe that for low
energies, the white light emission is not correlated anymore with other
spectral diagnostics, and this is the reason
why the U-band energy varies over more than an order of magnitude while
the Balmer lines show little variation (Fig. 3a). For a given spectral
line energy the U-band flux may span the entire flux range from 0 to
![]() 1028 erg. In other words, we believe that the U-band is a good
tracer of the entire flare energy only for a U-band peak flux greater than
1028 erg. In other words, we believe that the U-band is a good
tracer of the entire flare energy only for a U-band peak flux greater than
![]() 1028 ergs. In Fig. 3a we may therefore distinguish three regions:
(i) low energy flares (U-band flux below 1028 ergs) for which the
U-band is not a good tracer of the energy released, (ii) medium energy
flares for which the gradient can be explained by flare kernel models, and
(iii) high energy flares for which the gradient increases, and for which
the Balmer emission is increasingly dominated by radiative pumping.
1028 ergs. In Fig. 3a we may therefore distinguish three regions:
(i) low energy flares (U-band flux below 1028 ergs) for which the
U-band is not a good tracer of the energy released, (ii) medium energy
flares for which the gradient can be explained by flare kernel models, and
(iii) high energy flares for which the gradient increases, and for which
the Balmer emission is increasingly dominated by radiative pumping.
| Star | UT | Date | U-band | H |
H |
Ca II K | Ratio | Ratio |
| max. flux | max. flux | max. flux | max. flux | H I/Ca II | H I imp./ | |||
| (erg/s) | Imp. | Grad. | (erg/s) | Imp./Grad. | HI Grad. | |||
| (erg/s) | (erg/s) | - | ||||||
| UV Ceti | 11:19 | 08/09/79 | 2.9E29 | 2.1E27 | - | 1.6E26 | 13/- | - |
| Prox Cen | 8:21 | 25/03/84 | - | - | 1.4E26 | 4.5E25 | -/3.1 | - |
| Prox Cen | 8.50 | 25/03/84 | 5.3E26 | 1.9E26 | - | 4.5E25 | 4.2/- | - |
| AD Leo | 2:40 | 28/03/84 | 1.7E29 | 1.6E27 | - | <2E26 | >8/- | - |
| AD Leo | 3:22 | 28/03/84 | 7.7E29 | 4.8E27 | 4.8E27 | 1.1E27 | 4.5/4.5 | 1.0 |
| UV Ceti | 1:53 | 06/12/84 | - | - | 9.1E25 | 6.8E25 | -/1.3 | - |
| UV Ceti | 2:03 | 06/12/84 | - | - | 6.5E25 | 3.5E25 | -/1.9 | - |
| UV Ceti | 2:29 | 06/12/84 | - | - | 1.5E26 | 6.1E25 | -/2.5 | - |
| UV Ceti | 2:43 | 06/12/84 | 1.5E27 | 2.0E26 | - | 8.4E25 | 2.4/- | - |
| UV Ceti | 3:16 | 06/12/84 | - | - | 1.2E26 | 9.6E25 | -/1.3 | - |
| UV Ceti | 3:29 | 06/12/84 | 2.2E27 | 2.6E26 | - | 7.7E25 | 3.4/- | - |
| YZ CMi | 19:55 | 04/03/85 | 4.4E28 | 9.0E26 | - | 5.7E26 | 1.6/- | - |
| AD Leo | 4:40 | 12/04/85 | 8.6E30 | 7.1E28 | 1.0E29 | 2.6E28 | 2.7/3.9 | 0.71 |
| AT Mic | 1:12 | 20/08/85 | 7.7E30 | 9.6E28 | 1.3E29 | 3.2E28 | 3.0/4.0 | - |
| T48 | 13:00 | 04/12/85 | - | - | - | - | - | - |
| II Peg | 2:10 | 17/08/89 | 6.4E31 | 6.7E29 | 5.2E29 | 1.9E29 | 3.5/2.7 | 1.3 |
| Gl 866 | 3:27 | 11/06/91 | 6.5E27 | 1.6E26 | - | 7.0E25 | 2.3/- | - |
| Gl 866 | 3:56 | 11/06/91 | 8.1E27 | 3.7E26 | - | 3.7E25 | 10/- | - |
| Gl 866 | 4:24 | 11/06/91 | - | 4.3E26 | - | 9.2E25 | 4.7/- | - |
| AD Leo | 0:45 | 14/03/98 | 1.9E30 | 9.0E28 | (3.5E28) | 3.4E28 | 2.7/1.0 | 2.6 |
We show in Fig. 3b the Ca II K line flux as a function of the U-band flux. The Ca II K line flux increases as the U-band flux increases but more slowly. For a five orders of magnitude increase in the U-band flux, the Ca II K line flux increased by only 3.5 orders of magnitude. However, as already mentioned above for the Balmer line-U-band correlation, this may be due to small flares: for small flares the spectral line fluxes show little variation for a change of one order of magnitude in the U-band. This is not the case for medium and large flares where there is a one to one correlation between the line flux and the U-band flux. As already reported above, we believe this occurs for small flares because the U-band is not a good tracer of the flare energy. Above 1028 erg the Ca II K line flux seems to increase with the U-band flux with a slope close to one. This means that the magnitude of the gradual phase is directly proportional to the flare energy input.
The H![]() line flux during the gradual phase as a function of the
U-band flux is shown in Fig. 3c. Like the Ca II K line for medium
and large flares, we find
a gradient of
line flux during the gradual phase as a function of the
U-band flux is shown in Fig. 3c. Like the Ca II K line for medium
and large flares, we find
a gradient of ![]() 0.99, very close to one. Again, this shows that the
magnitude of the gradual phase is directly proportional to that of the
impulsive phase. This proves that the flare plasmas during the gradual phase
are linearly related to the energy released during the
impulsive phase. How this plasma is produced and related to the energy
release is unknown at this stage, but observations indicate that it has
a coronal nature (see Sect. 3).
0.99, very close to one. Again, this shows that the
magnitude of the gradual phase is directly proportional to that of the
impulsive phase. This proves that the flare plasmas during the gradual phase
are linearly related to the energy released during the
impulsive phase. How this plasma is produced and related to the energy
release is unknown at this stage, but observations indicate that it has
a coronal nature (see Sect. 3).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fig5.eps}\end{figure}](/articles/aa/full/2003/03/aah3294/Timg31.gif) |
Figure 5: We plot here the variations in the fluxes of the Balmer series as a function of the flux in the Balmer continuum at threshold, when an excess white light at about the Balmer continuum irradiates the quiescent atmosphere (from H90). These variations can be compared to the empirical correlation in Fig. 3a. |
| Open with DEXTER | |
Figure 3d shows the Ca II K line flux during the gradual phase as a
function of the H![]() line flux during this same phase. They are
linearly correlated and the slope of the correlation is 0.941 (Table 2),
which shows again that both the H
line flux during this same phase. They are
linearly correlated and the slope of the correlation is 0.941 (Table 2),
which shows again that both the H![]() and the Ca II K lines
grow linearly together. On average, according to the correlation (Table 2),
the ratio of the H
and the Ca II K lines
grow linearly together. On average, according to the correlation (Table 2),
the ratio of the H![]() line to the Ca II K line is about 2.6.
This means that the ratio of the amounts of plasma emitting in the
Balmer lines and the calcium lines remain constant for all
flares. This again supports the argument that these lines are emitted by
a cool coronal plasma that cools in time in a similar manner for all flares
(Sect. 3). However, the slight difference in the slope of the correlation
to unity implies that the H
line to the Ca II K line is about 2.6.
This means that the ratio of the amounts of plasma emitting in the
Balmer lines and the calcium lines remain constant for all
flares. This again supports the argument that these lines are emitted by
a cool coronal plasma that cools in time in a similar manner for all flares
(Sect. 3). However, the slight difference in the slope of the correlation
to unity implies that the H![]() line to Ca II K line ratio
varies from 1.95 to 3.39 over the entire energy range. This may be due to
the fact that a radiative pumping process also takes place during the
gradual phase for the large flares. Indeed,
the plasma also emmits a substantial amount of radiation in the Balmer
recombination continuum that will stimulate the Balmer line emission from
the surrounding chromosphere. This will produce additional Balmer line emission
during the gradual phase.
line to Ca II K line ratio
varies from 1.95 to 3.39 over the entire energy range. This may be due to
the fact that a radiative pumping process also takes place during the
gradual phase for the large flares. Indeed,
the plasma also emmits a substantial amount of radiation in the Balmer
recombination continuum that will stimulate the Balmer line emission from
the surrounding chromosphere. This will produce additional Balmer line emission
during the gradual phase.
Figure 3e shows the H![]() line flux during the gradual phase as a
function of the H
line flux during the gradual phase as a
function of the H![]() line flux during the impulsive phase. The slope
of the correlation is 0.93 (Table 2), again very close to 1. This is
further evidence that the emission produced during the gradual phase directly
depend on the impulsive phase. This also agrees with the finding that the
Balmer line fluxes are correlated with the calcium line fluxes (Fig. 3d) and
that both lines are correlated to the U-band (Figs. 3b and 3c).
line flux during the impulsive phase. The slope
of the correlation is 0.93 (Table 2), again very close to 1. This is
further evidence that the emission produced during the gradual phase directly
depend on the impulsive phase. This also agrees with the finding that the
Balmer line fluxes are correlated with the calcium line fluxes (Fig. 3d) and
that both lines are correlated to the U-band (Figs. 3b and 3c).
We also investigated the behaviour of the Balmer to Ca II flux line ratio (Table 4) as a function of the U-band energy and the time delays. We found no correlation between the line ratio and other parameters. The line ratio is usually between 2 and 4 except for a couple of flares (Table 4). This means, as highlighted by other correlations (e.g. Fig. 3d), that both the Balmer lines and Ca II lines grow simultaneously when the whole flare energy grows. The reason why, in a couple of flares, the Ca II emission is abnormally weak is unclear. Maybe in these instances the proportion of higher temperature plasma remains higher, and the flare plasmas do not undergo a normal cooling process, as discussed in Sect. 3.
In Fig. 6a we plot the rise time in the Ca II K line as a function of the U-band flux. As the correlation does not seem linear, we performed a fit with a second degree polynomial (Table 2). It shows that the more energetic the flare is, the longer the rise time in the gradual phase, or in other words, large flares last longer than small flares. This property is rather puzzling, it means, according to Gurzadyan (1984) models, that the plasma during the gradual phase has a lower density for large flares than for small flares. Figures 6b and 4c show a similar trend although in these cases the correlations seem linear. This agrees with our finding that we did not have linear correlations for other relationships involving the U-band (Figs. 3a and 3b) whereas we had linear correlations with line fluxes (e.g. Figs. 3c and 3d).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{fig6a_flare_2.eps}\hspace*{2...
...includegraphics[width=7.2cm,clip]{fig6c_flare_2.eps}\hspace*{9.6cm}
\end{figure}](/articles/aa/full/2003/03/aah3294/Timg32.gif) |
Figure 6: In figures a) to c), we show the U-band and line maximum fluxes as a function of delays in the spectral lines. The two parameters correlate which shows that basically, large flares last longer than small flares. |
| Open with DEXTER | |
As mentioned above, the reason why larger flares should have lower densities is unclear. In the framework of flare plasma cooling models (Gurzadyan 1984) one possibility would be that the flare plasma has a higher initial temperature for larger flares. It would then take longer for the plasma to cool down and reach the maximum emisivity (Gurzadyan 1984), hence the rise times in the Balmer and calcium lines would be lengthened. But if the density was the same for small and large flares then the decay times should be identical, which is not observed (Figs. 2b to 2d and 6d). There is therefore no simple explanation with the present models as to why the larger flares last longer and why they have lower densities during the gradual phase. An alternative explanation is that secondary energy release takes place during large flares which lengthens their duration.
It is also interesting to note that the larger flares on RS CVn systems, even though they may have somewhat different properties, last even longer (e.g. Baliunas et al. 1984; Linsky et al. 1989; Foing et al. 1994). The correlations found here (Figs. 6a to 6c) may therefore extend to flares on RS CVn systems.
Spectral lines of different species exhibit quite different behaviour in their broadening during a flare (H92a, Hawley & Pettersen 1991; Garcia-Alvarez 2001). This aspect of the flare as well as possible broadening mechanisms were already extensively commented by H92a. Here, we will focus our attention on how the broadening in the Balmer lines varies with the U-band flux. Previous evidence for Stark and opacity broadening suggest the presence of high density kernels during the flare impulsive phases (H92a). Has the density of these kernels any dependence on the magnitude of the flare? Large broadening seems to coincide with powerful white light emission, with the maximum attained during maximum white light (H92a, Hawley & Pettersen 1991; Garcia-Alvarez 2001). This maximum is followed by a monotonic decay of the line widths. There seems therefore to be some degree of correlation between the line width and the white light intensity during a flare.
H92a already investigated the dependence of the Balmer line widths on the white
light intensity. Here we augment his dataset with other observations.
We show in Fig. 7 the FWHM of H![]() ,
H
,
H![]() ,
H8 and H9 versus the U-band flux for flares on AD Leo (2:40 and 3:22 UT on 28 March 1984, Rodonò et al. 1989, 4:40 UT on the 12 April 1985,
Hawley & Pettersen 1991), YZ CMi (Doyle et al. 1988a; Zarro & Zirin
1985),
UV Ceti (de Jager et al. 1989; Phillips et al. 1988), Proxima Cen (PC2
flare) and AT Mic (Garcia-Alvarez et al. 2001). Filled circles are for the
impulsive phase only, open circles are for the gradual phase.
,
H8 and H9 versus the U-band flux for flares on AD Leo (2:40 and 3:22 UT on 28 March 1984, Rodonò et al. 1989, 4:40 UT on the 12 April 1985,
Hawley & Pettersen 1991), YZ CMi (Doyle et al. 1988a; Zarro & Zirin
1985),
UV Ceti (de Jager et al. 1989; Phillips et al. 1988), Proxima Cen (PC2
flare) and AT Mic (Garcia-Alvarez et al. 2001). Filled circles are for the
impulsive phase only, open circles are for the gradual phase.
![\begin{figure}
\par\includegraphics[width=13.75cm,clip]{fig7_flare_2.eps}\end{figure}](/articles/aa/full/2003/03/aah3294/Timg35.gif) |
Figure 7:
FWHM of the H |
| Open with DEXTER | |
Broadening during the impulsive phase is much larger in average than
during the gradual phase. Typical values are respectively in the
range [5 Å; 16 Å] and [2 Å; 7 Å]. Note that the lower limit of 2 Å
is often set by the instrumental resolution. The data shows a clear trend for
increased broadening with white light intensity, both during the impulsive
and gradual phases. In fact, we may distinguish three energy domains for the
impulsive phase measurements in
this diagram: the small flares with U-band energies lower than
![]() 1025 erg/Å, the medium size flares from
1025 erg/Å, the medium size flares from ![]() 1025 erg/Å to
1025 erg/Å to ![]()
![]() erg/Å, and the large flares for energies larger than
erg/Å, and the large flares for energies larger than
![]()
![]() erg/Å. For small flares, we believe that the kernels
may not reach a sufficiently high density so as to dominate the Balmer
line emission. In this case, the Balmer emission originates from various
areas such as in solar two-ribbon flares, and the broadening is of the same
order than that observed during the gradual phase of larger flares. In
other words, as in Sect. 4 we propose that observations are evidence that
the U-band is no longer a good tracer of the energy released during the
flare. For U-band energies above
erg/Å. For small flares, we believe that the kernels
may not reach a sufficiently high density so as to dominate the Balmer
line emission. In this case, the Balmer emission originates from various
areas such as in solar two-ribbon flares, and the broadening is of the same
order than that observed during the gradual phase of larger flares. In
other words, as in Sect. 4 we propose that observations are evidence that
the U-band is no longer a good tracer of the energy released during the
flare. For U-band energies above ![]() 1025 erg/Å, the FWHM clearly
increases as a function of energy up to a value of about 15 Å. This increase
is in agreement with the results obtained for the kernel model atmospheres
(H92a), and shows that, the larger the flare, the larger is the pressure
in the flare kernels, and therefore the higher is the energy of the particle
beams.
1025 erg/Å, the FWHM clearly
increases as a function of energy up to a value of about 15 Å. This increase
is in agreement with the results obtained for the kernel model atmospheres
(H92a), and shows that, the larger the flare, the larger is the pressure
in the flare kernels, and therefore the higher is the energy of the particle
beams.
For large flares (U-band energies above ![]()
![]() erg/Å), the
situation seems more puzzling. As was shown in Sect. 4.2, we can interpret
the data for large flares in Fig. 3a only if we invoke an increasing
contribution to the Balmer lines arising from the radiative pumping effect on
the surrounding chromosphere. If this indeed occurs, then we should observe a
progressive decrease in the Balmer maximum widths as the U-band energy
increases because the Balmer lines are not broadened by this process. This
is indeed what we observe in Fig. 7 for the flare on AD Leonis (Hawley &
Pettersen 1991). However for the flare on AT Mic (Garcia-Alvarez et al. 2001)
we observe a broadening that is still quite large; about 10 Å. Therefore, for
U-band energies above
erg/Å), the
situation seems more puzzling. As was shown in Sect. 4.2, we can interpret
the data for large flares in Fig. 3a only if we invoke an increasing
contribution to the Balmer lines arising from the radiative pumping effect on
the surrounding chromosphere. If this indeed occurs, then we should observe a
progressive decrease in the Balmer maximum widths as the U-band energy
increases because the Balmer lines are not broadened by this process. This
is indeed what we observe in Fig. 7 for the flare on AD Leonis (Hawley &
Pettersen 1991). However for the flare on AT Mic (Garcia-Alvarez et al. 2001)
we observe a broadening that is still quite large; about 10 Å. Therefore, for
U-band energies above ![]()
![]() erg/Å it seems that there is an
increasing contribution from the radiative pumping process for some flares but
not all.
erg/Å it seems that there is an
increasing contribution from the radiative pumping process for some flares but
not all.
A large scattering in FWHM for a given U-band energy is not only expected because of a probable large variety in the flare phenomenon, but also because of the changing sites for flare occurrence (disk and limb flares); indeed, according to the model calculations, the modification of the flare integrated intensities and line profiles is large for different propagation angles when the plasma density is high (H92a).
It is reasonable to assume in first approximation that the maximum intensity of suspected particule beams scale with the strength of the magnetic field in the flaring loops. Now, magnetic loops on a dMe star are limited in strength, to maybe a few KG or tens of KG. This saturation in the field strength will cause the particle beams to saturate in energy for a given amount of energy released, or for a given U-band flare intensity (assuming the U-band is a good tracer of the total energy budget). In addition, because the chromospheric pressure depends primarily on the total energy deposited, then the maximum chromospheric pressure will also be limited for a given U-band energy. On account of the dependence of the line widths with chromospheric pressure (H92a), thus, we expect such a scatter diagram to delineate an upper envelope in the FWHM for a given white light flux. This envelope is visible in Fig. 7, and the line FWHM clearly increase with the U-band flux. Assuming that the kernel contribution dominate the Balmer line flux, this maximum envelope defines the maximum particle beam intensity for a given U-band flux. It is therefore possible in principle to recover from Fig. 7 the maximum beam energy and intensity as a function of the U-band flux.
It is important to note that the rise in the line widths is very rapid in the
![]() 1025 erg/Å to
1025 erg/Å to ![]()
![]() erg/Å energy range.
What happens at energies higher than
erg/Å energy range.
What happens at energies higher than ![]()
![]() erg/Å? First of all
lets investigate how the Balmer
contribution from the flare kernels can evolve towards higher energies.
Lets investigate the two cases, when the magnetic field strength saturates
and when it does not, and therefore when the particle beam energy saturates and
when it does not. If it indeed saturates, then, so will the maximum
chromospheric pressure and the line width. In this case larger flares are
due to larger flaring areas and not to a higher beam intensity or energy.
If the kernels are still the main contributor to the Balmer emmission, then
we should observe a plateau (saturation) in the line widths at higher
energies. The situation is not clear because of a lack of observations, but
according to Fig. 7 there may be a saturation in the widths, if not a
decrease for large flares. This indicates that larger flares involve larger
areas rather than higher energy particle beams. On the other hand, the
AD Leo flare observed by Hawley & Pettersen (1991) indicates that for some
flares, as already found for the Balmer flux (Sect. 4.2 and Fig. 3a), the
contribution to the Balmer emission due to other sources (radiative pumping,
backwarming, lower density coronal plasmas) increasingly dominate.
erg/Å? First of all
lets investigate how the Balmer
contribution from the flare kernels can evolve towards higher energies.
Lets investigate the two cases, when the magnetic field strength saturates
and when it does not, and therefore when the particle beam energy saturates and
when it does not. If it indeed saturates, then, so will the maximum
chromospheric pressure and the line width. In this case larger flares are
due to larger flaring areas and not to a higher beam intensity or energy.
If the kernels are still the main contributor to the Balmer emmission, then
we should observe a plateau (saturation) in the line widths at higher
energies. The situation is not clear because of a lack of observations, but
according to Fig. 7 there may be a saturation in the widths, if not a
decrease for large flares. This indicates that larger flares involve larger
areas rather than higher energy particle beams. On the other hand, the
AD Leo flare observed by Hawley & Pettersen (1991) indicates that for some
flares, as already found for the Balmer flux (Sect. 4.2 and Fig. 3a), the
contribution to the Balmer emission due to other sources (radiative pumping,
backwarming, lower density coronal plasmas) increasingly dominate.
If the particle beam energy does not saturate, then the maximum
chromospheric pressure will increase with increasing U-band flux: the very
rapid rise in the line widths implies that a width of ![]() 37 Å will be
reached for a U-band flux of 1028 erg/Å! Indeed, for chromospheric
pressures even higher than those studied by H92a, Stark broadening dominates
the line formation and yields very broad profiles. Moreover, opacities
become also very large and the line formation approaches that of a black-body.
In other words, the Balmer lines progressively vanish in strength (because of
opacity) and become very broad because of the large Stark broadening.
Therefore, we are in a situation where the line equivalent widths fall
with increasing U-band intensity and become so broad that they would appear
to contribute only to the line wings. Hence, in the case when the beam
energy does not saturate, the contribution from the kernels, naturally
vanishes out of sight such that for large flares there remains only the
contributions from other flare plasmas, except in the line wings. Here,
we have a natural explanation so as why in some flares the observed line
widths fall with energy for energies larger than
37 Å will be
reached for a U-band flux of 1028 erg/Å! Indeed, for chromospheric
pressures even higher than those studied by H92a, Stark broadening dominates
the line formation and yields very broad profiles. Moreover, opacities
become also very large and the line formation approaches that of a black-body.
In other words, the Balmer lines progressively vanish in strength (because of
opacity) and become very broad because of the large Stark broadening.
Therefore, we are in a situation where the line equivalent widths fall
with increasing U-band intensity and become so broad that they would appear
to contribute only to the line wings. Hence, in the case when the beam
energy does not saturate, the contribution from the kernels, naturally
vanishes out of sight such that for large flares there remains only the
contributions from other flare plasmas, except in the line wings. Here,
we have a natural explanation so as why in some flares the observed line
widths fall with energy for energies larger than ![]()
![]() erg/Å.
erg/Å.
To conclude, we find that; (i) for energies lower than 1025 erg/Å,
flare kernels are not dense enough to dominate the Balmer emission
and the U-band is not a good tracer of the flare energy, (ii) for energies in
the range ![]() 1025 erg/Å to
1025 erg/Å to ![]()
![]() erg/Å,
the flare kernels dominate the Balmer emission and give rise to a rapid
increase in the line widths, (iii) for energies larger than
erg/Å,
the flare kernels dominate the Balmer emission and give rise to a rapid
increase in the line widths, (iii) for energies larger than
![]()
![]() erg/Å, the situation is not clear. The kernel contribution
may progressively vanish, either naturally because the chromospheric pressure
still increases, or because the contribution of other plasmas increases,
or both. But it seems that for some flares the kernel contribution is still
large, and such flares may be scaled up versions of medium size flares. In
this case we should observe a saturation in the line widths.
erg/Å, the situation is not clear. The kernel contribution
may progressively vanish, either naturally because the chromospheric pressure
still increases, or because the contribution of other plasmas increases,
or both. But it seems that for some flares the kernel contribution is still
large, and such flares may be scaled up versions of medium size flares. In
this case we should observe a saturation in the line widths.
It is important to remark that in any case the widths attain a maximum for
U-band energies of the order of ![]()
![]() erg/Å, and do not increase
for higher energies. This shows that either large flares are scaled up versions
of medium size flares, or that the contribution to the Balmer emission due to
other sources than the kernels (radiative pumping, backwarming, lower density
coronal plasmas) dominate.
erg/Å, and do not increase
for higher energies. This shows that either large flares are scaled up versions
of medium size flares, or that the contribution to the Balmer emission due to
other sources than the kernels (radiative pumping, backwarming, lower density
coronal plasmas) dominate.
We may also note that the gradient depicted for gradual phase measurements also suggests that densities or turbulence in non-kernel plasmas increase with the flare magnitude. This could indicate that backwarming effects on the atmosphere surrounding the flare are also magnified. Here again, the large scatter points to the probability that varying processes are at work.
We compiled all the simultaneous data of the Balmer lines and the U-band, during the impulsive phase. The results are shown in Fig. 8. In this figure we included the flares on; AD Leonis, 28/03/1984 2:40 UT and 3:22 UT, 12/04/1985 4:40 UT, 14/03/1998 0:45 UT, UV Ceti 08/09/1979 11:19 UT, 06/12/1984 2:43 UT and 3:29 UT, Prox Cen 25/03/1984 8:50 UT, YZ CMi 04/03/1985 19:55 UT, Gl 866 11/06/1991 3:27 UT and 3:56 UT, AT Mic 20/08/1985 1:12 UT. This diagrame is similar to Fig. 3a except that here we included all the points during the impulsive phase and not only the maximum flux.
When only the continuum flux measurement was available in spectrophotometry,
we transformed the continuum flux into U-band flux assuming (Lacy et al. 1976):
| (2) |
![\begin{figure}
\par\includegraphics[width=13.7cm,clip]{fig8_flare_2.eps}\end{figure}](/articles/aa/full/2003/03/aah3294/Timg40.gif) |
Figure 8:
Flux in the H |
| Open with DEXTER | |
Observations of the impulsive phase are correlated, and we fitted this correlation with a linear relation (Table 2). On the contrary, observations of the gradual phase are not correlated, and in fact the impulsive phase delineates a lower limit in the Balmer line fluxes for a given U-band flux. It is interesting to note that this corrrelation is valid for flares that span nearly 5 orders of magnitude in the U-band and that occur on different stars. This emphasizes that a universal mechanism is at work during the impulsive phase, that relates the formation of the U-band and the Balmer lines from the weakest flares to the largest ones. Other similar correlations between soft X-rays and radio fluxes or soft X-rays and Balmer line fluxes (Butler 1993; Benz & Gudel 1994) also indicate that emissions at different wavelengths are intimately related.
H92a showed that two leading mechanims could be responsible for the observed correlation; i) the dense flare kernels, and ii) the radiative pumping of the surrounding chromosphere by the white light. In the case of the flare kernels, both the white light intensity and the Balmer line intensity grow when the electron pressure increases, and because their growth is directly dependent on electron pressure, the two are correlated. However, H92a models cover only one order of magnitude in the U-band flux and cannot therefore explain the entire correlation. Hence, there is a need for a larger grid of model atmospheres, especially towards lower chromospheric pressures. It is important to note that, although larger flares are expected to cover larger areas, a simple scaling of the smaller flares cannot explain the observations. Indeed, if large flares were simply scaled up versions of smaller flares, then the correlation would have a slope of one. Even though the slope tends to increase towards the end of the energy range (Fig. 3a), the slope is generally smaller over most of the observed domain. Moreover we obtained a slope of 0.62 for the observations reported in Fig. 8 (Table 2). Therefore, simple scaling cannot explain the observations.
Models that mimic the effect of the radiative pumping by the white light on the chromosphere produce correlations with a slope between 0.6 and 1.7 (Houdebine 1992a; Houdebine 1990). Moreover they can cover more than three orders of magnitude in the U-band intensity. The M.A.1 series of model atmospheres in H90 agree rather well with observations, giving a slope close to the one observed in most of the U-band energy range. However, according to the variation of the Balmer FWHM as a function of U-band (Fig. 7) it is unlikely that this process is entirely responsible for the observed correlation between the Balmer line flux and the U-band flux. We propose that there is a combination of the two mechanisms as well as an increasing area of the flare at the lower atmospheric levels (kernels).
We compiled all the available data sets that include time-resolved spectroscopy in the 3600 Å-4500 Å wavelength range. We first analysed the flare time profile characteristics in terms of impulsive and gradual phases, and found a general description that holds for all the flares observed: namely, the flare is composed of an impulsive phase and a gradual phase which have different physical properties, and which arise in different proportions for different flares. The main signature of the impulsive phase is an impulsive behaviour in the Balmer line fluxes, always accompanied by a white light counterpart. The gradual phase evolves more slowly and has no white light counterpart. We found that all large flares are combined flares, i.e., they have strong distinct impulsive and gradual phases. Conversely, small flares can appear either totally dominated by the gradual or the impulsive phase.
We measured the rise and decay times in the time profiles of the Balmer and Ca II lines. We showed that the time profiles obey very precise laws that are valid for all flares in spite of their great variety in spectral signatures. These laws provide important constraints for modelling the flare phenomenon, future models will have to predict spectral line time-profiles that are identical for flares that have decay times from a couple of minutes to a couple of hours or more. In this respect, we found that the simple thermal cooling model proposed by Gurzadyan (1984, see also Houdebine et al. 1991) can reproduce very simply the observed features. However, in this case, observations also imply that small flares are compact and dense while larger flares have a lower density, which remains rather puzzling. In addition, we found that the constant ratio in the delays of the line time-profiles seem difficult to explain with X-ray backwarming models of the chromosphere.
We measured the maximum fluxes in the U-band and in spectral lines for both the impulsive and the gradual phases. The U-band and Balmer line fluxes correlate very well over more than 5 orders of magnitude. Moreover, the correlation is not linear and the gradient is generally smaller than 1, which shows that large flares are not simply scaled up versions of smaller flares, but that precise mechanisms that control both the U-band and the Balmer line formation are at work. As far as these mechanims are concerned, we establish that the flare kernel models and the radiative pumping models of Houdebine (1990, 1992a) can be combined to reproduce the observations. Other correlations between the spectral line fluxes, and the U-band flux, essentially demonstrate that the fluxes during the gradual phase and the impulsive phase grow together by the same rate.
Further correlations between the fluxes and the time delays in the spectral lines are evidence that, the more powerful the flare, the longer it lasts. As mentioned above, in the framework of Gurzadyan (1984) models, this implies that, the more powerfull the flare, the lower its density, at least for the plasmas concerned during the gradual phase. This remains unexplained at this stage. An alternative explanation is that more secondary energy release take place during the gradual phase of large flares, than during smaller flares.
The study of the Balmer line full width half maximum shows that the picture is likely to be more complex than expected. It seems that the description of the flares is best when divided into three subgroups; the small flares, the medium size flares, and the large flares. For the former, line broadening remains small and does not seem to depend on the flare U-band energy, probably because this latter feature is not a good diagnostic of the whole energy released. For intermediate energy flares, the line widths increase rapidly with the U-band energy, which seems evidence that, at this stage, emission from dense kernels dominates the overall Balmer emission. For larger flares, the line widths seem to reach a plateau. We interpret this as being a consequence of the kernel Balmer signature becoming very broad and vanishing away, and, as the radiative pumping process becomes more efficient, progressively taking over the Balmer emission, or because larger flares are simply scaled up versions of medium size flares.
Finally, we investigated in more detail the Balmer emission during the impulsive phase as a function of the U-band emission. We find that the correlation between the two parameters during the impulsive phase does in fact delimit a lower boundary in the Balmer-U-band diagram. The data shows that the Balmer emission and the U-band emission during the impulsive phase are correlated. We understand this correlation as being the direct signature of both dense kernel emission and the radiative pumping process taking place in the surrounding chromosphere.
We found that the simple characteristics of the flare flux time-profiles in visible spectroscopy provide valuable constraints for the modelling of stellar flares. Moreover, our correlations provide new insights into solar flare physics, and we suggest that observations of the sun as a star (whole sun observations) should be performed in the future to allow further comparison between solar and stellar flares. Future spectroscopic observations of flares, should be performed with a sufficiently high time resolution (at least 10 s), in particular if one wants to investigate the impulsive phase in detail. It would also be of particular interest to study the behaviour of other spectral lines, especially higher temperature transition region lines (such as the helium lines) and lower temperature lines such as Mg II or Ca I lines, in order to find out if similar correlations apply to them. Finally, future models will have to account for the numerous correlations obtained in this study, that apply to all flares.
Acknowledgements
This work was supported by a PPARC Research Fellowship (Grant PPA/G/S/2000/00076).