A&A 397, 997-1010 (2003)
DOI: 10.1051/0004-6361:20021589

Hipparcos red stars in the $HpV_{\rm T2}$ and $VI_{\rm C}$ systems[*],[*]

I. Platais1,2 - D. Pourbaix1,[*] - A. Jorissen1, $^{\star\star\star}$ - V. V. Makarov2,3 - L. N. Berdnikov4 - N .N. Samus5,4 - T. Lloyd Evans6 - T. Lebzelter7 - J. Sperauskas8

1 - Institut d'Astronomie et d'Astrophysique, Université Libre de Bruxelles, CP 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium
2 - Universities Space Research Association, Division of Astronomy and Space Physics, 300 D Street SW, Washington, D.C. 20024, USA
3 - U.S. Naval Observatory, 3450 Massachusetts Ave., NW, Washington D.C. 20392-5420, USA
4 - Sternberg Astronomical Institute and Isaac Newton Institute of Chile, Moscow Branch, 13 Universitetskij Prosp., Moscow 119992, Russia
5 - Institute of Astronomy, Russian Academy of Sciences, 48 Pyatnitskaya Str., Moscow 119017, Russia
6 - School of Physics and Astronomy, University of St Andrews, North Haugh, St Andrews, Fife, Scotland KY16 9SS
7 - Institut für Astronomie, Universität Wien, Türkenschanzstr. 17, 1180 Vienna, Austria
8 - Vilnius University Observatory, Ciurlionio 29, Vilnius 2009, Lithuania

Received 20 September 2002 / Accepted 28 October 2002

Abstract
For Hipparcos M, S, and C spectral type stars, we provide calibrated instantaneous (epoch) Cousins V-I color indices using newly derived $HpV_{\rm T2}$ photometry. Three new sets of ground-based Cousins VI data have been obtained for more than 170 carbon and red M giants. These datasets in combination with the published sources of VI photometry served to obtain the calibration curves linking Hipparcos/Tycho $Hp-V_{\rm T2}$ with the Cousins V-I index. In total, 321 carbon stars and 4464 M- and S-type stars have new V-I indices. The standard error of the mean V-I is about 0.1 mag or better down to $Hp\approx9$ although it deteriorates rapidly at fainter magnitudes. These V-I indices can be used to verify the published Hipparcos V-I color indices. Thus, we have identified a handful of new cases where, instead of the real target, a random field star has been observed. A considerable fraction of the DMSA/C and DMSA/V solutions for red stars appear not to be warranted. Most likely such spurious solutions may originate from usage of a heavily biased color in the astrometric processing.

Key words: stars: late type - stars: carbon - techniques: photometric - techniques: radial velocities


1 Introduction

The Hipparcos Catalogue (ESA 1997) includes two sets of Cousins V-Icolor indices - a functional V-I (entry H75 in the main Hipparcos Catalogue) and a best available V-I at the time of the Catalogue's release (entry H40). This color index is an important temperature indicator for late-type stars (Dumm & Schild 1998; Bessell et al. 1998). Since only 2989 Hipparcos stars are listed as having direct measurements of the Cousins V-I index, nineteen different methods of variable accuracy were used to obtain V-I photometry (see ESA 1997, Sect. 1.3, Appendix 5). In numerous cases the reductions of Hipparcos V-I photometry relied heavily upon the satellite's star mapper photometry - the Tycho $B_{\rm T}-V_{\rm T}$ color indices. However, the Tycho photometric system alone is not well-suited for the studies of fainter red stars. A combination of intrinsically low fluxes from these stars in the $B_{\rm T}$ bandpass and a short crossing time ($\sim$22 ms) of the star mapper's four vertical slits resulted in low S/N ratios. This, in combination with the residual bias that was not fully corrected by the de-censoring analysis (Halbwachs et al. 1997) in deriving the Tycho photometry for faint stars, diminishes the reliability of much of the published Hipparcos V-I indices for stars with $V-I\ga1.5$. As demonstrated by Koen et al. (2002), the listed Hipparcos V-I photometry of red stars shows a disappointingly large scatter with respect to the ground-based photoelectric V-Imeasurements. In extreme cases the disagreement can reach up to 2-3 mag.

Our interest in the V-I photometry of red stars is primarily motivated by the potential effect of incorrect V-I color indices on the chromaticity corrections in Hipparcos astrometry. On average, a one magnitude offset in the V-I value could introduce a $\sim$1 mas bias in the star's position (abscissa) along the scan direction. Besides grossly incorrect V-Iindices for some red stars (Koen et al. 2002), there is a systematic color bias related to neglecting in the Hipparcos reductions the intrinsic color variation in large amplitude variables such as Miras.

In retrospect, the Hipparcos V-I photometry would have gained considerably from the parallel-in-time ground-based V-I observations of stars with extreme colors and/or considerable color variability. For a number of reasons, most importantly, a prorogated decision to choose the V-I index, this opportunity was lost. Is it possible to improve the Hipparcos V-I photometry now? Here we attempt to answer this question. It appears that high-grade V-I photometry for red stars is possible down to $V\approx8$ and may even be used to obtain an estimate of effective temperatures. In general, the re-calibrated V-I photometry is useful in identifying some difficult cases in the Hipparcos Catalogue, such as red and variable stars in binary systems. Throughout the paper we refer to Cousins V-I color indices, unless it is explicitly stated otherwise.

  
2 Ground-based Cousins VI photometry

The advantages of the broadband Cousins VRI photometric system such as high internal precision and maintaining this precision over the whole range of spectral types are discussed by Bessell (1979). This system emerged with the advent of Ga-As photocathode photomultipliers in the early 1970s. There are two issues which should be considered in the broadband photometry of red stars. First, the majority of cool red stars are variable and no standard stars are available redder than $V-I\approx3$. Second, the presence of numerous molecular bands in the spectra of red stars requires stable and easily reproducible bandpasses in order to avoid possible nonlinear transformations from the instrumental to the standard system. In other words, to exclude the transformation uncertainties, such stars must be observed in the natural Cousins VRI system, i.e. using the same filters and detector. Examination of the published sources of Cousins VRI photometry indicates that many extremely red Hipparcos stars actually lack this photometry. Therefore, we have obtained new sets of UBVRI photometry of the Southern carbon stars and BVI photometry for the reddest M and C spectral-type stars.

2.1 Carbon star photometry at SAAO

The observations of 85 carbon stars including a few hydrogen-deficient (Hd) stars were made in 1984 and 1987 using the single channel Modular Photometer on the 0.5 m reflector at the Sutherland station of the SAAO. The photometer uses a Hamamatsu R943-02 GaAs photomultiplier and a filter set which reproduces the Johnson UBV and Cousins $(RI)_{\rm C}$ photometric systems, with a need for only very small linear and non-linear terms in transformations onto the standard system. The observations were made with frequent reference to the E-region standard stars of Menzies et al. (1989). The results of $UBV(RI)_{\rm C}$ photometry are provided in Table 1. The CGCS numbers are those in Stephenson (1989). The last column indicates the total number of observations, usually obtained over 2-3 nights. The standard error of individual observations is about 0.01 mag. It was necessary, however, to extrapolate the color system as some of the stars here are redder than any standard star in one color or another and in any case these are carbon stars (or helium stars in the case of Hd stars) whose colors differ systematically from the oxygen-rich M spectral type standard stars. In addition, most of our programme stars are variable to some degree. All cases with apparent variability or uncertain photometry are marked by (v) or (:), accordingly. Since in the UBVRI photoelectric photometry the aperture size varied from $20\hbox{$^{\prime\prime}$ }$ to  $40\hbox{$^{\prime\prime}$ }$, a nearby optical component, marked in Table 1, may affect the accuracy of our photometry.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f1.eps} \end{figure} Figure 1: Differences between the V-magnitude (top panel) and V-I color index (bottom panel) from Table 1 and that of Walker (1979). A relatively large spread visible in the top panel is mainly due to thevariability.

The generally good agreement (Fig. 1) with the data of Walker (1979), whose observations were made with separate blue and red sensitive photomultipliers and a different filter set, give added confidence to the results.


 

 
Table 1: SAAO photometry of selected carbon stars.
CGCS HIP GCVS V B-V U-B R-I V-I n CGCS HIP GCVS V B-V U-B R-I V-I n
177   AM Scl 12.33 2.16 3.42: 1.02 1.85 3 3810     10.39 1.41 0.90 0.83 1.63 5
196 5809   10.02 1.33 1.34 0.59 1.09 5 3813     11.02v 2.39 2.61 1.30 2.45 4
258     10.19 1.31 1.16 0.61 1.12 6 3842 85750   9.37 1.88 2.02 0.88 1.66 5
327 10472 V Ari 8.71 2.19 2.45 1.16 2.15 6 3855a     11.20 1.30 0.91 0.64 1.19 2
378 12028   8.16 1.24 0.77 0.60 1.09 4 3864a   V450 Sco 10.30v 2.38 3.56: 1.50 2.82 4
576 17933   8.30 1.65 1.72 0.75 1.41 6 3938 88584 W CrA 9.95 1.89 1.83 0.99 1.81 4
639 19269   10.66 1.23 0.68 0.72 1.43 4 3939   V1783 Sgr 10.53 1.54 1.01 0.94 1.74 3
725 21051   8.91 1.14 1.12 0.55 1.04 6 3957 88887   9.80 1.52 1.18 0.96 1.87 4
1380 31725   9.37 1.37 1.28 0.58 1.07 3 3958     10.45 1.34 0.95 0.66 1.23 6
1460 33042 KY CMa 10.75 2.73 4.00: 1.33 2.42 4 3966a     11.06v 1.95 1.76 1.05 1.95 4
1489 33550 RV Mon 6.88 2.65 7.16:     3 3992 89783 FO Ser 8.42 1.85 1.85 1.15 2.21 3
1507 33794 V614 Mon 7.32v 1.76 2.14: 1.13   4 4021 90694   9.90 1.39 0.92 0.81 1.60 3
1659 35549 MY CMa 10.63 2.44 3.08: 1.36 2.55 3 4042     11.13 2.08 2.01 1.05 1.90 3
1790     9.58 1.85 2.15 1.11 2.07 3 4070     9.33 1.29 1.00 0.58 1.06 3
1871a     10.16 1.23 0.82 0.56 1.02 3 4086 91929 RV Sct 10.02 2.35 2.52 1.54 2.92 3
1968 38787 V406 Pup 7.62v 3.20: 4.60: 1.40   4 4094 92115   9.49 0.83 0.47 0.42 0.67 3
2153 40805 V433 Pup 9.54v 1.67 1.66 1.07 2.05 3 4145 93181 V4152 Sgr 9.33 1.16 0.84 0.57 0.94 1
2331 43093 UZ Pyx 7.32 2.01 2.99 1.09   4 4168     9.95 1.29 1.22 0.59 1.10 4
2449 45295 GM Cnc 8.65 1.57 1.50 1.00 1.93 3 4179a 94049   10.29 1.26 0.83 0.60 1.14 3
2759 50994   9.53 1.30 1.07 0.59 1.09 4 4194 94294 V1445 Aql 11.31 2.08 2.35: 1.31 2.51 3
2787     9.48 1.29 0.96 0.60 1.11 5 4196     10.82 1.42 1.24 0.68 1.31 3
2829 52271   7.08 1.33 1.16 0.59 1.11 4 4229 94940 V1942 Sgr 7.06 2.56 4.45:     1
2852 52656 TZ Car 8.71v 2.10 2.60 1.30 2.50 4 4247 95289   6.96 1.07 0.58 0.57 0.97 1
2925 53810   8.33 1.16 1.08 0.55 1.05 4 4498     11.14 1.32 1.19 0.61 1.12 3
2975 54806   10.16 1.44 1.14 0.85 1.64 4 4524a 98117   9.18 1.21 0.61 0.54 1.01 3
2986   DI Car 10.5 v 1.4 v 1.30v 0.64v 1.2v 6 4567 98223   9.35 2.03 2.06 0.92 1.73 4
3001 55448 V905 Cen 10.51v 1.80 1.87 1.15 2.20 4 4595 98542 V1468 Aql 10.36 2.04 2.55 1.16 2.13 3
3066 56551   8.76 1.06 0.51 0.51 0.92 4 4598 98538 V1469 Aql 8.37 2.08 2.52 0.96 1.77 3
3141 58513 DD Cru 8.87 2.20 2.94: 1.04 2.03 4 4614 98958   8.05 1.07 0.97 0.51 0.98 3
3199   TV Cen 8.02v 2.74 2.89 1.42 2.57 5 4873 101277 BI Cap 9.67v 1.42 1.09 0.95 1.85 3
3227 60534 S Cen 7.66v 1.89 2.70: 1.11 2.10 5 4972 102726   10.30 1.29 0.92 0.63 1.14 3
3286 62401 RU Vir 9.97v 4.63 5.10: 1.99 3.42 4 4978 102706   8.16v 1.28 0.94 0.58 1.14 3
3335 63955   8.50 1.17 1.03 0.54 1.01 4 5147 104522   9.82 1.56 1.49 0.97 1.86 6
3405 66070 V971 Cen 8.50 1.87 2.12 1.02 1.94 5 5227 105212   9.67 1.26 0.87 0.57 1.06 5
3492 70339 RS Lup 9.62v 2.69 4.70: 1.35 2.46 5 5408 107349 BU Ind 10.15v 1.45 1.28 0.95 1.85 4
3545     10.95 1.40 0.80 0.77 1.44 5 5420 107490 RR Ind 9.34v 2.84v 5.29v 1.31v 2.36v 7
3558     10.42 1.51 1.26 1.01 1.98 5 5561 108953 HP Peg 8.89 1.45 1.13 0.61 1.15 2
3606 75694 HM Lib 7.48v 1.20 0.86 0.61 1.07 4 5627     10.71 1.72 1.63 0.82 1.50 3
3657     9.84 1.59 1.32 0.69 1.28 5 5761 113150   10.82 1.17 0.55 0.59 1.11 6
3672 79484   10.36 1.69 1.46 0.77 1.42 5 5823 114509   9.26 1.22 0.81 0.60 1.11 5
3707 81254 LV TrA 8.30 0.95 0.67 0.45 0.72 5 5937 117467   8.48 1.37 1.30 0.62 1.15 5
3756 83387 T Ara 9.03v 2.78 4.90: 1.40 2.55 5 5980 168   9.55 1.12 0.48 0.51 0.96 4
3765     9.11 1.39 1.26 0.65 1.25 4                  

a
Close companion: 1871 ( $9\hbox{$^{\prime\prime}$ }$ separation, bright); 3855 ( $15\hbox{$^{\prime\prime}$ }$); 3864 ( $11\hbox{$^{\prime\prime}$ }$); 3966 ( $15\hbox{$^{\prime\prime}$ }$, bright), 4179 ( $14\hbox{$^{\prime\prime}$ }$), 4524 ( $13\hbox{$^{\prime\prime}$ }$ & $18\hbox{$^{\prime\prime}$ }$).

2.2 Photometry of red stars at Siding Spring Observatory

In March-April 2002 additional $BVI_{\rm C}$ photometry for 47 very red Hipparcos carbon and M stars was secured at the Siding Spring Observatory, Australia. The data were obtained using the 24 inch reflector and a single channel photometer. A cooled unit containing a Hamamatsu GaAs photomultiplier tube and a set of filters allow us to match closely the Cousins photometric system, in the same way as was done at SAAO. Each night a set of the E-region standards (Menzies et al. 1989) was measured to obtain the atmospheric extinction coefficients and the transformation coefficients to the standard system. Mean transformation coefficients for this run were as follows: $\xi_{V}=0.005$, $\xi_{B-V}=1.010$, and $\xi_{V-I_{\rm C}}=1.015$ (see Berdnikov & Turner 2001, Eq. (2)). Hence the instrumental system is very close to the standard BVIC system, which greatly alleviates the problem of color-related extrapolation in the reductions of very red programme stars. Every 60-90 min two standard stars (red and blue) were used to define instantaneous zeropoints in the transformation relations. Some very bright programme stars were observed with the addition of an Oriel 50550 neutral density filter. The $BVI_{\rm C}$ photometry is presented in Table 2.


 

 
Table 2: BVI photometry at Siding Spring.
HIP GCVS JD -2 450 000 V B-V V-I
23203 R Lep 2353.915 11.63 4.60 3.75
23636 T Lep 2376.883 12.18 1.75 5.92
24055 U Dor 2376.977 8.61 1.62 4.17
    2378.889 8.62 1.60 4.17
25004 V1368 Ori 2376.871 10.07 3.53 3.48
25673 S Ori 2376.874 8.71 1.65 4.66
28041 U Ori 2376.870 10.22 1.87 5.40
    2378.880 9.94 2.00 5.45
29896 GK Ori 2353.919 9.96 4.22 3.52
34413 W CMa 2361.980 6.74 2.69 2.43
35793 VY CMa 2353.922 8.19 2.28 3.28
39967 AS Pup 2376.928 9.01 1.50 4.61
    2378.919 9.01 1.48 4.60
40534 R Cnc 2376.925 11.22 2.26 5.77
    2378.931 11.31 2.30 5.81
41061 AC Pup 2376.908 8.99 3.23 2.78
    2378.933 9.04 3.31 2.80
43905 T Cnc 2353.926 8.23 4.31 3.29
48036 R Leo 2353.929 7.28 1.71 5.02
53085 V Hya 2354.036 7.34 4.66 3.61
53809 R Crt 2354.038 8.43 2.01 4.81
57607 V919 Cen 2354.039 6.93 1.59 4.15
63642 RT Vir 2354.175 8.25 1.81 4.67
64569 SW Vir 2354.178 7.09 1.72 4.53
67419 W Hya 2354.179 8.42 2.44 5.64
69754 R Cen 2354.178 7.48 1.94 4.22
70969 Y Cen 2354.181 8.12 1.60 4.50
75393 RS Lib 2354.182 10.79 1.96 5.41
80365 RT Nor 2354.183 10.08 1.01 0.94
80488 U Her 2379.168 8.68 1.60 4.84
80550 V Oph 2357.168 9.21 4.13 3.19
82392 V TrA 2364.266 8.16 2.23 2.24
84876 V1079 Sco 2354.185 9.40 3.31 3.34
85617 TW Oph 2357.168 7.86 4.24 3.32
85750   2357.174 9.36 1.93 1.65
86873 SZ Sgr 2357.170 8.78 2.36 2.73
87063 SX Sco 2357.172 7.65 2.86 2.65
88341 V4378 Sgr 2379.172 10.37 2.97 3.24
88838 VX Sgr 2379.174 9.20 2.82 4.34
89739 RS Tel 2357.254 10.01 0.85 0.77
90694   2357.252 9.93 1.37 1.61
93605 SU Sgr 2357.258 8.33 1.73 4.39
93666 V Aql 2357.260 6.78 3.98 3.07
98031 S Pav 2379.201 7.82 1.64 4.63
99082 V1943 Sgr 2379.195 7.67 1.77 4.58
99512 X Pav 2357.256 8.97 1.91 4.92
100935 T Mic 2357.265 7.68 1.78 4.76


2.3 VRI photometry of red variables with APT

Since 1996 the University of Vienna has been obtaining UBV(RI)Cphotometry in Arizona using two 0.75 m automatic photoelectric telescopes[*] (APT) located on the grounds of Fairborn Observatory. The photometer of the APT dubbed Amadeus (Strassmeier et al. 1997), has an EMI-9828 S-20/B multi-alkali cathode photomultiplier, which is sensitive up to $\sim$900 nm. This photomultiplier in combination with filters close to those suggested by Bessell (1976) reproduces a $V(RI)_{\rm C}$ system close to the one used by Walker (1979). In 1997 a monitoring programme of nearly 60 late spectral type semiregular and irregular variables was initiated. Typical light curves resulting from this programme can be found in Lebzelter (1999) and Kerschbaum et al. (2001). A complete sample of light curves will be published elsewhere (Lebzelter et al., in preparation). In Table 3 we present median V, $V-I_{\rm C}$, and an intercept a0 and slope a1 from the fit V-I vs. V for 45 selected Hipparcos variables used in the following calibration (Sect. 3). The total number of observations n is indicated in the last column.


 

 
Table 3: APT photometry of selected red variables.
HIP GCVS V $V-I_{\rm C}$ a0 a1 n
4008 VY Cas 9.49 4.14 0.66 0.366 217
5914 Z Psc 6.85 2.54 -0.18 0.396 49
6191 AA Cas 8.24 3.47 0.00 0.422 206
10472 V Ari 8.52 2.07 -1.15 0.379 30
17821 BR Eri 7.15 3.16 -0.15 0.465 270
21046 RV Cam 8.16 3.81 0.38 0.420 326
22667 o1 Ori 4.84 2.50 -0.10 0.536 83
32083 VW Gem 8.32 2.41 -0.86 0.391 36
33369 BG Mon 9.66 2.46 -1.40 0.400 35
41061 AC Pup 9.05 2.83 -1.42 0.474 360
41201 FK Hya 7.29 3.48 0.22 0.446 388
43063 EY Hya 9.60 4.49 1.01 0.366 85
44601 TT UMa 9.02 3.68 -0.17 0.427 425
44862 CW Cnc 8.70 4.03 0.90 0.360 67
56976 AK Leo 8.54 2.87 -1.37 0.497 68
57504 AZ UMa 8.50 3.97 0.57 0.400 440
59108 RW Vir 7.33 3.63 0.66 0.405 377
61022 BK Vir 7.81 4.24 2.13 0.268 98
61839 Y UMa 8.39 4.40 1.92 0.295 411
66562 V UMi 7.91 2.92 -0.95 0.488 78
69449 EV Vir 6.91 2.62 -1.05 0.533 223
70236 CI Boo 6.48 2.93 -0.63 0.549 182
70401 RX Boo 7.43 4.33 2.97 0.184 105
71644 RV Boo 8.24 4.06 1.30 0.333 190
73213 FY Lib 7.24 3.65 0.30 0.460 225
74982 FZ Lib 7.10 3.04 -1.00 0.570 367
78574 X Her 6.28 3.92 1.60 0.371 346
80259 RY CrB 9.63 4.02 0.24 0.393 255
80704 g Her 4.86 3.47 1.23 0.461 291
81188 TX Dra 7.26 2.96 -0.58 0.488 153
81747 AX Sco 8.73 4.00 -0.60 0.527 120
82249 AH Dra 7.54 3.52 0.00 0.465 301
84027 CX Her 9.86 4.04 1.85 0.225 33
84329 UW Her 7.97 3.42 -0.29 0.464 298
84346 V438 Oph 9.12 4.26 2.41 0.199 164
93989 V398 Lyr 7.39 3.30 -0.32 0.490 265
95173 T Sge 9.29 4.66 2.45 0.236 276
96919 V1351 Cyg 6.56 3.06 0.00 0.466 226
102440 U Del 6.77 3.61 0.88 0.402 299
103933 DY Vul 7.09 3.58 0.55 0.425 207
107516 EP Aqr 6.63 4.01 2.16 0.279 183
109070 SV Peg 8.67 4.47 0.18 0.490 69
110099 UW Peg 8.89 3.39 -0.82 0.473 207
112155 BD Peg 8.66 3.82 0.56 0.376 159
113173 GO Peg 7.37 2.66 -0.76 0.464 168


2.4 Published sources of VI photometry

Only two large surveys of relatively bright red stars are available in the $VI_{\rm C}$system - a survey of the Southern carbon stars (Walker 1979) and the recent photometry of nearly 550 Hipparcos M stars (Koen et al. 2002). Additional literature on the $VI_{\rm C}$ photometry of Hipparcos red stars is not rich, therefore we included some other sources containing Johnson $VI_{\rm J}$photometry. We used normal color indices for M0 to M8 spectral type stars (Celis 1986, Table 4) to obtain the following relationship between the Johnson $V-I_{\rm J}$ and Cousins $V-I_{\rm C}$:

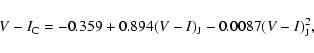\begin{displaymath}V-I_{\rm C}=-0.359+0.894(V-I)_{\rm J}-0.0087(V-I)_{\rm J}^{2}, \end{displaymath} (1)

defined for the giants of M spectral type. This is valid for zirconium (S-type) stars, and probably usable for carbon stars as well, throughout the $V-I_{\rm J}$ range from 1.9 to 8.7 mag. Note that this relationship yields a bluer color index, by $\sim$0.1, than a similar relationship from Hipparcos Catalogue (ESA 1997, vol. 1). A list of all sources used in this paper to calibrate V-I photometry is given in Table 4. It contains the reference, the number of stars n, spectral type, photometric system, and remarks. This list is not complete since we deliberately left out a few sources for the further independent comparisons.


 

 
Table 4: Selected sources of VI photometry.
Source n Type System Remarks
Bagnulo et al. (1998) 1 C Cousins  
Barnes (1973) 11 M Johnson narrow-band I
Celis (1982) 24 M Kron(?) $\sim$Johnson I
Celis (1986) 20 M Cousins  
Eggen (1972) 30 C Eggen $\sim$Cousins I
de Laverny et al. (1997) 2 C Cousins  
Kizla (1982) 36 C, M Johnson  
Koen et al. (2002) 80 M Cousins only V<8.4
Lee (1970) 43 M Johnson  
Mendoza & Johnson (1965) 33 C Johnson  
Olson & Richer (1975) 11 C Johnson  
Percy et al. (2001) 16 C, M Johnson  
Walker (1979) 119 C Cousins  
Table 1 61 C Cousins this study
Table 2 42 C, M Cousins this study
Table 3 45 C, M Cousins this study


2.5 Radial velocities

Although radial velocities have no direct bearing on the photometry, they could be used to identify spectroscopic binaries and hence shed light on possible discrepancies in the photometry caused by duplicity. We selected 19 Hipparcos carbon stars, mostly R type. The radial velocity measurements were made with a Coravel-type spectrometer using the Steward Observatory 1.6 m Kuiper Telescope at Mt. Bigelow, Arizona in February, 2002. Additional measurements were also obtained with the Moletai Observatory 1.65 m telescope in Lithuania and the 1.5 m telescope of the Turkish National Observatory near Antalya. A detailed description of the spectrometer is given in Upgren et al. (2002). On average, the estimated precision of a single measurement is 0.7 km s-1. A total of 61 measurements of radial velocity are given in Table 5, where columns 1-6 are Hipparcos number, carbon star number from Stephenson (1989), GCVS variable star name (Kholopov et al. 1985-1995), Julian date, heliocentric radial velocity and its estimated standard error, both in km s-1. More details on the observing and reduction procedure can be found in Upgren et al. (2002). By examining the ratio of external and internal error in accordance with Jasniewicz & Mayor (1988), it is evident that two stars in Table 5, HIP 53522 and 53832, are new SB1 spectroscopic binaries, although the time span is too short for the orbit determination. Both stars are suspected CH-like carbon stars (Hartwick & Cowley 1985), which adds more weight to the paradigm that most CH stars are binaries.


 

 
Table 5: Radial velocities of R and other selected carbon stars.
HIP CGCS GCVS JD-2 450 000 ${\it RV}_{\rm hel}$ $\sigma_{\it RV}$ HIP CGCS GCVS JD-2 450 000 ${\it RV}_{\rm hel}$ $\sigma_{\it RV}$
26927 1035 $\cdots$ 2327.617 42.5 0.6 53832 2919 $\cdots$ 2327.946 5.2 0.7
      2332.630 42.2 0.6       2332.843 3.4 0.6
29896 1222 GK Ori 2330.729 54.6 1.5       2363.492 -2.8 0.7
$\cdots$ 1226 V1393 Oria 2332.641 34.2 0.6       2368.389 -3.1 0.7
29961 1230 V1394 Ori 2327.658 70.8 0.7       2382.344 -5.5 0.7
31829 1337 NY Gem 2327.732 -123.0 0.8       2386.347 -6.4 0.7
32187 1373 V738 Mon 2327.706 60.3 0.7       2399.392 -8.9 0.7
      2332.650 61.2 0.7       2403.329 -8.4 0.7
33369 1474 BG Mon 2327.752 71.4 0.7       2419.261 -11.5 0.7
      2333.745 71.6 0.7       2423.270 -12.1 0.7
      2350.255 71.4 0.7 58786 3156 $\cdots$ 2349.500 -21.3 0.7
34413 1565 W CMa 2330.686 18.9 0.6       2368.400 -21.4 0.7
      2333.737 19.6 0.6       2386.299 -21.2 0.7
35681 1622 RU Cam 2350.266 -24.4 0.6 62944 $\cdots$ $\cdots$ 2327.992 8.5 0.6
      2356.253 -26.3 0.7       2332.853 6.5 0.6
      2375.335 -24.9 0.7       2363.504 6.7 0.6
38242 1891 $\cdots$ 2327.760 13.7 0.7       2368.416 6.2 0.6
      2332.664 15.7 0.7       2382.382 7.3 0.6
39118 1981 $\cdots$ 2327.772 95.5 0.7 63955 3335 $\cdots$ 2327.957 -9.2 0.7
      2332.670 96.2 0.7       2332.919 -10.1 0.6
44812 2428 $\cdots$ 2327.917 20.2 0.7 69089 $\cdots$ $\cdots$ 2330.980 -20.3 0.6
      2350.314 20.1 0.8       2332.906 -20.3 0.7
      2375.300 20.7 0.7       2359.572 -21.4 0.6
50412 2715 $\cdots$ 2349.486 -84.8 0.7       2382.449 -20.2 0.6
      2386.284 -84.9 0.7       2399.479 -20.9 0.6
53354 2892 $\cdots$ 2330.801 4.7 0.7            
      2332.827 5.8 0.8            
53522 2900 $\cdots$ 2327.938 28.0 0.6            
      2369.333 31.5 0.7            
      2375.326 33.3 0.7            
      2382.336 34.9 0.7            
      2386.337 34.3 0.7            
      2399.377 36.3 0.7            
      2403.322 37.5 0.7            
      2419.255 37.5 0.7            
      2423.255 38.5 0.7            

% latex2html id marker 6831 $\textstyle \parbox{14cm}{ $^a$\space Not HIP 29899. See Table~\ref{tab:off}.}$


  
3 Deriving V-I from Hipparcos Hp

The central idea of this study is to derive new sets of V-I color indices for red stars bypassing all various methods used in the original derivation of V-I (ESA 1997). We abandon the calibration methods based upon the ground-based B-V or Tycho $B_{\rm T}-V_{\rm T}$ for two reasons. First, the B-V color index, at least for carbon stars, is a poor representative of effective temperature due to the severe blanketing effect by molecular bands (Alksne et al. 1991) in the BV bandpasses. Second, many Hipparcos red stars have such a large B-V color index that their measurements are uncertain or, in the case of Tycho magnitudes, missing due to extremely low fluxes in the $B_{\rm T}$bandpass. In this sense the potential of Tycho $B_{\rm T}V_{\rm T}$ photometry for red stars is limited. However, there is a color index, $Hp-V_{\rm T}$, which to our knowledge, has been used neither in the Hipparcos reductions nor the following studies.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f2.eps} \end{figure} Figure 2: Normalized response curves for the Hipparcos Hp (solid line), Tycho $V_{\rm T}$ (short-dashed line), and Cousins I(long-dashed line) bandpasses. The corresponding curves are taken from Bessell (1990, 2000).

The normalized Hp and $V_{\rm T}$response curves provided by Bessell (2000) indicate only a 21 nm difference in the mean wavelength (see Fig. 2). This wavelength is calculated assuming a flat spectral energy distribution (SED) which is definitely not the case for late-type stars. If we account for the observed spectral energy distribution, e.g., from Gunn & Stryker (1983), then for an M7III spectral-type star (HIP 64569) the difference in the effective wavelengths of the two filters reaches 150 nm. The SEDs for the two carbon stars HIP 99 and 95777 yield an 84 and 94 nm difference in the effective wavelength, respectively. It is the extended red response of the S20 photocathode of Hipparcos main detector - Image Dissector Tube, which makes the $Hp-V_{\rm T}$ index fairly sensitive in the K-M spectral range (see ESA 1997, vol. 1, Fig. 1.3.4). We employ this property to calibrate V-I for late-type stars using $Hp-V_{\rm T}$.

3.1 Tycho photometry

First trials using the published Tycho $V_{\rm T}$ photometry indicated two problems. First, a large fraction of red stars lack Tycho photometry. Second, the $V_{\rm T}$ photometry shows a progressively increasing bias at faint magnitudes ( $V_{\rm T}>9$). This effect is illustrated by Fig. 3 where $Hp-V_{\rm T}$ values are abnormally small at Hp>8, equivalent to the "brightening'' of $V_{\rm T}$ at these Hp magnitudes.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f3.eps} \end{figure} Figure 3: Bias in the $Hp-V_{\rm T}$ at Hp>8 originating from original Tycho $V_{\rm T}$ magnitudes for a bright Mira  T  Cep  = HIP  104451 (top panel). If the $V_{\rm T2}$ epoch photometry is used, the bias disappears (bottom panel). A straight line is fitted to the data in the bottom panel and then just overplotted in the top panel.

It is suspected that the de-censoring technique (Halbwachs et al. 1997) has failed to completely correct the faint-magnitude bias. Therefore, it was decided to make use of the Identified Counts Data Base, ICDB (Fabricius & Makarov 2000b) - a by-product of the Tycho-2 data re-processing (Høg et al. 2000).

All transits of about 2.5 million stars included in the Tycho-2 Catalogue are represented in the ICDB by sequences of 13 time-ordered photon counts, separately for the inclined and vertical slits, and the $B_{\rm T}$ and $V_{\rm T}$ bandpasses. Combined with some instrument calibration files, this data base is sufficient to reproduce a complete astrometric solution for any Tycho-2 star, including its possible binarity status, photometric variability, etc. In this paper, we exploit the possibility to extract epoch photometry for selected stars by estimating the signal at the pre-computed, mission-averaged astrometric position.

The working version of Tycho-2 epoch photometry was derived some time ago for a search of a particular kind of variable stars, although it has not been implemented in the construction of the Tycho-2 Catalogue. It should be noted that, even though based on the same observational data, the Tycho-2 epoch photometry used here differs significantly from the published Tycho epoch photometry (ESA 1997). Nevertheless, the global calibrations of our current epoch photometry are consistent with the Tycho mission-average calibrations. On the star-by-star level, the Tycho-2 processing (both astrometric and photometric) is based on a single so-called Maximum Cross-Correlation estimator, while the original Tycho epoch photometry is the result of a series of successive linear and non-linear filterings (Halbwachs et al. 1997; ESA 1997, vol. 4). The main difference in the reduction procedure is that for a given star in Tycho-2, the determination of astrometric parameters was done over all collected transits at once; whereas in Tycho, a complete cycle of astrometric and photometric reductions was performed for each transit.

The latter method proved to be unreliable at a low signal-to-noise ratio, as the noise may mimic a signal from the star and produce a spurious astrometric detection and a subsequent false photometric estimate at the derived location. Such false detections tend to be abnormally bright, which then produce a bias in the faint magnitudes and hence necessitate the de-censoring analysis (Halbwachs et al. 1997) as the lesser of two evils.

The Tycho-2 epoch photometry is largely free of this de-censoring bias, since all photometric estimations are made at the correct location of a star image (within the astrometric precision), and all observations are retained. Still, Tycho-2 epoch photometry can only find restricted applications due to a possibly high background and contamination from other stars which could be present in the $40\hbox{$^\prime$ }$-long slits of the star mapper.

We will denote the re-processed Tycho photometry as $V_{\rm T2}$ to distinguish it from the original Tycho $V_{\rm T}$ epoch photometry.

  
3.2 Relationship Hp-V $_{\mathsfsl {T2}}$ vs. Hp

Due to the differences in spectral features, we kept the processing of carbon and oxygen- and zirconium-rich (M, S) stars separately. There are 321 carbon stars and 4464 stars of M and S spectral type, which have a pair of Hp and $V_{\rm T2}$ values. These stars were selected according to the listed spectral type in the Hipparcos Catalogue (field H76) but not fainter than Hp=11. In the case of a missing spectral type, we included the stars having Hipparcos V-I>1.5. Finally, the stars of K spectral-type were also considered if their V-I>2. Note that for the Hipparcos photometry we used the so-called $Hp_{\rm dc}$ magnitude estimate derived from the unmodulated part of a signal intensity (ESA 1997), since the mean photometric parameters have been obtained from $Hp_{\rm dc}$. In addition, the ground-based photoelectric photometry is always integrated over some aperture (usually with ${\ \hbox{$\scriptstyle/\mkern-13mu\mathchar''20D $ }}=15{-}30\hbox{$^{\prime\prime}$ }$) centered onto the target and hence, the flux from any object within this aperture is going to be included. However, in Tycho-2 photometry, if the star was found to be a binary (minimum separation $\sim$ $0\hbox{$.\!\!^{\prime\prime}$ }4$), only the brightest component has been retained and subsequently used for this study. Because of that, the color index $Hp-V_{\rm T2}$ of resolved binaries could be biased to some degree and thus, should be considered with caution.

For each star, the color index $Hp-V_{\rm T2}$ was visually examined as a function of Hpignoring the listed status flags. A pair of $Hp,V_{\rm T2}$ photometry was deleted if it deviated from the mean trend by more than $3\sigma$.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f4.eps} \end{figure} Figure 4: The distribution of mean standard errors for red stars from Hp photometry (solid dots) and Tycho-2 $V_{\rm T2}$ data (crosses) as a function of median Hp magnitude. The large scatter in the distribution of $V_{\rm T2}$ errors is due to the variability - observations of Miras generate the largest scatter. The lower envelope of the same error distribution reflects the contribution by photon noise.

As seen in Fig. 4 the precision of $Hp-V_{\rm T2}$ is driven by the precision of the $V_{\rm T2}$ photometry. A rapidly deteriorating error budget at Hp>9actually poses a problem of reliability of calculated slopes in the $Hp-V_{\rm T2}$ vs. Hp plot. We opted for an interactive and iterative linear fit to find a slope, i.e., gradient $\nabla_{HpV_{\rm T}}=\Delta(Hp-V_{\rm T2})/\Delta{Hp}$ and an intercept. It was decided to keep all datapoints unless any were clearly deviant or there was a peculiar trend usually due to very faint or corrupted $V_{\rm T2}$ epoch photometry. It should be noted that we were not able to find a perceptible difference in the color of variable stars observed at the same magnitude on the ascending or descending part of a lightcurve. In the case of a constant star or large uncertainties in the $V_{\rm T2}$ photometry, only the mean $Hp-V_{\rm T2}$ has been calculated. We note that Hp can be predicted for any $V_{\rm T2}$ via

 \begin{displaymath}Hp={b_0+V_{\rm T2} \over 1-b_1}, \end{displaymath} (2)

where b0 is the intercept and b1 is the slope from a linear fit. This simple relationship is crucial in bridging the ground-based VI photometry and Hipparcos Hp photometry (see Sect. 3.3).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f5.eps} \end{figure} Figure 5: Calculated gradients $\Delta (Hp-V_{\rm T2})/\Delta Hp$ as a function of observed Hp amplitude within the 5-to-95 percentile range, Hp95-Hp5, for 136 carbon stars (top panel) and 906 M and S stars (bottom panel). For M and S stars, the gradient is correlated with the amplitude of the brightness variation as indicated by a linear fit.

The calculated color gradients $\nabla_{HpV_{\rm T}}$ vs. the observed amplitude in Hp within the 5-to-95 percentile range, Hp95-Hp5, are shown in Fig. 5, separately for 136 carbon and 906 M and S stars. For both groups of stars, the color gradient ranges between -0.1 and -0.45. For carbon stars, the mean gradient is $\langle\nabla_{HpV_{\rm T}}\rangle=-0.24$, whereas it is -0.26 for the M and S stars. This indicates that on average the gradient $\nabla_{HpV_{\rm T}}$ is only marginally sensitive to the C/O ratio in the atmospheres of red stars. On the other hand, for M and S stars, the gradient is definitely correlated with the amplitude of a brightness variation in Hp - the color gradient increases at the rate -0.025 per mag of amplitude. Similarly, the gradient is correlated with the median V-I for M and S stars: this merely reflects another correlation between the amplitude of brightness variation and median V-I.

  
3.3 V - I calibration curves

We have not been able to find any ground-based $V-I_{\rm C}$ data for the red stars concurrent with the Hipparcos lifetime. To relate the ground-based V-I observations to Hipparcos/Tycho photometry we postulate that a star's luminosity-color relation (encapsulated by parameters b0 and b1 in Eq. (2)) is constant over several decades and adopt the $V_{\rm T2}$ magnitude as a proxy to tie ground-based observations into the Hipparcos $HpV_{\rm T2}$ system. In practice, it involves two important steps. First, the ground based V magnitude should be transformed into the system of Tycho $V_{\rm T}$. This is not trivial for red stars, therefore we provide step-by-step instructions explaining how to do that for carbon and M, S stars. Second, the derived $V_{\rm T2}$ magnitude now allows us to find the corresponding Hp value using Eq. (2) and thus, the color $Hp-V_{\rm T2}$. Only then, it is possible to relate a ground-based measurement of V-I to the corresponding $Hp-V_{\rm T2}$ value and be reasonably certain that both measurements are on the same phase of a light curve in the case of variable stars. As demonstrated by Kerschbaum et al. (2001), there is no phase shift between the variability in the V and $I_{\rm C}$ bandpasses for asymptotic giant branch stars, a dozen of which can also be found in Table 3. A small and consistent rms scatter of the residuals in the linear fits given in Table 3 for additional M stars and a few carbon stars, is another reassuring sign of the lack of a phase shift - a crucial assumption in the calibration procedure.

3.3.1 Carbon stars

Many carbon stars are too faint in the $B_{\rm T}$ bandpass, hence their $B_{\rm T}-V_{\rm T}$color index is either unreliable or is not available at all. Therefore, we first derived a relationship between the ground-based $(V-I)_{\rm C}$ and $(B-V)_{\rm J}$ using the Walker (1979) data:

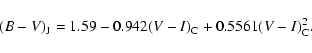\begin{displaymath}(B-V)_{\rm J}=1.59-0.942(V-I)_{\rm C}+0.5561(V-I)_{\rm C}^{2}. \end{displaymath} (3)

Then, the $B_{\rm T}-V_{\rm T}$ can be easily estimated using Eq. (1.3.31) in ESA (1997), vol. 1:

\begin{displaymath}(B_{\rm T}-V_{\rm T})=1.37(B-V)_{\rm J}-0.26. \end{displaymath} (4)

Finally, knowing the ground-based V-magnitude and employing Eq. (1.3.34) in ESA (1997), vol. 1, we derive

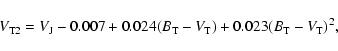\begin{displaymath}V_{\rm T2}=V_{\rm J}-0.007+0.024(B_{\rm T}-V_{\rm T})+0.023(B_{\rm T}-V_{\rm T})^{2}, \end{displaymath} (5)

which in combination with Eq. (2) yields the corresponding $Hp-V_{\rm T2}$.

3.3.2 M and S stars

Owing to some, albeit weak, dependence of TiO absorption upon the surface gravity, the stars of spectral type M can be divided into giants and dwarfs (main sequence stars). All stars in our sample with Hipparcos parallaxes smaller than 10 mas are considered to be giants. For M giants, $V_{\rm T2}$ follows directly from Eq. (1.3.36) (see ESA 1997, vol. 1):

 \begin{displaymath}V_{\rm T2}=V_{J}+0.20+0.03(V-I-2.15)+0.011(V-I-2.15)^{2}. \end{displaymath} (6)

To calculate a similar relationship for M dwarfs, we used the data from Koen et al. (2002):

 \begin{displaymath}V_{\rm T2}=V_{J}+0.20+0.042(V-I-2.15). \end{displaymath} (7)

As expected, Eqs. (6) and (7) are very similar so that, considering the uncertainties involved, our V-I photometry is not sensitive to the surface gravity. Equation (6) or (7) in combination with Eq. (2) then yields $Hp-V_{\rm T2}$.

3.3.3 Calibration curves

From the sources listed in Table 4, we have chosen 274 measurements of V-I for carbon stars and 252 for M and S stars. Quite often there is more than one V-I measurement for a given star. In the case of multi-epoch ground-based V-I data, we first obtained a linear fit to V-I as a function of V (e.g., Table 3). The coefficients of that fit were used to estimate the V-I index of variable stars at maximum brightness. The corresponding $Hp-V_{\rm T2}$ color index at maximum brightness has the advantage of being relatively insensitive to the uncertainties affecting the $Hp-V_{\rm T2}$ vs. Hp relation at its faint end (see Figs. 3 and 4). This is especially important at the blue end of the relationship between V-I and $Hp-V_{\rm T2}$ (corresponding to the maximum brightness in the case of variable stars) requires more care due to its steepness.

The calibration curves for oxygen (actually M and S) stars and carbon stars are presented in Fig. 6.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f6.eps} \end{figure} Figure 6: Color-color transformation for M and S stars (left panel) and carbon stars (right panel). The red end of this transformation ( $Hp-V_{\rm T2}<-1.5$) for carbon stars is uncertain due to the lack of intrinsically very red Hipparcos calibrating carbon stars.

Since many calibrating stars are fainter than Hp=8, the scatter is mainly along the $Hp-V_{\rm T2}$ axis (see also Fig. 4). The relationship between $V-I_{\rm C}$ and $Hp-V_{\rm T2}$ cannot be represented by a single polynomial, hence we provide segments of calibration curves along with a color interval of their validity (Table 6). Within this interval, a Hipparcos $(V-I)_{\rm H}$ is

 \begin{displaymath}(V-I)_{\rm H}=\sum_{k=0}^4 c_k (Hp-V_{\rm T2})^{k}. \end{displaymath} (8)


 

 
Table 6: Polynomial transformation from $Hp-V_{\rm T2}$ to $V-I_{\rm C}$.
Spectral Type Color Range c0 c1 c2 c3 c4
M, S $-0.20>Hp-V_{\rm T2}\geq-0.80$ 1.296 -6.362 -5.128 -1.8096 0.0
M, S $-0.80>Hp-V_{\rm T2}\geq-2.50$ 2.686 -1.673 0.0 0.0 0.0
C $-0.20>Hp-V_{\rm T2}\geq-1.77$ 1.297 -4.757 -4.587 -2.4904 -0.5343
C $-1.77>Hp-V_{\rm T2}\geq-2.00$ 3.913 0.0 0.0 0.0 0.0


To calculate an epoch $(V-I)_{\rm H}$, one should use the epoch Hp photometry and obtain $Hp-V_{\rm T2}=b_0+b_1\times{Hp}$ (see Eq. (2)). Then, a polynomial transformation given by Eq. (8) and Table 6 leads directly to the desired $(V-I)_{\rm H}$ color index. However, there are numerous cases when it was not possible to determine a slope b1 in the $Hp-V_{\rm T2}$ vs. Hp plot, although the amplitude of Hp variations indicated a likely change in $Hp-V_{\rm T2}$ as well. Therefore, for all such stars with a light amplitude having the range between maximum and minimum luminosities, $\Delta Hp>0.15$ (see entries H50-H49, ESA 1997, vol. 1), we adopted the mean slope, i.e., the mean gradient given in Sect. 3.2. A difficulty then is to find a point in the $Hp-V_{\rm T2}$ vs. Hp plot, to which the mean slope can be applied in order to estimate an intercept b0. The median of the 3-5 brightest values of Hp and the corresponding median $Hp-V_{\rm T2}$ color were adopted for such a "reference'' point.

An important issue is to verify the system of our $(V-I)_{\rm H}$ photometry for red stars. The differences between the new median $(V-I)_{\rm H}$ and the best available Hipparcos V-I photometry (entry H40) are plotted in Fig. 7.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f7.eps} \end{figure} Figure 7: Hipparcos median V-I (ESA 1997, entry H40) vs. newly derived median $(V-I)_{\rm H}$ in this study. The reasons for some very large discrepancies are discussed in Sect. 4.1.

On average the two systems are consistent. The very red carbon stars are an exception because their $(V-I)_{\rm H}$ color indices reach saturation, whereas the Hipparcos V-I index is not restrained. Then, there are numerous cases where the newly derived $(V-I)_{\rm H}$ values differ considerably from those in the Hipparcos Catalogue - in extreme cases up to 3-4 mag. A closer look at these cases indicates various reasons for such discrepancies. It could be duplicity, an incorrect target, severe extrapolation in color, etc. Noteworthy is the fact that the $I_{\rm C}$ bandpass given in ESA (1997) is $\sim$30 nm wider on the red side than the one published by Bessell (1979). Uncertainty in the location of the red-side cutoff of the $I_{\rm C}$-bandpass owing to different detectors is known to be a major source of a small color-dependent bias (<0.1 mag) in the ground-based photometry of red stars.

3.3.4 Verification of the new ${\mathsfsl V}$ - ${\mathsfsl I}$ color

From the variety of available sources, we have chosen the two largest sets of ground-based Cousins V-I data to test our $(V-I)_{\rm H}$ color indices; that is Koen et al. (2002) for M stars and Walker (1979) for carbon stars. We also selected the data of Lahulla (1987), which is an independent source of V-I, albeit in the system of Johnson VI which was not used in the calibration.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f8.eps} \end{figure} Figure 8: Differences between our instantaneous $(V-I)_{\rm H}$ color index and those of Koen et al. (2002); Lahulla (1987); Walker (1979). The upper two panels represent M stars, whereas the bottom panel contains carbon stars. The accuracy of our calibrated V-I colors is clearly insufficient in the case of faint M dwarfs, which represent a large fraction of the Koen et al. (2002) sample.

The differences, $(V-I)_{\rm H}-(V-I)_{\rm C}$, are plotted as a function of ground-based V (Fig. 8). For the Walker (1979) and Lahulla (1987) datasets, the mean offset $\langle(V-I)_{\rm H}-(V-I)_{\rm C}\rangle$ is not more than +0.01 mag; the scatter of individual differences is 0.12 mag. The Koen et al. (2002) data are instrumental to test the reliability of $(V-I)_{\rm H}$ for early-type M stars, both dwarfs and giants. We note that at $V-I\approx2$ the calibration curve is very steep (left panel, Fig. 6). At this V-I, a variation in $Hp-V_{\rm T2}$ by only 0.01 mag corresponds to a 0.05 mag change in V-I. For relatively bright Hipparcos stars (V<9), the mean offset $\langle(V-I)_{\rm H}-(V-I)_{\rm C}\rangle$ is +0.04 but it increases to +0.20 for fainter stars (9<V<11). The scatter also rises from 0.13 to 0.40 in these two intervals. A noticeable bias in the mean $(V-I)_{\rm H}$ towards faint magnitudes might be an indication of some residual systematic error either in the Hipparcos Hp epoch photometry or in Tycho-2 $V_{\rm T2}$ magnitudes. As expected, rapidly increasing errors in $V_{\rm T2}$ as a function of magnitude (Fig. 4) clearly set a limitation on the accuracy of $(V-I)_{\rm H}$.

4 New V-I and some applications

We have calculated instantaneous (epoch) $(V-I)_{\rm H}$ color indices for 4414 M stars, 50 S stars from the list by van Eck et al. (1998), and 321 carbon stars, which include R, N, and Hd sub-types. A condensed version of this effort is presented in Table 7[*], which contains HIP number, GCVS name for variable stars, median Hp magnitude (entry H44, ESA 1997, vol. 1), 5-to-95 percentile Hp range or the Hp "amplitude'', coefficients b0,b1 (if b1 has not been determined, it is set equal to zero), median V-I from this study, spectral type (M, S, or C).

We note that about 2% of Hipparcos M, S, and C stars do not have adequate Tycho-2 photometry and, hence, are not given in Table 7. Those include some very bright stars and a number of faint stars. More than a dozen stars of intermediate brightness with 8.0>Hp>5.0failed in the Tycho-2 photometry reductions due to poor astrometry, high background and/or a parasitic signal, which corrupted the signal from the target object.

  
4.1 Remarks on individual carbon stars

We used the derived $(V-I)_{\rm H}$ color index and in some cases individual slopes from the $Hp-V_{\rm T2}$ vs. Hp plot to scrutinize the identity of some Hipparcos carbon stars. If an anonymous field star is measured instead of a real carbon star, it could yield a positive slope in the fit of $Hp-V_{\rm T2}$ vs. Hp. This is because the Hp measures have been overcorrected, using a V-I color index appropriate for an expected carbon star but not for the actual target. On the other hand, the Tycho-2 $V_{\rm T2}$ photometry appears to be insensitive to the color a star really has. The net result is a very small or even positive slope. After identifying such cases, we checked the 2MASS Atlas Images for the true location of a carbon star in question. The offset in position is given in Table 8. If a carbon star has incorrect coordinates in Alksnis et al. (2001), it is coded by "GCGCS:'' in Remarks. If an incorrect identification is already acknowledged in the Hipparcos Catalogue, it is indicated by the "HIP note'' in Remarks. In the case of contradictory spectral classifications, we list only the alternative classification, since in nearly all such cases Hipparcos spectral type is "R...''. None of them can be found in Alksnis et al. (2001); therefore, the true identity of these stars has yet to be confirmed by spectroscopic means. An exception is HIP 94049 = CGCS 4179 which is a genuine carbon star (Houk, private communication; see also Table 1).


 

 
Table 8: Upper part: erroneous Hipparcos pointings of carbon stars or a contradictory spectral classification with Hipparcos indicating "R...'' spectral type. The offsets in coordinates, $\Delta $RA and $\Delta $Dec, are given in (s) and ( $\hbox {$^{\prime \prime }$ }$), respectively, in the sense "true position-Hipparcos''. Lower part contains significant corrections "true position-GCGCS'' required in Alksnis et al. (2001) to the positions of non-Hipparcos R stars from Table 1.
HIP CGCS $\Delta $RA $\Delta $Dec Remarks
4266       M0 (SAO)
14055       M0 (SAO)
21392       M0 (SAO)
22767 808 -21.0 +9 HIP note
24548 893 0.0 -242  
29564       M0 (SAO)
29899 1226 +3.4 +26 GCGCS:
35015 1615 +7.1 -146 GCGCS:
35119 1616 +0.3 +59 HIP note, GCGCS:
37022 1787 -2.6 +32 HIP note, GCGCS:
39337 2007 +16.7 +31  
40765       G1V (Houk & Swift 1999)
44235       not C-star? (Stephenson 1989)
75691 3614 +8.38 +94 GCGCS:
83404 3762 -0.4 -197 GCGCS:
85148 3820 -1.6 +58 GCGCS:
88170       M0 (SAO)
94049       C-star, not F5V
95024 4241 +5.3 +10 HIP note, GCGCS:
106599 5371 -7.7 +4 HIP note, GCGCS:
113840       M0 (SAO)
118252 5970 -2.3 -13 HIP note, GCGCS:
  258 -3.0 0  
  3765 -0.6 -42  
  3810 +10.3 +10  
  3813 +0.4 +9  
  3864 +0.3 -10  
  3939 +0.5 -2  
  3966 0.0 +25  
  4042 +0.8 -2  
  4168 +0.8 -14  
  4498 +3.7 -35  


  
4.2 Duplicity and V - I color index


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f9.eps} \end{figure} Figure 9: Comparison of the V-I color indices used in the preparation of the Hipparcos Catalogue (H75) with those rederived from a color transformation based on $Hp-V_{\rm T2}$. Only red stars with spectral types  M and  S are considered. Single-star solutions are depicted by black dots, whereas the open symbols denote more complex solutions (hexagons - component solutions  C; triangles - acceleration solutions  G; squares - Variability-Induced Mover (VIM) solutions  V; stars - stochastic solutions  X). It is worth noting that nearly all datapoints in the upper right corner of the diagram correspond to complex solutions, thus hinting at problems encountered in the Hipparcos data processing for these stars.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{ms3108f10.eps} \end{figure} Figure 10: A histogram showing the fraction of red stars with a DMSA C, G, V or X solution in the Hipparcos Catalogue (field H59), as a function of Hp magnitude, for three different sets of $\Delta (V-I)=(V-I)_{\rm H}-(V-I)_{\rm H75}$, where $(V-I)_{\rm H}$ is the newly derived median color index and $(V-I)_{\rm H75}$ is Hipparcos median V-I (entry H75). The unshaded histogram shows the fraction of these DMSA solutions among the stars with $\Delta (V-I)>2$; hatched for $2\ge \Delta (V-I)>1$; and dark-shaded for $1\ge \Delta (V-I)>-1$. The fraction of G, C, V, and X solutions clearly correlates with $\Delta (V-I)$; except for the faintest stars which always have a large fraction of G, C, V, X solutions.

Perhaps, the star HIP 12086 = 15 Tri is a prototype of a very rare but characteristic Hipparcos problem due to the neglected poor input coordinates. The declination of HIP 12086 listed in the Hipparcos Input Catalogue (ESA 1992) is off by $10\hbox{$^{\prime\prime}$ }$, hence in the detector's instantaneous field of view (see ESA 1997, vol. 3, Fig. 5.2) the signal has apparently been affected by the sensitivity attenuation profile. This kind of bias is absent in the star mapper's instrumentation. As a result, there is a very large positive slope in the $Hp-V_{\rm T2}$ vs. Hp plot. Not only is the Hp photometry clearly corrupted but the astrometry is also degraded as indicated by unusually large errors in the astrometric parameters. A similar effect of poor Hipparcos performance is known to be present, if the targets were wide binaries with separations in the range $\sim$ $15\hbox{$^{\prime\prime}$ }{-}20\hbox{$^{\prime\prime}$ }$ (Fabricius & Makarov 2000a). Here we list such binaries among red stars when the epoch Hp photometry is clearly biased: HIP 7762, 13714 & 13716, 17750, 18465, 45343, 57473, 86961, 87820, 108943, 116191, 114994. We note that from this list the revised astrometry is already available for HIP 17750, 86961, 87820, 116191 (Fabricius & Makarov 2000a).

Strictly speaking the V-I index derived in this study for Hipparcos binary and multiple stars could be affected by the component(s) and, hence should be considered with caution. On the other hand, a peculiar V-I value may very well signal a genuine problem, be it of astrophysical or instrumental character. With this in mind, we examined the location of complex astrometric solutions in the plot given in Fig. 7. It turns out that certain areas, as seen in Fig. 9, are heavily populated by such cases. Why is it so? It is helpful to look at the relative fraction of DMSA C,G,V, and X solutions as a function of differences between our median $(V-I)_{\rm H}$ and Hipparcos $(V-I)_{\rm H75}$. Figure 10 shows that the relative fraction of supposedly complex systems, i.e., binary or multiple stars, is abnormally high for red stars. For $\Delta(V-I)>1$ and Hp<10 (see unshaded and hatched areas in Fig. 10), the relative fraction of such systems is 40% and higher as compared to only $\sim$$10\%$ among the stars having correct $(V-I)_{\rm H75}$ index (dark-shaded histogram).

Table 9 lists all red stars with $(V-I)_{\rm H}-(V-I)_{\rm H75}>2$. As indicated from comparisons with an independent ground based V-I color index (see Col. 3 in Table 9), such differences are real. In essence, the stars listed in Table 9 have been processed with the $(V-I)_{\rm H75}$ color index off by more than 2 mag! Among such stars, the fraction of DMSA C,G,V, and X solutions - nearly 75% - is conspicuous in itself. For example, in the case of HIP 19488 and HIP 91703, it is evident that speckle interferometry could not confirm duplicity and, hence the Hipparcos DMSA/C solution must be spurious. This is nearly a watertight result since the limiting angular resolution of speckle interferometry (Mason et al. 1999; Prieur et al. 2002) is 2-3 times higher than the separation given in the Hipparcos Catalogue. The other stars with a DMSA/C solution listed in Table 9 have not been observed so far under similar conditions nor are they listed in the Fourth Catalog of Interferometric Measurements of Binary Stars[*], so that their possible spurious nature has yet to be established. Nevertheless, the high fraction of failed confirmations of binarity for Hipparcos stars with a DMSA/C solution (e.g., Mason et al. 1999, 2001; Prieur et al. 2002) is indicative that many such solutions might be spurious. We suspect that the phenomenon of such non-existent binaries among the red stars could very well be rooted in the improper chromaticity correction applied to these stars due to the poor knowledge of their true V-I color.


   
Table 9: All M, S spectral type stars with $\Delta (V-I)_{\rm H}=(V-I)_{\rm H}-(V-I)_{\rm H75}>2$ (Col. 2), where $(V-I)_{\rm H}$ is a color index from this study. When available, $\Delta (V-I)_{\rm0}=(V-I)_{\rm H}-(V-I)_{\rm obs}$, where $(V-I)_{\rm obs}$ is the ground-based photoelectric measurement. The stars are ordered by increasing amplitude of variability $\Delta Hp$(Col. 4). The column labelled DMSA provides a type of Hipparcos solution assuming more than one component. Angular separation between components, $\rho $, is given for DMSA/C solutions only.
HIP $\Delta (V-I)_{\rm H}$ $\Delta(V-I)_{\rm0} $ $\Delta Hp$ Hp DMSA $\rho (\hbox{$^{\prime\prime}$ })$ Remarks
19488 2.41   0.13 9.535 C 0.18 unresolved (Mason et al. 1999)
78501 2.19   0.14 10.285 C 0.17  
24661 2.31   0.15 10.170      
87221 2.61   0.19 8.763 C 0.17  
87433 2.27 -0.44 0.28 8.537      
76296 2.26   0.33 8.878 C 0.16  
42068 2.33 -0.49 0.41 8.511 C 0.18  
91703 2.65   0.46 8.799 C,V 0.21 unresolved (Prieur et al. 2002)
7762 2.03   0.48 8.615 X   companion star at $20\hbox{$^{\prime\prime}$ }$
84346 2.05   0.61 8.454 V   unresolved (Prieur et al. 2002)
100404 2.14 -0.76 0.61 8.464 V   unresolved (Mason et al. 2001)
37433 2.17   0.64 8.984      
56533 2.64   0.65 8.581 C 0.24  
84004 2.40   0.78 7.499 X    
80259 2.19   0.91 9.017 V   unresolved (Prieur et al. 2002)
16328 2.10   0.98 9.612 C 0.30  
90850 2.32   1.38 11.001      
78872 2.06 -0.47 1.70 9.841 G    
703 2.43 -0.59 2.09 11.112 V    
9767 2.19   2.10 9.773 V    
11093 2.52 0.16 2.10 9.756 V    
89886 3.27   2.26 10.883      
96031 2.29   2.64 10.512      
75393 3.06 0.32 2.73 8.554 V    
16647 3.23   2.87 10.376 V    
81026 2.66   2.89 11.538      
1901 2.61 1.27 2.97 10.705 V   unresolved (Prieur et al. 2002)
86836 3.43   3.15 11.196 V    
47066 2.61 0.87 3.49 10.073 V    
57642 2.32 0.78 3.60 9.968 V    
60106 2.04   3.81 9.854      
110451 2.01   3.90 11.460      
94706 2.81 0.67 3.97 10.826 V   T Sgr: composite spectrum
25412 2.39 0.29 4.00 9.974 V    
33824 2.02 0.97 4.05 9.922      

4.3 Empirical effective temperatures of red stars

Due to very complex spectra the red stars are cumbersome objects for getting their effective temperature - one of the fundamental stellar parameters. From different vantage points this has been investigated, e.g., by Bessell et al. (1998), Bergeat et al. (2001), Houdashelt et al. (2000). Although the Cousins V-I color index may not be the optimal color to calibrate effective temperature due to the strong influence by molecular absorption bands and possible reddening, nevertheless we attempted to derive an empirical calibration of effective temperatures for carbon and M giants. We used median $(V-I)_{\rm H}$ for Hipparcos stars having interferometric angular diameter measurements in K ( $\lambda=2.2$ $\mu$m) bandpass (Dyck et al. 1996; van Belle et al. 1997, 1999) and corresponding effective temperature estimates. It is expected that the interstellar reddening is low for the chosen Hipparcos stars because of their relative proximity to the Sun. In total, from these sources of effective temperature determinations, we selected 27 small amplitude ( $\Delta Hp < 0.5$) M giants in the range 3.6>V-I>1.5 and 16 carbon stars ( 3.8>V-I>2.4) with no restriction on variability. Similarly to Dumm & Schild (1998) we adopted a linear relationship

 \begin{displaymath}\log T_{\rm eff}=d_0+d_1(V-I). \end{displaymath} (9)

For M giants, a least squares fit using Eq. (9) yields $d_0=3.749\pm0.014$, $d_1=-0.087\pm0.007$, and the standard error $\sigma_{\rm T}=110$ K. For carbon stars the coefficients from the fit are: $d_0=3.86\pm0.06$, $d_1=-0.153\pm0.021$, and the standard error $\sigma_{\rm T}=210$ K. Apparently, the effective temperature scale is not satisfactory for carbon stars in terms of its precision. The color mismatch between our median $(V-I)_{\rm H}$ and the color of a variable star at the time of interferometric observation can only partly explain the noted large scatter. Another reason might include an unaccounted for circumstellar extinction, carbon abundance and metallicity effects on the color, and rather large errors in the effective temperature determination. The latter is discussed in detail by Dyck et al. (1996). An alternative scale of effective temperatures for carbon stars is given by Bergeat et al. (2001), although it may have the same kind of inherent problems. We note that the slope d1 for M giants is 2.5 times larger than in Dumm & Schild (1998). The main reason for that is a stretched color scale of Hipparcos V-I (see Fig. 7). It is felt that the empirical effective temperature scale based on V-I color has a limited use, in particular for carbon stars. Near infrared observations in JHKL bandpasses should be used to obtain better estimates of effective temperature for the coolest stars. With the advent of large optical interferometers the number of precise angular diameters for cool and red stars undoubtedly will increase substantially. However, an equal effort should be invested in deriving reliable bolometric fluxes, which are equally important in establishing a precise scale of effective temperatures.

5 Summary and conclusions

The main result of this work is demonstrating the feasibility of the $Hp-V_{\rm T2}$ color index in studies of red stars. This color index is tightly correlated with the Cousins V-Icolor and, thus, allows us to derive an independent estimate of $(V-I)_{\rm H}$ for carbon, M and S stars. Such estimates are indispensable in the analysis of red variable stars, which have been little studied in the Cousins VI system.

We have shown that a considerable fraction of Hipparcos best estimates of V-I color index (entry H40, ESA 1997) for red stars might be in error by more than a full magnitude. Conspicuously, among the most discrepant cases we find an unusually large number of DMSA C, G, V, and X solutions implicating a binary or multiple star status for these stars. On the other hand, extensive speckle interferometric observations have largely failed to confirm the binarity, despite the 2-3 times better angular resolution. This strongly suggests that some DMSA C, G, V, X solutions are not real and maybe due to the poor knowledge of the V-I color index, which served as a measure of star's color in both photometric and astrometric reductions by the Hipparcos consortia.

However, our attempts have not succeeded in improving the astrometry for single red stars. It was expected that an incomplete correction for the chromaticity effects should leave a color-related "jitter'' in the abscissa data at the level of 1-3 mas due to incorrect V-I, used in accounting for these effects. Surprisingly, we were not able to find clear traces of residual chromaticity effects, for instance, in carbon star Hipparcos astrometry. Either they have been somehow accounted for in the original Hipparcos reductions or they are insignificant.

On the other hand, the re-analysis of so-called Variability-Induced Movers (VIM) has benefited substantially from the new set of $(V-I)_{\rm H}$color indices. As indicated in Sect. 4.2, some of the DMSA/V solutions are suspected to be not warranted. Much finer analysis of all DMSA/V solutions for red stars (Pourbaix et al. 2002) provides strong evidence that nearly half of DMSA/V solutions are not justified, mainly thanks to reliable V-I colors now available at all phases of lightcurve for long-period variables such as Miras. This knowledge of V-I colors could be useful to further investigate other difficult systems having an extreme and changing color in combination with hints of duplicity, which can be resolved with interferometric means.

Acknowledgements
We thank A. Alksnis, C. Barnbaum, C. Fabricius, N. Houk, U. Jørgensen, D. Kilkenny, B. Mason, J. Percy, and G. Wallerstein for their expert advice and help at various stages of this project. This work is supported in part by the ESA Prodex grant C15152/NL/SFe(IC). I. P. would like to thank the staff of IAA for their generous hospitality during his stay in Brussels. L.N.B. thanks the staff of Siding Spring Observatory for hospitality and technical support. T.L.E. thanks his former colleagues at SAAO, especially R. M. Banfield and A. A. van der Wielen, for their assistance. T.L. has been supported by the Austrian Academy of Science (APART programme). The work with the Vienna APT has been made possible by the Austrian Science Fund under project numbers P14365-PHY and S7301-AST. J.S. acknowledges a travel support from the National Science Foundation grant AST 98-19777 to USRA. Illuminating comments and a number of suggestions by the referee, M. Bessell, are also greatly appreciated. This research has made use of the SIMBAD database operated at CDS, Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.

References

 

Copyright ESO 2003