A&A 397, 1143-1149 (2003)
DOI: 10.1051/0004-6361:20021557

The FERRUM Project: Experimental transition probabilities of [Fe II] and astrophysical applications

H. Hartman1 - A. Derkatch2 - M. P. Donnelly3 - T. Gull4 - A. Hibbert3 - S. Johansson1 - H. Lundberg5 - S. Mannervik2 - L.-O. Norlin6 - D. Rostohar2 - P. Royen2 - P. Schef2


1 - Atomic Astrophysics, Lund Observatory, Lund University, Box 188, 221 00 Lund, Sweden
2 - Physics Department, Stockholm University, AlbaNova University Center, 106 91 Stockholm, Sweden
3 - Department of Applied Mathematics and Theoretical Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland
4 - NASA/Goddard Space Flight Center, Code 681, Greenbelt, MD 20771, USA
5 - Department of Physics, Lund Institute of Technology, Box 118, 221 00 Lund, Sweden
6 - Physics Department, Royal Institute of Technology, AlbaNova University Center, 106 91 Stockholm, Sweden

Received 10 September 2002 / Accepted 25 October 2002

Abstract
We report on experimental transition probabilities for thirteen forbidden [Fe II] lines originating from three different metastable Fe II levels. Radiative lifetimes have been measured of two metastable states by applying a laser probing technique on a stored ion beam. Branching ratios for the radiative decay channels, i.e. M1 and E2 transitions, are derived from observed intensity ratios of forbidden lines in astrophysical spectra and compared with theoretical data. The lifetimes and branching ratios are combined to derive absolute transition probabilities, A-values.

We present the first experimental lifetime values for the two Fe II levels a4G9/2 and b2H11/2 and A-values for 13 forbidden transitions from a6S5/2, a4G9/2 and b4D7/2 in the optical region. A discrepancy between the measured and calculated values of the lifetime for the b2H11/2 level is discussed in terms of level mixing.
We have used the code CIV3 to calculate transition probabilities of the a6D-a6S transitions.

We have also studied observational branching ratios for lines from 5 other metastable Fe II levels and compared them to calculated values. A consistency in the deviation between calibrated observational intensity ratios and theoretical branching ratios for lines in a wider wavelength region supports the use of [Fe II] lines for determination of reddening.

Key words: atomic data - stars: individual: Eta Carinae - ISM: dust, extinction


1 Introduction

By definition metastable states cannot decay through electric dipole (E1) radiation and have therefore long radiative lifetimes ($\approx$1 s). They are, in general, collisionally deexcited in laboratory plasmas. However, in dilute astrophysical plasmas with low probabilities for collisions the metastable states can decay radiatively in magnetic dipole (M1) or electric quadrupole transitions (E2), emitting so called forbidden lines. Such lines can dominate in emission line spectra of low density regions and can be the major cooling agent of dilute plasmas. The use of forbidden lines in the diagnostics of a plasma requires the knowledge of the transition probabilities. These are obtained from theoretical calculations since experimental data require measurements of both the radiative lifetime and the branching fractions. Neither of these measurements is easily performed in the laboratory.

The first identification of forbidden Fe II lines, [Fe II], was done in the pioneering work by Merrill (1928) on the emission line spectrum of $\eta $ Carinae. The identification was stimulated by Bowen's explanation of the nebular lines as M1 transitions between states within the ground configuration of O III (Bowen 1928). The high spatial resolution of the Hubble Space Telescope (HST) made it possible to show that the narrow, strong nebular [Fe II] lines in $\eta $ Car emanate from compact gas ejecta (Davidson et al. 1995), close to the central star. Later HST/STIS spectra (Gull et al. 1999; Gull & Ishibashi 2001) show the distribution of [Fe II] in the proximity of the star. It is clear that [Fe II] provides possibilities to improve the diagnostics of the ejecta of this mysterious star.

The presence of strong [Fe II] lines in the ejecta of $\eta $ Car has initiated the present laboratory study, where we combine measurements of radiative lifetimes of four metastable Fe II levels with theoretical and observational data for the branching fractions in order to get absolute transition probabilities, A-values. As is the situation with A-values (or gf-values) of allowed lines, we will only be able to provide experimental data for a few forbidden lines. The main bulk of the data for astrophysical analyses must be supplied by theoretical calculations. It is therefore important to try to get an estimate of the accuracy of the calculated data by experiments. The radiative lifetime of the upper level of a forbidden transition is the atomic parameter that offers a comparison between theory and experiment. We have in our experiments chosen such metastable states of Fe II which are associated with strong nebular [Fe II] lines. One level is known to be affected by level mixing (Johansson 1978) and will provide a critical test of the theoretical calculations.

In the present paper we describe briefly the lifetime measurements in Sect. 2. A more detailed discussion is given in previous papers (Mannervik et al. 1996; Rostohar et al. 2001b). In Sect. 3 we discuss in detail the method of getting branching ratios from astrophysical observations by using HST/STIS spectra of $\eta $ Carinae and its ejecta. New calculations using the CIV3 code on the a6D-a6S transitions are reported in Sect. 4. The lifetimes of four metastable levels of Fe II and transition probabilities for 13 [Fe II] lines are presented in Sect. 5. In Sect. 6 we illustrate the effect of level mixing.

2 Lifetime measurement of metastable Fe II levels

The atomic structure of Fe II is complex due to seven valence electrons in one, two or even three open shells. The low complex of even parity configurations (3d + 4s)7 has 62 metastable levels in the energy range 0-4.7 eV. All of these levels are easily populated in stellar atmospheres of moderate temperature, which explains the richness in Fe II absorption lines in stellar spectra. The levels are also populated in dilute astrophysical plasmas, where they decay radiatively by forbidden transitions. The potential use of the [Fe II] lines in the diagnostics of astrophysical plasmas is a strong incentive for measuring the radiative lifetime of some metastable states.

The radiative lifetimes of metastable states are typically 6-8 orders of magnitude longer than those of the states decaying by E1 radiation. Consequently, a completely different technique has to be used. Firstly, the Fe+ ions have to be stored in a low-density environment during the measurement to avoid collisional quenching. Secondly, the ions have to be stored under controlled conditions for a time comparable to the lifetime. Thirdly, among all the Fe+ ions produced and stored, the ones populating the metastable state to be measured have to be unambigously selected and recognized.

A suitable method that meets these criteria has been developed at CRYRING, the storage ring facility at Manne Siegbahn Laboratory (MSL) in Stockholm (Abrahamsson et al. 1993). This method, which is called the laser probing technique (LPT) (Lidberg et al. 1999; Mannervik 2002), has been applied to Fe II (Rostohar et al. 2001b). The Fe+ ions were produced from FeCl2 in an ion source, accelerated up to an energy of 40 keV and injected into a storage ring. The long radiative lifetimes of the metastable levels require that the ring is evacuated to a pressure of 10-11 torr to avoid collisional quenching with the rest gas. The particular state to be measured is selected by irradiating the iron beam with monochromatic light from a cw laser tuned at a frequency matching an allowed transition to a higher state. The metastable state is thus depleted and excited to a state of opposite parity. This short-lived state decays in a fast transition and the corresponding fluorescence signal is detected. The laser probing pulse is systematically applied at different time delays after the injection of the iron beam into the storage ring. Thus, the number of fluorescent photons is monitored as a function of time and a lifetime curve is obtained. Certain correction and normalization procedures have to be applied, and all such details are given in previous papers (e.g. Rostohar et al. 2001a; Rostohar et al. 2001b). Examples of lifetime curves are given in Fig. 1.

  \begin{figure} \par\rotatebox{270}{\resizebox{!}{88mm}{\includegraphics[width=8.8cm,clip]{3076f1.ps}}} \end{figure} Figure 1: Typical lifetime curves (after corrections) for the levels a4G9/2 and b2H11/2.
Open with DEXTER

3 Measurements of branching ratios using astrophysical spectra

The relevant parameter in astrophysical analyses is the transition probability (Aik) which is related to the measurable quantities, branching fraction (BFik) and radiative lifetime ($\tau_{i}$) by

\begin{displaymath}A_{{ik}}= BF_{{ik}}/\tau_{i} \end{displaymath} (1)

where

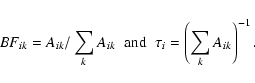\begin{displaymath}BF_{ik}=A_{{ik}}/\sum_{k}{} A_{{ik}} \hspace {0.2cm} {\rm and... ...e {0.2cm} \tau_{i}= \left ( \sum_{k}{} A_{{ik}}\right)^{-1}. \end{displaymath} (2)

The upper and lower states are denoted by i and k, respectively. BFik is obtained by measuring the intensity (in photons per second) of the emission line $\lambda_{{ik}}$ relative to the total intensity of all emission lines from level i.

Lifetimes of metastable states are typically 6-8 orders of magnitude longer than of ordinary excited levels, and the transition probabilities of the forbidden lines are accordingly very small. To avoid collisional quenching of the metastable states a very low electron density (typically 105 cm-3) is required in a plasma emitting observable forbidden lines. In general, this also means that a low concentration of ions is required throughout an extended source. Thus, the combination of low density and low transition probability makes dilute, extended astrophysical plasmas the best environment to produce forbidden lines of significant flux, where the low volume density is compensated by a large column density. In rare cases, forbidden lines have been observed in laboratory sources allowing accurate wavelength measurements (Eriksson 1965).

We have considered two ways to get the BF's and to derive the A-values:
1) Measure the relative intensities of the relevant [Fe II] lines in astrophysical spectra;
2) Use theoretical calculations of forbidden transitions in Fe II.

We have finally chosen a combination of the two, but before describing the procedure, we comment on the two different methods. The main argument against using astrophysical spectra is of course that we want to derive the atomic parameter values in an independent way and use them in the astrophysical analysis. A practical problem with the astrophysical spectra is that the intensities are affected by interstellar extinction and may not provide the "true'' branching fractions. Also, a nebular emission line may be blended with other lines from the same or another ion. This makes the intensity measurements less reliable, even if the blending component is known. The general problem with method 2) is the difficulty in estimating reliable uncertainties of calculated values.

We will adopt the following approach: We construct a reddening curve for one particular spectrum of ejecta near $\eta $ Car by using theoretical BF's for a number of [Fe II] lines. We correct the observed intensities of the lines under investigation and use them to derive branching fractions.

3.1 Construction of a reddening curve for $\eta $ Carinae

We have measured the observed intensities (in photons per s) of 14 [Fe II] lines in the HST/STIS spectrum of two compact gaseous condensations (called the Weigelt blobs B and D, Weigelt & Ebersberger 1986) of $\eta $ Carinae and grouped the lines according to their upper energy level. These lines have been observed at three occasions: March 1998, February 1999 and March 2000. The line ratios from the different observations show consistent results. We used the March 1998 data for the analysis since the lines of interest are less affected by blending of other lines. The observed intensity ratio between pairs of lines from a common upper level, i.e. the uncalibrated branching ratio, is compared to the theoretical branching ratio. For the latter we have used the calculations by Quinet et al. (1996) as they give a good agreement with the experimental lifetimes (Rostohar et al. 2001b). By using a standard reddening curve (Osterbrock 1989) with a wavelength dependent exponential degrading of the intensity, we can derive the amount of reddening for each line pair. If the exponential function is a good approximation the different line pairs would give the same value of the exponential constant C. By averaging over 11 pairs of [Fe II] lines, we derive a value of $C=1.6\pm 0.4$. The variation in C is caused by line blending, by uncertainties in the flux measurements and in the calculations of transition probabilities. Some of the linepairs used may have larger errors according to a note in proof on the paper by Quinet et al. (1996). This has been taken into consideration when deriving the uncertainties of the A-values. However, there is some evidence that nebular reddening in the Homonculus may not follow the standard interstellar reddening curve.

  \begin{figure} \par\rotatebox{90}{\resizebox{!}{88mm}{\includegraphics[width=8.8cm,clip]{3076f2.ps}}} \end{figure} Figure 2: HST/STIS spectrum of the blob spectrum of Eta Carinae showing the strong lines a6D-a6S.
Open with DEXTER


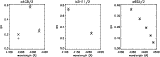  \begin{figure} \par\resizebox{14cm}{!}{\includegraphics{3076f3.eps}} \end{figure} Figure 3: Branching ratios for the metastable levels a4G9/2, b2H11/2 and a6S5/2. Crosses ($\times $) mark the astrophysical values corrected for reddening and the (+) mark the theoretical values (Quinet et al. 1996).
Open with DEXTER

3.2 Calibrated branching ratios

We use the reddening curve to derive calibrated intensities and branching fractions for the forbidden lines associated with the four metastable Fe II levels, for which we have experimental lifetimes. For one of the levels, a6S, the lines fall in a very narrow region (4280-4480 Å, see Fig. 2) so we can, to a first approximation, neglect the effect of reddening. We compare the BF's derived from the nebular intensities with calculated BF's (Quinet et al. 1996) in Fig. 3, and find an extremely good agreement.

We have repeated the same procedure for two other levels, b2H11/2 and a4G9/2, which also have their main branches within 100 and 200 Å, respectively. The agreement is reasonable good, as shown in Fig. 3 even if one line from a4G9/2 is blended. The line at $\lambda 4177$ in the $\eta $ Car spectrum is a blend of the two Fe II transitions a4F9/2-a4G9/2 and a2D5/2-z4D7/2. This affects the branching fractions for all lines from the $a^4{\rm G}_{9/2}$ level. To estimate the contribution of the allowed transition to the observed nebular feature, we have measured the flux from other nebular lines from the same upper level, z4D7/2. Based on the calculations by Raassen & Uylings (2000) and on solar spectrum observations (Thevenin 1989), we estimate the contribution from the a2D5/2-z4D7/2 line to be $\sim$20% of the observed emission feature in $\eta $ Carinae.

Based on this good agreement we can now, in principle, combine the theoretical BF's with measured lifetimes for these three levels and derive absolute transition probabilities (see results in Sect. 4).


  \begin{figure} \par\rotatebox{270}{\resizebox{!}{88mm}{\includegraphics[width=8.8cm,clip]{3076f4.ps}}} \end{figure} Figure 4: A-values for transitions from the upper level b4D7/2 for different values of the reddening constant C. The theoretical values (HFR and SST) are from Quinet et al. (1996).
Open with DEXTER

The branches from the fourth level, b4D7/2, are spread over a large wavelength interval, 3100-5600 Å, and the effect of reddening is not negligible. In Fig. 4 we show the transition probabilities derived from the stellar intensities, which are corrected for reddening at three different values of C located around the adopted value of 1.6. Assuming that the standard formula for interstellar reddening is a good approximation we see that the error introduced by the uncertainty in the C value is rather small. A change in C of 0.5 introduces a change in the BF of $\sim$10% for the UV lines around 3400 Å and $\sim$20% for the lines at 5500 Å.

4 Calculations of transitions probabilities


 

 
Table 1: Optimisation processes for the radial functions.
Orbital Configurations included Symmetry
     
4p 3d54s4p y6P$^{\rm o}$
5p 3d64p, 3d65p z6P$^{\rm o}$
6p 3d6np; n=4,5,6 z6D$^{\rm o}$
7p 3d6np; n=4,5,6,7 z6F$^{\rm o}$
5s 3d54s4p, 3d55s4p y6P$^{\rm o}$
6s 3d5msnp; m,n=4,5,6 y6P$^{\rm o}$
4d 3d64p, 3d54s4p, 3d44s4p4d y6P$^{\rm o}$
5d 3d64p, 3d54s4p, 3d54p4d, 3d54p5d z6P$^{\rm o}$
4f 3d64s, 3d54p4f a6D



 

 
Table 2: Optimised radial function parameters for Fe II.
nl cjnl Ijnl $\zeta_{jnl}$   nl cjnl Ijnl $\zeta_{jnl}$   nl cjnl Ijnl $\zeta_{jnl}$
5s 0.07552 1 19.02548   4d 0.63694 3 5.15025   7p 14.57355 2 0.91682
  -0.27401 2 9.35791     -0.92313 4 1.90298     -35.18975 3 1.57708
  0.57776 3 5.07754               18.84919 4 1.93717
  -1.03497 4 2.43824   5d 0.44144 3 4.73722     166.94166 5 1.93650
  0.97510 5 1.29982     -0.77547 4 2.61070     -366.00070 6 2.15513
            1.04299 5 1.28493     200.95182 7 2.40962
6s 0.06441 1 18.38583                    
  -0.16284 2 11.31165   4p 5.70277 2 1.44819   4f 1.00000 4 2.44380
  4.62987 3 2.03315     -1.88413 3 4.04161          
  -10.89075 4 2.13989     -3.85906 4 2.46303          
  7.93749 5 2.07416                    
  -1.98787 6 1.49966   5p 0.67165 2 2.83628          
            -0.78204 3 4.21964          
7s 0.97432 1 0.30972     5.72815 4 0.85910          
  -1.45676 2 1.62185     -6.48385 5 1.00256          
  11.78939 3 1.45012                    
  -28.95904 4 1.58546   6p 1.19932 2 10.90063          
  31.20386 5 1.64232     -1.37372 3 10.06883          
  -15.20386 6 1.64979     7.29654 4 1.35418          
  1.40099 7 1.11660     -16.45629 5 1.35122          
            9.70525 6 1.40443          



 

 
Table 3: Ab initio and fine-tuned results for calculation including all one- and two-electron changes from (3d64s, 3d54s4d) 6D and (3d54s2, 3d54s5s, 3d54p2, 3d54s4d) 6S.
Transition Ab initio resultsFine-tuned results
Upper level Lower level $\Delta E$ (cm-1) fl Al (s-1)$\Delta E$ (cm-1) fl Al (s-1)
              
a6S5/2 a6D9/2 22020.67 0.0846 0.977723317.40 0.0894 1.6247
  a6D7/2 21643.88 0.0837 0.903022932.64 0.0886 1.2042
  a6D5/2 21355.16 0.0830 0.636722649.56 0.0879 0.8533
  a6D3/2 21151.27 0.0825 0.406122455.02 0.0875 0.5469
  a6D1/2 21029.86 0.0823 0.197722340.36 0.0873 0.2671


The present work uses CI wave functions of the form

 \begin{displaymath} \Psi({J}) = \sum_{i=1}^{M} a_i \Phi_i(\alpha_iL_iS_iJ) \end{displaymath} (3)

generated by the code CIV3 (Hibbert 1975; Hibbert et al. 1991). For a specific choice of configuration state functions (CSFs) $\{\Phi_i\}$, where the angular momentum coupling scheme is defined by $\{\alpha_i\}$, the variationally optimal expansion coefficients $\{a_i\}$ are the eigenvector components of the diagonalized Hamiltonian whose typical element is $H_{ij}= ~<\Phi_i\vert H\vert\Phi_j>$. The corresponding eigenvalue is an upper bound to the energy of the particular state. In particular, if the eigenvalues $\{E_i\}$ are ordered so that $E_1<E_2< \cdots$, then

 \begin{displaymath} E_i \geq E_i^{\rm exact} \end{displaymath} (4)

is a consequence of the Hylleraas-Undheim theorem.

The Hamiltonian used to determine the final wave functions consists of the non-relativistic Schrödinger Hamiltonian along with the following relativistic operators associated with the Breit-Pauli approximation: mass-correction, Darwin, spin-spin, spin-other-orbit and spin-orbit terms. However, the spin-spin-contact and the orbit-orbit terms, which do not contribute directly to fine-structure separations, are not included in the calculations.

The CSFs of all states are constructed from a common set of one-electron orbitals of the form

 \begin{displaymath} \frac{1}{r} P_{nl}(r) Y_l^{m_l}(\theta,\phi) \chi_{m_s}(\sigma) \end{displaymath} (5)

where the radial functions in Eq. (5) are expressed in analytic form as a linear combination of normalized Slater-type orbitals (STOs):

 \begin{displaymath} P_{nl}(r) = \sum_{j=1}^{k} c_{jnl}\chi_{jnl}(r) \end{displaymath} (6)

and where the STOs take the form

 \begin{displaymath} \chi_{jnl}(r) = \left[ \frac{(2\zeta_{jnl})^{2I_{jnl}+1}}{(2I_{jnl})!} \right]^{1/2} r^{I_{jnl}} \exp(-\zeta_{jnl}r). \end{displaymath} (7)

Equations (4) constitute a set of variational principles allowing the optimisation of the radial function parameters on one or more of the energy eigenvalues of the Hamiltonian matrix. The integers $\{I_{jnl}\}$ are kept fixed but the exponents $\{\zeta_{jnl}\}$ and the coefficients $\{c_{jnl}\}$ in Eq. (7) may be treated as variational parameters to be optimised subject to the orthonormality conditions:

 \begin{displaymath} \int_{0}^{\infty} P_{nl}(r)P_{n^{\prime}l}(r) {\rm d}r = \delta_{nn^{\prime}} ; \hspace*{1.0cm} l < n^{\prime} \leq n. \end{displaymath} (8)

The optimisation of the radial functions on, for example, the energy of just one state would lead to a serious imbalance in the accuracy to which the full set of states under consideration would be represented. Hence different orbitals are optimised on different eigenvalues, so that all the states are of a comparable level of accuracy. In the present work, the 1s, 2s, 2p, 3s, 3p, 3d, 4s functions were taken from the ground state Hartree-Fock functions given by Clementi & Roetti (1974): hence they are all optimised on the a6D state. In the present calculations we used the radial functions previously optimised in our calculations of the a6D - z6P$^{\rm o}$ transitions (Donnelly & Hibbert 2001). The additional orbitals consist of 5s, 6s, 4p, 5p, 6p, 4d, 5d, 4f. The method of optimisation (involving only the non-relativistic Schrödinger Hamiltonian) is displayed in Table 1 and the radial function parameters are given in Table 2.
   
Table 4: Lifetimes (in s) of metastable Fe II levels.
    b4D7/2 a6S5/2 a4G9/2 b2H11/2
Garstang (1962)   0.618 0.326 0.856 10.1
Nussbaumer et al. (1981)     0.235    
Quinet et al. (1996) SST 0.567 0.262 0.755 6.59
  HFR 0.500 0.220 0.694 5.20
Rostohar et al. (2001b)   0.53(3) 0.23(3)    
This work (exp)       0.65(2) 3.8(3)
This work (calc)     0.222    
$\textstyle \parbox{9.5cm}{ SST$~=~$ Superstructure; HFR$~=~$ Relativistic Hartree-Fock.}$


We give in Table 3 both our ab initio results of oscillator strengths and the corresponding values obtained after the "fine-tuning'' of the calculated energy levels. This process (Brage & Hibbert 1989) makes small adjustments to the diagonal elements of the Hamiltonian matrix so as to bring the calculated eigenvalue differences into agreement with the corresponding experimental energy differences. This process has proved effective in improving the accuracy of calculated oscillator strengths (Hibbert 1996). The adopted A-values are inserted in Table 5 and compared with the new experimental and previously calculated values.

5 Results and discussion

Radiative lifetimes of metastable states in Fe II were first measured for two levels, a6S5/2 and b4D7/2, and they were reported in Rostohar et al. (2001b). In the present paper we report on the lifetime measurement of two more levels, a4G9/2 and b2H11/2. All values are presented in Table 4, where we also compare with theoretical calculations by Garstang (1962), Nussbaumer et al. (1981), Quinet et al. (1996) and our new calculations. The theoretical lifetimes are obtained by taking the inverse sum of all A-values (see Eq. (1)), which is the parameter calculated by the codes. Nussbaumer et al. (1981) made calculations only for the system of sextet levels, and the good agreement between their value for the a6S term and our experimental value implies that LS coupling is a good approximation for the low-level system in Fe II. Our new calculations of the a6S lifetime are also in very good agreement with the measured lifetime.

Quinet et al. (1996) have made calculations using both the relativistic Hartree-Fock (HFR) method in the Cowan code (Cowan 1981) and the Superstructure (SST) code (Eissner et al. 1974; Nussbaumer & Storey 1978). The SST code gives systematically larger lifetimes values than HFR, but there is no consistency as to which code gives the better value, judged from the experimental values. The values calculated by Garstang (1962) are consistently larger than the experimental values.

The branching fractions derived from the emission line spectrum of gas ejecta in $\eta $ Carinae have been corrected for reddening (see Sect. 3.1). For lines within a limited spectral region this correction is very small. For the other lines separated by about 2500 Å the error introduced is the main contribution to the total uncertainty.

From some of the metastable levels there are a few transitions with significant branching fractions that are not observed in the nebular spectra. Most fall in wavelength regions not covered by the observations. A few are weak transitions from the levels of interest that are too faint to be observed in the stellar spectrum. For all these lines we have used the calculations by Quinet et al. (1996) to estimate the missing branching fractions, the sum of which results in the residual. The residual is 3.5% for a4G9/2 and 0.1% for a6S5/2.

For b2H11/2 we observe only the two transitions down to a4F. There are two more lines with significant branching ratios, resulting in a residual of 26%. It is interesting to note that the major decay channels (74%) for b2H11/2 are the transitions to a4F, the same channels as for a4G. This is a sign of the level mixing between b2H and a4G, which is further discussed and illustrated in Sect. 6. The lines responsible for the residual BF appear at 9682 Å, which is heavily blended, and at 2.03 $\mu$, which is outside the observed region. The large residual makes it too uncertain to derive experimental A-values for the two transitions observed from b2H11/2. However, the calculated branching ratio for these two lines is in good agreement with the observed intensity (see Fig. 3). In Table 6 we give adjusted theoretical A-values, i.e. theoretical branching fractions combined with the measured lifetime.

As the forbidden lines from $b^4{\rm D}_{7/2}$ appear in a wider wavelength range, 3100-5600 Å, the branching fractions for the transitions depend on the reliability of the reddening curve discussed in Sect. 3.1. However, instead of adopting the calculated A-values for these lines we have used the theoretical A-values for 14 lines to derive the final branching fractions from the observed intensity ratios in the $\eta $ Carinae spectrum corrected for reddening, as described in Sect. 3. Consequently, the uncertainties of these BF's are larger than for the lines from the three other levels. The calculated residual is 11% for b4D7/2.

For the A-values with astrophysical branching ratios and experimental lifetimes we have estimated the uncertainties, which are included in Table 5. The uncertainties of the lifetime and the branching fractions are treated as independent. In the uncertainty of the BF effects from instrument calibration, intensity measurements, calculated residual and reddening are included.

   
Table 5: A-values (in s-1) for [Fe II] lines from a4G9/2, a6S5/2 and b4D7/2.
Transition Experimental   Theoretical
Upper level Lower level $\lambda$ (Å) This work   This work Qa(SST) Qb(HFR) Gc Nd
                   
a4G9/2 a4F9/2 4177 0.29(0.05) (bl)     0.184 0.194 0.14  
  a4F7/2 4276 0.83(0.07)     0.750 0.819 0.65  
  a4F5/2 4352 0.36(0.04)     0.345 0.380 0.31  
                   
a6S5/2 a6D9/2 4287 1.53(0.22)   1.625 1.37 1.65 1.12 1.53
  a6D7/2 4359 1.19(0.21)   1.204 1.02 1.22 0.82 1.141
  a6D5/2 4413 0.84(0.13)   0.853 0.725 0.858 0.58 0.812
  a6D3/2 4452 0.53(0.08)   0.547 0.465 0.548 0.37 0.522
  a6D1/2 4474 0.26(0.04)   0.267 0.227 0.267 0.18 0.255
                   
b4D7/2 a6D9/2 3175 0.23(0.03)     0.190 0.208 0.22  
  a4F9/2 3376 0.96(0.10)     0.846 0.981 0.73  
  a4F7/2 3440 0.23(0.03)     0.289 0.326 0.24  
  a4P5/2 5551 0.18(0.04)     0.149 0.176 0.13  
  a4P3/2 5613 0.10(0.03)     0.0808 0.0934 0.073  
$\textstyle \parbox{14cm}{ $^{a,b}$\space Quinet et~al. (\cite{QLZ96}); $^c$\space Garstang (\cite{G62}); $^d$\space Nussbaumer et~al. (\cite{NPS81}).}$


6 Mixing of the a4G9/2 and the b2H11/2 levels

The largest deviation between experimental and theoretical lifetimes occurs for the b2H11/2 level, where the experimental value is more than 25% smaller than the calculated value. Faster decays or more decay channels are thus available for b2H11/2 than predicted by theory. The result is a verification of the level mixing between b2H11/2 and a4G11/2, which has been observed earlier in the study of permitted lines of Fe II (Johansson 1978). The lifetime of the a4G11/2 level is predicted to be about 10 times shorter than the lifetime of b2H11/2. Unfortunately, due to frequency limitations in the probing laser we have not been able to measure the effect due to mixing on the lifetime of a4G11/2.

An astrophysical "proof'' for the level mixing is the observation of the b2H11/2-z6F9/2 transition at 6269.97 Å in the solar spectrum, which contradicts all statements about good LS coupling in the lower part of the energy level diagram of Fe II. The transition is a result of level mixing of both the upper and the lower states, i.e. b2H11/2 is mixed with a4G11/2 and z6F9/2 is mixed with z4F9/2. Thus, the observed line is an appendage to the strong a4G11/2-z4F9/2transition at 5316.61 Å (Multiplet 49). The line was not identified in the atlas of the solar spectrum by Moore et al. (1966). Since the transition probablilty is very sensitive to a small change in the eigenvector composition of an energy level, there is probably not a need for a large mixing to account for a change in radiative lifetimes that matches the observed deviation from the calculated value.

7 Conclusion

Experimental transition probabilities of 13 lines from three of the four metastable Fe II levels, for which we have measured the radiative lifetimes, have been derived according to Eq. (1). The values are inserted in Table 5 together with values from previous calculations. For the fourth level we give 3 adjusted A-values (Table 6). We also give an estimate of the uncertainty of the transition probabilities, see Table 5, which are in the range 10-30%.
 

 
Table 6: A-values (s-1) for transitions from b2H11/2. The branching fractions from Quinet et al. (SST, 1996) are combined with the experimental lifetime from this work.
Transition $\lambda$(Å) A-value (s-1)
Upper level Lower level    
       
b2H11/2 a4F9/2 4114 0.14
  a4F7/2 4211 0.058
  a2G9/2 9682 0.036


Acknowledgements
We are grateful to the staff of the CRYRING facility and appreciate their efforts to provide stable laboratory conditions. This work is supported by the Swedish Research Council (VR). H. Hartman acknowledges travel support from the Swedish Royal Academy of Science (KVA). We also wish to thank PPARC, UK, for support under Grant GR/L20276. The HST/STIS observations were performed under HST proposal 7302. This research has made use of NASA's Astrophysics Data System Bibliographic Services.

References

 

Copyright ESO 2003