A&A 397, 871-881 (2003)
DOI: 10.1051/0004-6361:20021572

[C II] emission and star formation in late-type galaxies

II. A model[*]

D. Pierini1,2 - K. J. Leech3 - H. J. Völk4


1 - Ritter Astrophysical Research Center, The University of Toledo, Toledo, OH 43606, USA
2 - Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse, 85748 Garching, Germany
3 - ISO Data Centre, Astrophysics Division, ESA Space Science Dept., PO Box 50727 Madrid, Spain
4 - Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany

Received 16 August 2001 / Accepted 29 October 2002

Abstract
We study the relationship between gas cooling via the [C II] ( $\rm\lambda = 158~\mu m$) line emission and dust cooling via the far-IR continuum emission on the global scale of a galaxy in normal (i.e. non-AGN dominated and non-starburst) late-type systems. It is known that the luminosity ratio of total gas and dust cooling, $L_{{\rm C~II}}/L_{{\rm FIR}}$, shows a non-linear behaviour with the equivalent width of the $\rm H \alpha$ ( $\rm\lambda = 6563~\AA$) line emission, the ratio decreasing in galaxies of lower massive star-formation activity. This result holds despite the fact that known individual Galactic and extragalactic sources of the [C II] line emission show different [C II] line-to-far-IR continuum emission ratios. This non-linear behaviour is reproduced by a simple quantitative theoretical model of gas and dust heating from different stellar populations, assuming that the photoelectric effect on dust, induced by far-UV photons, is the dominant mechanism of gas heating in the general diffuse interstellar medium of the galaxies under investigation. According to the model, the global $L_{{\rm C~II}}/L_{{\rm FIR}}$ provides a direct measure of the fractional amount of non-ionizing UV light in the interstellar radiation field and not of the efficiency of the photoelectric heating. The theory also defines a method to constrain the stellar initial mass function from measurements of $L_{{\rm C~II}}$ and $L_{{\rm FIR}}$. A sample of 20 Virgo cluster galaxies observed in the [C II] line with the Long Wavelength Spectrometer on board the Infrared Space Observatory is used to illustrate the model. The limited statistics and the necessary assumptions behind the determination of the global [C II] luminosities from the spatially limited data do not allow us to establish definitive conclusions but data-sets available in the future will allow tests of both the reliability of the assumptions behind our model and the statistical significance of our results.

Key words: galaxies: ISM - galaxies: spiral - galaxies: stellar content - infrared: galaxies - infrared: ISM - ISM: lines and bands


1 Introduction

The [C II]( $\rm ^2 P_{3/2}-{}^2 P_{1/2}$) ( $\rm\lambda = 157.7409~\mu m$) transition of singly ionized carbon is globally the dominant cooling line in the general diffuse Interstellar Medium (ISM), excluding H II regions (Dalgarno & McCray 1972; Tielens & Hollenbach 1985; Wolfire et al. 1995). Excitation of the $\rm ^2 P_{3/2}$ level of $\rm C^{+}$ is due to inelastic collisions with either neutral hydrogen atoms, molecules or electrons (Dalgarno & McCray 1972; Stacey 1985; Kulkarni & Heiles 1987).

Heating of the neutral interstellar gas is thought to be mainly due to photoelectrons (de Jong 1980) emitted by dust grains and Polycyclic Aromatic Hydrocarbons that are exposed to ultraviolet radiation from stars, both in the general diffuse ISM (Heiles 1994; Wolfire et al. 1995) and in the denser standard Photodissociation Regions (PDRs), at the interfaces between molecular clouds and H II regions (Tielens & Hollenbach 1985; Bakes & Tielens 1998). This photoelectric effect is essentially due to non-ionizing far-UV photons with $h \nu \ge 6~\rm eV$, as determined by the typical values of the work functions of the grain surfaces. In the field of a galaxy, this radiation is dominated by B3 to B0 stars with $5 \leq M \leq 20~M_{{\rm\odot}}$ (e.g. Xu et al. 1994). In addition, hotter, more massive stars will contribute locally.

Earlier studies of the innermost regions of gas-rich and starburst galaxies (Crawford et al. 1985; Stacey et al. 1991; Carral et al. 1994) have found that the [C II] line intensity, $I_{{\rm C~II}}$, is typically a few $\rm\times$10-3 of the far-IR continuum emission from the dust, heated by the stellar continuum emission. This fraction is of the same order of magnitude as the theoretical efficiency of the photoelectric heating, suggesting that the ratio between the far-IR continuum emission from dust and the stellar far-UV emission is constant (e.g. Kaufman et al. 1999).

With the advent of the Long Wavelength Spectrometer (LWS) (Clegg et al. 1996) on-board the ESA's Infrared Space Observatory (ISO) (Kessler et al. 1996), it has been possible to detect the [C II] line emission of large samples of normal, i.e. non AGN-dominated and non-starburst, galaxies (e.g. Malhotra et al. 1997, 2000, 2001; Smith & Madden 1997; Leech et al. 1999). Based on the last two data-sets and on that of Stacey et al. (1991), Pierini et al. (1999 - hereafter referred to as P99) have discovered a non-linear dependence of the ratio between the [C II] line intensity and the total far-IR continuum intensity FIR (as defined in Helou et al. 1985), $I_{{\rm C~II}}/I_{{\rm FIR}}$, on the equivalent width of the $\rm H \alpha$ line emission at $\rm\lambda = 6562.8~\AA$ ( ${\rm H} \alpha~EW$). The latter is proportional to the ratio between the stellar Lyman continuum and the stellar red continuum and is a tracer of the recent mass-normalized star formation rate (SFR), where mass normalization is in terms of the stellar red luminosity, and is linked to the star formation history of an individual galaxy (Kennicutt et al. 1994). In particular, P99 found that $I_{{\rm C~II}}/I_{{\rm FIR}}$ is about $\rm 4 \times 10^{-3}$ in the "normal star-forming'' galaxies (with ${\rm H} \alpha~EW \ge 10$ Å), while it decreases continuously with decreasing ${\rm H} \alpha~EW$ for "quiescent'' galaxies (with ${\rm H} \alpha~EW < 10$ Å). They qualitatively interpreted this drop in terms of a dominant "[C II]-quiet'' component of the far-IR emission in quiescent late-type galaxies, which are mainly identified with early-type spirals (cf. Leech et al. 1999). In these galaxies, dust heating is increasingly dominated by the general interstellar radiation field (ISRF), due to stars of low mass ( $ M < 5~M_{{\rm\odot}}$) (e.g. Xu et al. 1994). However, stars with $ M < 5~M_{{\rm\odot}}$ can not produce any substantial photoelectric effect on dust grains, for physical reasons which have to do with the depth of the Fermi level in the solids that constitute dust grains. In this sense such galaxies are "[C II]-quiet''. The picture of P99 has been recently invoked by Malhotra et al. (2000) in order to explain the low values of $L_{{\rm C~II}}/L_{{\rm FIR}}$ (1.2- $\rm 2.2 \times 10^{-3}$) of four nearby E/S0 galaxies observed with LWS.

Boselli et al. (2002) discuss the use of the [C II] luminosity as a diagnostic of the SFR in non IR-luminous galaxies, in place of e.g. the $\rm H \alpha$ luminosity, on the basis of empirical correlations. Their investigation carries on the seminal study of Stacey et al. (1991) and the later one of P99. They also review the empirical knowledge of the relationship between the [C II] line emission and the far-IR continuum emission from dust in different interstellar media and compare the [C II] line-to-far-IR continuum emission ratio for different Galactic and extragalactic sources of the [C II] line emission in more details than in P99.

In this paper, we present and discuss a simple but nontrivial theoretical model for the global energetics (per unit of galactic mass) of gas cooling via the [C II] line emission and dust cooling via far-IR emission in normal galaxies. This model is aimed at interpreting the relationship between global [C II] line-to-far-IR continuum emission ratio and massive star formation activity per unit of mass for normal galaxies, as suggested by the results of P99 and Malhotra et al. (2000). In particular, the trend found by P99 holds despite the fact that individual sources of the [C II] line emission have different [C II] line-to-far-IR continuum emission ratios (Stacey et al. 1991; P99; Boselli et al. 2002). The model presented here is due to H. J. Völk. It employs two moments of the stellar initial mass function (IMF) and two corresponding averages of the star formation rate (SFR) per unit of mass. We adopt standard characterizations of the IMF, assumed to be universal, in agreement with much of the evidence available in the literature (e.g. Meyer et al. 2000 and references therein) and with the expectations of self-regulating star formation models of disk-galaxies (e.g. Silk 1997). By its very nature, this model does not account for the dependence of the [C II] line emission on the astrophysical properties of the individual sources of this emission, like density of the gas and far-UV intensity of the local radiation field. For this kind of investigations we refer the reader to Heiles (1994), Wolfire et al. (1995), Kaufman et al. (1999) and references therein.

The two samples of Virgo cluster member late-type galaxies observed by Leech et al. (1999) and by Smith & Madden (1997) provide us with a total sample of 24 normal spirals with a large dynamic range in SF history and with homogeneous measurements of the observables of our interest (cf. Sect. 2). These two samples are weakly affected by Malmquist bias, because of the cluster depth (e.g. Gavazzi et al. 1999).

The previous LWS measurements are used to constrain the model, after a correction for the limited aperture of LWS (not introduced by P99), described and discussed in Sect. 2. This correction is admittedly not fully certain but is physically well motivated. In addition, the corrected [C II] line-to-far-IR continuum emission ratios are consistent with those determined within the LWS beam area, directly from the previous LWS data and the ISOPHOT (Lemke et al. 1996) data of Tuffs et al. (2002), for 10 of the sample galaxies (cf. Sect. 2). Finally, the correction leads to a result consistent with that of P99, as shown in Sect. 3.

The limited statistics of the data available to us nevertheless do not allow us to definitively confirm or disprove the theory and its quantitative consequences for the IMF. However, the model has an intrinsic astrophysical value and larger data sets, which will be available in the near future, will allow a detailed test. Therefore, the reader interested exclusively in the model may skip Sects. 2 and 3 and go directly to Sect. 4, where we introduce the model, and from there to Sect. 5, where we interpret the behaviour of $L_{{\rm C~II}}/L_{{\rm FIR}}$ with the mass-normalized massive SFR, reproduced in Sect. 3 (see also P99). A discussion of our results is contained in Sect. 6, while Sect. 7 gives a summary of our conclusions.

2 The galaxy sample and complementary data

2.1 The sample

The ISO Guaranteed Time program VIRGO combines studies of a deep optically complete, volume-limited sample of spiral, irregular and blue compact dwarf galaxies, selected from the Virgo Cluster Catalogue (VCC) of Binggeli et al. (1985) (Tuffs et al. 2002). In particular, 19 spiral galaxies (18 with $B_{{\rm T}} \le 12.3$ mag, plus NGC 4491 with $B_{{\rm T}} = 13.4$ mag) could be observed by Leech et al. (1999 - hereafter referred to as L99) with LWS in the spectral region around the [C II] line. Fourteen galaxies were detected in the [C II] line at a signal-to-noise ratio above $\rm 3 \sigma$ and upper limits were set to the other 5. Assuming a distance of 21 Mpc from Virgo, the 70 $^{\prime\prime}$ LWS half power beam-width (HPBW) corresponds to $\sim$7 kpc and encompasses at least one exponential disk scale-length for most of the sample galaxies, with the exception of those with an optical major axis larger than 5 arcmin. We note that a slightly larger (80 $^{\prime\prime}$) beam size has been determined by Lloyd (2000) for LWS. However, the discrepancy in the adopted LWS beam size does not affect the following results.

Five further VCC spiral galaxies with $12.5 \le B_{{\rm T}} \le 13.9$ mag were observed by Smith & Madden (1997 - hereafter referred to as SM97) with LWS in the [C II] line region. The latter 5 galaxies complement the previous 19, so that the total sample of 24 Virgo cluster member galaxies represents normal spirals with a large dynamic range in mass-normalized massive SFR ( ${\rm H} \alpha~EW \le 71$ Å) and in morphological type (from S0a to Sd).

According to P99, we divide the total sample of galaxies into quiescent and normal star-forming galaxies according to the values of ${\rm H} \alpha~EW < 10$ Å and $\ge $10 Å, respectively. $\rm H \alpha +[N~II]$(6548, 6583 Å) equivalent widths are available for 20 out of 24 (20/24) galaxies either from long-slit (from 3 to 7 arcmin) spectroscopy of their central region (Kennicutt & Kent 1983) or from CCD imaging (G. Gavazzi, private communication).

All the 19 galaxies of the L99 subsample have been imaged by Boselli et al. (1997) in the $K^{\prime}$-band ( $\rm\lambda = 2.1~\mu m$) and in the H-band ( $\rm\lambda = 1.65~\mu m$). Since the 5 galaxies of the SM97 subsample lack CCD measurements in these two near-IR bands, we convert their VCC total B-band ( $\rm\lambda = 0.55~\mu m$) magnitudes into $K^{\prime}$-band ones via the relation between the colour index $B_{\rm T}-K^{\prime}$ and the Hubble type found by Boselli et al. (1997). Furthermore, we convert these $K^{\prime}$-band magnitudes into H-band ones via the average $H-K^{\prime}$ colour of spiral galaxies of all Hubble types (0.26 mag), found by these authors.

18/24 galaxies have total nonthermal radio fluxes at 1.4 GHz, listed in Gavazzi & Boselli (1999). For 21/24 objects, we have selected detections/upper limits for their total IRAS 60 $\rm\mu m$ and 100 $\rm\mu m$ fluxes from either Rice et al. (1988) or Soifer et al. (1989) or Moshir et al. (1990), according to their relative optical sizes with respect to the IRAS HPBW.

The parameters of the total sample of 24 VCC late-type galaxies observed with LWS, relevant to this analysis, are given in Table 1 as follows:
Column 1: the NGC and VCC denominations;
Column 2: the morphological type, as listed in the VCC;
Column 3: logarithm of the length of major axis, as listed in de Vaucouleurs et al. (1991 - hereafter referred to as RC3);
Column 4: logarithm of the axial ratio, as listed in the RC3;
Column 5: the $\rm H \alpha +$[N II] equivalent width (H$ \alpha~EW$ for short);
Column 6: the total H-band magnitude, determined and corrected for Galactic extintion and galaxy inclination according to Gavazzi & Boselli (1996);
Column 7: the total nonthermal radio flux at 1.4 GHz;
Column 8: the total IRAS flux at 60 $\rm\mu m$;
Column 9: the total IRAS flux at 100 $\rm\mu m$;
Column 10: the observed [C II] line flux;
Column 11: references of the [C II] data.

  
Table 1: Galaxy parameters.
\begin{table} \begin{displaymath} \begin{array}{p{\linewidth}cccrrrrrrc} \hli... ...te{Ho97}). \item[$^{{g}}$ ] Sy 2 (Ho et~al. \cite{Ho97}). \end{list} \end{table}

In Table 1, notes identify the 7 early-type galaxies which are claimed to host nuclear activity typical of a LINER/AGN. The presence of an AGN increases both the [C II] line emission and the nonthermal radio emission of these galaxies in a way that is hard to predict quantitatively. As an example, however, an extra nonthermal radio emission due to the production of energetic electrons without star formation by an AGN will lead to secondary electrons on grains which will act like photoelectrons heating the gas. For NGC 4394 (Keel 1983), NGC 4569 and NGC 4579 (Stauffer 1982), claims of non-stellar nuclear activity were raised before the selection and observation of our sample. On the other hand, NGC 4192 (Barth et al. 1998), NGC 4569 and NGC 4579 (Ho et al. 1997) have recently been defined as transition spirals, while NGC 4438 (Ho et al. 1997) seems to be a marginal candidate for non-stellar nuclear activity. The phenomenology of the Virgo cluster spiral galaxy nuclear regions has not yet been established (e.g. Rauscher 1995), since different types of LINER (i.e. photoionized by a stellar continuum or by an active galactic nucleus) cannot easily be distinguished from one another (e.g. Alonso-Herrero et al. 2000). Moreover, these 7 galaxies have values of the IRAS far-IR colour f(60)/f(100) in the range 0.28-0.58, which indicates dust colour temperatures not particularly warm, and consistent both with the average far-IR colours of AGNs (0.58, with a dispersion of 0.20) and of non-AGN galaxies (0.40, with a dispersion of 0.12) found by Bothun et al. (1989). Given this, we still consider it reasonable to include these 7 VCC galaxies as part of our sample of normal late-type galaxies.

On the other hand, the 8 VCC Sc/Scd galaxies of our sample, detected both in the [C II] line and at 1.4 GHz, are not known to host any LINER/AGN activity. These galaxies define the subsample of normal star-forming galaxies.

2.2 Data analysis

The best way to get the [C II] line-to-far-IR continuum emission ratio on a galactic scale is to integrate over complete maps in each emission. Since this is not possible at the moment of writing, two options are left. One would be to take the [C II] pointings, relate the [C II] flux in them to the far-IR flux in a similar sized beam and take this ratio as representative of the whole galaxy, as suggested by the referee. IRAS beams are messy, so this is not the best way, but, for 10 of the galaxies listed in Table 1 and detected in the [C II] line emission (i.e. NGC 4178, 4192, 4293, 4394, 4429, 4438, 4450, 4491, 4569 and 4579), high signal-to-noise strip maps exist at 60 and $\rm 100~\mu m$, obtained by Tuffs et al. (2002) with the 40 arcsec HPBW instrument ISOPHOT (Lemke et al. 1996). Tuffs et al. have extracted the ISOPHOT far-IR photometry by fitting a model of the far-IR surface brightness distribution to the data. Thus, for these 10 galaxies, [C II] line-to-far-IR continuum emission ratios may be measured within the LWS beam size. However, it is not straightforward to conclude that these ratios represent the true total ratios. The second option is to adopt a [C II] line "growth curve'', but such a tool is not available at the moment of writing. A coarse spatial distribution of the [C II] line emission is known only for few individual galaxies, where it is found to be complex (e.g. Madden et al. 1993). We decided that a way out of this "impasse'' is to take the IRAS fluxes as the total far-IR ones and determine an aperture correction for the observed [C II] line fluxes on the basis of the most commonly accepted physical interpretation of the [C II] line emission. We will test the total [C II] line-to-far-IR continuum emission ratios obtained with our method from the LWS and IRAS measurements against those obtained with the method suggested by the referee, i.e. from the LWS and ISOPHOT data in our possession.

We adopt a simple analytical formula to extrapolate the total [C II] line flux from the observed one, which is based on the assumptions that i) the average ratio between the total [C II] line luminosity and the total 1.4 GHz radio continuum luminosity, as results of massive star formation activity, is constant in galaxies of the same Hubble type and that ii) the radial surface brightness profile of the [C II] line emission is homologous in galaxies of different Hubble type. We note that at this relatively low frequency, the contribution of the thermal Bremsstrahlung to the radio continuum emission of late-type galaxies is weak (e.g. Gioia et al. 1982).

In the normal star-forming galaxies, almost the same young stellar populations responsible for the gas heating (Sect. 1) dominate the SN rate (cf. X94), and, therefore, the production of Cosmic Ray electrons and nonthermal radio continuum emission. Since the corresponding UV radiation is essentially absorbed inside the galaxy by the dust grains, also the total number of photoelectrons and therefore the gas heating per $\rm C^{+}$-atom is only dependent on the UV luminosity and thus on the formation rate of massive stars. Almost the same is true for the total nonthermal radio emission (Lisenfeld et al. 1996). This carries over to the quiescent galaxies, although the fraction of SN Ia to SN II plus SN Ib may be larger than in the previous objects (cf. X94). These galaxies are close to becoming or are in fact already "radio-quiet'' (Condon et al. 1991) as well as [C II]-quiet (P99). Finally, whatever the massive star formation activity of the galaxy is, gas cooling and SNe are disk phenomena in predominantly non-interacting galaxies like ours (cf. the case of the "Antennae'' studied by Nikola et al. 1998). These astrophysical considerations support our assumptions.

It may sound dangerous to extrapolate the total [C II] line flux from the radio synchrotron emission in order to interpret the total gas-to-dust cooling flux ratio, given the existence of the radio/far-IR correlation (Rickard & Harvey 1984; Dickey & Salpeter 1984; de Jong et al. 1985; Helou et al. 1985; see also Condon et al. 1991; X94). However, the aperture correction is necessary and we consider this extrapolation as a very reasonably physically motivated way to achieve it. This correction has a larger impact for the larger galaxies of our sample, which are expected to have both larger radio and far-IR continuum emissions, as a consequence of well-established scaling effects (e.g. X94). Most of the galaxies largely undersampled by LWS are early-types, as shown by their values of the "coverage factor'' CF (defined as the ratio between the area of the LWS beam and the projected optical galaxy area, as defined in the RC3) between 10 and 100 per cent (Pierini et al. 2001). Nonetheless, for these objects, the behaviour of the total $L_{{\rm C~II}}/L_{{\rm FIR}}$ with the ${\rm H} \alpha~EW$ (Sect. 3) is consistent with that reported by P99, where no aperture correction to the LWS data was applied. On the basis of this consistency, we conclude that the aperture correction here introduced does not bias our following conclusions.

  \begin{figure} \par\includegraphics[width=8.8cm]{AA1818f1.ps} \end{figure} Figure 1: The ratio between the [C II] line luminosity, as derived from the observed flux, and the total radio continuum luminosity at 1.4 GHz, $L_{{\rm C~II}}/L_{{\rm 1.4~GHz}}$, vs. the "coverage factor'' CF, as defined in the text. Hereafter, filled circles represent the normal star-forming galaxies, empty circles represent the quiescent ones and asterisks represent galaxies without available H$ \alpha~EW$ (see text). Large empty circles and squares mark objects identified as Seyfert/LINER galaxies, respectively, while arrows mark lower and upper limits. Only the 15 galaxies with detected fluxes in both the emissions are plotted. The solid line represents Eq. (1).
Open with DEXTER

The LWS beamsize probed the [C II] line emission of the 8 VCC Sc/Scd galaxies of our sample up to relatively large galactocentric distances (Pierini et al. 2001). Moreover, there are no existing claims of LINER/AGN activity for these galaxies. For all these reasons, the subsample defined by these 8 Sc/Scd galaxies is adopted to investigate the dependence of the ratio between the [C II] line emission (within the LWS beam) and the total radio continuum luminosity, $L_{{\rm C~II}}/L_{{\rm 1.4~GHz}}$, on the CF.

As a functional form for the LWS aperture correction, we adopt the simple linear equation y = a x + b, where $y = \log~L_{{\rm C~II}}/L_{{\rm 1.4~GHz}}$ and $x = \log~CF$. According to our assumptions, $\log~L_{{\rm C~II}}/L_{{\rm 1.4~GHz}}$ is expected to decrease with decreasing values of $\log~CF$ as a consequence only of the reduced fraction of the [C II] line emission probed by LWS, so that the parameter a is independent of the Hubble type. In contrast, the constant term b, defining the intrinsic ratio between the total [C II] line luminosity and the total 1.4 GHz radio continuum luminosity, depends to first order on the average star formation history of a galaxy, i.e. on the Hubble type of the galaxy (Kennicutt et al. 1994). We may also expect that b depends to second order on the presence of an AGN and on the relationship between global properties of the ISM and Hubble type, if any.

Figure 1 shows the plot of $\log~L_{{\rm C~II}}/L_{{\rm 1.4~GHz}}$ vs. $\log~CF$ for all the galaxies with available obervables, $L_{{\rm C~II}}$ being determined from the observed [C II] line flux assuming a distance of 21 Mpc for Virgo. Hereafter, quiescent galaxies, normal star-forming galaxies and galaxies without measured H$ \alpha~EW$ are represented by empty circles, filled circles and asterisks, respectively. We also mark those galaxies with claimed non-stellar nuclear activity (cf. Sect. 2.1) by large circles and squares, respectively. In Fig. 1, the solid line reproduces the least-squares fit of equation

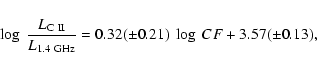\begin{displaymath}\log~\frac{L_{{\rm C~II}}}{L_{{\rm 1.4~GHz}}} = 0.32 (\pm 0.21)~\log~CF + 3.57 (\pm 0.13), \end{displaymath} (1)

obtained for the 8 Sc/Scd galaxies.

We note that the parameter a is different from 0 only at the $\rm 1 \sigma$ level, maybe as a result of the limited statistics. Nevertheless, we correct the observed [C II] line fluxes of all the galaxies (listed in Col. 10 of Table 1) to total ones via the multiplicative term $10^{0.32~\times~\log~CF}$.

  \begin{figure} \par\includegraphics[width=8.8cm]{AA1818f2.ps} \end{figure} Figure 2: Comparison of the ratio of the total [C II] line luminosity, obtained from the correction for the LWS aperture (Eq. (1)) and from the total IRAS far-IR continuum luminosity FIR (as defined by Helou et al. 1985), $L_{{\rm C~II}}/L_{{\rm FIR}}$, and the ratio of the observed [C II] line luminosity and the ISOPHOT far-IR continuum luminosity FIR within the LWS beam area, $L_{{\rm C~II}}/L_{{\rm FIR_{{\rm LWS}}}}$. Only the 10 galaxies with available LWS, ISOPHOT and IRAS measurements are plotted (see text).
Open with DEXTER

The method previously illustrated is admittedly crude but its feasibility may be tested against the data, as previously mentioned. In fact, ratios between the observed [C II] line luminosity and the far-IR continuum luminosity FIR (Helou et al. 1985) within the LWS beam may be obtained from the existing ISOPHOT photometry (Tuffs et al. 2002). Tuffs et al. show that the ISOPHOT photometry at 60 and $\rm 100~\mu m$ is consistent with the analogous IRAS photometry. Thus we have obtained aperture photometry of 10 sample galaxies with available LWS, ISOPHOT and IRAS data (i.e. NGC 4178, 4192, 4293, 4394, 4429, 4438, 4450, 4491, 4569 and 4579) at 60 and $\rm 100~\mu m$, after deconvolving the models of Tuffs et al. with the ISOPHOT beam, assumed to be reproduced by a two-dimensional circular gaussian of 40 arcsec full-width-at-half-maximum (FWHM).

Figure 2 shows the comparison between the total [C II] line-to-far-IR FIR emission ratios ( $\log~L_{{\rm C~II}}/L_{{\rm FIR}}$ on the y-axis) and the [C II] line-to-far-IR FIR emission ratios within the LWS beam area ( $\log~L_{{\rm C~II}}/L_{{\rm FIR_{{\rm LWS}}}}$ on the x-axis). The total ratio $\log~L_{{\rm C~II}}/L_{{\rm FIR}}$ is obtained by applying the aperture correction (Eq. (1)) to the observed LWS [C II] line flux and from the total IRAS fluxes at 60 and $\rm 100~\mu m$, according to Helou et al. (1985). Conversely, $\log~L_{{\rm C~II}}/L_{{\rm FIR_{{\rm LWS}}}}$ is obtained from the observed [C II] line flux and from the integration of the far-IR surface brightness distribution at 60 and $\rm 100~\mu m$, as obtained with ISOPHOT, within the LWS beam area. We assume an error of 5 per cent in the model ISOPHOT fluxes and an error of 30 per cent in the ISOPHOT absolute calibration.

The ratios estimated through these two different methods are consistent within the uncertainties and the approximations in both methods, especially when considering the difference between a total value and a rather local one. This is not trivial. Thus, we conclude that most of the emission both in the [C II] line and in the far-IR continuum comes from the regions probed by LWS, at least for our sample galaxies, as assumed by P99. "A posteriori'' this result supports the assumptions behind the correction for the LWS aperture, especially when considering that 9 of the previous 10 galaxies are not among those used to determine this aperture correction. Thus, we conclude that the estimates of the total [C II] line fluxes, obtained through the aperture correction of Eq. (1), are robust.

  \begin{figure} \par\includegraphics[width=6.5cm]{AA1818f3.ps} \end{figure} Figure 3: The ratio between the [C II] line luminosity and the total far-IR continuum luminosity FIR (as defined by Helou et al. 1985), $L_{{\rm C~II}}/L_{{\rm FIR}}$, vs. CF, prior to a) and after b) the correction for the LWS aperture. Only the 21 galaxies with available measurements are plotted.
Open with DEXTER

3 $\vec{L}_{{\rm C~II}}/\vec{L}_{{\rm FIR}}$ vs. H $\alpha~{\vec {EW}}$ in normal late-type galaxies

In Figs. 3a,b, we plot the ratio between the [C II] line luminosity and the total far-IR continuum luminosity FIR (Helou et al. 1985), $\log~L_{{\rm C~II}}/L_{{\rm FIR}}$, vs. $\log~CF$ prior to and after the correction for the LWS aperture effects, respectively. Although this correction affects the values of $L_{{\rm C~II}}/L_{{\rm FIR}}$ of individual galaxies, there is no definite global trend of $L_{{\rm C~II}}/L_{{\rm FIR}}$ with CF in Fig. 3a and, a fortiori, in Fig. 3b.

The early-type spiral galaxies with claimed non-stellar nuclear activity (cf. Sect. 2.1) are among those with the lowest values of $L_{{\rm C~II}}/L_{{\rm FIR}}$ in Figs. 3a,b, but their total $L_{{\rm C~II}}/L_{{\rm FIR}}$ (Fig. 3b) is on average more than one order of magnitude higher than that of the "[C II]-deficient'' galaxies identified by Malhotra et al. (1997), with IRAS far-IR colours between 0.6 and 1.4. For the same galaxies, the mean value of $L_{{\rm C~II}}/L_{{\rm FIR}}$ is intermediate between the range 1.2- $\rm 2.2 \times 10^{-3}$ spanned by 4 nearby E/S0 galaxies observed with LWS (Malhotra et al. 2000) and the mean value of $L_{{\rm C~II}}/L_{{\rm FIR}}$ of VCC galaxies of later Hubble types (Fig. 3b). This result suggests that the non-stellar nuclear activity claimed for some of our galaxies does not affect systematically their values of $L_{{\rm C~II}}/L_{{\rm FIR}}$. We conclude that $L_{{\rm C~II}}/L_{{\rm FIR}}$ is, on average, lower for quiescent galaxies than for normal star-forming ones, even though the scatter is large.

The average ratio between the [C II] line emission and the far-IR continuum emission is consistent with the theoretical efficiency of the photoelectric heating of the gas, as found by previous authors (cf. Sect. 1).

Figure 4 shows the dependence of the total $L_{{\rm C~II}}/L_{{\rm FIR}}$ on the ${\rm H} \alpha~EW$ for the 19/24 galaxies of our sample with available observables. Here, the galaxy out of bounds is NGC 4491, with H$ \alpha~EW$ consistent with 0 Å.

The distribution in Fig. 4 is much more regular than the one reproduced in Fig. 3b. For the 6 normal star-forming galaxies detected both in the [C II] line and in the far-IR, the mean value of $L_{{\rm C~II}}/L_{{\rm FIR}}$ is equal to $\rm 7.9 \times 10^{-3}$ with a dispersion of $2.1 \times 10^{-3}$. This figure is still consistent with the analogous mean value of $\sim$ $ 4 \times 10^{-3}$ obtained by P99 for an heterogeneous sample of normal star-forming galaxies without any kind of aperture correction. For the quiescent galaxies, $L_{{\rm C~II}}/L_{{\rm FIR}}$ drops continuously with decreasing values of the H$ \alpha~EW$, in agreement with P99. Finally, galaxies with claimed non-stellar nuclear activity do not behave in a peculiar way in Fig. 4.

These results strengthen those obtained by P99. In fact, P99 assumed that the bulk of the IRAS far-IR continuum emission of their VCC galaxies originated within the region sampled by the aperture of LWS (set equal to 80 arcsec) for each galaxy. P99 assumed implicitly that the characteristic FWHM of the IRAS $\rm 60~\mu m$ and $\rm 100~\mu m$ continuum emissions of normal galaxies was defined by the IRAS observations of the nearby Sab galaxy NGC 5713 (see Lord et al. 1996), which indicate that the FWHM of the IRAS $\rm 25~\mu m$ and $\rm 60~\mu m$ emissions of this galaxy is about 1/5 of its optical diameter. The LWS HPBW indeed encompasses 1/5 of the galaxy's optical diameter in VCC galaxies with $\log~D \le 1.76$, i.e. for all the objects observed with LWS, with the exception of NGC 4192, NGC 4438 and NGC 4569 (cf. Table 1). As seen in Sect. 2.2 this assumption seems to hold for the present case. Conversely, the values of $L_{{\rm C~II}}/L_{{\rm FIR}}$ adopted by P99 for their subsample of galaxies observed by Stacey et al. (1991) did not suffer because of a marked difference in beam size of the [C II] and far-IR observations. Here, we confirm that the dependence of $L_{{\rm C~II}}/L_{{\rm FIR}}$ on the H$ \alpha~EW$ found by P99 is not due either to their assumption or to the inclusion of LINER/AGN candidates in their sample.

  \begin{figure} \par\includegraphics[width=8.8cm]{AA1818f4.ps} \end{figure} Figure 4: $L_{{\rm C~II}}/L_{{\rm FIR}}$ vs. the equivalent width of the H$\alpha $ line, H$ \alpha~EW$. $L_{{\rm C~II}}$ is corrected for the LWS aperture. Only the 19 galaxies with available measurements are plotted. The galaxy out of bounds is NGC 4491, with H$ \alpha~EW$ consistent with $\rm 0~\AA$. The non-linear relation between $L_{{\rm C~II}}/L_{{\rm FIR}}$ and H$ \alpha~EW$ found by P99 is confirmed.
Open with DEXTER

4 The model

P99 interpreted the non-linear relation between $L_{{\rm C~II}}/L_{{\rm FIR}}$ and the H$ \alpha~EW$ under the assumption that photoelectric heating is the dominant mechanism of gas heating in the diffuse ISM of normal spiral galaxies, on the scale of a galaxy. The existence of a lower characteristic far-UV photon energy threshold for the photoelectric effect on the dust, coupled to the different massive SFRs of galaxies of different morphology (cf. Kennicutt et al. 1994), qualitatively explains why quiescent early-type spiral galaxies have lower values of $L_{{\rm C~II}}/L_{{\rm FIR}}$ than normal star-forming late-type ones.

Here, we introduce a simple quantitative model in order to describe this behaviour, based both on generally accepted concepts of galaxy star formation history and on observations. We adopt mass-normalized quantities, in order to eliminate simple scaling effects among galaxies of different masses. Mass-normalization is in terms of the total near-IR luminosity. The latter is, in fact, a good estimate of the bulk of the mass of the old stellar population, which dominates the mass of the "luminous matter'' of giant galaxies (Aaronson et al. 1979).

In our theoretical modelling, we adopt the formalism introduced by Xu et al. (1994 - hereafter referred to as X94), in their interpretation of the properties of the radio/far-IR correlation for normal late-type galaxies. We refer the reader to X94 for further details and discussion of the physical justification of the parameterization introduced hereafter.

The galaxy mass M is estimated as follows:

\begin{displaymath}M = \frac{L_{H}}{2.05 \times 10^{25}~{{\rm [W~\mu m^{-1}]}}}~~~~(M_{{\rm {\odot}}})~, \end{displaymath} (2)

where LH is the H-band luminosity.

The mass-normalized total IRAS far-IR continuum (FIR) emission within the wavelength range of 40-120 $\rm\mu m$ is expressed through the following formula:

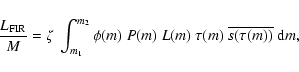\begin{displaymath}\frac{L_{{\rm FIR}}}{M} = \zeta~\int_{m_1}^{m_2} \phi (m)~P (m)~L (m)~\tau (m)~\overline{s (\tau (m))}~{\rm d}m, \end{displaymath} (3)

with $\zeta = 1/1.8$ denoting the fraction of the FIR emission contained within 40-120 $\rm\mu m$, which is quite a constant factor among galaxies (Helou et al. 1985), $m_1 = 1~M_{{\rm\odot}}$ and $m_2 = 100~M_{{\rm\odot}}$ specifying the mass range of stars which are responsible for the heating of the dust (we ignore stars less massive than the Sun because they contribute little to the dust heating and take an upper cut-off of the IMF of $100~M_{{\rm\odot}}$). The stellar initial mass function (IMF) is denoted by $\phi (m)$, the probability of the light of a star of mass m to be absorbed by dust by P (m). Finally, L (m) and $\tau (m)$ are the Main Sequence (MS) luminosity and life time of a star of mass m, respectively, and

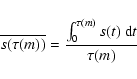\begin{displaymath}\overline{s (\tau (m))} = \frac{ \int_{0}^{\tau (m)} s (t)~{\rm d}t}{\tau (m)} \end{displaymath} (4)

is the star formation rate (per unit of mass) averaged over the life time of this star.

The total energy emitted during the MS life of a star of given mass m, $L (m) \times \tau (m)$, is given by:

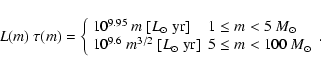\begin{displaymath}L (m)~\tau (m) = \left\{ \begin{array}{ll} 10^{9.95}~m~[L_{{\... ...mbox{$5 \le m < 100~M_{{\rm\odot}}$ } \end{array}. \right . \end{displaymath} (5)

According to X94, 60 per cent of the radiation from stars more massive than $5~M_{{\rm\odot}}$ is absorbed and then reradiated in the far-IR by the dust, while the absorption probability of radiation from stars with $1 \le m < 5~M_{{\rm\odot}}$ is 30 per cent.

We consider six different IMFs (Salpeter 1955; Miller & Scalo 1979; Kennicutt 1983; Kroupa et al. 1993; X94; Scalo 1998) and, in each case, we assume that the IMF is universal (cf. Meyer et al. 2000) and independent of the SFR. For each IMF, we calculate the normalization factor from the definition:

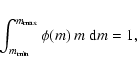\begin{displaymath}\int_{m_{{\rm min}}}^{m_{{\rm max}}} \phi (m)~m~{\rm d}m=1, \end{displaymath} (6)

imposing continuity at the values of m corresponding to a change of the IMF slope and taking the lower stellar mass $m_{{\rm min}} = 1~M_{{\rm\odot}}$ and the upper stellar mass $m_{{\rm max}} = 100~M_{{\rm\odot}}$.

Thus we rewrite $L_{{\rm FIR}}/M$ as:

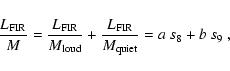\begin{displaymath}% \frac{L_{{\rm FIR}}}{M} = \frac{L_{{\rm FIR}}}{M_{\rm loud}}+\frac{L_{\rm FIR}}{M_{\rm quiet}}= a~s_8 + b~s_9~, \end{displaymath} (7)

where the suffix "loud'' ("quiet'') defines the far-IR component due to stars more (less) massive than $5~M_{{\rm\odot}}$, which are (are not) responsible for the photoelectric heating (Sect. 1).

The quantities s8 and s9 (in units of $\rm yr^{-1}$) define the star formation rates (per unit of mass) averaged over times of $\rm 10^8~yrs$ and $\rm 3 \times 10^9~yrs$, respectively. MS life times shorter than $\rm 10^8~yrs$ correspond to stars more massive than $5~M_{{\rm\odot}}$, while MS life times between $\rm 10^8~yrs$ and few $\rm\times 10^9~yrs$ characterize stars with $1 \le m < 5~M_{{\rm\odot}}$. Given the previous assumptions, the quantities a and b (in units of $L_{{\rm\odot}}~{M_{{\rm\odot}}}^{-1}~\rm yr$) depend only on the IMF. We discuss this interesting aspect in further detail in Sect. 5.2. In Table 2, we show the values of the parameters a and b, obtained from Eq. (3) through (6), corresponding to the adopted IMFs.

  
Table 2: "a'' and "b'' as functions of the IMF.
\begin{table} \begin{displaymath} \begin{array}{p{0.3\linewidth}ccc} \hline\hl... ...o '98 & 8.73 & 4.08 & 0.68\\ \hline \end{array} \end{displaymath} \end{table}

The mass-normalized total [C II] line luminosity is expressed as follows:

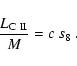\begin{displaymath}\frac{L_{{\rm C~II}}}{M} = c~s_8~. \end{displaymath} (8)

The parameter c (in units of $L_{{\rm\odot}}~{M_{{\rm\odot}}}^{-1}~\rm yr$) is assumed to depend on the IMF and, to second order, on the efficiency of the photoelectric effect in galaxies of different far-UV field strengths (cf. Bakes & Tielens 1994), i.e. of different morphological classification. Eventually, the latter dependence concerns effects due to metallicity and properties of dust and ISM, whether these properties are dependent on Hubble type. This formula provides a physical justification for the use of the [C II] line emission as a tracer of star formation in non AGN-dominated and non-starburst galaxies. This aspect is discussed by Boselli et al. (2002) and not here.

Finally, from Eqs. (7) and (8) it follows that:

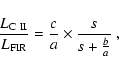\begin{displaymath}\frac{L_{{\rm C~II}}}{L_{{\rm FIR}}} = \frac{c}{a} \times \frac{s}{s+\frac{b}{a}}~, \end{displaymath} (9)

where

\begin{displaymath}s = \frac{s_8}{s_9}~\cdot \end{displaymath} (10)

According to these two equations, $L_{{\rm C~II}}/L_{{\rm FIR}}$ tends to c/a for s >> b/a and to (c/b) s for s << b/a.

5 Results

5.1 On the relation between gas cooling, dust cooling and star formation history of individual galaxies

In theory, the ratio between gas cooling via the [C II] line emission and dust cooling via the far-IR continuum emission depends only on the parameter c and on the two average SFRs (per unit of mass) s8 and s9, once the IMF is chosen. Hereafter, we adopt the X94 IMF for illustrative purposes.

We assume that galaxies of the same Hubble type (HT) have the same characteristic SF time scale. Under the further assumption that s9 is the median of the values of s8 of individual galaxies of the same morphology (X94), we derive the median values of s9 and c for each Hubble type as follows:

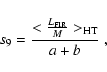\begin{displaymath}s_9 = \frac{<\frac{L_{{\rm FIR}}}{M}>_{{\rm HT}}}{a+b}~, \end{displaymath} (11)


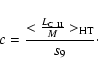\begin{displaymath}c = \frac{<\frac{L_{{\rm C~II}}}{M}>_{{\rm HT}}}{s_9}\cdot \end{displaymath} (12)

We remind the reader that the median is especially appropriate as a measure of central tendency of a skewed distribution of data. For the present illustrative purposes, we estimate the mean values of $L_{{\rm FIR}}/M$ and $L_{\rm C~II}/M$ for any given morphological type represented by the galaxy sample described in Sect. 2.1 instead. This choice allows the comparison of the mean value of $L_{{\rm C~II}}/L_{{\rm FIR}}$ found for the normal star-forming galaxies to that found by P99 for similar objects.

In Fig. 5, we plot the mass-normalized total [C II] luminosity vs. the mass-normalized total far-IR continuum luminosity for the 20 Virgo cluster galaxies with available suitable observables. In Figs. 5a-c only the 18 objects in the three groups Sa/Sab, Sb/Sbc, Sc/Scd are shown, since only for these three groups of morphological types we can constrain our model.

  \begin{figure} \par\includegraphics[width=10.8cm]{AA1818f5.ps} \end{figure} Figure 5: The mass-normalized total (i.e. corrected for the LWS aperture) [C II] luminosity, $L_{\rm C~II}/M$, vs. the mass-normalized total far-IR continuum luminosity FIR, $L_{{\rm FIR}}/M$. The 18 galaxies of the three groups of morphological classes for which the available observables may constrain the model, i.e. Sa/Sab a), Sb/Sbc b) and Sc/Scd c), are plotted. In each panel, the solid line represents the values of $L_{\rm C~II}/M$ obtained from Eq. (13). All the 20 galaxies with available suitable observables are plotted, superposed to the relation expressed by Eq. (13) for the Sa/Sab group d). It is evident that the available statistics are not sufficent to fully characterize the dependence of the model parameters on the galaxy morphology.
Open with DEXTER

In Fig. 5d we show all the 20 objects superimposed on the model curve obtained for the Sa/Sab galaxies as a reference. In each panel, the solid line represents the logarithmic value of $L_{\rm C~II}/M$ obtained as follows:

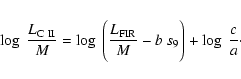\begin{displaymath}\log~\frac{L_{{\rm C~II}}}{M} = \log~\Bigg( \frac{L_{{\rm FIR}}}{M} - b~s_9\Bigg) + \log~\frac{c}{a}\cdot \end{displaymath} (13)

From inspection of Fig. 5, we obtain that:
1.
the model relation between $\log~L_{{\rm C~II}}/M$ and $\log~L_{{\rm FIR}}/M$ is non-linear for any given morphological classification;
2.
in the model, $L_{{\rm C~II}}/L_{{\rm FIR}}$ drops with decreasing values of $L_{{\rm FIR}}/M$, independent of galaxy classification, but this drop takes place at a characteristic value of $L_{{\rm FIR}}/M \sim b~s_9$, increasing with galaxy lateness;
3.
$L_{{\rm C~II}}/L_{{\rm FIR}}$ tends to first order to the same asymptotic value c/a at sufficiently high values of $L_{{\rm FIR}}/M$ for galaxies of different Hubble types;
4.
the galaxy distribution shown in Fig. 5 is consistent with the relation between current star formation activity and galaxy lateness (cf. Kennicutt et al. 1994; Boissier & Prantzos 2000), even though the non-linearity of the model is not well covered by the available data points;
5.
the statistics are not yet sufficient to characterize the dependence of the model parameters on the galaxy morphology;
6.
therefore the statistics are not yet sufficient to derive any quantitative difference induced by the assumed IMF (cf. Sect. 5.2).
We emphasize that only large statistical samples can prove or disprove the validity of the model. Nevertheless these illustrative results are quite encouraging.

5.2 A new method of constraining the stellar IMF

The theory of Sect. 4 allows us to express the mass-normalized total [C II] and far-IR continuum luminosities in terms of combinations of two star formation rates (per unit of mass), s8 and s9, averaged over 108 and $3 \times 10^9$ years, respectively, weighted by the two parameters a and b, depending only on the IMF.

Galaxies of a given morphological type distribute along a non-linear relation in the $\log~L_{{\rm C~II}}/M$- $\log~L_{{\rm FIR}}/M$ plane, according to the ratio between s8 and s9 in such a way that

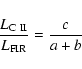\begin{displaymath}\frac{L_{{\rm C~II}}}{L_{{\rm FIR}}} = \frac{c}{a+b} \end{displaymath} (14)

when $s_8 \sim s_9$, and that, conversely,

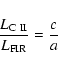\begin{displaymath}\frac{L_{{\rm C~II}}}{L_{{\rm FIR}}} = \frac{c}{a} \end{displaymath} (15)

when s8 is large compared to s9.

If the luminosities involved in these two equations were available for a large statistically complete sample of normal galaxies, it would be straightforward to derive an accurate value of a/(a+b) from Eqs. (14) and (15). Since a/(a+b) is sensitive to the IMF (cf. Col. 4 of Table 2), one can effectively constrain the stellar IMF via measurements of gas and dust cooling.

6 Discussion

According to different studies (de Jong 1980; Tielens & Hollenbach 1985; Bakes & Tielens 1994, 1998; Wolfire et al. 1995; Kaufman et al. 1999), the heating of the interstellar gas is mainly due to collisions with photoelectrons ejected from different dust components, when illuminated by far-UV photons. Contrary to gas heating, dust heating is due also to the general ISRF (e.g. Condon et al. 1991; X94; Popescu et al. 2000), although the consensus is not unanimous.

Early detailed models of gas heating (e.g. Tielens & Hollenbach 1985) considered only the relatively dense atomic interstellar environments dominated by the far-UV field, where dust heating is also dominated by the emission from stars more massive than $5~M_{{\rm\odot}}$. Therefore, these models naturally interpreted the ratio between gas cooling via the [C II] line emission and dust cooling via the far-IR continuum emission as a direct measure of the efficiency of the photoelectric effect on dust grains. In an analogous way, the early studies of the [C II] line emission in external galaxies (Crawford et al. 1985; Stacey et al. 1991; Carral et al. 1994) targeted the innermost regions of gas-rich and starburst galaxies, where both the fractional content of molecular gas (e.g. Pierini et al. 2001) and the contribution of the OB associations to the ISRF (e.g. Bronfman et al. 2000) are large. Since these stellar populations are associated with dense PDRs, it is no surprise that the previous models were successful in interpreting the phenomenology and the energetics of gas cooling in most of the galaxies observed in the [C II] line region for the first time.

Adopting the PDR models of Kaufman et al. (1999), Malhotra et al. (2001) have found that a significant fraction of the total [C II] line emission of normal galaxies is associated with PDRs very close to star formation regions. By contrast, Madden et al. (1993) have shown that the diffuse components of the ISM, associated with the atomic hydrogen, are responsible for the [C II] line emission on scales larger than a galactic nucleus. In the inner regions of a galaxy, the contribution of the diffuse ionized medium is also non negligible (Heiles 1994; Negishi et al. 2001). These results have been supported by P99, on the basis of the observations made by L99 and SM97 with LWS, and confirmed by Pierini et al. (2001), via a comparison with models of the diffuse ISM of Wolfire et al. (1995). We believe that the solution to this dilemma rests in the differences not only among the galaxy regions probed by observations (Pierini et al. 2001) but also in the massive star formation activity of the sample objects.

As far as orders of magnitude are concerned, even on a galactic scale the average ratio between the [C II] line intensity, as measured by the LWS, and the IRAS far-IR continuum emission FIR (Helou et al. 1985) is consistent with the theoretical efficiency of gas heating via the far-UV light induced photoelectric effect on different dust components (cf. Lord et al. 1996). However, P99 discovered that, to first order, this ratio is a function of the massive star formation activity for normal late-type galaxies. This result holds despite the fact that individual Galactic and extragalactic sources of the [C II] line emission show different values of the [C II] line-to-far-IR emission ratio (e.g. Stacey et al. 1991; P99; Boselli et al. 2002). In Sect. 5.1 we have reproduced the trend observed by P99 with a theoretical model, under the assumption (X94) that the time evolution of the SFR has an exponential law, where the characteristic time scale increases with galaxy lateness. This parametric model is supported both by theoretical results on galaxy evolution and by observations. As a result, we find that the global $L_{{\rm C~II}}/L_{{\rm FIR}}$ is a direct measure of the fractional content of far-UV photons in the ISRF of individual normal galaxies, whatever the components of the ISM (dense PDRs, diffuse atomic/ionized gas), where gas heating takes place, are, and not of the efficiency of the photoelectric heating.

Since massive star formation declines faster with time in spiral galaxies of earlier types, on average, these galaxies are expected to have low values of $L_{{\rm C~II}}/L_{{\rm FIR}}$. The opposite is true for the late-type spiral galaxies. A particularly low production of far-UV photons (per unit of mass) naturally explains the non-detection of 4 early-type spirals, none of which associated with an AGN, which were observed by L99 with LWS in the [C II] line region (cf. Table 1 in Sect. 2.1). This scenario has been recently invoked by Malhotra et al. (2000) in order to qualitatively explain the low values of $L_{{\rm C~II}}/L_{{\rm FIR}}$ (1.2-2.2 $\rm\times 10^{-3}$) of 4 nearby E/S0 galaxies observed with LWS, in agreement with the earlier interpretation of P99. According to the model, the efficiency of the photoelectric heating (on a galactic scale) may be derived if the absolute value of the global far-UV field strength is known. The latter is not simply proportional to the far-IR emission from dust (Sect. 4), given the relative contributions of non-ionizing UV and the general interstellar radiation field to the dust heating.

7 Conclusions

We have investigated the relationship between gas cooling via the [C II] ( $\rm\lambda = 158~\mu m$) line emission and dust cooling via the far-IR continuum emission in normal (i.e. non-AGN dominated and non-starburst) late-type galaxies. It is known that to first order the luminosity ratio between total gas and dust cooling, $L_{{\rm C~II}}/L_{{\rm FIR}}$, shows a non-linear behaviour with the equivalent width of the $\rm H \alpha$ ( $\lambda = 6563$ Å) line emission, the ratio decreasing in galaxies of lower global massive star formation activity. This trend holds despite the fact that individual Galactic and extragalactic sources of the [C II] line emission show different values of the [C II] line-to-far-IR emission ratio.

This non-linear behaviour is reproduced by a simple quantitative model of gas and dust heating from different stellar populations, under the assumption that the photoelectric effect on dust induced by far-UV photons is the dominant mechanism of gas heating in the general diffuse interstellar medium of these galaxies. This model employs two moments of the stellar initial mass function (IMF) and two corresponding averages of the star formation rate (SFR) per unit of mass. According to the model, $L_{{\rm C~II}}/L_{{\rm FIR}}$ directly measures the fractional amount of the non-ionizing UV light in the interstellar radiation field and not the efficiency of the photoelectric heating.

A sample of 20 Virgo cluster galaxies is used to illustrate the model. The insufficient statistics and the assumptions behind the determination of the global [C II] luminosities from the spatially limited LWS data do not yet allow us to definitively confirm or disprove the model. When measurements of the total [C II] line emission and of the other quantities invoked by our model will be available for large statistical samples of non-AGN and non-starburst galaxies, we shall be able to characterize the behaviour of $L_{{\rm C~II}}/L_{{\rm FIR}}$ with the H$ \alpha~EW$ for each Hubble type and to reproduce it. The same wealth of data will allow us to test the astrophysical assumptions behind our model, via the comparison of the average star formation rates as derived from the [C II] line and other line/continuum emissions. Finally, it will also quantitatively constrain the IMF, if universal, given the dependence of the results on the IMF.

Acknowledgements
We are grateful for the support of this work to the Deutsche Agentur für Raumfahrt Angelegenheiten, through DARA project number 50-OR-9501B. D.P. acknowledges support also through Grant NAG5-9202 from the National Aeronautics and Space Administration to the University of Toledo.
We are indebted to G. Gavazzi for providing us with optical data prior their publication.
We are grateful to the referee, G. J. Stacey, for his useful comments which improved the quality of this paper in its final version.

References

 

Copyright ESO 2003