A&A 397, 771-776 (2003)
DOI: 10.1051/0004-6361:20021523

Combined VLBI/GPS series of precession-nutation and comparison with IAU2000 model

J. Vondrák 1 - C. Ron 1 - R. Weber2


1 - Astronomical Institute, Academy of Sciences of the Czech Republic, Bocní II, 141 31 Prague 4, Czech Republic
2 - Institute of Geodesy and Geophysics, University of Technology Vienna, Gusshausstrasse 27-29, 1040 Vienna, Austria

Received 24 July 2002 / Accepted 3 October 2002

Abstract
The IAU adopted in 2000 a new model of precession-nutation that is to be used from January 1, 2003. It is based on the theory of nutation for the rigid Earth by Souchay et al. (1999) and the transfer function of a complicated geophysical Earth model computed by Mathews et al. (2002). Some of the constants of this model are derived from the celestial pole offsets observed by Very Long-Baseline Interferometry (VLBI). Since 1994, series of celestial pole offset rates, observed by Global Positioning System (GPS), have been made available.

The observations of Earth Orientation Parameters (EOP) made by different techniques have specific behavior at different frequencies. VLBI is very stable in long-term sense but does not provide very dense observations; satellite methods (such as GPS) have a good short-term precision and high resolution but their long-term stability is not good. The recently proposed method of combined smoothing (Vondrák & Cepek 2000) is capable of combining non-evenly distributed observations of a parameter with its observed rates, obtained in epochs that do not need to be identical with the epochs of the observed parameter.

Using this method, the combination of VLBI-based celestial pole offsets with the GPS-based celestial pole offset rates is presented, and compared with the new IAU2000 model of precession-nutation. The new model is shown to agree with the combined solution at the level of present observational accuracy, and the Free Core Nutation (FCN) is shown to be dominant in the residuals.

Key words: reference systems - Earth - techniques: miscellaneous - methods: numerical


1 Introduction

The IAU at its 24th General Assembly in 2000 adopted a series of resolutions, mostly concerning fundamental astronomy. One of these, B1.6, "recommends that, beginning on 1 January 2003, the IAU 1976 Precession Model and IAU 1980 Theory of Nutation, be replaced by the Precession-nutation Model IAU 2000A...''. The new model is based on the rotation theory of the rigid Earth REN-2000 by Souchay et al. (1999) and transfer function calculated for a non-rigid Earth model (Mathews et al. 2002; Buffet et al. 2002). The Earth model used consists of the mantle, the fluid outer and the solid inner core, and includes also mantle and inner core anelasticity, ocean tide effects, electromagnetic couplings of the mantle and the solid inner core with the fluid outer core, annual atmospheric tide and relativistic effects (geodesic precession and nutation).

A few basic parameters of the model are estimated by a fit to VLBI observations of precession-nutation during the past two decades or so (Herring et al. 2002). The VLBI technique, with the history going back to 1976, uses extragalactic sources as reference points, and therefore the EOP derived from VLBI are directly referred to the recently adopted International Celestial Reference Frame - ICRF (Ma et al. 1998; Feissel & Mignard 1998).

However, these are not the only observations of precession-nutation available at present. Recently the Global Positioning System (GPS), using the observations of navigation satellites, demonstrated its capability of measuring the rates (time derivatives) of precession-nutation angles (Rothacher et al. 1999).

Satellite methods, unlike the VLBI, measure the orientation of the Earth with respect to satellite orbits, and therefore are not capable of measuring directly the Earth's orientation with respect to the ICRF. Because the modelling of satellite orbits in space is a complicated task (their motion is subject to many influences, both gravitational and non-gravitational) and some of the orbital elements are correlated with some EOP, the exact and stable tie to ICRF is very difficult. Therefore, the satellite methods can provide only the time derivatives of those Earth orientation parameters that are sensitive to ICRF (i.e., Universal time and precession-nutation). As demonstrated by Weber (1996, 2001), GPS observations can thus deliver unique contribution to the nutation spectrum in the high frequency range (up to 14 days).

So we have a series of celestial pole offsets (i.e., the differences between the observed and modelled precession-nutation) in longitude $\Delta\psi$ and obliquity $\Delta\epsilon$ measured by one technique (VLBI) and their rates $\Delta\dot\psi$, $\Delta\dot\epsilon$ measured independently by another technique (GPS). This is a typical example when the recently proposed method of combined smoothing, introduced shortly by Vondrák & Gambis (2000) and described in detail by Vondrák & Cepek (2000) can be used.

This method was applied to combine celestial pole offsets from VLBI and GPS on a shorter time interval of only 3 years (1997.0-2000.0) by Vondrák et al. (2002a; 2002b), where the combination was compared with the new IAU precession-nutation theory and with the preliminary nutation theory of the International Earth Rotation Service (IERS) 1996, and on the interval of 6 years (1994.3-2000.3) by Vondrák & Ron (2002), where our combination was compared with the standard combination C04 of the IERS. These comparisons revealed that the agreement between the combination VLBI/GPS and the new IAU model of precession-nutation is better than the agreement between the standard IERS solution C04 and the same model. This means that the solution C04 (that uses only VLBI observations) probably lacks the higher frequency part that can be added by using also GPS observations.

Here we apply the method to combine the data covering a much longer interval (almost 8 years), using a slightly different approach, to demonstrate the capability of the method and to confirm the validity of the new model IAU2000A.

2 The method of combined smoothing

The method has been described in detail in the papers cited above, so only its main ideas are outlined briefly. The solution is based on two independent series of measurements: of the same time function whose analytical expression is unknown. We are looking for a smooth curve that fits both observed series well, by minimizing a weighted sum of three parameters S, F and $\overline{F}$, expressing the smoothness of the curve and its fidelity to both series, respectively:

 \begin{displaymath} Q=S+\varepsilon F + \overline{\varepsilon}\overline{F}=\min ... ...ow~ \frac{\partial Q}{\partial y_{i}}=0, \quad i=1,2,\ldots N. \end{displaymath} (1)

The "coefficients of smoothing'' $\varepsilon$, $\overline{\varepsilon}\geq 0$ acts as weighting factors, expressing the relative importance of the three parameters: the larger these coefficients, the better the fit to observations but the rougher the curve. The choice of the numerical values of coefficients of smoothing, based on numerous experiments with simulated data (Vondrák & Cepek 2001; Vondrák et al. 2002b), led to the following conclusion.

Provided the minimum period $P_{\min}$ of the signal is known and the resolution of observations is 7 days for function values, 1 day for time derivatives, the optimal choice is

 \begin{displaymath} \varepsilon=\left( \frac{12.6}{P_{\min}}\right)^6,\ \overline{\varepsilon}= \left( \frac{16.9}{P_{\min}}\right)^4. \end{displaymath} (2)

This choice assures that the smoothing is sufficiently weak not to suppress the signal contained in both series of the input data, and at the same time sufficiently strong to suppress the high frequency noise of the observations.

3 The input data used

The method of combined smoothing is now applied to the following two series of data, covering the interval 1994.3-2002.0:

Both series, that are referred to standard IAU 1976 precession and 1980 nutation, are described in detail below.

3.1 VLBI data

The astrometric/geodetic VLBI observations are now coordinated within the International VLBI Service (IVS). It provides, so far only since 1999.0, the official combined solution of EOP at weekly intervals. Before that date, there exist competing solutions prepared independently by several analysis centers. In this study we use the newest solution, IVS02001, that is linked to the ITRF2000 reference frame (Steinforth & Nothnagel 2002; IVS 2002).

The IERS, on the other hand, provides a combination of EOP based on all available observations, i.e. not only by VLBI but also by other space techniques. Its standard combined solution, C04, is given at daily intervals and its celestial pole offset part is based solely on VLBI solutions as provided by different analysis centers.

Since we found no significant difference between the IERS C04 and IVS combined solutions, we simply took the interval 1994.3-1999.0 for the former (for each 7th day only) and 1999.0-2002.0 for the latter, and merged them into a single series.

3.2 GPS data

The GPS observations are coordinated within the International GPS Service (IGS) that, however, does not provide celestial pole offset rates on a regular basis. The only analysis center that provides them is the Center for Orbit Determination in Europe (CODE).

Since March 1994 nutation rates have been computed at CODE using GPS data collected by the global IGS network. We may parameterize a nutation offset in longitude and obliquity w.r.t. the IAU 1980 model by means of a simple linear function over a three day interval

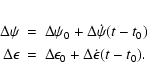
\begin{eqnarray*}\Delta\psi&=&\Delta\psi_0 + \Delta\dot\psi(t-t_0)\\ \Delta\epsilon&=&\Delta\epsilon_0 + \Delta\dot\epsilon(t-t_0). \end{eqnarray*}


Because of the correlations between the orbital elements and the nutation offsets, the initial quantities at each interval $\Delta\psi_0$, $\Delta\epsilon_0$ have to be constrained to the reference model and only their rates are obtained from the solution. As long as the perturbing accelerations acting on the GPS satellites can be modelled accurately enough over a given time interval (e.g., 3 days), the rates can be estimated.

These values were demonstrated by Weber (1996), Rothacher et al. (1999) or Weber (2001) to deliver unique contributions to the nutation spectrum in the high frequency range and to provide an independent check of present-day nutation models. Here we use the GPS-based celestial pole offsets covering the interval 1994.3-2002.0, with a gap of about 3 months in 2000. This gap is due to a change of the computer operating system which caused a loss of the relevant daily normal equation systems. To recover the data, daily parameter estimation batches (least squares adjustment) based on the already available observations at the single difference level have to be performed in the very near future.

4 The combined solution


  \begin{figure} \par\includegraphics[width=12cm,clip]{MS2950F1.eps} \end{figure} Figure 1: Combined smoothing ( $\varepsilon=34~\rm{day}^{-6}$, $\overline{\varepsilon}=34~\rm{day}^{-4}$) of celestial pole offsets in longitude $\Delta\psi / \Delta\dot{\psi}$ from VLBI/GPS. Full lines depict the combination, gray triangles the observations and gray crosses the residuals (enlarged scale on the right, upper plot only).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{MS2950F2.eps} \end{figure} Figure 2: Combined smoothing ( $\varepsilon=34~\rm{day}^{-6}$, $\overline{\varepsilon}=34~\rm{day}^{-4}$) of celestial pole offsets in obliquity $\Delta\epsilon / \Delta\dot\epsilon$ from VLBI/GPS. Full lines depict the combination, gray triangles the observations and gray crosses the residuals (enlarged scale on the right, upper plot only).
Open with DEXTER

We revealed, in our previous study made over a shorter time span (Vondrák et al. 2002b), large systematic errors with a dominant period around 60 days and an amplitude of about 0.1 mas/day in GPS-based rates of celestial pole offsets. Although the method of combined smoothing is able to suppress the influence of these errors substantially, we found that a small part (about ten per cent) still "leaks'' into the final product.

Our first "remedy'' for this problem (Vondrák et al. 2002a; Vondrák & Ron 2002) was to filter out the long-period part (i.e., all periodic variations longer than 30 days) from the GPS-based celestial pole offset rates, before the combination was made. However, we found later that by following this approach we got rid not only of the systematic errors but also of a part of the signal in this frequency range, i.e., there are distinct systematic deviations with semiannual and annual periods that are related to radiation pressure mismodelling in GPS orbits, but containing also signal pertaining to nutation terms.

Therefore, in this study, the GPS-based values have been "calibrated'' to fit, in a long-periodic sense (for periods 30 days and longer) to VLBI celestial pole offsets. The aim of the calibration is to remove the long-periodic part of GPS-based celestial pole offset rates that disagrees with VLBI observations and, at the same time, to retain the short-periodic part that is better monitored by GPS. To this end, we used a simple method similar to the one used by the IGS to derive Universal time from GPS-based length-of-day changes (Mireault et al. 1999; Kouba et al. 2000). Namely we integrated, in each 14-day interval, the celestial pole offset rates by GPS and compared the result with the difference of celestial pole offsets by VLBI at the beginning and end of the interval. The difference, divided by 14, was then removed from each GPS value within the interval. The method of combined smoothing was then applied to the corrected series.

To compute the combination, we used the coefficients of smoothing $\varepsilon=34~\rm{day}^{-6}$, $\overline{\varepsilon}=34~\rm{day}^{-4}$, calculated from Eq. (2) for $P_{\min}=7~\rm {days}$. This choice assures that all periodic variations with periods of 7 days and longer are passed by the filter completely while periods shorter than 2 days are totally suppressed. The results are shown in Figs. 1 and 2, for each component separately, upper plots depicting the celestial pole offsets, lower plots their rates. In both figures, the full lines show the combinations, gray triangles the individual observations and gray crosses (upper plots only) the residuals on an enlarged scale, in order to show the details. The a posteriori uncertainties, computed from the residuals, are compared with the a priori values, provided by the IVS and CODE, in the table below.

Uncertainties in $\Delta\psi$ $\Delta\dot\psi$ $\Delta\epsilon$ $\Delta\dot\epsilon$
  [mas] [mas/day] [mas] [mas/day]
a priori 0.087 0.079 0.033 0.033
a posteriori 0.093 0.249 0.024 0.086

It is clear that the a priori and a posteriori uncertainties for the VLBI ( $\Delta\psi$, $\Delta\epsilon$) are almost equal, but the values for GPS ( $\Delta\dot\psi$, $\Delta\dot\epsilon$) are much different - the a posteriori values are about three times larger than the a priori values. This shows that the uncertainties of GPS results estimated at CODE are highly underestimated (they take into consideration only a random part of the errors, not the systematic effects caused by orbital mismodelling). Therefore the a priori values of uncertainties reflect rather precision than accuracy.

In this respect, it is interesting to have a look at the spectrum of the residuals. Therefore, we made the spectral analysis of the residuals of both time series, using the Fast Fourier Transform (FFT) with the Parzen window (Press et al. 1992) in a complex form, applied to complex quantities \( R_{\Delta\psi}\sin\epsilon_\circ+{\rm i}R_{\Delta\epsilon} \)and \( R_{\Delta\dot\psi}\sin\epsilon_\circ+{\rm i} R_{\Delta\dot\epsilon}\)(where R stands for the residual) for VLBI and GPS, respectively. The result is shown in Fig. 3.

It is evident that while the spectrum for VLBI is very low and flat, with no dominant peaks, the spectrum for GPS is much different. It is relatively flat for high frequencies, say for periods shorter than 10 days, but rather peaky for frequencies ranging from 8 to 25 cpy (i.e., periods between 14 and 45 days). This part of the spectrum seems to come from an orbital modelling artefact, because of the high correlations between the orbital elements and celestial pole offsets (these are estimated simultaneously in GPS solutions). Systematic effects in this frequency range are however reflected in residuals only, not in the combined solution. Longer periods are not present, thanks to the calibration to VLBI described above that removed this part of the spectrum prior to combination.

5 Comparison of the combined solution with IAU2000A model of precession-nutation

The combined solution is now compared with the new model IAU2000A of precession-nutation. In this model, we considered not only the new periodic nutation terms but also the corrections to the IAU 1976 precession $\Delta\psi_{\rm A}$ and the secular change in the obliquity $\Delta\omega_{\rm A}$, and the biases $\xi_0$, $\eta_0$ in the direction of the Celestial Intermediate Pole (CIP) at J2000.0 from the direction of the pole of the Geocentric Celestial Reference System (GCRS); for details see Herring et al. (2002) or McCarthy & Capitaine (2002). The following formulae were used to calculate the differences:

 
$\displaystyle \delta\psi=\Delta\psi_{\rm C}-\Delta\psi_{\rm IAU}- (\Delta\psi_A+\xi_0/\sin\epsilon)$      
$\displaystyle \delta\epsilon=\Delta\epsilon_{\rm C}-\Delta\epsilon_{\rm IAU} -(\Delta\omega_A+\eta_0),$     (3)

in which $\Delta\psi_{\rm C}$, $\Delta\epsilon_{\rm C}$ denote the combined results, $\Delta\psi_{\rm IAU}$, $\Delta\epsilon_{\rm IAU}$ are the differences between the new and old nutation series, calculated from the tables worked out for this purpose by Ron (2002), and

\begin{eqnarray*}\Delta\psi_{\rm A}&=&-2.9965(t-2000.0)~{\rm mas},~\xi_0=-16.617... ..._{\rm A}&=&-0.2524(t-2000.0)~{\rm mas},~\eta_0=-6.819~{\rm mas}. \end{eqnarray*}


The differences $\delta\psi$, $\delta\epsilon$ are graphically displayed in Fig. 4; there is no obvious bias or trend. Nevertheless, they were further analyzed in order to find the statistical characteristics of the differences between our combination and the new IAU model. The biases and both biased and unbiased uncertainties found are given (in mas) in the table below:

  $\delta\psi\sin\epsilon$ $\delta\epsilon$
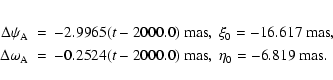
bias 0.019 -0.013
$\sigma_{\rm biased}$ 0.272 0.276
$\sigma_{\rm unbiased}$ 0.271 0.276


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2950F3.eps} \end{figure} Figure 3: Spectral analysis of the residuals - upper plot for VLBI, lower plot for GPS.
Open with DEXTER

The biases that we find here are very small and statistically insignificant, which is also reflected in the fact that biased and unbiased sigmas are practically equal. This confirms the values $\xi_0$, $\eta_0$ proposed by McCarthy & Capitaine (2002).

The FFT spectrum of the differences $\delta\psi\sin\epsilon+{i}\delta\epsilon$ is depicted in Fig. 5. A dominant peak is found for the period of about 455 days. This peak is rather broad, due to the relative shortness of the interval studied (containing only 6 periods of this term); the uncertainty of the estimated period can easily reach a few tens of days, due to the frequency step of the spectrum of about 0.09 cpy. This period is close to the theoretically expected period of FCN (430 days), so our study allows us to identify this peak with the FCN. A smaller peak exists at the period around 58 days, most probably caused by a residual systematic error of GPS orbit mismodelling (e.g., due to lunar forces with bi-monthly period). There are also some more peaks (with amplitudes lower than observational noise) that can partly be identified with existing nutation terms. The evident decrease of the amplitudes in the short-periodic part is caused by the weak smoothing applied in the combination.

6 Discussion

The method of combined smoothing proves to be a good tool to combine VLBI and GPS observations of celestial pole offsets. It is demonstrated that the GPS-based celestial pole offsets suffer from long-periodic systematic errors with a dominant period around 58 days that is however removed almost completely in the process of combining these parameters with VLBI data.

It seems that using the GPS information in combination with VLBI yields a better estimation of celestial pole offsets than using VLBI alone; GPS thus provides an important high-frequency contribution that would be missing if only VLBI observations are used. The improvement of the fit is achieved mainly in the high-frequency domain, because the parameters of the IAU2000 model are frequency independent, in the sense that the frequency dependence is explicitly taken into account in the formula whose parameters are estimated from VLBI observations. VLBI is very precise at frequencies outside the short period band, and in principle could provide a good estimation of the geophysical parameters; the main constraints of the new model come from annual, semi-annual and 18.6-year terms. Additionally, the nutation terms around a fortnightly period derived from our new combination can be used in the future to further improve the model.

The comparison of the combined solution provides a test of the new IAU precession-nutation model confirming its validity, at the level of present observational accuracy. The dominant peak found in the residuals can be identified with FCN, at the level of uncertainty of our estimation.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2950F4.eps} \end{figure} Figure 4: Differences between the combined solution and model IAU2000A.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2950F5.eps} \end{figure} Figure 5: Amplitude spectrum of the differences combined solutionminus IAU2000A precession-nutation model.
Open with DEXTER

Acknowledgements
The authors express their gratitude to the Ministry of Education of the Czech Republic for the grant No. LN00A005, the Product Center for EOP of the IERS for providing the series C04, IVS for providing the combined EOP solution IVS2001.eops and Center for Orbit Determination in Europe (CODE) for providing the solution of celestial pole offset rates. The help of the reviewer, Véronique Dehant, was indispensable for improving the text.

References

 
Copyright ESO 2003