We study a recently observed gravitational microlensing peak in the V-band light curve of Q2237+0305A using a relatively simple physical model, but one that is highly consistent with the data (the best-fit reduced
A&A 397, 517-525 (2003)
DOI: 10.1051/0004-6361:20021535
L. J. Goicoechea1 - D. Alcalde2 - E. Mediavilla2 - J. A. Muñoz2
1 - Departamento de Física Moderna, Universidad de Cantabria,
Avda. de Los Castros s/n, 39005 Santander, Spain
2 -
Instituto de Astrofísica de Canarias,
C/ Vía Láctea s/n, 38200 La Laguna, Spain
Received 17 July 2002 / Accepted 7 October 2002
Abstract
We study a recently observed gravitational microlensing peak in the V-band
light curve of Q2237+0305A using a relatively simple physical model, but one
that is highly consistent with the data (the best-fit reduced ![]() is
very close to 1). The source quasar is assumed to be a Newtonian
geometrically-thin and optically-thick accretion disk. The disk has an
arbitrary orientation, and both blackbody and greybody emission spectra are
considered. When the electron-photon scattering plays a role, the greybody
spectrum will be a simplified version of the exact one. In our model, the
microlensing variability results from the source crossing a caustic straight
line. The main goal of our work is to estimate the black hole mass and the mass
accretion rate in QSO 2237+0305 as well as to discuss the power and the weakness
of the technique, some possible improvements, and future prospects from
multifrequency monitoring of new microlensing peaks. We also put into
perspective the new methodology and the results on the central engine in QSO 2237+0305. From the fitted microlensing parameters and reasonable
dynamical/cosmological constraints, it is concluded that QSO 2237+0305 harbours
a central massive black hole: 107
is
very close to 1). The source quasar is assumed to be a Newtonian
geometrically-thin and optically-thick accretion disk. The disk has an
arbitrary orientation, and both blackbody and greybody emission spectra are
considered. When the electron-photon scattering plays a role, the greybody
spectrum will be a simplified version of the exact one. In our model, the
microlensing variability results from the source crossing a caustic straight
line. The main goal of our work is to estimate the black hole mass and the mass
accretion rate in QSO 2237+0305 as well as to discuss the power and the weakness
of the technique, some possible improvements, and future prospects from
multifrequency monitoring of new microlensing peaks. We also put into
perspective the new methodology and the results on the central engine in QSO 2237+0305. From the fitted microlensing parameters and reasonable
dynamical/cosmological constraints, it is concluded that QSO 2237+0305 harbours
a central massive black hole: 107 ![]() < M < 6
< M < 6 ![]() 108
108 ![]() .
While the information about the central dark mass is very interesting, the mass
accretion rate is not so well constrained. The typical values of the disk
luminosity/Eddington luminosity ratio are in the
.
While the information about the central dark mass is very interesting, the mass
accretion rate is not so well constrained. The typical values of the disk
luminosity/Eddington luminosity ratio are in the
![]() range,
where
range,
where
![]() 1 is the emissivity relative to a blackbody and the
highest
1 is the emissivity relative to a blackbody and the
highest
![]() ratio corresponds to the largest deflector motion.
Therefore, in order to verify
ratio corresponds to the largest deflector motion.
Therefore, in order to verify
![]() 1, a relatively small projected
peculiar motion of the lens galaxy and a greybody emission seem to be favored.
1, a relatively small projected
peculiar motion of the lens galaxy and a greybody emission seem to be favored.
Key words: gravitational lensing - galaxies: nuclei - quasars: general - quasars: individual: Q2237+0305
The optical continuum from a QSO could originate from a geometrically-thin
and optically-thick standard accretion disk. This standard scenario is able
to explain most of the non-variable background component, whereas the
fluctuations on different time scales may be caused by different mechanisms
(accretion disk instabilities, supernova explosions in a circumnuclear stellar
region, and so on). The Newtonian model of a standard accretion disk around a
black hole was introduced by Shakura & Sunyaev (1973). In this model, the
released gravitational energy is emitted as a multitemperature blackbody
radiation, where
![]() is the temperature at radius r. Thus, in the
absence of extinction, the emitted and observed intensities obey Planck laws
is the temperature at radius r. Thus, in the
absence of extinction, the emitted and observed intensities obey Planck laws
![]() and
and
![]() ,
respectively, where the emitted temperature and the observed
one are related through the cosmological redshift of the source
,
respectively, where the emitted temperature and the observed
one are related through the cosmological redshift of the source ![]() :
:
![]() .
As the emitted temperature profile depends on the black hole
mass and the mass accretion rate, the actually observed intensity profile
.
As the emitted temperature profile depends on the black hole
mass and the mass accretion rate, the actually observed intensity profile
![]() is determined from the two physical
parameters of the source. In a general situation we must take into account an
extinction factor
is determined from the two physical
parameters of the source. In a general situation we must take into account an
extinction factor
![]() due to dust in the host galaxy of the
quasar and any galaxy in the line of sight including a possible lens
galaxy and the Milky Way. A relativistic version of the Shakura & Sunyaev
model was presented by Novikov & Thorne (1973) and Page & Thorne (1974). The
relativistic model should be a useful tool to describe the physics of the
innermost layers of the disk. However, as we are interested in the emissivity
of a wide optical source from an inner edge of several Schwarzschild radii up
to an outer edge of 102-103 Schwarzschild radii, to a first
approximation, we can ignore the relativistic effects and take the Newtonian
picture.
due to dust in the host galaxy of the
quasar and any galaxy in the line of sight including a possible lens
galaxy and the Milky Way. A relativistic version of the Shakura & Sunyaev
model was presented by Novikov & Thorne (1973) and Page & Thorne (1974). The
relativistic model should be a useful tool to describe the physics of the
innermost layers of the disk. However, as we are interested in the emissivity
of a wide optical source from an inner edge of several Schwarzschild radii up
to an outer edge of 102-103 Schwarzschild radii, to a first
approximation, we can ignore the relativistic effects and take the Newtonian
picture.
When a lensed quasar crosses a microcaustic, an important fluctuation in the flux of one of its images is seen, i.e., a gravitational microlensing high-magnification event (HME) appears. The microlensing light curve of the image involved is given by convolving the observed intensity distribution with the corresponding magnification pattern. Therefore, the behaviour of the HME depends on the physical properties of the source quasar, and this fact opens discussion on the structure of the source from the analysis of the prominent microlensing event (e.g., Rauch & Blandford 1991; Jaroszynski et al. 1992). In principle, if we assume a standard accretion disk as the source of the optical continuum, a measurement of the black hole mass and the mass accretion rate may be possible and, recently, several papers have indicated that the study of an individual HME may be used to infer these parameters (Yonehara et al. 1998; Agol & Krolik 1999; Mineshige & Yonehara 1999; Yonehara et al. 1999; Shalyapin 2001; Yonehara 2001).
Very recently, the GLITP (Gravitational Lenses International Time Project)
collaboration has monitored the four images of QSO 2237+0305 in the V and
R bands. In each optical band, the GLITP light curve for the brightest image,
Q2237+0305A, traced the peak of one HME with unprecedented quality (Alcalde
et al. 2002). The global flat shape for the light curve of the faintest image,
Q2237+0305D, suggested that the intrinsic signal is globally stationary, and
this result supported the contention that the global variability in Q2237+0305A
is exclusively caused by microlensing. The peak of the HME was fitted to the
microlensing curves resulting from face-on circularly-symmetric sources
crossing a single straight fold caustic, and it was determined that the only
source models totally consistent with the GLITP data are the Newtonian standard
accretion disk and its simplified versions (Shalyapin et al. 2002). The uniform
and Gaussian disks led to an excessively high value of the reduced chi-square,
but the simplified variants of the Newtonian standard accretion disk gave
excellent results: the best fits are in very good agreement with the
observations and the upper limits on the source size are highly reasonable. To
avoid a possible anomalous ratio of fitted background fluxes
F0R/F0V,
one needs to consider additional R light, which is emitted from an extended
region (e.g., Jaroszynski et al. 1992). This possible R-band extended source is
however irrelevant in the estimation of the compact source size as well as in
the measurements of the central mass and the accretion rate from the technique
presented in this paper. Unfortunately, from the framework used by
Shalyapin et al. (2002), we cannot measure the physical parameters of the
engine. One can only determine a relationship between the black hole mass
(M), the mass accretion rate (
![]() ), and the quasar velocity perpendicular
to the caustic line (
), and the quasar velocity perpendicular
to the caustic line (![]() ). Even from some reasonable velocity range,
there is no way to separately infer M and
). Even from some reasonable velocity range,
there is no way to separately infer M and
![]() .
.
In this paper (Sect. 2), we introduce a novel expression of the microlensing
light curve when a Newtonian standard source crosses a single straight fold
caustic. This novel approach permits one to break the degeneracy in the
estimation of M and
![]() ,
and so to measure these parameters for a source
with an
arbitary orientation. In Sect. 3, from the V-band microlensing peak found
by the GLITP collaboration, we obtain estimates of the black hole mass and the
mass accretion rate in QSO 2237+0305. In Sect. 4 we present the main conclusions
and put into perspective the technique and the new results on the central engine
in QSO 2237+0305.
,
and so to measure these parameters for a source
with an
arbitary orientation. In Sect. 3, from the V-band microlensing peak found
by the GLITP collaboration, we obtain estimates of the black hole mass and the
mass accretion rate in QSO 2237+0305. In Sect. 4 we present the main conclusions
and put into perspective the technique and the new results on the central engine
in QSO 2237+0305.
Yonehara et al. (1998) and Shalyapin et al. (2002) previously studied the
microlensing light curve associated with a Newtonian standard source that
crosses a single straight fold caustic. Yonehara et al. (1998) presented the
expected light curve when a face-on source (
![]() ,
,
![]() yr-1) is strongly magnified by a
given caustic line, while Shalyapin et al. (2002) discussed the time evolution
of the monochromatic flux for a face-on source (the inner and outer edges were
assumed to be
yr-1) is strongly magnified by a
given caustic line, while Shalyapin et al. (2002) discussed the time evolution
of the monochromatic flux for a face-on source (the inner and outer edges were
assumed to be
![]() and
and
![]() ,
respectively) near to a
generic caustic line. Using the theoretical light curve reported by Shalyapin
et al. and an observed HME, one is able to obtain information on the size of
the involved source quasar, provided that some interval of the quasar velocity
,
respectively) near to a
generic caustic line. Using the theoretical light curve reported by Shalyapin
et al. and an observed HME, one is able to obtain information on the size of
the involved source quasar, provided that some interval of the quasar velocity
![]() might be inferred from observational data. However, their approach
does not permit a measurement of the two main parameters of the source: the
central mass and the mass accretion rate.
might be inferred from observational data. However, their approach
does not permit a measurement of the two main parameters of the source: the
central mass and the mass accretion rate.
Here we show the behaviour of an HME caused by a generic Newtonian
standard accretion disk (with finite inner and outer edges, and an arbitrary
orientation) crossing a generic caustic straight line, and more importantly, a
framework in which it is possible to measure the physical properties of the
black hole-accretion disk complex. We begin with a basic ingredient of the
monochromatic radiation flux: the observed intensity profile. The observed
intensity from a part of the disk at (r,![]() )
is given by
)
is given by
![\begin{displaymath}%
I_{\nu}(r) = \epsilon_{\nu} B_{\nu}[T(r)] = \frac{2h\nu^3}{c^2}
\frac{\epsilon_{\nu}}{\exp [h\nu/kT(r)] - 1},
\end{displaymath}](/articles/aa/full/2003/02/aa2922/img27.gif) |
(1) |
![\begin{displaymath}%
T(r) = \left[\frac{3}{8\pi} \frac{GM}{\sigma r^3} \left(\fr...
...ac{r_{{\rm in}}}{r}}\right)\right]^{1/4} (1 + z_{\rm s})^{-1}.
\end{displaymath}](/articles/aa/full/2003/02/aa2922/img28.gif) |
(2) |
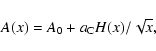 |
(3) |
| (4) |
![$\displaystyle K_{\nu} \int_{r_{{\rm in}}}^{r_{{\rm out}}}
\frac{r {\rm d}r}{\ex...
...\frac{H[x(r,\psi;x_{\rm c})]}{\sqrt{x(r,\psi;x_{\rm c})}}\right\} {\rm d}\psi ,$](/articles/aa/full/2003/02/aa2922/img45.gif) |
(5) |
In order to derive the microlensing light curve from Eq. (5), we firstly
calculated the integral over ![]() .
The angular integration led to
.
The angular integration led to
![\begin{displaymath}%
\int_{0}^{2\pi} \left[1 + \frac{a_{\rm C}}{A_0} \frac{H(x)}...
...i \left[ 1 + \frac{a_{\rm C}}{\pi A_0 \sqrt{rf}} G(q) \right],
\end{displaymath}](/articles/aa/full/2003/02/aa2922/img48.gif) |
(6) |
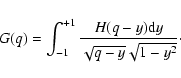 |
(7) |
![$\displaystyle = 2\pi K_{\nu} \int_{r_{{\rm in}}}^{r_{{\rm out}}}
\left[1 \!+\! ...
...\sqrt{rf}} G(x_{\rm c}/rf)\right]
\frac{r {\rm d}r}{\exp [h\nu/kT(r)] - 1}\cdot$](/articles/aa/full/2003/02/aa2922/img52.gif) |
(8) |
![$\displaystyle A_{\nu} \int_{1}^{\xi_{{\rm max}}}
\left\{1 + \frac{B}{\sqrt{\xi}} G\left[C(t - t_0)/\xi\right]\right\}$](/articles/aa/full/2003/02/aa2922/img56.gif) |
|
![$\displaystyle \times\frac{\xi {\rm d}\xi}{\exp \left[0.054 \left(\frac{\nu}{10^...
...
\rm {Hz}}\right) D \xi^{3/4} \left(1 - 1/\sqrt{\xi}\right)^{-1/4}\right] - 1},$](/articles/aa/full/2003/02/aa2922/img57.gif) |
(9) |
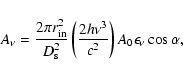 |
(10) |
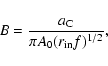 |
(11) |
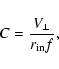 |
(12) |
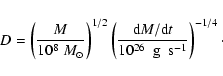 |
(13) |
In practice one must compare the theoretical law (9) with the brightness record
of a QSO image during a HME. In the comparison, the frequency ![]() will be the
central frequency of the optical band in which the observations were made, and
as mentioned above,
will be the
central frequency of the optical band in which the observations were made, and
as mentioned above,
![]() = 100 (
= 100 (
![]() = 300 Schwarzschild
radii) or
= 300 Schwarzschild
radii) or
![]() = 300 (
= 300 (
![]() 1000 Schwarzschild radii) are
plausible choices of the edge ratio. Therefore, at a given
1000 Schwarzschild radii) are
plausible choices of the edge ratio. Therefore, at a given
![]() (e.g.,
100), the goal is to estimate the values of the parameters
(e.g.,
100), the goal is to estimate the values of the parameters ![]() ,
,
![]() ,
C, D, and t0 by fitting the observed HME. Once the parameters C and Dhave been measured, from Eqs. (12)-(13) we make the relations:
,
C, D, and t0 by fitting the observed HME. Once the parameters C and Dhave been measured, from Eqs. (12)-(13) we make the relations:
![\begin{displaymath}%
\mu_{\rm BH} = 10^{-4} \hspace{0.07in} V_{\perp}\left({\rm ...
.../ \left[fC \hspace{0.07in} \left({\rm day}^{-1}\right)\right],
\end{displaymath}](/articles/aa/full/2003/02/aa2922/img69.gif) |
(14) |
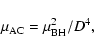 |
(15) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2922f1.eps} \end{figure}](/articles/aa/full/2003/02/aa2922/Timg74.gif) |
Figure 1:
Probability distribution of the factor related to the
orientation of the source. The shading region represents the 1 |
| Open with DEXTER | |
The GLITP collaboration has recently reported information relating to the peak of a microlensing high-magnification event detected in both V-band and R-band brightness records of Q2237+0305A, which was observed with an excellent sampling rate of about three times the OGLE one (Alcalde et al. 2002). The event was discovered by the OGLE team (Wozniak et al. 2000), who followed the evolution of the whole V-band HME. In a first paper, from the GLITP V-band and R-band peaks, Shalyapin et al. (2002) have analyzed the nature and size of the V-band and R-band sources in QSO 2237+0305. To do this, they used a family of source models. All the models led to theoretical microlensing curves with the same number of free parameters. This approach (comparison between models causing four-parametric theoretical curves) is very useful for discussion of the feasibility of different scenarios. The authors concluded that only two rough versions of the Newtonian standard scenario are clearly consistent with the observed optical peaks. Thus we know that a Newtonian standard accretion disk is in agreement with the GLITP monitoring of Q2237+0305A, and in principle, it is possible to measure the central mass and the flow of matter (see Sect. 2).
In our microlensing experiment, the functional relation presented in Eq. (9) is
investigated by comparing it with the observed value of
![]() at a given
frequency and for various epochs
t1,t2,...,tN. A value of
at a given
frequency and for various epochs
t1,t2,...,tN. A value of
![]() is
also assumed. The goal is to find the parameters
is
also assumed. The goal is to find the parameters ![]() ,
,
![]() ,
C, D,
and t0 of the theoretical microlensing curve which best describe the
observational data. To make the fit, two different chi-square minimizations
have been carried out. The most elementary procedure is to form a grid of
points in the free parameters and evaluate the
,
C, D,
and t0 of the theoretical microlensing curve which best describe the
observational data. To make the fit, two different chi-square minimizations
have been carried out. The most elementary procedure is to form a grid of
points in the free parameters and evaluate the ![]() function at each of
these points. The point with the smallest value is then the minimum. Therefore,
we have studied a reduced grid using some MATHEMATICA packages. The procedure is
called RGMath and it is based on the ideas discussed in Sect. 2.3 of
Shalyapin et al. (2002). Basically, as we like to fit a theoretical curve that
is linear in two parameters (
function at each of
these points. The point with the smallest value is then the minimum. Therefore,
we have studied a reduced grid using some MATHEMATICA packages. The procedure is
called RGMath and it is based on the ideas discussed in Sect. 2.3 of
Shalyapin et al. (2002). Basically, as we like to fit a theoretical curve that
is linear in two parameters (![]() and
and ![]() ), and non-linear
in C, D, and t0, the equations of minimization
), and non-linear
in C, D, and t0, the equations of minimization
![]() lead to
analytic relations:
lead to
analytic relations:
![]() ,
,
![]() .
In this scheme, the number of effective parameters is reduced to three, and one
can work with a 3D grid instead of a 5D one. As the procedure is quite time
consuming, we initially formed a 3D grid with moderate resolution, i.e., the
size of the grid step was reasonable, but relatively large. So, from RGMath
at moderate resolution, we inferred an initial best solution and some
uncertainties associated with it. Another procedure is called DSFor and it
is related to a version of the simplex method. We wrote a FORTRAN program to apply
a downhill simplex methodology (Nelder & Mead 1965) to our problem. The
simplexes will be the simplest geometrical figures in 5 dimensions having 6
vertices (points). The technique begins by choosing a point (vertice) in the 5D
parameter space. The program then generates an initial simplex, and after,
repeated calculations are made while varying the vertices of the initial
simplex in some way, until a local minimum is reached. The
.
In this scheme, the number of effective parameters is reduced to three, and one
can work with a 3D grid instead of a 5D one. As the procedure is quite time
consuming, we initially formed a 3D grid with moderate resolution, i.e., the
size of the grid step was reasonable, but relatively large. So, from RGMath
at moderate resolution, we inferred an initial best solution and some
uncertainties associated with it. Another procedure is called DSFor and it
is related to a version of the simplex method. We wrote a FORTRAN program to apply
a downhill simplex methodology (Nelder & Mead 1965) to our problem. The
simplexes will be the simplest geometrical figures in 5 dimensions having 6
vertices (points). The technique begins by choosing a point (vertice) in the 5D
parameter space. The program then generates an initial simplex, and after,
repeated calculations are made while varying the vertices of the initial
simplex in some way, until a local minimum is reached. The ![]() function
may have different local minima around different points tested by the method,
and consequently, to find the global minimum
function
may have different local minima around different points tested by the method,
and consequently, to find the global minimum
![]() we must make a 5D
grid, and apply the downhill simplex technique to all the points in the grid.
In the first stage with this alternative task (search for minima in the 5D
parameter space), the resolution was not very good. Once the initial best solution
we must make a 5D
grid, and apply the downhill simplex technique to all the points in the grid.
In the first stage with this alternative task (search for minima in the 5D
parameter space), the resolution was not very good. Once the initial best solution
![]() = (
= (![]() ,
,
![]() ,
C*, D*, t0*) is known (via
RGMath or DSFor), it is possible to refine it and estimate accurate
errors for the relevant parameters C and D. If the vector
,
C*, D*, t0*) is known (via
RGMath or DSFor), it is possible to refine it and estimate accurate
errors for the relevant parameters C and D. If the vector ![]() =
(
=
(![]() ,
,
![]() ,
C, D, t0) of parameter values is perturbed away from
,
C, D, t0) of parameter values is perturbed away from
![]() ,
then
,
then ![]() increases. So, we can draw high-resolution "parabolic''
laws
increases. So, we can draw high-resolution "parabolic''
laws
![]() and
and
![]() ,
where, for example,
,
where, for example,
![]() represents the minima of the
represents the minima of the ![]() function for values
of C around C*. The C range within which
function for values
of C around C*. The C range within which
![]() 1 defines the 1
1 defines the 1![]() confidence interval in the estimation of C and
the interval
confidence interval in the estimation of C and
the interval
![]() 1 is related to the
1
1 is related to the
1![]() confidence interval in the estimation of D. The
confidence interval in the estimation of D. The ![]() confidence
interval in the generic parameter p corresponds to the region bounded by
confidence
interval in the generic parameter p corresponds to the region bounded by
![]() = k2 (k = 1, 2,...).
= k2 (k = 1, 2,...).
| Procedure |
|
fC (day-1) | D | t0 (JD-2 450 000) | ||
| RGMath | 100 | 2.78 | 1.37 | 0.23+0.13-0.06 | 0.59+0.30-0.23 | 1481.4 |
| DSFor | 100 | 2.96 | 1.35 | 0.23+0.14-0.08 | 0.60+0.35-0.26 | 1481.9 |
The high-resolution fit to the GLITP V-band light curve for Q2237+0305A appears
in Table 1. The central frequency is ![]() = 5.52
= 5.52 ![]() 1014 Hz, and we
adopted
1014 Hz, and we
adopted
![]() = 100. We note that the uncertainties presented in Table 1
are 1
= 100. We note that the uncertainties presented in Table 1
are 1![]() intervals. Moreover, instead of direct measurements of the parameter C, 1
intervals. Moreover, instead of direct measurements of the parameter C, 1![]() confidence intervals for the relevant factor fC (see Eq. (14)) are
quoted in Table 1. During an advanced stage of the project, we also obtained rough
estimates of the errors in
confidence intervals for the relevant factor fC (see Eq. (14)) are
quoted in Table 1. During an advanced stage of the project, we also obtained rough
estimates of the errors in ![]() and
and ![]() .
From DSFor we inferred
.
From DSFor we inferred
![]()
![]() Jy and
Jy and
![]()
![]() Jy.
In Fig. 2 we show the details to obtain the best values of C and the standard
errors. The figure presents three
Jy.
In Fig. 2 we show the details to obtain the best values of C and the standard
errors. The figure presents three
![]() trends, which were derived
from RGMath at moderate resolution (dashed line), RGMath at high
resolution (solid line), and DSFor at high resolution (dotted line). The
1
trends, which were derived
from RGMath at moderate resolution (dashed line), RGMath at high
resolution (solid line), and DSFor at high resolution (dotted line). The
1![]() box corresponding to the RGMath (high resolution) procedure is
plotted with a thin line. Looking at both Table 1 and Fig. 2, two important
conclusions
appear: (1) the fit is stable against a change in the fitting method (RGMath
or DSFor), and (2) a change from moderate to high resolution does not strongly
perturb the parabolic law. Taking into account these last conclusions, we used the
RGMath task (moderate resolution) to test the influence of the
box corresponding to the RGMath (high resolution) procedure is
plotted with a thin line. Looking at both Table 1 and Fig. 2, two important
conclusions
appear: (1) the fit is stable against a change in the fitting method (RGMath
or DSFor), and (2) a change from moderate to high resolution does not strongly
perturb the parabolic law. Taking into account these last conclusions, we used the
RGMath task (moderate resolution) to test the influence of the
![]() value in the parameter estimation. We concluded that a change in
value in the parameter estimation. We concluded that a change in
![]() (from 100 to 300) does not modify the estimates of fC and D. In principle, a fit to
the GLITP R-band light curve for Q2237+0305A could be useful to improve the
parameter estimation. However, the GLITP R-band microlensing peak does not permit
one to infer the parameters C and D with errors similar to the previous ones
(from the V-band peak). The ratio between the 1
(from 100 to 300) does not modify the estimates of fC and D. In principle, a fit to
the GLITP R-band light curve for Q2237+0305A could be useful to improve the
parameter estimation. However, the GLITP R-band microlensing peak does not permit
one to infer the parameters C and D with errors similar to the previous ones
(from the V-band peak). The ratio between the 1![]() R-band interval and the
1
R-band interval and the
1![]() V-band interval is >2.4 for C and
V-band interval is >2.4 for C and ![]() 1.5 for D. Due to
these relatively large errors from the R-band brightness record, we only
considered the estimates in Table 1. More properly, we took
fC =
0.23+0.13-0.06 day-1 and
D = 0.59+0.30-0.23 (RGMath
solution) to determine the possible values of
1.5 for D. Due to
these relatively large errors from the R-band brightness record, we only
considered the estimates in Table 1. More properly, we took
fC =
0.23+0.13-0.06 day-1 and
D = 0.59+0.30-0.23 (RGMath
solution) to determine the possible values of
![]() and
and
![]() .
We
remark that the accretion-disk model is consistent with the V-band and R-band
light curves. The best-fit reduced
.
We
remark that the accretion-disk model is consistent with the V-band and R-band
light curves. The best-fit reduced ![]() is very close to one in both optical
filters, and we can see the good agreement between best-fits and observational
trends in Fig. 3. In the top panel, the observed V-band fluxes are compared with
the best-fit from RGMath at high resolution (solid line), while in the
bottom panel, the R-band record is compared with the best-fit from RGMath
at moderate resolution (dashed line). The fit in the R band led to best values
of C = 0.375 day-1 and D = 0.45, which are totally consistent with the
blue parameters given in Table 1. However, the R-band data are relatively
noisy in comparison to the V-band ones, and this fact does not permit a parameter
estimation in the red band with uncertainties similar to the blue
errors.
is very close to one in both optical
filters, and we can see the good agreement between best-fits and observational
trends in Fig. 3. In the top panel, the observed V-band fluxes are compared with
the best-fit from RGMath at high resolution (solid line), while in the
bottom panel, the R-band record is compared with the best-fit from RGMath
at moderate resolution (dashed line). The fit in the R band led to best values
of C = 0.375 day-1 and D = 0.45, which are totally consistent with the
blue parameters given in Table 1. However, the R-band data are relatively
noisy in comparison to the V-band ones, and this fact does not permit a parameter
estimation in the red band with uncertainties similar to the blue
errors.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2922f2.eps} \end{figure}](/articles/aa/full/2003/02/aa2922/Timg98.gif) |
Figure 2:
Behaviour of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{MS2922f3.eps} \end{figure}](/articles/aa/full/2003/02/aa2922/Timg99.gif) |
Figure 3: Observed fluxes and best-fits. In the top panel (V-band), it is showed the best-fit from RGMath at high resolution (solid line). In the bottom panel (R-band), it appears the best-fit from RGMath at moderate resolution (dashed line). |
| Open with DEXTER | |
Kayser et al. (1986) showed that the effective transverse velocity of the
source consists of three terms related to the transverse peculiar velocity of
the source quasar (
![]() ), the transverse peculiar velocity of the
deflector (
), the transverse peculiar velocity of the
deflector (
![]() ), and the transverse peculiar motion of the observer
(
), and the transverse peculiar motion of the observer
(
![]() ). The word "transverse'' denotes "perpendicular to the line of
sight'', and the effective transverse velocity is given by
). The word "transverse'' denotes "perpendicular to the line of
sight'', and the effective transverse velocity is given by
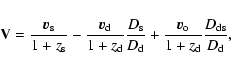 |
(16) |
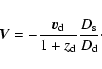 |
(17) |
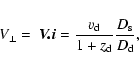 |
(18) |
Only one direct measurement of
![]() is currently available. The
measurement is an upper limit on V, and consequently on
is currently available. The
measurement is an upper limit on V, and consequently on ![]() ,
which was
inferred from the analysis of the light curves of the system (Wyithe et al. 1999). So we have decided to adopt a velocity range based on the relation
(18) and the relevant observational data. Firstly, one must find plausible values
of
,
which was
inferred from the analysis of the light curves of the system (Wyithe et al. 1999). So we have decided to adopt a velocity range based on the relation
(18) and the relevant observational data. Firstly, one must find plausible values
of ![]() ,
and with this aim, we analyzed a catalog of galaxy data that is included
in the electronic archives of the CDS (Centre de Données astronomiques de
Strasbourg). The catalog is a part of the Mark III full catalog of redshifts and
distances (Willick et al. 1997), and it contains redshifts
in the CMB frame and both forward and inverse Tully-Fisher (TF) distances of 1355 spiral galaxies (Mathewson et al. 1992).
As it is well-known, the
differences
,
and with this aim, we analyzed a catalog of galaxy data that is included
in the electronic archives of the CDS (Centre de Données astronomiques de
Strasbourg). The catalog is a part of the Mark III full catalog of redshifts and
distances (Willick et al. 1997), and it contains redshifts
in the CMB frame and both forward and inverse Tully-Fisher (TF) distances of 1355 spiral galaxies (Mathewson et al. 1992).
As it is well-known, the
differences
![]() are the projected peculiar motions of the spirals,
i.e.,
are the projected peculiar motions of the spirals,
i.e.,
![]() ,
where
,
where
![]() are the unit vectors pointing
towards the galaxies. In Fig. 4 we can see two very similar histograms showing
two distributions of
are the unit vectors pointing
towards the galaxies. In Fig. 4 we can see two very similar histograms showing
two distributions of
![]() .
The darker line represents
the results from the inverse TF distances (
.
The darker line represents
the results from the inverse TF distances (
![]() ), while the other line
traces the behaviour from the forward TF distances (
), while the other line
traces the behaviour from the forward TF distances (
![]() ). Inhomogeneous
Malmquist bias-corrected distances
). Inhomogeneous
Malmquist bias-corrected distances
![]() are quoted in the catalog, which
were computed using the density field obtained through the IRAS 1.2 Jy redshift
survey. From the distributions in Fig. 4, we concluded that the mean value is
are quoted in the catalog, which
were computed using the density field obtained through the IRAS 1.2 Jy redshift
survey. From the distributions in Fig. 4, we concluded that the mean value is
![]() = 663 km s-1. This average will be within the interval of allowed
values of
= 663 km s-1. This average will be within the interval of allowed
values of ![]() .
As a lower limit we took 100 km s-1, i.e.,
.
As a lower limit we took 100 km s-1, i.e.,
![]() 100 km s-1, in agreement with the observed distributions [P(
100 km s-1, in agreement with the observed distributions [P(
![]() 50 km s-1)
50 km s-1) ![]() 6%] and discarding a situation in which both
6%] and discarding a situation in which both
![]() and
and ![]() have a value
have a value ![]() 50 km s-1. On the other hand, the
distributions
50 km s-1. On the other hand, the
distributions
![]() were obtained with a sample including field spirals and
cluster spirals, and it is evident that amplitudes of the projected peculiar
velocities in excess of 1000 km s-1 cannot be rejected. However, the lens
galaxy is not placed inside a rich cluster or close to a group of clusters,
and thus, one may assume an upper limit of 1000 km s-1, i.e.,
were obtained with a sample including field spirals and
cluster spirals, and it is evident that amplitudes of the projected peculiar
velocities in excess of 1000 km s-1 cannot be rejected. However, the lens
galaxy is not placed inside a rich cluster or close to a group of clusters,
and thus, one may assume an upper limit of 1000 km s-1, i.e.,
![]() 1000 km s-1. To derive a reasonable range for
1000 km s-1. To derive a reasonable range for ![]() ,
the
second basic ingredient is the factor
,
the
second basic ingredient is the factor
![]() .
This factor depends on
the redshifts (
.
This factor depends on
the redshifts (![]() and
and ![]() )
and the matter/energy content of the universe
(cosmological parameters). In this paper we consider the two standard flat
cosmologies: (1)
)
and the matter/energy content of the universe
(cosmological parameters). In this paper we consider the two standard flat
cosmologies: (1) ![]() = 1,
= 1, ![]() = 0, and (2)
= 0, and (2) ![]() = 0.3,
= 0.3,
![]() = 0.7. As usual,
= 0.7. As usual, ![]() is the present density parameter and
is the present density parameter and
![]() is the present reduced cosmological constant. So, each plausible
value of
is the present reduced cosmological constant. So, each plausible
value of ![]() leads to two solutions for
leads to two solutions for ![]() .
Taking into account
the whole range 100
.
Taking into account
the whole range 100 ![]()
![]() (km s-1)
(km s-1) ![]() 1000, the characteristic
redshifts of the system, and the two standard cosmologies, it is found that
765
1000, the characteristic
redshifts of the system, and the two standard cosmologies, it is found that
765 ![]()
![]() (km s-1)
(km s-1) ![]() 10 548.
10 548.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{MS2922f4.eps} \end{figure}](/articles/aa/full/2003/02/aa2922/Timg138.gif) |
Figure 4: Probability distributions of the amplitudes of the projected peculiar motions of 1355 nearby spiral galaxies (see Mathewson et al. 1992). The darker line corresponds to the results from the inverse Tully-Fisher distances, and the other line represents the results from the forward Tully-Fisher distances, which were corrected for an inhomogeneous Malmquist bias. |
| Open with DEXTER | |
Our results (1![]() measurements of M and
measurements of M and
![]() for two
cosmologies and different values of
for two
cosmologies and different values of ![]() )
are presented in Table 2. We tested
four representative values of
)
are presented in Table 2. We tested
four representative values of ![]() (see Sect. 3.2). The black hole mass is
reasonably well constrained. For a universe with a zero cosmological
constant and a very small projected motion of the deflector,
the microlensing data suggest the existence of a central black hole having a
mass of
(see Sect. 3.2). The black hole mass is
reasonably well constrained. For a universe with a zero cosmological
constant and a very small projected motion of the deflector,
the microlensing data suggest the existence of a central black hole having a
mass of ![]() 3.3
3.3 ![]() 107
107 ![]() .
The most massive black hole is
inferred for a universe with a nonzero cosmological constant (
.
The most massive black hole is
inferred for a universe with a nonzero cosmological constant (![]() = 0.7)
and a very large projected velocity of the deflector. In that case,
= 0.7)
and a very large projected velocity of the deflector. In that case, ![]() 4.6
4.6 ![]() 108
108 ![]() .
Apart from these "individual'' estimates,
the main result is the global range for M. We concluded that the dark
mass in the heart of the quasar should be larger than 107
.
Apart from these "individual'' estimates,
the main result is the global range for M. We concluded that the dark
mass in the heart of the quasar should be larger than 107 ![]() and smaller than 6
and smaller than 6 ![]() 108
108 ![]() .
.
With regard to the mass accretion rate, the situation is quite intricate.
Firstly, we cannot obtain individual lower limits, since all the 1![]() estimates are consistent with
estimates are consistent with
![]() = 0. Therefore, only typical values
and upper limits are showed in Table 2. The fact that the 1
= 0. Therefore, only typical values
and upper limits are showed in Table 2. The fact that the 1![]() error
bars on the accretion rate turn out to be compatible with zero is related to the
(dis)abilities of the new technique. We fitted the parameters C and D (together
with
error
bars on the accretion rate turn out to be compatible with zero is related to the
(dis)abilities of the new technique. We fitted the parameters C and D (together
with ![]() ,
,
![]() ,
and t0), and used Eqs. (14)-(15) to estimate the
physical properties of the central engine: M and
,
and t0), and used Eqs. (14)-(15) to estimate the
physical properties of the central engine: M and
![]() .
Considering the
results in Table 1, fC is determined with a relative error of about 40 per cent,
while the relative error in D is of about 45 per cent. If we take a given value
of the cosmological parameters and vd, then the relative error in M will be
of about 40 per cent, i.e., similar to the relative error in fC (see Eq. (14)
and the results on M in Table 2). However, unfortunately, Eq. (15) indicates us
that
.
Considering the
results in Table 1, fC is determined with a relative error of about 40 per cent,
while the relative error in D is of about 45 per cent. If we take a given value
of the cosmological parameters and vd, then the relative error in M will be
of about 40 per cent, i.e., similar to the relative error in fC (see Eq. (14)
and the results on M in Table 2). However, unfortunately, Eq. (15) indicates us
that
![]() depends on both (fC)2 and D4. Due to this fact, the accuracy
in the determination of
depends on both (fC)2 and D4. Due to this fact, the accuracy
in the determination of
![]() is very poor, or in other words, the relative
error in
is very poor, or in other words, the relative
error in
![]() is greater than 100 per cent.
is greater than 100 per cent.
| Cosmology | M (108 |
|
|
| 100 | 0.33+0.09-0.19 | 1.5 (<3.9) | |
| 300 | 1.00+0.26-0.56 | 13.2 (<34.8) | |
| 663 | 2.21+0.58-1.25 | 64.3 (<170.0) | |
| 1000 | 3.33+0.87-1.88 | 146.2 (<386.7) | |
| 100 | 0.46+0.12-0.26 | 2.8 (<7.3) | |
| 300 | 1.38+0.36-0.78 | 25.0 (<66.1) | |
| 663 | 3.04+0.79-1.72 | 122.1 (<322.8) | |
| 1000 | 4.59+1.20-2.59 | 277.7 (<734.4) |
Secondly, a realistic scenario should incorporate the electron-scattering
opacity, which could play an important role at inner regions of the accretion disk
(Shakura & Sunyaev 1973). The local radiation energy flux is determined by the
gravitational energy release
![]() .
In the outer regions, where the free-free
processes give the main contribution to the opacity, a Planck spectrum is formed.
The radiation energy flux must be
.
In the outer regions, where the free-free
processes give the main contribution to the opacity, a Planck spectrum is formed.
The radiation energy flux must be
![]() ,
and from
,
and from
![]() we obtain the standard thermal law. In the inner regions of
the disk, the electron-photon scattering presumably plays a role in the opacity,
so these regions radiate less efficiently than a blackbody:
we obtain the standard thermal law. In the inner regions of
the disk, the electron-photon scattering presumably plays a role in the opacity,
so these regions radiate less efficiently than a blackbody:
![]() with
with
![]() 1. If one defines a constant factor
1. If one defines a constant factor
![]() 1 to be the emissivity relative to a blackbody, then the
corresponding radiation energy flux will be
1 to be the emissivity relative to a blackbody, then the
corresponding radiation energy flux will be
![]() .
At small radii the real disk could be hotter than the standard disk without
electron-photon scattering, i.e.,
.
At small radii the real disk could be hotter than the standard disk without
electron-photon scattering, i.e.,
![]() .
Therefore we can
consider two simple pictures: a global blackbody spectrum (
.
Therefore we can
consider two simple pictures: a global blackbody spectrum (
![]() = 1
along all the disk), i.e., the standard one, and a global greybody spectrum
(
= 1
along all the disk), i.e., the standard one, and a global greybody spectrum
(
![]() 1 along all
the disk). This last simplification was suggested by Rauch & Blandford (1991),
who introduced the greybody spectra in microlensing studies. When a generalized
model is considered (
1 along all
the disk). This last simplification was suggested by Rauch & Blandford (1991),
who introduced the greybody spectra in microlensing studies. When a generalized
model is considered (
![]() 1), we must re-interpret the results of
1), we must re-interpret the results of
![]() as measurements of
as measurements of
![]() .
In this way, the typical
values of
.
In this way, the typical
values of
![]() vary in the interval (1-300)
vary in the interval (1-300)
![]()
![]() yr-1.
For
yr-1.
For
![]() = 1, we derive a typical range of 1-300
= 1, we derive a typical range of 1-300 ![]() yr-1,
while for
yr-1,
while for
![]() = 0.1, the typical mass accretion rates are 0.1-30
= 0.1, the typical mass accretion rates are 0.1-30 ![]() yr-1.
yr-1.
We showed the time evolution of a microlensing HME caused by a generic
Newtonian geometrically-thin and optically-thick standard accretion disk
crossing a generic caustic straight line. Given a lensed QSO, in order to
estimate the mass of its central black hole and the accretion rate, we can
compare the theoretical law with a gravitational microlensing HME observed
in some image of the far source. This technique was applied to the gravitational
mirage QSO 2237+0305, whose brightest image experienced an important change in
flux during the 1999-2000 seasons (Wozniak et al. 2000). The peak of the
dramatic variation in Q2237+0305A (Alcalde et al. 2002) led to very interesting
information on the black hole in the core of the source and an interval of
typical values for the mass accretion rate. The main source of uncertainty
comes from our lack of knowledge about the peculiar motion of the lens galaxy
in the direction perpendicular to the caustic line (![]() ). To accurately
determine the typical flow of matter, it is also necessary to know the physical
processes involved in the emissivity of the disk. Although the standard
scenario does not incorporate the electron-photon scattering, in general, it
could strongly distort the standard Planck spectrum at the innermost layers of
the disk (e.g., Shakura & Sunyaev 1973; Malkan 1983).
). To accurately
determine the typical flow of matter, it is also necessary to know the physical
processes involved in the emissivity of the disk. Although the standard
scenario does not incorporate the electron-photon scattering, in general, it
could strongly distort the standard Planck spectrum at the innermost layers of
the disk (e.g., Shakura & Sunyaev 1973; Malkan 1983).
From 1![]() estimates of the relevant parameters in the theoretical
microlensing curve, we inferred 1
estimates of the relevant parameters in the theoretical
microlensing curve, we inferred 1![]() measurements of the black hole mass
and the accretion rate for a set of
measurements of the black hole mass
and the accretion rate for a set of ![]() values, which represents the whole
range of reasonable choices (see a detailed discussion in Sect. 3.2).
Taking into account all the individual estimates in Table 2, one obtains that
QSO 2237+0305 contains a massive black hole: 107
values, which represents the whole
range of reasonable choices (see a detailed discussion in Sect. 3.2).
Taking into account all the individual estimates in Table 2, one obtains that
QSO 2237+0305 contains a massive black hole: 107 ![]() < M < 6
< M < 6 ![]() 108
108 ![]() .
The information about the mass accretion rate is very much
poorer. The main result consists of a typical interval for
.
The information about the mass accretion rate is very much
poorer. The main result consists of a typical interval for
![]() .
This interval
is of (1-300)
.
This interval
is of (1-300)
![]()
![]() yr-1, where
yr-1, where
![]() = 1 if
the free-free processes are dominant (standard source) and
= 1 if
the free-free processes are dominant (standard source) and
![]() 1
when the scattering plays a role (e.g., Rauch & Blandford 1991). In
spite of the fact that the range of typical determinations of
1
when the scattering plays a role (e.g., Rauch & Blandford 1991). In
spite of the fact that the range of typical determinations of
![]() is not
excessively broad, all the individual 1
is not
excessively broad, all the individual 1![]() measurements are in agreement
with no accretion, but a flow of matter of almost
measurements are in agreement
with no accretion, but a flow of matter of almost
![]()
![]() yr-1 cannot be ruled out. On the other hand, one direct constraint on
vd was recently reported by Wyithe et al. (1999). This group
is involved in a project to
interpret the QSO 2237+0305 microlensing light-curves, and as a part of the
program, they derived an upper limit of
yr-1 cannot be ruled out. On the other hand, one direct constraint on
vd was recently reported by Wyithe et al. (1999). This group
is involved in a project to
interpret the QSO 2237+0305 microlensing light-curves, and as a part of the
program, they derived an upper limit of
![]() 500 km s-1, where
500 km s-1, where ![]() is the galactic transverse velocity (
is the galactic transverse velocity (![]() = 1,
= 1, ![]() = 0).
Therefore, considering that
= 0).
Therefore, considering that
![]() 500 km s-1 and
500 km s-1 and
![]() 100 km s-1, we find a central value of
100 km s-1, we find a central value of ![]() = 300 km s-1. For a flat
universe with a zero cosmological constant and a projected motion of
= 300 km s-1. For a flat
universe with a zero cosmological constant and a projected motion of ![]() =
300 km s-1, the typical source parameters are: M = 108
=
300 km s-1, the typical source parameters are: M = 108 ![]() and
and
![]()
![]()
![]() yr-1.
yr-1.
Several modeling aspects can be improved. For example, one must
include the effects of general relativity. One may also incorporate a new
theoretical law in the gallery of models: the time evolution of a microlensing
event generated by an accretion disk passing close to a cusp caustic. Efforts
in both directions are now in progress, and we will consider these improvements
in future studies of new QSO 2237+0305 microlensing peaks. Fortunately, using
the present model and monitoring the events that occur in the components of the
system, the future prospects are very promising. Thus, from 10 microlensing
peaks monitored in ten different optical bands (blue bands are required to avoid
the possible contamination by other sources of light as the extrapolated
IR power law spectrum, and therefore, the possible perturbation of the chromatic
amplitude ![]() which is defined in Eq. (10) for a blackbody emission; see,
for example, Malkan 1983), we must be able to noticeably
reduce the current uncertainty in the microlensing parameter D: from about 0.3 (see Table 1) to 0.03. In a similar way, if each peak is recorded at 10 frequencies, the error in each C value will be lowered in a factor of about 3, i.e., from a mean uncertainty of
which is defined in Eq. (10) for a blackbody emission; see,
for example, Malkan 1983), we must be able to noticeably
reduce the current uncertainty in the microlensing parameter D: from about 0.3 (see Table 1) to 0.03. In a similar way, if each peak is recorded at 10 frequencies, the error in each C value will be lowered in a factor of about 3, i.e., from a mean uncertainty of ![]() 0.1 day-1 to
0.1 day-1 to ![]() 0.03 day-1. As a result of new detailed monitoring programs, accuracies of 5-10%
in the microlensing parameters C and D can be easily achieved in the next
years. If a global dataset is made for each microlensing peak (tracing the time
evolution of the spectrum), and it is fitted to a model with six free parameters:
A, B, C, D, t0, and
0.03 day-1. As a result of new detailed monitoring programs, accuracies of 5-10%
in the microlensing parameters C and D can be easily achieved in the next
years. If a global dataset is made for each microlensing peak (tracing the time
evolution of the spectrum), and it is fitted to a model with six free parameters:
A, B, C, D, t0, and ![]() (
(![]() =
=
![]() ,
,
![]() =
=
![]() ), the accuracy could be even better than a few percent.
However, as it was previously remarked, we need a robust estimation of
the lens galaxy motion to accurately measure the black hole mass. This "dynamical
problem'' is the only pitfall to obtain a robust measurement of the amount of
dark mass in the centre of QSO 2237+0305. From another point of view, if an
independent estimate of M were available, we would deduce the effective quasar
velocity
), the accuracy could be even better than a few percent.
However, as it was previously remarked, we need a robust estimation of
the lens galaxy motion to accurately measure the black hole mass. This "dynamical
problem'' is the only pitfall to obtain a robust measurement of the amount of
dark mass in the centre of QSO 2237+0305. From another point of view, if an
independent estimate of M were available, we would deduce the effective quasar
velocity ![]() involved in the different microlensing events as well as
the value of
involved in the different microlensing events as well as
the value of
![]() .
Through a reasonable collection of
.
Through a reasonable collection of ![]() data, one may derive the effective transverse velocity of the
quasar (V), which is a basic piece in some microlensing analyses. Up to now
we focussed on the parameters (C, D) and the properties of the source,
however, the parameters (
data, one may derive the effective transverse velocity of the
quasar (V), which is a basic piece in some microlensing analyses. Up to now
we focussed on the parameters (C, D) and the properties of the source,
however, the parameters (![]() ,
,
![]() )
are also relevant for other studies.
For example, if a multiband monitoring of a microlensing peak is available,
we may estimate the ratios
)
are also relevant for other studies.
For example, if a multiband monitoring of a microlensing peak is available,
we may estimate the ratios
![]() .
These ratios will be
directly related to the extinction ratios
.
These ratios will be
directly related to the extinction ratios
![]() ,
and consequently, to the global (host galaxy + lens galaxy + Milky Way)
extinction law.
,
and consequently, to the global (host galaxy + lens galaxy + Milky Way)
extinction law.
Finally, we wish to put the new technique into perspective to determine the
physical parameters of a far quasar and the measurements for QSO 2237+0305.
Evidence for central black holes in local galaxies comes from small rotating
gaseous and stellar disks discovered with the Hubble Space Telescope, VLBI
observations of H2O masers in Keplerian rotation in some galactic nuclei,
and near-infrared measurements of the radial and proper motions of stars in
the cluster at the centre of the Galaxy (e.g., Ford et al. 1998). Analyzing
these gravitational signatures of massive black holes, the typical values of
the black hole masses vary between ![]() 3
3 ![]() 106
106 ![]() for the Milky
Way (Genzel et al. 1997; Ghez et al. 1998) and
for the Milky
Way (Genzel et al. 1997; Ghez et al. 1998) and ![]() 3
3 ![]() 109
109 ![]() for M87 (Ford et al. 1996; Macchetto et al. 1997). The central dark mass can
be also measured in far AGNs using two classical methods: analyses of the blue
and ultraviolet regions of the rest-frame spectra (e.g., Malkan 1983; Sun &
Malkan 1989) and observations of the time delays between the variations of
the continua and the variations of the broad emission lines (e.g., Wandel et al. 1999). The reverberation technique provides an estimate of
the size of the broad-line region (BLR) as well as the central mass of a quasar
at redshift
for M87 (Ford et al. 1996; Macchetto et al. 1997). The central dark mass can
be also measured in far AGNs using two classical methods: analyses of the blue
and ultraviolet regions of the rest-frame spectra (e.g., Malkan 1983; Sun &
Malkan 1989) and observations of the time delays between the variations of
the continua and the variations of the broad emission lines (e.g., Wandel et al. 1999). The reverberation technique provides an estimate of
the size of the broad-line region (BLR) as well as the central mass of a quasar
at redshift
![]() .
If the line-emitting gas is gravitationally bound to the central
black hole, the virial theorem implies that
.
If the line-emitting gas is gravitationally bound to the central
black hole, the virial theorem implies that
![]() ,
where
,
where
![]() is the FWHM of the emission profile of the BLR at distance
is the FWHM of the emission profile of the BLR at distance
![]() .
Therefore, measuring the lag
.
Therefore, measuring the lag ![]() between an intrinsic event at the central
continuum source and the reply (reverberation) at the BLR, one obtains the size
between an intrinsic event at the central
continuum source and the reply (reverberation) at the BLR, one obtains the size
![]() =
=
![]() and the dark mass M (e.g., Vestergaard 2002
and references therein). Apart from the reverberation mapping technique, there
is a straightforward method to get the parameters M and
and the dark mass M (e.g., Vestergaard 2002
and references therein). Apart from the reverberation mapping technique, there
is a straightforward method to get the parameters M and
![]() .
A comparison
between the blue-ultraviolet excess flux of a QSO (over the extrapolated
infrared power-law spectrum) and the theoretical integrated disk spectrum
permits to deduce the two physical quantities (e.g., Malkan 1983). In a
pioneering work, Shields (1978) found M = 109
.
A comparison
between the blue-ultraviolet excess flux of a QSO (over the extrapolated
infrared power-law spectrum) and the theoretical integrated disk spectrum
permits to deduce the two physical quantities (e.g., Malkan 1983). In a
pioneering work, Shields (1978) found M = 109 ![]() and
and
![]() = 3
= 3 ![]() yr-1 for a Newtonian blackbody disk modelling the central
engine in 3C 273. To make the fits, Malkan (1983) used a relativistic standard
accretion disk. The theoretical model included the effects of general relativity,
but the inclination and scattering atmosphere were ignored. For a sample of 6 quasars and assuming nonrotating black holes, the "big blue bumps'' can be fitted
by spectra of disks around massive (
yr-1 for a Newtonian blackbody disk modelling the central
engine in 3C 273. To make the fits, Malkan (1983) used a relativistic standard
accretion disk. The theoretical model included the effects of general relativity,
but the inclination and scattering atmosphere were ignored. For a sample of 6 quasars and assuming nonrotating black holes, the "big blue bumps'' can be fitted
by spectra of disks around massive (![]() 108
108 ![]() )
black holes.
The author also concluded that the six high-luminosity quasars are emitting
energy at approximately their Eddington limits. The effects of disk inclination
have been more recently considered by Sun & Malkan (1989), while the effects
of electron scattering were discussed by Wandel & Petrosian (1988). In this
paper we applied an alternative methodology to determine (M,
)
black holes.
The author also concluded that the six high-luminosity quasars are emitting
energy at approximately their Eddington limits. The effects of disk inclination
have been more recently considered by Sun & Malkan (1989), while the effects
of electron scattering were discussed by Wandel & Petrosian (1988). In this
paper we applied an alternative methodology to determine (M,
![]() ): the
monitoring of a lensed quasar when a microlensing HME occurs (e.g., Yonehara et al. 1998; Agol & Krolik 1999). The method can be seen as a complementary tool
to prove the existence of massive dark objects and accretion disks in the
centre of far QSOs. Taking as reference values M = 108
): the
monitoring of a lensed quasar when a microlensing HME occurs (e.g., Yonehara et al. 1998; Agol & Krolik 1999). The method can be seen as a complementary tool
to prove the existence of massive dark objects and accretion disks in the
centre of far QSOs. Taking as reference values M = 108 ![]() and
and
![]()
![]()
![]() yr-1 (see here above),
the estimate of the central dark mass in QSO 2237+0305 is consistent
with data of other galaxy nuclei. However, the accretion rate is relatively
large for a blackbody disk (
yr-1 (see here above),
the estimate of the central dark mass in QSO 2237+0305 is consistent
with data of other galaxy nuclei. However, the accretion rate is relatively
large for a blackbody disk (
![]() = 1). As
= 1). As
![]() ,
where L is the total disk luminosity and
,
where L is the total disk luminosity and
![]() is the
Eddington luminosity, one obtains
is the
Eddington luminosity, one obtains
![]() 3 for
3 for
![]() = 1,
= 1,
![]() 1 for
1 for
![]() = 0.3, and
= 0.3, and
![]() 0.3 for
0.3 for
![]() = 0.1. Therefore, to avoid meaningless results (
= 0.1. Therefore, to avoid meaningless results (
![]() ),
the electron-photon scattering must play a role.
),
the electron-photon scattering must play a role.
Acknowledgements
We would like to thank Vyacheslav Shalyapin for his insights on fitting procedures. We also thank Joachim Wambsganss and the anonymous referee for support during the project and useful comments, respectively. The GLITP observations were made with Nordic Optical Telescope (NOT), which is operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de Los Muchachos of the Instituto de Astrofísica de Canarias (IAC). We are grateful to the technical team of the telescope for valuable collaboration during the observational work. This work was supported by the P6/88 project of the IAC, Universidad de Cantabria funds, DGESIC (Spain) grant PB97-0220-C02, and the Spanish Department for Science and Technology grants AYA2000-2111-E and AYA2001-1647-C02.
The function G(q) is defined from Eq. (7) of the main text. For q > 1, we can
rewrite G(q) as
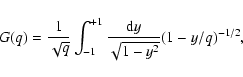 |
(A.1) |
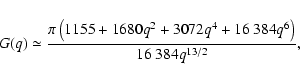 |
(A.2) |
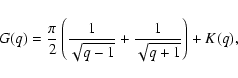 |
(A.3) |
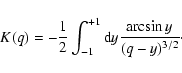 |
(A.4) |
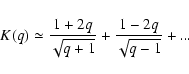 |
(A.5) |
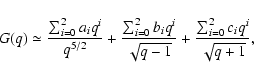 |
(A.6) |
For q < 1, it is more difficult to obtain useful approaches to G(q). After some
tests, we considered the combination of a smooth law (i.e.,
d0 + d1 q + d2 q2 +
...) and a trend that is singular at q = 1 (i.e.,
![]() ). At
-1 < q < 1, from the combined law we infer a good fit
). At
-1 < q < 1, from the combined law we infer a good fit
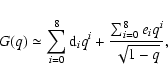 |
(A.7) |