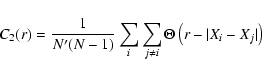A&A 397, 401-403 (2003)
DOI: 10.1051/0004-6361:20021528

The use of luminosity effects to calculate scaling regimes in the galaxy distribution

R. Thieberger

Physics Department, Ben Gurion University, Beer Sheva, 84105, Israel

Received 30 April 2002 / Accepted 5 June 2002

Abstract
This work is a continuation of a previous publication Thieberger and Spiegel concerning the use of two dimensional catalogues in unraveling the large scale distribution of galaxies. Since the data in two-dimensional catalogues are more plentiful than those in three dimensions, the luminosity method can be helpful in using two dimensional data to unravel the nature of the three dimensional distribution. In this work we analyse the Cfa catalogue and demonstrate that the results indicate a distribution of two dimensions in the nearer range and three dimensions in the farther range. The possibility of a different regime for very short distances is discussed.

Key words: galaxies: general - cosmology: large-scale structure of Universe


1 Introduction

Standard cosmology is based on the assumption that the universe is spatially homogeneous, at least on scales sufficiently large to justify its approximation by a Friedmann-Lemaître-Robertson-Walker (FLRW) model. The high isotropy measured in the cosmic microwave background radiation (CMBR) is usually taken as strong evidence in support of this hypothesis.

The structures seen in galaxy catalogues - groups, clusters and superclusters, distributed along voids, filaments and walls - are not viewed as contradicting this Principle, as the common opinion is that the scales on which the universe is assumed to be homogeneous are much larger than those subtended by these structures. However, the consensus on a homogeneous feature of structures, even on very large scales, has never been complete (see e.g. Pietronero 1987).

In more recent times, three-dimensional galaxy catalogues have been made available, they support the findings of approximate self-similarity in the large-scale distribution of galaxies within prescribed scale intervals (Provenzale 1991). Since the data in two-dimensional catalogues are more plentiful than those in three dimensions and are likely to remain so for some time (Cress et al. 1996), it seems worthwhile to discuss further the ways in which the two-dimensional data may be used to unravel the nature of the three-dimensional distribution. The basic issue in analyzing a two-dimensional catalogue goes back to work on stellar statistics (Trumpler & Weaver 1953). The significant point in the stellar studies was the effect of the luminosity distribution of the observed objects on the projected distributions.

The general outline of this issue, which is the main concern of our present attempt has been given previously (Thieberger & Spiegel 2002). Just as in the abovementioned publication, we shall leave out of the account some other features of the galaxy case that remain to be considered in detail, namely source evolution and cosmological effects (Spedalere & Schucking 1980; Ribeiro 1995; Celerier & Thieberger 2000).

In this study we limit ourselves to a three dimensional catalogue so as to be able to evaluate the results. Therefore we chose the cfa catalogue, which has been widely studied, and therefore where we can perform all necessary comparisons so as to understand more precisely our approach.

One of our motivations for the present study comes from our interest in trying to distinguish the different scaling regimes that may exist in the galaxy distribution, though on different length scales. It has been suggested (Murante et al. 1998) that three scaling regimes may be discerned in the distribution of galaxies: on the smallest scales the results are consistent with a distribution of density singularities; in the intermediate range, there is scaling behaviour suggestive of flat structures such as Zeldovitch (1970) favored; on the largest scales, the data indicate a homogeneous distribution of galaxies with nonfractal behavior. This categorization is based on the results of an analysis of three-dimensional catalogues. However, it has to be admitted that those data may as yet not be adequate to clearly decide such issues and that is why we wish to consider whether we may reliably use two-dimensional catalogues for immediate needs. Because of statistical problems, we find it at the moment difficult to study the close region behaviour, therefore we will limit ourselves in this study to the two other regions namely, the two dimensional region and the three dimensional one.

Before describing our calculations, we devote the two next sections to a short description of the correlation integral method and to a brief outline of the influence of luminosity effects by imposing a Schechter luminosity function on the objects of study and attempt to see how this influences the distribution of the projected objects, or rather of their apparent magnitudes. Then we devote a section to a model catalogue so as to help us understand the results of the observational data.

2 The correlation integral method

Calculating dimensions for galaxies enters into difficulty for the cases when the distribution is fractal (Coleman & Pietronero 1992). A robust characterization of the structures of point sets is given by the correlation integral (Grassberger & Procaccia 1983), defined as:

 \begin{displaymath}C_2(r)= {1\over {N^{\prime}(N-1)}}\sum_i \sum_{j\ne i} \Theta\left(r - \vert{X}_i - {X}_j\vert\right) \end{displaymath} (1)

where $\Theta$ is the Heaviside function. The inner summation is over the whole set of N-1 galaxies with coordinates Xj, $j\ne i$, and the outer summation is over a subset of $N^{\prime}$ galaxies, taken as centers, with coordinates Xi. By taking only the inner $N^{\prime}$ galaxies as centers we allow for the effect of the finiteness of the sample (see e.g. Sylos Labini et al. 1998).

We may interpret C2(r) as ${\cal N}(r)/N$ where ${\cal N}(r)$ is the average number of galaxies within a distance r of a typical galaxy in the set. As r goes to zero, C2 should go to zero and, for general distributions, we express this conclusion as $C_2 \propto r^{D_2}$. The exponent D2 is called the correlation dimension and it is necessarily $\le$3 for an embedding space of dimension three. When D2 is not an integer, the distribution is called fractal (Mandelbrot 1982).

In Eq. (1) we have a double summation. In certain cases, for example when we have a pencil beam, this inner region has to be very small and so sometimes one has to use just the distances from a single point. This of course results in a strong deterioration of the statistics. For comparison, we will perform such calculations and we will call it the "pencil beam method" (the dimension obtained will be denoted by $D_{\rm PB}$, comparing it to the usual "Grassberger Procaccia method" (with dimension  $D_{\rm GP}$).

3 Luminosity effects

In considering the distribution on the celestial sphere of galaxies or of radio sources the role of the intrinsic luminosities of the observed objects must be allowed for. Such effects appear in N(>f), the number of galaxies detected whose flux density exceeds a given value, f (Peebles 1993). As is done in Thieberger and Spiegel, we assume that the luminosity function of the objects in our study is independent of position and of time.

A galaxy at distance r is bright enough to be seen at flux density, f, if its luminosity exceeds L. Using a characteristic luminosity L*, for normalization one can express the mean number of galaxies per steradian brighter than f by (Peebles 1993):

 \begin{displaymath}N(>f)={\rm const.} \int^{\infty }_0 r^{D-1} {\rm d}r \psi \left(4 \pi r^2f/L_*\right) \end{displaymath} (2)

D being the dimension of the galaxy distribution, whether fractal or regular. $\psi (x)$, is proportional to the probability that a galaxy at distance r is included in the catalogue. For a Schechter model (Schechter 1976),

 \begin{displaymath}\psi (x)=\int^{\infty }_x w^{\alpha } \exp^{-w} {\rm d}w. \end{displaymath} (3)

Here $\alpha =-1.07$ and x=L/L*.

Lets consider our specific problem. We assume that (see Murante et al. 1998) at short distances we have a dimension D=2 ("Zeldovitch panckakes") and at large distances we have homogenous distribution (i.e. D=3). In this picture we have ignored the very close region where we probably have D=1 (the singularity picture). Then we can modify Eq. (2), and write:

 \begin{displaymath}N(>f)\sim f^{-1} \int^{r^*_0}_0 y {\rm d}y \psi \left(y^2\rig... ...1.5} \int^{\infty}_{r^*_0} y^2 {\rm d}y \psi \left(y^2\right). \end{displaymath} (4)

Here $y=4 \pi r^2f/L_* $, and $r^*_0 = r_0 \sqrt{4 \pi f/L_*}$. r0 is the value at which we change the dimension from two to three. It is easy to see that for the limit of small f the value of the slope $\log N(>$f) vs. $\log f$ tends to D=3, and for large f it tends to D=2. We used this equation to evaluate numerically the dimension, for the whole range of f, by calculating an array of values of f vs. N(>f), making a numerical integration of Eq. (4). We obtained then the dimension by a least squares fit. This analysis resulted in D=2.9 for very small f, and going fast towards the value of D=2, for large f. These results are of course quite obvious, the only point we wanted to clarify is the extension of the transition zone between 2 and 3 dimensions. We found that this transition zone is larger than the zone where f tends to zero and that quite small values of f already give a dimension D=3, i.e. are already behaving as very large f. In the next section we will perform a number of model catalogue calculations in order to study the relations between the results obtained by the luminosity method versus the integral correlation method. We will also compare that to the "beam pencil method'' as was explained in the previous section. The reason is that we wish to stress that in the "luminosity method" we are forced to consider only the luminosities relative to the observer, i.e. just for one galaxy.

4 The model catalogues

In order to understand the results which we obtain from an observational catalogue, we constructed a number of representative model catalogues. We took N1 points in a box 0 to 500 (arbitrary units), and around each point on a plane we put N2 points at distances up to PL units, in each direction on the plane. To each point we attributed a "luminosity'' obtained according to the Schechter function distribution (Eq. (2)). In most of the catalogues we considered the cases were we had in our box around 20 000 points ( $N_1 \times N_2$ minus the points which fall outside the box limits). This value was chosen so as to be of the same order of magnitude as the Cfa catalogue. In this way we can examine the reliability of the results for the real catalogue. Just for the sake of learning about the improvement obtained for larger catalogues, we checked also a few cases of a larger amount of points. In the following table we compare the results to the ones obtained by the use of correlation integrals (Grassberger & Procaccia 1983). In the table we compare our results also to the pencil beam method. The dimensions are denoted by $D_{\rm GP}$ and $D_{\rm PB}$ appropriately. In this table we give also the results obtained by performing the dimension analysis via the luminosity effect. Using the $\log(f)$ versus $\log(N(>$f)) results, we calculate the appropriate dimensions. The result is denoted by $D_{\rm L}$ in the table.

In addition to the main purpose of the table, which is the comparison beween the different methods, for a variaty of cases, we also obtain an indication of the errors for the different models. The cases of pure two or three dimensional models (the last four lines in the table) give good agreement and when the number of points is increased (see last line) the errors even for the luminosity case start to decrease considerably. The main reason for the larger overall errors in the top five lines is the consequence of our model where some points "see'' more three dimensional points then others depending on their location on the planes. This problem, being an artifact, should be less pronounced in the true catalogues.


 
Table 1: Dimension calculation for different model catalogues.
N1 N2 PL $D_{\rm GP}$ $D_{\rm L}$ $D_{\rm PB}$
150 150 50 2.3 $\pm $ 0.1 2.5 $\pm $ 0.1 2.5 $\pm $ 0.2
300 150 50 2.6 $\pm $ 0.1 2.6 $\pm $ 0.1 2.8 $\pm $ 0.2
300 300 50 2.6 $\pm $ 0.0 2.6 $\pm $ 0.1 2.6 $\pm $ 0.2
6 4800 200 2.2 $\pm $ 0.2 2.3 $\pm $ 0.2 2.4 $\pm $ 0.3
3700 6 50 2.95 $\pm $ .05 2.9 $\pm $ 0.1 3.0 $\pm $ 0.1
1 20 k 250 2.00 $\pm $ .00 2.00 $\pm $ .04 2.01 $\pm $ .03
20 k 1 .1 3.00 $\pm $ .00 2.9 $\pm $ 0.1 2.98 $\pm $ .05
80 k 1 .1 3.00 $\pm $ .00 2.9 $\pm $ 0.1 3.00 $\pm $ .03
320 k 1 .1 3.00 $\pm $ .00 2.94 $\pm $ .03 2.99 $\pm $ .02


We wish to remark here that there are problems concerning the validity of the results both for very small f and for large f. For small f the finite size of our box results in the limit being f dependent, which is an artifact. For large f only a smaller and smaller fraction of the points reach the "observer", resulting in bad statistics. So we check the average dimension over the range of f where we thought the results were reliable.

5 Observational catalogue

In this section we describe the dimensions that we obtain based on the three dimensional data of the Cfa Catalogue of redshifts (Huchra et al. 1995), which is a compilation from several sources. A previous analysis using the standard method, described in Sect. 2, was performed, for an older catalogue, by Provenzale et al. (1997).

We wish to compare the results of the correletion integral method and the luminosity method. The correlation integral method gives for the near galaxies D=1.9 and for the far galaxies D=2.6. The luminosity method gives for the mostly near (as explained in the previous section) D=2.1, and for the mostly far ones: D=2.8.

In these cases we do not have a way to put error bars on the values. So to get a feel for the possible error, we attribute to each galaxy a luminosity obtained in the same manner as in the model catalogue, instead of using the values of the luminosities in the real Cfa catalogue. We chose nine different sets of random numbers. In this way we could obtain the error on the average and obtained an error of about $ \pm 0.2$. These are encouraging results demonstrating that although the errors for the luminosity method are somewhat larger than the ones for the correlation integral method, they are in a reasonable range. Of course if one has a large two dimensional catalogue and a relatively much smaller three dimensional catalogue (as is at the moment the case) then the larger number of galaxies in the two dimensional catalogue will make the errors smaller then the one obtained from analysing a red shift catalogue.

6 Discussion and conclusion

Our calculations show that we obtain the same kind of results both for the correlation integral method and the luminosity method. We tried to estimate the possible errors on the results and it seems to us that they are somewhat larger for the luminosity method. So if we have a three dimensional catalogue most probably the correlation integral give a more reliable result, but as the two dimensional catalogues are much larger, most probably the luminosity method is more reliable.

Acknowledgements
The author wants to thank Professor E.A. Spiegel for many valuable discussions concerning this work.

References

 

Copyright ESO 2003