A&A 397, 747-756 (2003)
DOI: 10.1051/0004-6361:20021536
D. Katz 1,2 - F. Favata 1 - S. Aigrain 1,3 - G. Micela 4
1 - Astrophysics Division - Research and Science Support
Department of ESA, ESTEC,
Postbus 299, 2200 AG Noordwijk, The Netherlands
2 -
Observatoire de Paris, GEPI, Place Jules Janssen,
92195 Meudon, France
3 -
Institute of Astronomy, Madingley Road, Cambridge,
UK
4 -
Osservatorio Astronomico di Palermo,
Piazza del Parlamento 1, 90134 Palermo, Italy
Received 8 March 2002 / Accepted 15 October 2002
Abstract
The high-resolution optical spectra of the two X-ray active
binaries RS CVn stars HD 113816 (IS Vir) and HD 119285 (V851 Cen)
are analysed and their Na, Mg, Al, Si, Ca, Sc, Ti, Co and Ni
contents determined, in the framework of a larger program of chemical
analysis of RS CVn stellar atmosphere.
The analysis of IS Vir and V851 Cen
is performed with three different LTE methods. In the first one,
abundances are derived for a large set of transitions (among which 28 Fe I lines, spanning a broad interval in excitation potential and
equivalent width, and 6 Fe II transitions) using measured equivalent
widths and Kurucz LTE model atmospheres as input for the MOOG software
package. The input atmospheric parameters and abundances are iteratively
modified until (i) the Fe I abundances exhibit no trend with
excitation potential or equivalent width, (ii) Fe I and Fe II average abundances are the same and (iii) Fe and
Alpha elements average abundances are consistent with the input values.
The second method follows a similar approach, but uses a restricted
line list (without the Fe I "low excitation potential''
transitions) and relies on the B-V and V-I colour indices to determine
the temperature. The third method uses the same restricted line list
as the second method and relies on fitting the 6162 Å Ca I line wing
profiles to derive the surface gravity. The reliability of these
methods is investigated in the context of single line RS CVn stars. It
is shown that the V-I photometric index gives, on a broader sample of stars, significantly
cooler estimates of the effective temperature than the B-V index.
All approaches give results in good agreement with each other,
except the V-I based method. The analysis of IS Vir and V851 Cen results
in both cases in their primaries being giant stars of near-solar
metallicity. Their parameters as derived with the first method
are respectively
![]() K,
K,
![]() ,
,
![]() and
and
![]() K,
K,
![]() and
and
![]() .
In the case of V851 Cen the
derived iron content is significantly higher than a previous
determination in the literature. Both stars exhibit relative
overabundances of several elements (e.g. Ca) with respect to the
solar mix.
.
In the case of V851 Cen the
derived iron content is significantly higher than a previous
determination in the literature. Both stars exhibit relative
overabundances of several elements (e.g. Ca) with respect to the
solar mix.
Key words: stars: fundamental parameters - stars: abundances - stars: individual: HD 113816, HD 119285
Since the advent of high-energy astronomy, active binaries have been studied in more and more detail thanks to their very high activity levels, several orders of magnitude higher than e.g. in the Sun. In the Sun the modest rotation level induces a correspondingly modest level of magnetic activity and sunspot cover, even at solar maximum, a modest fraction of the solar surface. In active binaries on the other hand the tidally locked rotation is likely to induce significant transformations in the stellar structure, and also manifests itself through much higher levels of magnetic activity. Doppler imaging techniques have also produced evidence for very large starspot groups (see e.g. Rice & Strassmeier 2001 and previous papers in the series). A good understanding of the structure and evolutionary state of active binaries can thus help to understand coronal phenomena at their extreme levels.
One new area of investigation which has opened up since the advent of enhanced resolution X-ray spectroscopy is the study of the metal abundance in coronal plasmas. Abundance values significantly lower than solar have been derived (see e.g. Jordan et al. 1998 for a review). In the Sun it is observed that the coronal abundances are not the same as the photospheric ones, with elements being selectively enhanced (Feldman 1998) on the basis of their first ionisation potential (FIP). The possibility that some elements are actually depleted is also not ruled out (Jordan et al. 1998). Detailed individual coronal abundances of other stars are now becoming available, and thus a new question arises: the relationship between photospheric and coronal abundances.
To study this issue it is, however, obviously necessary to have a detailed knowledge of the photospheric abundances of the stars under investigation. The iron photospheric abundances of most of the active stars which are the subject of detailed investigation in e.g. X-rays, are not at all well known, and the situation is worse for the other metals. There are several reasons for this, including (for the active binaries) the difficulty of performing detailed spectroscopic studies of binary stars with a significant rotation velocity, which tends to broaden and blend the spectral lines, making the analysis difficult. Note that, in the case of cool active stars, photometric abundance indices seem to produce biased results, giving lower abundances than determined spectroscopically (Favata et al. 1997) and thus cannot be used for a detailed comparison of photospheric and coronal abundances.
Randich et al. (1994) have conducted a study on a significant sample of objects (67 components in 54 systems), using effective temperatures derived from the B-V index (which is, however, sensitive to both metal abundances and interstellar reddening) and surface gravities estimated from the spectral type and the luminosity class or when radii and masses were known these were directly computed. Iron and lithium abundances were derived by comparison with a grid of synthetic spectra covering a domain of 25 Å around the 6708 Å Li I doublet. The main result from the above study is that a large fraction of its sample is composed of metal deficient stars (around 60% of the stars display a metallicity equal or lower than -0.4 dex). At the same time a large fraction of their stars are Li rich.
Ottmann et al. (1998) studied a much more limited sample of (in general hotter)
objects, but with a much more detailed and purely spectroscopic
analysis, determining Fe, Mg and Si abundances through an equivalent
widths based analysis. Temperatures were derived fitting the wings of
the H![]() and H
and H![]() Balmer lines, and gravities were estimated
in a similar way, by comparing the wings of two strong lines to
synthetic profiles. Their study presents results for 5 systems in
common with Randich et al. (1994), deriving, in 4 cases out of the 5, [Fe/H]
abundances larger by 0.1 to 0.3 dex. They also compared the
metallicities of the photosphere and corona (the latest extracted from
the literature) in II Peg and
Balmer lines, and gravities were estimated
in a similar way, by comparing the wings of two strong lines to
synthetic profiles. Their study presents results for 5 systems in
common with Randich et al. (1994), deriving, in 4 cases out of the 5, [Fe/H]
abundances larger by 0.1 to 0.3 dex. They also compared the
metallicities of the photosphere and corona (the latest extracted from
the literature) in II Peg and ![]() And, showing that the X-ray
derived coronal abundance is lower than the photospheric value by one
order of magnitude.
And, showing that the X-ray
derived coronal abundance is lower than the photospheric value by one
order of magnitude.
We have thus started a detailed study of the photospheric abundances in a sample of 28 RS CVn stars, aiming at providing consistently-derived abundances of several elements in their photosphere. They will be useful to address the issues of RS CVn metallicity distribution, abundance pattern(s) and mixing processes. They will also serve as a starting point for the comparison with the coronal abundances once our sample objects will have been observed by either Chandra or XMM. The sample selection as well as the observations are presented in Sect. 2.
RS CVn stars are characterised by a high level of activity, which may modify their photospheric properties. Therefore, the methods commonly used for the study of non active stars should be carefully checked before being applied to RS CVn. The aim of this paper is to compare different spectral analysis techniques, to investigate their reliability in the study of single line RS CVn stars. In order to do so, two stars of the sample, the slow rotators, single lines spectroscopic binaries (SB1) IS Vir and V851 Cen, are analysed using three different methods (Sect. 3). In addition, the consistency of the B-V, V-R and V-I indices as temperature indicators is studied on a larger set of 8 single lined sample stars (Sect. 3.6). The results of the three methods are compared in Sect. 4. The parameters and chemical compositions of IS Vir and V851 Cen are discussed in Sect. 5. The analysis of the remaining SB1 sample stars as well as the study of double lines spectroscopic binaries (SB2) will be the subject of future papers.
The most extensive catalog of active binaries remains the one of
Strassmeier et al. (1993), which we have thus used as parent
sample for our observing program. We have selected, from it, 28 systems (18 SB1 and 10 SB2), bright enough (![]() )
to be observed
with the instrument used (FEROS on the ESO 1.52 m telescope) at
sufficiently high S/N in a reasonable time (1 hr maximum). We have
made sure that a number of systems in our sample were also present in
the work of Randich et al. (1994), in order to simplify the
comparison of the two studies. The selected stars are all systems with
moderate projected rotational velocity (
)
to be observed
with the instrument used (FEROS on the ESO 1.52 m telescope) at
sufficiently high S/N in a reasonable time (1 hr maximum). We have
made sure that a number of systems in our sample were also present in
the work of Randich et al. (1994), in order to simplify the
comparison of the two studies. The selected stars are all systems with
moderate projected rotational velocity (
![]() km s-1),
to limit the blending of the lines.
km s-1),
to limit the blending of the lines.
The spectra were acquired in January 2000, with the fibre fed cross-dispersed echelle spectrograph FEROS, mounted on the ESO 1.52 m telescope at La Silla. The spectral range covered is 3600-9200 Å, with a resolution of 48 000. The spectral reduction (i.e. bias subtraction, flat field correction, order extraction and merging and wavelength calibration) has been performed during the observations with the "FEROS Data Reduction Software'' (URL: http://www.ls.eso.org/lasilla/Telescopes/2p2T/E1p5M/ FEROS/offline.html) available on the mountain. Most of the targets were observed 2 or 3 times (for a total of 49 spectra) to detect possible modifications of line profiles and allow a good filtering of the cosmic rays.
In this paper, 2 SB1 sample stars, IS Vir and V851 Cen, are analysed.
Table 1 summarises their visual apparent magnitudes,
number of exposures, mean resulting signal to noise ratios
(per pixel) and projected rotational velocities, ![]() ,
(from Strassmeier et al. 1993).
,
(from Strassmeier et al. 1993).
| HD Num. | Id. | V | Nb | S/N | |
| (km s-1) | |||||
| HD 113816 | IS Vir | 8.32 | 3 | 170 | 6.0 |
| HD 119285 | V851 Cen | 7.67 | 1 | 150 | 6.5 |
Three different approaches were used for the analysis of IS Vir and V851 Cen.
The first one is a "classical'' iterative LTE analysis. Measured equivalent widths of 10 different elements (among which 28 Fe I lines, spanning a broad interval in excitation potential and equivalent widths, and 6 Fe II transitions) were converted in abundances, using the MOOG (Sneden 1973) software packages. The complete list of lines used is given in Table 2, while their selection is discussed in Sect. 3.2. MOOG uses model atmospheres and atomic data (wavelength, excitation potential, gf values) to compute theoretical curves of growth, from which the abundances are derived. Kurucz LTE plane parallel models (Kurucz 1993a, see Sect. 3.5) and Kurucz atomic data (Kurucz & Bell 1995) were used, except for gf values which were, in majority, adjusted by comparison with the solar spectrum (Sect. 3.3).
The atmospheric parameters and abundances were obtained by iteratively
modifying the effective temperature, surface gravity, metallicity,
mean alpha element overabundance and micro-turbulence velocity of the
input model and rederiving the abundances until
(i) the Fe I transition abundances exhibited no
trend with excitation potential
or logarithm of reduced equivalent width![]() , (ii) Fe I and Fe II
lines gave the same average abundances (ionisation equilibrium) and (iii)
the iron and alpha elements average abundances were consistent
with those of the input model atmosphere.
, (ii) Fe I and Fe II
lines gave the same average abundances (ionisation equilibrium) and (iii)
the iron and alpha elements average abundances were consistent
with those of the input model atmosphere.
Each of these diagnostics is sensitive to changes of several of the input atmospheric parameters. Given a set of observed equivalent widths, the slope of Fe I abundance as a function of excitation potential decreases with effective temperature, is very slightly sensitive to surface gravity and metallicity and increases with micro-turbulence. The slope of Fe I abundances as a function of logarithm of reduced equivalent width increases with effective temperature, decreases with surface gravity, is very slightly sensitive to metallicity and strongly decreases with micro-turbulence. Around the convergence point, the mean Fe I abundance is weakly sensitive to changes of the atmospheric parameters, while the mean Fe II abundance decreases significantly with effective temperature and increases significantly with surface gravity.
"Low excitation potential'' neutral iron group transitions have been
reported to yield, in giant stars, lower abundances than their "high
excitation'' counterparts (Ruland et al. 1980; Drake & Smith 1991).
This behaviour is usually attributed to non-LTE effects
due to the low density of the photosphere. As presented in
Sect. 5, the first analysis of IS Vir and V851 Cen
leads to the result that both of them are giants.
It was therefore necessary to test whether the results of the first
analysis had been affected by non-LTE effects, via the "low excitation
potential'' transitions. Both stars were then reanalysed without
the "low excitation potential'' transitions. Following the Ruland et al. (1980)
study of LTE departure as a function of excitation potential,
all Fe I lines with
![]() eV were discarded from the
initial selection. This, of course, makes it impossible to rely on the
slope of the Fe I transition abundances as a function
of excitation potential
to constrain the atmospheric parameters, because the
remaining interval,
eV were discarded from the
initial selection. This, of course, makes it impossible to rely on the
slope of the Fe I transition abundances as a function
of excitation potential
to constrain the atmospheric parameters, because the
remaining interval,
![]() eV, is too limited.
Another "diagnostic'' was therefore needed to avoid the LTE analysis
solution being degenerated.
eV, is too limited.
Another "diagnostic'' was therefore needed to avoid the LTE analysis
solution being degenerated.
In IS Vir and V851 Cen second analysis, photometric colour indices were used. The effective temperatures were derived from the B-V index for IS Vir, and from the B-Vand V-I indices for V851 Cen (the two colours leading to different temperatures, V851 Cen was analysed two times, using each index separately). Surface gravities, micro-turbulences and abundances were estimated in the same way as in the first method, using the same set of lines (but excluding the "low excitation potential'' Fe I transitions). In the case of the B-V/temperature transformation, which is metallicity sensitive, the two steps were iterated until convergence. The conversion of photometric indices into effective temperatures, as well as the consistency of different colour indices as RS CVn stars temperature estimator is discussed in more details in Sect. 3.6.
As discussed in Sect. 3.6, the photometric indices present a major drawback: in several RS CVn stars, different colours yield different effective temperatures. Therefore, analyses based on photometric indices are not consistent and reliable enough to identify any possible non-LTE effect that might affect the first method. IS Vir and V851 Cen were thus analysed a third time.
Instead of the "low excitation potential'' Fe I transitions or
the photometric colour indices, the third method makes
use of information
contained in the wings of the 6162 Å Ca I transition.
In IS Vir and V851 Cen, the 6162 Å Ca I line is a "strong'' line,
and therefore its wing profiles are strongly sensitive to surface
gravity. As the 6162 Å Ca I wing profiles are also sensitive
to effective temperature, micro-turbulence velocity and iron
and calcium abundances, the analysis was performed in an iterative way.
The atmospheric parameters determined with the second method were
used as starting parameters. In a first step, the surface gravity was
derived by comparing the 6162 Å Ca I line wing profiles to a
library of synthetic profiles (this step is detailed in Sect. 3.7).
In a second step, the measured equivalent widths of the set of lines
used in the second method were converted to abundances, using the LTE
analysis program MOOG. The surface gravity of the MOOG input atmospheric
model was the one derived during the first step.
Effective temperature, surface gravity, micro-turbulence
velocity and abundances were obtained by iteratively modifying the
input
![]() ,
,
![]() ,
,
![]() and
and
![]() and rerunning
the two steps until (i) the Fe I transitions exhibited no trend
with logarithm of reduced equivalent width, (ii) Fe I and Fe II lines gave the same average abundances and (iii) the iron
and calcium average abundances were consistent with the input abundances.
and rerunning
the two steps until (i) the Fe I transitions exhibited no trend
with logarithm of reduced equivalent width, (ii) Fe I and Fe II lines gave the same average abundances and (iii) the iron
and calcium average abundances were consistent with the input abundances.
Another "classical diagnostic'' is often used to derive the
effective temperature: the adjustment of the Balmer lines wing
profiles. In F- and G-type stars, the wings of the Balmer lines are
very sensitive to the effective temperature (the width of the wings
monotically increasing with
![]() ), while very slightly sensitive
to the surface gravity or the metallicity. As a consequence Balmer lines
are very good temperature indicators above
), while very slightly sensitive
to the surface gravity or the metallicity. As a consequence Balmer lines
are very good temperature indicators above
![]() K
(Cowley & Castelli 2002),
and were effectively used by, e.g., Ottmann et al. (1998) in their analysis
of hotter active binaries. Below this threshold, Balmer line wings
become less temperature sensitive and are no longer useful
as estimators. Since most of the 18 SB1 stars in our present sample are
classified early K-type stars, Balmer line profile adjustment could not
be used to derive their temperatures. However, even at higher temperature,
the presence of activity (filled in lines, or emission) makes it necessary
to be very careful in the use of Balmer lines as temperature indicators in
RS CVn stars.
K
(Cowley & Castelli 2002),
and were effectively used by, e.g., Ottmann et al. (1998) in their analysis
of hotter active binaries. Below this threshold, Balmer line wings
become less temperature sensitive and are no longer useful
as estimators. Since most of the 18 SB1 stars in our present sample are
classified early K-type stars, Balmer line profile adjustment could not
be used to derive their temperatures. However, even at higher temperature,
the presence of activity (filled in lines, or emission) makes it necessary
to be very careful in the use of Balmer lines as temperature indicators in
RS CVn stars.
Both IS Vir and V851 Cen are relatively cool
and therefore exhibit a lot of blended features. A first selection of
unblended or "slightly'' blended lines (lines that can be reliably
deblended) has therefore been performed starting from a synthetic
spectrum of parameters
![]() K,
K,
![]() and
and
![]() ,
covering the wavelength range
5000-8000 Å (the bluer part of the spectrum suffers so heavily
from blending as to be effectively useless in the present context).
This spectrum was computed with Piskunov's SYNTH program
using atomic parameters from the VALD database
(Piskunov et al. 1995; Kupka et al. 1999;
Kupka et al. 2000) and a Kurucz model atmosphere (Kurucz 1993a).
The lines chosen in the
synthetic spectrum were then examined, one by one, in the two sample
spectra. For each star, lines which appeared asymmetric or showed an
unusually large width, were assumed blended with unidentified lines
and therefore discarded from the initial sample. Lines whose profiles
overlapped with the position of one of the telluric lines listed in
"Rowland's table of the solar spectrum''
(Moore et al. 1966) were also discarded. Note that the lines concerned are
not necessarily the same from star to star because of the radial
velocity differences.
,
covering the wavelength range
5000-8000 Å (the bluer part of the spectrum suffers so heavily
from blending as to be effectively useless in the present context).
This spectrum was computed with Piskunov's SYNTH program
using atomic parameters from the VALD database
(Piskunov et al. 1995; Kupka et al. 1999;
Kupka et al. 2000) and a Kurucz model atmosphere (Kurucz 1993a).
The lines chosen in the
synthetic spectrum were then examined, one by one, in the two sample
spectra. For each star, lines which appeared asymmetric or showed an
unusually large width, were assumed blended with unidentified lines
and therefore discarded from the initial sample. Lines whose profiles
overlapped with the position of one of the telluric lines listed in
"Rowland's table of the solar spectrum''
(Moore et al. 1966) were also discarded. Note that the lines concerned are
not necessarily the same from star to star because of the radial
velocity differences.
Ideally, one would like to rely only on weak lines (lines on the
linear part or close to the knee of the curve of growth, i.e.
approximately W < 70 mÅ) to perform detailed analysis.
Unfortunately, in the case of "cool'' stars exhibiting a moderate
rotational velocity, the number of reliable and unblended lines is
rather small.
Even for the two slow rotators analysed here, IS Vir and V851 Cen, Na
and Mg are derived from "strong'' lines (respectively around 100 and 150 mÅ). In order to quantify the effect of "strong'' lines on the
results, V851 Cen has been analysed (method 3) with two sets of
Fe I lines: the first made of 20 lines with ![]() mÅ,
the second made of these plus 11 lines with
mÅ,
the second made of these plus 11 lines with
![]() mÅ (see Table 2).
The two studies give very similar results, with negligible differences
(
mÅ (see Table 2).
The two studies give very similar results, with negligible differences
(
![]() ,
,
![]() ,
,
![]() km s-1,
km s-1,
![]() and a few hundredths of dex for the other elements;
the largest difference being
and a few hundredths of dex for the other elements;
the largest difference being
![]() dex). The
results presented in Table 7 have been obtained with
the large set of lines: "weak'' plus "strong''.
dex). The
results presented in Table 7 have been obtained with
the large set of lines: "weak'' plus "strong''.
As many damping constants are poorly known, all the lines that may have
been significantly van der Walls broadened (
![]() )
were discarded from the analysis. In the remaining transitions, the van der Waals
damping process is a minor contributor to the equivalent widths.
MOOG's Unsöld approximation option was used to take into account
van der Waals damping in the computation of theoretical curves of growth.
)
were discarded from the analysis. In the remaining transitions, the van der Waals
damping process is a minor contributor to the equivalent widths.
MOOG's Unsöld approximation option was used to take into account
van der Waals damping in the computation of theoretical curves of growth.
Many of the lines used in this analysis don't have accurate oscillator
strengths reported in the literature. We have thus determined, from a
solar spectrum, the oscillator strengths of most of the lines (see
below) used in the
present analysis. Their equivalent widths were measured in a high
S/N ratio (
![]() )
moon spectrum extracted from the
archive of the first FEROS commissioning period (fall 1998). Their
oscillator strengths were then adjusted using a Kurucz
model atmosphere with
)
moon spectrum extracted from the
archive of the first FEROS commissioning period (fall 1998). Their
oscillator strengths were then adjusted using a Kurucz
model atmosphere with
![]() K,
K,
![]() and
micro-turbulence
and
micro-turbulence ![]() km s-1, so that a spectral
analysis made with the same approach as for IS Vir and V851 Cen stars
(i.e. deriving abundances with the MOOG LTE analysis software packages)
reproduced the Kurucz solar
abundances. In order to be consistent with Kurucz models and
opacities, we kept the old Fe I solar abundance,
km s-1, so that a spectral
analysis made with the same approach as for IS Vir and V851 Cen stars
(i.e. deriving abundances with the MOOG LTE analysis software packages)
reproduced the Kurucz solar
abundances. In order to be consistent with Kurucz models and
opacities, we kept the old Fe I solar abundance,
![]() ,
instead of the meteoritic value
,
instead of the meteoritic value
![]() .
As
the analysis performed here is purely differential with respect to the
Sun, the use of the "old'' Fe value has no consequence on the
results derived. In order to avoid degrading the accuracy of the
oscillator strengths with equivalent widths' measurement errors, only
lines with
.
As
the analysis performed here is purely differential with respect to the
Sun, the use of the "old'' Fe value has no consequence on the
results derived. In order to avoid degrading the accuracy of the
oscillator strengths with equivalent widths' measurement errors, only
lines with
![]() mÅ were calibrated on the Sun. For the
weaker lines, we kept the Kurucz theoretical values (Kurucz & Bell 1995).
The characteristics of the selected lines are listed in
Table 2, with their wavelengths, excitation potentials and
adopted oscillator strengths. When available, oscillator strengths
from the literature, extracted from Edvardsson et al. (1993),
Neuforge-Verheecke & Magain (1997) and Feltzing & Gonzalez (2001) are also listed.
mÅ were calibrated on the Sun. For the
weaker lines, we kept the Kurucz theoretical values (Kurucz & Bell 1995).
The characteristics of the selected lines are listed in
Table 2, with their wavelengths, excitation potentials and
adopted oscillator strengths. When available, oscillator strengths
from the literature, extracted from Edvardsson et al. (1993),
Neuforge-Verheecke & Magain (1997) and Feltzing & Gonzalez (2001) are also listed.
The FEROS spectra were straightened by segments of 200 to 400 Å. In each of them, intervals of the continuum were selected by comparison with a Kurucz synthetic spectrum. Those series of intervals were adjusted by low degree polynomials, which in turn were used to straighten the different domains. In slow rotators, such as IS Vir and V851 Cen, the fitting of the continuum is relatively simple. This is not true for intermediate rotators which display very few intervals at continuum level. There is then a risk to underestimate the position of the continuum. An underestimation of 0.5% of the continuum, would lead to an error of 5% on the equivalent widths and 0.05 dex on the abundances (on "weak'' lines).
The equivalent widths were measured with the IRAF![]() (Jacoby 1998) task splot, assuming Gaussian profiles.
They are compiled in Table 2.
(Jacoby 1998) task splot, assuming Gaussian profiles.
They are compiled in Table 2.
The analysis were performed using Kurucz' LTE plane parallel atmospheric
models, computed without the overshooting option and for a value of the
length of the convective cell over the pressure scale height
![]() .
This later value has been shown to give
a better description of Balmer H
.
This later value has been shown to give
a better description of Balmer H![]() and H
and H![]() line profiles
than the previous value of 1.25 (Fuhrmann et al. 1993; van't Veer-Menneret & Megessier 1996).
line profiles
than the previous value of 1.25 (Fuhrmann et al. 1993; van't Veer-Menneret & Megessier 1996).
| HD Num. | l | b | d | E(B-V) |
|
|
B-V |
|
|
|
|
|
| (B-V) | (V-R) | (V-I) | ||||||||||
| HD 26354 | 262 | -46 | 35 | 0.03 | 0.02 | 0.04 | 0.88 | 0.52 | 0.99 | 4963 | 4927 | 4824 |
| HD 34802 | 289 | -32 | 180 | 0.06 | 0.04 | 0.08 | 1.03 | 0.57 | 1.09 | 4746 | 4602 | 4546 |
| HD 61245 | 258 | -12 | 111 | 0.03 | 0.02 | 0.04 | 1.01 | 0.54 | 1.02 | 4785 | 4704 | 4687 |
| HD 72688 | 255 | 3 | 131 | 0.02 | 0.02 | 0.03 | 0.93 | 0.47 | 0.91 | 4945 | 4973 | 4936 |
| HD 81410 | 254 | 19 | 120 | 0.04 | 0.03 | 0.06 | 0.98 | 0.53 | 1.02 | 4844 | 4740 | 4687 |
| HD 106225 | 287 | 53 | 125 | 0.01 | 0.00 | 0.01 | 0.99 | 0.58 | 1.13 | 4824 | 4569 | 4472 |
| HD 119285 | 309 | 1 | 76 | 0.03 | 0.02 | 0.05 | 1.05 | 0.60 | 1.15 | 4708 | 4507 | 4436 |
| HD 136905 | 356 | 40 | 95 | 0.07 | 0.04 | 0.09 | 0.96 | 0.53 | 1.01 | 4884 | 4740 | 4708 |
The use of photometric indices to derive effective temperature is a classical technique commonly used to analyse non-active stars. In the present work we are however considering stars with a very high level of magnetic activity, which also produces large photospheric spots. Their high activity level could thus affect their spectral energy distribution and therefore their colour indices. In the case of the metallicity, large discrepancies between photometric and spectroscopic estimates were reported by Gimenez et al. (1991) and Favata et al. (1997).
In order to check the relative consistency of different colour
indices, we derived, for 8 SB1 objects from our program
(hereafter referred to as test stars), with good quality
Hipparcos parallaxes and B-V,
![]() and
and
![]() indices either from Cutispoto (1998) or
Cutispoto et al. (2001), the effective temperatures corresponding to the three
colours.
There was no recent
measurement of the V-R or V-I colour indices reported in the literature
for IS Vir, which, therefore, has not been included in the test stars sample.
The visual extinction (i.e. A(V)) was
derived using the model of Arenou et al. (1992) and converted in
colour excesses using the coefficients :
E(B-V) = 0.302 A(V),
indices either from Cutispoto (1998) or
Cutispoto et al. (2001), the effective temperatures corresponding to the three
colours.
There was no recent
measurement of the V-R or V-I colour indices reported in the literature
for IS Vir, which, therefore, has not been included in the test stars sample.
The visual extinction (i.e. A(V)) was
derived using the model of Arenou et al. (1992) and converted in
colour excesses using the coefficients :
E(B-V) = 0.302 A(V),
![]() and
and
![]() (Schlegel et al. 1998). Galactic coordinates, distances (pc)
and colour excesses of the tests stars are summarised in Table 3.
(Schlegel et al. 1998). Galactic coordinates, distances (pc)
and colour excesses of the tests stars are summarised in Table 3.
The colours were converted into effective temperatures
using the empirical calibration for F0V to K5V main sequence stars of
Alonso et al. (1996) (HD 26354) and for F0 to K5 giant stars of
Alonso et al. (1999) (for the 7 others), initially assuming
solar metallicities. The 8 test stars were classified as either main
sequence or evolved stars, by comparing their absolute magnitudes with
the Bertelli et al. (1994) isochrones. To convert the
![]() and
and
![]() indices measured by Cutispoto (1998) and Cutispoto et al. (2001) into the
indices measured by Cutispoto (1998) and Cutispoto et al. (2001) into the
![]() and
and
![]() indices used by
Alonso et al. (1996) and Alonso et al. (1999), we used the Bessell (1979)
transformations,
indices used by
Alonso et al. (1996) and Alonso et al. (1999), we used the Bessell (1979)
transformations,
![]() and
and
![]() .
The colour indices as well as the
corresponding effective temperatures are summarised in
Table 3.
.
The colour indices as well as the
corresponding effective temperatures are summarised in
Table 3.
In all cases, the
![]() index lead to
temperatures systematically cooler (from 10 to 350 K with a mean of 175 K)
than the B-V index. In 6 cases out of 8, the
index lead to
temperatures systematically cooler (from 10 to 350 K with a mean of 175 K)
than the B-V index. In 6 cases out of 8, the
![]() indices give
temperatures significantly cooler than B-V (and slightly warmer
than
indices give
temperatures significantly cooler than B-V (and slightly warmer
than
![]() ), with differences ranging
from 80 to 255 K.
), with differences ranging
from 80 to 255 K.
In order to check if the discrepancies between the effective temperatures
derived from B-V, and those derived from V-I, were artefacts of the
adopted transformations, we compared Alonso et al. (1999) calibrations
with those for giant stars of McWilliam (1990). In the ranges of
colour relevant to our test stars:
![]() and
and
![]() ,
the differences between the
2 systems never exceed 40 and 20 K. We also computed
the mean differences
,
the differences between the
2 systems never exceed 40 and 20 K. We also computed
the mean differences
![]() over 7 evolved test stars (i.e. all test stars but HD 26354)
with the 2 calibrations and found
respectively 181 K (Alonso et al. 1999) and 180 K
(McWilliam 1990), in perfect agreement.
over 7 evolved test stars (i.e. all test stars but HD 26354)
with the 2 calibrations and found
respectively 181 K (Alonso et al. 1999) and 180 K
(McWilliam 1990), in perfect agreement.
Alonso et al. (1996) and Alonso et al. (1999) calibrations have been derived for single stars and their validity is established only for single systems. A binary system, in which both components contribute significantly to the total flux, and at the same time differ in colours, will deviate from the colour/temperature relations. Of course, in most cases, a large difference in colour also means a large difference in brightness and therefore a small contribution of the secondary to the overall system colours.
The possible role of binarity in the discrepancies observed in the
test stars, between the B-Vand V-I temperatures, was investigated via a synthetic
grid of binary systems (computed using the isochrones of
Bertelli et al. 1994, for solar metallicity). This grid contains all possible
arrangements of primary and secondary components ranging from the top of the
giant branch to K7 dwarf (![]() 3900 K) by steps of 50 K. Several system
ages have been considered: 0.5, 1, 2, 3, 4, 5, 8, 10 and 12 Gyr.
Each arrangement is characterised by the effective
temperature
3900 K) by steps of 50 K. Several system
ages have been considered: 0.5, 1, 2, 3, 4, 5, 8, 10 and 12 Gyr.
Each arrangement is characterised by the effective
temperature![]() , evolutionary stage (dwarf or giant),
visual absolute magnitude and B-V and V-I colour indices of
each component and of the global system.
, evolutionary stage (dwarf or giant),
visual absolute magnitude and B-V and V-I colour indices of
each component and of the global system.
For each of the 8 test stars, we searched
the grid for the synthetic binary system with similar
B-V temperature and visual absolute magnitude (i.e. within ![]()
![]() of the test star parameters) that showed the largest difference
between the temperatures derived from B-V and V-I indices.
To take into account that all the test stars are single line
systems, only systems with secondary component at least 2.5 mag fainter than the primary were considered.
of the test star parameters) that showed the largest difference
between the temperatures derived from B-V and V-I indices.
To take into account that all the test stars are single line
systems, only systems with secondary component at least 2.5 mag fainter than the primary were considered.
In the case of the dwarf star HD 26354, the largest discrepancy between the B-V and V-I diagnostics is around 150 K (assuming a 1 Gyr old system with a 5200 K subdwarf as primary component and a 3900 K dwarf as secondary component). For the 7 evolved test stars, the "strongest differences'' range from 18 to 67 K with a mean of 41 K. This mean value of 41 K is small compared to the mean difference of 181 K derived from the real colours of the same 7 test stars. Moreover, the above 18 to 67 K differences represent "extreme'' cases among a large number of combinations of primary and secondary components, whose B-V and V-I colour indices lead to very similar effective temperatures. Therefore, the binarity may play a minor role in the discrepancy between the B-V and V-I temperatures, but is most likely not the dominant effect.
Unlike the
![]() transformation, both the B-V and
V-R vs. temperature relations of Alonso et al. (1999) are
sensitive to metallicity. To test whether the
above discrepancy can be solved by adjusting the iron abundances, we
performed a full detailed analysis on 4 of the previous stars,
namely HD 26354, HD 34802, HD 106225 and HD 119285, using the
second method together with the B-V index. The derived metallicities
and corresponding B-V effective temperatures are presented in
Table 4. V-I temperatures are also listed for comparison.
The metallicities of HD 34802 and HD 119285
are close to solar and therefore their temperatures are fairly similar
to those listed in Table 3. HD 26354 exhibits an iron
overabundance which increases the difference between the B-V and
V-I temperatures by about 120 K. The moderate deficiency of HD 106225,
reduces by 100 K the discrepancy between B-V and V-I, but the difference
is still about 250 K. Therefore the metallicity is unlikely to explain the
temperature discrepancy derived through the two indices, discrepancy which
may be due to stellar activity.
transformation, both the B-V and
V-R vs. temperature relations of Alonso et al. (1999) are
sensitive to metallicity. To test whether the
above discrepancy can be solved by adjusting the iron abundances, we
performed a full detailed analysis on 4 of the previous stars,
namely HD 26354, HD 34802, HD 106225 and HD 119285, using the
second method together with the B-V index. The derived metallicities
and corresponding B-V effective temperatures are presented in
Table 4. V-I temperatures are also listed for comparison.
The metallicities of HD 34802 and HD 119285
are close to solar and therefore their temperatures are fairly similar
to those listed in Table 3. HD 26354 exhibits an iron
overabundance which increases the difference between the B-V and
V-I temperatures by about 120 K. The moderate deficiency of HD 106225,
reduces by 100 K the discrepancy between B-V and V-I, but the difference
is still about 250 K. Therefore the metallicity is unlikely to explain the
temperature discrepancy derived through the two indices, discrepancy which
may be due to stellar activity.
| HD Num. |
|
|
|
| (B-V) | (V-I) | ||
| HD 26354 |
|
5085+85-77 | 4824 |
| HD 34802 |
|
4793+65-57 | 4546 |
| HD 106225 |
|
4723+38-33 | 4472 |
| HD 119285 |
|
4674+29-27 | 4436 |
The wings of "strong'' lines are collisionally broadened and therefore
gravity sensitive. In the third method, we take advantage of this
behaviour to derive the surface gravity of our stars. The wings of one
of those "strong'' lines are compared to a library of synthetic lines
spanning a large range in gravities. In a first step the grid is
searched for the most similar synthetic profile. In a second step the
difference of gravity between the best synthetic match and the
observed profile is estimated. Variations of this method have been
successfully used by several authors (e.g.
Drake & Smith 1991). Several "strong'' lines are present in the FEROS
spectral interval: the magnesium green triplet (
![]() Å), the neutral calcium red triplet (
Å), the neutral calcium red triplet (
![]() Å) and the ionised calcium infrared triplet
(
Å) and the ionised calcium infrared triplet
(
![]() Å). We used the 6162 Å
neutral calcium line whose profile is more sensitive to surface
gravity than the two other transitions of the triplet. This line
looses relatively quickly its sensitivity to gravity below
Å). We used the 6162 Å
neutral calcium line whose profile is more sensitive to surface
gravity than the two other transitions of the triplet. This line
looses relatively quickly its sensitivity to gravity below
![]() .
For more evolved stars it is more accurate to rely on the Ca
II triplet lines, whose strengths increase with decreasing
gravity. A grid of about 1600 synthetic spectra was computed with the
Kurucz' ATLAS9 (Kurucz 1993a) and SYNTHE
(Kurucz 1993b) software packages. It covers the
parameter space
.
For more evolved stars it is more accurate to rely on the Ca
II triplet lines, whose strengths increase with decreasing
gravity. A grid of about 1600 synthetic spectra was computed with the
Kurucz' ATLAS9 (Kurucz 1993a) and SYNTHE
(Kurucz 1993b) software packages. It covers the
parameter space
![]() K (by
steps of 250 K),
K (by
steps of 250 K),
![]() (by steps of 0.5),
(by steps of 0.5),
![]() km s-1,
km s-1,
![]() and
and
![]() and +0.4. Each spectrum ranges from 6000 to 6250 Å with an initial resolution of 300 000.
and +0.4. Each spectrum ranges from 6000 to 6250 Å with an initial resolution of 300 000.
The 6162 Å calcium line is not only sensitive to gravity, but
also to effective temperature, metallicity,
micro-turbulence and, of course, calcium abundance. As a
consequence, the first step in the estimation of gravity is to fix
those four parameters. The synthetic grid is then interpolated to
compute a new sub-grid at the chosen values of
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
keeping
,
keeping ![]() as the only degree
of freedom. The 10 spectra of this sub-grid are then compared with the
observed spectrum. For each comparison, the flux of the synthetic and
observed spectra are adjusted by least squares, finding the
coefficients a0 and a1 that minimise the expression:
as the only degree
of freedom. The 10 spectra of this sub-grid are then compared with the
observed spectrum. For each comparison, the flux of the synthetic and
observed spectra are adjusted by least squares, finding the
coefficients a0 and a1 that minimise the expression:
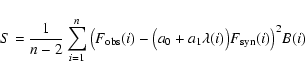 |
(1) |
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{2450f1.eps}
\end{figure}](/articles/aa/full/2003/02/aa2450/Timg80.gif) |
Figure 1: Comparison of a portion the IS Vir spectrum (thick line) and the interpolated profile (thin line). The open circles show the pixels that have been used in the interpolation. |
| Open with DEXTER | |
Once the most similar synthetic spectrum (hereafter referred as pivot)
is identified, the difference of gravity between this "twin''
synthetic profile and the observed one is derived, using a variant of
the atmospheric parameters optimal extraction method
(Cayrel et al. 1991). The 6162 Å Ca I profile is projected on the
grid, assuming that between two neighbouring synthetic spectra, the
gravity evolved linearly with the logarithm of the flux:
![]() ,
where
,
where
![]() ,
,
![]() and
and
![]() are respectively the observed
and pivot fluxes and the flux of the one out of the pivot's two
synthetic neighbours that is most similar to the observed profile.
The projection is performed by least squares, searching for the
coefficients u, a0 and a1 that minimise the expression:
are respectively the observed
and pivot fluxes and the flux of the one out of the pivot's two
synthetic neighbours that is most similar to the observed profile.
The projection is performed by least squares, searching for the
coefficients u, a0 and a1 that minimise the expression:
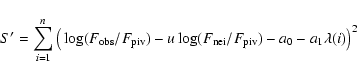 |
(2) |
The gravity of the star is then given by
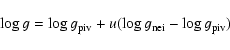 |
(3) |
| Id. | S/N |
|
|
|
||
| Sun | 380 | 5777 | 4.44 | 0.00 |
1.0 | 4.42 |
| Sun | 270 | " | " | " |
" | 4.39 |
| Sun | 140 | " | " | " |
" | 4.43 |
| Sun | 160 | " | " | " |
" | 4.43 |
| Sun | 120 | " | " | " |
" | 4.41 |
| Sun | 200 | " | " | " |
" | 4.48 |
| Sun | 220 | " | " | " |
" | 4.46 |
| HD 1835 | 140 | 5771 | 4.44 | 0.15 |
1.0 | 4.56 |
| HD 10307 | 200 | 5882 | 4.33 | 0.02 |
1.0 | 4.24 |
| HD 24040 | 150 | 5594 | 4.50 | 0.07 |
1.0 | 3.95 |
| HD 28099 | 110 | 5761 | 4.50 | 0.17 |
1.0 | 4.48 |
| HD 85503 | 180 | 4540 | 2.20 | 0.29 |
1.2 | 2.14 |
| HD 86728 | 130 | 5742 | 4.21 | 0.12 |
1.0 | 4.37 |
| HD 95128 | 180 | 5855 | 4.25 | 0.00 |
1.0 | 4.14 |
| HD 113226 | 140 | 4990 | 2.70 | 0.11 |
1.6 | 2.33 |
| HD 114710 | 90 | 5979 | 4.40 | 0.08 |
1.0 | 4.22 |
| HD 115383 | 110 | 5920 | 3.96 | 0.10 |
1.3 | 4.16 |
| HD 146233 | 240 | 5803 | 4.34 | 0.03 |
1.0 | 4.48 |
| HD 184406 | 80 | 4450 | 2.47 | 1.8 | 2.64 | |
| HD 186408 | 160 | 5820 | 4.26 | 0.07 |
1.0 | 4.31 |
| HD 186427 | 140 | 5762 | 4.38 | 0.06 |
1.0 | 4.39 |
| HD 187691 | 160 | 6101 | 4.22 | 0.09 |
1.0 | 4.21 |
| HD 217014 | 160 | 5757 | 4.23 | 0.15 |
1.0 | 4.24 |
| HD 219134 | 150 | 4727 | 4.50 | 0.05 |
1.0 | 4.55 |
The reliability of the method was tested on a subsample of the
ELODIE![]() library of standard stars
(Soubiran et al. 1998; Prugniel & Soubiran 2001). This library, in
addition to the spectra, provides values of
library of standard stars
(Soubiran et al. 1998; Prugniel & Soubiran 2001). This library, in
addition to the spectra, provides values of
![]() ,
,
![]() and
and
![]() for each star. The ELODIE spectra are relatively
similar in characteristics to FEROS spectra, with a resolution of 42 000 and a wavelength domain ranging from 3900 to 6800 Å. We
applied the gravity determination method to 24 spectra from the
library: 7 spectra of the Sun (Moon), 17 main sequence star spectra
and 4 evolved star spectra. We assumed a calcium abundance proportional to
the solar one (
for each star. The ELODIE spectra are relatively
similar in characteristics to FEROS spectra, with a resolution of 42 000 and a wavelength domain ranging from 3900 to 6800 Å. We
applied the gravity determination method to 24 spectra from the
library: 7 spectra of the Sun (Moon), 17 main sequence star spectra
and 4 evolved star spectra. We assumed a calcium abundance proportional to
the solar one (
![]() )
for all stars, a
micro-turbulence of 1 km s-1 for the main sequence stars and
searched the literature for the micro turbulence of the evolved
objects. Table 5 list the stars used, their adopted
atmospheric parameters and the surface gravities estimated with our
method. The average difference between the estimated and the
bibliographic gravities is -0.02 with a dispersion of 0.16.
A test performed on IS Vir has shown that systematically shifting
the calcium line fitting gravity diagnostic by
)
for all stars, a
micro-turbulence of 1 km s-1 for the main sequence stars and
searched the literature for the micro turbulence of the evolved
objects. Table 5 list the stars used, their adopted
atmospheric parameters and the surface gravities estimated with our
method. The average difference between the estimated and the
bibliographic gravities is -0.02 with a dispersion of 0.16.
A test performed on IS Vir has shown that systematically shifting
the calcium line fitting gravity diagnostic by
![]() modifies the third method result
by
modifies the third method result
by
![]() K,
K,
![]() ,
,
![]() dex and
dex and
![]() km s-1.
This error is accounted for in the error bars given for IS Vir and
V851 Cen in Tables 6 and 7.
km s-1.
This error is accounted for in the error bars given for IS Vir and
V851 Cen in Tables 6 and 7.
| meth. 1 | meth. 2 | meth. 3 | |||||||||
| n | <> | n | <> | n | <> | ||||||
|
|
4720 | 100 | 4690 | 150 | 4780 | 185 | |||||
| 2.65 | 0.25 | 2.55 | 0.41 | 2.75 | 0.45 | ||||||
| 1.65 | 0.08 | 1.65 | 0.11 | 1.60 | 0.13 | ||||||
|
|
44 | +0.04 | 0.08 | 36 | +0.02 | 0.13 | 36 | +0.09 | 0.16 | ||
|
|
1 | +0.23 | 0.04 | 1 | +0.23 | 0.04 | 1 | +0.23 | 0.04 | ||
|
|
1 | +0.17 | 0.06 | 1 | +0.18 | 0.06 | 1 | +0.18 | 0.06 | ||
|
|
3 | +0.18 | 0.06 | 3 | +0.19 | 0.07 | 3 | +0.16 | 0.08 | ||
|
|
7 | +0.06 | 0.05 | 7 | +0.07 | 0.08 | 7 | +0.02 | 0.11 | ||
|
|
4 | +0.11 | 0.04 | 4 | +0.10 | 0.04 | 4 | +0.13 | 0.06 | ||
|
|
1 | +0.05 | 0.05 | 1 | +0.03 | 0.09 | 1 | +0.08 | 0.12 | ||
|
|
2 | +0.05 | 0.04 | 2 | +0.04 | 0.04 | 2 | +0.06 | 0.05 | ||
|
|
2 | -0.04 | 0.07 | 2 | -0.04 | 0.07 | 2 | -0.04 | 0.08 | ||
|
|
9 | -0.10 | 0.03 | 9 | -0.10 | 0.04 | 9 | -0.10 | 0.04 | ||
| meth. 1 | meth. 2 (B-V/V-I) | meth. 3 | |||||||||||||
| n | <> | n | <> | n | <> | n | <> | ||||||||
|
|
4700 | 80 | 4670 | 150 | 4440 | 100 | 4780 | 160 | |||||||
| 3.00 | 0.27 | 2.90 | 0.42 | 2.25 | 0.32 | 3.23 | 0.41 | ||||||||
| 1.50 | 0.07 | 1.50 | 0.12 | 1.60 | 0.10 | 1.40 | 0.13 | ||||||||
|
|
46 | -0.13 | 0.07 | 36 | -0.14 | 0.12 | 36 | -0.31 | 0.10 | 36 | -0.04 | 0.15 | |||
|
|
1 | +0.30 | 0.03 | 1 | +0.29 | 0.04 | 1 | +0.28 | 0.04 | 1 | +0.27 | 0.04 | |||
|
|
1 | +0.41 | 0.07 | 1 | +0.39 | 0.07 | 1 | +0.44 | 0.07 | 1 | +0.35 | 0.04 | |||
|
|
3 | +0.46 | 0.07 | 3 | +0.46 | 0.08 | 3 | +0.51 | 0.10 | 3 | +0.41 | 0.08 | |||
|
|
6 | +0.15 | 0.04 | 6 | +0.14 | 0.07 | 6 | +0.26 | 0.06 | 6 | +0.08 | 0.09 | |||
|
|
4 | +0.22 | 0.04 | 4 | +0.21 | 0.06 | 4 | +0.14 | 0.05 | 4 | +0.22 | 0.06 | |||
|
|
2 | +0.24 | 0.10 | 2 | +0.22 | 0.13 | 2 | +0.06 | 0.10 | 2 | +0.30 | 0.15 | |||
|
|
2 | +0.19 | 0.04 | 2 | +0.17 | 0.05 | 2 | +0.12 | 0.05 | 2 | +0.18 | 0.05 | |||
|
|
2 | +0.07 | 0.04 | 2 | +0.06 | 0.04 | 2 | +0.04 | 0.04 | 2 | +0.06 | 0.05 | |||
|
|
9 | -0.06 | 0.03 | 9 | -0.07 | 0.04 | 9 | -0.09 | 0.03 | 9 | -0.06 | 0.04 | |||
The atmospheric parameters and abundances derived for IS Vir and V851 Cen,
with the three methods outlined in Sect. 3,
are presented in
Tables 6 and 7.
The error bars were derived in several steps. First, the 1 ![]() errors
on each of the "individual'' diagnostics (e.g. average slope of Fe I
abundances versus excitation potentials relation)
were calculated. They were then propagated to obtain the "individual''
errors on the atmospheric parameters and abundances. Finally, those
"individual'' errors were quadratically summed.
errors
on each of the "individual'' diagnostics (e.g. average slope of Fe I
abundances versus excitation potentials relation)
were calculated. They were then propagated to obtain the "individual''
errors on the atmospheric parameters and abundances. Finally, those
"individual'' errors were quadratically summed.
Our concern with the first method was that Fe I "low excitation potential'' transitions may be affected by non-LTE effects. This does not seem the case neither for IS Vir nor for V851 Cen since, in both cases, methods 1 and 3 (the first using Fe I "low excitation potential'' iron transitions and the other not) give results in good agreement. Cooler or more evolved stars might, of course, exhibit stronger departure from LTE and would require some careful checking.
The B-V index leads to effective temperatures in very good agreement
with those derived with the first method and 90 and 110 K lower,
for IS Vir and V851 Cen respectively, than those derived with the third
method. Given the error bars of the second and third methods (respectively 150 and 185 K for IS Vir and 150 and 160 K for V851 Cen), their results
are compatible within less than one sigma error. As already presented
in Sect. 3.6, the temperature derived for V851 Cen from the
![]() index is about 230 K lower than the one derived from B-V.
This is respectively 260 and 340 K lower than the temperatures obtained
via the first and third methods.
Neither IS Vir, nor V851 Cen display a significant departure
from the B-V/temperature relation of non-active stars,
whereas the V-I index deviate from the V-I/temperature
calibration. This behaviour may be due to the presence of
activity.
index is about 230 K lower than the one derived from B-V.
This is respectively 260 and 340 K lower than the temperatures obtained
via the first and third methods.
Neither IS Vir, nor V851 Cen display a significant departure
from the B-V/temperature relation of non-active stars,
whereas the V-I index deviate from the V-I/temperature
calibration. This behaviour may be due to the presence of
activity.
The third method exhibits fairly large error bars. This is in part due to its dependency on the knowledge of the calcium abundance, which relies on four lines (2 of them being on the "plateau'' of the curve of growth) and in part due to the propagation, on the final results, of the error bars on the surface gravity (derived by calcium wings fitting, see Sect. 3.7). Nonetheless it has the merit of relying on criteria which present few risks of being affected by non-LTE or activity effects, as well as being self-consistent. As discussed above, the results of methods 1 and 3 are consistent.
The following discussion is based on the parameters derived with the first method (using both "low'' and "high'' excitation potential transitions). Opting for the parameters derived with one of the two other methods (at the exception of V-I temperature diagnostic) would not significantly alter the conclusions.
IS Vir is a giant star of near-solar metallicity. Its position
in the H-R diagram (using
![]() determined in this work
and Mv derived from
Hipparcos parallaxes) is plotted in Fig. 2 (circle),
together with four isochrones of respective ages 0.5, 1.0, 5.0 and 10 Gyr, derived using solar metallicity
(Bertelli et al. 1994). The mass and bolometric magnitude tabulated by
Bertelli et al. (1994) for a 1 Gyr old star with
determined in this work
and Mv derived from
Hipparcos parallaxes) is plotted in Fig. 2 (circle),
together with four isochrones of respective ages 0.5, 1.0, 5.0 and 10 Gyr, derived using solar metallicity
(Bertelli et al. 1994). The mass and bolometric magnitude tabulated by
Bertelli et al. (1994) for a 1 Gyr old star with
![]() K,
K,
![]() and
and
![]() ,
correspond
to a surface gravity of
,
correspond
to a surface gravity of
![]() ,
in perfect agreement
with the spectroscopic gravity derived here. This area of
the H-R diagram is too dense to
determine the evolutionary stage of the star, i.e. whether it is at
the beginning of the giant branch or a giant of the clump, or its age
(error bars on
,
in perfect agreement
with the spectroscopic gravity derived here. This area of
the H-R diagram is too dense to
determine the evolutionary stage of the star, i.e. whether it is at
the beginning of the giant branch or a giant of the clump, or its age
(error bars on
![]() are still compatible at the 1.5
are still compatible at the 1.5 ![]() level with a 5 or 10 Gyr clump star
level with a 5 or 10 Gyr clump star![]() ). Its chemical mix is somewhat
different from the the solar one, with Na, Mg, Al and Ca exhibiting
overabundances of 0.1 to 0.2 dex with respect to Fe. The Na and Mg abundances should be considered with caution, since they both rely on
a single line of the curve of growth "plateau''. The ratio [Ni/Fe] is
somewhat lower than in the Sun.
). Its chemical mix is somewhat
different from the the solar one, with Na, Mg, Al and Ca exhibiting
overabundances of 0.1 to 0.2 dex with respect to Fe. The Na and Mg abundances should be considered with caution, since they both rely on
a single line of the curve of growth "plateau''. The ratio [Ni/Fe] is
somewhat lower than in the Sun.
V851 Cen is a slightly metal-poor evolved star. Its position in
the H-R diagram (Fig. 2, square) shows that it is
a several Gyr old
star, starting the ascension of the giant branch. The 10 Gyr isochrone
leads to a gravity of
![]() for a temperature of 4700 K, in
reasonable agreement with the spectroscopic determination. Its
chemical composition displays some similarities with the one of IS Vir,
with (stronger) overabundances of Na, Mg, Al and Ca ranging from +0.2 to +0.5 dex. In addition Si, Sc and Ti are also over-abundant by +0.15 to +0.25 dex.
for a temperature of 4700 K, in
reasonable agreement with the spectroscopic determination. Its
chemical composition displays some similarities with the one of IS Vir,
with (stronger) overabundances of Na, Mg, Al and Ca ranging from +0.2 to +0.5 dex. In addition Si, Sc and Ti are also over-abundant by +0.15 to +0.25 dex.
V851 Cen is one of the stars studied by Randich et al. (1993).
With a value of
B-V = 1.07 they derived an effective temperature of
![]() K, very close to our (B - V) photometric determination
(
K, very close to our (B - V) photometric determination
(
![]() K) and 50 K colder than our first method
estimate. They found a gravity larger by
K) and 50 K colder than our first method
estimate. They found a gravity larger by
![]() .
The largest discrepancy between our analysis and theirs
concern the metallicity, as they derived an iron abundance of
.
The largest discrepancy between our analysis and theirs
concern the metallicity, as they derived an iron abundance of
![]() ,
,
![]() -0.5 dex lower than our determination.
-0.5 dex lower than our determination.
As a caveat, it should be reminded that abundances have been derived, here, under the assumption of an atmosphere which can be represented through a single plane parallel model and that the lines were formed under LTE conditions. Clearly, the behaviour of the colour indices described above shows that this assumption is likely to be a simplification of reality in these stars. On the other hand, it is reassuring to note that three different methods lead to converging results. However, as shown in Tables 6 and 7, while the absolute abundance values depend on the effective temperature, most abundance ratios (i.e. Na, Mg, Al, Ca, Ti, Co and Ni over Fe) appears relatively insensitive to the assumed temperature. Therefore, even in an atmosphere which is a superposition of models with different effective temperatures, the abundance pattern should remain largely unchanged. In general, all the other analyses of abundances in active stars have also been carried out under the same assumptions, so that the resulting bias, if present, should be common to all works.
![\begin{figure}
\par\includegraphics[angle=90,width=8.8cm,clip]{2450f2.eps}
\end{figure}](/articles/aa/full/2003/02/aa2450/Timg115.gif) |
Figure 2: The position of IS Vir (circle) and V851 Cen (square) in the H-R diagram using the temperatures derived here, plotted with four solar metallicity isochrones of respective ages 0.5, 1.0, 5.0 and 10.0 Gyr (from top to bottom) from Bertelli et al. (1994). |
| Open with DEXTER | |
The high-resolution optical spectra of the two X-ray active binaries RS CVn stars HD 113816 (IS Vir) and HD 119285 (V851 Cen) have been analysed, using three different techniques. The techniques have been compared in order to establish their respective merits and drawbacks. The present results show that the Fe I low excitation potential transitions do not appear significantly affected by non-LTE effects, and, as a consequence, the iron excitation equilibrium is a reliable diagnostic in the two studied RS CVn. At the same time, the V-I photometric index gives significantly colder (and by comparison with the other approaches, likely underestimated) effective temperatures than the B-V index.
Both IS Vir and V851 Cen are found to be near-solar metallicity giants, with the latter somewhat underabundant in Fe (but significantly more metal rich, for V851 Cen, than found by Randich et al. 1994). Both stars present overabundances with respect to the solar pattern of their Na, Mg, Al and Ca to Fe ratios. In addition IS Vir exhibits a modest underabundance in Ni, while V851 Cen shows overabundances of Si, Sc and Ti. The analysis of a large sample will be interesting to see whether this apparent peculiar abundance pattern is a general characteristic of active binaries.
Acknowledgements
We are very grateful to R. Kurucz, C. Sneden and the VALD people for making their software packages and atomic and molecular data available to the community. We would like to thank F. Arenou, B. Barbuy, V. Hill, M. Spite, F. Spite, C. van 't Veer, I. Pillitteri and J. Drake for the very fruitful discussions and advice.
| IS Vir | V851 Cen | ||||||
| (eV) | (Ka 02) | (Ed 93) | (Ne 97) | (Fe 01) | W (mÅ) | W (mÅ) | |
|
Na I;
|
|||||||
| 6154.226 | 2.10 | -1.580 | -1.61 | -1.58 | 102.4 | 95.6 | |
| Mg I;
|
|||||||
| 5711.088 | 4.35 | -1.653 | 155.1 | 158.4 | |||
| Al I;
|
|||||||
| 6698.673 | 3.14 | -1.867 | -1.837 | -1.89 | 65.7 | 69.5 | |
| 7084.643 | 4.02 | -1.136 | 57.3 | 66.0 | |||
| 7835.309 | 4.02 | -0.689 | -0.78 | 83.3 | 93.3 | ||
| Si I;
|
|||||||
| 6029.869 | 5.98 | -1.550 | 26.8 | 20.0 | |||
| 6125.021 | 5.61 | -1.490 | -1.54 | -1.55 | 50.8 | 41.8 | |
| 6155.134 | 5.62 | -0.730 | -0.77 | 82.7 | 72.9 | ||
| 6194.416 | 5.87 | -1.540 | 26.7 | 21.8 | |||
| 6195.433 | 5.87 | -1.570 | 32.3 | 24.8 | |||
| 6237.319 | 5.61 | -1.010 | -1.15 | 74.8 | 67.8 | ||
| 6721.848 | 5.86 | -1.080 | -1.16 | 57.7 | |||
| Ca I;
|
|||||||
| 5867.562 | 2.93 | -1.591 | -1.61 | -1.534 | -1.61 | 76.9 | 68.5 |
| 6156.023 | 2.52 | -2.410 | 53.0 | 50.2 | |||
| 6166.439 | 2.52 | -1.100 | -1.20 | -1.078 | -1.22 | 133.4 | 127.4 |
| 6455.598 | 2.52 | -1.370 | -1.344 | -1.48 | 125.3 | 120.9 | |
| Sc II;
|
|||||||
| 6245.637 | 1.51 | -1.010 | -1.066 | 81.8 | 78.9 | ||
| 6320.851 | 1.50 | -1.800 | 26.9 | ||||
| Ti I;
|
|||||||
| 5766.359 | 3.29 | 0.329 | 46.5 | 46.1 | |||
| 6098.658 | 3.06 | -0.010 | -0.07 | 42.5 | 39.9 | ||
| Fe I;
|
|||||||
| 5833.926 | 2.61 | -3.730 | 65.5 | 47.1 | |||
| 5855.076 | 4.61 | -1.730 | -1.72 | -1.646 | -1.70 | 52.0 | 41.1 |
| 5856.088 | 4.29 | -1.750 | -1.76 | 72.0 | 61.1 | ||
| 5861.109 | 4.28 | -2.480 | -2.50 | -2.491 | 34.8 | 24.0 | |
| 6012.210 | 2.22 | -3.990 | 86.0 | 69.2 | |||
| 6027.051 | 4.08 | -1.290 | 110.2 | 94.0 | |||
| 6056.005 | 4.73 | -0.550 | 106.6 | 92.2 | |||
| 6078.491 | 4.80 | -0.451 | 115.2 | 100.3 | |||
| 6079.008 | 4.65 | -1.150 | 88.5 | 76.3 | |||
| 6093.643 | 4.61 | -1.540 | -1.443 | 58.0 | 45.9 | ||
| 6094.373 | 4.65 | -1.770 | -1.698 | -1.74 | 47.0 | 35.2 | |
| 6098.244 | 4.56 | -1.970 | -1.861 | 45.5 | 34.2 | ||
| 6151.617 | 2.18 | -3.510 | -3.49 | -3.404 | -3.489 | 122.1 | 103.8 |
| 6157.728 | 4.08 | -1.360 | -1.40 | -1.44 | 119.2 | 97.6 | |
| 6165.360 | 4.14 | -1.670 | -1.69 | -1.684 | 83.8 | 71.9 | |
| 6307.854 | 3.64 | -3.599 | 25.8 | 17.8 | |||
| 6335.330 | 2.20 | -2.450 | 171.9 | ||||
| 6336.823 | 3.69 | -0.910 | 162.5 |
| IS Vir | V851 Cen | ||||||
| (eV) | (Ka 02) | (Ed 93) | (Ne 97) | (Fe 01) | W (mÅ) | W (mÅ) | |
| 6385.718 | 4.73 | -2.010 | -1.962 | -1.98 | 33.8 | 24.0 | |
| 6436.406 | 4.19 | -2.550 | 39.1 | 29.5 | |||
| 6593.870 | 2.43 | -2.472 | 152.2 | ||||
| 6699.141 | 4.59 | -2.180 | -2.215 | 27.4 | 19.6 | ||
| 6713.743 | 4.80 | -1.640 | -1.547 | 46.2 | 31.5 | ||
| 6725.356 | 4.10 | -2.380 | -2.277 | 47.3 | 34.3 | ||
| 6726.666 | 4.61 | -1.212 | -1.239 | 78.1 | 65.5 | ||
| 6750.152 | 2.42 | -2.741 | -2.801 | 159.8 | 134.8 | ||
| 6793.258 | 4.08 | -2.580 | 42.9 | 29.5 | |||
| 6806.843 | 2.73 | -3.300 | -3.27 | 100.4 | 86.2 | ||
| 6810.262 | 4.61 | -1.150 | -1.186 | 87.8 | 76.8 | ||
| 6857.249 | 4.08 | -2.280 | 53.8 | 43.4 | |||
| 6861.937 | 2.42 | -3.990 | 81.7 | 65.1 | |||
| 6862.493 | 4.56 | -1.590 | 62.8 | 50.2 | |||
| 7142.517 | 4.96 | -1.139 | 78.2 | 58.0 | |||
| 7148.725 | 4.28 | -2.297 | 51.6 | 44.2 | |||
| 7411.153 | 4.28 | -0.418 | 157.5 | 132.1 | |||
| 7447.394 | 4.96 | -1.144 | 75.5 | 57.0 | |||
| 7498.530 | 4.14 | -2.320 | -2.29 | 63.1 | 50.5 | ||
| 7563.010 | 4.84 | -1.656 | 44.5 | ||||
| 7583.788 | 3.02 | -2.040 | 152.4 | 131.8 | |||
| 7748.269 | 2.95 | -1.760 | 184.0 | 165.0 | |||
| 7780.557 | 4.47 | -0.151 | 145.5 | ||||
| 7807.909 | 4.99 | -0.614 | 90.5 | 81.0 | |||
| Fe II;
|
|||||||
| 5991.376 | 3.15 | -3.727 | -3.718 | 44.6 | 29.9 | ||
| 6084.111 | 3.20 | -3.988 | -3.968 | 31.0 | |||
| 6149.258 | 3.89 | -2.874 | -2.96 | -3.00 | 48.1 | 32.1 | |
| 6247.557 | 3.89 | -2.419 | -2.55 | 63.6 | 48.1 | ||
| 6432.680 | 2.89 | -3.758 | -3.80 | 56.1 | 38.8 | ||
| 6456.383 | 3.90 | -2.235 | -2.40 | 79.4 | 55.5 | ||
| Co I;
|
|||||||
| 6595.864 | 3.71 | -0.647 | 26.7 | 20.8 | |||
| 7838.134 | 3.97 | -0.300 | 25.0 | 21.2 | |||
| Ni I;
|
|||||||
| 5805.213 | 4.17 | -0.580 | 62.1 | 51.2 | |||
| 6111.066 | 4.09 | -0.790 | -0.96 | -0.739 | -0.86 | 62.2 | 52.2 |
| 6176.807 | 4.09 | -0.170 | -0.37 | -0.27 | 90.9 | 80.8 | |
| 6204.600 | 4.09 | -1.110 | -1.17 | -1.063 | -1.146 | 46.9 | 33.6 |
| 6598.593 | 4.24 | -0.860 | -0.883 | -0.94 | 55.4 | 39.9 | |
| 6772.313 | 3.66 | -0.910 | -1.082 | 83.4 | 70.9 | ||
| 7525.111 | 3.64 | -0.516 | -0.64 | 120.5 | 106.3 | ||
| 7555.598 | 3.85 | 0.074 | 131.1 | 111.5 | |||
| 7797.586 | 3.90 | -0.172 | -0.40 | 119.7 | 105.2 |