A&A 397, 353-359 (2003)
DOI: 10.1051/0004-6361:20021518
P. Oberti1 - A. Vienne2
1 - Observatoire de la Côte d'Azur,
BP 4229, 06304 Nice Cedex 4, France
2 -
Institut de mécanique céleste et de calcul des éphémérides,
UMR 8028 du CNRS and
Université de Lille, 1 impasse de l'Observatoire, 59000 Lille, France
Received 1 August 2002 / Accepted 10 October 2002
Abstract
A tridimensional model including the perturbation due to
Saturn's oblateness provides accurate solutions for the motions of
Tethys and Dione's Lagrangian satellites Telesto,
Calypso, and Helene. Expanded around the Lagrangian points and
compared to numerical simulations to check their reliabilities, the solutions
are fitted to almost twenty years of data thanks to recently published
observations. User-friendly compact series give Telesto,
Calypso, and Helene's positions and velocities in the mean
ecliptic and equinox of J2000.
Key words: planets and satellites: individual: Saturn - planets and satellites: general - celestial mechanics
Recently published observations of Tethys and Dione's Lagrangian satellites Telesto, Calypso, and Helene (Veiga & Vieira Martins 2000; Veiga et al. 2002), give an opportunity to revisit and improve the theory of their motions to face an almost 2-decade observation time span.
The mass ratios Tethys/Saturn
(
![]() )
and Dione/Saturn
(
)
and Dione/Saturn
(
![]() )
ensure the stability of the Lagrangian points L4and L5 in the Restricted Circular 3-Body Problem. Due to the 1:1-resonance
with the companion, a satellite around these positions shows librations in its
motion resulting in a tadpole-shaped orbit in a rotating reference frame.
Expansions around the equilibrium positions provided accurate solutions in the
bidimensional case (Deprit & Rom 1970).
)
ensure the stability of the Lagrangian points L4and L5 in the Restricted Circular 3-Body Problem. Due to the 1:1-resonance
with the companion, a satellite around these positions shows librations in its
motion resulting in a tadpole-shaped orbit in a rotating reference frame.
Expansions around the equilibrium positions provided accurate solutions in the
bidimensional case (Deprit & Rom 1970).
Pointed out as a significant perturbation by numerical simulations, Saturn's oblateness (through the first zonal coefficient of Saturn's potential developed in spherical harmonics) was then introduced in the model by addition of perturbing terms in the second and following orders of the previously expanded non-perturbed Hamiltonian (Oberti 1990).
This new theory, now developed in a tridimensional context, deals with the perturbation at the uppermost level of the expansion, the quadratic part of the Hamiltonian (generally called H0), improving the convergence of the solution and offering an explicit generalization suitable for other studies.
Moreover, the model could prove useful for the analysis of the CASSINI space probe's accurate observations of these faint satellites that should be obtained during its nearing exploration of the Saturnian system.
For the sake of convenience, computations are carried out in
dimensionless units (Szebehely 1967). The distance between the
primaries, and the sum of their masses (called
![]() for the second
primary and
for the second
primary and ![]() for Saturn), are assumed to be unity. The reference
frame is a barycentric rotating frame with a rotational period of
for Saturn), are assumed to be unity. The reference
frame is a barycentric rotating frame with a rotational period of ![]() (in
dimensionless time
(in
dimensionless time ![]() ), where the value of k will be computed in order to
insure a consistent model involving fixed primaries. The xy-plane contains the
primaries, the x-axis being located along the primaries and positively
oriented from Saturn toward the second primary.
), where the value of k will be computed in order to
insure a consistent model involving fixed primaries. The xy-plane contains the
primaries, the x-axis being located along the primaries and positively
oriented from Saturn toward the second primary.
The theory will be expanded around L4. Dealing with the symmetrical point L5 requires only slight modifications indicated in Sect. 7.
With
![]() ,
L4 is located at the point
,
L4 is located at the point
![]() .
.
Let x, y, z be the satellite's Cartesian coordinates and Px, Py, Pz their conjugate variables in the barycentric rotating frame.
The Hamiltonian of the motion is:
![\begin{eqnarray*}H={1\over2}\left(P_x^2+P_y^2+P_z^2\right)-k\left(xP_y-yP_x\righ...
...er r^2}\left(1-{3z^2\over r^2}\right)\right]
-{\mu\over\Delta},
\end{eqnarray*}](/articles/aa/full/2003/01/aa2969/img9.gif)
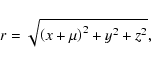
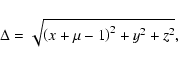
L4 is no longer an equilibrium position (Sharma & Subba Rao
1976). The conditions:
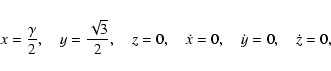
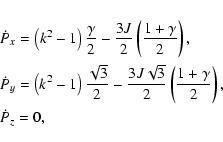
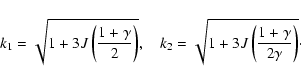
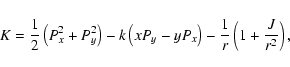
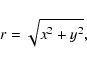
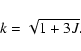
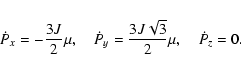
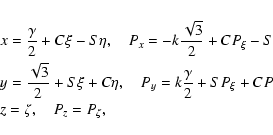
Applying the transformation turns the Hamiltonian into:
![\begin{eqnarray*}H={1\over2}\left(P_\xi^2+P_\eta^2+P_\zeta^2\right)
-k\left(\xi...
...1
-{3~\zeta^2\over r^2}\right)\right]-{{1-\gamma}\over2\Delta},
\end{eqnarray*}](/articles/aa/full/2003/01/aa2969/img26.gif)
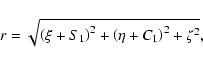
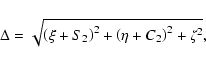
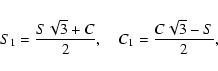
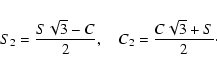
Using, for example, the software Mathematica, we expand the
functions of the coordinates in the vicinity of
![]() :
:
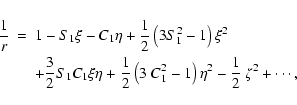
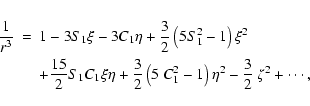
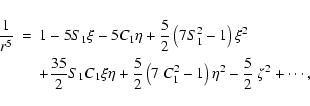
Neglecting the remainder:
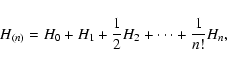
Defining:
![\begin{displaymath}\alpha={3\over4}\left[1+5J\left({1+\gamma\over2}\right)\right...
...a={3\over4}\left[\gamma+5J\left({1+\gamma\over2}\right)\right],\end{displaymath}](/articles/aa/full/2003/01/aa2969/img39.gif)
![\begin{eqnarray*}H_0&=&{1\over2}\left(P_\xi^2+P_\eta^2+P_\zeta^2\right)
-k\left...
...ft[-1-9J\left({1+\gamma\over2}\right)\right]{\zeta^2\over2}\cdot
\end{eqnarray*}](/articles/aa/full/2003/01/aa2969/img40.gif)
Removing the ![]() -term leads to:
-term leads to:
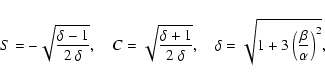
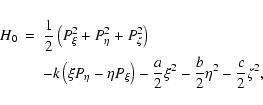
![\begin{displaymath}a={1\over2}\left[1-{3\over2}~\delta+3J\left({1
+\gamma\over2}\right)\left(3-{5\over2}~\delta\right)\right],\end{displaymath}](/articles/aa/full/2003/01/aa2969/img46.gif)
![\begin{displaymath}b={1\over2}\left[1+{3\over2}~\delta+3J\left({1
+\gamma\over2}\right)\left(3+{5\over2}~\delta\right)\right],\end{displaymath}](/articles/aa/full/2003/01/aa2969/img47.gif)
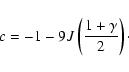
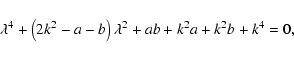
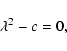
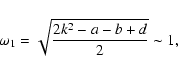
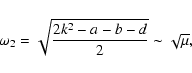
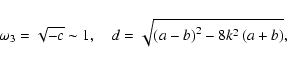
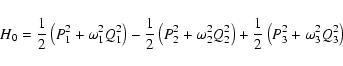
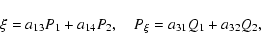
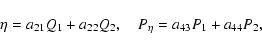
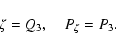
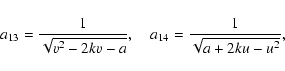
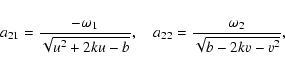
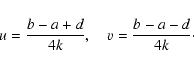
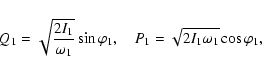
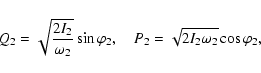
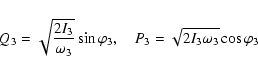
Normalizing H0, the
![]() -variables are suitable for
performing a nth-order Lie transformation
-variables are suitable for
performing a nth-order Lie transformation
![]() on the approximation H(n) of the Hamiltonian of the motion (Deprit 1969). First, the last two
canonical transformations are applied to the components H1, H2, ...,
Hn for dealing with
on the approximation H(n) of the Hamiltonian of the motion (Deprit 1969). First, the last two
canonical transformations are applied to the components H1, H2, ...,
Hn for dealing with
![]() -variables. Then, the Lie algorithm is
carried out using an algebraic processor from the University of Namur (Moons
1991). It results in a nth-order normalized Hamiltonian depending
only on the variables
-variables. Then, the Lie algorithm is
carried out using an algebraic processor from the University of Namur (Moons
1991). It results in a nth-order normalized Hamiltonian depending
only on the variables
![]() ,
providing nth-order solutions in the
vicinity of the equilibrium position.
,
providing nth-order solutions in the
vicinity of the equilibrium position.
The Lie algorithm was carried out up to the fourth order mainly to accurately compute the frequencies of the motion (they are only updated at even steps). It gives the theory a better reliability for prediction. Non-significant solution terms (with respect to the statistics of the solution) will be removed after the fit to the observations.
The development process is a bit less straightforward than in the case of the geosynchronous satellite because of extra terms that are not canceled by the orientation of the normal frame (Oberti 1994). To increase the convergence, each even generator has to be completed by polynomials in the action variables devoted to removing solution terms having the unfortunate propensity to grow too fast.
The value of the theory in the dimensionless space, at a selected time
![]() ,
depends on six internal parameters: three amplitudes I01,
I02, I03, and three phases
,
depends on six internal parameters: three amplitudes I01,
I02, I03, and three phases
![]() ,
,
![]() ,
,
![]() (dropping the primes to save writing). When going back to the real world,
another two (external) parameters can be fitted for fine tuning: the
companion's longitude
(dropping the primes to save writing). When going back to the real world,
another two (external) parameters can be fitted for fine tuning: the
companion's longitude ![]() at
at ![]() (its initial value is provided by
the companion's theory) and the scaling factor r0 between the theoretical
space and the actual one (its initial value is computed from the companion's
observed period).
(its initial value is provided by
the companion's theory) and the scaling factor r0 between the theoretical
space and the actual one (its initial value is computed from the companion's
observed period).
With an expansion around the equilibrium position, the accuracy of the theory strongly depends on the satellite's libration amplitude, and its ability to correctly represent the motion increases with the development order. To check the inner limits of the theory (due to the finite expansion of the Hamiltonian), the solution was fitted by least squares (internal parameters only) to a numerical integration of the same Hamiltonian system over twenty years.
With initial values causing libration amplitudes of 10, 20, 30, 40, and 50
degrees, the accuracy is of order 10-6, 10-4, 10-3, 10-2,
and
![]() arcsec. Helene's libration amplitude being of
order 30 degrees, and Telesto and Calypso's much smaller, the
theory qualifies for the job regarding this test.
arcsec. Helene's libration amplitude being of
order 30 degrees, and Telesto and Calypso's much smaller, the
theory qualifies for the job regarding this test.
The theory assumes a non-Keplerian circular motion for the second primary and doesn't take into account the neighboring satellites. To check the outer limits of the theory (due to this more complex environment), the solution was fitted by least squares to simulated observations generated at each observation time by a numerical integration of the studied satellite. The numerical model, including the first six Saturn's satellites (Vienne & Duriez 1995; Duriez & Vienne 1997) was previously fitted to the actual observations.
When only the six internal parameters are fitted, the precision strongly depends on the initial time chosen for the series through the induced companion's initial position. Its average value is of order 0.15 arcsec for the three satellites. Allowing the fit of the companion's initial longitude removes this dependency, and the precision is about 0.03 arcsec for Helene, 0.05 arcsec for Telesto, and 0.08 arcsec for Calypso. The effect of the last parameter (the scaling factor) is barely visible. Despite a greater libration amplitude, Helene's motion seems to be a bit more accurately modeled, possibly because the motion of Tethys is less regular than Dione's.
Here again, the theory pass the test for the three satellites.
The last test shows the relevance of the model: without or with Saturn's oblateness (IJ=0 or 1) and bidimensional or tridimensional (ID=2 or 3). To remove any side effects, the companion's longitude and the scaling factor were fitted in every case. The resulting precisions are summarized in Table 1, in arcsec, for the different values of IJ/ID. Comparatively to the basic model (0/2), only the combination of the two extensions seems to make the difference...
| Model | Helene | Telesto | Calypso |
| 0/2 | 0.20 | 0.60 | 0.75 |
| 0/3 | 0.15 | 0.40 | 0.65 |
| 1/2 | 0.10 | 0.55 | 0.60 |
| 1/3 | 0.03 | 0.05 | 0.08 |
They are performed using the observations from Reitsema (1981a, 1981b) obtained in 1980 and 1981 for Helene (20 obs.), Telesto (2 obs.), and Calypso (4 obs.), the observations from Oberti et al. (1989) obtained in 1981, 1982, 1984, and 1985 for Helene (133 obs.), Telesto (46 obs.), and Calypso (93 obs.), the observations from Veiga & Vieira Martins (2000) obtained in 1985 and 1987 for Helene (22 obs.), and the observations from Veiga et al. (2002) obtained in 1995 and 1996 for Helene (46 obs.), Telesto (13 obs.), and Calypso (19 obs.), the latter being deduced from the positions of the major satellites as exposed in Vienne et al. (2001).
For each satellite, three different fits were performed using first the observations from 1980 to 1987, then the observations from 1995 to 1996, and finally all the observations. The precisions of the resulting solutions are summarized in Table 2, in arcsec. The residuals from Veiga et al. (2002) were 0.15 arcsec for Helene, 1.43 arcsec for Telesto, and 0.42 arcsec for Calypso.
The selected solutions are the ones computed from the whole set of observations. Deduced from these solutions, the respective libration angles for Helene, Telesto, and Calypso are of order 28.5, 4.5, and 10.5 degrees, and their respective long-period libration periods are of order 783, 662.5, and 663.5 days.
| Data | Helene | Telesto | Calypso |
| 1980-1987 |
|
|
|
| 1995-1996 |
|
|
|
| 1980-1996 |
|
|
|
For each satellite, the fitted solution gives the Cartesian
coordinates and their conjugate variables in the theoretical space. They are
developed in trigonometric polynomials involving three time-depending angles
![]() ,
,
![]() ,
,
![]() :
:
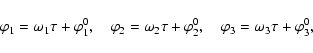
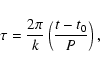
Obtaining the saturnicentric positions X, Y, Z and velocities
![]() ,
,
![]() ,
,
![]() (where dots stand for derivation with respect to
the real time) referred to the mean ecliptic and equinox of J2000 requires
several steps. With the notations of the first canonical transformation:
(where dots stand for derivation with respect to
the real time) referred to the mean ecliptic and equinox of J2000 requires
several steps. With the notations of the first canonical transformation:
![\begin{displaymath}\left(\matrix{X\cr\noalign{\smallskip } Y\cr\noalign{\smallsk...
...gn{\smallskip }
y\cr\noalign{\smallskip } z\cr}\right)\right],\end{displaymath}](/articles/aa/full/2003/01/aa2969/img99.gif)
![\begin{displaymath}\left(\matrix{\dot X\cr\noalign{\smallskip } \dot Y\cr\noalig...
...(1-\gamma\right)\cr\noalign{\smallskip } P_z\cr}\right)\right],\end{displaymath}](/articles/aa/full/2003/01/aa2969/img100.gif)
The signs of y and Px are changed for Calypso to take into account its position near L5.
Then, the series are shortened giving the three amplitudes I01,
I02, I03 their numerical values and removing non-significant terms, and
the frequencies of the four angles are multiplied by ![]() (and called
(and called
![]() ,
,
![]() ,
,
![]() ,
and
,
and ![]() )
to deal directly with a more realistic
time.
)
to deal directly with a more realistic
time.
The signs of ![]() ,
,
![]() ,
and
,
and ![]() are changed for Calypso to
take into account its position near L5.
are changed for Calypso to
take into account its position near L5.
The frequencies (rd/day) and phases (rd) for Helene, Telesto, and Calypso, together with their saturnicentric positions (a.u.) and velocities (a.u./day), referred to the mean ecliptic and equinox of J2000, are summarized in Tables 3-8.
Each coordinate is the sum of the corresponding numerical coefficients
multiplied by the cosine (f=0) or sine (f=1) of the angle ![]() computed
by:
computed
by:
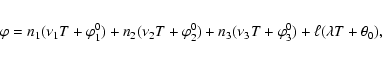
A downloadable FORTRAN code for the theory is available at: ftp://www.imcce.fr/pub/ephem/satel/htc20/
The comparison with numerical simulations shows the model's efficiency to deal with Lagrangian satellites similar to Tethys and Dione's companions (with small and moderate libration amplitudes). With almost twenty years of observations, the precision obtained when fitting each satellite's theory gives a rather good level of confidence for predictions.