A&A 397, 305-318 (2003)
DOI: 10.1051/0004-6361:20021487

Magnetic twist and writhe of active regions

On the origin of deformed flux tubes

M. C. López Fuentes1 - P. Démoulin2 - C. H. Mandrini1 - A. A. Pevtsov3 - L. van Driel-Gesztelyi 2,4,5,6


1 - Instituto de Astronomía y Física del Espacio, CC. 67, suc. 28, 1428 Buenos Aires, Argentina
2 - Observatoire de Paris, LESIA, FRE 2461 (CNRS), 92195 Meudon, France
3 - National Solar Observatory, Sacramento Peak, Sunspot, NM 88349, USA
4 - Centre for Plasma Astrophysics, K.U. Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
5 - Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
6 - Konkoly Observatory, Budapest, Pf. 67, 1525, Hungary

Received 18 July 2002 / Accepted 10 October 2002

Abstract
We study the long term evolution of a set of 22 bipolar active regions (ARs) in which the main photospheric polarities are seen to rotate one around the other during several solar rotations. We first show that differential rotation is not at the origin of this large change in the tilt angle. A possible origin of this distortion is the nonlinear development of a kink-instability at the base of the convective zone; this would imply the formation of a non-planar flux tube which, while emerging across the photosphere, would show a rotation of its photospheric polarities as observed. A characteristic of the flux tubes deformed by this mechanism is that their magnetic twist and writhe should have the same sign. From the observed evolution of the tilt of the bipoles, we derive the sign of the writhe of the flux tube forming each AR; while we compute the sign of the twist from transverse field measurements. Comparing the handedness of the magnetic twist and writhe, we find that the presence of kink-unstable flux tubes is coherent with no more than 35% of the 20 cases for which the sign of the twist can be unambiguously determined. Since at most only a fraction of the tilt evolution can be explained by this process, we discuss the role that other mechanisms may play in the inferred deformation. We find that 36% of the 22 cases may result from the action of the Coriolis force as the flux tube travels through the convection zone. Furthermore, because several bipoles overpass in their rotation the mean toroidal (East-West) direction or rotate away from it, we propose that a possible explanation for the deformation of all these flux tubes may lie in the interaction with large-scale vortical motions of the plasma in the convection zone, including also photospheric or shallow sub-photospheric large scale flows.

Key words: magnetic fields - methods: data analysis - Sun: interior - Sun: magnetic fields - Sun: photosphere


   
1 Introduction

Active regions (ARs) have long been thought to be the manifestation of the emergence of buoyant magnetic flux tubes having the typical shape of the letter $\Omega $ (Zwaan 1985 and references therein). These tubes are supposed to be formed at the base of the convection zone (CZ) from the global toroidal component of the solar magnetic field (Parker 1993). After ascending through the CZ and emerging, their cross-sections with the photosphere are observed as magnetic field concentrations forming ARs. The orientation of positive and negative polarities of ARs with respect to the East-West direction is opposite in both hemispheres and reverses from one solar cycle to the next (see Babcock 1961), obeying the so called Hale-Nicholson law (Hale & Nicholson 1925). Another fact observed is the tendency of the preceding polarity to lie closer to the solar equator than the following one, known as Joy's law (see Hale et al. 1919), the name of this relationship can be attributed to Zirin (1988, p. 307).


  \begin{figure} \par\includegraphics[width=11cm,clip]{ms2921f1.eps} \end{figure} Figure 1: Magnetic flux tubes distorted from the typical $\Omega $-loop shape. The sketch in the left panel shows an almost rigid flux tube with negative writhe; then, as it emerges across the photosphere (horizontal planes) the orientation of the bipolar flux concentrations changes (they rotate) clockwise. Correspondingly, in the right panel, a flux tube with positive writhe will appear as a bipole rotating counterclockwise.
Open with DEXTER

However, several ARs do not follow the Hale-Nicholson law and/or the Joy's law, but their magnetic polarities show proper motions that are not compatible with the emergence of a planar flux tube (Cannon & Marquette 1991; Tanaka 1991; Lites et al. 1995; Leka et al. 1996; Pevtsov & Longcope 1998b). The evolution of these peculiar ARs has often been associated with the emergence of distorted magnetic flux tubes. In particular, there are examples of deformed flux tubes that are suspected to be formed by the development of a kink instability (Linton et al. 1998).

In a recent paper (López Fuentes et al. 2000), we have analyzed the evolution of a bipolar AR (NOAA 7912) in which the main polarities were observed to turn one around the other during several solar rotations. AR 7912 appeared on the southern hemisphere as a non-Hale region for cycle 22 in October 1995, becoming a Hale region three solar rotations later (January 1996) after the main polarities were seen to turn by more than 180 degrees. After discarding photospheric or shallow sub-photospheric flows that are unlikely to explain why the AR was initially formed with a non-Hale orientation, we interpreted this evolution as the emergence of a very distorted magnetic flux tube in which the sign of the twist (a measure of the turning of the field lines around the axis of the flux tube) was different from the sign of the writhe (a measure of the spatial turning of the axis of the flux tube). In a flux tube where the kink instability has developed the sign of the twist and the writhe should be the same because, as the instability grows, part of the twist is transferred into writhe (e.g. Linton et al. 1999). Then, we concluded that a kink instability could not be at the origin of the tube deformation. We proposed that it was due to the interaction of the flux tube with surrounding plasma motions during its emergence through the CZ.

In this work we analyze in detail a set of 22 bipolar flux concentrations, and their subsequent reappearances on the solar disk, in which the main polarities are observed to rotate one around the other. We refer to these ARs as rotating tilt-angle ARs (RTARs). Each reappearance of a given flux concentration is simply called an AR, which is named using the first NOAA number found in SGD as given in Tables 1 and 2. As in the case of AR 7912, we interpret their evolution as due to the emergence of deformed flux tubes. In order to test the role of the kink instability to originate the flux-tube deformation, we analyze magnetic field observations and obtain the signs of the twist and the writhe. To determine the sign of the writhe we study the evolution of the tilt angle of the AR, which is defined as the angle that the axis joining the flux-weighted centers of the main polarities form with the solar equator. We measure this angle in synoptic magnetic maps obtained by the National Solar Observatory at Kitt Peak (NSO/KP). On the other hand, using the linear force-free field equation ( $\vec{\nabla} \times \vec{B}= \alpha \vec{B}$, where $\alpha $ is a constant), we compute from vector magnetograms obtained mainly at Mees Solar Observatory (MSO) the value of the parameter, $\alpha _{\rm best}$, that best fits to the data. The sign of $\alpha _{\rm best}$ is then used as a proxy for the sign of the twist.

In Sect. 2, we describe the data used, together with the procedure and criteria followed to determine the writhe of ARs. We outline briefly the method used to compute the sign of the twist in Sect. 3. A summary and an interpretation of the results is presented in Sect. 4. We discuss the relevance of the kink instability as the origin of the deformation of the flux tubes, and we analyze the role that other mechanisms, such as the Coriolis force and external rotational motions of the plasma in the CZ or at/near the photospheric surface, may have in the observed evolution. Finally, in Sect. 5 we conclude.


  \begin{figure} \par\includegraphics[width=10cm,clip]{ms2921f2.eps} \end{figure} Figure 2: Typical synoptic map from NSO/KP. White (black) concentrations correspond to positive (negative) magnetic flux. Bipolar ARs are easily identified as pairs of flux concentrations. The magnetic field has been saturated above (below) 100 G (-100 G). This particular map corresponds to Carrington rotation number 1930 that started on November 28, 1997. The AR shown in Fig. 3 is first seen on this map (top right corner). The horizontal continuous line is the solar equator.
Open with DEXTER

   
2 Inferring the writhe of flux tubes from the evolution of the main polarities

   
2.1 The relation between the tilt evolution and the writhe

The observed global evolution of RTARs can a priori be the consequence of either the drag of plasma flows forcing the magnetic flux-tube to rotate or its own internal dynamics. In the first case, for example, photospheric or shallow sub-photospheric vortex motions can be present where some ARs emerge. After the emergence of a classical planar $\Omega $-loop, the drag force applied by such vortex motions could force the main polarities to rotate as observed in RTARs. Observations to test such hypothesis are not presently available. Another possibility is that the $\Omega $-loop was distorted from its planar shape in the CZ itself. In such a case the observed rotation of the polarities is a consequence of the flux tube morphology as it moves across the photosphere. In the present work we test this second possibility; in particular, the possible development of a kink instability in the CZ. Then, as done previously (López Fuentes et al. 2000), we can obtain the sign of the writhe of the tube from the sense of rotation of the main polarities along the AR life time. Figure 1 shows two almost rigid flux tubes with their axis distorted in a helix-like curve. The different planes correspond to consecutive cross-sections of the flux tubes, giving the evolution of the relative positions of the opposite polarities as the deformed flux tubes are emerging. As time goes on, the magnetic flux concentrations present different tilt angles from which we can derive the sign of the writhe. A clockwise rotation of the polarities indicates a negative (left-handed) writhe, and a counterclockwise a positive (right-handed) writhe. In these examples the flux concentrations rotate at photospheric level by 180 deg., but the writhe can be inferred in the same way for any significant rotation.

   
2.2 The data set used

We have used NSO/KP synoptic maps (see ftp://argo.tuc.noao.edu/kpvt/synoptic/README) to measure systematically the tilt angle of ARs. The maps consist of rectangular arrays built from daily full-disk magnetograms using a triangular weighted integration. The result of this procedure is arranged in an array from right to left (West to East) as time evolves. The arrays have a 360 by 180 pixels format; then, each pixel in the horizontal direction corresponds to a heliographic longitude degree, while in the vertical direction they correspond to the sinus of the latitude in heliographic coordinates. Each pixel contains the time and space averaged magnetic flux per unit surface crossing the photosphere at a given position on the Sun. Projection effects are taken into account by correcting the flux according to the real solar area covered by a particular pixel and by supposing that the photospheric field is radial. Figure 2 shows one of these maps as an example, it is possible to identify the ARs as pairs of black and white concentrations corresponding to negative and positive magnetic flux, respectively.


  \begin{figure} \par\includegraphics[width=10.5cm,clip]{ms2921f3.eps} \end{figure} Figure 3: Evolution of AR 8113 from December 1997 to February 1998. The December 3 magnetogram corresponds to Carrington rotation 1930 shown in Fig. 2. These images come from Kitt Peak full disk magnetograms obtained on the dates appearing on the panels. Note the change in the tilt angle along the four solar rotations (see also Fig. 5 right panel). The flux is saturated above (below) 100 (-100) G. Each panel covers an area of $450 \times 300 \hbox {$^{\prime \prime }$ }$. North is up and West is to the right.
Open with DEXTER

   
2.3 Description of the procedure

We have developed a routine that allows us to compare successive synoptic maps, and to select from them ARs that survive more than one solar rotation by visual inspection. In particular, we are interested in those ARs where a systematic evolution of the tilt angle is observed. An example of such regions (AR 8113) is shown in Fig. 3, where the variation of the tilt angle of the bipole is clearly seen. A strong dispersion of the flux is also evident in the last two solar rotations. Once a flux concentration is selected, we isolate from the synoptic map a submatrix including it. We compute from the data in this submatrix the flux weighted mean longitude ($\phi$) and latitude ($\lambda$) of the positive (P) and negative (N) magnetic polarities:

 \begin{displaymath}\phi_{\rm P,N} = \frac{\sum \phi \vert B\vert}{\sum \vert B\v... ... P,N} = \frac{\sum \lambda \vert B\vert}{\sum \vert B\vert}~, \end{displaymath} (1)

where B is the magnetic flux crossing the photosphere associated to each pixel. The summation is done over the pixels where |B| is above a given value $B_{\rm min}$, for which we have chosen 10 G (higher values, e.g. 100 G, give similar results for the first appearance of an AR, but they do not allow us to follow its decaying phase long enough). From the previous parameters, we compute the mean longitude and latitude, $\bar{\phi} = (\phi_{\rm P}+\phi_{\rm N})/2$ and $\bar{\lambda} = (\lambda_{\rm P}+\lambda_{\rm N})/2$. The dipolar size, S, and the tilt angle, $\varphi$, of the AR are defined as:
  
S = $\displaystyle R_{\hbox{$\odot$ }} \sqrt{(\phi_{\rm P} - \phi_{\rm N})^2 \cos^2\bar{\lambda} + (\lambda_{\rm P} -\lambda_{\rm N})^2} ,$ (2)
$\displaystyle \varphi$ = $\displaystyle \arctan \left( \frac{\lambda_{\rm P} - \lambda_{\rm N}} { (\phi_{\rm P} - \phi_{\rm N}) \cos \bar{\lambda} } \right) ,$ (3)

where $R_{\hbox{$\odot$ }}$ is the solar radius (and both longitude and latitude are in radians).

We have also quantified the dispersion of the polarities measuring the flux weighted mean size of both, positive and negative, flux concentrations as:

 \begin{displaymath}R_{\rm P,N}=R_{\hbox{$\odot$ }} \frac{\sum \sqrt{(\phi - \ph... ...lambda_{\rm P,N})^2}\vert B\vert} {\sum \vert B\vert} \cdot \end{displaymath} (4)

The quantities given by Eqs. (1-4) are computed for all the successive appearances of the selected ARs. We have also computed the total magnetic flux by simply adding the values of the flux in the pixels where the field is above $B_{\rm min}$. These values are kept in a data base that covers two and a half solar cycles.

The present study is limited to a set of 22 ARs for which we can derive both the sign of the writhe and the $\alpha _{\rm best}$. The main results are summarized in Tables 1 and 2. The ARs are grouped according to their reappearances on the solar disk along successive solar rotations. We have obtained the NOAA numbers from the Greenwich Observatory archives (see e.g. http://science.nasa.gov/ssl/pad/solar/greenwich.htm), comparing the heliographic coordinates of the identified ARs to the positions of sunspots provided in the archives.

   
2.4 The criteria to identify reappearances of flux concentrations

To test that the supposed reappearances of a flux concentration indeed correspond to the same AR observed in successive solar rotations, we have applied certain criteria that we describe in this section. First of all, the longitude and latitude of an AR cannot differ by more than a few heliographic degrees when differential rotation is taken into account. On the other hand, we also require that the evolution of the magnetic flux follows what is expected in the case of a flux concentration that is emerging, growing and dispersing afterwards. These criteria have been implemented in a code to filter the data set built by visual inspection.

Because of the effect of differential rotation, ARs that lie at higher latitudes appear progressively shifted to decreasing longitudes. This effect was corrected using the classical expression for differential rotation ( $\omega (\lambda)$):

 \begin{displaymath} \omega (\lambda) = a + b \sin ^{2} \lambda + c \sin ^{4} \lambda . \end{displaymath} (5)

We have taken $a=14.38 \deg$/day, $b=-1.95 \deg$/day and $c=-2.17 \deg$/day, as given by the cross-correlation analysis of Kitt Peak magnetograms from 1975 to 1991 (Komm et al. 1993a). These values are very close to the recent ones deduced from seismology measurements using MDI (e.g. Charbonneau et al. 1999 and references therein). Because the values of the published coefficients (a,b,c) are very close, the association of magnetic bipoles along successive Carrington rotations is independent on the precise coefficient choice.

We consider that the position of an AR in a given rotation cannot differ by more than 5 heliographic degrees in latitude and 8 degrees in longitude from the previous rotation, to be identified as the same flux tube. With this range of confidence, we are taking into account that the position of an AR can change from one solar rotation to the next due only to changes in the photospheric distribution of the flux. This interval is small enough to eliminate confusion with surrounding ARs and, at the same time, is large enough to include the influence of the meridional drift of magnetic concentrations, as discussed below.

Our measurements show the meridional drift of ARs during their evolution. The mean meridional velocity (latitudinal displacement divided by time averaged along several rotations) is within $\approx$1.8 m s-1 to $\approx$8.1 m s-1 (giving a shift in the range [ $0.3^\circ,1.7^\circ$] for one Carrington rotation). The average value for all the ARs is $\approx$$5.5 \pm 2$ m s-1, this value is coherent with the one found by Komm et al. (1993b) from the study of Kitt Peak magnetic maps.

Concerning the evolution of the size of the polarities in an AR, it has been observed that as the flux disperses the size increases with time (Harvey 1993; van Driel-Gesztelyi 1998). In this aspect, our criterion is that $R_{\rm P,N}$cannot decrease from one solar rotation to the next for a given concentration to be considered as the reappearance of the same flux system. We have also imposed that the magnetic flux of the AR can have only one maximum. Using these criteria, we try to remove from our set cases of nearby and successive emergences of magnetic flux that form a complex of activity (Gaizauskas et al. 1983). Such multiple emergences can result in a change in the tilt that is not related to the writhe of the individual flux tubes. Since these tests are not enough to fully eliminate these multiple emergences, we further inspect the magnetic evolution of each selected AR to verify that the change in the tilt was not critically influenced by them.

After applying the just discussed criteria to the original data set, we identify a total number $\approx$300 RTARs, from June 1975 to December 2000. We will analyze here only those cases for which we can determine both the sign of the writhe and of the twist. A statistical study of the complete set and its relation to solar activity will be included in a future paper (López Fuentes et al., in preparation), preliminary results of this work have been discussed in Mandrini et al. (2002).


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{ms2921f4.eps} \par\end{figure} Figure 4: Three different examples of the evolution of the flux in ARs. The top panel corresponds to an AR that we start observing during its decaying phase. The middle panel shows the most typical case, an AR with an initial phase of increasing flux and a long lasting decay. The bottom panel corresponds to the evolution of a strange case in which the flux increase lasts several solar rotations, decreasing later on. The continuous line corresponds to the positive flux and the dashed line to the negative one.
Open with DEXTER

   
2.5 Evolution of the magnetic flux

The analyzed RTARs have no peculiar characteristics in terms of the evolution of the magnetic flux as compared to the classical ARs (not or weakly rotating). The mean flux is of the order of 1022 Mx, which is the average value for the group of strong bipoles forming ARs (Wang & Sheeley 1989). The selection of strong bipoles is implicitly associated with the duration of one Carrington rotation because of their characteristic decay time. ARs typically decay at a rate of 1 to 2 $ \times 10^{20}$ Mx/day (Schrijver & Zwaan 2000, pp. 114-115); then, small ARs of $5 \times 10^{21}$ Mx survive for about 25-50 days, while the smaller ones are excluded. We have also found that the magnetic flux is higher for ARs where S(dipolar size) is larger, in agreement with previous results (e.g. Wang & Sheeley 1989; Howard 1992).

Figure 4 shows three ARs representing different cases of flux evolution. The first example (Fig. 4 top panel) corresponds to AR 7790 in which the magnetic flux decreases continuously. This means that this AR has been identified after its emergence phase has ended, and so we observe it along its decaying phase (5 solar rotations). The second case shown in Fig. 4 (middle panel) is AR 6940 in which the increase of flux lasts just from the first to the second solar rotation, then this AR has probably been selected at the beginning of its emergence. The bottom panel corresponds to AR 8674 in which the flux increases during most of its lifetime, the decaying phase starts as late as the fourth solar rotation in which it is observed.

In general, the magnetic flux of ARs evolves in such a way that it shows an initial rapid increase (in a time scale of weeks), followed by a long lasting decay (in a time scale of months, see Harvey 1993; van Driel-Gesztelyi 1998). Nevertheless, we have observed cases in which the flux increase lasts as long as 3 solar rotations, much more than what is usually believed (see previous references). This long-term flux increase is observed only in a small number of the RTARs, 3 over 22 regions (AR 8674 in Fig. 4 shows the longest period of flux increase, while in the other two cases the flux increases only from the first to the third rotation). We may ask ourselves if this behavior is inherent to the RTARs but, since very little is known about their long term evolution, a further investigation based on a larger data set is needed (López Fuentes et al., in preparation).

   
2.6 Tilt of active regions

The evolution of the tilt angle for 8 ARs is shown in Figs. 5 and 6 for the northern and southern hemisphere, respectively. The mean orientation of the positive and negative polarities of ARs with respect to the East-West direction is opposite in both hemispheres, and reverses from one solar cycle to the next (Hale-Nicholson law). The observed orientation is the one shown in Figs. 5 and 6, but, when discussing the plausible mechanisms originating the variation in the tilt, it is better to remove these hemispheric and cycle dependences. More precisely, we set in Tables 1 and 2 the origin of the tilt angle in the East-West direction following the Hale-Nicholson law. With this convention, the relaxation, or not, to the East-West direction is easily seen (Sect. 4.6).

The errors in the tilt are computed combining the independent errors coming from each pixel. In practice, this is done by propagating the error of each parameter (position and field strength) on which the tilt depends to first order in Eq. (3), and taking afterwards the square root of the summation of the terms in the propagation to the second power. We assume that the error in the position is half a pixel of the synoptic map and that the error per pixel in the magnetic field is 5 G. This last value is a large upper bound since the flux in each pixel of a synoptic map is computed averaging several individual magnetograms for which the errors are of $\approx$7 G per pixel, this implies an error of about 0.5 G per pixel in the synoptic map (using only the classical propagation of errors). However, there are certain systematic errors in the original data used to build up the synoptic maps, such as a deficit of flux in strong field regions that we cannot take into account (Harvey J., private communication). We have found that, when taking 5 G for the field error, the contribution due to the error in the flux is in general of the same order as the contribution due to the error in the position.

   
2.7 The contribution of differential rotation to the tilt change

Differential rotation certainly contributes to modify the tilt angle of ARs. The effect of differential rotation is maximum when the drag force at the photospheric surface becomes so efficient that it couples the magnetic flux tube to the surrounding plasma. To subtract the contribution of differential rotation at the photosphere from Eq. (3), we have divided each Carrington rotation in several temporal steps to make our computation more precise. The variation of the tilt angle corrected in this way is illustrated in Figs. 5 and 6 for several ARs from the North and South hemispheres. The fifth and sixth columns of Tables 1 and 2 show the total rotation angle (final minus initial tilt angle) computed with and without the effect of differential rotation. The errors in $\Delta \varphi $ and $\Delta \varphi _{\rm cor.}$, computed as described in Sect. 2.6, are almost the same; that is why, we have included them only for the $\Delta \varphi _{\rm cor.}$ values.

Differential rotation has its most significant effect when the AR is oriented in the North-South direction, which is rare according to the Hale-Nicholson law. In the present data set, we find that this is the case of AR 4711 and of two ARs with an important tilt change; AR 8100 that rotates $\approx$ $150^{\circ}$ and AR 8113 that rotates $\approx$ $140^{\circ}$ when no correction for the differential rotation is applied. These two last examples start as "normal'' ARs in the sense of the Hale-Nicholson law, but become non-Hale ARs later on. The influence of differential rotation is clearly evident in these two ARs since most of the change in the tilt angle after their third appearances is provided by it (Figs. 5 and 6); however, a significant total rotation angle is still present ($\approx$ $-60^{\circ}$ and $\approx$ $74^{\circ}$, respectively).

The results summarized in Tables 1 and 2, together with polar plots similar to those in Figs. 5 and 6 for the full set analyzed here, show that for most of the ARs $\Delta \varphi $ and $\Delta \varphi _{\rm cor.}$ have comparable values. In the few cases discussed above, where differential rotation has a large effect, a significant rotation of the AR polarities still remains. Then, we conclude that differential rotation is not the main mechanism responsible for the rotation of the bipoles. In all cases, the correction of the tilt angle by differential rotation does not change its sign (which is equivalent to keep the inferred sign of the writhe unchanged) and, therefore, it does not alter our conclusions.


  \begin{figure} \par\includegraphics[width=15cm,clip]{ms2921f5.eps} \end{figure} Figure 5: Four RTARs observed on the North hemisphere between 1986 and 1998. The center of the polar plots corresponds to the position of the center of the negative polarity, while the arrows and squares indicate the relative position of the positive polarity. The tilts are shown as measured on the Sun, except that they are corrected for differential rotation (Sect. 2.7). The AR NOAA numbers appear in the upper left corner of the panels and the labels indicate the dates of the successive reappearances of the ARs. Three of these ARs (AR 6805, AR 7433, AR 8113) rotate in the counterclockwise (CCW) direction and one (AR 7618) in the clockwise (CW) one.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=15cm,clip]{ms2921f6.eps} \end{figure} Figure 6: Idem Fig. 5 for the South hemisphere. Two of these ARs (AR 6100, AR 7518) rotate in the CCW direction and two (AR 8100, AR 8563) in the CW one. The tilt angles are corrected for differential rotation.
Open with DEXTER

   
3 Determination of the twist of RTARs

   
3.1 The data used

It is not possible to obtain a direct measurement of the twist of the magnetic flux tubes that form ARs. Nevertheless, computations of the global value of the force-free field parameter, $\alpha _{\rm best}$, provide a proxy for the sign of the magnetic twist in the tubes forming ARs (see Sect. 3.5). Except for two regions (AR 4711 and AR 6100), for which we have data from the magnetograph of the Marshall Space Flight Center (MSFC) (Hagyard 1982), we have used vector magnetograms from the Haleakala Stokes Polarimeter at MSO (Mickey 1985) to determine $\alpha _{\rm best}$. This instrument provides Stokes I, Q, U and V profiles of the Fe I $\lambda\lambda$ 6301.5, 6302.5 Å doublet with a 25 mÅ pixel-1 dispersion. A typical magnetogram consists of a 2' x 2' array with a spatial resolution of less than 3'' and is completed in about one hour. Each raster point provides the strength of the magnetic field components parallel and transverse to the line of sight, as well as the azimuth of the transverse field (for a detailed description of the data processing see i.e. Pevtsov & Canfield 1998a). The azimuth has a 180 degree ambiguity that is resolved by the method described in Canfield et al. (1993). To avoid projection effects the magnetograms are transformed to disk-center heliographic coordinates.

   
3.2 The computation of $\mathsfsl{\alpha_{best}}$

In force-free magnetic field configurations the rotation of the field and the magnetic field itself are related by: $\vec{\nabla} \times \vec{B}= \alpha \vec{B}$. The projection of the force-free equation in the z direction (being z normal to the photosphere) gives:

 \begin{displaymath}\frac{\partial B_y}{\partial x} - \frac{\partial B_x}{\partial y} = \alpha B_z~. \end{displaymath} (6)

In this way maps of $\alpha $can be created from vector magnetograms. These maps show in general a large variation of $\alpha $ (both in sign and magnitude) within an AR. However, there is frequently a given overall sign of $\alpha $associated to an AR. A single value of $\alpha _{\rm best}$ for the linear force-free field that best fits the AR magnetic field is obtained by a least-squares method (Pevtsov et al. 1995). When more than one magnetogram is available for a particular AR, we compute the standard deviation that is shown in the third column in Tables 1 and 2 as the error of $\alpha _{\rm best}$.

   
3.3 $\mathsfsl{\alpha_{best}}$ in the selected ARs

When data are available for the successive rotations of the same AR, we find in general a coherent sign for $\alpha _{\rm best}$. However, there are 4 cases where the sign of $\alpha _{\rm best}$ changes along the evolution of the region; these cases are: AR 6855, AR 8243, AR 7518, AR 8100 (NOAA numbers of the first appearances). For the first two cases the change in the sign of $\alpha _{\rm best}$ is significant (see Table 2), so we will not use these ARs in our analysis. For AR 7518, the change in the sign of $\alpha _{\rm best}$ occurs only in the last appearance and its error is much larger than its mean value; therefore, we consider that this measurement is irrelevant. Finally, the evolution of AR 8100 along five solar rotations has been studied in detail (Green et al. 2002) by us; we have found (using coronal observations) that, except in the first rotation, the twist was always positive. Then, we have decided to include AR 7518 and AR 8100 (considering in this case a positive twist) in our study. For some of the 20 remaining ARs (ARs 7417, 7433, 7618, 7882, 8293, 8674) the value of $\alpha _{\rm best}$ is largely uncertain; so that, within the error bars, there is a non-null probability that the twist has the opposite sign to the mean $\alpha _{\rm best}$. However, we have decided to keep such cases because there is still significant information in them. The uncertainties in $\alpha _{\rm best}$ are reflected in Fig. 7.

   
3.4 Hemispheric rule

Seehafer (1990) showed that the helicity is predominantly negative in the northern hemisphere and positive in the southern one. This result was confirmed and quantified computing $\alpha _{\rm best}$ by Pevtsov et al. (1995, 2001), Longcope et al. (1998) and Tian et al. (2001). The dominance of negative (resp. positive) $\alpha _{\rm best}$ in the northern (resp. southern) hemisphere is in the range of 62% to 75%.

Our sample (see Tables 1 and 2) includes one order of magnitude less ARs than the previous studies, having a low statistical significance. Nevertheless, we see almost the same tendency in the RTARs for hemispheric dominance; that is to say, if we consider the measurements of $\alpha _{\rm best}$ for each rotation independently, as done in the previous studies, we have a dominance of 18 negative values of $\alpha _{\rm best}$ over 23 cases (so 78%) for the northern hemisphere, and a dominance of 12 positive values over 17 cases (so 70%) for the southern hemisphere. If we count only the magnetic flux tubes (relating successive rotations, a procedure which takes into account the physics but decreases the statistics), the dominance turns out to be 10 over 12 cases, so 83%, and 6 over 8 so 75%, respectively. The slightly higher values of the dominance percentages found for the RTARs are not statistically meaningful to claim for any typical property. As for the magnetic flux (Sect. 2.5), RTARs are similar to what we may call "normal'' ARs with a flux large enough to survive more than one rotation.

   
3.5 Interpretation of $\mathsfsl{\alpha_{best}}$

It is not straightforward to interpret the meaning of $\alpha _{\rm best}$ in terms of the original properties of the magnetic flux tubes in the CZ. Because magnetic measurements are obtained in a region of the atmosphere where the magnetic field is still confined by the plasma, the magnetic field is expected to keep most of its subphotospheric properties; in particular, $\alpha _{\rm best}$ is a trace of how the tube was twisted. But this is not a quantitative measurement of the twist because magnetograms give information at only a few cuts of the magnetic tube. Moreover, the subphotospheric twist is expected to be progressively transferred to the corona by torsional Alfvén waves (Longcope & Welsch 2000). Keeping this in mind, we will focus only in the sign of $\alpha _{\rm best}$ as a proxy for the sign of the magnetic "twist'' in the flux tube.

   
4 Possible origin of RTARs

The development of the kink instability in the CZ has been several times invoked to explain the peculiar evolution of some ARs. The detailed analysis of a particular RTAR, as well as the review of other published examples (López Fuentes et al. 2000), have shown that few cases can be explained as due to the kink instability. The main objective of the present study is first to test this hypothesis on the largest set of data presently available; that is to say, ARs where the sign of the writhe and the twist can be both unambiguously determined. After doing so, we will explore other possible mechanisms that can be at the origin of the RTARs.


  
Table 1: List of the RTARs for the South hemisphere. The first column gives the NOAA number of each appearance for which $\alpha _{\rm best}$ is available, NOAA numbers that do not belong to the same magnetic flux tube are separated by a blank line. The second column gives the date of the central meridian passage (CMP) of the corresponding NOAA region. The following four columns show, respectively, the value of the force free parameter $\alpha _{\rm best}$ (in units of 10-8 m-1), the tilt angle for the first rotation $\varphi _{0}$ in degrees (computed as described in Sect. 2.6, and taken as 0 when the bipole is oriented in the East-West direction following the Hale-Nicholson law), the total rotation angle of the AR not corrected ( $\Delta \varphi $) and corrected ( $\Delta \varphi _{\rm cor.}$) for differential rotation. The total rotation angles are computed for the full period in which each AR is observed in the synoptic maps (not just when vector magnetograms were available). The last column indicates the way the AR evolves with respect to East-West direction (a: rotates away from it, o: rotates towards but overpasses it by more than 10$^{\circ }$, r: relaxes to it within 10$^{\circ }$, t: rotates towards without reaching it within 10$^{\circ }$) and the possible deformation mechanism (C: Coriolis force, K: kink instability, ?: unidentified).
\begin{table} \par\begin{displaymath} \begin{array}{lc\vert crrr\vert rr} \hline... ...4.3&31.&-42.&-40.\pm7.& r & C \\ \hline \end{array}\end{displaymath}\end{table}


  
Table 2: Idem Table 1 for the North hemisphere.
\begin{table} \begin{displaymath} \begin{array}{lc\vert crrr\vert rr} \hline\hli... ...6/07/98&~~7.8~~~~~~~& & & & & \\ \hline \end{array}\end{displaymath}\end{table}

   
4.1 How do RTARs rotate?

The set of RTARs studied here rotate in a coherent way; that is to say, the sense of rotation is always the same along their evolution. However, we have found that in 7 cases, after correcting for differential rotation, the general rotation trend changes either between the second and third solar rotations or at the end of the AR evolution (see e.g. AR 8100 in Fig. 6). The angle by which the RTARs rotate back is always of a few degrees, so, of the same order as the error in the total rotation angle ( $\Delta \varphi $ or $\Delta \varphi _{\rm cor.}$); therefore, this does not alter the general trend.

We can now investigate which is the direction towards which most of the bipoles relax; that is to say, which is the last observed direction of the axis joining both polarities. We find that 8 ARs relax to the East-West direction (where we have set the origin of tilt angle) within $10^{\circ}$; those marked with an ron the left side of the last column in Tables 1 and 2 (this can be easily seen by adding $\varphi _{0}$to $\Delta \varphi _{\rm cor.}$). Moreover, only 2 ARs (those marked with a t on the left side of the last columns in Tables 1 and 2) relax towards this direction without reaching it, but both are peculiar ARs; AR 4711 starts with a very large tilt angle and AR 7762 is a non-Hale AR. It is worth noting that these 10 cases have an evolution similar to the average of the sunspot groups as found by Howard et al. (2000, and references therein). However, our results are based on much longer time scales (several Carrington rotations) while the relaxation towards the mean tilt found by Howard et al. occurs on a 3 to 6 days time scale. Longcope & Choudhuri (2002) have modeled this behavior as the relaxation of the turbulent perturbations set in the magnetic flux tube when it crosses the upper part of the CZ.

An important fraction of the ARs (7/22, those marked with an o on the left side of the last columns in Tables 1 and 2) rotates towards the East-West direction, but after reaching it, they continue rotating and overpass it by more than $10^{\circ}$ (with a mean value of $30^{\circ}$). This kind of ARs have been found previously by Cannon & Marquette (1991, their regions 1-4). In a previous work Marquette & Martin (1988) studied in detail region 1, that rotates by $\approx$600, and found that the origin of the rotation was neither due to the emergence of new flux, nor to the interaction with the surrounding field (the AR is isolated). We found also a smaller fraction of ARs (5/22) that rotate away from the East-West direction. The number of cases in each of the above categories is the same if we do not correct for differential rotation.

   
4.2 Twist versus writhe

$\alpha _{\rm best}$ and $\Delta \varphi _{\rm cor.}$ are proxies for the twist and for the writhe of the magnetic flux tubes, respectively. They are two independent measurements for each AR and any correlation between them can give clues on the physical mechanisms creating RTARs.

Figure 7 illustrates the results shown in Tables 1 and 2. The values of $\alpha _{\rm best}$ plotted in this figure correspond to the average of the measurements for each AR. We have omitted AR 7882 for the sake of clarity, since both its average $\alpha _{\rm best}$ and error bar are considerably larger than the others. ARs 6855 and 8243 have also been omitted since, as discussed in Sect. 3.3, the sign of $\alpha _{\rm best}$ changes along their evolution. The errors in $\alpha _{\rm best}$ correspond to the average of the errors computed in the way described in Sect. 3. The errors on $\Delta \varphi _{\rm cor.}$ are derived as explained in Sect. 2.6.

In the set of 20 bipolar flux concentrations (ARs and their reappearances), there are 7 that have the same sign of twist and writhe and 13 for which the signs are different. Some cases have low values for $\alpha _{\rm best}$ or $\Delta \varphi $, so, one wonders about their significance; however, taken as a whole Fig. 7 indicates an anticorrelation between twist and writhe.


  \begin{figure} \par\includegraphics[width=10cm,clip]{ms2921f7.eps} \end{figure} Figure 7: Twist vs. writhe for the studied ARs. The proxy for the twist is $\alpha _{\rm best}$ (Sect. 3) and the proxy for the writhe is total rotation angle corrected for differential rotation (noted $\Delta \varphi _{\rm cor.}$, see Sect. 2). The value of $\alpha $ plotted in the ordinate is the average of the measured values of $\alpha _{\rm best}$ for each AR (see Tables 1 and 2). North hemispheric RTARs are plotted with asteriks and South hemispheric ones with diamonds.
Open with DEXTER

   
4.3 Comparison to previous studies

Canfield & Pevtsov (1998) and Tian et al. (2001) have analyzed the relationship between the tilt angle and the twist of ARs. Both studies differ from our analysis in two important points: first, these authors analyze the ARs individually (they do not identify all the reappearances of the same flux tube), and second, they analyze the tilt (not the variation of the tilt). In the previous works, the tilt angle of each appearance, which is considered as an independent region, is used as a proxy of the writhe of the magnetic flux tube (we will refer below to this proxy as writhe $_{\rm (tilt)}$). This approach assumes that the flux tube is rooted to a toroidal field, and that the observed tilt is a proxy for the deformation of the flux tube from a planar geometry (for which the writhe is null). Then, the approach in Canfield & Pevtsov (1998) and Tian et al. (2001) is related, but clearly different from the one taken by us (a proxy of the writhe is the long-term evolution of the flux concentrations with no hypothesis made about the rooted part of the flux tube, see Sect. 2.1 and Fig. 1).

The results of Canfield and Pevtsov (1998) show a dominantly positive (resp. negative) writhe $_{\rm (tilt)}$ in the northern (resp. southern) hemisphere, which is a confirmation of Joy's law. They also find a dominant negative (resp. positive) twist in the northern (resp. southern) hemisphere. But their results show a positive correlation between the twist and writhe $_{\rm (tilt)}$ (which is not intuitive taking into account that both hemispheric rules have been verified by them). Tian et al. (2001) also find that both hemispheric rules are fulfilled in their survey of 286 ARs, but contrary to Canfield and Pevtsov, Tian et al. show that 60% of the ARs have opposite sign of twist and writhe $_{\rm (tilt)}$ (in both hemispheres). Our results are similar to those of Tian et al., around 65% (13/20 cases for which the sign of the twist can be unambiguously determined) of the ARs show an anticorrelation between the signs of writhe and twist.

   
4.4 Conservation of magnetic helicity

The magnetic flux tubes that form ARs are most probably formed at the base of the convective zone (CZ) from the global toroidal component of the solar magnetic field (Parker 1993). Both 2-D (Emonet & Moreno-Insertis 1998) and 3-D models (Abbett et al. 2000; Fan 2001) predict that only flux tubes with a certain amount of twist would survive to the interaction with the surrounding plasma as they travel through the CZ. Then, an AR observed at the photosphere is formed by a flux tube which initially starts rising with some finite amount of magnetic helicity in the form of twist (T0). Later on, during its transit through the CZ, its magnetic helicity will remain roughly constant for the following reasons. First, magnetic helicity is weakly dissipated in a plasma with a large magnetic Reynolds number (it is dissipated only on the global diffusion time scale, Berger 1984). Second, the magnetic helicity of the flux tube can change only if there is an input from its footpoints (in the tachocline), but the dynamo works in a time scale much longer than the CZ transit time of the tube (which typically is of the order of one month).

However, an internal transfer between twist and writhe helicity can occur. In particular, any helicoidal-like distortion of the flux tube axis will introduce writhe helicity W1. Because of helicity conservation, this induces a change in the twist helicity, which becomes T1, so that:

 
T0=T1+W1 . (7)

There are various mechanisms that are able to transform the flux tube axis to introduce writhe. These can be: an internal instability of the tube (such as the kink mode), or the Coriolis force acting on the ascending tube, or the drag action of external convective flows. Depending on the mechanism, W1 is related in a different way to some characteristic parameters of the flux tube (such as T0 or its latitude) so that the behavior of W1 traces the underlying mechanism.


  
Table 3: Results of the comparison between twist and writhe. We list the number of ARs having the same (opposite) sign of twist (T) and writhe (W) separately for the two hemispheres and added up.
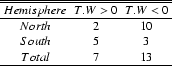\begin{table} \begin{displaymath} \begin{array}{ccc} \hline\hline Hemisphere ... ...5 & 3 \\ Total & 7 & 13 \\ \hline \end{array} \end{displaymath} \end{table}

   
4.5 Kink instability

The MHD kink instability has been studied by many authors in the context of laboratory, coronal and CZ plasmas (see e.g. Baty 1997; Linton et al. 1999 and references there in). The instability occurs when a magnetic flux tube is twisted above a critical value. As the instability proceeds, the flux tube untwists by one turn (for the most unstable mode m=1), reducing the magnetic stress that originates the instability. However, because of the conservation of magnetic helicity (Eq. (7)), the twist helicity is transformed into writhe helicity. Then, in the new equilibrium, the axis of the flux tube lies on a deformed helix with a rotation of one turn.

In contrast with a classical $\Omega $ loop, which is planar, a flux tube where the kink instability has developed will have the geometry shown in Fig. 1. The kink instability is then a possible mechanism for the origin of the RTARs (Sect. 2). However, one characteristic of the kink instability is that W1 should have the same handedness (i.e. same sign) as T1 (because the instability develops only for large twist so that |T0|>|W1|).

The results of Sect. 4.2 show that only 7 (those marked with a K on the right side of the last columns in Tables 1 and 2), over the 20 ARs for which the sign of the twist can be determined, have the same twist and writhe sign, but 13 ARs have opposite signs (Table 3). That is to say, at most only $\approx$35% of the ARs can be associated with the formation of kinked flux tubes (in the sense given by the kink instability). These ARs tend in general to have large values of $\alpha _{\rm best}$, as illustrated in Fig. 7 (first and third quadrant); this agrees with the fact that the kink instability develops in tubes having an excess of twist. However, AR 7912 analyzed in López Fuentes et al. (2000) is a clear example of an AR having a large twist, deduced from coronal field extrapolations (so, different from the approach used here), and still showing a different sign of twist and writhe.

It is worth mentioning that the fact that the signs of twist and writhe are the same does not imply that the deformation of the flux tube is due to the kink instability. Having the same sign is a necessary, but not a sufficient, condition to confirm the kink instability as the process responsible of the deformation. Other processes may still be at the origin of the distortion of those tubes with the same sign of twist and writhe. Moreover, another physical process is necessarily acting in ARs which have different sign of twist and writhe.

   
4.6 Coriolis force

A possible mechanism is the action of the Coriolis force on the plasma during the emergence of the flux tube. This has exhaustively been studied in relation to Joy's law (D'Silva & Choudhuri 1993; Fan et al. 1994; Schüssler et al. 1994; Caligari et al. 1995). A review on these works can be found in Fisher et al. (2000).

As a flux tube emerges through the CZ, the Coriolis force deforms its main axis introducing writhe helicity. If the flux tube is in the North (South) hemisphere the acquired writhe is positive (negative). Because of magnetic helicity conservation (Eq. (7)), this adds an oppositely directed twist in the tube, which is negative (positive) in the North (South) hemisphere. This is in agreement with the observed hemispheric rule for the mean twist (Sect. 3.4). In this scenario, the tilt angle is expected, first to satisfy Joy's law on average (leader closer to the equator); then, to change in the counterclockwise (clockwise) direction in the northern (southern) hemisphere. If the flux tube remains anchored to the bottom of the CZ through this long-term evolution, the expected final direction of the bipole is East-West (the direction of the toroidal field), while if disconnection occurs earlier this direction will not be reached and the further evolution of the magnetic field is the result of turbulent diffusion and advection by large scale flows (Fan et al. 1994).

To check the relevance of the Coriolis force as the main mechanism to originate the flux tube deformation, let us first see how many RTARs rotate in the right sense to be explained by this mechanism. Looking at our results in Tables 1 and 2, we find that from the 13 ARs that cannot be associated with the kink instability, 12 have the appropriate sense of rotation. Besides, from the 7 ARs that can be related to a deformation of flux tubes because of a kink instability, 3 can alternatively be originated by the Coriolis force (they satisfy Joy's law and rotate towards the East-West direction). These 3 cases should have an initial twist T0 that is opposite to the hemispheric rule (as observed, see Tables 1 and 2), of the same sign and larger in magnitude than W1, to still have W1and T1 of the same sign. Summarizing, we find that 15 out of 22 ARs rotate in the direction expected when the Coriolis force has deformed the flux tube.

If we also require that a flux tube deformed by the Coriolis force should evolve as described in the above second paragraph, relaxing to the East-West direction (see also Sect. 4.1), we find that only 9 of the 15 ARs that rotate in agreement with the action of Coriolis force are coherent with that scenario (those marked with a C on the right side of the last columns in Tables 1 and 2). Therefore, only $\approx$41% of the full set of studied RTARs (9/22 cases) fulfill these two requirements (correct sense of rotation for the Coriolis force and relaxation to the toroidal direction). We conclude that, under our assumptions, the rotation of the polarities for most of the studied ARs is not coherent with the effect of the Coriolis force on the ascending flux tube.

   
4.7 Convective-zone motions

Section 4.5 shows that the dominant mechanism driving the variation of the tilt angle does not have an internal origin in the magnetic flux tube. We have analyzed only the kink mode, since buoyancy and pressure are unable to distort the flux tube axis on an helix-like path. We have also shown that the Coriolis force can only account for 9 out of 22 of the studied cases. The RTARs, which can be attributed neither to the kink instability nor to the action of the Coriolis force, have been marked with a "?'' (for unidentified) on the left side of the last columns in Tables 1 and 2, and they also amount to $\approx$41% of the full set (9/22 cases). At this point, we have to consider the interaction of the flux tube with the external plasma via the drag force, which can be very efficient in coupling them, specially if the subphotospheric flux tube is split in several thinner tubes (e.g. Zwaan 1987).

Large scale vortex motions are presently difficult to infer from the data. Nevertheless, Ambroz (2001 and references therein) claimed for the detection of large scale vortex with a spatial size of the order of 200 Mm and with a time scale of 4 Carrington rotations. The results are deduced using the Wilcox Solar Observatory synoptic maps and a local correlation tracking algorithm. Such vortex motions, which may be present at the photosphere or at larger depths, are still an open possibility to explain the origin of some RTARs. They may act deforming a flux tube from its planar $\Omega $ shape while it travels through the CZ, or after the emergence of a classical planar $\Omega $-loop forcing the photospheric polarities to rotate. On the theoretical side, Longcope et al. (1998) propose that the turbulent velocities in the CZ can, via the drag force, deform the axis of an ascending magnetic flux tube. The writhe of the flux tube is modified inducing twist via magnetic helicity conservation (Eq. (7)). The derived mean tilt angle and its dispersion compare favorably with the corresponding observations. Although the buffeting of flux tubes by CZ turbulence can be invoked as the origin of the variation of the tilt angle found in the 22 studied ARs, our selection criteria (clear rotation and availability of vector magnetograms) compel us to use a too biased and too small sample, and do not let us arrive at a conclusion about a mechanism which is by nature of statistical origin.

   
5 Conclusion

We focus this study on the long term evolution of a set of bipolar active regions (ARs) in which the main polarities were seen to rotate one around the other (named as rotating tilt-angle ARs, RTARs). Differential rotation contributes only partially to the change of the tilt angle of the bipoles and it is not the main mechanism. In principle, a possible origin of the observed evolution is the nonlinear development of a kink-instability that occurs in the convection zone (CZ) when the tube is twisted above a critical value. The development of this instability creates a flux tube with a non-planar axis geometry (introducing magnetic helicity in the form of writhe). Then, RTARs can result from the emergence of magnetic flux tubes that are distorted with respect to the classical planar $\Omega $-loop shape. The main objective of this study has been to test this possibility using the largest available set of ARs. We have inferred the sign of the writhe of RTARs computing the variation of their tilt angle from synoptic maps and we have used photospheric vector magnetograms to determine the sign of the magnetic twist. The intersection of the set of RTARs and the set of ARs for which vector magnetograms are available amounts to 22 cases.

A main characteristic of the kink instability is that the flux tube axis is distorted having the same handedness as the twist, so this mechanism necessarily implies that the sign of twist and writhe should be the same. Comparing the handedness of the magnetic twist and writhe, we find that the presence of kink-unstable flux tubes is coherent with no more than 35% of the studied cases; so, at most, only a fraction (7/20) of these RTARs can be explained by this process. This confirms previous results derived when investigating a few cases (only 2 cases over 5 could be explained by the kink instability, see López Fuentes et al. 2000). With such a small percentage, we conclude that the kink instability cannot be the main mechanism at the origin of the observed rotation of the polarities in the studied subset of ARs.

Another possible mechanism is the action of the Coriolis force on the ascending flux tubes in the CZ. In particular, Coriolis force is invoked to explain Joy's law (leader spot closer to the equator). However, we have found no systematic relaxation of the bipoles towards the toroidal direction, rather an important fraction of the ARs (7/22) rotates towards the toroidal direction and then overpasses it by more than  $10^{\circ}$. A similar fraction (5/22) rotates away from the toroidal direction. Therefore, only $\approx$41% (9/22) of the RTARs can be originated by the Coriolis force. Another possible mechanism, which can create the RTARs (9/22) that cannot be explained either by the kink instability, or by the Coriolis force, is the action of large scale vortexes and/or turbulent flows in the CZ or photosphere; these may couple to the ascending or already emerged flux tube through the drag force.

Summarizing, after showing that differential rotation cannot explain the change of the tilt, our results demonstrate that none of the two mechanisms we have tested can be considered as the main cause of the deformation of the flux tubes forming the RTARs. The fraction of ARs that can be explained by any of them is equivalent: 7/20 for the kink instabilty and 9/22 for the Coriolis force. Furthermore, none of the mechanisms excludes the other, which makes it even more difficult to distinguish between them. For the cases that can be attributed to neither of them (9/22), we have proposed the action of large scale vortexes in the CZ, or in the photosphere or near sub-photosphere. These motions impose no clear signature on the emerging flux tubes and, in fact, they could be acting on all the RTARs. Moreover, if RTARs rotate mainly because of photospheric or shallow sub-photospheric motions; then, any signature of the processes that could deform the flux tube before emergence might be completely washed out. As mentioned above, our sample is too biased by the kind of ARs that we have chosen to analyze, those showing a coherent change in their tilt angle along several solar rotations. Besides, the fact that we wanted to test the relevance of the kink instability restricted our sample even more. It will be the objective of a next paper to study the kinetic properties of a much larger set of ARs (López Fuentes et al., in preparation) to determine the role of the Coriolis force and of large scale turbulent plasma motions in the CZ on the observed large tilt angle variation.

Finally, it is worth mentioning that models of kink-unstable tubes have been proposed to explain a particular kind of ARs, the so-called $\delta$-spot configurations (Linton et al. 1998, 1999; Fan et al. 1999). Basically, they are formed by two strong opposite polarities very close together sharing the same penumbra. Such configurations, if present in ARs, appear in their early stages, while our study addresses the long-term evolution of ARs. Then, it has to be tested on a daily basis, whether $\delta$-spot configurations rotate in such a way that their writhe and twist have dominantly the same sign. This first test will tell us if $\delta$-spot configurations are likely to be a consequence of the kink-instability in the CZ. If this first test is successful, a further test would be to estimate the amount of twist in the flux tube to check if it is large enough to trigger the kink instability (this critical value depends on the twist distribution in the tube). Probably, this second test will be possible in a near future with the next generation of vector magnetographs, and the computation of the coronal magnetic helicity budget (a way to estimate the total helicity present initially in the flux tube, see Démoulin et al. 2002).

Acknowledgements
We acknowledge the referee, Dr. E. N. Parker, for his helpful suggestions. M.L.F. acknowledges the Observatoire de Paris, Meudon, for financial support. C.H.M. and P.D. acknowledge financial support from ECOS (France) and SETCIP (Argentina) through their cooperative science program (A01U04). L.v.D.G.was supported by the Research Fellowship F/01/004 of the K.U. Leuven and by the Hungarian Government grants OTKA T-032846, T-038013. P.D. and L.v.D.G. acknowledge the Hungarian-French S&T cooperative program. The NSO/Kitt Peak data used here are produced cooperatively by NSF/NSO, NASA/GSFC, and NOAA/SEL. The National Solar Observatory (NSO) is operated by the Association of Universities for Research in Astronomy (AURA, Inc) under cooperative agreement with the National Science Foundation (NSF).

References

 

Copyright ESO 2003