A&A 397, 147-157 (2003)
DOI: 10.1051/0004-6361:20021560

The stellar activity-rotation relationship revisited: Dependence of saturated and non-saturated X-ray emission regimes on stellar mass for late-type dwarfs[*]

N. Pizzolato1 - A. Maggio1 - G. Micela1 - S. Sciortino1 - P. Ventura2


1 - INAF - Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
2 - INAF - Osservatorio Astronomico di Roma, Via Frascati 33, 00040 Monteporzio, Italy

Received 14 May 2002 / Accepted 1 October 2002

Abstract
We present the results of a new study on the relationship between coronal X-ray emission and stellar rotation in late-type main-sequence stars. We have selected a sample of 259 dwarfs in the B-V range 0.5-2.0, including 110 field stars and 149 members of the Pleiades, Hyades, $\alpha $ Persei, IC 2602 and IC 2391 open clusters. All the stars have been observed with ROSAT, and most of them have photometrically-measured rotation periods available. Our results confirm that two emission regimes exist, one in which the rotation period is a good predictor of the total X-ray luminosity, and the other in which a constant saturated X-ray to bolometric luminosity ratio is attained; we present a quantitative estimate of the critical rotation periods below which stars of different masses (or spectral types) enter the saturated regime. In this work we have also empirically derived a characteristic time scale, $\tau _{\rm e}$, which we have used to investigate the relationship between the X-ray emission level and an X-ray-based Rossby number $R_{\rm e} = P_{\rm rot}/\tau_{\rm e}$: we show that our empirical time scale $\tau _{\rm e}$ resembles the theoretical convective turnover time for $0.4 \lesssim M/M_{\odot} \lesssim 1.2$, but it also has the same functional dependence on B-V as $L_{\rm bol}^{-1/2}$ in the color range $0.5 \lesssim B-V \lesssim 1.5$. Our results imply that - for non-saturated coronae - the $L_{\rm x}$ -  $P_{\rm rot}$ relation is equivalent to the $L_{\rm x}/L_{\rm bol}$ vs. $R_{\rm e}$ relation.

Key words: stars: activity - stars: late-type - X-rays: stars


   
1 Introduction

Magnetic activity in late-type main-sequence stars is an observable manifestation of the stellar magnetic fields. The generation and amplification of surface magnetic fields in solar-like stars are commonly considered the end result of a complex dynamo mechanism, whose efficiency depends on the interaction between differential rotation and subphotosferic convection into the stellar interior. In this context, stellar rotation must play a very important role, and numerous studies have searched for relationships between magnetic activity and rotation. This connection has been explored ever since the pioneering work by Wilson (1966) and the study by Kraft (1967). At first, the rotation-activity relationship was considered to be an indirect one, through stellar age: in fact, Skumanich (1972), compared the rotation and the Ca II emission luminosity for Pleiades, Ursa Major, Hyades stars and the Sun, and showed that both the chromospheric emission and the rotation velocity decay roughly as the inverse square root of the age. According to Frazier's data (Frazier 1970), Ca II emission intensity (in a 1.1 Å band centered on the K-line) varies linearly with surface magnetic field strength, thus making appropriate to link the stellar Ca II emission luminosity with the average magnetic field strength. Thus, the Skumanich's work was the first to suggest the activity-rotation relationship as a causal consequence of the dynamo action, because of the indirect observation of the proportionality law between the average surface magnetic field and the stellar rotation.

When comparing any radiative measure of stellar magnetic activity with the stellar angular velocity, for stars of comparable effective temperature and gravity, one finds that activity increases monotonically with increasing angular velocity for rotation periods exceeding $\sim$1-2 days. The correlation between X-ray luminosity and rotation was first discovered for RS CVn systems by Walter & Bowyer (1981) and was generalized by Pallavicini et al. (1981) for late-type stars (F7 to M5), independently from the luminosity class, as $L_{\rm x} \approx 10^{27}(v_{\rm rot})^{2}$ erg s-1, being  $v_{\rm rot}$ the rotational velocity in km s-1. In the last 20 years many other authors have investigated the correlation between several chromospheric and coronal magnetic activity indicators and stellar rotation rate in both field stars and cluster members (Maggio et al. 1987; Dobson & Radick 1989; Stepien 1994; Hempelmann et al. 1995; Randich et al. 1996, to cite a few). For stars of a given spectral type, hence given radius, the X-ray vs. rotation relationship does not hold for very fast rotators (Micela et al. 1985). Obviously, if one were to increase $v_{\rm rot}$ into the Pallavicini's equation, extremely large X-ray luminosities are obtained. What is observed instead is that the most active stars reach a maximum X-ray luminosity such that $L_{\rm x}/L_{\rm bol}\approx 10^{-3}$ (Vilhu 1984; Vilhu & Walter 1987), where $L_{\rm bol}$ indicates the star's bolometric luminosity. The saturation limit appears to extend all the way along the main sequence from G-type stars to the latest M dwarfs (Fleming et al. 1993); using $L_{\rm x}/L_{\rm bol}$ as activity indicator for stars in the Pleiades and $\alpha $ Persei open clusters, Stauffer et al. (1994) and Randich et al. (1996), respectively, found a trend of increasing log $L_{\rm x}/L_{\rm bol}$ with the rotation velocity up to $\sim$15 km s-1, while stars with higher velocities have $L_{\rm x}/L_{\rm bol}$ near the saturation level. It is yet unclear whether this saturation effect is caused by an intrinsic change in the behavior of the dynamo, or it is merely a sign of a limiting coronal emission reached because the star runs out of the available surface area to accommodate more active regions (Jardine & Unruh 1999).

In this context, we have studied the dependence of the X-ray emission on the stellar rotation in late-type main-sequence stars, using a sample of both field stars and members of open clusters, which includes more K and M-type dwarfs than in previous studies. In particular, we have investigated the relationships between X-ray luminosity or X-ray to bolometric luminosity ratio and the rotation period for stars grouped in selected mass or color ranges. In the first part of this paper we show that the rotation period by itself appears to be a good predictor of the stellar X-ray luminosity down to a critical value, below which the coronal emission saturates, and we explore how the transition from the non-saturated to the saturated X-ray emission regime depends on stellar properties, such as the spectral type and the mass.

The magnetic dynamo mechanism operates in a highly conductive fluid (plasma) subject to convective and rotational motions whose characteristic time scales are, respectively, the convective turnover time - i.e. the period of circulation within a convective cell - and the stellar rotation period. The Rossby number $R_{\rm o}=P_{\rm rot}/\tau_{\rm conv}$, i.e. the ratio between the measured rotation period, $P_{\rm rot}$, and the convective turnover time, $\tau_{\rm conv}$, was introduced in the context of stellar magnetic activity by Noyes et al. (1984), and since then, used by many authors (Micela et al. 1984; Schmitt et al. 1985; Maggio et al. 1987; Dobson & Radick 1989; Stepien 1994; Hempelmann et al. 1995; Randich 2000 - to cite a few) as the quantity best-suited to parameterize the level of stellar magnetic activity. Using the Rossby number, all these authors have investigated the dependence of coronal and chromospheric emission levels on the spectral type, stellar age and evolutionary stage for different samples of late-type stars. In all these works, however, the Rossby number was always calculated as the ratio of the rotation period, a measured quantity, with the convective turnover time estimated by means of some empirical color-dependent function $\tau_{\rm e}(B-V)$, usually the one provided by Noyes et al. (1984), which resembles the theoretical  $\tau_{\rm conv}$. Moreover, although this function was originally derived for main-sequence stars with 0.5<B-V<1.4 (but based on 5 points only redder than B-V=1.0), several authors have applied such an empirical Rossby number out of its range of applicability (for example, Maggio et al. 1987 have used this function to evaluate  $\tau _{\rm e}$ for stars of luminosity class IV, or Giampapa et al. 1998 and Randich 2000 for cluster stars younger and redder than the Noyes's dwarfs). To check the validity of this approach, in the second part of this paper we have empirically determined a new  $\tau_{\rm e}(M)$, as a function of stellar mass, based on the analysis of the same star sample introduced above, and we have investigated whether the use of our X-ray-based Rossby number effectively helps in our physical understanding of X-ray emission as a magnetic dynamo phenomenon.

In Sect. 2 we present the stellar sample used for the present work, and discuss some observational issues related to the completeness of the sample; in Sect. 3 we explore the dependence of the relationship between X-ray emission and rotation period on both stellar mass and color, while in Sect. 4 we determine an X-ray-derived empirical Rossby number and discuss its physical meaning. Section 5 is devoted to the conclusions.

   
2 Selection of a sample of main-sequence stars

In order to study the relationship between activity and rotation on a solid basis we have selected a sample of 259 solar-type dwarfs in the color range 0.5<B-V<2.0, consisting of 110 field stars and 149 stars belonging to the Pleiades ($\sim$100 Myr), Hyades ($\sim$700 Myr), $\alpha $ Persei ($\sim$50 Myr), IC 2602 ($\sim$30 Myr) and IC 2391 ($\sim$30 Myr) open clusters. It represents a significant extension of the sample ($\sim$70 stars) used by Stepien (1994) for an investigation similar - in some respects - to the one carried out in the present work; in particular, our sample is characterized by a better coverage of stars in the low-mass end of the HR diagram (B-V>1.4).

All the selected stars were observed with ROSAT, but the main selection constraint was the availability of photometrically-measured rotational periods (with few exceptions described below); in fact, this sample covers the period range $0.2<P_{\rm rot}<50$ days almost uniformly up to $B-V \sim 1.6$. We have rejected stars known as close binary systems in order to reduce as much as possible the contamination on both X-ray luminosity and rotation due to stellar companions. All the selected field dwarfs and cluster stars are listed in Tables 1 and 2, respectively; for each star, these tables contain the stellar ID, Hipparcos distance, B-V color, V magnitude, rotation period, X-ray emission data, stellar mass and the original references.

In order to take into account the effect on the B-V color due to the interstellar absorption, we have assumed a constant reddening value 0.04 for all the Pleiades stars, 0.1 for $\alpha $ Persei, 0.006 for IC 2391 and 0.04 for IC 2602 members, as already done in previous works (Micela et al. 1999; Randich et al. 1996; Patten & Simon 1996; Prosser et al. 1996, respectively). The B-V colors listed in Table 2 are the de-reddened colors (B-V)0. Hyades members and field stars are much closer to us and hence their colors are not significantly affected by reddening. A color-magnitude diagram for all the stars in the sample is shown in Fig. 1.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f1.eps} \end{figure} Figure 1: Color-magnitude diagram for all 259 selected stars. Squares and crosses indicate cluster members and field stars respectively, while the solid line represents the zero-age-main-sequence location by Siess et al. (2000).
Open with DEXTER

In the B-V color range 0.5-1.4, most of the stars are located near the theoretical zero-age-main-sequence (Siess et al. 2000), with the exception of few members of the IC 2602 cluster and few field stars lying significantly above the main-sequence location: these outliers could be binary systems still present in the sample, pre-main-sequence stars, or field stars starting their evolution across the Hertzsprung gap. We do not have any a priori reason to exclude these stars from our sample, since the X-ray emission from both pre-main-sequence stars and evolved stars with B-V>0.5 (corresponding to a mass $M<1.5~M_{\odot}$ on the main-sequence) very likely has the same coronal origin as in other solar-type dwarfs where a magnetic dynamo mechanism is at work (see Pizzolato et al. 2000, for evolved stars); "anomalously'' high X-ray emission levels could be expected only for close binary systems not yet recognized as such. For 1.4<B-V<1.6, the locus traced by cluster members appears to be systematically above that traced by field stars, because these low-mass cluster members are still in a pre-main-sequence phase of stellar evolution. Again, in the assumption that the X-ray emission from the younger pre-main-sequence stars has a common magnetic origin with the other sources, we have decided to keep these objects in our sample, carrying on our analysis on the most extended sample as possible.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f2.eps} \end{figure} Figure 2: Rotation period as a function of the B-V color for all 259 selected stars. Squares and crosses indicate cluster members and field stars respectively; the arrows mark the field stars with periods derived from $v\sin i$ data.
Open with DEXTER

Finally, it is worth noticing that the low-mass end of our H-R diagram (B-V>1.6) is occupied only by field stars because of the lack of rotational periods for late M-type dwarfs in clusters. All the stars selected for this study were detected with ROSAT. The X-ray luminosities and part of the X-ray to bolometric luminosity ratios have been retrieved from the original papers[*]. In particular, we have adopted the published $L_{\rm x}/L_{\rm bol}$ for those stars belonging to the Pleiades, $\alpha $ Persei, IC 2602 and IC 2391 open clusters, and for the field M dwarfs of our sample selected from Delfosse et al. (1998). The bolometric luminosities of such cluster stars have been computed by using the Johnson's (1966) data for B-V<1.34, while the Monet et al. (1992) transformation between the bolometric correction and the V-I color has been used for all the cluster members (including the two Hyades stars) redder then B-V=1.34. Then, we have verified that the bolometric luminosities computed via the Monet et al. (1992) transformation and those derived with the bolometric correction curve vs. (R-I)C color used by Delfosse et al. (1998) differ by less than 2%. For this reason, we have decided to adopt the calibration of Delfosse et al. (1998) also for the other field stars of the sample having B-V>1.34, for which we have obtained the (R-I)C values from the Kron R-I listed in the CNS3 catalogue (Gliese & Jahreiss 1991), by means of the Bessel (1983) transformation. Finally, for all the field stars with B-V<1.34 in our sample and for the Hyades cluster members with similar colors we have estimated the bolometric correction from the B-V color with the transformations by Flower (1996). In fact, comparison between the bolometric luminosities based on the Johnson's (1966) calibration and those obtained by using the Flower (1996) calibration shows a measured scatter also lower than 2%.

All rotation periods used in the following analysis are derived from photometric measurements (see references in Tables 1 and 2) except for 16 M-type field stars in Delfosse et al. (1998), for which the periods are calculated from $v\sin i$ data and accurate determinations of the stellar radii (Beuermann et al. 1999). These stars are marked with an arrow on the rotation period in all the relevant figures of this paper.

In Fig. 2 we show the rotation periods vs. B-V color for the whole sample: the low-velocity field dwarfs and the high-velocity cluster stars improve the completeness of our sample with respect to previous works, from the point of view of the covered range of rotation periods, especially for  $0.5\lesssim B-V\lesssim 1.6$.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f3.eps} \end{figure} Figure 3: X-ray luminosity vs. rotation period of field dwarfs (crosses) and cluster stars (squares). Leftward arrows indicate field stars with periods derived from $v\sin i$ data.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f4.eps} \end{figure} Figure 4: X-ray to bolometric luminosity ratio vs. rotation period for field dwarfs (crosses) and cluster stars (squares). The meaning of the leftward symbols is the same as in Fig. 3.
Open with DEXTER

   
3 X-ray emission vs. stellar rotation

   
3.1 Overview of the activity-rotation relationships

In this section we show our new results on the relationship between coronal X-ray emission and rotation for solar-type stars. In Figs. 3 and 4 we have plotted, respectively, the X-ray luminosity and the X-ray to bolometric luminosity ratio vs. stellar rotation period for all the stars in our sample.

Both $L_{\rm x}$ and $L_{\rm x}/L_{\rm bol}$ increase with increasing rotation rate (decreasing period) as already noted in previous works (e.g. Pallavicini et al. 1981), and as expected from qualitative arguments based on the $\alpha\Omega$-type shell dynamo theory. In particular, both $L_{\rm x}$ and  $L_{\rm x}/L_{\rm bol}$increase by more than 2 orders of magnitude for decreasing rotation periods from $\sim$50 days to $\sim$4 days; in this non-saturated regime the spread in the $L_{\rm x}$ vs. $P_{\rm rot}$ relationship appears slightly lower than in the $L_{\rm x}/L_{\rm bol}$ vs. $P_{\rm rot}$ case; a more quantitative determination of the spread will be given in the next section. For rotation periods lower than $P_{\rm rot}\sim4$ days, the spread in $L_{\rm x}$ (Fig. 3) becomes much larger than in $L_{\rm x}/L_{\rm bol}$ (Fig. 4), because of the mixing of M-type field dwarfs, having $L_{\rm x}<10^{29}$ erg s-1, with younger cluster members with spectral types G-K-M, having $L_{\rm x}>10^{29}$ erg s-1.


   
Table 3: Results of the analysis of the correlations of the X-ray emission vs. rotation period as a function of the stellar mass.

Mass range		 Number of log $L_{\rm x}^{\rm sat}$ log $(L_{\rm x}/L_{\rm bol})^{\rm sat}$ $P_{\rm sat}^{L_{\rm x}}$ $P_{\rm sat}^{L_{\rm x}/L_{\rm bol}}$ log $\tau_{\rm e}^{*}$
  stars (erg s-1)   (days) (days) (days)

$1.10<M/M_{\odot}<1.29$		 34 $30.0\pm0.5 $ $-3.9\pm0.5$ $2.3\pm1.8$ $2.2\pm1.8$ $0.9\pm0.4$
$1.03<M/M_{\odot}<1.10$ 34 $30.3\pm0.3$ $-3.2\pm0.3$ $1.5\pm1.6$ $1.4\pm1.6$ $1.1\pm0.3$
$0.98<M/M_{\odot}<1.03$ 34 $30.1\pm0.3$ $-3.2\pm0.3$ $2.0\pm1.6$ $2.2\pm1.6$ $1.2\pm0.3$
$0.93<M/M_{\odot}<0.98$ 34 $30.1\pm0.4$ $-3.1\pm0.4$ $1.9\pm1.6$ $2.1\pm1.6$ $1.3\pm0.3$
0.87 $<M/M_{\odot}<0.93$ 34 $ 29.8\pm0.3$ $-3.1\pm0.3$ $3.0\pm1.5$ $3.0\pm1.5$ $1.4\pm0.2$
0.79 $<M/M_{\odot}<0.87$ 34 $29.5\pm0.2$ $-3.2\pm0.2$ $3.1\pm1.5$ $3.3\pm1.5$ $1.5\pm0.2$
0.63 $<M/M_{\odot}<0.78$ 34 $29.3\pm0.2$ $-3.1\pm0.2 $ $3.5\pm1.5$ $3.3\pm1.5$ $1.5\pm0.2$
0.22 $<M/M_{\odot}<0.60$ 21 $28.2\pm0.2$ $-3.3\pm0.2$ >10.8 >13.1 >2.0

* Adopted scaling: log $\tau_{\rm e}(1M_{\odot})=1.1$ days.


  \begin{figure} \par\includegraphics[width=12.5cm,clip]{MS2680f5.eps} \end{figure} Figure 5: X-ray luminosity vs. rotation period for stars in 8 different mass ranges. Cluster members are indicated with squares, field stars having measured periods with crosses and field dwarfs having periods derived from $v\sin i$ data with leftward arrows. Solid lines indicate the broken power laws with fixed exponents obtained by the fitting procedure. The dashed line is used to evidence the paucity of the data in the lowest mass bin.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12.5cm,clip]{MS2680f6.eps} \end{figure} Figure 6: X-ray to bolometric luminosity ratio vs. rotation period for stars in the same mass ranges as in Fig. 5. The meaning of the symbols and of the solid lines is the same as in Fig. 5.
Open with DEXTER

On the other hand, the X-ray emission reaches a saturation level that is clearly evident in the $L_{\rm x}/L_{\rm bol}$ vs. $P_{\rm rot}$ diagram (Fig. 4). In this diagram some of the stars with the shortest rotation periods appear to emit at a saturation level somewhat lower than the canonical value $L_{\rm x}/L_{\rm bol}\sim10^{-3}$: this behavior has been ascribed to the so-called "supersaturation phenomenon" (Prosser et al. 1996); the significance and the interpretation of this behavior is still a matter of debate (James et al. 2000; Stepien et al. 2001) and the issue will not be addressed in this paper.

In the past, the rotation-activity relationship has been studied for stars of different spectral types or in selected color bins, in order to investigate the dependence of such a relationship on stellar properties (i.e. the characteristics of the convection zone). In our study we have chosen to carry out our analysis by studying the X-ray emission vs. rotation correlation primarily as a function of the stellar mass and, subsequently, also as a function of the B-V color. There are two reasons for this choice: (i) the stellar mass is the best indicator of global stellar properties (i.e. the characteristics of the stellar structure), and it allows us a direct comparison with results based on theoretical stellar structure models (see Sect. 4.1); (ii) the color-based analysis is most useful for ease of comparison with results reported in previous studies.

   
3.2 Dependence of saturated and non-saturated X-ray emission on stellar mass

In order to study the dependence of different X-ray emission regimes on stellar parameters, we have derived the mass for each star in our sample. We have first compared the theoretical mass-luminosity relationships based on the models by Kim & Demarque (1996), Ventura et al. (1998) and Siess et al. (2000), at fixed stellar ages between 0.2 Gyr - the age of the youngest model in Kim & Demarque (1996) - and 5 Gyr: we have verified that in the mass range $0.5<M/M_{\odot}<1.2$, covered by all these models, the three relationships never deviate from each other by more than $10\%$ in mass. Eventually, we have decided to adopt the mass-luminosity relationship reported by Siess et al. (2000), because their results cover a wider mass and age ranges than available from other works. In our specific case, we have estimated stellar masses from $0.22~M_{\odot}$ to  $1.29~M_{\odot}$ by interpolating between several relationships at different ages in the range 30 Myr - 5 Gyr and assuming 5 Gyr as the most appropriate age for field stars.

In order to investigate how the observed spread of the X-ray emission levels depends on the stellar mass, we have explored the relationships $L_{\rm x}$ vs. $P_{\rm rot}$ and $L_{\rm x}/L_{\rm bol}$ vs. $P_{\rm rot}$ separately in 8 mass-selected subsamples (Figs. 5 and 6, respectively). The stars were distributed among the subsamples in such a way that exactly the same number of objects (34) fall in each mass range, with the exception of the last bin, which contains the remaining 21 objects (Table 3).

Essentially in all cases two distinct correlation regimes exist: (i) at high rotation periods the emission level (either $L_{\rm x}$ or  $L_{\rm x}/L_{\rm bol}$) increases as a power-law function of  $P_{\rm rot}$in any subsample, while at low rotation periods the emission reaches the saturation level $L_{\rm x}/L_{\rm bol}\approx 10^{-3}$, with no dependence on  $P_{\rm rot}$. Note that the spread in the X-ray emission vs. rotation relationship is rather small in each of these plots, except in the highest and lowest mass ranges where part of the scatter is possibly due to their relatively larger widths, i.e. to the inclusion in the same bin of stars with masses differing by up to $\sim$ $0.4~M_{\odot}$.

In order to obtain a parameterization of the X-ray emission vs. rotation relationship for both saturated and non-saturated coronal sources having different masses, we have fitted the data in each mass bin with a broken power law or, in other terms, a piece-wise linear function in log variables.

As a first step we have performed our fitting by leaving all the parameters free to vary (the slopes and intercepts of the two lines in the log-log diagrams): in the non-saturated regime, the exponent of the power law was found consistently equal to -2 for any subsample, within statistical errors, while in the saturated regime the power-law exponent resulted statistically consistent with 0.

In the next step, the period at which saturation occurs ( $P_{\rm rot}^{\rm sat}$) and the saturation X-ray emission level ( $L_{\rm x}^{\rm sat}$or ( $L_{\rm x}/L_{\rm bol}$) $^{\rm sat}$) have been determined, for each mass range, as free parameters of the piece-wise power-law functions with fixed exponents (0 and -2). Note that for $1.10<M/M_{\odot}<1.29$ only few stars are in the saturated regime while for $0.22<M/M_{\odot}<0.60$ all stars - except one - are saturated (Figs. 5 and 6). The results of such analysis are reported in Table 3.


   
Table 4: Results of the analysis of the correlations of the X-ray emission vs. rotation period as a function of the B-V color.

B-V color range		 Number of log $L_{\rm x}^{\rm sat}$ log $(L_{\rm x}/L_{\rm bol})^{\rm sat}$ $P_{\rm sat}^{L_{\rm x}}$ $P_{\rm sat}^{L_{\rm x}/L_{\rm bol}}$ log $\tau_{\rm e}^{*}$
  stars (erg s-1)   (days) (days) (days)

0.50 <B-V< 0.60		 34 $30.1\pm0.4$ $-3.6 \pm 0.4$ $1.8 \pm 1.6$ $1.6 \pm 1.6$ $1.0 \pm 0.3$
0.61 <B-V< 0.71 34 $30.3 \pm 0.4$ $-3.1\pm0.4$ $1.6 \pm 1.7$ $1.3 \pm 1.7$ $1.1\pm0.3$
0.72 <B-V< 0.84 34 $30.2 \pm 0.3$ $-3.1\pm0.3$ $1.8 \pm 1.5$ $1.7 \pm 1.5$ $ 1.2 \pm 0.2$
0.84 <B-V< 0.91 34 $29.9 \pm 0.3$ $-3.2\pm0.3$ $2.6 \pm 1.5$ $2.4 \pm 1.5$ $1.3 \pm 0.2$
0.91 <B-V< 1.06 34 $29.9 \pm 0.3$ $-3.0 \pm 0.3$ $2.8 \pm 1.5$ $2.4 \pm 1.5$ $1.4\pm0.2$
1.07 <B-V< 1.35 34 $29.4 \pm 0.2$ $-3.2\pm0.2$ $4.1 \pm 1.5$ $3.5\pm1.5$ $1.5\pm0.2$
1.36 <B-V< 1.54 34 $29.2 \pm 0.3$ $-3.2\pm0.2$ $4.0 \pm 1.5$ $3.7 \pm 1.5$ $1.5\pm0.2$
1.55 <B-V< 1.90 21 $28.3 \pm 0.2$ $-3.3\pm0.2$ >9.7 >23.9 >2.3

* Adopted scaling: log $\tau_{\rm e}(B-V)_{\odot}=1.1$ days.

In Fig. 7 we show the variation of the X-ray luminosity saturation level and the $L_{\rm x}/L_{\rm bol}$ saturation level vs. stellar mass: the X-ray luminosity saturation level decreases from $L_{\rm x}\approx2\cdot10^{30}$ erg s-1 to $L_{\rm x}\approx10^{28}$ erg s-1, between $M/M_{\odot}\approx 1.1$ and $M/M_{\odot}\approx 0.4$, while the $L_{\rm x}/L_{\rm bol}$ saturation level remains almost fixed at $\approx 10^{-3}$, except for the point at $\sim$ $1.2~M_{\odot}$ ( $L_{\rm x}/L_{\rm bol}\approx 10^{-4}$). The rotation period at which saturation occurs (Fig. 7, right panel) increases from $P_{\rm rot}^{sat}\sim 1.5$ days for solar-mass dwarfs to $P_{\rm rot}^{sat}\sim4$ days for dwarfs with half the solar mass, for both the X-ray emission indicators. These values are essentially in agreement with the recent saturation periods reported by Stauffer et al. (1994): in fact their results (2 days at 1 $M_{\odot}$and 4.5 days at about 0.4 $M_{\odot}$) differ from our findings for a quantity well within the associated errors.


  \begin{figure} \par\includegraphics[width=12.5cm,clip]{MS2680f7.eps} \end{figure} Figure 7: Results of the fitting analysis reported in Table 3: the left and central panel show, respectively, the variation of $L_{\rm x}$ and  $L_{\rm x}/L_{\rm bol}$ saturation level with the stellar mass; the right panel shows variation of the rotation period at which saturation of $L_{\rm x}$ (triangles) and $L_{\rm x}/L_{\rm bol}$ (squares) occurs vs. stellar mass. The horizontal segments indicate the ranges of the mass bins, with the vertical error bar (or lower limit) located at the median value of the masses for the stars in each bin.
Open with DEXTER

In order to show the global behavior of the X-ray emission vs. rotation relations and their dependence on the adopted activity indicator ($L_{\rm x}$ or $L_{\rm x}/L_{\rm bol}$) and on the stellar mass, we have plotted in Fig. 8 all the relations obtained by the fitting procedure in each mass-selected subsample. The relation between $L_{\rm x}$ and  $P_{\rm rot}$ (Fig. 8, left panel) in the non-saturated regime is identical for all mass bins, while the saturation is reached at decreasing rotation periods and increasing X-ray luminosity levels for increasing mass. Note the complementary behavior of the $L_{\rm x}/L_{\rm bol}$ vs. $P_{\rm rot}$ case (Fig. 8, right panel): the saturation occurs approximately at the same level of $L_{\rm x}/L_{\rm bol}\approx 10^{-3}$ for $M<1.1~M_{\odot}$, but the mass-dependence of $P_{\rm rot}^{\rm sat}$ - which is the same as in the $L_{\rm x}$ vs. $P_{\rm rot}$ relationships - induces a spread in the $L_{\rm x}/L_{\rm bol}$ power-laws which describe the behavior of the non-saturated stars.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{MS2680f8.eps}\hspace*{4mm} \includegraphics[width=6.5cm,clip]{MS2680f9.eps} \end{figure} Figure 8: Collection of all the best-fit relations between X-ray emission and rotation period shown in Figs. 5 and 6 for the stars in all the mass ranges considered.
Open with DEXTER

   
3.3 Dependence of saturated and non-saturated X-ray emission on $\mathsfsl {B-V}$ color

We have also performed a complementary investigation of the dependence on B-V color of the correlation of the X-ray emission with the stellar rotation period. We have followed the same criteria of analysis previously described for the case of the study of the activity-rotation connection in selected mass bins. The functional dependences on B-V color of the X-ray emission saturation level and of the rotation period at which saturation occurs are essentially identical to those shown in Fig. 7, except for the x-axis values. It is worth noticing that for low mass main sequence stars ( $M<0.6~M_{\odot}$, B-V>1.3) the B-V color is not a good proxy of fundamental stellar parameters such as the mass, the effective temperature, the bolometric luminosity and the depth of the convection zone. On the other hand, the results described in this section (reported in Table 4) are the most adequate to be compared with similar results obtained in the past by other authors.

   
4 X-ray emission vs. Rossby number

The historical importance of the Rossby number is strictly related to the dynamics of the magnetic fields embedded and frozen in the plasma. As already anticipated in Sect. 1 the Rossby number $R_{\rm o}=P_{\rm rot}/\tau_{\rm conv}$ is usually considered a good indicator of the efficiency of the dynamo mechanism in the generation and amplification of the stellar magnetic fields, and consequently of the stellar magnetic activity. However, while the rotation period can be directly measured, $\tau_{\rm conv}$ is usually empirically determined (Noyes et al. 1984; Stepien 1994) or derived from theoretical models (Gilliland 1985; Kim & Demarque 1996; Pizzolato et al. 2001).

The study of the relationship between X-ray emission and rotation in different mass ranges (or spectral classes), described in the previous section, allowed us to clearly separate saturated stars from non-saturated stars and, therefore, it made possible a new determination of an empirical X-ray-based Rossby number. In order to evaluate this parameter for all the stars in our sample we have determined an empirical X-ray-derived function of the stellar mass, $\tau_{\rm e}(M)$, and we have used this function as an empirical time scale in place of  $\tau_{\rm c}$, the convective turnover time. In this section we show how the ratio $R_{\rm e} = P_{\rm rot}/\tau_{\rm e}$ effectively provides us with a unique, mass-independent prediction of the X-ray emission level, for both saturated and non-saturated stars, a property which makes $R_{\rm e}$ possibly preferable to  $P_{\rm rot}$.

   
4.1 Empirical determination of the Rossby number from X-ray data

Following the original idea of Noyes et al. (1984), and a working approach similar to that adopted by Stepien (1994), we have explored the possibility to obtain an improvement in the correlation between activity and rotation by using the Rossby number $R_{\rm e}=P_{\rm rot}/\tau_{\rm e}(M)$ instead of the rotation period, where $\tau_{\rm e}(M)$ is a mass-dependent function derived from the observational data available.

Our work is characterized by two improvements with respect to the Stepien (1994) work: (i) a larger sample, including more stars in all rotation ranges and more low-mass stars, and (ii) a quantitative separation of the two X-ray emission regimes, a crucial point for the determination of the mass dependent function  $\tau_{\rm e}(M)$.

We have first considered the family of power laws:

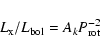\begin{displaymath}L_{\rm x}/L_{\rm bol}=A_k P_{\rm rot}^{-2} \end{displaymath} (1)

which describe the behavior of the non-saturated stars in Fig. 8 (right panel), with Ak dependent on the mass range considered. We stress that Stepien (1994) made no distinction between saturated and non-saturated stars in his activity-rotation relationships.

A single relationship for all the stars in our sample can be obtained by scaling:

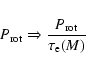\begin{displaymath}P_{\rm rot} \Rightarrow \frac{P_{\rm rot}}{\tau_{\rm e}(M)} \end{displaymath} (2)

where the mass-dependent function $\tau_{\rm e}(M)$ can be obtained as (Ak/C)1/2, with C= const., so that

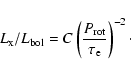\begin{displaymath}L_{\rm x}/L_{\rm bol}= C \left(\frac{P_{\rm rot}}{\tau_{\rm e}}\right)^{-2} \cdot \end{displaymath} (3)

The new variable $P_{\rm rot}/\tau_{\rm e}$ can be dubbed "X-ray empirical Rossby number" and denoted by $R_{\rm e}$. An important point is that, by using this empirically-derived Rossby number, we may effectively describe the activity level, represented by $L_{\rm x}/L_{\rm bol}$, as a single mass-independent function of the parameter $R_{\rm e}$, taking into account both the rotation and any effect linked to differences in internal stellar structure for stars of different masses (Fig. 9).


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f10.eps} \end{figure} Figure 9: X-ray to bolometric luminosity ratio vs. empirical Rossby number for all the stars in our sample. The meaning of the symbols is the same as in Fig. 3.
Open with DEXTER

It is to be mentioned, however, that the adopted procedure does not permit to determine absolute values of  $\tau _{\rm e}$, but only the functional dependence of such an empirical time scale on the stellar mass; the function  $\tau _{\rm e}$ must be properly scaled in order to be compared with other empirical or model-derived convective turnover times. The value of  $\tau _{\rm e}$ listed in Table 3 for each mass range was obtained by applying a constant scaling factor such that the value of  $\tau _{\rm e}$ for solar-mass stars matches the Noyes's semi-empirical prediction of the convective turnover time of the Sun. The relationship between this  $\tau _{\rm e}$ and the stellar mass has been used to calculate the values of $R_{\rm e}$ plotted in Fig. 9.

In Fig. 10 we show a comparison between the function  $\tau_{\rm e}(M)$ and the theoretical convective turnover time, $\tau_{\rm c}$, derived from two stellar structure models, the model by Kim & Demarque (1996) and the more recent model by Ventura et al. (1998). The latter was employed for the computation of the characteristic turnover time also for stars with $M<0.5~M_{\odot}$, including fully-convective stars with $M/M_{\odot}=0.3$ and $M/M_{\odot}=0.2$. Both models give a global estimate of this time scale by integrating over the whole convective region. For ease of comparison the function $\tau_{\rm e}(M)$ in Fig. 10 is scaled in such a way that our empirical time scale for a solar-mass star coincides with the theoretical convective time predicted by Ventura et al. (1998). We find that the empirically X-ray-derived function  $\tau _{\rm e}$ follows  $\tau_{\rm c}$ for stars in the mass range 0.6-1.2; for lower-mass stars, the empirical timescale is still in agreement with the model convective time, even if the paucity of stars with $P_{\rm rot}>10$ days makes the comparison particularly critical.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f11.eps} \end{figure} Figure 10: Comparison between our empirically-determined  $\tau _{\rm e}$(asterisks), and theoretical predictions by Kim & Demarque (dash-dotted line) and by Ventura et al. (1998) (dashed line). Horizontal lines cover the mass ranges considered, while the asterisks are placed at the median of the masses of the corresponding bin.
Open with DEXTER

In order to compare our empirical time scale with the values computed with the Noyes et al. (1984) formula, we have completed our analysis by deriving  $\tau _{\rm e}$ also as a function of the B-V color, using the results reported in Sect. 3.3. In Fig. 11 we have plotted the Noyes function and our empirical $\tau_{\rm e}(B-V)$, properly scaled as in Table 3. The two formulations are very similar for 0.5<B-V<1.0, and our data confirm the Noyes's prediction also in the B-V range 1.0-1.4, where the Noyes study was based on the data of 5 stars only (dashed line in Fig. 11). For B-V>1.4 we find an indication of increasing  $\tau _{\rm e}$as already seen in Fig. 10 for stars with $M<0.5~M_{\odot}$.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f12.eps} \end{figure} Figure 11: Comparison between empirically-determined  $\tau _{\rm e}$(asterisks), scaled $L_{\rm bol}^{-1/2}$ (squares), and the Noyes et al. (1984) semi-empirical formulation (thin solid and dashed line).
Open with DEXTER

4.2 Alternative interpretation of the empirical Rossby number

In Sect. 3.2 we have already demonstrated that a single power-law provides a good mass-independent description of the $L_{\rm x}$ vs. $P_{\rm rot}$ relationship, for non-saturated stars. Does the $L_{\rm x}/L_{\rm bol}$ vs. $R_{\rm e}$ relationship represent a real improvement?

The scaling:

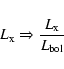\begin{displaymath}L_{\rm x} \Rightarrow \frac{L_{\rm x}}{L_{\rm bol}} \end{displaymath} (4)

introduces a color-dependent vertical shift of the power-laws, which can be compensated by the horizontal shift provided by the scaling:

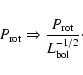\begin{displaymath}P_{\rm rot} \Rightarrow \frac{P_{\rm rot}}{L_{\rm bol}^{-1/2}}\cdot \end{displaymath} (5)

In fact, we show in Fig. 11 that the empirically-determined color function $\tau_{\rm e}(B-V)$ is equivalent to $L_{\rm bol}^{-1/2}$, except for a constant scaling factor, where $L_{\rm bol}$ was computed as the mean value of the bolometric luminosities of the stars in each color bin. The above argument suggests that for stars in the non-saturated regime the two relationships $L_{\rm x}$ vs. $P_{\rm rot}$and $L_{\rm x}/L_{\rm bol}$ vs. $R_{\rm e}$ are equivalent.

On the other hand, for saturated stars, the X-ray luminosity is related only to  $L_{\rm bol}$. From this point of view, we can argue that there is no need to invoke a Rossby number: $P_{\rm rot}$ is the only parameter required to described the behavior of the non-saturated stars, while $L_{\rm bol}$ is the crucial parameter in the saturated regime.

An alternative interpretation can be sustained by noting that the $L_{\rm x}/L_{\rm bol}$ vs. $R_{\rm e}$ relationship describes adequately both saturated and non-saturated stars. From this second point of view, we are left with one open issue: if we accept $R_{\rm e}$ as a fundamental dimensionless parameter of the dynamics of plasma flows in the stellar interiors, determining also the efficiency of the dynamo action, then the stellar activity level is best represented by the ratio $L_{\rm x}/L_{\rm bol}$, but why the X-ray emission level should be determined by the bolometric luminosity?

In any case, the observed agreement between the functional forms of $L_{\rm bol}^{-1/2}$ and $\tau_{\rm e}(B-V)$ seems to indicate a possible physical link between the stellar bolometric luminosity and the "effective" time scale relevant for the dynamo action. Future investigations on fully-convective late M-type dwarfs or stars in evolutionary phases across the Hertzsprung gap, will allow us to test in more detail whether stellar activity in these stars can be described in the same framework as in main sequence stars.

A final point is illustrated in Fig. 12 which shows an interesting almost linear relationship between our empirical convective turnover time and the rotation period at which the saturated X-ray emission is reached. This plot suggests that the saturation is triggered when a critical value of the ratio between these two time scales is reached, and this value is almost independent from the stellar mass, at least for main-sequence stars. Moreover, since  $\tau _{\rm e}$ scales as  $L_{\rm bol}^{-1/2}$, also $P_{\rm rot}^{\rm sat}$ scales in the same way; to a good approximation:

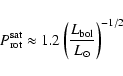\begin{displaymath}P_{\rm rot}^{\rm sat}\approx 1.2\left(\frac{L_{\rm bol}}{L_{\odot}}\right) ^{-1/2} \end{displaymath} (6)

which is accurate within a factor two.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS2680f13.eps} \end{figure} Figure 12: Relationship between our empirical time scale and the rotation period at which the saturated X-ray emission is reached.
Open with DEXTER

   
5 Summary and conclusions

Our study has confirmed that a single relationship between  $L_{\rm x}/L_{\rm bol}$ and an empirical Rossby number $R_{\rm e}$ can be obtained for main sequence late-type stars having different masses or spectral types (i.e. different properties of the convection zone). The importance of our result rests on the inclusion - for the first time with respect to past works by Noyes et al. (1984) and by Stepien (1994) - of very late-type stars with $M<0.5~M_{\odot}$, comprising some fully convective stars. For the first time we have also determined the functional dependence on the stellar mass of an empirically X-ray-derived characteristic time scale, $\tau _{\rm e}$, and, independently, we have carried out our analysis also with the B-V color.

However, the clear observational link between $L_{\rm x}/L_{\rm bol}$and the empirical Rossby number does not imply by itself the interpretation of the mass-dependent quantity  $\tau_{\rm e}(M)$ as a convective time. For this reason, we have performed a comparison between our empirical time scale and the theoretical values of the convective turnover time, $\tau_{\rm c}$. We have confirmed that the function  $\tau_{\rm e}(M)$ is very similar to  $\tau_{\rm c}$ for stars in the entire mass range considered (Fig. 10). For fully-convective late-type stars with $M<0.3~M_{\odot}$, we have shown that $\tau_{\rm e}(M)$ is still consistent with the corresponding values predicted by theoretical models. This is a new and significant result, because of insufficient data in previous works for such a comparison.

Another important point is that the function $\tau_{\rm e}(B-V)$ turns out to have the same functional shape as $L_{\rm bol}^{-1/2}$, in the range 0.5<B-V<1.5. For this reason we can assert that for non-saturated stars the $L_{\rm x}$ vs. $P_{\rm rot}^{-2}$relationship is equivalent to the relationship $L_{\rm x}/L_{\rm bol}\propto (P_{\rm rot}/\tau_{\rm e})^{-2}$.

The analysis developed to investigate the physical meaning of an empirical X-ray-derived Rossby number has forced us to revisit the relationship between X-ray emission and rotation. Our results show that the coronal X-ray emission increases roughly as a power law of the stellar rotation period independently of the stellar mass or spectral class, thus demonstrating that the stellar rotation dominates over convection in the magnetic dynamo operating in non-saturated late-type dwarfs, including stars with $M<0.5~M_{\odot}$.

On the other hand, the X-ray emission level from saturated stars depends only on  $L_{\rm bol}$, and hence it appears to be dependent on the characteristics of the stellar structure.

In this contest, the most important result is that, independently of the X-ray emission indicator used in our study, the X-ray emission saturation occurs below a critical rotation period, $P_{\rm rot}^{\rm sat}$, increasing with decreasing stellar mass, in a way that we have quantitatively estimated.

Equivalently, we have also demonstrated that $P_{\rm rot}^{\rm sat}$scales as  $L_{\rm bol}^{-1/2}$: this link suggests that the saturation of the X-ray emission in late-type main sequence stars can be considered as an effect depending on the properties of the convective region as well as an effect depending on the total energy budget available in the star. We believe that in the near future the study of the activity-rotation connection in samples of stars having different evolutionary stages will enable us to test on a more solid basis the relationship between the characteristic time scale  $\tau _{\rm e}$ and the bolometric luminosity, thus contributing to complete our current picture of the stellar magnetic activity.

Acknowledgements
The authors acknowledge partial support for this work from Agenzia Spaziale Italiana, Ministero dell'Università e della Ricerca Scientifica e Tecnologica and CNAA. F. D'Antona is also gratefully acknowledged for clarifying discussions, and we also thank the referee S. Randich for her useful comments and suggestions.

References

 

Online Material


   
Table 1: Field dwarf sample.
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
Sun - 0.66 -26.78 25.38 1a 27.37 1b -6.23 1.09
DK Leo 20.41 1.37 9.3 7.98 2 28.90 2 -3.96 0.82
GL 83.1 4.48 1.80 12.28 <0.52 3 27.33 3 -3.72 0.31
G 99-49 5.38 1.68 11.33 <0.50 3 28.01 3 -3.41 0.42
G 165-08 7.94 1.57 11.45 <0.28 3 28.31 3 -3.19 0.48
GL 166C 4.85 1.67 11.17 <2.11 3 28.02 3 -3.41 0.41
GL 182 26.67 1.37 9.6 1.86 2 29.00 2 -3.96 0.84
G 188-38 8.96 1.72 11.99 <0.52 3 28.44 3 -3.14 0.45
GL 234A 4.12 1.71 11.12 <0.39 3 27.75 3 -3.62 0.39
GL 285 5.93 1.59 11.2 2.78 2 28.50 2 -3.23 0.44
GL 338B 6.27 1.42 7.64 <10.17 3 27.51 3 -4.90 0.75
GL 380 4.87 1.36 6.60 <11.67 3 27.45 3 -5.04 0.79
GL 388 4.69 1.54 9.4 2.60 2 28.30 2 -3.61 0.55
GL 490 18.09 1.42 10.6 3.17 2 28.90 2 -3.41 0.69
GL 493.1 8.13 1.75 13.40 <0.21 3 27.92 3 -3.21 0.33
GL 494 11.43 1.44 9.8 1.54 2 29.00 2 -3.25 0.68
GL 551 1.30 1.90 11.05 42.00 4 27.04 5 -3.78 0.22
GL 673 7.72 1.36 7.54 <11.94 3 27.64 3 -4.96 0.79
GL 685 14.09 1.45 9.9 18.60 2 27.40 2 -4.92 0.71
GL 791.2 8.70 1.65 13.05 <0.32 3 27.88 3 -3.43 0.36
GL 860B 4.03 1.62 9.59 <0.41 3 27.38 3 -3.70 0.51
GL 873 5.05 1.60 10.2 4.38 2 28.60 2 -3.12 0.50
GL 875 14.00 1.48 9.85 1.60 2 29.00 2 -3.29 0.71
GL 890 21.86 1.41 10.6 0.43 2 29.00 2 -3.37 0.73
GL 896B 6.24 1.65 12.40 <0.20 3 28.62 3 -2.58 0.36
GJ 1154A 8.40 1.77 13.73 <0.65 3 27.77 3 -3.28 0.31
GJ 1156 6.54 1.88 13.81 <0.87 3 27.65 3 -3.39 0.26
HD 1835 20.39 0.66 6.4 7.70 2 28.90 2 -4.67 1.08
LHS 3376 7.30 1.83 13.48 <0.22 3 27.30 3 -3.64 0.30
HD 3651 11.11 0.85 5.9 48.00 2 27.60 2 -5.70 1.00
HD 4628 7.46 0.88 5.8 38.00 2 27.00 2 -6.01 0.93
HD 10360 8.15 0.88 5.76 30.00 6 27.13 7 -5.97 0.95
HD 10361 8.13 0.86 5.81 39.00 6 27.13 7 -5.94 0.95
HD 10476 7.47 0.84 5.2 35.20 6 26.64 8 -6.59 0.98
HD 10700 3.65 0.72 3.5 34.50 6 27.04 9 -6.21 1.00
HD 11507 11.09 1.43 8.8 15.80 2 27.70 2 -4.76 0.75
HD 13445 10.91 0.82 6.17 30.00 6 27.61 9 -5.56 0.97
HD 14802 21.93 0.60 5.19 9.00 6 29.60 9 -4.50 1.22
HD 16160 7.21 0.97 5.8 45.00 2 27.30 2 -5.71 0.92
HD 16673 21.54 0.52 5.8 7.40 2 28.80 2 -5.03 1.15
HD 17051 17.24 0.56 5.4 7.90 6 28.78 9 -5.02 1.15
HD 17925 10.38 0.87 6.0 6.60 2 28.70 2 -4.51 0.98
HD 20630 9.16 0.68 4.8 9.40 2 28.90 2 -4.62 1.07
HD 22049 3.22 0.88 3.7 11.30 2 28.20 2 -4.92 0.95
HD 25998 21.34 0.52 5.5 3.00 6 29.54 9 -4.40 1.18
HD 26913 20.89 0.70 6.96 7.20 6 29.20 9 -4.18 1.03
HD 26965 5.04 0.82 4.41 37.10 6 27.61 9 -5.59 0.98
HD 30495 13.32 0.64 5.5 7.60 2 28.70 2 -4.86 1.08
HD 32147 8.81 1.06 6.22 47.40 6 27.18 9 -5.87 0.92


 
Table 1: (continued)
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
HD 35296 14.66 0.53 5.0 5.00 2 29.30 2 -4.52 1.15
HD 36435 19.57 0.78 7.01 11.20 6 28.43 10 -4.90 1.01
HD 36705 14.94 0.83 6.6 0.51 2 30.30 2 -2.97 0.99
HD 38392 8.97 0.94 6.15 17.30 6 28.27 9 -4.77 0.93
HD 39587 8.66 0.59 4.4 5.20 2 29.10 2 -4.51 1.10
HD 42807 18.12 0.66 6.5 7.80 2 28.60 2 -4.83 1.04
HD 43834 10.15 0.72 5.09 32.00 6 27.46 9 -6.05 1.06
HD 52698 14.62 0.90 6.71 26.00 6 28.49 10 -4.74 0.98
HD 53143 18.41 0.81 6.81 16.40 6 28.69 10 -4.67 1.02
HD 72905 14.27 0.62 5.6 4.10 2 29.10 2 -4.47 1.08
HD 75332 28.69 0.52 6.22 4.00 6 29.56 9 -4.35 1.17
HD 76151 17.09 0.67 6.0 15.00 6 28.34 9 -5.24 1.08
HD 78366 19.14 0.60 5.9 9.70 6 28.95 9 -4.75 1.12
HD 81809 31.24 0.64 5.38 40.20 6 28.10 9 -6.25 1.29
HD 82106 12.68 1.00 7.22 13.30 6 28.30 10 -4.64 0.91
HD 82558 18.34 0.91 7.8 1.70 2 29.50 2 -3.50 0.93
HD 82885 11.18 0.77 5.41 18.60 6 28.38 9 -5.10 1.05
HD 95650 11.66 1.47 9.5 2.94 2 28.50 2 -3.80 0.71
HD 95735 2.55 1.51 7.5 48.00 2 26.80 2 -5.12 0.60
HD 97334 21.72 0.60 6.4 7.60 2 29.10 2 -4.51 1.09
HD 98712 13.16 1.36 8.7 11.60 2 28.50 2 -4.08 0.79
HD 101501 9.54 0.74 5.3 16.00 2 28.20 2 -5.17 1.03
HD 102077 48.66 0.91 8.92 1.80 2 30.00 2 -3.40 1.02
HD 114613 20.48 0.70 4.85 33.00 6 28.36 9 -5.85 1.24
HD 114710 9.15 0.58 4.3 12.40 2 28.20 2 -5.50 1.12
HD 115383 17.95 0.58 5.2 3.30 2 29.10 2 -4.82 1.17
HD 115404 11.23 0.92 6.6 19.00 2 27.80 2 -5.25 0.94
HD 118100 19.79 1.18 9.3 3.96 2 29.20 2 -3.38 0.81
HD 128620 1.35 0.71 -0.01 29.00 6 27.34 10 -6.45 1.13
HD 128621 1.35 0.88 1.33 42.00 6 27.34 10 -5.97 1.00
HD 131156A 6.70 0.72 4.7 6.20 2 28.60 2 -4.70 1.01
HD 131977 5.91 1.11 5.74 44.60 6 27.54 9 -5.38 0.89
HD 136202 24.53 0.54 5.04 16.00 6 27.64 9 -6.61 1.27
HD 141004 11.75 0.60 4.4 18.00 2 27.70 2 -6.18 1.16
HD 147513 12.87 0.62 5.38 8.50 6 28.96 9 -4.61 1.08
HD 147584 12.11 0.55 4.91 13.00 6 29.11 9 -4.58 1.12
HD 149661 9.78 0.81 5.7 23.00 2 28.30 2 -4.96 0.99
HD 152391 16.94 0.75 6.6 11.10 2 28.70 2 -4.66 1.02
HD 154417 20.38 0.58 6.0 7.60 2 28.80 2 -4.91 1.12
HD 155885 5.98 0.86 5.33 21.11 6 28.28 9 -4.71 0.93
HD 155886 5.46 0.85 5.29 20.69 6 28.28 9 -4.65 0.91
HD 156026 5.97 1.16 6.3 18.00 2 27.50 2 -5.23 0.85
HD 160346 10.71 0.96 6.5 36.00 2 27.70 2 -5.36 0.94
HD 165185 17.37 0.62 5.95 5.90 6 29.17 9 -4.43 1.09
HD 165341 5.09 0.86 4.03 19.70 2 28.20 2 -5.18 1.02
HD 166620 11.10 0.87 6.37 42.00 11 26.92 12 -6.19 0.96
HD 176051 14.98 0.59 5.22 16.00 6 28.06 9 -5.70 1.13
HD 185144 5.77 0.79 4.70 29.00 6 27.61 9 -5.58 0.98
HD 187691 19.39 0.55 5.10 10.00 6 28.05 9 -5.97 1.20
HD 190007 13.11 1.12 7.5 29.30 2 27.90 2 -5.01 0.89


 
Table 1: (continued)
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
HD 190406 17.67 0.61 5.8 14.50 2 28.10 2 -5.58 1.11
HD 191408 6.05 0.87 5.31 45.00 6 26.60 7 -6.42 0.93
HD 194012 26.13 0.51 6.17 7.00 6 28.36 9 -5.49 1.16
HD 197481 9.94 1.44 8.6 4.85 2 29.40 2 -3.19 0.75
HD 201091 3.48 1.17 5.2 37.90 2 27.20 2 -5.51 0.84
HD 201092 3.50 1.37 6.0 48.00 2 27.20 2 -5.32 0.78
HD 206860 18.39 0.58 6.0 4.70 2 29.00 2 -4.62 1.10
HD 209100 3.63 1.06 4.69 22.00 6 27.20 9 -5.69 0.89
HD 216803 7.64 1.10 6.5 10.30 2 28.30 2 -4.54 0.87
HD 219834B 20.8 0.91 7.6 42.00 2 27.70 2 -5.49 0.97
HD 224930 12.40 0.67 5.75 33.00 6 27.51 9 -5.90 1.04

References: [1a]: Lang, Astroph. Data (1992), [1b]: Peres et al. (2000), [2]: Hempelmann et al. (1995), [3]: Delfosse et al. (1998), [4]: Benedict et al. (1993), [5]: Marino et al. (2000), [6]: Saar et al. (1997), [7]: Schmitt et al. (1995), [8]: Marino et al. (2002), [9]: Huensch et al. (1998), [10]: Huensch et al. (1999), [11]: Noyes et al. (1984), [12]: Stepien (1994).


   
Table 2: Cluster stars: Pleiades, IC 2602, IC 2391, $\alpha $ Persei and Hyades.
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
Pleiades
HCG 71 127 1.37 14.36 2.98 3 29.21 2 -2.80 0.72
HII-34 127 0.88 11.84 6.60 4 28.98 2 -4.04 0.93
HII-133 127 1.31 14.14 1.36 3 29.43 2 -3.01 0.74
HII-191 127 1.31 14.38 3.10 3 29.40 2 -2.98 0.72
HII-263 127 0.84 11.51 4.82 3 29.79 1 -3.43 0.96
HII-293 127 0.66 10.79 4.25 4 29.13 2 -4.29 1.03
HII-314 127 0.60 10.44 1.47 4 30.28 2 -3.22 1.06
HII-320 127 0.88 10.92 4.58 4 30.20 1 -3.26 1.01
HII-324 127 1.01 12.87 0.42 4 29.85 2 -2.83 0.84
HII-335 127 1.26 13.65 0.27 3 29.34 1 -3.24 0.78
HII-345 127 0.84 11.57 0.84 3 30.08 1 -3.15 0.95
HII-357 127 1.21 13.20 3.40 4 29.47 1 -3.17 0.81
HII-625 127 0.78 11.46 0.43 4 30.19 2 -2.92 0.96
HII-686 127 1.35 13.43 0.40 4 29.40 1 -3.24 0.79
HII-708 127 0.58 10.01 1.05 4 29.78 2 -3.89 1.11
HII-727 127 0.51 9.58 1.20 4 29.85 1 -4.06 1.15
HII-738 127 0.75 11.04 0.83 3 30.25 2 -3.04 1.00
HII-739 127 0.58 9.45 2.69 4 30.29 2 -3.61 1.16
HII-879 127 1.03 12.79 7.38 4 28.98 1 -3.85 0.85
HII-882 127 1.02 12.95 0.58 4 29.67 1 -3.11 0.83
HII-883 127 1.08 13.05 7.20 3 28.98 1 -3.75 0.83
HII-930 127 1.22 14.08 1.39 3 29.15 2 -3.20 0.74
HII-1032 127 0.71 10.98 1.31 3 30.15 1 -3.27 1.01
HII-1124 127 0.94 12.20 6.20 2 29.47 2 -3.43 0.90
HII-1136 127 0.72 11.34 0.53 4 30.16 1 -3.05 0.97
HII-1280 127 1.40 14.45 0.30 2 29.44 2 -2.65 0.71
HII-1305 127 1.15 13.52 0.39 3 29.37 1 -3.25 0.79
HII-1332 127 0.98 12.41 8.29 4 29.27 1 -3.57 0.88
HII-1512 127 1.26 13.51 8.20 3 28.94 1 -3.68 0.79
HII-1531 127 1.23 13.46 0.48 4 29.25 1 -3.23 0.79
HII-1532 127 1.23 13.87 0.78 3 29.58 1 -3.01 0.76
HII-1653 127 1.17 13.38 0.74 3 29.59 2 -2.99 0.80
HII-2034 127 0.92 12.53 0.55 4 29.97 1 -2.75 0.87
HII-2244 127 0.95 12.46 0.58 4 29.99 2 -2.82 0.87
HII-2284 127 0.74 11.23 10.08 4 29.16 1 -4.20 0.98
HII-2341 127 0.68 10.81 8.21 4 29.09 1 -4.35 1.02
HII-2548 127 1.29 13.90 7.40 4 28.98 2 -3.52 0.76
HII-2741 127 0.97 12.53 5.01 4 29.38 2 -3.41 0.87
HII-2786 127 0.56 10.19 2.21 3 29.37 1 -4.30 1.09
HII-2881 127 0.93 11.45 4.17 4 29.90 2 -3.30 0.96
HII-2927 127 1.22 13.85 0.26 4 29.34 2 -3.10 0.76
HII-2966 127 1.46 14.74 4.60 3 28.97 2 -3.36 0.69
HII-3063 127 1.13 13.42 0.89 4 29.61 2 -2.93 0.79
HII-3163 127 0.97 12.65 0.42 4 29.78 2 -2.96 0.86
HII-3197 127 1.03 11.98 0.44 3 30.14 2 -2.91 0.92
IC 2602
B134 161 0.91 10.66 6.80 5 30.02 6 -3.69 1.07
R15 161 0.89 11.75 3.60 5 30.34 6 -2.96 0.97
R24 161 1.39 14.61 1.25 5 29.46 6 -3.07 0.73


 
Table 2: (continued)
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
R26 161 1.50 15.14 5.70 5 28.84 6 -3.57 0.66
R27 161 1.46 14.35 4.50 5 29.11 6 -3.57 0.76
R29 161 1.07 12.73 2.21 5 29.65 6 -3.21 0.90
R31 161 1.55 15.08 0.49 5 29.56 6 -2.94 0.67
R32 161 1.59 15.06 4.00 5 29.30 6 -3.16 0.67
R43 161 0.91 12.14 0.78 5 30.06 6 -3.01 0.94
R44 161 1.51 14.88 5.50 5 28.90 6 -3.60 0.70
R50 161 1.52 14.75 6.40 5 29.41 6 -3.19 0.71
R52 161 1.03 12.19 0.39 5 29.74 6 -3.33 0.94
R53 161 1.57 15.39 0.41 5 29.41 6 -3.12 0.63
R56 161 1.39 13.64 4.10 5 29.66 6 -2.99 0.83
R57 161 1.56 15.59 8.70 5 29.11 6 -3.30 0.60
R58 161 0.61 10.57 0.57 5 30.41 6 -3.22 1.08
R66 161 0.64 11.07 3.30 5 29.72 6 -3.76 1.02
R70 161 0.65 10.92 4.30 5 29.08 6 -4.44 1.04
R72 161 0.60 10.89 1.05 5 30.51 6 -3.01 1.04
R77 161 1.43 14.12 10.10 5 29.00 6 -3.66 0.79
R83 161 0.58 10.70 1.67 5 30.04 6 -3.55 1.06
R88 161 1.16 12.71 0.20 5 29.46 6 -3.54 0.91
R89 161 1.20 12.97 4.80 5 29.41 6 -3.49 0.89
R92 161 0.63 10.26 2.00 5 30.03 6 -3.72 1.13
R93 161 1.33 13.79 6.70 5 29.11 6 -3.60 0.82
R94 161 1.35 13.33 2.60 5 29.46 6 -3.56 0.86
R95 161 0.83 11.73 1.20 5 30.28 6 -2.90 0.97
R96 161 1.21 12.94 1.82 5 29.74 6 -3.18 0.89
$\alpha $ IC 2391
VXR 12 146 0.84 11.86 3.86 15 29.63 15 -3.63 0.95
VXR 14 146 0.57 10.45 1.32 15 30.17 15 -3.59 1.08
VXR 35a 146 0.99 12.56 0.53 15 30.11 15 -3.00 0.91
VXR 38a 146 1.23 13.36 2.78 15 29.64 15 -3.32 0.85
VXR 41 146 1.25 13.57 5.80 15 29.66 15 -3.21 0.83
VXR 42a 146 1.54 15.88 1.81 15 29.35 15 -3.04 0.55
VXR 45a 146 0.80 10.70 0.22 15 30.10 15 -3.62 1.05
VXR 47 146 1.43 13.96 0.26 15 29.57 15 -3.41 0.80
VXR 62a 146 0.85 11.73 0.50 15 30.04 15 -3.30 0.96
VXR 70 146 0.63 10.85 2.67 15 29.84 15 -3.77 1.04
VXR 72 146 0.72 11.46 3.23 15 30.18 15 -3.21 0.98
VXR 76a 146 1.04 12.76 4.86 15 29.93 15 -3.11 0.90
VXR 77a 146 0.50 9.91 0.65 15 30.18 15 -3.77 1.17
$\alpha $ Persei
HE 520 185 0.69 11.69 0.60 7 30.29 7 -3.10 1.05
HE 601 185 0.63 11.43 3.63 8 29.77 7 -3.71 1.08
HE 622 185 0.69 11.63 0.81 7 30.44 7 -2.98 1.05
HE 699 185 0.61 11.27 0.33 7 30.36 7 -3.19 1.09
AP 15 185 1.19 14.12 0.65 7 29.58 7 -3.08 0.79
AP 25 185 0.78 12.25 3.71 8 30.12 7 -3.07 0.99
AP 28 185 0.95 13.09 3.47 8 29.80 7 -3.09 0.90
AP 37 185 0.86 12.61 2.40 8 29.96 7 -3.11 0.95
AP 41 185 0.71 12.03 5.50 9 29.45 7 -3.82 1.01
AP 43 185 0.87 12.84 0.56 7 29.99 7 -3.00 0.92


 
Table 2: (continued)
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
AP 56 185 0.90 13.00 0.36 7 29.72 7 -3.21 0.91
AP 60 185 1.60 15.74 0.32 7 29.40 7 -3.16 0.67
AP 63 185 0.82 12.29 0.22 7 29.81 7 -3.37 0.98
AP 70 185 0.88 12.83 6.40 9 29.68 7 -3.33 0.93
AP 72 185 0.87 12.78 6.30 9 28.70 7 -4.30 0.93
AP 75 185 1.17 13.82 2.82 8 29.43 7 -3.32 0.82
AP 86 185 1.22 14.31 0.21 7 29.30 7 -3.29 0.78
AP 93 185 0.83 11.99 0.62 7 30.18 7 -3.13 1.01
AP 96 185 1.42 14.55 0.35 8 29.64 10 -3.11 0.76
AP 97 185 0.77 12.08 4.78 8 29.52 7 -3.74 1.00
AP 98 185 0.86 12.80 6.20 9 29.11 7 -3.90 0.93
AP 100 185 1.03 12.80 0.21 7 29.72 7 -3.37 0.93
AP 101 185 1.24 13.89 3.20 9 29.37 10 -3.42 0.81
AP 102 185 0.70 11.96 4.26 8 29.68 10 -3.65 1.02
AP 108 185 0.93 12.92 3.89 8 29.80 10 -3.21 0.92
AP 109 185 1.43 15.84 0.25 8 29.49 10 -2.82 0.66
AP 110 185 0.82 12.27 5.13 8 29.48 10 -3.76 0.98
AP 112 185 1.05 13.68 2.69 8 29.57 10 -3.19 0.83
AP 114 185 1.06 13.40 1.30 9 29.26 7 -3.55 0.86
AP 117 185 0.85 13.05 0.47 7 29.89 7 -3.00 0.90
AP 118 185 0.71 12.06 0.32 8 30.14 7 -3.11 1.01
AP 149 185 0.72 11.71 0.32 7 30.23 7 -3.14 1.04
AP 158 185 0.75 11.93 3.23 8 29.40 10 -3.96 1.02
AP 189 185 0.84 13.05 0.63 8 30.02 10 -2.92 0.90
AP 193 185 0.79 12.28 0.74 8 30.30 7 -2.84 0.98
AP 197 185 0.90 12.31 5.62 8 29.52 7 -3.70 0.98
AP 199 185 0.88 12.10 1.82 8 29.99 7 -3.30 1.00
AP 201 185 1.04 13.08 3.75 9 29.85 10 -3.14 0.90
AP 211 185 1.39 15.07 0.29 8 29.42 10 -3.05 0.73
AP 212 185 0.87 13.24 7.10 9 29.45 10 -3.47 0.88
Hyades
VB 21 45 0.81 9.14 8.98 11 28.78 13 -4.43 0.98
VB 25 45 0.99 9.61 12.64 11 28.58 14 -4.50 0.94
VB 26 45 0.74 8.62 9.39 11 28.56 13 -4.83 1.03
VB 31 45 0.57 7.47 5.44 11 29.09 13 -4.72 1.14
VB 43 45 0.91 9.40 10.26 11 28.36 13 -4.78 0.95
VB 50 45 0.60 7.62 7.10 11 29.74 13 -4.02 1.13
VB 52 45 0.60 7.80 7.96 11 29.01 13 -4.67 1.11
VB 59 45 0.54 7.49 4.98 11 29.34 13 -4.46 1.14
VB 63 45 0.65 8.08 7.73 11 29.09 13 -4.49 1.08
VB 64 45 0.66 8.14 8.67 11 28.90 13 -4.66 1.07
VB 65 45 0.54 7.42 5.87 11 29.06 13 -4.76 1.15
VB 69 45 0.75 8.64 11.52 11 28.76 13 -4.63 1.02
VB 73 45 0.61 7.82 7.41 11 29.05 13 -4.63 1.11
VB 79 45 0.83 8.94 11.38 11 28.59 13 -4.70 1.00
VB 91 45 0.88 8.92 9.36 11 28.54 13 -4.78 1.00
VB 92 45 0.74 8.66 9.04 11 28.67 13 -4.71 1.02
VB 97 45 0.63 7.92 8.55 11 28.89 13 -4.75 1.10
VB 102 45 0.60 7.54 6.46 11 29.19 13 -4.60 1.13
VB 174 45 1.04 9.98 11.88 11 28.51 14 -4.45 0.90


 
Table 2: (continued)
Name Distance B-V V Period Ref. log L$_{\rm X}$ Ref. log L$_{\rm X}/$L $_{\rm bol}$ Mass
  (pc)     (days)   (erg s-1)     (M$_{\odot}$)
VB 175 45 1.03 10.28 10.82 11 28.19 14 -4.64 0.88
VB 190 45 1.32 10.71 3.66 11 29.48 14 -3.33 0.84
VA 486 45 1.49 12.10 2.42 12 29.44 14 -3.17 0.74
VA 512 45 1.53 14.26 8.80 12 28.82 13 -3.29 0.55

References: [1]: Micela et al. (1999), [2]: Stauffer et al. (1994) [3]: Krishnamurthi et al. (1998), [4]: Prosser et al. (1995), [5]: Barnes et al. (1999), [6]: Randich et al. (1995), [7]: Randich et al. (1996) and reference there in, [8]: Prosser & Grankin (1997), [9]: Allain et al. (1996), [10]: Prosser et al. (1996), [11]: Radick et al. (1987), [12]: Prosser et al. (1995) [13]: Stern et al.(1995), [14]: Pye et al.(1994), [15]: Patten & Simon (1996).

Copyright ESO 2003