The present calculations showed that two reaction channels are involved in the
hydrogen atom dissociations from HCNH on the ground state potential energy surface
(![]() or 2A' states) expressed by
or 2A' states) expressed by
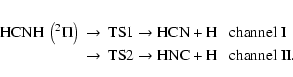
![\begin{figure}
\par\includegraphics[width=10cm,clip]{aa2614f2.eps}\end{figure}](/articles/aa/full/2003/01/aa2614/Timg24.gif) |
Figure 2:
Optimized structures of HCNH system. The values were calculated at the
MP4SDQ/cc-pVTZ level. Bond lengths and angles are in Å and in degrees, respectively.
Experimental geometrical parameters are
|
The total energies and potential energy curve calculated at the MP4SDQ/cc-pVTZ,
QCISD/aug-cc-pVTZ, MP4SDQ/aug-cc-pVTZ, QCISD/6-311++G(2df, 2pd), and
QCISD/6-311++G(3df, 3pd) levels are given in Fig. 3.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{aa2614f3.eps} %
\end{figure}](/articles/aa/full/2003/01/aa2614/Timg25.gif) |
Figure 3: Potential energy curve for the hydrogen atom decomposition of HCNH calculated for several levels. The structures at each stationary point were obtained at the MP4SDQ/cc-pVTZ level (see Fig. 1). |
| HCNH | TS1 | TS2 | HCN + H | HNC + H | |
| MP4SDQ/cc-pVTZ | 0.0 | 34.8 | 38.5 | 23.0 | 34.4 |
| MP4SDQ/aug-cc-pVTZ | 0.0 | 34.8 | 39.1 | 20.8 | 35.4 |
| QCISD/6-311++G(2df,2pd) | 0.0 | 33.7 | 40.4 | 23.1 | 37.3 |
| QCISD/6-311++G(3df,3pd) | 0.0 | 33.8 | 40.7 | 23.4 | 37.6 |
| QCISD/aug-cc-pVTZ | 0.0 | 33.5 | 40.4 | 23.2 | 37.7 |
Harmonic vibrational frequencies of HCNH, TS1, TS2, HCN and HNC were
calculated at the MP4SDQ/6-311++G(d, p) level. The results are summarized in Table 2.
Inclusion of zero-point vibrational energies changed relative energies to the low-energy
region. However, TS1 is always lower in energy than that of TS2.
| HCNH | TS1 | TS2 | HCNa + H | HNCb + H | |
| 1 | 3541.1(a') | 1801.9i(a') | 931.8i(a') | 3475.9( |
3860.9( |
| 2 | 3070.3(a') | 3491.0(a') | 3853.7(a') | 2121.5( |
2053.3( |
| 3 | 2246.3(a') | 2359.6(a') | 2043.5(a') | 739.6( |
484.5( |
| 4 | 1203.5(a') | 881.9(a
|
518.9(a
|
739.6( |
484.5( |
| 5 | 982.5(a
|
774.2(a') | 423.8(a') | ||
| 6 | 859.8(a') | 559.7(a') | 355.3(a') | ||
| ZPE | 17.0 | 11.6 | 10.3 | 10.1 | 9.8 |
|
|
0.0 | 28.1 | 33.7 | 16.3 | 30.5 |
|
a Experimental values were measured to be 3311.5, 2096.9 and 712.0 cm-1 (Shimanouchi
et al. 1992).
b Experimental values were measured to be 3652, 2023.9 and 464.2 cm-1 (Pettersson 1998). |
For comparison, vibrational frequencies of the molecules at the stationary points for
the deuterium dissociation reactions,
![\begin{eqnarray*}\rm DCND^+ ~ \left(^2\Pi\right)+ e^- &\to&\rm [DCND]^* \\ &\to&...
...~ channel~I(D)\\
&\to& \rm TS2(D) \to DCN + D~~~ chennel~II(D)
\end{eqnarray*}](/articles/aa/full/2003/01/aa2614/img28.gif)
| DCND | TS1(D) | TS2(D) | DCN + D | DNC + D | |
| 1 | 2642.0(a') | 1337.1i(a') | 683.5i(a') | 2723.3( |
2905.7( |
| 2 | 2399.2(a') | 2816.8 (a') | 2899.7(a') | 1950.6( |
1964.8( |
| 3 | 2039.3(a') | 2075.2(a') | 1955.4(a') | 589.7( |
383.2( |
| 4 | 954.8(a') | 718.7(a
|
410.1(a
|
589.7( |
383.2( |
| 5 | 720.7(a
|
639.7(a') | 353.6(a') | ||
| 6 | 630.4(a') | 410.6(a') | 257.7(a') | ||
| ZPE | 13.4 | 9.5 | 8.4 | 8.4 | 8.1 |
|
|
0.0 | 29.6 | 35.4 | 18.2 | 32.4 |
| Stationary point | frequency | |||||
| Reaction of HCND | ||||||
| HCND | 3553.6 | 2448.3 | 2058.6 | 1079.1 | 865.6 | 742.8 |
| TS1 | 1353.9i | 3499.7 | 2328.1 | 891.3 | 744.5 | 452.6 |
| TS2 | 933.9i | 2907.0 | 1958.1 | 417.3 | 412.0 | 279.4 |
| Reaction of DCNH | ||||||
| DCNH | 3083.2 | 2629.8 | 2204.2 | 1153.9 | 863.9 | 685.3 |
| TS1 | 1794.8i | 2836.5 | 2099.9 | 724.0 | 696.6 | 492.9 |
| TS2 | 688.3i | 3867.2 | 2042.7 | 519.9 | 390.0 | 309.2 |
On the basis of the energetics and vibrational frequencies, reaction rates for channels I and II were calculated as a function of internal energy (E) of HCNH using RRKM theory including tunneling effects. The results are given in Fig. 3. At lower internal energy, channel I was significantly dominant. The curves of reaction rates for channel I and II crossed each other at E = 48 kcal/mol. Channel II becomes dominant at higher energies. At E = 4.4 eV, which corresponds to the electron affinity of HCNH+ (Shiba et al. 1998), the branching ratio for HCN/HNC was calculated to be 0.3. The corresponding branching ratio for DCN/DNC was calculated to be 2.8 at E = 4.4 eV, which is significantly larger than the reaction of the hydrogen atom. This is due to the isotope effect in deuterium.
For comparison, the ratios for the H or D atom dissociation reactions of DCNH and HCND were calculated. The ratio of DNC/HCN is calculated to be 5.9 for HCND, is 0.63 in DCNH.
Copyright ESO 2003