Based on gas dynamical calculations in a fixed galactic potential with
a weak bar-like distortion,
we estimated errors in mass estimation from the rotation curves,
and calculated the probability that observations would
suffer from such errors.
We found that, as well as the final morphologies of gas disks,
the probability strongly depends on the pattern speed of a bar
![]() ,
and weakly on the bar strength
,
and weakly on the bar strength
![]() .
Among our nine models,
the probability for the errors becomes maximal for the models
with
.
Among our nine models,
the probability for the errors becomes maximal for the models
with
![]() ;
the 15%
of them have an error of a factor of five in mass estimation, if we observe
the disks from an arbitrary viewing angle, and if we define
rotation curves as the highest-velocity envelope of the p-v diagrams.
Even in those erroneous cases, the galactic
mass is not overestimated by more than a factor of six.
In all of our models, the overestimation in mass is more probable
than the underestimation.
We consider only some particular cases for
a weak bar, thus cannot obtain general conclusions.
The above estimation however must be a guideline to consider the central
galactic mass derived from an observed rotation curve.
;
the 15%
of them have an error of a factor of five in mass estimation, if we observe
the disks from an arbitrary viewing angle, and if we define
rotation curves as the highest-velocity envelope of the p-v diagrams.
Even in those erroneous cases, the galactic
mass is not overestimated by more than a factor of six.
In all of our models, the overestimation in mass is more probable
than the underestimation.
We consider only some particular cases for
a weak bar, thus cannot obtain general conclusions.
The above estimation however must be a guideline to consider the central
galactic mass derived from an observed rotation curve.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{h3838f10.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg108.gif) |
Figure 10: Same as Fig. 9, but rotation curves are derived by taking the density-weighted mean velocity rather than the most rapidly rotating envelope of the p-v diagram. |
Conventionally, rotation curves have been often defined as
the peak-intensity velocity or intensity-weighted mean velocity of
p-v diagrams. However, Sofue (1996) pointed out that these methods
underestimate the rotation velocity, particularly in the central region,
because the finite beam size causes the confusion with the gas with lower
line-of-sight velocities on the p-v diagram; this effect is also
demonstrated in Koda et al. (2002, in their Fig. 15). For rotation curves
in highly inclined galaxies, this confusion can not be avoidable.
Alternatively, the envelope-velocity of the p-v diagram is better suited
to trace the central mass distribution (Sofue 1996; Sofue & Rubin 2001).
Therefore we defined the highest-envelope velocity as our rotation curves
in the above study. Here we repeat the same analysis for a comparison,
using rotation curves derived from the density-weighted mean velocity,
and shows the results in Fig. 10.
![]() s are always less than those in Fig.
9, and are almost zero at
s are always less than those in Fig.
9, and are almost zero at
![]() .
This means that
the mass derived from the mean-velocity rotation curves are
almost always underestimated in the central regions of galaxies.
These results suggest that the conventional method for deriving rotation
curves from p-v diagrams is not also relevant to estimate the mass in
galaxies with bar-like distortions.
.
This means that
the mass derived from the mean-velocity rotation curves are
almost always underestimated in the central regions of galaxies.
These results suggest that the conventional method for deriving rotation
curves from p-v diagrams is not also relevant to estimate the mass in
galaxies with bar-like distortions.
Sofue et al. (1999) showed that most of the rotation curves rise steeply from the
centers, reaching high velocities of about
![]() in the
innermost regions. Owing to the large fraction of the rotation curves with
these high central velocities, they discussed the idea
that these velocities should be attributed to massive cores rather than to
bars.
We may have a chance to statistically clarify whether or not the massive
cores exist by comparing a probability such as ours with the observed
fraction of rotation curves with high central velocities.
When we define the probability P averaged in all types of barred
and non-barred galaxies by
in the
innermost regions. Owing to the large fraction of the rotation curves with
these high central velocities, they discussed the idea
that these velocities should be attributed to massive cores rather than to
bars.
We may have a chance to statistically clarify whether or not the massive
cores exist by comparing a probability such as ours with the observed
fraction of rotation curves with high central velocities.
When we define the probability P averaged in all types of barred
and non-barred galaxies by
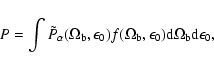 |
(9) |
Acknowledgements
We are grateful to Y. Sofue for fruitful discussions. We also thank an anonymous referee and H. J. Habing, the editor, for useful comments. J.K. was financially supported by the Japan Society for the Promotion of Science (JSPS) for Young Scientists.
Copyright ESO 2002