A&A 396, 867-876 (2002)
DOI: 10.1051/0004-6361:20021461
1 - Institute of Astronomy, University of Tokyo
2-21-1, Osawa, Mitaka, Tokyo 181-0015, Japan
2 -
National Astronomical Observatory,
2-21-1, Osawa, Mitaka, Tokyo 181-8588, Japan
Received 12 July 2002 / Accepted 1 October 2002
Abstract
Rotation curves are often used to estimate the mass distribution of spiral
galaxies, assuming that the circular velocities of the interstellar medium
balance with the galactic centrifugal force.
However, non-circular motions caused by a non-axisymmetric gravitational
potential, such as a stellar bar, may disturb the velocity field, resulting
in errors in mass estimation, especially in the central regions of
galaxies. This is because
the line-of-sight velocity depends on the viewing angles in
a non-axisymmetric flow.
Observing rotation curves of edge-on galaxies in time-dependent
numerical simulations from different viewing angles,
we obtain errors in the estimation of galactic mass from the rotation curves.
In the most extreme case,
the ellipticity of gas orbits is as high as
![]() in the central regions, even if the bar potential is weak.
When rotation curves are defined as the highest velocity envelope of
position-velocity diagrams, the mass estimated from the rotation curves
is larger than the true mass by a factor of five for 15% of the viewing
angles, and the ratio between the apparent mass and true mass is less
than six for any viewing angle.
The overestimation in mass occurs more frequently than the underestimation.
in the central regions, even if the bar potential is weak.
When rotation curves are defined as the highest velocity envelope of
position-velocity diagrams, the mass estimated from the rotation curves
is larger than the true mass by a factor of five for 15% of the viewing
angles, and the ratio between the apparent mass and true mass is less
than six for any viewing angle.
The overestimation in mass occurs more frequently than the underestimation.
Key words: galaxies: fundamental parameters (masses) - galaxies: ISM - galaxies: kinematics and dynamics - hydrodynamics
Rotation curves in their outer regions are generally flat
(Rubin et al. 1980, 1982, 1985), indicating massive dark halos
surrounding their optical disks (Kent 1987).
In their central regions, many rotation curves rise steeply
from the centers, reaching the high velocity seen
in the outer flat rotation curves: typically 100-300
![]() within a central
within a central ![]() radius (Sofue 1996; Sofue et al. 1999).
These high velocities may indicate central massive cores
of about
radius (Sofue 1996; Sofue et al. 1999).
These high velocities may indicate central massive cores
of about
![]() within a central
within a central ![]() radius (Sofue 1996; Sofue et al. 1999; Takamiya & Sofue 2000).
radius (Sofue 1996; Sofue et al. 1999; Takamiya & Sofue 2000).
However, the gas in galactic disks does not necessarily show pure circular rotation, especially in the central regions. Bar-like distortions of the stellar system can drive non-circular (elliptical) motions for the gas. As a result, the apparent rotation curves do not represent the correct mass distribution. For example, if the elliptical orbits were aligned by chance with the line-of-sight, we would overestimate the mass (Sakamoto et al. 1999). The effect of non-circular motion on position-velocity diagrams has been intensively studied in theoretical calculations (Bureau & Athanassoula 1999; Athanassoula & Bureau 1999).
In this paper, we quantitatively study the errors in estimating the mass from rotation curves in galaxies with a weak bar, and calculate the probability that the observed mass suffers from such errors. Even if the bar-like distortion of the gravitational potential is very weak, the gas velocity-field can be non-axisymmetric (Wada 1994). In order to obtain the velocity-field of the gas in a weak bar potential, we performed Smoothed Particle Hydrodynamics (SPH) simulations (Sect. 2). Using the numerical results, we estimate the probability of overestimating the central galactic mass (Sect. 3). We discuss the implications of our results in Sect. 4.
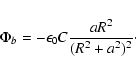 |
(4) |
Our potential model has the benefit of being capable of analytically investigating gaseous orbits in the bar potential (Wada 1994), and has been well-studied in numerical simulations for the bar-driven gas fueling into galactic centers (Wada & Habe 1992, 1995), the gas kinematics in the Galaxy (Wada et al. 1994), the spatial distribution of mass-to-light ratio in a galaxy NGC 4321 (Wada et al. 1998), and the effects of a central black hole (Fukuda et al. 1998, 2000).
We fix
![]() and
and
![]() ;
the corresponding rotation
curve is shown in Fig. 1. The gas reaches the maximum circular
rotation velocity at
;
the corresponding rotation
curve is shown in Fig. 1. The gas reaches the maximum circular
rotation velocity at
![]() with a rotational period of
with a rotational period of
![]() .
Figure 2 shows the radial changes of frequencies,
.
Figure 2 shows the radial changes of frequencies, ![]() and
and
![]() ,
where
,
where ![]() and
and ![]() are circular and epicyclic
frequencies respectively. We set the pattern speed of the bar
are circular and epicyclic
frequencies respectively. We set the pattern speed of the bar
![]() at 0.4, 0.8, and 1.5 times the maximum of
at 0.4, 0.8, and 1.5 times the maximum of
![]() ,
indicated by horizontal
lines. Models with
,
indicated by horizontal
lines. Models with
![]() and
and
![]() have two inner Lindblad resonances (ILR),
while those with
have two inner Lindblad resonances (ILR),
while those with
![]() have no ILR.
have no ILR.
![]() is set to 0.05, 0.10,
and 0.15. Our nine models are listed in Table 1.
is set to 0.05, 0.10,
and 0.15. Our nine models are listed in Table 1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3838f1.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg41.gif) |
Figure 1:
Rotation curve from the axisymmetric potential, Eq. (3),
with the core radius
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3838f2.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg42.gif) |
Figure 2:
Radial changes of frequencies, |
| Open with DEXTER | |
The gas is initially distributed in a uniform-density disk
with an
![]() radius,
following pure circular-rotation that balances the centrifugal force.
The gas temperature is assumed to be a constant
radius,
following pure circular-rotation that balances the centrifugal force.
The gas temperature is assumed to be a constant
![]() ,
corresponding to the sound
speed of about
,
corresponding to the sound
speed of about
![]() ,
throughout evolution. The total gas mass is assumed to
be 5% of the total stellar mass within the radius of
,
throughout evolution. The total gas mass is assumed to
be 5% of the total stellar mass within the radius of
![]() .
The results are not significantly affected by the total gas mass,
because thermal pressure is much smaller than the rotational energy,
and we do not calculate self-gravity of the gas.
We advance the calculations up to about
.
The results are not significantly affected by the total gas mass,
because thermal pressure is much smaller than the rotational energy,
and we do not calculate self-gravity of the gas.
We advance the calculations up to about
![]() .
.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{h3838f3.eps}
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg51.gif) |
Figure 3:
Gas dynamical evolution in model E:
(
|
| Open with DEXTER | |
Gas dynamics in a barred potential have been well studied in numerical simulations
(Wada & Habe 1992; Heller & Shlosman 1994; Piner et al. 1995; Fukuda et al. 1998; Athanassoula & Bureau 1999). Our models evolve consistently with these
simulations.
Figure 3, model E, shows a typical evolution.
Three phases of the evolution can be seen in this model:
(a) linear perturbation phase,
![]() ,
(b) transient phase,
,
(b) transient phase,
![]() ,
and
(c) quasi-steady phase,
,
and
(c) quasi-steady phase,
![]() .
.
The characteristic structure appearing during the evolution depends strongly
on the positions
of resonances, i.e. the pattern speed of the bar
![]() .
In phase (a),
leading and trailing spiral arms are formed around the inner (
.
In phase (a),
leading and trailing spiral arms are formed around the inner (
![]() )
and
outer (
)
and
outer (
![]() )
ILRs respectively at
)
ILRs respectively at
![]() .
These resonant-driven spirals are expected in a linear
theory (Wada 1994).
While the outer trailing arms remain with increasing density contrasts,
the inner leading arms evolve into an oval ring, or a gaseous bar
(t= 71-107
.
These resonant-driven spirals are expected in a linear
theory (Wada 1994).
While the outer trailing arms remain with increasing density contrasts,
the inner leading arms evolve into an oval ring, or a gaseous bar
(t= 71-107![]() ), i.e. phase (b). The oval ring first leads the stellar bar
(
), i.e. phase (b). The oval ring first leads the stellar bar
(
![]() ), rotating opposite to the gas rotation (
), rotating opposite to the gas rotation (
![]() ), and being
aligned with the stellar bar (
), and being
aligned with the stellar bar (
![]() ), and thereafter, the system
develops toward a quasi-steady phase, i.e. phase (c). The ellipticity of
the nuclear ring grows as high as
), and thereafter, the system
develops toward a quasi-steady phase, i.e. phase (c). The ellipticity of
the nuclear ring grows as high as
![]() .
The ripple seen in the outer arms at
.
The ripple seen in the outer arms at
![]() would originate
in the Kelvin-Helmholtz instability (Piner et al. 1995).
Gas dynamics and structure in the inner region of the disk
are not affected by this instability.
would originate
in the Kelvin-Helmholtz instability (Piner et al. 1995).
Gas dynamics and structure in the inner region of the disk
are not affected by this instability.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3838f4.eps} \end{figure}](/articles/aa/full/2002/48/aah3838/Timg63.gif) |
Figure 4:
Final snapshots for all nine models. Different pattern speeds
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3838f5.eps} \end{figure}](/articles/aa/full/2002/48/aah3838/Timg64.gif) |
Figure 5: Final velocity fields for all nine models. The arrangement is the same as in Fig. 3. Arrows are drawn for 1500 out of total 30 000 gas particles. |
| Open with DEXTER | |
Figures 4 and 5 display the final snapshots and velocity
fields for nine models. Different pattern speeds
![]() and bar strength
and bar strength
![]() are arranged vertically and horizontally, respectively. It is evident
that the final structure depends strongly on
are arranged vertically and horizontally, respectively. It is evident
that the final structure depends strongly on
![]() ,
while
,
while
![]() changes
only the density contrasts.
Model A, B, and C have no ILRs, thus no spiral arms or ring in their inner
regions are formed.
The outer spiral arms are formed outside the radius of the corotation
resonance (CR) due to the outer Lindblad resonance (OLR).
Model D and F resemble model E. Model G, H and I also have arms and rings
similar to those in model E, but at different radii, corresponding to
the location of the ILRs.
Figure 5 clearly show that, in models D, E, F and G, most gaseous
orbits are x1-like, while in model H and I, the large separation
and low density between the two ILRs suffice to leave the gases on
x2-orbits, which form a stable oval ring, nearly perpendicular
to the stellar bar.
changes
only the density contrasts.
Model A, B, and C have no ILRs, thus no spiral arms or ring in their inner
regions are formed.
The outer spiral arms are formed outside the radius of the corotation
resonance (CR) due to the outer Lindblad resonance (OLR).
Model D and F resemble model E. Model G, H and I also have arms and rings
similar to those in model E, but at different radii, corresponding to
the location of the ILRs.
Figure 5 clearly show that, in models D, E, F and G, most gaseous
orbits are x1-like, while in model H and I, the large separation
and low density between the two ILRs suffice to leave the gases on
x2-orbits, which form a stable oval ring, nearly perpendicular
to the stellar bar.
In this section, we compare the apparent rotation curves obtained from the numerical results (Sect. 3.1) and the true rotation curves, then we get probability to overestimate/underestimate the galactic mass (Sects. 3.2 and 3.3).
We obtain a position-velocity (p-v) diagram by observing our calculated gas
disks edge-on, and then determine a rotation curve from the p-v diagram.
We assign gas particles in a position-velocity grid using the cloud-in-cell
method (Hockney & Eastwood 1981); the spacing for the grid is set to a typical resolution
in recent interferometry observations of the CO gas for Virgo galaxies,
i.e. ![]() (
(![]() 1
1
![]() )
in space and
)
in space and
![]() in velocity (Sofue in
private communication).
Then we determine a rotation curve by tracing the gas at the highest velocity
for each radius in the p-v diagram. Some examples for p-v diagrams and
rotation curves are shown in Fig. 6.
in velocity (Sofue in
private communication).
Then we determine a rotation curve by tracing the gas at the highest velocity
for each radius in the p-v diagram. Some examples for p-v diagrams and
rotation curves are shown in Fig. 6.
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3838f6.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg69.gif) |
Figure 6:
Position-velocity diagrams and rotation curves in model E,
observed from a variety of viewing angles, at
|
| Open with DEXTER | |
There are several ways to derive a rotation curve from an observed p-v diagram. One traces the peak-intensity velocity or intensity-weighted mean velocity at each radius (Rubin et al. 1980, 1982, 1985; Mathewson et al. 1992; Mathewson & Ford 1996), while another traces the 20% envelope of the peak-intensity velocity at each radius (Sofue 1996). These intensity-based methods cannot be applied to our density-based p-v diagram, because intensity is not a simple function of density, especially in edge-on systems. Compared with these methods, our method provides generally higher velocity.
We compare the observed rotation curves
![]() derived from p-v diagrams
in simulations (Sect. 3.1), with the true rotation curves
derived from p-v diagrams
in simulations (Sect. 3.1), with the true rotation curves
![]() from the gravitational potential (
from the gravitational potential (![]() ). We estimate the errors in rotation curves by
defining a function, i.e.
). We estimate the errors in rotation curves by
defining a function, i.e.
A rotation curve rises steeply from a galactic center, having a peak, or
at least a shoulder, at an innermost region, then reaching the flat
rotation. A central galactic mass is always estimated at the radius of
the peak or shoulder in observations (see Sofue et al. 1999).
We thus consider the case that the mass
is overestimated/underestimated at the radius of the first peak or shoulder.
The radius
depends on, and changes with a viewing angle for the gas disk (see Fig. 6).
Hence, we define a reference region of
![]()
![]() to which the above criterion, i.e. Eq. (6), is applied; in our
models the first peak or shoulder always fall in this region.
If Eq. (6) or (8) is satisfied in this
reference region, our observed rotation velocity differs from
the true velocity at least by a factor of
to which the above criterion, i.e. Eq. (6), is applied; in our
models the first peak or shoulder always fall in this region.
If Eq. (6) or (8) is satisfied in this
reference region, our observed rotation velocity differs from
the true velocity at least by a factor of
![]() .
.
![\begin{figure}
\par\includegraphics[width=9.8cm,clip]{h3838f7.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg90.gif) |
Figure 7:
Change of the probability
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3838f8.eps}
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg92.gif) |
Figure 8:
The probability that an observed rotation velocity would exceed
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11cm,clip]{h3838f9.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg93.gif) |
Figure 9:
The probability that an observed mass would exceed
|
| Open with DEXTER | |
Figure 8 shows the averaged probability
![]() as
a function of
as
a function of
![]() for all nine models.
Different pattern speeds
for all nine models.
Different pattern speeds
![]() and bar strengths
and bar strengths
![]() are arranged
vertically and horizontally, respectively, as in Fig. 4.
If the gas follows pure circular rotation, i.e.
are arranged
vertically and horizontally, respectively, as in Fig. 4.
If the gas follows pure circular rotation, i.e.
![]() ,
then these
,
then these
![]() -profiles must be a step function:
-profiles must be a step function:
![]() for
for
![]() and
and
![]() for
for
![]() .
However, the non-circular motion changes the
.
However, the non-circular motion changes the
![]() -profiles
as seen in the plots. In model E for example,
-profiles
as seen in the plots. In model E for example,
![]() at
at
![]() means that 80% of the rotation curves
means that 80% of the rotation curves
![]() observed
from random angles would apparently show higher velocities than the true
rotation curve
observed
from random angles would apparently show higher velocities than the true
rotation curve
![]() which traces the mass, and another 20% would show
lower velocities than the true one. Thus the overestimation in mass
occurs more frequently than the underestimation in model E.
which traces the mass, and another 20% would show
lower velocities than the true one. Thus the overestimation in mass
occurs more frequently than the underestimation in model E.
![]() at
at
![]() indicates that the observed rotation curve cannot be
overestimated by more than the factor of 2.4 in model E.
indicates that the observed rotation curve cannot be
overestimated by more than the factor of 2.4 in model E.
We discussed in Sect. 2.4 that the final structure depends strongly
on the pattern speed
![]() and a little on the bar strength
and a little on the bar strength
![]() .
This is also evident in Fig. 8; the global profiles in the
same
.
This is also evident in Fig. 8; the global profiles in the
same
![]() are quite similar, but
are quite similar, but
![]() increases slightly with
increasing
increases slightly with
increasing
![]() .
Models A, B and C have no ILRs, not showing non-axisymmetric structures in
the central regions (Sect. 2.4), thus the
.
Models A, B and C have no ILRs, not showing non-axisymmetric structures in
the central regions (Sect. 2.4), thus the
![]() -profiles
are similar to the step functions. Models D, E and F show the most prominent
streaming motions in their central regions,
and therefore they have the largest
-profiles
are similar to the step functions. Models D, E and F show the most prominent
streaming motions in their central regions,
and therefore they have the largest
![]() .
Although models G, H and I have the same
.
Although models G, H and I have the same
![]() ,
the
,
the
![]() -profile for model G is different from those for models H
and I, because gaseous x2-orbits remain in models H and I, but not in
model G (see Sect. 2.4).
-profile for model G is different from those for models H
and I, because gaseous x2-orbits remain in models H and I, but not in
model G (see Sect. 2.4).
Figure 9 shows the probability
![]() vs.
vs.
![]() .
All the plots show properties similar to those in Fig. 8.
In model E for example,
.
All the plots show properties similar to those in Fig. 8.
In model E for example,
![]() at
at
![]() means that
the central galactic mass derived from an observed rotation curve is
overestimated by a factor of five in the probability of 15%.
means that
the central galactic mass derived from an observed rotation curve is
overestimated by a factor of five in the probability of 15%.
![]() s
in all models become zero at
s
in all models become zero at
![]() ,
meaning that the central
mass from an observed rotation curve can be overestimated by at most
a factor of six in our models.
,
meaning that the central
mass from an observed rotation curve can be overestimated by at most
a factor of six in our models.
Based on gas dynamical calculations in a fixed galactic potential with
a weak bar-like distortion,
we estimated errors in mass estimation from the rotation curves,
and calculated the probability that observations would
suffer from such errors.
We found that, as well as the final morphologies of gas disks,
the probability strongly depends on the pattern speed of a bar
![]() ,
and weakly on the bar strength
,
and weakly on the bar strength
![]() .
Among our nine models,
the probability for the errors becomes maximal for the models
with
.
Among our nine models,
the probability for the errors becomes maximal for the models
with
![]() ;
the 15%
of them have an error of a factor of five in mass estimation, if we observe
the disks from an arbitrary viewing angle, and if we define
rotation curves as the highest-velocity envelope of the p-v diagrams.
Even in those erroneous cases, the galactic
mass is not overestimated by more than a factor of six.
In all of our models, the overestimation in mass is more probable
than the underestimation.
We consider only some particular cases for
a weak bar, thus cannot obtain general conclusions.
The above estimation however must be a guideline to consider the central
galactic mass derived from an observed rotation curve.
;
the 15%
of them have an error of a factor of five in mass estimation, if we observe
the disks from an arbitrary viewing angle, and if we define
rotation curves as the highest-velocity envelope of the p-v diagrams.
Even in those erroneous cases, the galactic
mass is not overestimated by more than a factor of six.
In all of our models, the overestimation in mass is more probable
than the underestimation.
We consider only some particular cases for
a weak bar, thus cannot obtain general conclusions.
The above estimation however must be a guideline to consider the central
galactic mass derived from an observed rotation curve.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{h3838f10.eps} %
\end{figure}](/articles/aa/full/2002/48/aah3838/Timg108.gif) |
Figure 10: Same as Fig. 9, but rotation curves are derived by taking the density-weighted mean velocity rather than the most rapidly rotating envelope of the p-v diagram. |
| Open with DEXTER | |
Conventionally, rotation curves have been often defined as
the peak-intensity velocity or intensity-weighted mean velocity of
p-v diagrams. However, Sofue (1996) pointed out that these methods
underestimate the rotation velocity, particularly in the central region,
because the finite beam size causes the confusion with the gas with lower
line-of-sight velocities on the p-v diagram; this effect is also
demonstrated in Koda et al. (2002, in their Fig. 15). For rotation curves
in highly inclined galaxies, this confusion can not be avoidable.
Alternatively, the envelope-velocity of the p-v diagram is better suited
to trace the central mass distribution (Sofue 1996; Sofue & Rubin 2001).
Therefore we defined the highest-envelope velocity as our rotation curves
in the above study. Here we repeat the same analysis for a comparison,
using rotation curves derived from the density-weighted mean velocity,
and shows the results in Fig. 10.
![]() s are always less than those in Fig.
9, and are almost zero at
s are always less than those in Fig.
9, and are almost zero at
![]() .
This means that
the mass derived from the mean-velocity rotation curves are
almost always underestimated in the central regions of galaxies.
These results suggest that the conventional method for deriving rotation
curves from p-v diagrams is not also relevant to estimate the mass in
galaxies with bar-like distortions.
.
This means that
the mass derived from the mean-velocity rotation curves are
almost always underestimated in the central regions of galaxies.
These results suggest that the conventional method for deriving rotation
curves from p-v diagrams is not also relevant to estimate the mass in
galaxies with bar-like distortions.
Sofue et al. (1999) showed that most of the rotation curves rise steeply from the
centers, reaching high velocities of about
![]() in the
innermost regions. Owing to the large fraction of the rotation curves with
these high central velocities, they discussed the idea
that these velocities should be attributed to massive cores rather than to
bars.
We may have a chance to statistically clarify whether or not the massive
cores exist by comparing a probability such as ours with the observed
fraction of rotation curves with high central velocities.
When we define the probability P averaged in all types of barred
and non-barred galaxies by
in the
innermost regions. Owing to the large fraction of the rotation curves with
these high central velocities, they discussed the idea
that these velocities should be attributed to massive cores rather than to
bars.
We may have a chance to statistically clarify whether or not the massive
cores exist by comparing a probability such as ours with the observed
fraction of rotation curves with high central velocities.
When we define the probability P averaged in all types of barred
and non-barred galaxies by
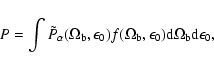 |
(9) |
Acknowledgements
We are grateful to Y. Sofue for fruitful discussions. We also thank an anonymous referee and H. J. Habing, the editor, for useful comments. J.K. was financially supported by the Japan Society for the Promotion of Science (JSPS) for Young Scientists.