

Up: Fundamental parameters of Galactic supergiants
Subsections
5 Discussion
The results obtained in the preceding section allow us to address four
important aspects of the properties of massive OB supergiants: the effective
temperature scale, the ionizing fluxes, the mass discrepancy and the wind
momentum-luminosity relationship.
With the inclusion of mass-loss, sphericity and line-blocking/blanketing we
derived lower temperatures than those quoted in Herrero et al. (2001),
where we have
used plane-parallel, hydrostatic models without line-blocking for all
stars except Cyg OB2 #7, for which a spherical model with mass-loss, but
without line-blocking was used. As we have covered various spectral types
from O3 to B1 in our analysis, we can obtain a temperature scale for O supergiants. We note however, that Cyg OB2 #4 is actually a luminosity
class III star, while #2 is probably of class II.
For our earlier supergiants (O3-O7) we find temperatures that are 4000 to 8000 K cooler than in Herrero et al. (2001),
while for the O9.5 I supergiant we
obtain 2000 K less and for the B1 star the temperature is now hotter, but
with a lower He abundance. These findings are in qualitative agreement with
theoretical expectations (e.g., Schaerer & Schmutz 1994) and with the recent
temperature scale for O dwarfs presented by Martins et al. (2002).
These authors
obtain lower temperatures for O dwarfs by 1500-4000 K when including
line-blanketing and sphericity.
Our temperature scale is shown in Fig. 12, together with the
one from Vacca et al. (1996) for O supergiants. The effective temperature scale
from these authors has been mainly derived from analyses using pure H-He,
plane-parallel, hydrostatic models, like those performed by
Herrero et al. (1992). It is
thus not surprising that our new scale is cooler.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f12.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg56.gif) |
Figure 12:
Our temperature scale for O supergiants (circles) compared
with the scale by Vacca et al. (1996) (triangles). New temperatures
are much lower, except for the relatively cool Cyg OB2 #2 (B1I).
Note that the entry at O7 is actually a luminosity class III star. |
In spite of the still low number statistics, we already appreciate some
interesting features in Fig. 12. First, from O3 to O9 we see a
smooth temperature decline into which Cyg OB2 #4 fits perfectly, despite its
luminosity class III. From this smoothness is excluded Cyg OB2 #11, much
cooler than the other O5 supergiant, Cyg OB2 #8C, and even cooler than the
O5.5 supergiant, Cyg OB2 #8A. The main difference in their properties is
the extreme Of character of Cyg OB2 #11, which thus appears to be related
to cooler temperatures. This is indicating to us that all spectral
signatures have a significance in terms of stellar parameters, and thus a
temperature scale using only spectral subtypes of O supergiants, with the various nuances in their
classification scheme, will neccesarily be of limited accuracy.
We also see that both temperature scales converge towards later spectral
types, until the B1 star, Cyg OB2 #2. This object has a temperature that
does not seem to fit into the general behaviour, although data are still too
scarce to know whether this has any significance.
The new temperature scale and the lower luminosities will have an influence
on other aspects, e.g., on the emergent ionizing fluxes that are now much
lower than in the older models, as we have seen in the discussion of Cyg OB2 #7.
Our treatment of UV metal line opacity is approximate (in the sense that we
use an approximate NLTE approach and suitably averaged lines opacities), and
we do not pretend to give a detailed description of the UV radiation field.
However, the emergent fluxes,
should be correct in an average sense (i.e., neglecting distinct spectral
features, see again Fig. 5), in particular concerning frequency
integrated quantities. (Note that the differences bluewards from He II 228 Å are mostly
due to different temperature
structures in the outer wind.)
Thus, we should obtain a rather correct description
of quantities extending over broad spectral regions, like the number of
photons capable of ionizing hydrogen.
This number, of course, is of extreme relevance to studies of H II regions surrounding the stars. Vacca et al. (1992)
have calculated ionizing fluxes
from plane-parallel, hydrostatic, LTE, line-blanketed Kurucz-models
(Kurucz 1992) and concluded, from a comparison with more elaborate
models available at that time (Schaerer & Schmutz 1994), that their ionizing fluxes
should be reliable. That would indicate that line-blocking/blanketing is
the major effect when calculating the UV continuum ionizing flux at a
given effective temperature.
Our calculations seem to support this conclusion, but also indicate that for
an application to H II regions further effects have to be considered.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f13.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg57.gif) |
Figure 13:
a) left: ionizing fluxes (photons cm-2 s-1) at
the stellar surface versus effective temperature. b) right: ionizing
luminosities (photons s-1) versus spectral type. Dots correspond
to the stellar analyses presented here and lines represent the calibrations
by Vacca et al. (1996) for O supergiants. |
In Fig. 13a we have plotted our calculated H ionizing fluxes versus
the effective temperature of the corresponding model. The dashed line gives
the calibration by Vacca et al. (1996)
for O supergiants (their Table 7). We see
that the agreement is good. Even more, the entry departing slightly from the
relation corresponds to Cyg OB2 #4, that has a luminosity class III. Note
that the ionizing fluxes are basically independent of stellar radius.
Thus, at given temperature the effects of metal line opacity remain the
major ingredient which detemine the emergent UV flux, and the differences
between NLTE and LTE models seem to be small regarding the integrated
hydrogen Lyman fluxes. (This behaviour should become significantly different
when, considering, e.g., He II ionizing fluxes because of the extreme
sensitivity of this ion to NLTE effects, in particular as function of
mass-loss.)
In Fig. 13b we have plotted the H ionizing luminosities as
function of spectral type. Here, the differences with the calibration
by Vacca et al. (1996) are apparent.
They clearly originate from our new relation
between spectral type and effective temperature (and our lower radii for
most stars, compared to the calibrations by Vacca et al. 1996), i.e., the stellar
luminosities at given subtype are now smaller. (This discrepancy
between both plots, of course,
results from the former inconsistency of calibrating spectral types via
unblanketed models, however calculating the number of ionizing photons
from blanketed ones).
Furthermore, for one case (Cyg OB2 #8A) we find that our ionizing
luminosities are larger as a consequence of the larger radius in this
particular case. Since the ionizing luminosity is the quantity which
really matters for the ionization of H II regions, our results
indicate that statistically there are fewer photons available compared
to earlier findings, but also that individual cases have to be studied in detail, because they can depart from the general trend.
The mass discrepancy is a term that was used by Herrero et al. (1992)
to refer to the
systematic difference between spectroscopically determined stellar masses of OB supergiants and their evolutionary counterparts. The latter were always
systematically larger, well beyond the error bars.
In Fig. 14 we have plotted the evolutionary mass (derived from the
"classical'' models by Schaller et al. (1992) without rotation) and the
spectroscopic masses obtained in our analysis for the Cyg OB2 supergiants.
We see that the situation is by no means satisfactory: despite the (very)
large errors adopted for the spectroscopic masses, three of the seven stars
still do not cross the one-to-one relation and for two other we find
only a marginal agreement. In fact, only two out of the seven stars have
masses that agree reasonably well. However, compared to previous diagrams
the situation seems to have improved: there is no clear systematic
trend any longer. Roughly the same number of data points lie on each
side of the
one-to-one relation and the apparent scatter might be related to problems in
the individual analyses.
Nevertheless it is somewhat too early to conclude that the atmosphere models
with sphericity, mass-loss and metal opacity agree with the evolutionary
models without rotation, and thus give the same answer in a statistical
sense. First, the large scatter in Fig. 14 still poses a question
for the masses of both set of models; and second, the stars in Cyg OB2
have moderate projected rotational velocities and are very young, with only
the earliest type exhibiting an enhanced He abundance. Thus, older or faster
rotating stars may have masses that disagree even more when derived using
different methods.
This result indicates that we badly need both a calibration of present mass
scales based on early type binaries (or any other reliable method), and CNO
abundances for isolated massive stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f14.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg58.gif) |
Figure 14:
A comparison of the spectroscopic and evolutionary
masses for the Cyg OB2 supergiants. Although there are still serious
differences, no obvious systematic trend is present. See text for
details and discussion. |
The original purpose of our work was to obtain a better constrained WLR for
Galactic O stars by using objects belonging to the same association, and
thus minimizing the scatter introduced by uncertainties in the relative
distances. The distance to Cyg OB2 and thus the derived luminosities may be
in error, but all determinations will be affected in a similar way.
Figure 15 displays the WLR obtained for our Cyg OB2 sample. Errors for
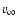 are taken from Herrero et al. (1991). The stars #8A, #8C, #4 and #10
follow a nice sequence with low scatter. Cyg OB2 #7 and #11 seem to lie
above this sequence. This is interesting because these stars display the
most extreme Of signatures in their spectra, which might be related to an
ionization change in the wind that could result in a different line-driving
force or to clumping effects that would produce an overestimation of the
mass-loss rate. Cyg OB2 #2 seems to lie below that relation, which is
consistent with the results by Kudritzki et al. (1991),
who found a different WLR (with
a lower offset) for the winds of early B supergiants, compared to the O-star
case. Our observed relation also agrees well with the theoretical WLR
derived by Vink et al. (2000) (the dashed line in Fig. 15).
are taken from Herrero et al. (1991). The stars #8A, #8C, #4 and #10
follow a nice sequence with low scatter. Cyg OB2 #7 and #11 seem to lie
above this sequence. This is interesting because these stars display the
most extreme Of signatures in their spectra, which might be related to an
ionization change in the wind that could result in a different line-driving
force or to clumping effects that would produce an overestimation of the
mass-loss rate. Cyg OB2 #2 seems to lie below that relation, which is
consistent with the results by Kudritzki et al. (1991),
who found a different WLR (with
a lower offset) for the winds of early B supergiants, compared to the O-star
case. Our observed relation also agrees well with the theoretical WLR
derived by Vink et al. (2000) (the dashed line in Fig. 15).
We have investigated whether a reduction in the outer minimum
electron temperature (that the model is allowed to reach, see
Santolaya-Rey et al. 1997, Sect. 3.1) might result in lower mass-loss rates for
Cyg OB2 #7 and #11. While we usually assume that
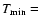 0.75
0.75
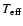 (a typical value for OB stars), calculations by Pauldrach
(private communication) indicate that this value can reach values as low as
0.40
(a typical value for OB stars), calculations by Pauldrach
(private communication) indicate that this value can reach values as low as
0.40
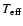 in extreme cases. This effect has usually no influence on an
analyis as performed here, where almost all considered lines are formed in a
region with temperatures beyond this minimum. "Only'' H
in extreme cases. This effect has usually no influence on an
analyis as performed here, where almost all considered lines are formed in a
region with temperatures beyond this minimum. "Only'' H
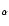 (and He II
(and He II 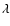 4686) might be affected in cases of extreme mass-loss,
which is the reason that we have investigated here this question.
Nevertheless, in all considered cases the resulting reduction of the derived
mass-loss rate was less than 20
4686) might be affected in cases of extreme mass-loss,
which is the reason that we have investigated here this question.
Nevertheless, in all considered cases the resulting reduction of the derived
mass-loss rate was less than 20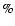 .
Thus, even accounting for this
uncertainty we cannot bring the position of these two stars into agreement
with the WLR defined by the other four O stars.
.
Thus, even accounting for this
uncertainty we cannot bring the position of these two stars into agreement
with the WLR defined by the other four O stars.
However, taking into account the error bars, our data are still compatible
with a unique relation including all seven stars. This is also shown in
Fig. 15, where we display two different regressions, one including
only Cyg OB2 #8A, #8C, #4 and #10, and one including all seven stars,
respectively. Interestingly, the relation obtained by including only the
O-supergiants, not shown for clarity, is still marginally compatible
with the position of the B-supergiant.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f15.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg60.gif) |
Figure 15:
The wind momentum-luminosity relationship obtained for
the Cyg OB2 supergiants. The dotted line gives the regression obtained by
including all stars, while the solid line gives the one obtained by
including only Cyg OB2 #8A, #8C, #4 and #10. The dashed line very close
to the solid one is the theoretical relation by Vink et al. (2000). The entry
with the highest luminosity is Cyg OB2 #8A and those close together are Cyg OB2 #7 and #11, the stars with extreme Of character. |
In Fig. 16 we show a comparison of our data points with those
obtained by Puls et al. (1996), updated by Herrero et al. (2000)
for some entries. We see
that both sets compare well, the most important difference being the fact
that the scatter in our data points is lower. However, at present it is not
possible to conclude whether this is a real improvement (as we have
expected) or an artefact of the low number statistics. We note that the
first possibility would imply that stars with extreme Of characteristics
follow a slightly different relation than normal O stars,
although we could not determine the reason for the relatively high position of
Cyg OB2 #7 and #11.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f16.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg61.gif) |
Figure 16:
A comparison of our results for Cyg OB2 OB-supergiants
(filled dots) with the results by Puls et al. (1996) and
Herrero et al. (2000). |
In Table 4 we compare the coefficients we have obtained for the WLR
(by weighted least-squares fits) using different samples (see above) as well
as those quoted by Kudritzki & Puls (2000) in their Table 2,
and the coefficients of the
theoretical relation provided by Vink et al. (2000).
A correct error treatment would require to take into account errors in
both axes and their correlation. This treatment is not simple and will be
presented elsewhere (Markova & Puls 2002). For the scope of the present paper
we have adopted as error an average of the errors obtained when considering
only those in the ordinate values (an underestimation) and when considering
the errors in abscissa and ordinate as uncorrelated (an overestimation).
Using both estimates for the errors, we have calculated the corresponding
regression, where the resulting values for slope and offset turned out to be
only marginally different. The final values quoted in Table 4 have
been obtained from a straight average of these results.
We see that in spite of the visual agreement found in Fig. 16,
our results differ significantly from those given by Kudritzki & Puls (2000),
in particular concerning the slope of the relation.
Kudritzki & Puls (2000) found a slope
of 1.51 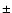 0.18, while, when excluding the B supergiant, we obtain values
from 1.74
0.18, while, when excluding the B supergiant, we obtain values
from 1.74 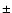 0.24 to 1.92
0.24 to 1.92 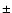 0.22. In addition, our values for the
vertical offset vary between 19.27 and 18.30, below the value of 20.69 of
Kudritzki & Puls (2000).
Although the error bars allow for marginal agreement,
the conclusion is that our relation is steeper and
thus
0.22. In addition, our values for the
vertical offset vary between 19.27 and 18.30, below the value of 20.69 of
Kudritzki & Puls (2000).
Although the error bars allow for marginal agreement,
the conclusion is that our relation is steeper and
thus
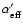 (=1/x) is smaller in our case. This indicates a
different slope of the line-strength distribution function (see Puls et al. 2000 and Kudritzki & Puls 2000, Sect. 4.1), i.e., a larger number of
weak lines.
(=1/x) is smaller in our case. This indicates a
different slope of the line-strength distribution function (see Puls et al. 2000 and Kudritzki & Puls 2000, Sect. 4.1), i.e., a larger number of
weak lines.
In contrast, we obtain very good agreement with the theoretical relation by
Vink et al. (2000).
Their relation, both in slope and offset, lies right between
our relation when considering all supergiants or only the moderate O, Of
stars, respectively. Our observations are thus compatible with a unique WLR
for all O supergiants, but favour a separation of the extreme O, Of stars.


Up: Fundamental parameters of Galactic supergiants
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f12.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f13.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f14.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f15.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3745f16.eps}\end{figure}](/articles/aa/full/2002/48/aah3745/Timg61.gif)