A&A 396, 1019-1028 (2002)
DOI: 10.1051/0004-6361:20021418
N.-E. Raouafi 1 - S. Sahal-Bréchot2 - P. Lemaire3
1 - Max-Planck-Institut für Aeronomie, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 -
Laboratoire d'Étude du Rayonnement et de la Matière en Astrophysique (LERMA), Observatoire de Paris-Meudon, 92195 Meudon, France
3 -
Institut d'Astrophysique Spatiale, Université Paris XI, 91405 Orsay Cedex, France
Received 2 May 2002 / Accepted 25 September 2002
Abstract
Numerical computation results of the linear polarization parameters of the
![]()
![]() coronal line are presented. They are based on theoretical results obtained by Raouafi (2002 and 2000), which give the Stokes parameters of a resonance scattering spectral line sensitive simultaneously to the Hanle effect and to the Doppler redistribution. In the present coronal case, the Hanle effect is due to the coronal magnetic field and the Doppler redistribution to the macroscopic motion of the scattering O5+ coronal ions (solar wind velocity field vector). Constraints on the coronal magnetic field vector and on the solar wind velocity field vector are obtained by comparing the numerical results and the linear polarization measurements of the
coronal line are presented. They are based on theoretical results obtained by Raouafi (2002 and 2000), which give the Stokes parameters of a resonance scattering spectral line sensitive simultaneously to the Hanle effect and to the Doppler redistribution. In the present coronal case, the Hanle effect is due to the coronal magnetic field and the Doppler redistribution to the macroscopic motion of the scattering O5+ coronal ions (solar wind velocity field vector). Constraints on the coronal magnetic field vector and on the solar wind velocity field vector are obtained by comparing the numerical results and the linear polarization measurements of the
![]()
![]() coronal line obtained through particular observations performed by SUMER/SoHO.
coronal line obtained through particular observations performed by SUMER/SoHO.
Key words: polarization - scattering - Sun: magnetic field - Sun: solar wind - Sun: corona - Sun: UV radiation
The present paper is the second of a series of papers on the interpretation of the linear polarization parameters of the
![]()
![]() coronal line (hereafter D2 line). The goal is the determination of the magnetic field vector and the velocity field vector (the solar wind velocity field vector) in the solar corona. The first paper (Raouafi et al. 2002) was limited to the interpretation in terms of velocity field only. They (Raouafi et al. 2002) showed that Doppler redistribution effect on the linear polarization of the
coronal line (hereafter D2 line). The goal is the determination of the magnetic field vector and the velocity field vector (the solar wind velocity field vector) in the solar corona. The first paper (Raouafi et al. 2002) was limited to the interpretation in terms of velocity field only. They (Raouafi et al. 2002) showed that Doppler redistribution effect on the linear polarization of the
![]() D2 coronal line gives results in agreement with the measurements done by using observations performed by the SUMER spectrometer (Solar Ultraviolet Measurements of Emitted Radiation: Wilhelm et al. 1995, 1997; Lemaire et al. 1997) operating on SoHO (the Solar and Heliospheric Observatory: Domingo et al. 1995). However, the obtained solutions correspond to velocity field vectors (solar wind velocity field vectors) with relatively high inclinations with respect to the polar axis. This is because observations show that the coronal structures in the polar holes are quasi-radial at low altitudes where SUMER/SoHO observations were done (1.29
D2 coronal line gives results in agreement with the measurements done by using observations performed by the SUMER spectrometer (Solar Ultraviolet Measurements of Emitted Radiation: Wilhelm et al. 1995, 1997; Lemaire et al. 1997) operating on SoHO (the Solar and Heliospheric Observatory: Domingo et al. 1995). However, the obtained solutions correspond to velocity field vectors (solar wind velocity field vectors) with relatively high inclinations with respect to the polar axis. This is because observations show that the coronal structures in the polar holes are quasi-radial at low altitudes where SUMER/SoHO observations were done (1.29 ![]() from the solar center). In the present paper, the interpretation in terms of both the magnetic field and the velocity field vectors is achieved.
from the solar center). In the present paper, the interpretation in terms of both the magnetic field and the velocity field vectors is achieved.
The
![]() D2 line is one of the strongest spectral lines emitted by the solar corona until high altitudes (Vial et al. 1980; Kohl et al. 1998; Xing Li et al. 1998; and other papers related to UVCS (Ultraviolet Coronagraph Spectrometer: Kohl et al. 1995, 1997) on SoHO. The
D2 line is one of the strongest spectral lines emitted by the solar corona until high altitudes (Vial et al. 1980; Kohl et al. 1998; Xing Li et al. 1998; and other papers related to UVCS (Ultraviolet Coronagraph Spectrometer: Kohl et al. 1995, 1997) on SoHO. The
![]() D2 line (and also the
D2 line (and also the
![]()
![]() line, hereafter D1 line) is formed in the chromosphere-corona transition region. In the corona, the O5+ ions are excited by the isotropic electronic collisions (do not create alignment in the Zeeman sub-levels of the excited ions) and by the unpolarized and partial anisotropic photons coming from the underlying transition region. The partial anisotropy of the radiation coming from the transition region creates the partial linear polarization of the
line, hereafter D1 line) is formed in the chromosphere-corona transition region. In the corona, the O5+ ions are excited by the isotropic electronic collisions (do not create alignment in the Zeeman sub-levels of the excited ions) and by the unpolarized and partial anisotropic photons coming from the underlying transition region. The partial anisotropy of the radiation coming from the transition region creates the partial linear polarization of the
![]() D2 coronal line. This linear polarization was detected for the first time by SUMER/SoHO (for more details, see Raouafi et al. 1999a). Taking advantage of its sensitivity to the linear polarization state of the observed radiation (Wilhelm et al. 1995; Hassler et al. 1997), SUMER/SoHO has been used to analyze the partial linear polarization of the
D2 coronal line. This linear polarization was detected for the first time by SUMER/SoHO (for more details, see Raouafi et al. 1999a). Taking advantage of its sensitivity to the linear polarization state of the observed radiation (Wilhelm et al. 1995; Hassler et al. 1997), SUMER/SoHO has been used to analyze the partial linear polarization of the
![]() D2 line observed in the south polar hole of the solar corona at
D2 line observed in the south polar hole of the solar corona at
![]() above the limb at March 19, 1996 (Raouafi et al. 1999a,b,c,d, 2002). The measured parameters have been reported in Raouafi (2000) and Raouafi et al. (2002): the measured degree of linear polarization is
above the limb at March 19, 1996 (Raouafi et al. 1999a,b,c,d, 2002). The measured parameters have been reported in Raouafi (2000) and Raouafi et al. (2002): the measured degree of linear polarization is ![]() and the rotation angle of the direction of linear polarization with respect to the tangent to the solar limb (Px) is equal to
and the rotation angle of the direction of linear polarization with respect to the tangent to the solar limb (Px) is equal to
![]() .
The mean intensity ratio of the
.
The mean intensity ratio of the
![]() doublet
doublet
![]() is equal to
is equal to
![]() .
.
The determination of the linear polarization parameters of the
![]() D2 coronal line is very important. This is because the coronal line width is of a few tens of km s-1 and then this line should be affected by the effect of the macroscopic velocity field of the scattering ions (which can be assimilated to the solar wind outflow velocity field). The effect of the macroscopic motion of the O5+ ions on the linear polarization parameters of the scattered photons is studied by Raouafi et al. (2002) (see also Raouafi 2002). This study gave strong constraints on the solar wind velocity field in the coronal polar holes.
D2 coronal line is very important. This is because the coronal line width is of a few tens of km s-1 and then this line should be affected by the effect of the macroscopic velocity field of the scattering ions (which can be assimilated to the solar wind outflow velocity field). The effect of the macroscopic motion of the O5+ ions on the linear polarization parameters of the scattered photons is studied by Raouafi et al. (2002) (see also Raouafi 2002). This study gave strong constraints on the solar wind velocity field in the coronal polar holes.
The polarization parameters of a spectral line sensitive to the Hanle effect depend both on the strength and direction of the magnetic field (Sahal-Bréchot et al. 1977; Bommier & Sahal-Bréchot 1978; Bommier et al. 1981; Bommier & Sahal-Bréchot 1982; Sahal-Bréchot et al. 1986; ...). On the one hand, the
![]() D2 line domain of sensitivity to the Hanle effect (Mitchell & Zemansky 1934) corresponds to magnetic field with strengths between few Gauss (
D2 line domain of sensitivity to the Hanle effect (Mitchell & Zemansky 1934) corresponds to magnetic field with strengths between few Gauss (![]() 3 Gauss) to more than 300 Gauss. On the other hand, the expected order of magnitude of the inner corona magnetic field is a few Gauss (this comes from theoretical models, but the coronal magnetic field has never been measured). Thus, one expects that the linear polarization of the
3 Gauss) to more than 300 Gauss. On the other hand, the expected order of magnitude of the inner corona magnetic field is a few Gauss (this comes from theoretical models, but the coronal magnetic field has never been measured). Thus, one expects that the linear polarization of the
![]() D2 line should be affected also by the coronal magnetic field (Sahal-Bréchot et al. 1986) in addition to the macroscopic velocity field of the O5+ ions (Raouafi et al. 2002).
D2 line should be affected also by the coronal magnetic field (Sahal-Bréchot et al. 1986) in addition to the macroscopic velocity field of the O5+ ions (Raouafi et al. 2002).
The present work is devoted to numerical computations of linear polarization parameters of the
![]() D2 coronal line by using theoretical results obtained by Raouafi (2000, 2002). In Sect. 2, We study the magnetic field effect alone on the linear polarization of the
D2 coronal line by using theoretical results obtained by Raouafi (2000, 2002). In Sect. 2, We study the magnetic field effect alone on the linear polarization of the
![]() D2 coronal line. In Sect. 3, we combine the magnetic field and the macroscopic velocity field effects. By comparing the numerical results with the observational ones, we obtain constraints on the solar wind velocity field and the coronal magnetic field vectors in the coronal polar holes.
D2 coronal line. In Sect. 3, we combine the magnetic field and the macroscopic velocity field effects. By comparing the numerical results with the observational ones, we obtain constraints on the solar wind velocity field and the coronal magnetic field vectors in the coronal polar holes.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{h3667_Figure1.eps}
\end{figure}](/articles/aa/full/2002/48/aah3667/Timg27.gif) |
Figure 1:
Definition of the axes and angles in the case where we take into account the effect of the magnetic field on the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3667_Figure2.eps}
\end{figure}](/articles/aa/full/2002/48/aah3667/Timg28.gif) |
Figure 2:
Variation of the linear polarization parameters (degree (top panel) and rotation angle of the polarization direction with respect to the tangent to the solar limb (medium panel)) given as a function of the azimuth angle (for different values of the polar angle) obtained by taking into account the effect of a magnetic field of 4 Gauss. Bottom panel gives the variation of the intensity ratio of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3667_Figure3.eps}
\end{figure}](/articles/aa/full/2002/48/aah3667/Timg29.gif) |
Figure 3: The same as Fig. 2 but for a magnetic field of 6 Gauss. |
| Open with DEXTER | |
In the present section, we take into account only the Hanle effect due to the coronal magnetic field on the
![]() D2 linear polarization parameters. We cancel the Doppler dimming term in the equations presented by Raouafi (2000, 2002). These equations giving the Stokes parameters of a resonance scattering spectral line sensitive to the Hanle and Doppler redistribution effects are general. They give the Stokes parameters as a function of the magnetic field vector and the velocity field vector of the scattering atoms (or ions). However, the equation structures show that both effects are decoupled. By canceling the magnetic field, we obtain results of Sahal-Bréchot et al. (1998), which give only the effect of the velocity field. To obtain the magnetic field effect alone, it is sufficient to eliminate the dimming term by canceling the macroscopic velocity field vector of the scattering ions, and we obtain the results of Sahal-Bréchot et al. (1986).
D2 linear polarization parameters. We cancel the Doppler dimming term in the equations presented by Raouafi (2000, 2002). These equations giving the Stokes parameters of a resonance scattering spectral line sensitive to the Hanle and Doppler redistribution effects are general. They give the Stokes parameters as a function of the magnetic field vector and the velocity field vector of the scattering atoms (or ions). However, the equation structures show that both effects are decoupled. By canceling the magnetic field, we obtain results of Sahal-Bréchot et al. (1998), which give only the effect of the velocity field. To obtain the magnetic field effect alone, it is sufficient to eliminate the dimming term by canceling the macroscopic velocity field vector of the scattering ions, and we obtain the results of Sahal-Bréchot et al. (1986).
In order to minimize the number of free parameters in the numerical calculations, it is useful to have an idea, even global, on the magnetic field "topology'' in the south coronal polar hole during the observations (March 1996). The polarimetric observations of the
![]() D2 coronal line performed by SUMER/SoHO were done during the minimum of the solar activity. The knowledge of the mean magnetic polarity of the Sun allows this ambiguity to be eliminated. The Ulysses ESA/NASA (European Space Agency/National Aeronautics and Space Administration) space mission which had measured the mean magnetic field of the Sun during this period of time: the south geographic pole of the Sun was also the negative pole of the mean magnetic field. Consequently, the mean magnetic field lines should be oriented toward the solar disk in the south hemisphere of the Sun and in particular in the south polar hole of the solar corona where the field lines are open (see Fig. 1). For the numerical computations, we consider a magnetic field vector oriented toward the solar disk but not necessary parallel to the polar axis. This is because magnetic field vectors parallel to the symmetry axis of the incident radiation have no effect on the linear polarization of the scattered radiation. Thus, the cylindrical symmetry of the incident radiation is not broken. In other words and from a theoretical point of view, this is equivalent to say that coherence terms do not appear in the density matrix of the scattered photons which means no changes for the polarization parameters.
D2 coronal line performed by SUMER/SoHO were done during the minimum of the solar activity. The knowledge of the mean magnetic polarity of the Sun allows this ambiguity to be eliminated. The Ulysses ESA/NASA (European Space Agency/National Aeronautics and Space Administration) space mission which had measured the mean magnetic field of the Sun during this period of time: the south geographic pole of the Sun was also the negative pole of the mean magnetic field. Consequently, the mean magnetic field lines should be oriented toward the solar disk in the south hemisphere of the Sun and in particular in the south polar hole of the solar corona where the field lines are open (see Fig. 1). For the numerical computations, we consider a magnetic field vector oriented toward the solar disk but not necessary parallel to the polar axis. This is because magnetic field vectors parallel to the symmetry axis of the incident radiation have no effect on the linear polarization of the scattered radiation. Thus, the cylindrical symmetry of the incident radiation is not broken. In other words and from a theoretical point of view, this is equivalent to say that coherence terms do not appear in the density matrix of the scattered photons which means no changes for the polarization parameters.
The magnetic field vector is defined by its strength B and by two angles ![]() and
and ![]() .
.
![]() is the polar angle made by the magnetic field vector and the polar axis (Pz). The azimuth angle
is the polar angle made by the magnetic field vector and the polar axis (Pz). The azimuth angle ![]() is that made by the projection of the magnetic field vector on the plane (xPy) with the tangent to the solar limb (Px). The definition of the different axes and the angles
is that made by the projection of the magnetic field vector on the plane (xPy) with the tangent to the solar limb (Px). The definition of the different axes and the angles ![]() and
and ![]() are given in Fig. 1.
are given in Fig. 1.
For the numerical calculations, we choose a range for the magnetic field strength from 1 to 10 Gauss, the polar angle ![]() varies from
varies from ![]() to
to ![]() and the azimuth angle from
and the azimuth angle from ![]() to
to ![]() .
.
As expected, magnetic field vectors parallel to the polar axis do not have any effect on the polarization parameters (degree and direction of the linear polarization) of the scattered photons (see top and medium panels of Figs. 2 and 3).
The curves giving the linear polarization degree, as a function of the azimuth angle ![]() ,
have quasi-sinusoidal shapes for magnetic field vectors inclined with respect to the polar axis. The amplitude of these curves increases with the polar angle and with the magnetic field strength. This is due to the fact that the major variation of the linear polarization degree is due to the transversal component (Bx and By) which increases with the polar angle and with the magnetic field strength.
,
have quasi-sinusoidal shapes for magnetic field vectors inclined with respect to the polar axis. The amplitude of these curves increases with the polar angle and with the magnetic field strength. This is due to the fact that the major variation of the linear polarization degree is due to the transversal component (Bx and By) which increases with the polar angle and with the magnetic field strength.
Maximum of depolarization of the scattered radiation corresponds to magnetic field vectors located around the plane of the sky in the half space (x<0) (Figs. 2 and 3). However, magnetic field vectors with directions around the plane of the sky in the half space (x>0) could be polarizing for the scattered line until a critical value of their strength beyond which they become depolarizing. This is due to the fact that the scattering angle ![]() is equal to
is equal to ![]() (for more details, see Fig. 5 in Raouafi et al. 2002). However, in the case of right angle scattering, the magnetic field is always depolarizing. In the interval of values where the magnetic field is polarizing and for a given value of the polar angle
(for more details, see Fig. 5 in Raouafi et al. 2002). However, in the case of right angle scattering, the magnetic field is always depolarizing. In the interval of values where the magnetic field is polarizing and for a given value of the polar angle ![]() ,
the linear polarization degree increases with the magnetic field strength until a critical limit beyond which it (the polarization degree) decreases when the magnetic field strength continues to increase (Fig. 2 and 3).
,
the linear polarization degree increases with the magnetic field strength until a critical limit beyond which it (the polarization degree) decreases when the magnetic field strength continues to increase (Fig. 2 and 3).
The curves giving the rotation angle of the linear polarization direction with respect to the tangent to the solar limb as a function of the azimuth angle are sinusoidal functions (medium panels of Figs. 2 and 3). This is due to the fact that the rotation of the direction of the linear polarization is mainly due to the magnetic field component along to the axis
![]() which is a sinusoidal function of the azimuth angle
which is a sinusoidal function of the azimuth angle ![]() .
The amplitude of these curves increases with the polar angle
.
The amplitude of these curves increases with the polar angle ![]() .
It increases also with the magnetic field strength (Figs. 2 and 3). This is for the same reasons as for the degree of linear polarization.
.
It increases also with the magnetic field strength (Figs. 2 and 3). This is for the same reasons as for the degree of linear polarization.
In the case of the velocity field alone, the extremes of the curves giving the linear polarization parameters (degree and the rotation angle of the polarization direction with respect to the tangent to the solar limb (Px)) are fixed (see Raouafi et al. 2002). However, in the present case (magnetic field alone), the curve extremes move when the magnetic field strength changes (Figs. 2 and 3).
Generally magnetic field vectors located in the half space (y>0) (vectors with directions around the scattering plane
![]() give positive rotation angles of the linear polarization direction (Figs. 2 and 3). However, magnetic field vectors with directions in the other half space (y<0) give negative rotation angles of the linear polarization direction with respect to the tangent to the solar limb (Px).
give positive rotation angles of the linear polarization direction (Figs. 2 and 3). However, magnetic field vectors with directions in the other half space (y<0) give negative rotation angles of the linear polarization direction with respect to the tangent to the solar limb (Px).
Bottom panels of Figs. 2 and 3 give the variation of the intensity ratio of the
![]() doublet as a function of the azimuth angle
doublet as a function of the azimuth angle ![]() for different values of the polar angle
for different values of the polar angle ![]() and for magnetic fields with strengths 4 and 6 Gauss, respectively. As for the polarization parameters, magnetic field vectors parallel to the symmetry axis of the incident radiation (Pz) do not have any effect on the intensity ratio
and for magnetic fields with strengths 4 and 6 Gauss, respectively. As for the polarization parameters, magnetic field vectors parallel to the symmetry axis of the incident radiation (Pz) do not have any effect on the intensity ratio
![]() ,
which is equal in this case to 2.927. The displacement of the curves giving the polarization parameters is also seen for the curves giving
,
which is equal in this case to 2.927. The displacement of the curves giving the polarization parameters is also seen for the curves giving
![]() .
.
For weak values of the magnetic field strength (<6 Gauss), the effect of the magnetic field on the linear polarization of the
![]() D2 coronal line and on the intensity ratio of the
D2 coronal line and on the intensity ratio of the
![]() doublet gives results in agreement with the observational measurements only for vectors with strong inclination angles with respect to the polar axis (Pz) (see Fig. 2; top panels of Fig. 9 and also first rows of Table 1 for B =4 and 5 Gauss and V=0 km s-1). For magnetic field vectors with strengths greater than 6 Gauss, the Hanle effect taken into account alone gives good results for vectors with medium and strong inclination angles with respect to the polar axis (see Fig. 3; top panel of Fig. 9 and also the first row of Table 1 for B =6 Gauss and V =0 km s-1). We should notice that the effect of magnetic field vectors with strengths lower than 3 Gauss
doublet gives results in agreement with the observational measurements only for vectors with strong inclination angles with respect to the polar axis (Pz) (see Fig. 2; top panels of Fig. 9 and also first rows of Table 1 for B =4 and 5 Gauss and V=0 km s-1). For magnetic field vectors with strengths greater than 6 Gauss, the Hanle effect taken into account alone gives good results for vectors with medium and strong inclination angles with respect to the polar axis (see Fig. 3; top panel of Fig. 9 and also the first row of Table 1 for B =6 Gauss and V =0 km s-1). We should notice that the effect of magnetic field vectors with strengths lower than 3 Gauss
![]() is sufficient to give results in agreement with the observations.
is sufficient to give results in agreement with the observations.
The results obtained by taking only into account the Hanle effect due to the coronal magnetic field vector correspond to vector with high inclination angle with respect to the polar axis. Such inclinations are not expected at low altitudes in the coronal polar holes where observations show that the magnetic field lines are almost along the radial direction. In the next section, we will study the effect of the combination of the effects of the coronal magnetic field and the solar wind velocity field vectors on the polarization parameters of the
![]() D2 line on the intensity ratio of the
D2 line on the intensity ratio of the
![]() doublet. This is in order to obtain better results than those obtained in the cases of the velocity field alone and the magnetic field alone.
doublet. This is in order to obtain better results than those obtained in the cases of the velocity field alone and the magnetic field alone.
![\begin{figure}
\par {\resizebox{\hsize}{!}{\includegraphics[clip]{h3667_Figure4.eps}} }\end{figure}](/articles/aa/full/2002/48/aah3667/Timg37.gif) |
Figure 4:
The polar angle |
| Open with DEXTER | |
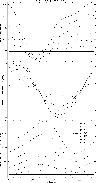 |
Figure 5: The linear polarization parameters (degree and the rotation angle of the polarization direction with respect to the tangent to the solar limb) given as a function of the azimuth angle (for different values of the polar angle) in the case of the combination of a magnetic field of 4 Gauss and a velocity field of 32 km s-1. The asymmetry of the curves giving the linear polarization degree is quiet remarkable. |
| Open with DEXTER | |
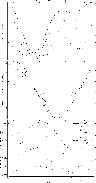 |
Figure 6: The same as Fig. 5 but for a magnetic field of 4 Gauss combined with a velocity field vector of 42 km s-1. |
| Open with DEXTER | |
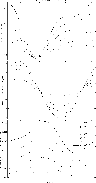 |
Figure 7: The same as Fig. 5 but for a magnetic field of 6 Gauss combined with a velocity field vector of 39 km s-1. |
| Open with DEXTER | |
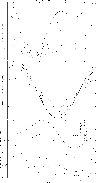 |
Figure 8: The same as Fig. 5 but for a magnetic field of 6 Gauss combined with a velocity field vector of 49 km s-1. |
| Open with DEXTER | |
In the inner corona, the plasma is confined in the magnetic field lines. This is because the magnetic pressure is much greater than that of the plasma
![]() .
Consequently, the macroscopic motion of the coronal material should be along the magnetic field lines. This is equivalent to say that the macroscopic velocity field vector of this material is parallel to the coronal magnetic field vector. In the south hemisphere of the Sun, the mean magnetic field lines are oriented toward the solar disk during the last minimum of the solar activity (Ulysses mission). However, the solar wind particles run away from the solar disk, which is equivalent to say that the macroscopic velocity field vector of these particles is oriented outward the solar disk. Consequently during the period of the observations, the magnetic field and the solar wind velocity field vectors in the south coronal polar hole are parallel but with opposite directions.
.
Consequently, the macroscopic motion of the coronal material should be along the magnetic field lines. This is equivalent to say that the macroscopic velocity field vector of this material is parallel to the coronal magnetic field vector. In the south hemisphere of the Sun, the mean magnetic field lines are oriented toward the solar disk during the last minimum of the solar activity (Ulysses mission). However, the solar wind particles run away from the solar disk, which is equivalent to say that the macroscopic velocity field vector of these particles is oriented outward the solar disk. Consequently during the period of the observations, the magnetic field and the solar wind velocity field vectors in the south coronal polar hole are parallel but with opposite directions.
For the numerical calculations, we consider a magnetic field vector parallel to the velocity field vector but with an opposite direction (the magnetic field is directed toward the solar disk). The magnetic field and the velocity field vectors are defined by their strengths (B and V) and by two angles ![]() (the polar angle) and
(the polar angle) and ![]() (the azimuth angle) (
(the azimuth angle) (![]() and
and ![]() have the same definition as in the previous section, see Fig. 4). We choose the following range of variation: the magnetic field strength B varies from 1 Gauss to 10 Gauss, the velocity field strength V varies from 0 to 100 km s-1,
have the same definition as in the previous section, see Fig. 4). We choose the following range of variation: the magnetic field strength B varies from 1 Gauss to 10 Gauss, the velocity field strength V varies from 0 to 100 km s-1, ![]() varies from
varies from ![]() to
to ![]() and
and ![]() varies from
varies from ![]() to
to ![]() .
For each couple
.
For each couple
![]() ,
we calculate the linear polarization parameters of the
,
we calculate the linear polarization parameters of the
![]() D2 scattered line along the line of sight (PZ) (degree and rotation angle of the direction of linear polarization with respect to the tangent to the solar limb) and the intensity ratio
D2 scattered line along the line of sight (PZ) (degree and rotation angle of the direction of linear polarization with respect to the tangent to the solar limb) and the intensity ratio
![]() of the
of the
![]() doublet.
doublet.
For the interpretation of the obtained numerical results, as for the case of the velocity field alone (Raouafi et al. 2002) or the magnetic field alone (previous section), we divide the polar angle ![]() range values into three sub-intervals:
range values into three sub-intervals:
As in the case of the Hanle effect alone or the Doppler redistribution alone, the combination of the effects of magnetic field and velocity field vectors parallel to the polar axis
![]() does not have any effect on the direction of linear polarization. It gives, for a given value of V, a linear polarization degree equal to that obtained by taking into account only the effect of the velocity field (see Figs. 5-8).
does not have any effect on the direction of linear polarization. It gives, for a given value of V, a linear polarization degree equal to that obtained by taking into account only the effect of the velocity field (see Figs. 5-8).
The curves giving the degree of linear polarization of the scattered photons as a function of the azimuth angle ![]() present an increasing asymmetry with the velocity filed strength V and also with the polar angle
present an increasing asymmetry with the velocity filed strength V and also with the polar angle ![]() .
This asymmetry decreases by increasing the magnetic field strength (top panels of Figs. 5-8). In fact, there is a competition between the magnetic field effect and the velocity field effect. By increasing the velocity field strength, the curves are more and more similar to those obtained in the case of the velocity field alone (Raouafi et al. 2002) and vice versa. Curves obtained in the case of the magnetic field alone and in the case of the velocity field alone are in fact the limit ones.
.
This asymmetry decreases by increasing the magnetic field strength (top panels of Figs. 5-8). In fact, there is a competition between the magnetic field effect and the velocity field effect. By increasing the velocity field strength, the curves are more and more similar to those obtained in the case of the velocity field alone (Raouafi et al. 2002) and vice versa. Curves obtained in the case of the magnetic field alone and in the case of the velocity field alone are in fact the limit ones.
The competition between the velocity field effect and the magnetic field effect on the linear polarization of the scattered radiation appears also in the shift of the curves giving the polarization degree (also those giving the rotation angle of the linear polarization direction) (Figs. 5-8). The extremes of these curves move toward weak values of the azimuth angle ![]() by increasing the velocity field strength for a given value of that of the magnetic field and toward high values of
by increasing the velocity field strength for a given value of that of the magnetic field and toward high values of ![]() by increasing the magnetic field strength for a given value of that of the velocity field. This corresponds to the shift variation of the curves observed in the case where we only take into account the effect of the magnetic field.
by increasing the magnetic field strength for a given value of that of the velocity field. This corresponds to the shift variation of the curves observed in the case where we only take into account the effect of the magnetic field.
As in the case of the magnetic field effect and the case of the velocity field effect taken separately into account, the curves giving the rotation angle of the polarization direction (with respect to the tangent to the solar limb) as a function of the azimuth angle ![]() are sinusoidal (medium panels of Figs. 5-8). The amplitude of curves giving the rotation angle of the polarization direction as a function of the azimuth angle increases with the polar angle
are sinusoidal (medium panels of Figs. 5-8). The amplitude of curves giving the rotation angle of the polarization direction as a function of the azimuth angle increases with the polar angle ![]() ,
with the velocity field strength and with the magnetic field strength. This is for the same reasons reported in Raouafi et al. (2002) and in the previous section of the present paper.
,
with the velocity field strength and with the magnetic field strength. This is for the same reasons reported in Raouafi et al. (2002) and in the previous section of the present paper.
Positive rotation angles of the polarization direction of significant values (
![]() ,
see Raouafi et al. 2002) are obtained for magnetic fields located in the vicinity of the scattering plane in the half-space (y>0) for weak values of the velocity field strength (
,
see Raouafi et al. 2002) are obtained for magnetic fields located in the vicinity of the scattering plane in the half-space (y>0) for weak values of the velocity field strength (![]() km s-1). For stronger velocity fields, positive rotation angles of the direction of polarization correspond to magnetic field vectors located in the vicinity of the plane of the sky.
km s-1). For stronger velocity fields, positive rotation angles of the direction of polarization correspond to magnetic field vectors located in the vicinity of the plane of the sky.
The effect of the combination of the coronal magnetic field and the solar wind velocity field on the intensity ratio of the
![]() doublet lines is given by the bottom panels of Figs. 5-8. The shapes of these curves are between those of the curves obtained in the case of the velocity field effect alone (Raouafi et al. 2002) and in the case of the magnetic field alone (previous section). The curves obtained in these latter cases are in fact the limit ones.
doublet lines is given by the bottom panels of Figs. 5-8. The shapes of these curves are between those of the curves obtained in the case of the velocity field effect alone (Raouafi et al. 2002) and in the case of the magnetic field alone (previous section). The curves obtained in these latter cases are in fact the limit ones.
The results obtained by combining the effects of the coronal magnetic field and solar wind velocity field vectors are presented for each value of the magnetic field strength as a function of the inclination angle interval by giving the outflow speed ranges of the scattering ions that give numerical results in agreement with the measurements.
![\begin{figure}
\par\includegraphics[width=4.35cm,clip]{h3667_Figure9_1.eps}\incl...
...ure9_3.eps}\includegraphics[width=4.35cm,clip]{h3667_Figure9_4.eps}
\end{figure}](/articles/aa/full/2002/48/aah3667/Timg51.gif) |
Figure 9:
|
| Open with DEXTER | |
|
![\begin{displaymath}\begin{minipage}[t]{5cm}
{\small\begin{tabular}[h]{ccc}
\hli...
...circ\rightarrow144^\circ$}\\
\end{tabular} }
\end{minipage} \end{displaymath}](/articles/aa/full/2002/48/aah3667/img52.gif)
|
If we limit ourselves to the effect of a magnetic field of 3 Gauss combined with the velocity field effect, the solar wind outflow speed depend on the direction of the magnetic field vector (and consequently on the direction of the velocity field vector). If we take into account only the effect of weakly inclined vectors with respect to the polar axis
![]() ,
we obtain numerical results compatible with the observations for speeds between 33 and 39 km s-1. In this case, the velocity field vectors are blue-shifting and in the quarter space
(x>0, y>0). If we take into account in addition the effects of magnetic field and velocity field vectors with medium inclinations, we obtain good results for velocity field vectors with strengths between 27 and 42 km s-1. However, if we take into account the effect of the all the vectors independently with their inclinations, we obtain good results for velocity field speeds between 21 and 48 km s-1. The directions of these magnetic field vectors (and thus of the velocity field vectors) depend on the strength of the velocity field. These results are summarized in the first part of Table 1.
,
we obtain numerical results compatible with the observations for speeds between 33 and 39 km s-1. In this case, the velocity field vectors are blue-shifting and in the quarter space
(x>0, y>0). If we take into account in addition the effects of magnetic field and velocity field vectors with medium inclinations, we obtain good results for velocity field vectors with strengths between 27 and 42 km s-1. However, if we take into account the effect of the all the vectors independently with their inclinations, we obtain good results for velocity field speeds between 21 and 48 km s-1. The directions of these magnetic field vectors (and thus of the velocity field vectors) depend on the strength of the velocity field. These results are summarized in the first part of Table 1.
For a magnetic field of 4 Gauss, the obtained results are similar to those obtained with a magnetic field of 3 Gauss. Providing that the velocity field be different from zero, the Hanle effect is able to give results consistent with the measurements. These results are summed up in Table 1 (see also Fig. 9).
In order to obtain good results, a magnetic field vector with a strength of 5 Gauss should be combined with velocity field vectors with strength ranges depending on the inclination angle interval as the following:
The effect of magnetic fields with strengths greater than 6 Gauss becomes more and more important. To obtain good results for medium inclined vectors, the effect of the velocity field vector of the scattering ions is no longer needed. But for weak values of the inclination angle, the effect of the velocity field vector is always necessary. To obtain results consistent with the measurements, and if we take into account the effect of
The temperature anisotropy observed by UVCS/SoHO at higher altitudes in the polar holes of the solar corona would have an important effect on the polarization parameters of the scattered radiation, particularly on the direction of the linear polarization. This anisotropy is interpreted by the ion-cyclotron effect that creates anisotropy in the velocity field distribution of the scattering ions. Theoretically, ion-cyclotron waves can exist everywhere in the solar corona until the chromosphere (E. Marsch, private communication). This would be taken into account and will be the topic of a further paper.
In the present paper and in Raouafi et al. (2002) as well, the considered velocity field distribution is a simple Maxwellian with a drift velocity field vector which describes the macroscopic motion of the scattering ions (solar wind velocity field vector). The polarization parameters of the
![]() D2 coronal line are more sensitive to the velocity field effect than to the magnetic field effect. However, these parameters could be more sensitive to an anisotropic velocity field distribution (in particular the direction of linear polarization). The effect of this latter will be the topic of a further paper.
D2 coronal line are more sensitive to the velocity field effect than to the magnetic field effect. However, these parameters could be more sensitive to an anisotropic velocity field distribution (in particular the direction of linear polarization). The effect of this latter will be the topic of a further paper.
Acknowledgements
The authors would like to thank an anonymous referee for critical and helpful comments on the manuscript.The SUMER project is supported by DLR, CNES, NASA, and ESA PRODEX programs (Swiss contribution). The SoHO is a mission of international cooperation between ESA and NASA.