A unique case of two zebra patterns related harmonically with ratio of
A&A 396, 1015-1018 (2002)
DOI: 10.1051/0004-6361:20021493
H. S. Sawant1 - M. Karlický2 - F. C. R. Fernandes1 - J. R. Cecatto1
1 - Instituto Nacional de Pesquisas Espaciais, INPE, CP 515, 12201-970 São José dos Campos, SP, Brazil
2 -
Astronomical Institute of the Academy of Sciences of the Czech Republic,
25165 Ondrejov, Czech Republic
Received 12 March 2002 / Accepted 24 September 2002
Abstract
A unique case of two zebra patterns related harmonically
with ratio of ![]() 1:2 was observed by distant radio telescopes at
São José dos Campos and Ondrejov Observatories. Accompanied
zebras show that the ratio of frequencies of the neighboring zebra
lines is in the range of 1.009-1.037. There is a tendency of a
decrease of this ratio with decreasing frequency within the specific
zebra pattern. Both facts speak in favour of plasma emission models
for the zebra pattern fine structure in radio burst continua.
1:2 was observed by distant radio telescopes at
São José dos Campos and Ondrejov Observatories. Accompanied
zebras show that the ratio of frequencies of the neighboring zebra
lines is in the range of 1.009-1.037. There is a tendency of a
decrease of this ratio with decreasing frequency within the specific
zebra pattern. Both facts speak in favour of plasma emission models
for the zebra pattern fine structure in radio burst continua.
Key words: plasmas - Sun: flares - Sun: radio radiation
The zebra patterns belong to fine structures of radio continua observed during solar flares. At metric wavelengths they have been known for a long time (e.g. Slottje 1972; Aurass & Chernov 1983). Rosenberg (1972) and later Zheleznyakov & Zlotnik (1975) modelled these structures in terms of the harmonics of the electron cyclotron modes. A similar model was suggested also by Kuijpers (1975). Other models (e.g. Chernov 1990) explained zebras by modulation of whistler packets.
With new radiospectrographs operating in the GHz frequency range the zebra patterns were discovered also in the 1-4 GHz range (Isliker & Benz 1994). These high-frequency zebras are relatively rare (Jiricka et al. 2001). Therefore their observation and comparison with models is important.
In the present paper, first, examples of high-frequency zebra patterns observed by both Brazilian Solar Spectroscope (BSS) (Sawant et al. 2001) and Ondrejov radiospectrograph during the June 6, 2000 flare are presented. Among them a unique case of harmonically related zebra patterns observed at distant sites is shown. Using the plasma emission model of Ledenev et al. (2001) these zebras are analysed and magnetic fields in radio sources are estimated.
| |
Figure 1: The 3 GHz radio flux record of two parts of the June 6, 2000 flare observed by the Ondrejov radiometer. The arrows indicate times of the zebra pattern observations in the 2.0-4.5 GHz and 1.2-1.7 GHz ranges - see also Tables 1 and 2. Note different time and flux scales in both parts of the figure. |
| Open with DEXTER | |
The June 6, 2000 flare classified as X2.3 was observed at 15:00-17:00 UT in the active region NOAA AR 9026. A full-halo coronal mass ejection and type II/IV bursts were reported in association with this flare (Solar Flare NOAA Report).
This flare was rich in high-frequency zebra patterns. A global
overview of observations of these zebras in comparison with the 3 GHz
radio flux record is shown in Fig. 1. Here it is shown that the
zebra patterns were recorded after the first flare maximum and close
to the secondary one. Parameters of the zebra patterns in the
1.2-1.7 and 2.0-4.5 GHz frequency ranges are given in Tables 1 and 2, respectively. The number of observed zebra lines is in the
interval of 2-8. The modulation depth Q of zebras (the ratio of
the maximum to minimum radio flux) is listed in the last columns of
Tables 1 and 2. Examples of the zebra patterns in the 1.2-1.7 GHz
and 2.0-4.5 GHz ranges and the corresponding frequency cuts are
shown in Figs. 2 and 3, respectively.
![\begin{figure}
\par\includegraphics[height=6.5cm,width=8.8cm,clip]{zebperf16314.ps}\end{figure}](/articles/aa/full/2002/48/aah3544/Timg3.gif) |
Figure 2: An example of the 1.2-1.7 GHz zebra pattern observed at 16:31:14 UT by the BSS, and its frequency cut. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6.8cm,width=8.8cm,clip]{a000606aobs.eps}\end{figure}](/articles/aa/full/2002/48/aah3544/Timg4.gif) |
Figure 3: An example of the 2.0-4.5 GHz zebra pattern observed at 15:43:12 UT by the Ondrejov radiospectrograph, and its frequency cut. |
| Open with DEXTER | |
| Zebra | Start | End | Freq. range | No. | Q |
| [UT] | [UT] | MHz | zebra | ||
| lines | |||||
| Z1 | 15:37:42 | 15:37:50 | 1590-1685 | 3 | 1.9 |
| Z2 | 15:42:51 | 15:42:52 | 1220-1265 | 3 | 1.6 |
| Z3 | 15:51:33 | 15:51:34 | 1245-1385 | 5 | 2.7 |
| Z4 | 15:54:43 | 15:54:47 | 1250-1395 | 6 | 1.4 |
| Z5 | 16:31:25 | 16:31:27 | 1500-1690 | 7 | 2.5 |
| Z6 | 16:32:12 | 16:32:25 | 1605-1685 | 4 | 1.7 |
| Z7 | 16:33:27 | 16:33:34 | 1420-1500 | 4 | 1.4 |
| Z8 | 16:34:00 | 16:34:06 | 1535-1680 | 7 | 2.2 |
The zebra patterns in the harmonic ratio of ![]() 1:2 are presented
in Fig. 4. In both the 1.2-1.7 GHz as well as the 2.0-4.5 GHz range
some zebra lines appear with varying intensity, simultaneously, and
at frequencies in fundamental (F)/ harmonic (H) ratio within the
accuracy of the receivers (about
1:2 are presented
in Fig. 4. In both the 1.2-1.7 GHz as well as the 2.0-4.5 GHz range
some zebra lines appear with varying intensity, simultaneously, and
at frequencies in fundamental (F)/ harmonic (H) ratio within the
accuracy of the receivers (about ![]() 20 MHz). The zebra lines in
the fundamental band are more intense than those in the harmonic one.
Furthermore, the zebra lines in the fundamental band are shorter in
time; after 15:37:45 UT only zebra lines in the harmonic band were
observed. A detailed comparison of zebra frequencies at 15:37:43.5 UT
shows zebra lines in the fundamental mode at 1620, 1640, and 1680 MHz. In the second harmonic mode, stripes are situated at 3200 MHz
(
20 MHz). The zebra lines in
the fundamental band are more intense than those in the harmonic one.
Furthermore, the zebra lines in the fundamental band are shorter in
time; after 15:37:45 UT only zebra lines in the harmonic band were
observed. A detailed comparison of zebra frequencies at 15:37:43.5 UT
shows zebra lines in the fundamental mode at 1620, 1640, and 1680 MHz. In the second harmonic mode, stripes are situated at 3200 MHz
(
![]() ?), 3280 MHz (
?), 3280 MHz (
![]() ), 3380 MHz (
), 3380 MHz (
![]() ?), and 3450 MHz.
?), and 3450 MHz.
| Zebra | Start | End | Freq. range | No. | Q |
| [UT] | [UT] | MHz | zebra | ||
| lines | |||||
| Z9 | 15:37:44 | 15:37:49 | 3300-3400 | 2 | 1.3 |
| Z10 | 15:43:12 | 15:43:13 | 3500-4000 | 6 | 1.2 |
| Z11 | 16:33:59 | 16:34:02 | 2000-2200 | 3 | 1.5 |
| Z12 | 16:38:58 | 16:39:00 | 2000-2600 | 8 | 1.4 |
| Z13 | 16:39:57 | 16:39:59 | 2000-2500 | 8 | 1.6 |
In observed zebras (Z1-Z13) we measured the ratio of frequencies of
the neighboring zebra lines (numbered for the specific zebra as
1, 2, ... from high to low frequencies) and the results are shown in
Table 3. The frequency ratios between the neighboring zebra lines are
designated as e.g. 1-2, which means the ratio of frequencies of the
zebra line 1 and 2. As can be seen these ratios are in the interval
1.009-1.037 and there is a tendency of a decrease of these ratios
towards higher numbers of zebra lines, i.e. towards lower frequencies
within the selected zebra. This trend was predicted in the
theoretical model for the zebra pattern emission by Ledenev et al.
(2001). In this model with the spatially distributed zebra line
sources, in the atmosphere where the magnetic field gradient is much
greater than that of the density gradient, the ratio of frequencies
of the neighboring zebra lines is expressed as
![\begin{displaymath}%
\frac{\omega_{s}}{\omega_{s+1}} = \frac{\omega_{pe s}}{\omega_{pe
s+1}} \left[\frac{s^3 (s+2)}{(s+1)^3(s-1)} \right]^{1/2},
\end{displaymath}](/articles/aa/full/2002/48/aah3544/img9.gif) |
(1) |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{zebra060600harmS.ps}\end{figure}](/articles/aa/full/2002/48/aah3544/Timg18.gif) |
Figure 4: The zebra pattern observed in harmonic ratio by BBS (upper) and Ondrejov (bottom) radio spectrographs. Notice the reversed color scale compared with Figs. 2 and 3. |
| Open with DEXTER | |
In this estimation the most critical aspect is the determination of
the s harmonic numbers for the zebra lines. It can be done by a
comparison of the highest frequency ratio in the specific zebra
pattern with the theoretical values. In our case, the best fit is s = 4 for the zebra line with the highest frequency. Then the magnetic
field strength can be determined in the different zebra pattern
sources as
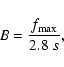 |
(2) |
| 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | B(G) | |
| Z1 | 1.024 | 1.009 | 150 | ||||
| Z2 | 1.020 | 1.016 | 113 | ||||
| Z3 | 1.037 | 1.023 | 1.024 | 1.024 | 124 | ||
| Z4 | 1.026 | 1.015 | 1.023 | 1.023 | 1.024 | 125 | |
| Z5 | 1.021 | 1.028 | 1.019 | 1.019 | 1.016 | 1.017 | 151 |
| Z6 | 1.015 | 1.018 | 1.016 | 150 | |||
| Z7 | 1.020 | 1.021 | 1.014 | 134 | |||
| Z8 | 1.018 | 1.015 | 1.019 | 1.009 | 1.016 | 1.013 | 150 |
| Z9 | 1.019 | 152 | |||||
| Z10 | 1.020 | 1.020 | 1.015 | 1.018 | 1.015 | 178 | |
| Z11 | 1.021 | 1.011 | 196 | ||||
| Z12 | 1.030 | 1.027 | 1.037 | 1.023 | 1.024 | 1.023 | 232 |
| Z13 | 1.031 | 1.028 | 1.023 | 1.024 | 1.030 | 1.023 | 223 |
In this paper examples of the high-frequency zebra patterns observed by both the Brazilian Solar Spectroscope and the Ondrejov radiospectrograph during the June 6, 2000 flare are shown. One of the patterns appears at frequencies of ratio 1:2 (fundamental/harmonic mode of the plasma frequency). This observation favours plasma emission models of zebra pattern continuum fine structure. The intensity of harmonic branch was weaker than that of the fundamental one. The modulation depths Q of zebras are 1.4-2.7 in the (1.2-1.7) GHz range and 1.2-1.6 in the (2.0-4.5) GHz range. These values are lower than those (2.7-3.4) reported by Aurass & Chernov (1983) for the zebras observed in the metric range. It was found that the ratio of frequencies of the neighboring zebra lines is in the range of 1.009-1.037 and there is a tendency of a decrease of this ratio with the decreasing frequency. (The uncertainty of 20 MHz in frequency measurements has a negligible effect on these results.) These facts are in good agreement with the Ledenev et al. (2001) model and that is why this model was used for magnetic field estimations. The magnetic field values in the zebra radio sources were found in the range of 113-232 G.
Acknowledgements
This work was supported by the grant IAA3003202 of the Academy of Sciences of the Czech Republic. F.C.R. Fernandes acknowledge receiving scholarship from FAPESP (99/10529-0). The authors thank to the referee, Dr. H. Aurass, for helpful comments and to H. Mészárosová for technical help.