A&A 396, L31-L34 (2002)
DOI: 10.1051/0004-6361:20021645

No observational proof of the black-hole event-horizon

M. A. Abramowicz1,3,4 - W. Kluzniak2,3,5 - J.-P. Lasota3


1 - Department of Astronomy and Astrophysics, Chalmers University, 412-96 Göteborg, Sweden
2 - Institute of Astronomy Johannes Kepler, University of Zielona Góra, Poland
3 - Institut d'Astrophysique de Paris, 98bis boulevard Arago, 75014 Paris, France
4 - Université Pierre et Marie Curie, Paris 6
5 - Centre d'Étude Spatiale des Rayonnements, 9 Av. Colonel-Roche, 31028 Toulouse, Cedex 4, France

Received 15 July 2002 / Accepted 8 November 2002

Abstract
Recently, several ways of verifying the existence of black-hole horizons have been proposed. We show here that most of these suggestions are irrelevant to the problem of the horizon, at best they can rule out the presence of conventional baryonic matter in the outer layers of black-hole candidates. More generally, we argue that it is fundamentally impossible to detect in electromagnetic radiation direct evidence for the presence of a black-hole horizon. This applies also to future observations, which would trace very accurately the details of the space-time metric of a body suspected of being a black hole. Specific solutions of Einsteins's equations lack an event horizon, and yet are indistinguishable in their electromagnetic signature from Schwarzschild black holes.


1 Introduction

One of the most remarkable predictions of General Relativity - a very well tested theory of gravity - is the existence of black holes, whose most distinctive feature is the presence of an event horizon. The black-hole horizon may only be a curiosity to astronomers, but it is of fundamental importance to theoretical physics (e.g., Bousso 2002 and references therein). It is also possible, as claimed by Babak & Grishchuk (2002), that arbitrarily small corrections to General Relativity (mass-term which might be required by the string/M-theory) may eliminate black holes. Therefore "... good science demands that we seek positive evidence in support of the black hole picture, and watch for credible evidence that the standard picture may not be quite right" (Peebles 2002).

The best black-hole candidates are found in Low Mass X-ray Binaries, in particular in their subclass called Soft X-ray Transients (SXTs), which are systems undergoing rare and powerful outbursts but spending most of their life in a low luminosity quiescent state (see Tanaka & Shibazaki 1996 for a review). It is generally believed that the compact component in these and other X-ray binary systems is either a star possessing a material surface (a neutron star or a quark star) or a black hole. The reason for this belief is that masses of compact bodies in X-ray binaries are clearly divided into two classes: those whose mass is less than $\sim$$3~M_\odot$, the maximum mass of a neutron star or a quark star (see e.g., Salgado et al. 1994; Stergioulas et al. 1999), and those whose mass is clearly larger than this value.

Compact members of the lower-mass class usually show clear evidence of a surface, such as stable and coherent pulsations or X-ray bursts. One can therefore safely conclude that in this case we are dealing with either neutron or quark stars.

Sources in the second class exhibit neither X-ray bursts, nor coherent pulsations. Since their masses exceed the maximum mass of neutron stars we know that they are not made from neutron-star or quark matter, usually they are called "black-hole candidates". If despite this nomenclature they have a surface, it may be physically different from that of neutron or quark stars. This must be taken into account when considering hypothetical physical processes on these hypothetical surfaces.

Narayan and collaborators (see e.g. Narayan et al. 2001 and references therein), attempted to give a positive proof in favor of black-hole existence by looking for the evidence of absence of surfaces in "black-hole candidates". They used two types of arguments. First, the claim is that properties of Advection Dominated Accretion Flows (ADAFs; Abramowicz et al. 1995; Narayan & Yi 1994, 1995a,b) can be used to prove the existence of event-horizons. Second, absence of X-ray bursts from these sources would prove the absence of surface.

In the following we show that such arguments are fundamentally flawed, because the laws of physics admit the presence of compact objects with no event horizons and the same observational signatures as black holes.

2 Proof by ADAFs

ADAFs describe accretion with very low radiative efficiency in which energy released by viscous torques removing angular momentum from the accreting matter is not radiated away but stored in the flow. If an ADAF forms around a black hole, the stored energy will be lost forever under the event horizon, whereas if the accreting body is a "star" this energy must be radiated away once matter lands on its surface. Therefore, the argument runs, black holes should be dimmer than neutron stars, quark stars, etc., if in both cases an ADAF is present.

The best systems in which this hypothesis could be tested are the soft X-ray transients. In SXTs, like in low-mass X-ray binaries in general, a compact body accretes matter lost by a Roche-lobe filling low-mass stellar companion. The accreting matter forms a disc whose instabilities trigger outbursts (see Lasota 2001 for a review of the instability model). Narayan et al. (1996; see also Lasota et al. 1996 and Narayan et al. 1997a) proposed that quiescent SXT discs are truncated and that the inner accretion flow forms an ADAF. This hypothesis has been recently vindicated from the theoretical point of view by Dubus et al. (2001) and is supported by observations (see Done 2002 for a review).

Narayan et al. (1997b) investigated quiescent luminosities of SXTs and found black-hole "candidates" to be dimmer, in accordance with the prediction of the ADAF model. They came to the conclusion that they found evidence for the presence of event horizons. Subsequent work (e.g. Lasota & Hameury 1998; Menou et al. 1999; Garcia et al. 2001) confirmed that black-hole "candidates" are indeed dimmer than systems known to contain neutron stars, or at least stars with a surface. This is a very strong argument in favour of the presence of event horizons. However, it is not a proof.

3 Arguments against evidence based on relative dimness of black hole candidates

Arguments against the most conservative conclusion that the relative dimness of black-hole candidates results from the presence of event horizons are of two, not unrelated, types.

First, it has been argued that the accretion flow in quiescent SXTs are not represented by ADAFs.

Narayan & Yi (1995a) and Blandford & Begelman (1999) argued (see however Paczynski 1998 and Abramowicz et al. 2000 for criticism of the argument) that ADAFs are subject to mass loss and therefore the dimness of quiescent SXTs could result from the low accretion rate onto the compact object - most of the matter being lost with the wind. However, such wind models do not offer an explanation of the luminosity difference between neutron-star systems and those presumed to contain black holes (Menou et al. 1999). Since the attempt to apply to these systems the windy-ADAF model of Quataert & Narayan (1999) failed, they proposed that the action of a magnetic propeller could be answer. However, a compelling signature of this effect has yet to be found.

Abramowicz & Igumenshchev (2001) suggested that the observed differences between quiescent luminosities of accreting black holes and neutron stars is well explained by the occurrence in such systems of a CDAF (Convection Dominated Accretion Flow; see Narayan et al. 2000) instead of an ADAF. They found that for low viscosities accretion flows around compact bodies form ADAFs only in their innermost regions but are convectively dominated at radii $R\ga 10^2~R_{\rm S}$ (where $R_{\rm S}=2GM/c^2$ is the Schwarzschild radius). In such flows emission comes mostly from the convective region; the radiative efficiency is independent of accretion rate and equals $\varepsilon_{\rm BH}= 10^{-3}$. Assuming that mass-energy accreted onto a neutron star is converted to photons with efficiency $\varepsilon_{\rm NS}\approx 0.1$, one obtains the observed ratio between black-hole and neutron-star luminosities. Unfortunately this cannot be the correct explanation of all of the luminosity difference (Lasota 2002) because, as already pointed out by Menou et al. (1999), if neutron stars in quiescent transient systems are to radiate with a 0.1 efficiency, some mass loss from the system must be assumed.

Another class of arguments asserts that X-rays in quiescent SXTs are not powered by the accretion flow.

Attempts to ascribe quiescent X-ray luminosity in black-hole systems to active stellar companions (Bildsten & Rutledge 2000) are not based on a sound theoretical foundation (Lasota 2001) and have been refuted by observations (Garcia et al. 2001; Kong et al. 2002).

Menou (2001) presented an argument based on the settling-flow model of Medvedev & Narayan (2001) in which the accretion flow arrives with very low angular momentum at the surface of a rapidly rotating neutron star. The quiescent X-ray luminosity is then due to rotational energy loss by the star. This requires viscous contact between the star and the accretion disk, and if, in contrast, black-hole candidates had a material surface at radii smaller than the inner-most stable orbit, the accretion flow would be supersonic and viscous contact impossible. Black-hole candidates would be dimmer because unable to lose their rotational energy (Menou 2001).

For an earlier review of this topic see Narayan et al. (2001).

4 Absence of X-ray bursts

There is direct evidence that compact bodies in X-ray binaries form (at least) two types of objects: their masses show a bimodal distribution (see Miller et al. 1998). Neutron star masses are all concentrated around the "canonical" value of 1.4 $M_\odot$ whereas the second class of bodies, the "black hole candidates", have higher masses in the range of $\sim$5 to 18 $M_\odot$ (see e.g. Narayan et al. 2001; Greiner et al. 2001).

In general, the maximum mass of a compact body can be expressed as $8.4\left(\varepsilon_0/10^{14}~{\rm g\ cm^{-3}} \right)^{-1/2}$ $M_\odot$, where $\varepsilon_0$ is the fiducial density above which the equation of state is taken to be described by a causality-limit equation of state (Rhoades & Ruffini 1974; Friedmann & Ipser 1987). Bahcall et al. (1990) showed that stars with a material surface can have masses as high as 10 $M_\odot$, if one is willing to entertain configurations of baryonic matter at sub-nuclear density (allowed by a mean-field description of nuclear interactions). Although Miller et al. (1998) shows that it is unlikely that bodies with masses larger than 10 $M_\odot$ are Q-stars - because this would require unrealistically low densities at which hadronic bulk matter would persist - "unlikely" is not a very satisfactory argument in favour of black-hole existence. One wishes for a more direct argument excluding Q-stars, and this has recently been attempted by Narayan & Heyl (2002), who point out that none of the SXTs with a measured mass function greater than $3~M_\odot$ is a type I burster.

Narayan & Heyl (2002) compute instability of accretion onto a hypothetical  $10~M_\odot$ star with a surface of radius between  $(9/8)~R_{\rm S}$ and  $3~R_{\rm S}$, and report that for a range of accretion rates compatible with observations of X-ray novae, the star is expected to give rise to an X-ray burst. The lack of observed X-ray burst in the high-mass SXTs strongly argues against the presence of a star with a surface composed of conventional cold matter. From this, the authors further conclude that black hole candidates cannot have a surface at all. We point out that some of the tacit assumptions underlying this latter inference may not be satisfied in the observed SXTs.

First, we note that a very compact object with a surface would be dimmer than a less compact object, simply because of redshift and light bending. If the surface is below the photon orbit, the fraction of "outward moving'' photons which escape to infinity is in the Schwarzschild metric

\begin{displaymath}{\Delta\Omega\over 2\pi} =1-\left[1-{27\over4}{(1-R_{\rm S}/R)\over( R/R_{\rm S})^2}\right]^{1/2}\cdot \end{displaymath} (1)

At one of the radii considered by Narayan and Heyl, $R/R_{\rm S}=9/8$, this factor and the redshift squared yield a luminosity at infinity which is equal to only 0.040 of the luminosity at the source. A source this compact and radiating at Eddington luminosity would be an order of magnitude dimmer than in Newtonian physics. However, there is a more fundamental doubt as to whether the lack of bursts necessarily implies the presence of an event horizon. "Black-hole candidates" cannot be composed of ordinary matter. X-ray burst calculations based on the assumption that the sources are neutron stars (of a mass so high as to contradict the laws of physics) are irrelevant to the question of the real nature of black-hole candidates.

To rule out all alternatives to black holes one needs to consider all theoretically possible compact configurations, especially those whose microscopic properties may differ from conventional matter. For example, it is possible that the accreted matter could be converted right away to a more exotic form, as it would be on contact with quark matter in the color-locked phase (Alford et al. 1998; Rapp et al. 1998), or with the skin of a gravastar (Mazur & Mottola 2001, see below). This could happen even at zero pressure of the accreting matter. No nuclei, no bursts.

Finally, as shown by Babak & Grishchuk (2002), in massive gravity even an arbitrarily small mass-correction suppresses the event horizon and produces a surface-less object (a naked "singularity") whose existence would be of fundamental importance, but which is observationally indistinguishable from a black hole.

5 Gravastars

Mazur & Mottola (2001) have recently found a new static, spherically symmetric, solution of Einstein's field equations. A gravastar, as it is called, has the standard vacuum Schwarzschild exterior. Its interior, filled with matter that has the equation of state $\rho = -p$, is described by the de Sitter solution, and is matched to the exterior vacuum solution in a very thin shell of thickness on the order of the Planck length, $\lambda_{\rm P} = 1.6 \times 10^{-33}$ cm.

The gravastar has no horizon or singularity. Its rigid surface is located at a radius just slightly greater than the gravitational radius, $R_* = R_{\rm S} + f\lambda_{\rm P}$, $f \sim 2$. There are several purely theoretical objections that one could raise against gravastars, none of them conclusive. For example, stellar-mass gravastars have entropy smaller than ordinary stars with the same masses and this would require extremely efficient cooling before gravastars could form during stellar collapse.

There is no observational way to distinguish what may seem to be a Schwarzschild black-hole from a gravastar. To see this, let us denote the surface redshift by

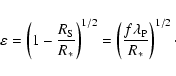\begin{displaymath}\varepsilon = \left ( 1 - {R_{\rm S} \over R_*} \right)^{1/2} = \left( {f\lambda_{\rm P} \over R_*} \right)^{1/2}\cdot \end{displaymath} (2)

For astrophysically interesting gravastars, with mass greater than $M_\odot$, i.e., $R_{\rm S} > 3\times 10^{5}$ cm, this quantity is very small,

\begin{displaymath}\varepsilon < 10^{-19} \ll 1. \end{displaymath} (3)

The power of any radiation emitted by the surface of a gravastar is greatly reduced because only the radiation within the solid angle  $27\varepsilon^2/4$ around the normal to the surface escapes to infinity (Eq. (1)). Further, because of gravitational redshift, the power of radiation received by a distant observer is only  $\varepsilon^2$ of what was emitted at the gravastar's surface. Therefore, the power emitted from the surface is reduced by

\begin{displaymath}\varepsilon^{4} < 10^{-75} \end{displaymath} (4)

by the time it reaches a distant observer. One should conclude that a gravastar with mass greater than $M_\odot$ is to a distant observer as black as a black hole.

6 Conclusions

We have argued that in the electromagnetic window it is fundamentally impossible to observationally verify the existence of a black-hole horizon. One could argue that it is not necessary to directly detect an event horizon - a black hole is a specific space-time metric. If so, it would suffice to determine that the space-time around a compact object corresponds to the Kerr solution of the Einstein equations.

One way to distinguish the Kerr metric from that of a rotating star (if no star can be the "source'' of the $a\neq 0$ Kerr metric, see Abramowicz et al. 1976), is through the study of orbital and other frequencies (e.g., epicyclic) of accreting matter moving in strong-field gravity (Kato 2001; Wagoner 2001; Abramowicz & Kluzniak 2001, 2002). Another method of determining the space-time geometry is by observation of the energy spectrum reflected from an accretion disc deep in the gravitational well of a compact object (Fabian et al. 1989, 2000).

Finally, the capture of stellar-mass compact objects by supermassive black holes in galactic nuclei produces gravitational radiation whose properties reflect the structure of black-hole space-time (Ryan 1995; Hughes 2001). Such gravitational radiation could be observed by the gravitational-wave antenna LISA.

Acknowledgements
We thank Pawe\l Mazur and Lonya Grishchuk for discussion, Bohdan Paczynski and the first referee, Ramesh Narayan, for the helpful comments.

References

 

Copyright ESO 2002